An efficient method for estimating failure possibility function by combining adaptive Kriging model with augmented fuzzy simulation

Abstract

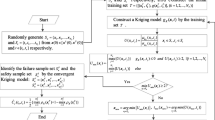
Failure possibility function (FPF) provides the relationship of failure possibility varying with distribution parameters of fuzzy inputs, and it is desired in the possibility-based design optimization under fuzzy uncertainty. However, estimating FPF by direct double-loop fuzzy simulation (DL-FS) requires large computational cost, since failure possibility needs to be repeatedly estimated corresponding to different discrete realizations of distribution parameters. For addressing this issue, an augmented fuzzy simulation (AFS) is proposed to improve the efficiency of estimating FPF. In AFS, the candidate sample pool (CSP) is first generated in an augmented space spanned by fuzzy inputs and their distribution parameters, on which the failure possibility at different distribution parameters can be estimated by the same CSP of AFS. Compared with DL-FS, the proposed AFS only needs one group of FS, which greatly reduces the computational cost and improves the efficiency of estimating FPF. Moreover, a Kriging model is adaptively embedded in the CSP of AFS by adopting U-learning and CSP reduction strategy, in which the convergent Kriging model trained in CSP of AFS is used to replace performance function for recognizing failure samples and estimating FPF. Since the number of the training samples for constructing the convergent Kriging model is much less than the size of CSP of AFS, the method combining adaptive Kriging with AFS can greatly improve the efficiency of estimating FPF, which is verified by the presented examples.

Appendices

Appendix A: The relationship between the U-learning function and the probability of the current Kriging model correctly recognizing the state of the sample point

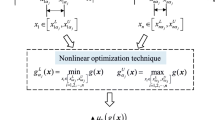
The U-learning function $U\left( {\varvec{x}} \right)$ proposed in Ref. [29] corresponds to the probability denoted as $P_{e} \left( {\varvec{x}} \right)$ of the current Kriging model $g_{K} \left( {\varvec{x}} \right)$ correctly recognizing the state of the sample point ${\varvec{x}}$ (also recognizing the symbol of the performance function value). The relationship between $U\left( {\varvec{x}} \right)$ and $P_{e} \left( {\varvec{x}} \right)$ can be expressed as follows, and the relationship has been discussed in detail in Ref. [35]

$$P_{e} \left( {\varvec{x}} \right) = \Phi \left( {\frac{{\left| {\mu_{{g_{K} }} \left( {\varvec{x}} \right)} \right|}}{{\sigma_{{g_{K} }} \left( {\varvec{x}} \right)}}} \right) = \Phi \left( {U\left( {\varvec{x}} \right)} \right),$$

(22)

where $\mu_{{g_{K} }} \left( {\varvec{x}} \right)$ and $\sigma_{{g_{K} }} \left( {\varvec{x}} \right)$ are the prediction mean and standard deviation provided by the current Kriging model $g_{K} \left( {\varvec{x}} \right)$, respectively. $\Phi \left( \cdot \right)$ is the cumulative distribution function of the standard normal variable. The smaller $U\left( {\varvec{x}} \right)$ is, the smaller $P_{e} \left( {\varvec{x}} \right)$ is. Since $P_{e} \left( {\varvec{x}} \right) \ge \Phi \left( 2 \right) = 97.7\%$ is a high probability corresponding to $U\left( {\varvec{x}} \right) \ge 2$, it is widely accepted that the current Kriging model $g_{K} \left( {\varvec{x}} \right)$ can accurately identify the value symbol of the performance function at ${\varvec{x}}$.

Appendix B: Common membership functions

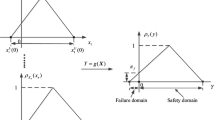
Table B1 lists several common membership functions, which include the normal type [36], the logarithmic normal type and the Gaussian type [37], and the triangular type and the trapezoid type.

Table B1 Several common membership functions