Skip to main content
SpringerLink
Log in

A decoupled credibility-based design optimization method for fuzzy design variables by failure credibility surrogate modeling

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

In order to make a good compromise of cost and safety with small data in the early structural design stage, a practical decoupled credibility-based design optimization method is developed in the presence of fuzzy uncertainty. In the proposed approach, failure credibility is constructed as optimization constraints estimated by fuzzy advanced first-order second-moment method. By approximating the fuzzy credibility constraint by the adaptive Kriging surrogate model, a fuzzy credibility-based design is decoupled to a common deterministic optimization so that various existing optimization algorithms can be easily applied. Compared to the traditional double-loop approach, the newly proposed method is more efficient and strongly practical for complicated engineering problems. Design results of three structural engineering examples also show advantages in accuracy and computation speed of the proposed method over the traditional double-loop approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Ashkzari A and Azizi A (2014) Introducing genetic algorithm as an intelligent optimization technique. In: Applied Mechanics and Materials vol. 568–570, pp 793–797

  • Azizi A (2017) Introducing a novel hybrid artificial intelligence algorithm to optimize network of industrial applications in modern manufacturing. Complexity, article vol. 2017, Art. no. 8728209

  • Azizi A (2019) Hybrid artificial intelligence optimization technique. In: SpringerBriefs in Applied Sciences and Technology, pp 27–47

  • Box GEP, Draper N (2007) Response Surfaces, Mixtures, and Ridge Analysis [M]. Second Edition (of Empirical Model-Building and Response Surfaces, 1987). Wiley

  • Bucher CG (1988) Adaptive sampling-an iterative fast sampling fast Monte Carlo procedure. Struct Saf 5(2):119–126

    Google Scholar 

  • Burges CJC (1998) A tutorial on support vector machines for pattern recognition. Data Min Knowl Disc 2(2):121–167

    Google Scholar 

  • Cai KY, Wen CY, Zhang ML (1991) Fuzzy variables as a basis for a theory of fuzzy credibility in the possibility context. Fuzzy Sets Syst 42(2):145–172

    MATH  Google Scholar 

  • Chen D, Hasselman TK, Neill DJ (1997) Reliability-based structural design optimization for practical applications. In: Proceedings of the 38th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics, and material conference, Kissimmee, AIAA-97-1403

  • Du X, Chen W (2004) Sequential optimization and reliability assessment method for efficient probabilistic design. J Mech Des 126(2):225–233

    Google Scholar 

  • Du L, Choi KK, Youn BD (2006) Inverse possibility analysis method for possibility-based design optimization. AIAA J 44(11):2682–2690

    Google Scholar 

  • Dubois D, Prade H (1988) Possibility theory: an approach to computerized processing of uncertainty. Plenum, New York

    MATH  Google Scholar 

  • Echard B, Gayton N, Lemaire M (2011) AK-MCS: an active learning reliability method combining Kriging and Monte Carlo simulation. Struct Saf 33:145–154

    Google Scholar 

  • Elishakoff I, Chamis CC (2001) Interrelation between safety factors and reliability

  • Elishakoff I, Haftka RT, Fang J (1994) Structural design under bounded uncertainty-optimization with anti-optimization [J]. Comput Struct 57(6):1401–1405

    MATH  Google Scholar 

  • Freudenthal AM (1961) Safety, reliability and structural design [J]. J Struct Div 87:1–16

    Google Scholar 

  • Hasofer AM, Lind NC (1974) An exact and invariant first order reliability format. ASCE J Eng Mech 100(1):111–121

    Google Scholar 

  • Jia B, Lu Z (2018) Root finding method of failure credibility for fuzzy safety analysis. Struct Multidiscip Optim 58(5):1917–1934

  • Kirjner-Neto C, Polak E, Der Kiureghian A (1998) An outer approximation approach to reliability-based optimal design of structures. J Optim Theory Appl 98(1):1–16

    MathSciNet  MATH  Google Scholar 

  • Kleijnen JPC (2009) Kriging metamodeling in simulation: a review. Eur J Oper Res 192(3):707–716

    MathSciNet  MATH  Google Scholar 

  • Kuschel N, Rackwitz R (1997) Two basic problems in reliability-based structural optimization. Math Methods Oper Res 46(3):309–333

    MathSciNet  MATH  Google Scholar 

  • Kuschel N, Rackwitz R (2000) Optimal design under time-variant reliability constraints. Struct Saf 22(2):113–127

    MATH  Google Scholar 

  • Liao KW, Ha C (2008) Application of reliability-based optimization to earth-moving machine: hydraulic cylinder components design process [J]. Struct Multidiscip Optim 36(5):523–536

    Google Scholar 

  • Liu JS (2001) Monte Carlo strategies in scientific computing. Springer, New York, p 114

    Google Scholar 

  • Liu B (2007) Uncertainty theory, 2nd edn. Springer

  • Liu C, Lv Z, Xu Y (2006) Reliability analysis for the crack growth of powder metallurgy turbine disk. Rare Metal Mater Eng 35(2):232–236

    Google Scholar 

  • Lombardi M (1998) Optimization of uncertain structures using non-probabilistic models [J]. Comput Struct 67:99–103

    MATH  Google Scholar 

  • Lophaven SN, Nielsen HB, Sondergaard J (2002) DACE, a matlab Kriging toolbox, version 2.0. Technical University of Denmark

  • Madsen HO, Friis Hansen F (1992) A comparison of some algorithms for reliability-based structural optimization and sensitivity analysis. In: Rackwitz R, Thoft-Christensen P (eds) Proceedings of the 4th IFIPWG 7.5 conference, Munich. Springer-Verlag, Berlin, pp 443–451

  • Melchers RE (1989) Importance sampling in structural system. Struct Saf 6(1):3–10

    Google Scholar 

  • Möller B, Graf W, Beer M (2000) Fuzzy structural analysis using α−level optimization. Comput Mech 26547–565

  • Mourelatos ZP, Zhou J (2005) Reliability estimation and design with insufficient data based on possibility theory. AIAA J 43(8):1696–1705

    Google Scholar 

  • Nikolaidis E, Burdisso R (1988) Reliability-based design optimization using probabilistic sufficiency factor. Comput Struct 28(6):781–788

    MATH  Google Scholar 

  • Rosenblueth E (1975) Point estimation for probability moments. Proc Natl Acad Sci 72(10):3812–3814

    MathSciNet  MATH  Google Scholar 

  • Royset JO, Der Kiureghian A, Polak E (2001) Reliability-based optimal structural design by the decoupling approach. Reliab Eng Syst Saf 73(3):213–221

    Google Scholar 

  • Tang ZC, Lu ZZ, Hu JX (2014) An efficient approach for design optimization of structures involving fuzzy variables. Fuzzy Sets Syst 225:52–73

    MathSciNet  Google Scholar 

  • Tu J, Choi KK (1999) A new study on reliability-based design optimization. J Mech Des 121(4):557–564

    Google Scholar 

  • Wang C, Matthies HG, Qiu Z (2017) Optimization-based inverse analysis for membership function identification in fuzzy steady-state heat transfer problem. Struct Multidisc Optim 57(4):1495–1505

  • Wu YT, Wang W (1998) Efficient probabilistic design by converting reliability constraints to approximately equivalent deterministic constraints. J Integr Des Process Sci 2(4):13–21

    Google Scholar 

  • Xu L, Lu W (2000) Crack growth failure probability of PM turbine disk [J]. Mech Sci Technol 19(2):210–212

    Google Scholar 

  • Zhang CY, Zhang Z, Fei C-W, Yuan Z-S, Wei J-S, Tang W-Z (2019) Fuzzy multi-SVR learning model for reliability-based design optimization of turbine blades. Materials (Basel) 12(15):2341

    Google Scholar 

Download references

Funding

This work was supported by the National Natural Science Foundation of China (Grant 51775439) and National Science and Technology Major Project (2017-IV-0009-0046).

Author information

Authors and Affiliations

  1. School of Aeronautics, Northwestern Polytechnical University, Xi’an, 710072, China

    Beixi Jia, Zhenzhou Lu & Lu Wang

Authors
  1. Beixi Jia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhenzhou Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lu Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhenzhou Lu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Responsible Editor: Somanath Nagendra

Publisher’s note

Springer Nature remains neutral with regard to jurisdictionalclaims in published maps and institutional affiliations.

Appendix A

Appendix A

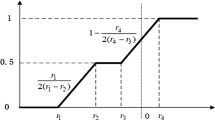
Common regular fuzzy credibility distributions and standard regular fuzzy credibility distributions

Table A.1 Regular fuzzy credibility distributions and their characteristics
Full size table
Table A.2 Standard regular fuzzy credibility distributions
Full size table

1.1 Replication of results

The original codes of the three examples in the Section 4 are available in the Supplementary materials, i.e., Test 1.m, Test 2.m and Test 3.m.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jia, B., Lu, Z. & Wang, L. A decoupled credibility-based design optimization method for fuzzy design variables by failure credibility surrogate modeling. Struct Multidisc Optim 62, 285–297 (2020). https://doi.org/10.1007/s00158-020-02487-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-020-02487-6

Keywords

Search

Navigation