An efficient method for solving the system failure possibility of multi-mode structure by combining hierarchical fuzzy simulation with Kriging model

Abstract

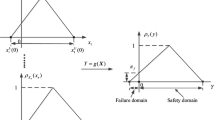
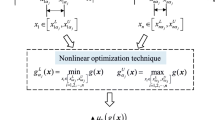
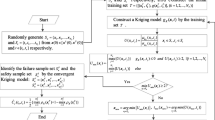
The system failure possibility of multi-mode structural system (referred to as system) under fuzzy uncertainty is the joint membership function of input vector at the system fuzzy design point, and it can reasonably measure the safety degree of the system. The system fuzzy simulation (S-FS) can be combined with adaptive Kriging model (AK-S-FS) to solve the system failure possibility. In the current AK-S-FS method, the system fuzzy design point is searched in the maximum value region of the fuzzy input vector corresponding to the 0 membership level, and its computational efficiency still needs to be improved. Thus, a hierarchical system fuzzy simulation combined with adaptive Kriging model (AK-HS-FS) method is proposed to improve the efficiency of searching the system fuzzy design point in this paper. The efficiency of the proposed AK-HS-FS method comes from the innovative strategies of three aspects. The first is the strategy of the hierarchical system fuzzy simulation (HS-FS). Compared with the S-FS with the system fuzzy design point searched roughly in the maximum possible value region, the strategy of the HS-FS is to exploratively expand the search region by transferring from a larger membership level to a smaller one. The overall search region of the system fuzzy design point can be reduced without losing the search accuracy in the HS-FS. The second is the strategy of the hierarchical training. Compared with training the system Kriging model in the combined candidate sample pool (CSP) of all layers, it is more time-saving to train the system Kriging model layer by layer in the hierarchical CSP. The third is the strategy of iteratively reducing the CSP. According to the properties of the system fuzzy design point and the probability properties of the Kriging prediction, the required time of training the system Kriging model can be further reduced by iteratively reducing the CSP, and the reduction of the CSP can ensure the accuracy without introducing any computational cost and complexity. The results of case studies fully verify that the AK-HS-FS is much more efficient than the AK-S-FS under satisfying the computational accuracy.

Appendices

Appendix 1: U-learning function

The U-learning function proposed by Echard et al. (2011) was based on the idea that only the sign of the performance function is important for estimating the failure probability. Here, we extended this learning function to the estimation of the system failure possibility due to that the system Kriging model only needs to accurately identify the value symbol of the system performance function. The U-learning function is shown as follows.

$$U({\varvec{x}}) = \frac{{\left| {\mu_{{g_{K} }} ({\varvec{x}})} \right|}}{{\sigma_{{g_{K} }} ({\varvec{x}})}},$$

(47)

which indicates the distance in Kriging standard deviations between the prediction and estimated limit surface. And it implies a reliability index on the risk of misjudging the sign of $g({\varvec{x}})$ by $g_{K} ({\varvec{x}})$. The smaller $U({\varvec{x}})$ means the much more uncertainty of the sign of $g({\varvec{x}})$. And as a reliability index, $U({\varvec{x}}) = 2$ corresponds to a probability of making a mistake on the sign of $\Phi ( - 2) = 0.023$. To get more details of U-learning, readers can refer to Ref. Echard et al. (2011).

Appendix 2: The relation between the U-learning function and the probability of the current Kriging model correctly recognizing the state of the prediction point

The Kriging prediction of an arbitrary point ${\varvec{x}}$ follows Gaussian distribution, i.e., $g_{K} ({\varvec{x}})\sim N(\mu_{{g_{K} }} ({\varvec{x}}),\sigma_{{g_{K} }} ({\varvec{x}}))$, where $\mu_{{g_{K} }} ({\varvec{x}})$ and $\sigma_{{g_{K} }} ({\varvec{x}})$ are, respectively, the prediction mean and standard deviation provided by the current Kriging model.

Based on the sign of $\mu_{{g_{K} }} ({\varvec{x}})$ and the prediction characteristic of the Kriging model $g_{K} ({\varvec{x}})$, the probability $P_{e}$ of the Kriging model $g_{K} ({\varvec{x}})$ correctly recognizing the sign of $g({\varvec{x}})$ can be discussed by the following two cases.

• (1) Case 1: $\mu_{{g_{K} }} ({\varvec{x}}) > 0$

  When the prediction value $\mu_{{g_{K} }} ({\varvec{x}}) > 0$, i.e., the state of ${\varvec{x}}$ predicted by Kriging model is safe. Since $g_{K} ({\varvec{x}})\sim N(\mu_{{g_{K} }} ({\varvec{x}}),\sigma_{{g_{K} }} ({\varvec{x}}))$, the probability $P_{1}$ of the sign of the performance function $g({\varvec{x}})$ being correctly recognized by the Kriging model (i.e., the probability of $g_{K} ({\varvec{x}}) > 0$) can be obtained by Eq. (48),

  $$\begin{aligned} P_{1} & = P\{ g_{K} ({\varvec{x}}) > 0\} = 1 - P\{ g_{K} ({\varvec{x}}) \le 0\} \\ \, & { = 1} - P\left\{ {\frac{{g_{K} ({\varvec{x}}) - \mu_{{g_{K} }} ({\varvec{x}})}}{{\sigma_{{g_{K} }} ({\varvec{x}})}} \le \frac{{0 - \mu_{{g_{K} }} ({\varvec{x}})}}{{\sigma_{{g_{K} }} ({\varvec{x}})}}} \right\} \\ \, & { = 1} - \Phi \left( {\frac{{0 - \mu_{{g_{K} }} ({\varvec{x}})}}{{\sigma_{{g_{K} }} ({\varvec{x}})}}} \right) = \Phi \left( {\frac{{\mu_{{g_{K} }} ({\varvec{x}})}}{{\sigma_{{g_{K} }} ({\varvec{x}})}}} \right) \\ \end{aligned}$$

  (48)

• (2) Case 2: $\mu_{{g_{K} }} ({\varvec{x}}) \le 0$

  When the prediction value $\mu_{{g_{K} }} ({\varvec{x}}) \le 0$, i.e., the state of ${\varvec{x}}$ predicted by Kriging model is failed. Similarly, the probability $P_{2}$ of the sign of the performance function $g({\varvec{x}})$ being correctly recognized by the Kriging model (i.e., the probability of $g_{K} ({\varvec{x}}) \le 0$) can be obtained by Eq. (49),

  $$\begin{aligned} P_{2} & = P\{ g_{K} ({\varvec{x}}) \le 0\} = P\left\{ {\frac{{g_{K} ({\varvec{x}}) - \mu_{{g_{K} }} ({\varvec{x}})}}{{\sigma_{{g_{K} }} ({\varvec{x}})}} \le \frac{{0 - \mu_{{g_{K} }} ({\varvec{x}})}}{{\sigma_{{g_{K} }} ({\varvec{x}})}}} \right\} \\ \, & = \Phi \left( {\frac{{0 - \mu_{{g_{K} }} ({\varvec{x}})}}{{\sigma_{{g_{K} }} ({\varvec{x}})}}} \right) = \Phi \left( {\frac{{|\mu_{{g_{K} }} ({\varvec{x}})|}}{{\sigma_{{g_{K} }} ({\varvec{x}})}}} \right). \\ \end{aligned}$$

  (49)

  Combining Eqs. (48) and (49), it is seen that no matter what the state of the sample predicted by Kriging model is, the probability of the sign of $g({\varvec{x}})$ being correctly recognized by Kriging model is

  $$P_{e} = \Phi \left( {\frac{{|\mu_{{g_{K} }} ({\varvec{x}})|}}{{\sigma_{{g_{K} }} ({\varvec{x}})}}} \right) = \Phi \left( {U({\varvec{x}})} \right),$$

  (50)

  where $U({\varvec{x}}) = |\frac{{\mu_{{g_{K} }} ({\varvec{x}})}}{{\sigma_{{g_{K} }} ({\varvec{x}})}}|$ is the U-learning function. The smaller $U({\varvec{x}})$ is, $P_{e}$ is smaller. Thus, for enhancing the ability of the Kriging model in accurately predicting the sign of $g({\varvec{x}})$, the new training sample ${\varvec{x}}_{{{\text{new}}}}$ can be selected as the sample with the smallest U-learning function $U({\varvec{x}})$ in the candidate sampling pool $S_{{\varvec{x}}}$, i.e.,

  $${\varvec{x}}_{{{\text{new}}}} = \arg \mathop {\min }\limits_{{{\varvec{x}} \in S_{{\varvec{x}}} }} U({\varvec{x}})$$

  (51)

  When $U({\varvec{x}}) > 2$, the probability of the sign of performance function being correctly recognized by the Kriging model is more than $\Phi \left( 2 \right) = 0.977$, i.e., the current Kriging model $g_{K} ({\varvec{x}})$ can correctly recognize the sign of performance function at ${\varvec{x}}$ with at least $\Phi (2) = 97.7\%$ probability. By taking this fact into consideration, $\mathop {\min }\limits_{{{\varvec{x}} \in S_{{\varvec{x}}} }} U({\varvec{x}}) > 2$ is generally taken as the stopping criteria to terminate the iteration process for updating the Kriging model.

Appendix 3: Common membership functions

The following Table 10 lists several common membership functions which include the normal type (Liu 2007b), the logarithmic normal type and the Gaussian type (Kundu 2015; Klimke 2006), the triangular type and the trapezoid type (Liu 2006).

Table 10 Several common membership functions