Abstract
Local exponential stabilization of the three-dimensional Navier–Stokes system to a given reference trajectory via receding horizon control (RHC) is investigated. The RHC enters as the linear combinations of a finite number of actuators. The actuators are spatial functions and can be chosen in particular as indicator functions whose supports cover only a part of the spatial domain.
Similar content being viewed by others
1 Introduction
In this paper, we are concerned with the following controlled Navier–Stokes system
where \(\varOmega \subset {\mathbb {R}}^3\) is a bounded domain with smooth boundary \(\partial \varOmega \), the vector valued function \({\mathbf {y}}(t,x)=(y_1(t,x),y_2(t,x),y_3(t,x))\) stands for the fluid velocities, the real valued function \({\mathbf {p}}(t,x)\) indicates the pressure field, and \(\hat{ {\mathbf {f}}}(t,x)=({\hat{f}}_1(t,x),{\hat{f}}_2(t,x),{\hat{f}}_3(t,x))\) is a source field. Moreover, \(\nu >0\) is the viscosity constant, \( {\mathbf {y}} \cdot \nabla \) denotes the differential operator \(y_1\partial _{x_1}+y_2\partial _{x_2}+y_3\partial _{x_3}\), and for \(N \in {\mathbb {N}}\) the vector valued functions \(\varvec{\Phi }_i(x) =\left( \Phi _{i1}(x),\Phi _{i2}(x),\Phi _{i3}(x)\right) \) with \(i = 1,\dots ,N\) are specified and defined as actuators. These actuators can be chosen as the indicator functions whose supports are contained in an open subset \(\omega \) of the domain \(\varOmega \).
The control objective here is to find a control vector \({\mathbf {u}}(t):=[ u_1(t), \dots , u_N(t) ] \in L^2((0,\infty );{\mathbb {R}}^N)\) by the receding horizon framework that steers system (1.1) to a reference trajectory \(\hat{ {\mathbf {y}}}\) satisfying
for any given \(\hat{ {\mathbf {y}}}_0\) in a neighbourhood of \({\mathbf {y}}_0\). Here, \(\hat{{\mathbf {y}}}(t,x)=( {\hat{y}}_1(t,x),{\hat{y}}_2(t,x),{\hat{y}}_3(t,x))\) and \(\hat{{\mathbf {p}}}(t,x)\) denote the associated fluid velocities and the pressure field, respectively. To be more precise, we show that there exists an \(r>0\) such that for every initial function \({\mathbf {y}}_0\) satisfying \(\Vert {\mathbf {y}}_0-\hat{{\mathbf {y}}}_0\Vert _{H^1_0(\varOmega ;{\mathbb {R}}^3)} \le r\), and the receding horizon state \({\mathbf {y}}_{rh}\) corresponding to the RHC \({\mathbf {u}}_{rh}({\mathbf {y}}_0) \in L^2((0,\infty );\mathbb {R}^N)\), it holds
where the positive constants \(c_V\) and \(\zeta \) are independent of \({\mathbf {y}}_0\).
One efficient approach for the stabilization of a class of continuous-time infinite-dimensional controlled systems is receding horizon framework, see e.g., [1,2,3,4,5] and the references therein. In this approach, a stabilizing RHC is constructed through the concatenation of a sequence of finite horizon open-loop optimal controls on overlapping temporal intervals covering \([0,\infty )\). These optimal control problems are computed according to a performance index function which enhances the desirable properties and structures of the control. Here, for every \(T \in (0, \infty ]\), we consider the following performance index function
for \(\beta > 0\) and initial pair \((t_0, {\mathbf {y}}_0) \in {\mathbb {R}}_+ \times H^1(\varOmega ; {\mathbb {R}}^3)\), where \(|\cdot |_2\) stands for the \(\ell _2\)-norm. The receding horizon framework bridges to a certain degree the gap between closed-loop control and open-loop control. The main issue is then to justify the stability of RHC. Depending on the structure of the underlying problem, this is usually done, by techniques involving the design of appropriate sequences of temporal intervals, using an adequate concatenation scheme, or adding terminal costs and\or constraints to the finite horizon problems. Due to the structure of the receding horizon framework, the resulting control acts as a feedback mechanism.
Considering the performance index function defined in (1.3), the stabilization of the control system (1.1) towards the trajectory \(\hat{{\mathbf {y}}}\) of (1.2) can be also reformulated as the following infinite horizon optimal control problem

In connection to the infinite horizon problem \(OP^o_{\infty }({\mathbf {y}}_0)\), the receding horizon framework delivers approximations to the solution of this problem which are considered suboptimal solutions.
We continue our investigations on the receding horizon framework for infinite horizon optimal control problems governed by partial differential equations, that we initiated in [2] for autonomous systems and, recently extended in [3] for time-varying infinite-dimensional linear systems. In this framework, the exponential stability and suboptimality of RHC are obtained by generating an appropriate sequence of overlapping temporal intervals and applying a suitable concatenation scheme. There is no need for terminal costs or terminal constraints imposed on the open-loop problems. Previously, this framework was investigated for finite-dimensional autonomous systems in e.g, [6, 7] and for discrete-time autonomous systems in e.g, [8, 9].
In the receding horizon approach, we choose a sampling time \(\delta >0\) and an appropriate prediction horizon \(T>\delta \). Then, we define sampling instances \(t_k :=k\delta \) for \(k=0\dots \). At every sampling instance \(t_k\), an open-loop optimal control problem is solved over a finite prediction horizon \((t_k,t_k+T)\). Then the optimal control is applied to steer the system from time \(t_k\) with the initial state \({\mathbf {y}}_{rh}(t_k)\) until time \(t_{k+1}:=t_k+\delta \) at which point, a new measurement of state is assumed to be available. The process is repeated starting from the new measured state: we obtain a new optimal control and a new predicted state trajectory by shifting the prediction horizon forward in time. The sampling time \(\delta \) is the time period between two sample instances. Throughout, we denote the receding horizon state- and control variables by \({\mathbf {y}}_{rh}(\cdot )\) and \({\mathbf {u}}_{rh}(\cdot )\), respectively. Also, \(({\mathbf {y}}_T^*(\cdot ;t_0,{\mathbf {y}}_0), {\mathbf {u}}^*_T(\cdot ;t_0,{\mathbf {y}}_0))\) stands for the optimal state and control of the optimal control problem with finite time horizon T, and initial function \({\mathbf {y}}_0\) at initial time \(t_0\). The receding horizon framework is summarized in Algorithm 1.

1.1 Related Work
Optimal control and feedback stabilization of the Navier–Stokes equations are still active research topics and a considerable amount of research has been devoted to these fields. Among them we can mention [10,11,12,13,14,15,16,17] for feedback stabilization, [18,19,20,21,22,23,24] for open-loop optimal control problems, and [25,26,27,28] for controllability results. We also quote the works [11, 19], where instantaneous control is employed for the Navier–Stokes system. In this approach, which is somehow related to RHC, discrete-in-time feedback control is computed by solving sequences of stationary optimal control problems at selected time instances.
While most of the literature on feedback stabilization is concerned with the stabilization of the Navier–Stokes equations to the steady-state, similarly to [14], we are interested in the stabilization towards a given reference trajectory by means of finite-dimensional controls. In this case, it is needed to derive the stabilizability results for a nonautonomous system, which requires different techniques compared to the case of autonomous systems, see e.g, [14, Introduction] for more details. We also refer the readers to [29,30,31] for more recent results concerning the stabilizability of the nonautonomous parabolic-like differential equations by finite-dimensional controls.
1.2 Contributions
This manuscript deals with the analysis of the RHC for the Navier–Stokes equations. Besides the fact that RHC has not been investigated for these equations before, the present paper also contains novelties compared to our recent investigations [1,2,3] on the analysis of RHC for infinite-dimensional systems: (i) Here our objective is to stabilize the system around a given reference trajectory. In this case, depending on the regularity of the given reference trajectory, in order to study the stability and well-posedness of RHC, we consider the translated controlled system. This system, obtained by subtracting (1.1) from (1.2), is a system of nonlinear time-varying equations and, thus, we are concerned with the local stabilizability of a nonautonomous system. (ii) For the three-dimensional Navier–Stokes equations, in order to ensure the uniqueness, we need to work with the so-called strong variational solutions. For this purpose, the stabilizability of the controlled system is investigated with respect to the \(H^1\)-norm. In this matter, in order to establish the exponential stability of RHC, we need to derive an observability type inequality with respect to the \(H^1\)-norm. (iii) For the three-dimensional Navier–Stokes equations, the existence of the global strong solution is only guaranteed for small initial data and forcing terms. Therefore, an extra effort needs to be made to guarantee both well-posedness of the open-loop subproblems and the smallness of the \(H^1\)-norm of the states at sampling instances \(t_k\) during the concatenation process within the receding horizon framework.
Furthermore, compared to the work [14] dealing with the stabilization of Navier–Stokes equations to reference trajectories, the present work differs not only in the fact that we employ and investigate the receding horizon framework for stabilization, but also that our theory allows the stabilization to less regular reference trajectories, and as actuators, we can use the indicator functions which are more practical in applications in comparison to the eigenfunctions of the Stokes operator.
1.3 Organization of the Paper
The rest of the paper is organized as follows: In Sect. 2, we introduce the notions and functional spaces used in the theory of the three-dimensional Navier–Stokes equations. Then, we review some preliminaries about the well-posedness and regularity of the solution to the translated system, which is obtained by subtracting (1.1) from (1.2). Based on four key properties, Sect. 3 deals with the stability and suboptimality of RHC. In Sect. 4, we investigate the local stabilizability of (1.1) around a given trajectory \(\hat{{\mathbf {y}}}\) by finitely many controllers. Further, sufficient conditions on the set of actuators are given, for which the stabilizability results hold. Then in Sect. 5, first the validity of the four properties given in Sect. 3 is established. Then the main results i.e., the local exponential stabilizability of the receding horizon state towards a given target trajectory and the suboptimality of RHC are proven. Finally, to improve the readability of the paper, we provide proofs to some of results from Sects. 2–4 only in the appendix.
2 Notation and Preliminaries
2.1 Functional Spaces and Translated Systems
We write \({\mathbb {R}}_+\) for the set of non-negative real numbers. For a Banach space X, we denote by \(\Vert \cdot \Vert _X\) the associated norm, by \(X'\) the associated dual space, and by \(\langle \cdot , \cdot \rangle _{X',X}\) the dual paring between \(X'\) and X. In the case that X is a Hilbert space, we use the scalar product \((\cdot ,\cdot )_X\). Further, \({\mathcal {L}}(X, Y )\) denotes the space of continuous linear operators from X to Y with the usual operator norm \(\Vert \cdot \Vert _{{\mathcal {L}}(X,Y)}\). In case \(X = Y\), we write \({\mathcal {L}}(X) :={\mathcal {L}}(X, X)\) instead. Let X and Y be Banach spaces, then for any open interval \((t_0,t_1) \subset {\mathbb {R}}_+\) we define
where the derivative \(\partial _t \) is taken in the sense of distributions. This space is endowed with the norm
We frequently use open intervals of the form \(I_{T}(t_0) :=(t_0,t_0+T)\subset {\mathbb {R}}_+\) with \(t_0 \in {\mathbb {R}}_+\) and \(T \in {\mathbb {R}}_+ \cup \{\infty \}\). Then, we denote \([t_0,t_0+T]\) and \([t_0, \infty )\), by \({\overline{I}}_{T}(t_0)\) and \({\overline{I}}_{\infty }(t_0)\), respectively.
Let \(\varOmega \subset {\mathbb {R}}^3\) be an open, bounded, and connected set with smooth boundary \(\partial \varOmega \). Throughout, for simplicity, we use the notations \({\mathbf {L}}^p:= L^p(\varOmega ;{\mathbb {R}}^3)\), \({\mathbf {W}}^{p,q}:= W^{p.q}(\varOmega ;{\mathbb {R}}^3)\) for \(p,q >0\), \({\mathbf {H}}^1_0:= H^1_0(\varOmega ;{\mathbb {R}}^3)\), and \({\mathbf {H}}^{-1} :=({\mathbf {H}}^1_0)'\). Similarly, for every open subset \(\omega \subset \varOmega \), we denote \({\mathbf {L}}^p(\omega ):= L^p(\omega ;{\mathbb {R}}^3)\) for \(p>0\), and \({\mathbf {H}}^1_0(\omega ):= H^1_0(\omega ;{\mathbb {R}}^3)\). We shall use the standard spaces of divergence-free vector fields
where \({\mathbf {n}}\) is the unit outward normal vector on \(\partial \varOmega \). The spaces H and V are the closure of the space \({\mathcal {D}}\) with respect to the \({\mathbf {L}}^2\)- and \({\mathbf {H}}^1_0\)-norms, respectively. It is wellknown that
with a densely compact embedding, and as a consequence, we recall from e.g., [32] that for an open interval \((t_0,t_1)\subset {\mathbb {R}}_+\) it holds
Moreover, if we denote the Leray projection on H by \( \varPi :{\mathbf {L}}^2 \rightarrow H\), we have \(\varPi (\nabla {\mathbf {p}})=0\) and can define the Stokes operator \({\mathcal {A}}: D({\mathcal {A}}) \rightarrow H\) by
The spaces H, V, and \(D({\mathcal {A}})\) are endowed with the scalar products
In order to define the weak variational form of the Navier–Stokes equations, we introduce the continuous bilinear form \(B : V \times V \rightarrow V'\) defined by
and trilinear form \(b:V\times V\times V \rightarrow {\mathbb {R}}\) defined by
It is wellknown from e.g., [33, Lemma 1.3.], that for b it holds that
Moreover, using standard Sobolev’s embeddings, we can obtain that
where c is a generic constant depending on \(\varOmega \).
We denote the nonlinear term in the Navier–Stokes equations by
For any given \(\hat{{\mathbf {y}}} \in V\), we define the linear operator \({\mathcal {B}}(\hat{{\mathbf {y}}}): V \rightarrow V'\) by
For specifying the regularity of the reference trajectory, we need to introduce the following Banach space
endowed with the norm \(\Vert {\mathbf {y}}\Vert _{L^{\infty }_{div}(I_{\infty }(0)\times \varOmega ; {\mathbb {R}}^3)}:=\Vert {\mathbf {y}}\Vert _{L^{\infty }(I_{\infty }(0)\times \varOmega ; {\mathbb {R}}^3)}\). Note that due the fact that \(L^{\infty }(I_{\infty }(0)\times \varOmega ; {\mathbb {R}}^3)\) is dual of \(L^1(I_{\infty }(0)\times \varOmega ; {\mathbb {R}}^3)\), we obtain that
where the subscript w stands for the weak measureability, see e.g., [34, Sects. 5.0 and 9.1].
For any given \(t_0 \in {\mathbb {R}}_+\), \(T \in {\mathbb {R}}_+ \cup \{ \infty \}\), and a fix \(\varvec{\sigma }> \frac{6}{5}\), we consider the spaces \({\mathfrak {W}}_{t_0,T}\) and \({\mathfrak {V}}_{t_0,T}\) for the measurable vector functions \({\mathbf {y}}=(y_1,y_1,y_3)\) defined in \(I_{T}(t_0) \times \varOmega \) satisfying
where \({\mathbf {L}}_{{{\,\mathrm{div}\,}}}^{\infty } :=\{ {\mathbf {y}}\in {\mathbf {L}}^{\infty } : {{\,\mathrm{div}\,}}{\mathbf {y}} = 0 \text { in } \varOmega \}\).
Further, for given \(t_0 \in {\mathbb {R}}_+\), \(T \in {\mathbb {R}}_+ \cup \{ \infty \}\), and \(\lambda \ge 0\), we will use the Banach space \( {\mathcal {V}}^{\lambda }_{t_0,T} \subset L^{\infty }(I_{T}(t_0); V)\cap L^2(I_{T}(t_0);D({\mathcal {A}}))\) endowed with the norm
These spaces will be used within the contraction mapping theorem for the existence results for the nonlinear system of equations.
Using the Leray projection and the notations introduced above, (1.1) and (1.2) can equivalently be written as
and
respectively. Setting \({\mathbf {v}} := {\mathbf {y}}- \hat{{\mathbf {y}}}\), \({\mathbf {v}}_0 := {\mathbf {y}}_0- \hat{{\mathbf {y}}}_0\), and subtracting (2.4) from (2.5), we come up with the following system of time-varying nonlinear differential equations
This system is called the translated system. Our control objective can now be expressed, equivalently, as the local exponential stabilization of the nonlinear time-varying system (2.6) to zero with respect to V-norm by means of RHC.
2.2 Local Existence and Estimates
In this section, we are concerned with the well-posedness and regularity of the system of nonlinear time-varying Eq. (2.6). Let \(\hat{{\mathbf {y}}}\) be the solution to (2.5) for a pair \((\hat{{\mathbf {y}}}_0, \hat{{\mathbf {f}}})\). Then for every initial function \({\mathbf {v}}_0\) and forcing term \({\mathbf {f}}\), we consider the auxiliary nonlinear system
and for \(\lambda \ge 0\) the auxiliary linear system
Throughout the paper, we impose the following regularity condition for the reference trajectory \(\hat{{\mathbf {y}}}\).
Assumption 1
Let \((\hat{{\mathbf {y}}}, \hat{{\mathbf {p}}})\) be a global smooth solution to (1.2), for which it holds with constants \({\hat{\epsilon }}>0\), \(\sigma > \frac{6}{5}\), and \(R>0\), that
Our stabilizability result is based on the concatenation of exact controllability controls on a family of finite intervals covering \([ 0, \infty )\). Here we used the exact controllability result given in [25, Proposition 1.] and, thus, the regularity condition (RA) is motivated by the one given in [25, p. 3].
Remark 1
Due to regularity condition (RA), for every \((t_0 ,T) \in {\mathbb {R}}^2_+\) the quantities \(\Vert \hat{{\mathbf {y}}}\Vert _{{\mathfrak {W}}_{t_0,T}}\) and \(\Vert \hat{{\mathbf {y}}}\Vert _{{\mathfrak {V}}_{t_0,T}}\) are bounded by constants depending only on \({\hat{\epsilon }}\), T, and R.
Lemma 1
Let \(\nu >0\) and \(\lambda \ge 0\) be given. Then, for every \((t_0,T,{\mathbf {v}}_0, {\mathbf {f}})\in {\mathbb {R}}_+^2\times H\times L^2(I_{T}(t_0);V')\), (2.8) admits a unique weak solution \( {\mathbf {v}} \in W(I_{T}(t_0);V,V')\) satisfying
Moreover, for every \((t_0,T,{\mathbf {y}}_0, {\mathbf {f}})\in {\mathbb {R}}_+^2\times V\times L^2(I_{T}(t_0);H)\), Eq. (2.8) admits a unique strong solution \({\mathbf {v}} \in W(I_{T}(t_0);D({\mathcal {A}}),H)\) satisfying
Finally, for every \((t_0,T,{\mathbf {v}}_0, {\mathbf {f}})\in {\mathbb {R}}_+^2\times H\times L^2(I_{T}(t_0);H)\), we have \(\sqrt{\cdot -t_0}{\mathbf {v}} \in W(I_{T}(t_0);D({\mathcal {A}}),H)\), and the corresponding estimate
The positive constants \(c_1\), \(c_2\), and \(c_3\) depend on \(\hat{{\mathbf {y}}}\), \(\lambda \), T, and \(\nu \).
Proof
The proof follows by using the standard arguments given in e.g. [33, Chapter 3] and estimates (2.3). Thus, we omit the proof here. \(\square \)
In the next proposition, we investigate the existence of the nonlinear system (2.7) for small pairs of initial functions \({\mathbf {v}}_0\) and forcing functions \({\mathbf {f}}\).
Proposition 1
For every given \(T>0\), there exists \(r = r(T)>0\) such that for every \((t_0,{\mathbf {v}}_0, {\mathbf {f}}) \in {\mathbb {R}}_+ \times V \times L^2(I_{T}(t_0);H)\) satisfying
eq. (2.7) admits a unique strong solution \({\mathbf {v}} \in W(I_{T}(t_0);D({\mathcal {A}}),H)\). Moreover, for this solution we have the following estimates
and
where the constant \(c_4\) depends on \(\hat{{\mathbf {y}}}\) and T, and the constant K depends on T, \(\hat{{\mathbf {y}}}\), \({\mathbf {v}}_0\), and \( {\mathbf {f}}\).
Proof
The proof is given in Appendix 1. \(\square \)
In the next Lemma, we establish an observability inequality which is essential for the exponential stability of RHC.
Lemma 2
Assume that for \(T>0\), \(r(T)>0\), and arbitrary given \((t_0,{\mathbf {v}}_0, {\mathbf {f}}) \in {\mathbb {R}}_+ \times V \times L^2(I_{T}(t_0);H)\) satisfying (2.12), system of equations (2.7) admits a solution \({\mathbf {v}} \in W(I_{T}(t_0);D({\mathcal {A}}),H)\). Then, for every \(\delta \) with \(0<\delta \le T\), we have
where the constants \(c_5\) depends on \(\delta \), T, \(\nu \), and \(\hat{{\mathbf {y}}}\).
Proof
The proof follows by energy estimates and it is given in Appendix 2. \(\square \)
3 Stability of RHC
This section is devoted to investigating the stability of RHC. For simplicity in presentation, we use the notations \({\mathbf {B}}:= [\varPi \varvec{\Phi }_1 , \dots ,\varPi \varvec{\Phi }_N ]\) for the set of actuators \( {\mathcal {U}}_{\omega } :=\{ \varvec{\Phi }_i \in \varvec{\mathbf {L}}^2 : i = 1, \dots , N\}\) with \(c_{{\mathcal {U}}_{\omega }}:=N\max _{ 1 \le i \le N} \Vert {\varvec{\Phi }_i}\Vert ^2_H\).
For any \(T \in {\mathbb {R}}_+ \cup \{ \infty \}\), \(t_0\ge 0\), \({\mathbf {v}}_0 \in V\), and \({\mathbf {u}} \in L^2( I_T(t_0) ; {\mathbb {R}}^N)\), we consider the following nonlinear time-varying controlled system

Then, for \({\mathbf {u}} =[u_1,\dots ,u_N ]^t\) we obtain
Further, due to Proposition 1, for every given \(T>0\), there exists a radius \(r_c:= \frac{1}{\max \{ 1, c_{{\mathcal {U}}_{\omega } }\}} r(T)\) such that for given triple \((t_0,{\mathbf {v}}_0,{\mathbf {u}}) \in {\mathbb {R}}^2_+\times V \times L^2(I_{T}(t_0); {\mathbb {R}}^N)\) satisfying
equation \(CS(T,t_0,{\mathbf {v}}_0)\) admits a unique solution \(y^{{\mathbf {u}}} \in W(I_{T}(t_0);D({\mathcal {A}}),H)\).
For the sake of convenience in presentation, we proceed the stability analysis of RHC with a general class of incremental functions which contains the one associated to (1.3) as a spacial case (See Remark 2). In this matter, for defining the optimal control problems associated to the receding horizon framework, we consider an incremental functions \(\ell : \mathbb {R}_+\times V\times {\mathbb {R}}^N \rightarrow \mathbb {R}_+\) satisfying
where the number \(\alpha _{\ell }>0\) is independent of \((t,{\mathbf {v}},{\mathbf {u}})\).
For every interval length \(T>0\), initial state \({\mathbf {v}}_0 \in V\), and initial time \(t_0\), we use frequently the finite horizon optimal control problems of the form

The solution of \(OP_{T}(t_0,{\mathbf {v}}_0)\) is denoted by the pair \(({\mathbf {v}}^*_T(\cdot ;t_0,{\mathbf {v}}_0), {\mathbf {u}}^*_T(\cdot ;t_0,{\mathbf {v}}_0 ))\). Then, the reeding horizon algorithm for dealing with the infinite horizon problem

is given in Algorithm 2.
Remark 2
It is easy to check that by setting
in \(OP_{T}(t_0,{\mathbf {v}}_0)\), (3.2) holds for \(\alpha _{\ell } :=\min \{ 1, \beta \}\) and Algorithm 1 can be equivalently expressed by Algorithm 2. To be more precise, due to (3.3) and using the fact that \({\mathbf {v}} = {\mathbf {y}} -\hat{{\mathbf {y}}}\), it can be easily verified that the finite horizon optimal control problems defined on the same temporal interval in both of Algorithms 1 and 2 are equivalent. Thus, both of these algorithms deliver the same RHC \({\mathbf {u}}_{rh}\) and approximations for the value functions. Hence, we restrict ourselves here to investigate the stability and suboptimality of RHCs obtained by Algorithm 2.

Definition 1
For any \({\mathbf {v}}_0 \in V\) the infinite horizon value function \(V_{\infty }: V \rightarrow {\mathbb {R}}_+\) is defined by
Similarly, for every \((T,t_0,{\mathbf {v}}_0) \in {\mathbb {R}}^2_+ \times V\), the finite horizon value function \(V_{T}: {\mathbb {R}}_+ \times V \rightarrow {\mathbb {R}}_+\) is defined by
In order to show the exponential stability and suboptimality of RHC obtained by Algorithm 2, we need to verify the following properties for \(CS(T,t_0,{\mathbf {v}}_0)\), the finite horizon value function \(V_T\), and open-loop problems \(OP_{T}(t_0,{\mathbf {v}}_0)\). Throughout, \(\mathrm {B}_r(\overline{{\mathbf {v}}})\) denotes a ball in V centred at \(\overline{{\mathbf {v}}}\) with radius \(r>0\).
-
P1
: There exists a radius \(r_s\) such that for every positive number T, \(V_T\) is globally decrescent on \(\mathrm {B}_{r_s}(0)\) with respect to the V-norm. That is, there exists a continuous, non-decreasing, and bounded function \(\gamma : {\mathbb {R}}_+ \rightarrow {\mathbb {R}}_+\) such that
$$\begin{aligned} V_T(t_0,{\mathbf {v}}_0) \le \gamma (T)\Vert {\mathbf {v}}_0\Vert ^2_{V} \quad \text { for every } (t_0,{\mathbf {v}}_0)\in {\mathbb {R}}_+ \times \mathrm {B}_{r_s}(0). \end{aligned}$$(3.4)
Since, in Algorithm 2, the solution of \(OP_{\infty }({\mathbf {v}}_0)\) is approximated by solving a sequence of the finite horizon open-loop optimal controls, we need a priori to guarantee that any of these optimal control problems in Step 2 of Algorithm 2 is well-posed.
For any given \(T>0\), there exists a radius \(r_e = r_e(T)\) such that for every \((t_0 ,{\mathbf {v}}_0) \in {\mathbb {R}}_+ \times \mathrm {B}_{r_{e}}(0)\) and \({\mathbf {u}}\) satisfying
we have the following properties:
-
P2
: \(CS(T,t_0,{\mathbf {v}}_0)\) is well-posed and its associated solution satisfies
$$\begin{aligned} \Vert {\mathbf {v}}\Vert ^2_{C({\overline{I}}_{T}(t_0);V)} \le {\bar{c}}_1 \left( \Vert {\mathbf {v}}_0\Vert ^2_{V}+\int \limits ^{t_0+T}_{t_0}|{\mathbf {u}}(t)|_2^2\,dt \right) , \end{aligned}$$(3.6)with a positive constant \({\bar{c}}_1 ={\bar{c}}_1(T)\).
-
P3
: Every finite horizon optimal control problem of the form \(OP_{T}(t_0,{\mathbf {v}}_0)\), over the set of all control \({\mathbf {u}}\) satisfying (3.5), admits a solution.
-
P4
: For every \(\delta \) with \(0<\delta \le T\), there exists a constant \({\bar{c}}_2= {\bar{c}}_2(\delta ,T)> 0\) such that
$$\begin{aligned} \Vert {\mathbf {v}}(t_0+\delta )\Vert ^2_{V} \le {\bar{c}}_2\left( \int \limits ^{t_0+\delta }_{t_0}\Vert {\mathbf {v}}(t)\Vert ^2_{V}dt+ \int \limits ^{t_0+\delta }_{t_0}|{\mathbf {u}}(t)|_2^2\,dt \right) . \end{aligned}$$(3.7)
The estimate (3.7) will be used to derive the exponential stability of RHC.
The validity of Properties P1-P4 will be addressed in Sect. 5. In particular, the justification of Property P1 is based on the stabilizability of (2.6) by finitely many controllers. This result will be investigated in Sect. 4.
For the sake of simplicity, throughout this section, we use the notation
Remark 3
Let Properties P1-P3 hold and \({\mathbf {v}}_0 \in \mathrm {B}_{r_e}(0)\cap \mathrm {B}_{r_s}(0)\) be given. Then, for every optimal control of \(OP_{T}(t_0,{\mathbf {v}}_0)\), the control constraint \(\Vert {\mathbf {u}}\Vert _{L^2(I_{T}(t_0); {\mathbb {R}}^N)}\le \sqrt{{\gamma (T)}/{\alpha _{\ell }}}\,\Vert {\mathbf {v}}_0\Vert _{V}\) is automatically satisfied and it is not needed to be imposed to \(OP_{T}(t_0,{\mathbf {v}}_0)\). In fact, due to (3.2) and (3.4) for every optimal control \({\mathbf {u}}^*_T(\cdot ;t_0,{\mathbf {v}}_0) \in L^2(I_{T}(t_0); {\mathbb {R}}^N)\) of \(OP_{T}(t_0,{\mathbf {v}}_0)\), we obtain that
Therefore, \(OP_{T}(t_0,{\mathbf {v}}_0)\) can be considered as an unconstrained problem.
Lemma 3
If P1-P3 hold and \(T>\delta >0\), then there exists a neighbourhood \(\mathrm {B}_{d_1}(0) \subset V\) with \(d_1=d_1(T)>0\) such that for every \((t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+ \times \mathrm {B}_{d_1}(0)\) the following inequalities hold
and
Proof
First observe that due to (3.8) in Remark 3, we have for every \({\mathbf {v}}_0 \in \mathrm {B}_{r_e}(0) \cap \mathrm {B}_{r_s}(0)\) that
Thus, using (3.4) and (3.6), we have for every \({\tilde{t}} \in [0,T]\) that
Choosing \(d_1:= \min \{\delta _1, \sqrt{\left( {\bar{c}}_1(T)(1+ \frac{\gamma (T)}{\alpha _{\ell }})\right) ^{-1}\delta ^2_1}\}\) with \(\delta _1 := \min \{r_s, r_e\} \), we obtain that
Now, we come to the verification of (3.9) for \({\mathbf {v}}_0 \in \mathrm {B}_{d_1}(0)\). Due to Bellman’s optimality principle, we have for every \(t^* \in [\delta , T]\) that
where \({\mathbf {v}}^{{\mathbf {u}}}\) in the above equality is the solution to \(CS(t^*-\delta ,t_0+\delta ,{\mathbf {v}}_T^*(t_0+\delta ;t_0,{\mathbf {v}}_0))\) for any \(\mathbf {u} \in L^2((t_0+\delta , t_0+t^*); \mathbb {R}^N)\) and in the last inequality, (3.4) and (3.11) were used.
To show (3.10), suppose that \(t^* \in [0,T]\) is given. Using Bellman’s principle and (3.4) and (3.11), we have
as desired. \(\square \)
Lemma 4
Suppose that P1-P3 hold, and for given \((T,\delta ,t_0,{\mathbf {v}}_0) \in {\mathbb {R}}^3_+ \times \mathrm {B}_{r_{e}}(0)\) with \(T>\delta \), properties (3.9) and (3.10) of Lemma 3 are satisfied. Then for the choice of
we have the following estimates
and
Proof
The proof is similar to the one given in [3, Lemma 2.4]. The only difference lies on the fact that here the estimates are with respect to the V-norm instead of H-norm. This requires that \({\mathbf {v}}_T^*(\cdot ;v_0,t_0) \in C({\overline{I}}_{T}(t_0);V)\) which is true according to Property P2. \(\square \)
Proposition 2
Suppose that P1-P3 hold and let \(\delta >0\) be given. Then there exist \(T^*>\delta \) and \(\alpha \in (0,1)\) such that for every \(T\ge T^*\) and \((t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+ \times \mathrm {B}_{d_1}(0)\) with \(d_1(T)\) defined in Lemma 3, the inequalities
and
hold, where \(\zeta \) is a positive number depending on \(\alpha \), \(\delta \), and T, but it is independent of \((t_0, {\mathbf {v}}_0)\).
Proof
The proof is given in Appendix 3. \(\square \)
Theorem 1
(Suboptimality and exponential stability) Suppose that P1-P4 hold and let a sampling time \(\delta >0\) be given. Then there exist numbers \(T^* > \delta \) and \(\alpha \in (0,1)\), such that for every fixed prediction horizon \(T \ge T^*\) and every \({\mathbf {v}}_0 \in \mathrm {B}_{d_2}(0)\) with \(d_2(T)>0\), the receding horizon control \({\mathbf {u}}_{rh}\) obtained from Algorithm 2 satisfies the suboptimality inequality
and the exponential stability inequality
where the positive numbers \(\zeta \) and \(c_V\) depend on \(\alpha \), \(\delta \), and T, but are independent of \({\mathbf {v}}_0\).
Proof
First we deal with (3.17). The right and left inequalities are obvious, thus we only need to verify the middle one. For fixed \(\delta >0\) we choose \(T^*\) and \(\alpha \) according to Proposition 2 and define \(d_2:= \min \{ \sqrt{\frac{\alpha _{\ell }d^2_1}{{\bar{c}}_2\gamma (T)}},d_1\}\), where \(T\ge T^*\), \(d_1\) is defined as in Lemma 3, and \({\bar{c}}_2 = {\bar{c}}_2(\delta ,T)\) is given in Property P4. For the moment, we will show by induction that for every integer \(k \ge 1\), the following conditions hold:
and
Induction base \(( k= 1)\): Since \(d_2 \le d_1\), the assumptions of Proposition 2 are applicable and we have
and
where \(\alpha \) and \(\zeta \) have been defined in Proposition 2.
Induction step: We assume that (3.19)–(3.21) hold for \(k=k'\) with \(k' \in {\mathbb {N}}\), we will show that (3.19)–(3.21) are also satisfied for \(k=k'+1\). Since \({\mathbf {v}}_{rh}(t_{k'}) \in \mathrm {B}_{d_1}(0)\), by Proposition 2 we have
and
Combining (3.22) and (3.23) with (3.20) and (3.21) for \(k = k'\), respectively, we can infer that
and
Moreover, due to the induction hypothesis ((3.19) for \(k = k'\)), P1 is applicable and by using (3.8) in Remark 3, we can write
Hence, for initial pair \((t_{k'},{\mathbf {v}}_{rh}(t_{k'}))\), Property P4 is also applicable and we can write that
Hence \({\mathbf {v}}_{rh}(t_{k'+1}) \in \mathrm {B}_{d_1}(0)\). From this together with (3.24) and (3.25), we can conclude the induction step and, thus, (3.19)–(3.21) hold for any \(k \in {\mathbb {N}}_0\).
Now, taking the limit \(k \rightarrow \infty \) in (3.20), we find
which concludes (3.17).
Now we turn to inequality (3.18). Using (3.27) and setting \(c'_V =\frac{ {\bar{c}}_2 \gamma (T)}{\eta \alpha _{\ell }}\) with \(\eta = e^{-\delta \zeta }\), we have
Moreover, for every \(t >0\) there exists a \(k \in {\mathbb {N}}\) such that \(t \in [t_k, t_{k+1}]\). Using (3.6), (3.26), and (3.28), we have for \(t \in [t_k, t_{k+1}]\) that
and therefore, by setting \(c_V :={\bar{c}}_1c'_V(1+\frac{\gamma (T)}{\alpha _{\ell }})\eta ^{-1}\), we are finished with the verification of (3.18) and the proof is complete. \(\square \)
Remark 4
if we had \(\alpha = 1\), the inequality (3.17) would imply the optimality of the RHC \({\mathbf {u}}_{rh}\). Since \(\gamma (T)\) is bounded and \(\delta \) is fixed, it follows from (7.10) that \(\lim _{T \rightarrow \infty } \alpha (T) = 1\). This means that, RHC is asymptotically optimal.
4 Stabilizability
In this section, we are concerned with the stabilizability results for (2.6) by finitely many controllers. The possibility of stabilization by a control associated with finitely many actuators has been studied in several papers, see e.g., [10, 11, 15, 29,30,31, 35]. Here, we follow the similar arguments as in [29,30,31].
We introduce a set of actuators \({\mathcal {U}}_{\omega }:=\{\varvec{\Phi }_i : i=1,\dots ,N \}\) supported in an open set \(\omega \subset \varOmega \). For this set of actuators, we prove, under some suitable conditions, the local stabilizability of the nonlinear system. This result is the key condition for the verification of Property P1. To provide \({\mathcal {U}}_{\omega }\) with \(\omega \subset \varOmega \), we use frequently a function \( \varrho = \varrho ({\omega }) \in L^{\infty }(\varOmega )\) satisfying
Then, for a given set \(\hat{{\mathcal {U}}}:=\{\hat{\varvec{\Phi }}_i : i=1,\dots ,N \} \subset {\mathbf {L}}^2\) and \(\varrho \) satisfying (4.1), we define
Further, without loss of generality, we assume that \({\mathcal {U}}_{\omega }\) is linearly independent.
To prove the local stabilizability of \(CS(\infty ,t_0,{\mathbf {v}}_0)\), first, we study the stabilizability of this controlled system without the nonlinear term \({\mathcal {N}}\). Then using the perturbation theory, we extend the result to the local stabilizability for the original controlled system with the nonlinearity. In this matter, we consider the following linear system
where \({\mathbf {q}} \in L^2( I_{\infty }(t_0);{\mathbf {L}}^2)\) stands for the control input and \({\mathbf {P}}_N : {\mathbf {L}}^2 \rightarrow {{\,\mathrm{span}\,}}{\hat{{\mathcal {U}}}} \subset {\mathbf {L}}^2\) is the orthogonal projection onto the span of \(\hat{{\mathcal {U}}}\). A stabilizing control \({\mathbf {q}} \) for (4.3) is constructed through concatenation of a sequence of controls on equidistant finite horizon intervals covering \([t_0,\infty )\). These controls are associated to the null controllability problems introduced in the next lemma.
Lemma 5
Suppose that \( \lambda \ge 0\), and a nonempty open set \(\omega \subset \varOmega \) be given. Further, assume that for the reference trajectory \(\hat{{\mathbf {y}}}\) regularity condition (RA) holds. Then for every \({\overline{T}}>0\), and \((t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+ \times H\), the following system
is null controllable with a constant \(c_{ob} =c_{ob}({\overline{T}},\lambda , \hat{{\mathbf {y}}})\). That is, there exists a control \(\eta ^* \in L^2(I_{{\overline{T}}}(t_0), {\mathbf {L}}^2(\omega ))\) satisfying
whose associated state at time \(t_0+{\overline{T}}\) is equal to zero.
Proof
By setting \(\overline{{\mathbf {v}}}(\tau ): = e^{-\frac{\lambda }{2} \tau } {\mathbf {v}}(\tau +t_0)\) for \(\tau \in (0, {\overline{T}})\), we can transform (4.4) to the following controlled system
where \(\overline{{\mathbf {y}}}(\tau ) := \hat{{\mathbf {y}}}(\tau +t_0)\) for \(\tau \ge 0\). Due to (RA), it follows for \(\overline{{\mathbf {y}}}\) that the terms \(\Vert \overline{{\mathbf {y}}}\Vert _{L_{{{\,\mathrm{div}\,}}}^{\infty }(I_{{\overline{T}}}(0)\times \varOmega ; {\mathbb {R}}^3)}\) and \(\Vert \partial _t \overline{{\mathbf {y}}}\Vert _{L^2(I_{{\overline{T}}}(0);{\mathbf {L}}^{\sigma })}\) with \(\sigma > \frac{6}{5}\) are bounded by a constant \({\bar{c}}={\bar{c}}({\hat{\epsilon }},R,{\overline{T}})\) which is independent of \(t_0\). We are now in the position to apply the null controllability result from [25, Proposition 1] for (4.6). According to this result, for a given \({\mathbf {v}}_0 \in H\), there exists a control \(\overline{{\eta }} ({\mathbf {v}}_0 )\in L^2(I_{{\overline{T}}}(0);{\mathbf {L}}^2(\omega )) \) which drives the system to zero at \({\overline{T}}\) and satisfies
where the constant \({\bar{c}}_{ob} = {\bar{c}}_{ob}({\overline{T}},\overline{{\mathbf {y}}})>0\) is related to the Carleman inequality given in [25, Lemma 1]. For the choice of \(\eta ^*(t):=e^{\frac{\lambda }{2}(t-t_0)}{\overline{\eta }}(t-t_0)\) with \(t\in I_{{\overline{T}}}(t_0)\), the control \(\eta ^*\in L^2(I_{{\overline{T}}}(t_0), {\mathbf {L}}^2(\omega ))\) steers (4.4) at time \(t_0+{\overline{T}}\) to zero and (4.5) holds for \(c_{ob}: ={\bar{c}}_{ob}e^{\frac{\lambda }{2} {\overline{T}}}\). \(\square \)
In the next proposition, we show that for every \((t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+\times H\), there exists a control \({\mathbf {q}}({\mathbf {v}}_0) \in L^2(I_{\infty }(t_0);{\mathbf {L}}^2)\) which steers exponentially system (4.3) to zero.
Proposition 3
(Uniform exponential stabilizability of (4.3)) Let \(\lambda >0\) and \( \varrho \in L^{\infty }(\varOmega )\) satisfying (4.1) be given. Then there exists a constant \(\varUpsilon :=\varUpsilon (\lambda ,\nu ,\hat{{\mathbf {y}}},\varrho )>0\) such that: If, for \(\hat{{\mathcal {U}}}\), \(\varrho \), and the identity mapping \(\mathrm {id} \in {\mathcal {L}}({\mathbf {L}}^2)\), the following holds
then the control system (4.3) is exponentially stabilizable. That is, for every \((t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+ \times H \), there exists a control \({\mathbf {q}}({\mathbf {v}}_0,\lambda ) \in L^2(I_{\infty }(t_0);{\mathbf {L}}^2)\) such that
and
where the constants \(\varTheta _1\) and \(\varTheta _2\) depend on \(\hat{{\mathbf {y}}}\), \(\hat{{\mathcal {U}}}\), \(\varrho \), and \(\nu \), but are independent of \((t_0,{\mathbf {v}}_0)\).
Proof
The proof is inspired by those given in [29, Theorem 2.10] and [31] with the deferences that here we deal with a system of equations and for the Navier–Stokes system, we need to deal with the Leray projection. For the sake of completeness, we give the proof in Appendix 4. \(\square \)
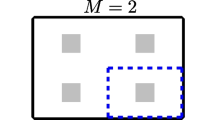
In the following, we present two examples of \(\hat{{\mathcal {U}}}\), for which the condition (COAC) is satisfied. These examples are inspired by those given in [29, Examples 2.11, 2.12] for parabolic equations. For simplicity, we assume that \(\omega \) is an open nonempty rectangle defined by
Due to [13, Definition A.1.2, Page 98], the Leray projection \(\varPi : {\mathbf {L}}^2 \rightarrow H\) can be naturally extended to a continuous operator from \( {\mathbf {H}}^{-1}\) to \( V'\). In this case, there exists a constant \(c_{\varPi }>0\) such that \(\Vert \varPi \Vert _{{\mathcal {L}}({\mathbf {H}}^{-1},V')} \le c_{\varPi }\) and, as a consequence, condition (COAC) holds provided that
For both the examples, we investigate the actuators component-wise. In this matter, for the sequence of scalar valued spatial functions \(\{ \phi _j \}^M_{j =1} \subset L^2(\varOmega )\), we consider the functions \(\varvec{\Psi }_{{\mathbf {j}}} \in {\mathbf {L}}^2\) defined by
Then we can define
where \(N = M^3\). For this setting, the orthogonal projection \({\mathbf {P}}_N: {\mathbf {L}}^2 \rightarrow {{\,\mathrm{span}\,}}\hat{{\mathcal {U}}} \) will have the form
where \(P_{M}: L^2(\varOmega ) \rightarrow {{\,\mathrm{span}\,}}(\{ \phi _j \}^M_{j =1} ) \) stands for the orthogonal projection from \(L^2(\varOmega ) \) onto \({{\,\mathrm{span}\,}}(\{ \phi _j \}^M_{j =1})\). Therefore, due to (4.11) and (4.14), condition (COAC) holds provided that
This means that, we only need to verify condition (COAC) component-wise. In each example, we choose \(\{ \phi _j \}^M_{j =1}\) in (4.12), and \(\varrho \) in such a way that (4.15) holds. In this case, for the corresponding \(\hat{{\mathcal {U}}}\) defined in (4.13) and the chosen \(\varrho \), Proposition 3 is applicable and \( {\mathcal {U}}_{\omega }\) defined in (4.2) is the desirable set of actuators.
Example 1
(Laplacian Eigenfunctions) Suppose that \(\{ \hat{{\phi }}_i \in C^{\infty }(\omega ) : i =1,2,3,\dots \}\) is a complete system of eigenfunctions associated to the negative of Laplacian \(-\varDelta \), which is defined on the domain \(\omega \) with homogeneous Dirichlet boundary conditions. We may also assume that these eigenfunctions are ordered with respect to the increasing sequence of the eigenvalues \(0<\lambda _1 \le \lambda _{2} \le \cdots \) with \(\lim _{i\rightarrow \infty } \lambda _i = \infty \). Moreover, let \(\varrho \in C^2({\overline{\varOmega }})\) satisfying (4.1) be given. For instance, \(\varrho \) can be chosen to be a bump function.
By defining the orthonormal projection \(P_M^{\omega }: L^2(\omega ) \rightarrow {{\,\mathrm{span}\,}}( \{{\phi }_i \}^M_{i=1})\) and setting \(\phi _j := {\mathcal {E}}_0 {\hat{\phi }}_j\) for \( j =1,\dots ,M \) with the extension-to-zero operator \({\mathcal {E}}_0: L^2(\omega )\rightarrow L^2(\varOmega )\), we obtain for every \(w \in L^2(\varOmega )\) and \(v \in H^1_0(\varOmega )\) that
Therefore, for these choices of \(\hat{{\mathcal {U}}}\) defined by (4.12)–(4.13) and \(\varrho \), condition (COAC) holds due to (4.15) if for a large enough \(N = M^3\) the following inequality holds
For \(\omega \) of the form (4.10), due to the asymptotic behaviour \(\lambda _M\ge D M^{\frac{2}{3}}\) from [36, Corollary 1] with
and \(|{\mathcal {B}}|\) denoting the volume of the unit ball in \({\mathbb {R}}^3\), we obtain the following estimate on the number of required actuators
Example 2
(Piecewise constant functions) Here we set \(\varrho :=\chi _{\omega }\) for (4.10), where \(\chi _{\omega }: \varOmega \rightarrow \{0,1\}\) is the characteristic function defined on \(\omega \). Then we consider the uniform partitioning of \(\omega \) to a family of sub-rectangles. For every \(i\in \{1,2,3\}\), the interval \((a_i,b_i)\) is divided into \(d_i \in {\mathbb {N}}\) intervals defined by \(I_{i,k_i}=(a_i+k_i\frac{{\bar{I}}_i}{d_i}, a_i+(k_i+1)\frac{{\bar{I}}_i}{d_i})\) with \(k_i\in \{0,1,\dots ,d_i-1\}\) and \({\bar{I}}_i:=b_i-a_i \). In this case, \(\omega \) is divided into \(M:=\prod ^3_{i =1} d_i\) sub-rectangles defined by
Then the set of actuators is defined by setting \(\phi _i := \frac{1}{\Vert 1_{R_i}\Vert _{L^2}}1_{R_i} \) with \( i=1,\dots ,M\) in (4.12), where \(1_{R_i}\) stands for the indicator function of \(R_i\). Then by following the arguments given in [29, Example 2.12] we can infer that
where \(\lambda _i\) is the smallest positive eigenvalue of the Laplace operator with homogeneous Neumann boundary conditions on the rectangle \(R_i\). That is, \(-\varDelta \Phi _i = \lambda _i \Phi _i \) in \(R_i\) and \(\partial _{\nu } \Phi _i = 0 \) on \(\partial R_i\). Further we have \(\lambda _i = \mu _M\pi ^2\) with \(\mu _M :=\{\frac{d^2_i}{{\bar{I}}^2_i} : i \in \{1,2,3\}\}\), since the partitions are uniform on any intervals \((a_i, b_i)\).
Since \(\mu _M \rightarrow 0\) ( equivalently \(\mu _N \rightarrow 0\)) as \(d_i\rightarrow 0\) for each \(i\in \{1,2,3\}\), due to (4.15) it can be shown that for this choice of \(\hat{{\mathcal {U}}}\) defined in (4.12)–(4.13), condition (COAC) is satisfied provided that the partitions are fine enough so that
Consequently, condition (COAC) is satisfied provided that \(\frac{d_{\min }}{{\bar{I}}} \ge \frac{c^2_{\varPi }\varUpsilon }{\pi ^2}\), where \(d_{\min }:=\min _{1\le i \le 3}d_i\) and \({\bar{I}}:= \max _{1\le i \le 3} {\bar{I}}_i\). Then the inequality \(\frac{M^2}{{\bar{I}}^{6}} \ge \frac{c^{6}_{\varPi }\varUpsilon ^3}{\pi ^{6}}\) is sufficient for (COAC) and we have the following lower bound on the number of actuators
Due to Proposition 3, system (4.3) is globally stabilizable and the control \({\mathbf {q}}({\mathbf {v}}_0)\in L^2(I_{\infty }(t_0); {\mathbf {L}}^2)\) can be taken as a bounded function of an initial function \({\mathbf {v}}_0 \in H\). Relying on this, in the following Proposition, we derive a stabilizing feedback law of the form
This feedback law enters the linear system (4.3) in the place of \(\varrho {\mathbf {P}}_N {\mathbf {q}}(t)\).
Proposition 4
Let \(\hat{{\mathbf {y}}}\), \(\lambda >0\), and \( \varrho \in L^{\infty }(\varOmega )\) satisfying (4.1) be given. Moreover, assume that for \(\hat{{\mathcal {U}}}\) and \(\varrho \), condition (COAC) holds with \(\varUpsilon =\varUpsilon (\lambda ,\nu ,\hat{{\mathbf {y}}},\varrho ) >0 \). Then depending on \((\hat{{\mathbf {y}}},\varrho ,\hat{{\mathcal {U}}},\lambda ,\nu )\), there exist a family of continuous operators \({\mathbf {K}}_{\lambda }(t): H \rightarrow {{\,\mathrm{span}\,}}{{\mathcal {U}}_{\omega }}\), and constants \(c_{{\mathbf {K}}}=c_{{\mathbf {K}}}(\hat{{\mathbf {y}}},\varrho ,\hat{{\mathcal {U}}},\lambda ,\nu )\) and \(\varTheta _3=\varTheta _3(\hat{{\mathbf {y}}},\varrho ,\hat{{\mathcal {U}}},\lambda ,\nu )\) such the following conditions are satisfied:
-
1.
The mapping \(t \mapsto {\mathbf {K}}_{\lambda }(t)\) is continuous in the weak operator topology, and its operator norm is bounded by \(c_{{\mathbf {K}}}\).
-
2.
For every pair \((t_0, {\mathbf {v}}_0) \in {\mathbb {R}}_+ \times H\), the following system
$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t {\mathbf {v}}(t)+\nu {\mathcal {A}} {\mathbf {v}}(t) + {\mathcal {B}}( \hat{{\mathbf {y}}}(t)){\mathbf {v}}(t) = \varPi {\mathbf {K}}_{\lambda }(t){\mathbf {v}}(t) \quad t \in I_{\infty }(t_0),\\ {\mathbf {v}}(t_0)= {\mathbf {v}}_0, \end{array}\right. } \end{aligned}$$(4.18)in the interval \(I_{\infty }(t_0)\) is well-defined and its solution satisfies
$$\begin{aligned} \Vert {\mathbf {v}}(t) \Vert ^2_H \le \varTheta _3 e^{-\lambda (t-t_0)} \Vert {\mathbf {v}}_0 \Vert ^2_{H} \quad \text {for all } t\ge t_0. \end{aligned}$$(4.19)
Proof
Due to Proposition 3, there exists at least a stabilizing control, namely \(\varrho {\mathbf {P}}_N{\mathbf {q}} \in L^2(I_{\infty }(t_0); {{\,\mathrm{span}\,}}{{\mathcal {U}}_{\omega }} )\). Using standard techniques based on the dynamical programming principle, one can construct a feedback operator satisfying the properties 1 and 2. The proof is given in [14, Sect. 3.2]. \(\square \)
In the next theorem, we show the local exponential stabilizability of the nonlinear system relying on the results of Proposition 4.
Theorem 2
Let the assumptions of Proposition 4 hold. Then there exist a family of continuous operators \(\tilde{{\mathbf {K}}}_{\lambda }(t): H \rightarrow {{\,\mathrm{span}\,}}{{\mathcal {U}}_{\omega }}\) and a constant \(c_{\tilde{{\mathbf {K}}}}=c_{\tilde{{\mathbf {K}}}}(\hat{{\mathbf {y}}},\varrho ,\hat{{\mathcal {U}}},\lambda ,\nu )\), for which the first statement in Proposition 4 holds. Further, there exists a radius \(r_s\) such that for every pair \((t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+ \times \mathrm {B}_{r_s}(0)\) with \(\mathrm {B}_{r_s}(0) \subset V\), the nonlinear system
is well-posed and its solution satisfies
where \( \varTheta _4= \varTheta _4(\hat{{\mathbf {y}}},\varrho ,\hat{{\mathcal {U}}},\lambda ,\nu )\).
Proof
The proof is provided in Appendix 5. \(\square \)
5 Main Result
In this section, we present the main result of the paper, i.e, the local exponential stability of the RHC obtained by Algorithm 1, or equivalently, by Algorithm 2 for the setting (3.3). Beforehand, we need to verify Properties P1-P4 for the incremental function \(\ell \) defined in (3.3). Clearly, in this case \(\ell \) satisfies (3.2) with \(\alpha _{\ell }:= \min \{ 1 , \beta \}\).
Proposition 5
Let \(T>0\) be given. Suppose that for chosen set of actuators \(\hat{{\mathcal {U}}} \subset H\), \(\lambda >0\), and \( \varrho \in L^{\infty }(\varOmega )\) satisfying (4.1), condition (COAC) holds with \(\varUpsilon =\varUpsilon (\lambda ,\nu ,\hat{{\mathbf {y}}},\varrho ) >0 \). Then there exist a radius \(r_s>0\) and a nondecreasing, continuous, and bounded function \(\gamma : {\mathbb {R}}_+ \rightarrow {\mathbb {R}}_+\) such that (3.4) holds for \(V_T\). Thus P1 holds.
Proof
Due to Theorem 2, there exist a uniformly bounded family of continuous operators \(\tilde{{\mathbf {K}}}_{\lambda }(t): H \rightarrow {{\,\mathrm{span}\,}}{{\mathcal {U}}_{\omega }}\) and a radius \(r_s\) such that for every pair \((t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+ \times \mathrm {B}_{r_s}(0)\) the feedback law \(\tilde{{\mathbf {K}}}_\lambda {\mathbf {v}}\) is exponentially stabilizing. By defining the linear isomorphism \({\mathcal {I}}: {{\,\mathrm{span}\,}}{{\mathcal {U}}_{\omega }} \rightarrow {\mathbb {R}}^N\), and setting \(\tilde{{\mathbf {u}}}({\mathbf {v}}_0) = ({\tilde{u}}_1, \dots , {\tilde{u}}_N)^t := {\mathcal {I}}\,\tilde{{\mathbf {K}}}_\lambda {\mathbf {v}}\), we obtain that
Using (4.21) and (5.1), we can infer that
where constant \(c_{{\mathcal {I}}}\) is related to \({\mathcal {I}}\). Due to the definition of \(V_T\) and using (4.21) and (5.2), we can write for any given \( (t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+ \times \mathrm {B}_{r_s}(0)\) that
Hence, by setting \(\gamma (T): =\frac{\varTheta _4(1+\beta c^2_{{\mathcal {I}}} c^2_{\tilde{{\mathbf {K}}}} )}{\lambda }\left( 1-e^{-\lambda T}\right) \), we are finished with the verification of Property P1. \(\square \)
In the next proposition, we investigate Properties P2-P4.
Proposition 6
(Verification of P2-P4) Suppose that the incremental function \(\ell \) is defined as in (3.3) and let \(T>0\) be given. Then there exists a ball \(\mathrm {B}_{r_e}(0) \subset V\) with radius \(r_e=r_e(T)\), such that for every \((t_0 , {\mathbf {v}}_0) \in {\mathbb {R}}_+ \times \mathrm {B}_{r_e}(0)\) and \({\mathbf {u}}\) satisfying
Properties P2-P4 hold. Here, \(\gamma \) is defined as in Proposition 5 and \(\alpha _{\ell } =\min \{1, \beta \}.\)
Proof
First we deal with the verification of P2. Due to Proposition 1, for every given \(T>0\), there exists a radius \(r =r(T)\) such that for every \((t_0,{\mathbf {v}}_0,{\mathbf {u}}) \in {\mathbb {R}}_+ \times V\times L^2(I_T(t_0);{\mathbb {R}}^N)\) satisfying
there is unique solution \({\mathbf {v}} \in W(I_{T}(t_0);D({\mathcal {A}}),H)\) to \(CS(T,t_0,{\mathbf {v}}_0)\) satisfying
with \(c_7\) depending on \(\hat{{\mathbf {y}}}\), T, and \(c_{{\mathcal {U}}_{\omega }}\).
Setting \(r_e(T):=( 1+ \frac{c_{{\mathcal {U}}_{\omega }} \gamma (T)}{\alpha _{\ell }})^{-1}r(T)\) we obtain for every \((t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+ \times \mathrm {B}_{r_e}(0)\) and \( {\mathbf {u}}\) satisfying (5.3) that
Hence, \(CS(T,t_0,{\mathbf {v}}_0)\) is well-posed and (3.6) follows from (5.5). Further, due to (2.14), (5.3), and (5.6), there exists a constant \({\bar{K}} ={\bar{K}}(T ,r_e,\hat{{\mathbf {y}}} )>0\) such that
This completes the verification of P2.
Now we turn to verification of P3. We show that for \((t_0 , {\mathbf {v}}_0) \in {\mathbb {R}}_+ \times \mathrm {B}_{r_e}(0)\) and the set of admissible controls \({\mathbf {u}}\) satisfying (5.3), \(OP_{T}(t_0,{\mathbf {v}}_0)\) with incremental function \(\ell \) defined in (3.3) admits a solution. The proof is based on the direct method in the calculus of variations. Due to the fact that \(J_T(t_0,{\mathbf {v}}_0;{\mathbf {u}})\) is nonnegative and the set of admissible controls is bounded, there exists a weakly convergent minimizing sequence \(\{ {\mathbf {u}}^n \}_{n} \subset L^2(I_{T}(t_0); {\mathbb {R}}^N)\) satisfying
with \(\sigma >0\) and \({\mathbf {u}}^n \rightharpoonup {\mathbf {u}}^*\) for \({\mathbf {u}}^*\) satisfying (5.3). Using (5.5) and (5.7), we find that the sequence of solutions \(\{ {\mathbf {v}}^n \}_{n} \in W(I_{T}(t_0);D({\mathcal {A}}),H)\) to \(CS(T,t_0,{\mathbf {v}}_0)\) corresponding to \(\{ {\mathbf {u}}^n \}_{n}\) are bounded in \(W(I_{T}(t_0); D({\mathcal {A}}),H)\) and it holds
We will next show that \({\mathbf {v}}^*\) is the solution corresponding to \(\mathbf {u^*}\). Using (2.3) we can write for every \({\mathbf {w}} \in W(I_{T}(t_0);D({\mathcal {A}}),H)\) that
where c depends only on \(\varOmega \), and \({\hat{c}} = {\hat{c}}({\hat{\epsilon }},T,R)\) due to Remark 1. Therefore, \({\mathcal {B}}(\hat{{\mathbf {y}}})\) is a continuous linear operator from \(L^2(I_{T}(t_0);D({\mathcal {A}}))\cap H^1(I_{T}(t_0);H)\) to \(L^2(I_{T}(t_0);H)\). Using this fact together with (5.8), we find that
Therefore, in order show that the solution \({\mathbf {v}}^* \in W(I_{T}(t_0);D({\mathcal {A}}),H)\) is corresponding to the control \({\mathbf {u}}^*\), it remains only to prove that \( {\mathcal {N}}({\mathbf {v}}^n) \rightharpoonup {\mathcal {N}}({\mathbf {v}}^*)\) in \(L^2(I_{T}(t_0);H)\). We can write
Further, for the terms in the last line of (5.11), we obtain
and
where \(c>0\) is a generic constant depending on \(\varOmega \), and in both of (5.12) and (5.13) we have used Agmon’s inequality [37, Lemma 13.2]
with \(c_{ag}\) depending on \(\varOmega \). Due to the fact that the embedding \(L^2(I_{T}(t_0);D({\mathcal {A}}))\cap H^1(I_{T}(t_0);H) \hookrightarrow L^2(I_{T}(t_0); V)\) is compact (see e.g., [38]) and the terms \(\Vert {\mathbf {v}}^n\Vert _{L^{\infty }(I_{T}(t_0);V)}\), \(\Vert {\mathbf {v}}^n -{\mathbf {v}}^*\Vert _{L^2(I_{T}(t_0);D({\mathcal {A}}))}\), \(\Vert {\mathbf {v}}^n -{\mathbf {v}}^*\Vert _{L^{\infty }(I_{T}(t_0);V)}\), \(\Vert {\mathbf {v}}^*\Vert _{L^{\infty }(I_{T}(t_0);V)}\), and \(\Vert {\mathbf {v}}^*\Vert _{L^2(I_{T}(t_0);D({\mathcal {A}}))}\) are bounded, we can conclude that
and, thus, \({\mathbf {v}}^* \in W(I_{T}(t_0);D({\mathcal {A}}),H)\) is the solution corresponding to the control \({\mathbf {u}}^*\). Since \({\mathbf {v}}^n \rightarrow {\mathbf {v}}^*\) strongly in \(L^2(I_{T}(t_0); V)\) and \({\mathbf {u}}^n \rightharpoonup {\mathbf {u}}^*\) in \(L^2(I_{T}(t_0); {\mathbb {R}}^N )\) we have
and, as a consequence, the pair \(({\mathbf {v}}^*, {\mathbf {u}}^*)\) is optimal. We are finished with the justification of P3.
Finally, due to (5.3) and (5.6), Lemma 2 is applicable. Using estimate (2.15) for any \(\delta \) with \(0< \delta \le T\), we obtain
where \({\bar{c}}_2(\delta ) := \max \{ c_{{\mathcal {U}}_{\omega }}, 1 \} c_5(\delta )\) and, thus, we complete the justification of P4. \(\square \)
Now we are in the position that we can present the main result. Beforehand, we denote the value function associated to \(OP^o_{\infty }({\mathbf {y}}_0)\) by \({\bar{V}}_{\infty }({\mathbf {y}}_0)\). That is
Theorem 3
Suppose that for a given regular enough \((\hat{{\mathbf {f}}}, \hat{{\mathbf {y}}}_0) \in L^2(I_{\infty }(0); {\mathbf {L}}^2) \times V\), the reference trajectories \((\hat{{\mathbf {y}}}, \hat{{\mathbf {p}}})\), as the solution to (1.2), satisfies (RA). Further, assume that for given \(\hat{{\mathcal {U}}}\subset H\), \(\lambda >0\), and \( \varrho \in L^{\infty }(\varOmega )\) satisfying (4.1), condition (COAC) holds with \(\varUpsilon =\varUpsilon (\lambda ,\nu ,\hat{{\mathbf {y}}},\varrho ) >0 \). Then, for any given \(\delta \), and the fixed set of actuators \({\mathcal {U}}_{\omega }: =\varrho \hat{{\mathcal {U}}}\), there exist numbers \(T^* =T^*(\delta ,{\mathcal {U}}_{\omega })>\delta \) and \(\alpha = \alpha (\delta ,{\mathcal {U}}_{\omega }) <1\) such that: For every fixed prediction horizon \(T \ge T^*\), and every \({\mathbf {y}}_0 \in \mathrm {B}_{d_2}( \hat{{\mathbf {y}}}_0 )\) with \(d_2 = d_2(T)>0\), the RHC \({\mathbf {u}}_{rh}\) obtained by Algorithm 1 satisfies the suboptimality inequalities
and the exponentially stable estimate
where \(\zeta \) and \(c_V\) depend on \({\mathcal {U}}_{\omega }\), \(\delta \), and T, but are independent of \({\mathbf {y}}_0\).
Proof
The proof is based on using Theorem 1. First due to Remark 2, for the setting (3.3) the both of Algorithms 1 and 2 are equivalent and yield the same RHC \({\mathbf {u}}_{rh}\). Thus, it is sufficient to consider Algorithm 2 for the setting (3.3). Further, due to Propositions 5 and 6 , Properties P1-P4 hold. Therefore, Theorem 1 is applicable, and, as a consequence, there exist numbers \(T^* =T^*(\delta ,{\mathcal {U}}_{\omega })>\delta \) and \(\alpha = \alpha (\delta ,{\mathcal {U}}_{\omega }) <1\) such that: For every fixed prediction horizon \(T \ge T^*\), and every \({\mathbf {v}}_0 \in \mathrm {B}_{d_2}(0)\) with \( d_2=d_2(T)>0\), the receding horizon \({\mathbf {u}}_{rh}\) obtained by Algorithm 2 satisfies (3.17) and (3.18) for \({\mathbf {v}}_0 = {\mathbf {y}}_0-\hat{{\mathbf {y}}}_0\). Therefore, using the fact that \({\mathbf {v}}_{rh} = {\mathbf {y}}_{rh}-\hat{{\mathbf {y}}}\), \({\bar{V}}_{\infty }({\mathbf {y}}_0) = V_{\infty }({\mathbf {v}}_0)=V_{\infty }({\mathbf {y}}_0- \hat{{\mathbf {y}}}_0) \), and \( J^o_{\infty }({\mathbf {u}}_{rh};0,{\mathbf {y}}_0) = J_{\infty }({\mathbf {u}}_{rh};0,{\mathbf {v}}_0)\) we can infer that (5.14) and (5.15) hold and the proof is complete. \(\square \)
Remark 5
Due to Theorem 3, condition (COAC) is the essential condition for the set of actuators for which the stabilizability of RHC holds. In view of Example 2, indicator functions supported on a fixed open subset of the domain can be chosen as the actuators.
In the next proposition, we derive an estimate for the pressure corresponding to the receding horizon control \({\mathbf {u}}_{rh}\).
Proposition 7
(Estimate for the pressure) Suppose that the assumptions of Theorem 3 hold and for given \(T> \delta >0\), the receding horizon control \({\mathbf {u}}_{rh}\) obtained by Algorithm 1 is stabilizing i.e., (5.14) and (5.15) are satisfied for a given \({\mathbf {y}}_0 \in \mathrm {B}_{d_2}( \hat{{\mathbf {y}}}_0 )\) with \(d_2 = d_2(T)>0\). Then for the pressure \({\mathbf {p}}_{rh}\) associated to \({\mathbf {y}}_{rh}\) as the solution of (1.1) for \({\mathbf {u}} ={\mathbf {u}}_{rh}\), we have \({\mathbf {p}}_{rh} \in L^2(I_{\infty }(0); H^1(\varOmega ))\) and
where \(c_{p}\) is independent of \({\mathbf {y}}_0\).
Proof
The proof of the well-posedness of the pressure \({\mathbf {p}}_{rh} \in L^2(I_{\infty }(0); H^1(\varOmega )) \) for the strong solution follows with the same argument as in the proof of [39, Theorem V.2.1]. Therefore, we restrict ourselves here to derive the estimate (5.16).
Throughout the proof c is a generic constant and does not depends on \({\mathbf {y}}_0\). Similarly to the proof of Theorem 3, we consider the translated equation obtained by subtracting (1.1) with \({\mathbf {u}} = {\mathbf {u}}_{rh}\) from (1.2)
where \({\mathbf {v}}_{rh} = {\mathbf {y}}_{rh}-\hat{{\mathbf {y}}}\), \({\mathbf {v}}_0 = {\mathbf {y}}_0-\hat{{\mathbf {y}}}_0\), and the pressure \({\bar{\mathbf {p}}}\) is defined by \( {\bar{\mathbf {p}}}: = {\mathbf {p}}_{rh}-\hat{{\mathbf {p}}}\). We will show that \({\bar{\mathbf {p}}} \in L^2(I_{\infty }(0); H^1(\varOmega ))\) and (5.16) holds. Beforehand we derive some auxiliary estimates. Projecting (5.17) to the divergence-free spaces, multiplying with \({\mathcal {A}}{\mathbf {v}}_{rh}\), integrating over \(\varOmega \), and using (2.3), we obtain
Using Young’s inequality and (3.18), we can write
Integrating (5.19) over \((0, \infty )\), using (3.17) and (3.18), together with the fact that
for \({\mathbf {u}}_{rh}=(({u}_{rh})_1, \dots ,({u}_{rh})_N)\) and
with R and \({\hat{\epsilon }}\) defined in (RA), we infer that
Further, similarly to (7.4), using (3.18), (5.21), and (5.22), it can be shown that
and, as a consequence, by using [39, Theorem IV.5.11], we conclude that
Moreover, using the fact that \(\Vert {\mathbf {v}}_{rh} \Vert _{ {\mathbf {H}}^2} \le {\tilde{c}} \Vert {\mathbf {v}}_{rh} \Vert _{D({\mathcal {A}})}\) with a constant \({\tilde{c}}>0\) (see e.g., [39, Proposition IV.5.9]), we can write
and
Now, due to (5.20), (5.23), (5.25), and (5.26), we know that \(\partial _t {\mathbf {v}}_{rh}\), \(( {\mathbf {v}}_{rh} \cdot \nabla ) {\mathbf {v}}_{rh}\), \(( \hat{{\mathbf {y}}} \cdot \nabla ) {\mathbf {v}}_{rh} + ( {\mathbf {v}}_{rh} \cdot \nabla ) \hat{{\mathbf {y}}} \), and \(\sum ^N_{i =1} (u_{rh})_i\varvec{\Phi }_i\) are in \(L^2(I_{\infty }(0);{\mathbf {L}}^2) \). Thus, we have
with
Choosing, as usual, \(\bar{{\mathbf {p}}}\) having a zero mean and using the Poincaré-Wirtinger inequality [39, Proposition III.2.39], we can conclude that \( \bar{{\mathbf {p}}} \in L^2(I_{\infty }(0); H^1(\varOmega ))\) with
and this completes the proof. \(\square \)
6 Conclusions
To sum up, we have established the local stabilizability of the three-dimensional Navier–Stokes system towards a given trajectory satisfying suitable regularity conditions via finite-dimensional RHC. This RHC enters as time depending linear combinations of a finite number of actuators. Our theory allows us to employ the indicator functions whose supports cover a part of the domain as actuators.
In this paper, we confined ourselves to the three-dimensional Navier–Stokes equations. Obviously, all the results remain also valid for the two-dimensional Navier–Stokes equations. We believe that for the two-dimensional case the local exponential stabilizability of the RHC can even be proven for the weakly variational solution, as a consequence, with respect to the H-norm.
References
Azmi, B., Boulanger, A.C., Kunisch, K.: On the semi-global stabilizability of the Korteweg-de Vries equation via model predictive control. ESAIM Control Optim. Calc. Var. 24(1), 237–263 (2018). https://doi.org/10.1051/cocv/2017001
Azmi, B., Kunisch, K.: On the stabilizability of the burgers equation by receding horizon control. SIAM J. Control. Optim. 54(3), 1378–1405 (2016). https://doi.org/10.1137/15M1030352
Azmi, B., Kunisch, K.: A hybrid finite-dimensional RHC for stabilization of time-varying parabolic equations. SIAM J. Control. Optim. 57(5), 3496–3526 (2019). https://doi.org/10.1137/19M1239787
Ito, K., Kunisch, K.: Receding horizon optimal control for infinite dimensional systems. ESAIM Control Optim. Calc. Var. 8, 741–760 (2002). https://doi.org/10.1051/cocv:2002032
Kunisch, K., Pfeiffer, L.: The effect of the terminal penalty in receding horizon control for a class of stabilization problems. ESAIM Control Optim. Calc. Var. 26, 26 (2020). https://doi.org/10.1051/cocv/2019037
Jadbabaie, A., Yu, J., Hauser, J.: Unconstrained receding-horizon control of nonlinear systems. IEEE Trans. Automat. Control 46(5), 776–783 (2001). https://doi.org/10.1109/9.920800
Reble, M., Allgöwer, F.: Unconstrained model predictive control and suboptimality estimates for nonlinear continuous-time systems. Automatica J. IFAC 48(8), 1812–1817 (2012). https://doi.org/10.1016/j.automatica.2012.05.067
Grimm, G., Messina, M.J., Tuna, S.E., Teel, A.R.: Model predictive control: for want of a local control Lyapunov function, all is not lost. IEEE Trans. Automat. Control 50(5), 546–558 (2005). https://doi.org/10.1109/TAC.2005.847055
Grüne, L.: Analysis and design of unconstrained nonlinear MPC schemes for finite and infinite dimensional systems. SIAM J. Control. Optim. 48(2), 1206–1228 (2009). https://doi.org/10.1137/070707853
Lasiecka, I., Priyasad, B., Triggiani, R.: Uniform stabilization of Navier–Stokes equations in critical \(l^q\)-based Sobolev and Besov spaces by finite dimensional interior localized feedback controls. Appl. Math. Optim. (2019). https://doi.org/10.1007/s00245-019-09607-9
Badra, M., Takahashi, T.: Stabilization of parabolic nonlinear systems with finite dimensional feedback or dynamical controllers: application to the Navier–Stokes system. SIAM J. Control. Optim. 49(2), 420–463 (2011). https://doi.org/10.1137/090778146
Lefter, C.: Feedback stabilization of 2D Navier–Stokes equations with Navier slip boundary conditions. Nonlinear Anal. 70(1), 553–562 (2009). https://doi.org/10.1016/j.na.2007.12.026
Barbu, V., Lasiecka, I., Triggiani, R.: Tangential boundary stabilization of Navier–Stokes equations. Mem. Am. Math. Soc. 181(852), 128 (2006). https://doi.org/10.1090/memo/0852
Barbu, V., Rodrigues, S.S., Shirikyan, A.: Internal exponential stabilization to a nonstationary solution for 3D Navier–Stokes equations. SIAM J. Control. Optim. 49(4), 1454–1478 (2011). https://doi.org/10.1137/100785739
Barbu, V., Triggiani, R.: Internal stabilization of Navier–Stokes equations with finite-dimensional controllers. Indiana Univ. Math. J. 53(5), 1443–1494 (2004). https://doi.org/10.1512/iumj.2004.53.2445
Breiten, T., Kunisch, K., Pfeiffer, L.: Feedback stabilization of the two-dimensional Navier–Stokes equations by value function approximation. Appl. Math. Optim. 80(3), 599–641 (2019). https://doi.org/10.1007/s00245-019-09586-x
Raymond, J.P.: Feedback boundary stabilization of the three-dimensional incompressible Navier–Stokes equations. J. Math. Pures Appl. 87(6), 627–669 (2007). https://doi.org/10.1016/j.matpur.2007.04.002
Wachsmuth, D.: Analysis of the SQP-method for optimal control problems governed by the nonstationary Navier–Stokes equations based on \(L^p\)-theory. SIAM J. Control. Optim. 46(3), 1133–1153 (2007). https://doi.org/10.1137/S0363012904443506
Choi, H., Hinze, M., Kunisch, K.: Instantaneous control of backward-facing step flows. Appl. Numer. Math. 31(2), 133–158 (1999). https://doi.org/10.1016/S0168-9274(98)00131-7
Hinze, M.: Instantaneous closed loop control of the Navier–Stokes system. SIAM J. Control. Optim. 44(2), 564–583 (2005). https://doi.org/10.1137/S036301290241246X
Bewley, T., Temam, R., Ziane, M.: Existence and uniqueness of optimal control to the Navier–Stokes equations. C. R. Acad. Sci. Paris Sér. I Math. 330(11), 1007–1011 (2000). https://doi.org/10.1016/S0764-4442(00)00299-8
Casas, E.: An optimal control problem governed by the evolution Navier–Stokes equations. In: Optimal control of viscous flow. SIAM, Philadelphia, PA (1998)
Casas, E., Chrysafinos, K.: Analysis of the velocity tracking control problem for the 3D evolutionary Navier–Stokes equations. SIAM J. Control. Optim. 54(1), 99–128 (2016). https://doi.org/10.1137/140978107
Kien, B.T., Rösch, A., Wachsmuth, D.: Pontryagin’s principle for optimal control problem governed by 3D Navier–Stokes equations. J. Optim. Theory Appl. 173(1), 30–55 (2017). https://doi.org/10.1007/s10957-017-1081-8
Fernández-Cara, E., Guerrero, S., Imanuvilov, O.Y., Puel, J.P.: Local exact controllability of the Navier–Stokes system. J. Math. Pures Appl. 83(12), 1501–1542 (2004). https://doi.org/10.1016/j.matpur.2004.02.010
Fursikov, A.V., Èmanuilov, O.Y.: Exact local controllability of two-dimensional Navier–Stokes equations. Mat. Sb. 187(9), 103–138 (1996). https://doi.org/10.1070/SM1996v187n09ABEH000160
Imanuvilov, O.Y.: Remarks on exact controllability for the Navier–Stokes equations. ESAIM Control Optim. Calc. Var. 6, 39–72 (2001). https://doi.org/10.1051/cocv:2001103
Rodrigues, S.S.: Local exact boundary controllability of 3D Navier–Stokes equations. Nonlinear Anal. 95, 175–190 (2014). https://doi.org/10.1016/j.na.2013.09.003
Breiten, T., Kunisch, K., Rodrigues, S.S.: Feedback stabilization to nonstationary solutions of a class of reaction diffusion equations of FitzHugh–Nagumo type. SIAM J. Control. Optim. 55(4), 2684–2713 (2017). https://doi.org/10.1137/15M1038165
Kröner, A., Rodrigues, S.S.: Remarks on the internal exponential stabilization to a nonstationary solution for 1D Burgers equations. SIAM J. Control. Optim. 53(2), 1020–1055 (2015). https://doi.org/10.1137/140958979
Phan, D., Rodrigues, S.S.: Stabilization to trajectories for parabolic equations. Math. Control Signals Syst. 30(2), 11 (2018). https://doi.org/10.1007/s00498-018-0218-0
Temam, R.: Infinite Dimensonal Dynamical Systems in Mechanics and Physics, vol. 68. Springer, New York (1997)
Temam, R.: Navier–Stokes Equations, Studies in Mathematics and its Applications, vol. 2: Theory and Numerical Analysis With an Appendix by F. Thomasset, 3rd edn. North-Holland Publishing Co., Amsterdam (1984)
Fattorini, H.O.: Infinite-dimensional optimization and control theory. Encyclopedia of Mathematics and its Applications, vol. 62. Cambridge University Press, Cambridge (1999). https://doi.org/10.1017/CBO9780511574795
Raymond, J.P., Thevenet, L.: Boundary feedback stabilization of the two dimensional Navier–Stokes equations with finite dimensional controllers. Discrete Contin. Dyn. Syst. 27(3), 1159–1187 (2010). https://doi.org/10.3934/dcds.2010.27.1159
Li, P., Yau, S.T.A.: On the Schrödinger equation and the eigenvalue problem. Commun. Math. Phys. 88(3), 309–318 (1983)
Agmon, S.: Lectures on Elliptic Boundary Value Problems. AMS Chelsea Publishing, Providence, RI (2010)
Simon, J.: Compact sets in the space \(L^p(0, T;B)\). Ann. Math. Pura Appl. 4(146), 65–96 (1987). https://doi.org/10.1007/BF01762360
Boyer, F., Fabrie, P.: Mathematical Tools for the Study of the Incompressible Navier–Stokes Equations and Related Models, Applied Mathematical Sciences, vol. 183. Springer, New York (2013). https://doi.org/10.1007/978-1-4614-5975-0
Acknowledgements
The author appreciates and acknowledges Prof. Karl Kunisch and Sergio S. Rodrigues for their helpful comments and insights on this manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL. The authors have not disclosed any funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have not disclosed any competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Proofs
Appendix A: Proofs
1.1 Appendix A.1: Proof of Proposition 1
Proof
We use the Banach fixed point theorem. For given \(\kappa >0\), we define the set
and the mapping \(\varPsi : {\mathcal {V}}^{0,\kappa }_{t_0,T} \rightarrow {\mathcal {V}}^0_{t_0,T} \), which maps a given function \( {\mathbf {z}} \in {\mathcal {V}}^{0,\kappa }_{t_0,T}\) to the solution of the following problem
That is, \(\varPsi ({\mathbf {z}}) ={\mathbf {w}}\). Then, we show that the unique solution to (2.7) is the fixed point of \(\varPsi \). First, using (2.3), we have for every \({\mathbf {z}} \in {\mathcal {V}}^{0,\kappa }_{t_0,T}\) that
Therefore, using Lemma 1 for \(\lambda = 0\), the linear system (7.1) has a strong solution for any \({\mathbf {z}} \in {\mathcal {V}}^{0,\kappa }_{t_0,T}\) and we can use the estimate (2.10).
Next we choose \(\kappa \) and r(T) such that the mapping \(\varPsi : {\mathcal {V}}^{0,\kappa }_{t_0,T} \rightarrow {\mathcal {V}}^{0,\kappa }_{t_0,T} \) is a contraction. Using (2.3) and (2.10) with \(\lambda =0\), we can write for every \({\mathbf {z}} \in {\mathcal {V}}^{0,\kappa }_{t_0,T}\) that
where c is a generic constant which depends only on \(\varOmega \). Setting \(\kappa : = 2c_2\) and choosing \(r^2 \le \frac{1}{4cc_2}\), we obtain \(c_2(1+c\kappa ^2 r^2) \le \kappa \) and, as a consequence, \(\varPsi \) maps the set \({\mathcal {V}}^{0,\kappa }_{t_0,T}\) into itself. Now it remains to show that the mapping \(\varPsi \) is a contraction for a small enough r. Let two functions \({\mathbf {z}}_1, {\mathbf {z}}_2 \in {\mathcal {V}}^{0,\kappa }_{t_0,T}\) be given. Then using (2.3), (2.10), and (7.1), we obtain that
where in the last inequality we set \(\kappa = 2c_2\). Thus, for given \({\bar{\gamma }}<1\), by choosing \(r^2 = \min \{ \frac{1}{4cc_2},\frac{{\bar{\gamma }}}{4cc^2_2}\}\), the mapping \(\varPsi \) is a contraction with rate \({\bar{\gamma }}\) and we can use the Banach fixed point theorem. Therefore, there exists a unique solution \({\mathbf {v}} \in {\mathcal {V}}^{0,\kappa }_{t_0,T}\) with \(\kappa = 2c_2\) to (2.7).
Now we turn to the verification of (2.13) and (2.14). Due to the definition of \({\mathcal {V}}^{0,\kappa }_{t_0,T}\), for \(c_4: = \kappa \) we obtain that
Further, due to (2.7), we can write
where the terms \(\Vert \hat{{\mathbf {y}}}\Vert _{L_w^{\infty }( I_{T}(t_0); {\mathbf {L}}_{{{\,\mathrm{div}\,}}}^{\infty })}\) and \(\Vert \nabla \hat{{\mathbf {y}}} \Vert _{L^2(I_{T}(t_0);L^{3}(\varOmega ;{\mathbb {R}}^{9}))} \le \Vert \hat{{\mathbf {y}}}\Vert _{{\mathfrak {V}}_{t_0,T}} \) are bounded due to Remark 1 and (RA). Thus, using (2.1), (7.3), and (7.4), the verification of (2.13) and (2.14) is complete. To show the uniqueness in the space \(L^{\infty }(I_{T}(t_0); V)\cap L^2(I_{T}(t_0);D({\mathcal {A}}))\), we suppose that an another solution \({\mathbf {p}}\) is given, then the difference of these solutions \({\mathbf {z}} := {\mathbf {v}}-{\mathbf {p}}\) satisfies
Taking the scalar product of (7.5) with \({\mathbf {z}}\) in H and proceeding some standard energy estimates (see, e.g., [33]), we will obtain that \({\mathbf {z}} = 0\). Thus, the proof is complete. \(\square \)
1.2 Appendix A.2: Proof of Lemma 2
Proof
Throughout the proof, c is a generic constant independent of \((t_0,{\mathbf {v}}_0, {\mathbf {f}})\). Multiplying (2.7) by \((t-t_0) {\mathcal {A}}{\mathbf {v}}(t)\) and integrating over \(\varOmega \) we obtain for almost every \(t \in I_{\delta }(t_0)\) that
Using (2.3), we have the following estimate
for the linear term \({\mathcal {B}}(\hat{{\mathbf {y}}}){\mathbf {v}}\), and the estimate
for the nonlinear term. Further, using (7.6)–(7.8), and Young’s inequality, we obtain
with c depending only on \(\varOmega \) and \(\nu \). Then, using (7.9) and Gronwall’s Lemma for the interval \(I_{\delta }(t_0)\), we obtain
where c depends also on T. Moreover, due to (2.12) and (2.13), we have
where in the last inequality we have use the fact that \(\Vert \hat{{\mathbf {y}}}\Vert ^2_{{\mathfrak {V}}_{t_0,\delta }} \le {\hat{c}}\) for a constant \( {\hat{c}}={\hat{c}}(\delta , R,{\hat{\epsilon }})\) independent of \(t_0\) (see Remark 1). Hence, by setting \(c_5: = \frac{1}{\delta }c e^{\left( \max \{\delta ,1\}{\hat{c}} + c_4r^2\right) }\), we are finished with the verification of (2.15). \(\square \)
1.3 Appendix A.3: Proof of Proposition 2
Proof
Due to the definition of \(\theta _1>0\) and \(\theta _2>0\) in Lemma 4, we can write
Therefore, there exist \(T^*>\delta \) and \(\alpha \in (0,1)\) such that \(1-\theta _2(T,\delta )\left( \theta _1(T,\delta )-1 \right) \ge \alpha \) for all \(T\ge T^*\). Then, using (3.13) and (3.14), we have for every \(T\ge T^*\) and \((t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+ \times \mathrm {B}_{d_1}(0)\) that
and, as a consequence, (3.15) holds
Now, we turn to verification of (3.16). Using (3.13) and (3.14) we have
Further, using (3.15) and (7.11) we can write
Therefore, by defining \(\eta :=(1+\frac{\alpha }{\theta _1\theta _2})^{-1}\), we have
Now by defining \(\zeta := \frac{|\ln \eta |}{\delta }\), we obtain the inequality (3.16). \(\square \)
1.4 Appendix A.4: Proof of Proposition 3
Proof
The proof is divided into two parts. We first prove the results for the case \(\nu = 1\). Then these results are extended to include any \(\nu >0\).
The case \(\nu = 1\): To verify the inequality (4.8) for given \(\lambda >0\) and \((t_0,{\mathbf {v}}_0) \in {\mathbb {R}}_+\times H\), it is sufficient to show that \({\mathbf {v}}_{\lambda }(t):=e^{\frac{\lambda }{2}(t-t_0)}{\mathbf {v}}(t)\) is uniformly bounded for \(t \ge t_0\) and a control \({\mathbf {q}}_{\lambda }\). Clearly, \({\mathbf {v}}_{\lambda }\) can be expressed as the solution to the following shifted system
for \({\mathbf {q}}_{\lambda }({\mathbf {v}}_0) \in L^2(I_{\infty }(t_0), {\mathbf {L}}^2)\). To find a control \({\mathbf {q}}_{\lambda }({\mathbf {v}}_0)\) generating a uniformly bounded \({\mathbf {v}}_{\lambda }\), we first decompose the interval \(I_{\infty }(t_0)\) for fixed \({\overline{T}}>0\) to a sequence of intervals defined by \(I_i := (t_0+i{\overline{T}},t_0+(i+1){\overline{T}})\) with \(i = 0,1,2,\dots \). Then, for any \(i\ge 0\), we use repeatedly the null controllability control for the following auxiliary system
where the initial functions \(\hat{{\mathbf {v}}}^i_0\) is specified from the previous null controllability problem, i.e., for \(i-1\). Due to Lemma 5, for any given \(\hat{{\mathbf {v}}}^i_0 \in H\), there exists a control \(\hat{{\eta }} ^i (\hat{{\mathbf {v}}}^i_0 )\in L^2(I_i;{\mathbf {L}}^2(\omega _1)) \) which drives the system to zero at \(t_0+(i+1){\overline{T}}\), and it satisfies
with \(c_{ob} = c_{ob}({\overline{T}})>0\).
For every \(i\ge 0\) and the control \({\eta }^i := 1_{\omega _1}\hat{{\eta }}^i\), we also consider the following controlled system
Now, using the fact that \({\eta }^i = \varrho {\eta }^i \varrho = {\eta }^i \varrho \) due to \(\varrho |_{\omega _1} = 1\), subtracting (7.15) from (7.13) with \({\eta }=\hat{{\eta }}^i\), and setting \( {\mathbf {d}}^i :={\mathbf {b}}^i- {\mathbf {v}}_{\lambda }\), we have
Further, using (2.9) for (7.16) and (7.14), we obtain
Now, setting \(\varUpsilon ({\overline{T}}):=c_{ob}({\overline{T}})c_1( {\overline{T}},\lambda ,\hat{{\mathbf {y}}})\) and defining \(\rho := \Vert \varPi \varrho (\mathrm {id}-{\mathbf {P}}_{N})\varrho \Vert ^2_{{\mathcal {L}}({\mathbf {L}}^2, V')} \varUpsilon ({\overline{T}})\), we have \(\rho <1\) due to (COAC). Hence, we can conclude that
The control \({\mathbf {q}}_{\lambda }({\mathbf {v}}_0) \in L^2(I_{\infty }(t_0);{\mathbf {L}}^2)\) is constructed by concatenation of the controls \(\eta ^i \in L^2(I_i;{\mathbf {L}}^2)\) for initial functions \(\hat{{\mathbf {v}}}^i_0:={\mathbf {v}}_{\lambda }(t_0+i{\overline{T}})\) for \(i\ge 1 \) and \(\hat{{\mathbf {v}}}^0_0:= {\mathbf {v}}_0\) for \(i =0\). Thus, using (7.17), we can write
For every \(t\ge t_0\), the exists \(j \in {\mathbb {N}}_0\) such that \(t \in [t_0+j {\overline{T}},t_0+(j +1){\overline{T}})\). Using estimate (2.9) for (7.15), (7.14), and (7.18), we can write
where \(\varTheta _1:= {\hat{c}}_{1}(1 +\Vert \varrho \Vert ^2_{L^{\infty }(\varOmega )} c_{ob}({\overline{T}}))\) and \({\hat{c}}_{1}\) depends on \(c_1( {\overline{T}},\lambda ,\hat{{\mathbf {y}}})\) and the continuous embedding \(H \hookrightarrow V'\). Thus, we can conclude (4.8).
Now we turn to the verification of (4.9). Setting \({\mathbf {q}}(t):=e^{\frac{-\lambda }{2}(t-t_0)}{\mathbf {q}}_{\lambda }(t)\) and using (7.14) and the fact that
we have
where \( \varTheta _2 := \frac{c_{ob}}{1-\rho }\). Hence, (4.9) holds.
The case \(\nu >0\): Let \(\nu >0\) be given. By setting \(\overline{{\mathbf {v}}}(\tau ):= {\mathbf {v}}(\frac{\tau }{\nu }+t_0)\) for \(\tau \in I_{\infty }(0)\), (4.3) can be transformed to the following controlled system
where \(\overline{ {\mathbf {y}}}(\tau ):= \frac{1}{\nu } \hat{{\mathbf {y}}}(\frac{\tau }{\nu }+t_0)\) for \(\tau \in I_{\infty }(t_0)\). In this case, (RA) holds for \(\overline{ {\mathbf {y}}}\) with \(\frac{R}{\nu }\) in place of R. Due to the first part of the proof, for any given \({\overline{\lambda }}>0\), there exists a constant \( {\overline{\varUpsilon }}:= {\overline{\varUpsilon }}({\overline{\lambda }},\overline{{\mathbf {y}}},\varrho )>0\) such that: If for \(\hat{{\mathcal {U}}}\) and \(\varrho \), the condition \(\Vert \varPi \varrho (\mathrm {id}-{\mathbf {P}}_{N})\varrho \Vert ^2_{{\mathcal {L}}({\mathbf {L}}^2, V')} < {\overline{\varUpsilon }}^{-1}\) holds. Then, for every \({\mathbf {v}}_0 \in H \), there exists a control \(\overline{{\mathbf {q}}}({\mathbf {v}}_0,{\overline{\lambda }}) \in L^2(I_{\infty }(0);{\mathbf {L}}^2)\) such that
where \( {\overline{\varTheta }}_1 = {\overline{\varTheta }}_1({\overline{\lambda }}, \overline{{\mathbf {y}}})\) and \({\overline{\varTheta }}_2 = {\overline{\varTheta }}_2({\overline{\lambda }}, \overline{{\mathbf {y}}})\). Now, choosing \({\overline{\lambda }} := \frac{\lambda }{\nu }\) and putting \({\mathbf {q}}(t):=\nu \overline{{\mathbf {q}}}(\nu (t-t_0))\) for \(t \in I_{\infty }(t_0)\) in (4.3), we obtain that
and
provided that (COAC) holds for \(\varUpsilon := {\overline{\varUpsilon }}(\frac{\lambda }{\nu },\overline{{\mathbf {y}}},\varrho )\). Thus, (4.8) and (4.9) hold for \(\varTheta _1(\lambda , \hat{{\mathbf {y}}},\nu ) = {\overline{\varTheta }}_1(\frac{\lambda }{\nu },\overline{{\mathbf {y}}})\) and \(\varTheta _2 =\nu {\overline{\varTheta }}_2(\frac{\lambda }{\nu }, \overline{{\mathbf {y}}})\), and the proof is complete. \(\square \)
1.5 Appendix A.5: Proof of Theorem 2
Proof
We use the Banach fixed point theorem. For given \(\kappa >0\), we define the set
where the Banach space \({\mathcal {V}}^{\lambda }_{t_0,\infty }\) is endowed with the norm
Further, we consider the mapping \(\varPsi : {\mathcal {V}}^{\lambda ,\kappa }_{t_0,\infty } \rightarrow {\mathcal {V}}^{\lambda }_{t_0,\infty }\), which maps a given function \( {\mathbf {z}} \in {\mathcal {V}}^{\lambda , \kappa }_{t_0,\infty }\) to the solution of the following problem
where \(\tilde{{\mathbf {K}}}_{\lambda }(t) := {\mathbf {K}}_{{\bar{\lambda }}}(t)\) with \({\mathbf {K}}_{{\bar{\lambda }}}(t)\) given in Proposition 4, and \( {\bar{\lambda }} \in (\lambda , 2\lambda ]\). Clearly, for this choice of operator \(\tilde{{\mathbf {K}}}_{\lambda }\), the first part of the theorem follows from Proposition 4 with \(c_{\tilde{{\mathbf {K}}}}(\lambda ):=c_{{\mathbf {K}}}({\bar{\lambda }})\).
We show that the unique solution to (4.20) is the fixed point of \(\varPsi \) with \(\varPsi ({\mathbf {z}}) ={\mathbf {w}}\). To do this, we choose \(\kappa \) and \(r_s\) such that the mapping \(\varPsi : {\mathcal {V}}^{\lambda , \kappa }_{t_0,\infty } \rightarrow {\mathcal {V}}^{\lambda ,\kappa }_{t_0,\infty }\) is a contraction. Throughout the proof c is a positive constant which does not depend on \({\mathbf {v}}_0\), \(r_s\), and \(\kappa \).
First step: we show that \(\varPsi : {\mathcal {V}}^{\lambda , \kappa }_{t_0,\infty } \rightarrow {\mathcal {V}}^{\lambda , \kappa }_{t_0,\infty }\). We fix \({\mathbf {z}} \in {\mathcal {V}}^{\lambda , \kappa }_{t_0,\infty }\). For \(t \ge s \ge t_0\), we denote by \({\mathbb {W}}(s,t)\) the evolution operator of the linear problem (4.18), which takes an initial function \({\mathbf {v}}_0 \in H\) at initial time \(t_0\) to \({\mathbf {v}}(t)\) at time t. In other words, we have
Then, for (7.23) we can write
Hence, using estimate (4.19) for \({\bar{\lambda }}\) with \(2\lambda \ge {\bar{\lambda }} > \lambda \), we have for \(t\ge t_0\) that
where we have used the fact that \(\Vert {\mathcal {N}}({\mathbf {z}}(s))\Vert _H \le \Vert {\mathbf {z}}(s)\Vert _V \Vert {\mathbf {z}}(s)\Vert _{D({\mathcal {A}})}\).
Further, by multiplying (7.23) by \(e^{\frac{{\bar{\lambda }}}{2}(\cdot -t_0)}\) and setting \({\mathbf {w}}_{{\bar{\lambda }}} := e^{\frac{{\bar{\lambda }}}{2}(\cdot -t_0)}{\mathbf {w}}\), we have
By deriving a similar estimate as (2.11) in Lemma 2 for (7.25), it can be shown for arbitrarily given \(T>0\) and initial pair \((t_0,{\mathbf {w}}_0)\in {\mathbb {R}}_+ \times V\) (\({\mathbf {w}}_0\) in place of \({\mathbf {v}}_0\)) that
where \(c_6\) depends on T, \({\bar{\lambda }}\), \(\tilde{{\mathbf {K}}}\), and \(\hat{{\mathbf {y}}}\), and is independent of \((t_0,{\mathbf {w}}_0)\). Using (7.26) together with (7.24), we can write for \({\hat{\epsilon }}>0\) and \(k \ge 1\) that
Therefore, due to the definition of \({\mathbf {w}}_{{\bar{\lambda }}}\), using a similar argument as in the proof of Proposition 3, and (7.27), we conclude that
Moreover, reconsidering (7.25) with \(\lambda \) in place of \({\bar{\lambda }}\) and multiplying it by \({\mathcal {A}}{\mathbf {w}}_{\lambda }\), we obtain
By integrating (7.29) from \(t_0\) to t and using Young’s inequality, we obtain for \(t\ge t_0\) that
Using (7.24), (7.28), and the fact that
with R and \({\hat{\epsilon }}\) defined in (RA), we obtain for every \(t \ge t_0 \) that
Now by choosing \(\kappa : = 2c\) and \(r_s \le \frac{1}{2c}\), we have \( c(1+ \kappa ^2r^2_s ) \le \kappa \) and, thus, we can conclude that \(\varPsi : {\mathcal {V}}^{\lambda , \kappa }_{t_0,\infty } \rightarrow {\mathcal {V}}^{\lambda , \kappa }_{t_0,\infty }\) and this finishes the verification of the first step.
Second step: we show that \(\varPsi \) is contraction for a radius \(r_s\). In a similar manner as in (7.2), it can be shown that
for a constant \({\tilde{c}}\) independent of \(r_s\). It is sufficient to choose \(r_s < \min \{ \frac{1}{{\tilde{c}}}, \frac{1}{2c} \} \), then clearly \(\varPsi \) is a contraction mapping.
Similarly to the proof of Proposition 1, it can be shown that \(\Vert \partial _t {\mathbf {v}} \Vert _{L^2(I_{\infty }(t_0);H)} \) is bounded. Therefore (4.20) is well-posed, and estimate (4.21) follows from (7.30). Next, we show that the solution of (4.20) is unique in \(L^{\infty }(I_{\infty }(t_0); V)\cap L^2(I_{\infty }(t_0);D({\mathcal {A}}))\). Let an another solution \({\mathbf {p}}\) be given, then the difference of these solutions \({\mathbf {z}} := {\mathbf {v}}-{\mathbf {p}}\) satisfies
Taking the scalar product of (7.31) with \({\mathbf {z}}\) in H, proceeding with some standard energy estimates (see, e.g., [33]), and due to the uniform boundedness of the feedback operator, we will obtain that \({\mathbf {z}} = 0\). Thus, the proof is complete. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Azmi, B. Stabilization of 3D Navier–Stokes Equations to Trajectories by Finite-Dimensional RHC. Appl Math Optim 86, 38 (2022). https://doi.org/10.1007/s00245-022-09900-0
Accepted:
Published:
DOI: https://doi.org/10.1007/s00245-022-09900-0