Skip to main content
SpringerLink
Log in

Bell-polynomial approach and Wronskian determinant solutions for three sets of differential–difference nonlinear evolution equations with symbolic computation

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

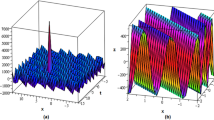
Under investigation in this paper are the Belov–Chaltikian (BC), Leznov and Blaszak–Marciniak (BM) lattice equations, which are associated with the conformal field theory, UToda\((m_1,m_2)\) system and r-matrix, respectively. With symbolic computation, the Bell-polynomial approach is developed to directly bilinearize those three sets of differential–difference nonlinear evolution equations (NLEEs). This Bell-polynomial approach does not rely on any dependent variable transformation, which constitutes the key step and main difficulty of the Hirota bilinear method, and thus has the advantage in the bilinearization of the differential–difference NLEEs. Based on the bilinear forms obtained, the N-soliton solutions are constructed in terms of the \(N \times N\) Wronskian determinant. Graphic illustrations demonstrate that those solutions, more general than the existing results, permit some new properties, such as the solitonic propagation and interactions for the BC lattice equations, and the nonnegative dark solitons for the BM lattice equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Valeo, E., Oberman, C., Perkins, F.W.: Saturation of the decay instability for comparable electronic and ion temperatures. Phys. Rev. Lett. 28, 340 (1972)

    Article  Google Scholar 

  2. Agrawal, G.P.: Nonlinear Fiber Optics. Academic, New York (2002)

    MATH  Google Scholar 

  3. Pitaevskii, L.P., Stringari, S.: Bose–Einstein Condensation. Cambridge University Press, Cambridge (2003)

    MATH  Google Scholar 

  4. Gao, X.Y.: Looking at a nonlinear inhomogeneous optical fiber through the generalized higher-order variable-coefficient Hirota equation. Appl. Math. Lett. 73, 143 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  5. Gao, X.Y.: Backlund transformation and shock-wave-type solutions for a generalized (3+1)-dimensional variable-coefficient B-type Kadomtsev-Petviashvili equation in fluid mechanics. Ocean Eng. 96, 245 (2015)

    Article  Google Scholar 

  6. Huang, Q.M., Gao, Y.T.: Wronskian, Pfaffian and periodic wave solutions for a (2+1)-dimensional extended shallow water wave equation. Nonlinear Dyn. 89, 2855 (2017)

    Article  MathSciNet  Google Scholar 

  7. Huang, Q.M., Gao, Y.T., Hu, L.: Breather-to-soliton transition for a sixth-order nonlinear Schrodinger equation in an optical fiber. Appl. Math. Lett. 75, 135 (2018)

    Article  MathSciNet  Google Scholar 

  8. Su, J.J., Gao, Y.T.: Dark solitons for a (2+1)-dimensional coupled nonlinear Schrodinger system with time-dependent coefficients in an optical fiber. Superlattices Microstruct. 104, 498 (2017)

    Article  Google Scholar 

  9. Deng, G.F., Gao, Y.T.: Integrability, solitons, periodic and travelling waves of a generalized (3+1)-dimensional variable-coefficient nonlinear-wave equation in liquid with gas bubbles. Eur. Phys. J. Plus 132, 255 (2017)

    Article  Google Scholar 

  10. Jia, S.L., Gao, Y.T., Zhao, C., Lan, Z.Z., Feng, Y.J.: Solitons, breathers and rogue waves for a sixth-order variable-coefficient nonlinear Schrodinger equation in an ocean or optical fiber. Eur. Phys. J. Plus 132, 34 (2017)

  11. Ghosh, S., Sarma, D.: Bilinearization of \(N = 1\) supersymmetric modified KdV equations. Nonlinearity 16, 411 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  12. Joshi, N., Lafortune, S., Ramani, A.: Hirota bilinear formalism and ultra-discrete singularity analysis. Nonlinearity 22, 871 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hone, A.N.W.: Lattice equations and \(\tau \)-functions for a coupled Painlevé system. Nonlinearity 15, 735 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  14. Sakai, H.: Casorati determinant solutions for the \(q\)-difference sixth Painlevé equation. Nonlinearity 11, 823 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  15. Anderson, B.P., Kasevich, M.A.: Macroscopic quantum interference from atomic tunnel arrays. Science 282, 1686 (1998)

    Article  Google Scholar 

  16. Trombettoni, A., Smerzi, A.: Discrete solitons and breathers with dilute Bose–Einstein condensates. Phys. Rev. Lett. 86, 2353 (2001)

    Article  Google Scholar 

  17. Kominis, Y., Bountis, T., Hizanidis, K.: Breathers in a nonautonomous Toda lattice with pulsating coupling. Phys. Rev. E 81, 066601 (2010)

    Article  MathSciNet  Google Scholar 

  18. Zakharov, V.E., Musher, S.L., Rubenchik, A.M.: Nonlinear stage of parametric wave excitation in a plasma. JETP Lett. 19, 151 (1974)

    Google Scholar 

  19. Picard, G., Johnston, T.W.: Instability cascades, Lotka–Volterra population equations, and Hamiltonian chaos. Phys. Rev. Lett. 48, 1610 (1982)

    Article  MathSciNet  Google Scholar 

  20. Musher, S.L., Rubenchik, A.M., Zakharov, V.E.: Weak Langmuir turbulence. Phys. Rep. 252, 177 (1995)

    Article  Google Scholar 

  21. Marquié, P., Bilbault, J.M., Remoissenet, M.: Observation of nonlinear localized modes in an electrical lattice. Phys. Rev. E 51, 6127 (1995)

    Article  Google Scholar 

  22. Gerdjikov, V.S., Baizakov, B.B., Salerno, M., Kostov, N.A.: Adiabatic \(N\)-soliton interactions of Bose–Einstein condensates in external potentials. Phys. Rev. E 73, 046606 (2006)

    Article  MathSciNet  Google Scholar 

  23. Levi, D., Martina, L., Winternitz, P.: Lie-point symmetries of the discrete Liouville equation. J. Phys. A 48, 025204 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  24. Baudouin, L., Ervedoza, S., Osses, A.: Stability of an inverse problem for the discrete wave equation and convergence results. J. Math. Pure Appl. 103, 1475 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  25. Al-Ghassani, A., Halburd, R.G.: Height growth of solutions and a discrete Painlevé equation. Nonlinearity 28, 2379 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  26. Yu, F.J.: Nonautonomous discrete bright soliton solutions and interaction management for the Ablowitz–Ladik equation. Phys. Rev. E 91, 032914 (2015)

    Article  MathSciNet  Google Scholar 

  27. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  28. Jia, T.T., Chai, Y.Z., Hao, H.Q.: Multi-soliton solutions and Breathers for the coupled nonlinear Schrodinger equations via the Hirota method. Math. Probl. Eng. 2016, 1741245 (2016)

    Google Scholar 

  29. Jia, T.T., Chai, Y.Z., Hao, H.Q.: Multi-soliton solutions and Breathers for the generalized coupled nonlinear Hirota equations via the Hirota method. Superlattices Microstruct. 105, 172 (2017)

    Article  Google Scholar 

  30. Deng, G.F., Gao, Y.T.: Solitons for the (3+1)-dimensional variable-coefficient coupled nonlinear Schrodinger equations in an optical fiber. Superlattices Microstruct. 109, 345 (2017)

    Article  Google Scholar 

  31. Huang, Q.M., Gao, Y.T., Jia, S.L., Wang, Y.L., Deng, G.F.: Bilinear Backlund transformation, soliton and periodic wave solutions for a (3+1)-dimensional variable-coefficient generalized shallow water wave equation. Nonlinear Dyn. 87, 2529 (2017)

    Article  Google Scholar 

  32. Su, J.J., Gao, Y.T.: Bilinear forms and solitons for a generalized sixth-order nonlinear Schrodinger equation in an optical fiber. Eur. Phys. J. Plus 132, 53 (2017)

    Article  Google Scholar 

  33. Weiss, J.: The Painlevé property for partial differential equations. II: Bäcklund transformation, Lax pairs, and the Schwarzian derivative. J. Math. Phys. 24, 1405 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  34. Estévez, P.G., Gordoa, P.R.: Darboux transformations via Painlevé analysis. Inverse Probl. 13, 939 (1997)

    Article  MATH  Google Scholar 

  35. Alagesan, T., Chung, Y., Nakkeeran, K.: Painlevé test for the certain (2 \(+\) 1)-dimensional nonlinear evolution equations. Chaos Solitons Fract. 26, 1203 (2005)

    Article  MATH  Google Scholar 

  36. Gilson, C., Lambert, F., Nimmo, J.J., Willox, R.: On the combinatorics of the Hirota \(D\)-operators. Proc. R. Soc. Lond. A 452, 223 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  37. Lambert, F., Loris, I., Springael, J., Willox, R.: On a direct bilinearization method: Kaup’s higher-order water wave equation as a modified nonlocal Boussinesq equation. J. Phys. A 27, 5325 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  38. Lambert, F., Springael., J.: On a direct procedure for the disclosure of Lax pairs and Bäcklund transformations. Chaos Solitons Fract. 12, 2821 (2001)

    Article  MATH  Google Scholar 

  39. Lambert, F., Springael, J.: Soliton equations and simple combinatorics. Acta Appl. Math. 102, 147 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  40. Wang, Y.F., Tian, B., Wang, M.: Bell-Polynomial approach and integrability for the coupled Gross–Pitaevskii equations in Bose–Einstein condensates. Stud. Appl. Math. 131, 119 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  41. Sun, W.R., Tian, B., Wang, Y.F., Zhen, H.L.: Soliton excitations and interactions for the three-coupled fourth-order nonlinear Schrödinger equations in the alpha helical proteins. Eur. Phys. J. D 69, 146 (2015)

    Article  Google Scholar 

  42. Qin, B., Tian, B., Liu, L.C., Wang, M., Lin, Z.Q., Liu, W.J.: Bell-polynomial approach and \(N\)-soliton solution for the extended Lotka–Volterra equation in plasmas. J. Math. Phys. 52, 043523 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  43. Belov, A.A., Chaltikian, K.D.: Lattice analogues of \(W\)-algebras and classical integrable equations. Phys. Lett. B 309, 268 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  44. Leznov, A.N.: Graded Lie algebras, representation theory, integrable mappings, and integrable systems. Theor. Math. Phys. 122, 211 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  45. Blaszak, M., Marciniak, K.: \(R\)-matrix approach to lattice integrable systems. J. Math. Phys. 35, 4661 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  46. Kupershmidt, B.A., Mathieu, P.: Quantum Korteweg–de Vries like equations and perturbed conformal field theories. Phys. Lett. B 227, 245 (1989)

    Article  MathSciNet  Google Scholar 

  47. Sasaki, R., Yamanaka, I.: Field theoretical construction of an infinite set of quantum commuting operators related with soliton equations. Commun. Math. Phys. 108, 691 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  48. Hikami, K.: The Baxter equation for quantum discrete Boussinesq equation. Nucl. Phys. B 604, 580 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  49. Hikami, K., Inoue, R.: Classical lattice \(W\) algebras and integrable systems. J. Phys. A 30, 6911 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  50. Sahadevan, R., Khousalya, S.: Similarity reduction, generalized symmetries and integrability of Belov–Chaltikian and Blaszak–Marciniak lattice equations. J. Math. Phys. 42, 3854 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  51. Toda, M.: Vibration of a chain with nonlinear interaction. J. Phys. Soc. Jpn. 22, 431 (1967)

    Article  Google Scholar 

  52. Mokross, F., Büttner, H.: Comments on the diatomic Toda lattice. Phys. Rev. A 24, 2826 (1981)

    Article  MathSciNet  Google Scholar 

  53. Dreyer, W., Herrmann, M., Mielke, A.: Micro–macro transition in the atomic chain via Whitham’s modulation equation. Nonlinearity 19, 471 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  54. Wang, H.Y., Hu, X.B., Tam, H.W.: On the two-dimensional Leznov lattice equation with self-consistent sources. J. Phys. A 40, 12691 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  55. Lane, A.M., Thomas, R.G.: \(R\)-matrix theory of nuclear reactions. Rev. Mod. Phys. 30, 257 (1958)

    Article  MathSciNet  Google Scholar 

  56. Belhout, A., Ouichaoui, S., Beaumevieille, H., Boughrara, A., Fortier, S., Kiener, J., Maison, J.M., Mehdi, S.K., Rosier, L., Thibaud, J.P., Trabelsi, A., Vernotte, J.: Measurement and DWBA analysis of the \(12C (6Li, d)\) 16O \(\alpha \)-transfer reaction cross sections at \(48.2\) MeV. \(R\)-matrix analysis of \(12C (\alpha, \gamma ) 16O\) direct capture reaction data. Nucl. Phys. A 793, 178 (2007)

    Article  Google Scholar 

  57. Nemnes, G.A., Iona, L., Antohe, S.: Thermo-electrical properties of nanostructured ballistic nanowires in the \(R\)-matrix formalism using the Implicitly Restarted Arnoldi Method. Physica E 42, 1613 (2010)

    Article  Google Scholar 

  58. Sahadevan, R., Khousalya, S.: Master symmetries for Volterra equation, Belov–Chaltikian and Blaszak–Marciniak lattice equations. J. Math. Anal. Appl. 280, 241 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  59. Zhang, D.J., Chen, D.Y.: The conservation laws of some discrete soliton systems. Chaos Solitons Fract. 14, 573 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  60. Hu, X.B., Zhu, Z.N.: A Bäcklund transformation and nonlinear superposition formula for the Belov–Chaltikian lattice. J. Phys. A 31, 4755 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  61. Hu, X.B., Tam, H.W.: Application of Hirota’s bilinear formalism to a two-dimensional lattice by Leznov. Phys. Lett. A 276, 65 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  62. Hu, X.B., Zhu, Z.N.: Some new results on the Blaszak–Marciniak lattice: Bäcklund transformation and nonlinear superposition formula. J. Math. Phys. 39, 4766 (1998)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Bo Qin, Bo Tian, Yu-Feng Wang & Ming Wang

  2. Department of Computer Science and Engineering, Hong Kong University of Science and Technology Clear Water Bay, Hong Kong, China

    Bo Qin

  3. College of Science, Minzu University of China, Beijing, 100081, China

    Yu-Feng Wang

  4. Ministry-of-Education Key Laboratory of Fluid Mechanics and National Laboratory for Computational Fluid Dynamics, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China

    Yu-Jia Shen

Authors
  1. Bo Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bo Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu-Feng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yu-Jia Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ming Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bo Tian.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qin, B., Tian, B., Wang, YF. et al. Bell-polynomial approach and Wronskian determinant solutions for three sets of differential–difference nonlinear evolution equations with symbolic computation. Z. Angew. Math. Phys. 68, 111 (2017). https://doi.org/10.1007/s00033-017-0853-1

Download citation

  • Received:

  • Revised:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-017-0853-1

Mathematics Subject Classification

Keywords

Search

Navigation