1 Background

Research work on unsteady fully developed laminar flow attributed to circumferential pressure gradient (unsteady Dean flow) and oscillating pressure gradient has remained very active in the past decade due its increasing applications in hemodynamics, biofluid mechanics, and engineering. The underlying phenomenon of fluid flow due to heat transfer has its setback as heat alters the rheological properties of fluids in most of the systems in the aforementioned applications. Consequently, it will be desirable to design systems in which the flows are driven by pressure and not convective current.

A theoretical analysis on laminar steady flow due to constant azimuthal pressure gradient in a channel can be dated back to the work of Dean [1, 2]. Richardson and Tyler [3] and Sexl [4] undertook an investigation on the motion of a viscous and incompressible fluid induced by an oscillating pressure gradient in a straight circular pipe. In context of blood flow in the human arterial system, the fully developed flow of a viscous and incompressible fluid with imposed periodic pressure gradient in a circular pipe was examined by Womersley [5]. Uchida [6], on the other hand, gave the exact solution for the steady motion of a viscous and incompressible fluid in a circular pipe driven by pressure gradient oscillating about a non-zero frequency. Afterwards, extensive survey has been carried out both experimentally and theoretically on this field of research by many workers. In an attempt to have an overview of this study, we shall consider the work of Seth and Jana [7], Mullin and Greated [8], Drake [9], Smith [10], and Badr [11].

Chamkha [12], using the cosine Fourier series and method of separation of variables, performed an analytical evaluation on transient flow of a viscous and electrically conducting fluid in a channel saturated with non-conducting dusty fluid particles in the presence of applied transverse magnetic field and an oscillating pressure gradient in the direction of flow. A fully developed flow due to an oscillatory pressure gradient with time-dependent curvature in a tube was reported by Waters and Pedley [13]. In recent past, Ansari et al. [14] solved numerically Navier-Stokes equations responsible for the motion of a viscous and incompressible fluid through a pipe driven by an oscillatory pressure gradient.

With regard to the continuing investigation, Tsangaris et al. [15] and Tsangaris and Vlachakis [16] reported the effect of an oscillating pressure gradient on unsteady laminar fully developed flow in the region between two concentric cylinders. The exact solution for unsteady rotating flow of a generalized Maxwell fluid in an infinite straight circular cylinder with oscillating pressure gradient was proposed by Zheng et al. [17]. Unsteady fully developed flow of a rarefied gas due a harmonically oscillating pressure gradient in a straight circular tube was studied by Tsimpoukis and Valougeorgis [18].

As the trend continues to unfold and facts are emerging, the phenomenon of an oscillating time-dependent pressure driven flow has not been fully understood even though experiments have been carried out and interpretation of the observable behaviors has been formulated. Jha and Yusuf [19] in an attempt to understand transient flow formation due to a steady circumferential pressure gradient (azimuthal pressure gradient) in a composite annulus, solved semi-analytically the governing momentum equations accountable for the flow in terms of modified Bessel functions. In their work, they utilized a numerical inversing technique known as Riemann-Sum Approximation approach (RSA) in transforming the Laplace domain solution to time domain and concluded that velocity of the fluid is an increasing function of time. Other related literatures that adopted this method of solution include the work of Jha and Odengle [20], Yusuf and Gambo [21], and Jha and Yahaya [22].

Recently, Jha and Yahaya [22, 23] adopting the same method of solution as Jha and Yusuf [19], scrutinized unsteady Dean flow of a viscous and incompressible fluid with constant pressure gradient. In their work, they considered the flow in a horizontal concentric cylinder and later extended the work to the case when the walls of the cylinder are porous in order to superimpose the radial flow. They obtained that an increasing time is desirable for an optimum velocity and skin friction (see Jha and Yahaya [22]). In addition, Jha and Yahaya [23] reported that the fluid velocity and skin friction are increasing functions of injection and time.

However, in spite of all these contributions, no research work has been done to semi-analytically examine the influence of an oscillating time-dependent pressure gradient on Dean flow. Although, there is a general agreement that the annular effects are influenced by time, frequency, and amplitude of the oscillating pressure gradient. However, other facets like the behavior of fluid in the annular gap with an increasing time at fixed frequency and amplitude were not elucidated. The aim of this article is to extend the work of Jha and Yahaya [22] by considering an oscillating time-dependent pressure gradient in addition to the azimuthal pressure gradient. The governing momentum equations are solved analytically in Laplace domain, and the Laplace domain solution is transformed to time domain using a numerical inversing technique known as Riemann-Sum Approximation (RSA). Comparison with previously established results is made at special case.

2 Methods

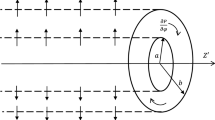
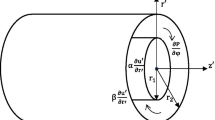
Unsteady fully developed laminar circumferential flow of a viscous and incompressible fluid in an infinite horizontal concentric cylinder is considered. It is assumed the cylinders are fixed and the fluid is Newtonian. The Z′-axis is taken as axis of the cylinder in the horizontal direction. The radii of the inner and outer cylinder are r1 and r2, respectively (see Fig. 1). Initially, at time t ′  ≤ 0, it is assumed that the fluid is at rest. At t ′  > 0, the flow is set in motion by the applied circumferential pressure gradient \( \left(\frac{\partial P}{\partial \varphi}\right) \) and the oscillating time-dependent pressure gradient in the direction of flow. The Navier-Stokes and continuity equations for unsteady fully developed \( \left(u{\prime}_{r^{\prime }}=0\right) \) flow of viscous incompressible fluid written in polar coordinate systems as functions of time and radial coordinates. The following partial differential equations are given as follows:

$$ \frac{\partial \left(r^{\prime }u{\prime}_{r\prime}\right)}{\partial r^{\prime }}+\frac{\partial u^{\prime }}{\partial \varphi }=0 $$
(1)
$$ \rho \left(\frac{\partial u{\prime}_{r\prime }}{\partial t^{\prime }}+u{\prime}_{r\prime}\frac{\partial u{\prime}_{r\prime }}{\partial r^{\prime }}+\frac{u^{\prime }}{r^{\prime }}\frac{\partial u{\prime}_{r\prime }}{\partial \varphi }-\frac{u{\prime}^2}{r^{\prime }}\right)=-\frac{\partial P}{\partial r^{\prime }}+\mu \left(\frac{\partial^2u{\prime}_{r\prime }}{\partial r{\prime}^2}+\frac{1}{r^{\prime }}\frac{\partial u{\prime}_{r\prime }}{\partial r^{\prime }}+\frac{1}{r^{\prime }}\frac{\partial^2u^{\prime }}{\partial {\varphi}^2}-\frac{u{\prime}_{r\prime }}{r{\prime}^2}-\frac{2}{r{\prime}^2}\frac{\partial u^{\prime }}{\partial \varphi}\right) $$
(2)
$$ \rho \left(\frac{\partial {u}^{\prime }}{\partial {t}^{\prime }}+{u}_{r^{\prime}}^{\prime}\frac{\partial {u}^{\prime }}{\partial {r}^{\prime }}+\frac{u^{\prime }}{r^{\prime }}\frac{\partial {u}^{\prime }}{\partial \varphi }-\frac{u_{r^{\prime}}^{\prime }{u}^{\prime }}{r^{\prime }}\right)=-\frac{\cos \left({\omega}_0^{\prime }{t}^{\prime}\right)}{r^{\prime }}\frac{\partial P}{\partial \varphi }+ $$
$$ \mu \left(\frac{\partial^2u^{\prime }}{\partial r{\prime}^2}+\frac{1}{r^{\prime }}\frac{\partial u^{\prime }}{\partial r^{\prime }}+\frac{1}{r{\prime}^2}\frac{\partial^2u^{\prime }}{\partial {\varphi}^2}-\frac{u^{\prime }}{r{\prime}^2}+\frac{2}{r{\prime}^2}\frac{\partial u^{\prime }}{\partial \varphi}\right) $$
(3)
Fig. 1
figure 1

Flow configuration and coordinate system

Full size image

As mentioned earlier, the cylinder is of infinite length and the flow is fully developed, thus

$$ u{\prime}_{r\prime }=0 $$
(4)

Following the approach of Tsangaris and Vlachakis [16], the governing momentum equation can be written as

$$ \rho \frac{u{\prime}^2}{r^{\prime }}=\frac{\partial P}{\partial r^{\prime }} $$
(5)
$$ \rho \frac{\partial u^{\prime }}{\partial t^{\prime }}=-\frac{\cos \left(\omega {\prime}_0{t}^{\prime}\right)}{r^{\prime }}\frac{\partial P}{\partial \varphi }+\mu \left(\frac{\partial^2u^{\prime }}{\partial r{\prime}^2}+\frac{1}{r^{\prime }}\frac{\partial u^{\prime }}{\partial r^{\prime }}-\frac{u^{\prime }}{r{\prime}^2}\right) $$
(6)

The initial and boundary conditions under consideration for the problem are

t′ ≤ 0 : u ′  = 0 for r1 ≤ r ′  ≤ r2

$$ {t}^{\prime }>0\left\{\begin{array}{c}u\hbox{'}=0\kern0.5em \mathrm{at}\kern0.5em r\hbox{'}={r}_1\\ {}u\hbox{'}=0\kern0.5em \mathrm{at}\kern0.5em r\hbox{'}={r}_2\end{array}\right. $$
(7)

Equations (5)–(7) has been rendered dimensionless using the following dimensionless quantities

$$ R=\frac{r^{\prime }}{r_1};\kern0.5em \lambda =\frac{r_2}{r_1};\kern0.5em t=\frac{v{t}^{\prime }}{r_1^2};\kern0.5em U=\frac{u^{\prime }}{U_0};{U}_0=\frac{-{r}_1\frac{\partial P}{\partial \varphi }{A}_0}{\rho v};\kern0.5em \omega =\frac{r_1^2\omega {\prime}_0}{v} $$
(8)

Equations (5) and (6) can be written in the dimensionless form as

$$ \frac{\partial U}{\partial t}=\frac{\cos \left(\omega t\right)}{R}+\left(\frac{\partial^2U}{\partial {R}^2}+\frac{1}{R}\frac{\partial U}{\partial R}-\frac{U}{R^2}\right) $$
(9)

Subject to the following initial and bound boundary conditions

t ≤ 0 : U = 0 for 1 ≤ R ≤ λ

$$ t>0\left\{\begin{array}{c}U=0\kern0.75em \mathrm{at}\ R=1\\ {}U=0\kern0.75em \mathrm{at}\ R=\lambda \end{array}\right. $$
(10)

Employing the classical Laplace transform technique, Eqs. (9) and (10) are transformed to the Laplace domain using \( \overline{U}\left(R,s\right)={\int}_0^{\infty }U\left(R,t\right){e}^{- st} dt \) where s is the Laplace parameter and (s > 0). Equations (9) and (10) in the Laplace domain are given as

$$ \frac{d^2\overline{U}}{d{R}^2}+\frac{1}{R}\frac{d\overline{U}}{dR}-\left(1+s{R}^2\right)\frac{\overline{U}}{R^2}=-\frac{s}{R\left({s}^2+{\omega}^2\right)} $$
(11)

Under the no slip boundary condition

$$ \left\{\begin{array}{c}\overline{U}=0\ \mathrm{at}\ R=1\\ {}\overline{U}=0\ \mathrm{at}\ R=\lambda \end{array}\right. $$
(12)

Following the work of Tsangaris et al. [15], the linear non-homogeneous differential equation in Eq. (11) can be reduced using the given transformation below

$$ \overline{U}\left(R,s\right)={\overline{U}}_h\left(R,s\right)+\frac{1}{R\left({s}^2+{\omega}^2\right)} $$
(13)

where \( {\overline{U}}_h\left(R,s\right) \) is the homogeneous solution of Eq. (11).

Thus, employing Eq. (13), the exact solution of Eq. (11) in the Laplace domain subject to boundary conditions (12) is given below

$$ \overline{U}\left(R,s\right)={B}_1{I}_1\left(R\sqrt{s}\right)+{B}_2{K}_1\left(R\sqrt{s}\right)+\frac{1}{R\left({s}^2+{\omega}^2\right)} $$
(14)

Where \( {B}_1=\frac{K_1\left(\lambda \sqrt{s}\right)-{\lambda}^{-1}{K}_1\left(\sqrt{s}\right)}{\left({s}^2+{\omega}^2\right)\left[{I}_1\left(\lambda \sqrt{s}\right){K}_1\left(\sqrt{s}\right)-{I}_1\left(\sqrt{s}\right){K}_1\left(\lambda \sqrt{s}\right)\right]} \), \( {B}_2=\frac{\lambda^{-1}{I}_1\left(\sqrt{s}\right)-{I}_1\left(\lambda \sqrt{s}\right)}{\left({s}^2+{\omega}^2\right)\left[{I}_1\left(\lambda \sqrt{s}\right){K}_1\left(\sqrt{s}\right)-{I}_1\left(\sqrt{s}\right){K}_1\left(\lambda \sqrt{s}\right)\right]} \)

The skin frictions at the outer surface of the inner cylinder and the inner surface of the outer cylinder are derived by differentiating Eq. (14) at R = 1 and R = λ, respectively

$$ \overline{\tau_1}\left(R,s\right)=R\frac{d}{dR}{\left.\left(\frac{\overline{U}\left(R,s\right)}{R}\right)\right|}_{R=1}=\sqrt{s}\left[{B}_1{I}_2\left(\sqrt{s}\right)-{B}_2{K}_2\left(\sqrt{s}\right)\right]-\frac{2}{\left({s}^2+{\omega}^2\right)} $$
(15)
$$ \overline{\tau_{\lambda }}\left(R,s\right)=R\frac{d}{dR}{\left.\left(\frac{\overline{U}\left(R,s\right)}{R}\right)\right|}_{R=\lambda }=\sqrt{s}\left[{B}_1{I}_2\left(\lambda \sqrt{s}\right)-{B}_2{K}_2\left(\lambda \sqrt{s}\right)\right]-\frac{2}{\lambda^2\left({s}^2+{\omega}^2\right)} $$
(16)

The vorticity of the fluid in the annular gap is given by

$$ \overline{\eta}\left(R,s\right)=\frac{1}{R}\frac{d}{dR}\left(R\overline{U}\left(R,s\right)\right)=\sqrt{s}\left[{B}_1{I}_2\left(R\sqrt{s}\right)-{B}_2{K}_2\left(R\sqrt{s}\right)\right]-\frac{2}{R^2\left({s}^2+{\omega}^2\right)} $$
(17)

It is relevant to note that the above Laplace domain solutions in Eq. (14)–(17) are to be transformed in order to determine the velocity, skin frictions and vorticity in time domain. Due to the intricate nature of the closed-form solutions, a numerical inversing procedure known as Riemann-Sum Approximation (RSA) employed by Jha and Odengle [20], Yusuf and Gambo [21], and Jha and Yahaya [22, 23] which is remarkable for its precision has been utilized in transforming Eq. (14)–(17) to time domain as follows:

$$ Z\left(R,t\right)=\frac{e^{\varepsilon t}}{t}\left[\frac{\overline{Z}\left(R,s\right)}{2}+\mathit{\operatorname{Re}}\left(\sum \limits_{n=1}^Q\overline{Z}\Big(R,\varepsilon +\frac{in\pi}{t}\right){\left(-1\right)}^n\right] $$
(18)

Where Z constitutes U, τ or η as the case may be, Re is the real part of the summation, \( i=\sqrt{-1} \) the imaginary number, Q is the number of terms involve in the summation, and ε is the real part of the Bromwich contour that is used in inverting Laplace transform. The Riemann-Sum Approximation (RSA) for the Laplace inversion involves a single summation for the numerical computation, of which its exactness is dependent on the value of ε and the truncation error prescribed by Q. Following Tzou [24], taking εt to be 4.7 gives the most desirable result.

In order to ascertain the validity of the present analysis, comparison with previously established results has been tabulated when the frequency of the oscillating time-dependent pressure gradient is taken as 0 (ω = 0) Tables 1 and 2

Table 1. Comparison of the present results obtained using the Riemann-Sum Approximation approach (RSA) with those of Jha and Yahaya [22] for the transient state velocity
Full size table
Table 2 Comparison of the present results obtained using the Riemann-Sum Approximation approach (RSA) with those of Jha and Yahaya [22] for the transient state skin frictions
Full size table

3 Results

In an attempt to understand the influence of time, frequency of oscillating time-dependent pressure gradient and the annular gap on the velocity, skin frictions and vorticity, a MATLAB program has been written to compute and generate line graphs and numerical values for the velocity, skin friction and vorticity. The present parametric study has been performed over a reasonable range of values 0.02 ≤ t ≤ 0.2 with t = 0.05 taken as reference point, 0 ≤ ω ≤ 10π, ω = π taken as reference point and λ = 2.0. The effects of the various dimensionless parameters on the flow formation are depicted graphically in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13. The combined action of a growing time, an increasing frequency of oscillating time-dependent pressure gradient and constant pressure gradient on the azimuthal velocity profile are shown in Figs. 2, 3, and 4. The effects of the controlling parameters on skin friction on the outer surface of the inner cylinder and inner surface of the outer cylinders are depicted in Figs. 5, 6, and 7 and Figs. 8, 9, 10, respectively. The rotation of fluid produced by the azimuthal pressure in the annular gap when the velocity is acted upon by time, frequency of oscillation, and constant pressure gradient are represented by Figs. 11, 12, and 13.

Fig. 2
figure 2

Velocity profile versus time t at ω = π

Full size image
Fig. 3
figure 3

Velocity profile versus frequency ω at t = 0.05

Full size image
Fig. 4
figure 4

Velocity profile versus time t as ω = 0

Full size image
Fig. 5
figure 5

Distribution of skin friction versus time at R = 1, ω = π

Full size image
Fig. 6
figure 6

Distribution of skin friction versus frequency ω at R = 1, t = 0.05

Full size image
Fig. 7
figure 7

Distribution of skin friction versus time t at R = 1, ω = 0

Full size image
Fig. 8
figure 8

Distribution of skin friction versus time t at R = λ, ω = π

Full size image
Fig. 9
figure 9

Distribution of skin friction versus frequency ω at R = λ, t = 0.05

Full size image
Fig. 10
figure 10

Distribution of skin friction versus time t at R = λ, ω = 0

Full size image
Fig. 11
figure 11

Vorticity versus time t at ω = π

Full size image
Fig. 12
figure 12

Vorticity versus frequency ω at t = 0.05

Full size image
Fig. 13
figure 13

Vorticity versus time t at ω = 0

Full size image

4 Discussion

Figure 2 shows the velocity profile as time passes for a fixed frequency of oscillation. It is observed that as time increases, the velocity gradually increases as it attains steady state. On the other hand, the velocity profile for different values of the frequency of the oscillating time-dependent pressure gradient and a fixed value of time is presented in Fig. 3. It is evident from Fig. 3 that as the frequency of oscillation increases harmonically, the velocity of the fluid decreases. This is ascribed to the fact that the oscillating pressure gradient is an increasing function of frequency alone, and its increase further reduces the fluid velocity in the annular gap.

Figure 4 exhibits the influence of time on a constant circumferential pressure gradient when the frequency of the oscillation is taken as 0. It is noted that as time passes, the fluid velocity is enhanced.

The distribution of skin friction at the outer wall of the inner cylinder for different values of time and frequency of the oscillating time-dependent pressure gradient are shown in Figs. 5 and 6. It is clear from Fig. 5 that as time passes with a fixed frequency of oscillation, the skin friction increases and later drops with further distance from the wall. It is interesting to note that the reverse trend is observed as time is fixed and the frequency of the oscillating time-dependent pressure gradient increases as depicted in Fig. 6.This is due to the fact that as the frequency increases harmonically, the fluid velocity gradually drops and consequently weakening the skin friction on the wall.

Figure 7 shows the influence of time on the skin friction at the outer surface of the inner cylinder with an applied constant pressure gradient. It is seen from Fig. 7 that the effect of time and a constant pressure gradient is to increase skin friction at the outer wall of the inner cylinder.

Figure 8 shows the effect of time with a fixed frequency of oscillation on skin friction at the inner wall of the outer cylinder. It is observed that as time passes, the skin friction increases attaining its maximum and drops gradually towards the wall.

The variation of skin friction at the inner wall of the outer cylinder with a fixed time and an increasing frequency of the oscillating time-dependent pressure gradient is demonstrated in Fig. 9. It is seen that the skin friction decreases as the frequency of the oscillating time-dependent pressure gradient is increased. In addition, the decreased is more pronounced on the walls of the cylinder. On the other hand, influence of time on the skin friction as the frequency of the oscillating time-dependent pressure gradient is taken as 0 is presented in Fig 10. Result shows that the skin friction decreases as time passes.

The effects of frequency of oscillation and time on the fluid vorticity are shown in Figs. 11, 12, and 13. It is observed that the vorticity increases initially and subsequently weakens as time passes. Although there is a general decrease in magnitude of the vorticity with further distance towards the wall of the outer cylinder as time increases, the decrease is subtle when the frequency is no longer oscillating but rather a constant pressure gradient as evident from Fig. 13.

5 Conclusions

The influence of time and an oscillating time-dependent pressure gradient on Dean flow has been analyzed. The closed-form solution of the governing momentum equation has been derived semi-analytically using the Laplace transformation technique in conjunction with Riemann-Sum Approximation (RSA) as a tool for inversion. The effect of various flow parameters on the flow formation has been represented pictorially. Findings suggest that the fluid velocity, skin frictions, and fluid vorticity can be minimized by increasing the frequency of oscillation. Furthermore, the azimuthal velocity is seen to increase steadily as time passes with an imposed frequency of oscillation, although the increase subtle as seen when a constant pressure gradient is applied.

5.1 Nomenclature

  • A0 Amplitude of oscillating pressure gradient

  • r1 Radius of the inner cylinder (m)

  • r2 Radius of the outer cylinder (m)

  • P Static pressure (Kg/ms2)

  • R Dimensionless radius

  • s Laplace parameter

  • t Dimensionless time (s)

  • U0 Reference velocity (m/s)

  • u′r′ Radial velocity (m/s)

  • u' Circumferential velocity (m/s)

  • U Dimensionless velocity

5.2 Greek letters

  • λ Radii ratio (r2/r1)

  • ρ Fluid density (Kg/m3)

  • η Vorticity

  • τ Skin friction

  • μ Dynamic viscosity of the fluid (Kg/ms)

  • ω Frequency of oscillating time-dependent pressure gradient