Background

Dielectric materials are widely used in mobile electronics, electrical transmission, and pulsed power applications [1]. There is an increasing demand for new nanodielectric materials, consisting of nanoparticle-filled polymers, for creating future electrical transmission and storage devices. One example is a new capacitor made from nanodielectrics that can store a large amount of energy and discharge it quickly with high-energy density [2]. The design of nanodielectrics is often multi-objective, for example, a tradeoff between dielectric constant and breakdown strength of dielectric materials has been observed [3]. It has been noted that small volume fractions of nanofillers can significantly improve the composites’ dielectric breakdown strength because of their high surface area/internal volume ratio [4]. To achieve design requirements under different application scenarios, a systematic computational design approach is needed to quickly explore the microstructure design space of nanodielectrics. In this work, we are developing characterization, reconstruction, and key microstructure feature identification techniques to support the computational design of nanodielectric systems.

A traditional material design follows a trial-and-error process with the focus on exploring the relationships between processing conditions and material properties. This empirical approach to material design is expensive and time consuming. In integrated computational materials engineering (ICME), a three-link (i.e., processing-structure-property) chain model that enables “microstructure-mediated design” has been proposed to facilitate the design of new materials [5, 6]. The microstructure material design problem can be formulated as an optimization problem, in which the desired material properties drive the design of microstructure first and then the corresponding processing conditions. As pointed out by Xu et al, ICME faces three design-related challenges: design representation, design evaluation, and design optimization [7]. Design representation requires quantitative representation of the design space of heterogeneous microstructures using a small set of design variables. Design evaluation is the process of assessing material properties for a given microstructure morphology, which often involves finite element modeling (FEM) and simulations. Design optimization searches for the optimal microstructure design to achieve the desired material properties. Using the design of nanodielectrics as a focal application, the main focus of this paper is on developing methods to support design representation and identify key microstructural design variables in material design.

A good design representation means an accurate quantitative description of microstructures that is easy to control from the perspective of simulation, design, and processing. In the existing work, methods have been developed to characterize and reconstruct microstructures for different material systems. They can be mainly classified into two categories: one is to use correlation functions (CFs) such as 2-point CF, 2-point cluster CF, and surface correlation [8–11]; the other is to use physical descriptors, such as volume fraction, particle size, and minimum distance between particles [12]. CF-based reconstruction often involves optimization procedures to minimize the error between the actual CF and the target ones. This approach has been extended for reconstructing multiphase microstructures, for which each phase has its own CF [13, 14]. Although CF-based approaches are flexible and can be adapted for different microstructures, it is computationally expensive and prohibitive for use as a part of the iterative material design procedure. In addition, CFs are infinitely dimensional. While coefficients of the functions can be treated as design variables, they lack physical meaning. The descriptor-based approach, on the other hand, is much more intuitive and offers low dimensionality of design variables with clear physical meaning. Toward this end, Xu et. al. [12, 15] proposed a descriptor-based approach to fully characterize particle-based microstructures by introducing three categories of descriptors: (1) composition: e.g., volume fraction; (2) dispersion: e.g., nearest center distance, interphase area, cluster number, local volume fraction, and orientation; (3) geometry: e.g., cluster area, equivalent radius, aspect ratio, eccentricity, roundness, compactness, tortuosity, pore size, and rectangularity.

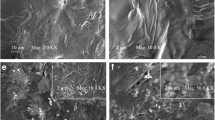
A descriptor-based approach is more efficient for generating statistically equivalent microstructures than the CF-based approach and has been found effective for polymer nanocomposites that have a relatively high volume fraction of filler (e.g., over 20 %) [7, 12]. In this work, the nanodielectric system of interest has a few special features (shown in Fig. 1):

  • Low volume fraction and small number of clusters

  • Uneven distribution of aggregates (heterogeneity)

  • Irregularly shaped large clusters that cannot be modeled using simple geometries like a sphere or ellipse (see Fig. 1c)

Fig. 1
figure 1

a, b Sample microstructures (binary TEM images) of nanodielectric materials. 1430 × 1430 pixels, physical size around 1 × 1 μm, red circles in (c) indicate examples of irregular clusters

Full size image

The volume fraction of the nanodielectric fillers ranges from 0.5 to 3 % over the samples available in our study (collected from several dielectric systems with similar polymer dielectric permittivity). When the filler phase is on the nanoscale, small filler loadings can result in significant property improvement because of the large interfacial area. When the volume fraction is high, aggregation is harder to control and the property enhancements are reduced. As a consequence, the distribution is heterogeneous after processing, which is the reason why, as shown in Fig. 1c, local aggregates (marked by circles) can be observed in these microstructures. In addition, the dispersion (ability to separate primary particles) depends on the particle/particle and particle/polymer attraction [16]. The greater the particle/polymer enthalpic incompatibility, the greater the driving force for agglomeration.

While the descriptor-based method is generally applicable for particle-based nanodielectrics, the original reconstruction algorithm requires the microstructures to be simple and the distribution of filler phase to be even, which is not always satisfied in low volume fraction nanodielectric systems. Therefore, the existing descriptor-based method needs to be tailored to suit the special features of nanodielectrics.

Material informatics [17, 18] is a growing area that exploits information technology and data science to represent, manage, and analyze material data for accelerating new material discovery and design. One of the common challenges associated with material informatics is the high dimensionality of the data and the design space. Recently, efforts have been made in microstructure dimensionality reduction via manifold learning [19] and principal components [20]. However, dimension reduction based only on microstructures does not reflect the influence of microstructure on the properties of interest. To address such limitations, our recent work applied a supervised learning algorithm by using structural information from images and material properties from simulations [21] as supervisory (response) signals. Even though the method can determine the relative importance of descriptors, it introduces subjectivity when determining the final set of design variables. In addition, this learning method is not capable of discriminating redundant features (descriptors); neither it is reliable for cases with a small number of sample images.

In this work, we employ the descriptor-based characterization and reconstruction method to the particular nanodielectric system of interest. To achieve more realistic characterization and more accurate reconstruction, the existing algorithms are modified considering the aforementioned special features of the nanodielectric system. To address the issue of irregularly shaped large clusters, a touching cell splitting algorithm [22] is incorporated to reproduce more realistic structures. To capture the unevenly distributed aggregates, we propose a decomposition and reassembly strategy for reconstruction that preserves local microstructural information. To overcome the limitations of the existing machine learning approach, a Structural Equation Modeling [23] approach is proposed in this work to choose the proper set of independent descriptors using the information learned from images. By introducing latent layers in mapping input and output relations, we are able to identify the relationships and dependencies among descriptors, which allow determination of a small set of key descriptors as design variables. Finally, we illustrate the obtained relationship between key microstructural descriptors and the dielectric properties to support design of a nanoscale silica/epoxy matrix system.

Methods

Descriptor-based characterization and reconstruction

With various microscopic imaging techniques, such as scanning electron microscopy [24] and transmission electron microscopy (TEM) [25], material microstructures can be represented by grayscale digital images. Descriptor characterization is a process for extracting statistical information about the structure descriptors from the images. Due to the heterogeneity of these microstructures, statistical moments are often used as a part of the descriptors. For instance, “cluster area” as a descriptor is best described by a statistical distribution rather than a single value. To reduce dimensionality in representation, the first several orders of statistical moments, such as mean and variance are often used rather than considering the whole distribution.

Once a microstructure is characterized by descriptors, a typical 2D or 3D reconstruction follows a sequential procedure [12]: (1) dispersion reconstruction: center positions of clusters are adjusted to match dispersion descriptors, e.g., the nearest center distances, using optimization algorithms such as simulated annealing (SA), (2) geometry reconstruction: the geometry is randomly generated for each cluster based on the geometry descriptors and geometry profiles are assigned to each cluster, (3) composition adjustment: the edge of clusters are modified to satisfy the composition descriptors such as the volume fraction.

Because the primary particle size is small in this system, noise in the grayscale TEM images is more likely to be recognized as particles in image processing. In this work, we first employ Gaussian filtering [26] to remove the influence of noise. Gaussian filtering utilizes a Gaussian kernel to smooth the image, which will remove isolated pixels. After the filtering process, the existing descriptor-based characterization and reconstruction algorithm as described earlier is employed.

Touching cell splitting method

In the existing descriptor-based characterization [7], all connected regions are considered clusters and are approximated by ellipses. However, for the nanodielectric system in our study, it is observed that the shapes of many connected regions are irregular, which introduces inaccuracy when using a simple ellipse approximation as shown in Fig. 2b.

Fig. 2
figure 2

Illustration of different cluster shapes. a High VF polymer nanocomposite with ellipse-shaped filler phase and (b) low VF nanodielectric system with irregular clusters

Full size image

To improve the characterization accuracy, a touching cell splitting algorithm [22] is applied to split large irregular clusters. The algorithm uses polygon approximation and ellipse fitting techniques to achieve the goal of separation. One simple example is shown in Fig. 3b, where one large cluster is split into three ellipses. To achieve this, the splitting algorithm follows three basic steps:

  1. 1)

    Polygon approximation of cluster edges

  2. 2)

    Identification of concave points and segmentation of cluster edges

  3. 3)

    Separation with ellipse fitting

Fig. 3
figure 3

a Basic idea of using polygon approximation for concavity calculation and b example splitting results

Full size image

A polygon approximation pre-process is first applied, to avoid the evaluation of concavity of each point on the edge of aggregates. This first step is beneficial for reducing the noise on the contour of aggregates as well as reducing the computational time, which is proportional to the number of points to be evaluated. As shown in Fig. 3a, after the polygon approximation using an octagon, the contour can be simply represented by a sequence of points (marked by blue dots), and the concavity at each location can be easily approximated by the angle difference between the neighbors:

$$ \begin{array}{l}a\left({P}_{\mathrm{pre}},{P}_c\right)={ \tan}^{-1}\left(\left({y}_{\mathrm{pre}}-{y}_c\right)/\left({x}_{\mathrm{pre}}-{x}_c\right)\right),\\ {}a\left({P}_{\mathrm{next}},{P}_c\right)={ \tan}^{-1}\left(\left({y}_{\mathrm{next}}-{y}_c\right)/\left({x}_{\mathrm{next}}-{x}_c\right)\right)\end{array} $$
(1)
$$ \begin{array}{l}\mathrm{concavity}\left({P}_c\right)=\left\{\begin{array}{l}\left|a\left({P}_{\mathrm{pre}},{P}_c\right)-a\left({P}_{\mathrm{next}},{P}_c\right)\right|, if\left|a\left({P}_{\mathrm{pre}},{P}_c\right)\right|<\pi, \\ {}\kern8em \pi \left|a\left({P}_{\mathrm{pre}},{P}_c\right)-a\left({P}_{\mathrm{next}},{P}_c\right)\right|,\mathrm{else}\end{array}\right.\\ {}\end{array} $$
(2)

where Pc is the location to be evaluated and Ppre, Pnext are the neighbor points next to it. Real concave points should satisfy the following rules:

  1. 1)

    concavity(Pc) ∈ (a1, a2), and

  2. 2)

    Line \( \frac{}{P_{\mathrm{pre}}{P}_{\mathrm{next}}} \) should not cross over the inner region of the aggregates.

The first rule indicates that a proper threshold interval of concavity needs to be set to select the candidates of real concave points. The choice of the interval varies for different material systems. Once the concave points are identified, the entire contour of aggregates can be represented by several segments to fit ellipses. To represent the ellipses, an implicit second order polynomial is utilized, i.e.:

$$ F=a{x}^2+bxy+c{y}^2+dx+ey+f. $$
(3)

Reconstruction using decomposition and reassembly

To deal with microstructures with local aggregates that are unevenly distributed over the whole image, we propose to first divide the image into subdomains and then reassemble small blocks of reconstructions to preserve local structural information. The proposed method follows three steps (shown in Fig. 4):

  1. 1)

    Divide the original microstructure into multiple equal size sub-blocks

  2. 2)

    Apply the 2D descriptor characterization and reconstruction algorithm to each sub-block

  3. 3)

    Randomly assemble the sub-block reconstructions to obtain the fully reconstructed microstructure

Fig. 4
figure 4

Flow chart of reconstruction by decomposition and random assembly of small blocks

Full size image

Our proposed method is inspired by the Morisita Index approach [27], which is used to analyze local versus global dispersions. The Morisita Index divides the original image using different sizes of small blocks, and then based on the number of particles in each block, a weighted index is calculated to represent the dispersion status of an image. Here we need to choose an appropriate block size based on a specific problem, but the basic idea is similar: let the sub-blocks keep the local information, which would be lost if characterization and reconstruction were directly applied to the global region. The size of the sub-blocks may influence the reconstruction accuracy. In this study, it is found that when the block size is slightly larger than the largest clusters in the microstructure, satisfactory results can be obtained. A decomposition and reassembly strategy was also employed in the evaluation of structure-property relationships and proved to be effective [28]. One additional advantage of the proposed method is that in some sub-blocks, there may be no particles. The block is then maintained as pure matrix (void space) in the reconstruction to ease computation as well as to capture the void space feature which has been used in literature to quantitatively characterize material microstructure dispersion [29, 30] in low volume fraction systems.

Identification of key microstructure descriptors

The procedure of our proposed Structural Equation Modeling-based approach is shown in Fig. 5. Structural Equation Modeling is a multivariate data analysis method that is often used in social science for problems with latent layers and path structures [31]. Considering that microstructures are measurements of structural characteristics, the concept of a measurement model in Structural Equation Modeling can be applied. By introducing latent layers (structural features) in mapping input and output relations, we are able to identify the relationships and dependencies among different descriptors. The whole procedure contains two main parts: First exploratory factor analysis (EFA) [32] is used to reduce descriptors and group them where the latent factors are also identified. Second, with the identified structure, the Partial Least Squares (PLS) technique [33] is applied to estimate the coefficients in Structural Equation Modeling. PLS is shown to be advantageous for problems with a small number of samples and can predict responses accurately [34–36]. In the first step, the original descriptors are grouped under a few number of latent factors after using the EFA, and each latent factor relates to several descriptors (called indicators) that reflects the latent factor. The extracted latent factors can be considered as categories of microstructure features, described by descriptors, and the grouped structure reflects the correlation patterns of descriptors. In the second step, response data such as microstructure CF or material properties is added as the supervisory signal to identify the underlying descriptor-CF or descriptor-property relationship, solved using the PLS algorithm

Fig. 5
figure 5

Flowchart of Structural Equation Modeling-based Machine Learning Method

Full size image

Two steps are shown: EFA and PLS-SEM. Responses can include both CF and properties. In contrast to our proposed approach described above, the existing machine learning technique for identifying key microstructure descriptors pre-specifies the categories of microstructure features (e.g., composition, dispersion, geometry). Such classification is experience-based and can become arbitrary as key microstructural features may vary from one material system to another. In this work, exploratory factor analysis is used to classify the descriptors into several groups by identifying the common factors underlying the original data set. If the observed variables are X1, X2, …, Xn (microstructural descriptors such as minimum distance between fillers in the context of this work), the common factors are F1, F2, …, Fm (latent microstructural features, e.g., dispersion status), and the unique factors are U1, U2, …, Un (the part of X that cannot be explained by F), the variables may be expressed as linear functions of the factors:

$$ \begin{array}{l}{X}_1={\lambda}_{11}{F}_1+{\lambda}_{12}{F}_2+\dots {\lambda}_{1m}{F}_m+{U}_1\hfill \\ {}{X}_2={\lambda}_{21}{F}_1+{\lambda}_{22}{F}_2+\dots +{\lambda}_{2m}{F}_m+{U}_2.\hfill \\ {}\vdots \hfill \\ {}{X}_n={\lambda}_{n1}{F}_1+{\lambda}_{n2}{F}_2+\dots +{\lambda}_{nm}{F}_m+{U}_n,\hfill \end{array} $$
(4)

Each of these equations is a regression equation; factor analysis seeks to find the coefficients λij (loadings on factors) that best reproduce the observed variables from the factors. If all coefficients are correlations and factors are uncorrelated, then the sum of the squared loadings for variable Xi, e.g., \( {\displaystyle \sum_j}{\lambda}_{ij}^2 \), shows the proportion of the variance of Xi explained by these factors. This is called the communality, and the larger the communality for each variable, the more successful the factor solution is.

The EFA helps us identify the common (latent) factors (F) that drive the variation of descriptors (X). Each latent factor can be associated with a specific microstructural feature. For example, equivalent radius and pore size are different measures of the clusters’ sizes, where the cluster size can be considered a latent factor, and both equivalent radius and pore size are observed indicators. The EFA process is implemented with three basic steps:

  1. Step 1:

    Determine the number of latent factors (exogenous variables) n

  2. Step 2:

    Conduct factor analysis with the n factors using proper rotation

  3. Step 3:

    Identify exogenous variables that are poor indicators of latent factors (uniqueness > 0.5) [32]

After identifying the proper structure model using EFA, a detailed Structural Equation Modeling analysis follows where the general structure can be found in Fig. 6. A detailed mathematical model of the presented structure is composed of three key equations:

Fig. 6
figure 6

Basic structure of Structural Equation Modeling. Circles represent latent variables, and squares represent indicators that we can observe and measure

Full size image
$$ {\boldsymbol{\upeta}}_{\left(m\times 1\right)}={\mathbf{B}}_{\left(m\times m\right)}{\boldsymbol{\upeta}}_{\left(m\times 1\right)}+{\boldsymbol{\Gamma}}_{\left(m\times n\right)}{\boldsymbol{\upxi}}_{\left(n\times 1\right)}+{\boldsymbol{\upzeta}}_{\left(m\times 1\right)}, $$
(5)
$$ {\mathbf{y}}_{\left(p\times 1\right)}={\boldsymbol{\Lambda}}_{y\left(p\times m\right)}{\boldsymbol{\upeta}}_{\left(m\times 1\right)}+{\boldsymbol{\upvarepsilon}}_{\left(p\times 1\right)}, $$
(6)
$$ {\mathbf{x}}_{\left(q\times 1\right)}={\boldsymbol{\Lambda}}_{x\left(q\times n\right)}{\boldsymbol{\upxi}}_{\left(n\times 1\right)}+{\boldsymbol{\updelta}}_{\left(q\times 1\right)}, $$
(7)

where m is the number of endogenous latent variables η, n is the number of exogenous latent variables ξ, and p and q are the number of indicators (x and y) and for endogenous and exogenous variables, respectively. In our study, microstructure descriptors (inputs) are the indicators of exogenous latent variables and microstructure CFs and material properties (outputs) are the indicators of endogenous latent variables. Λy and Λx are the loading coefficient matrix for indictors y and x, ζ is a structural error vector, B is the relation matrix among endogenous variables η, and matrix Γ describes the relations between endogenous variable η and exogenous variable ξ. ε and δ are both measurement errors.

Equation (5) shows the mathematical relationship of the structural model, the relationship between latent variables, while Eqs. (6) and (7) both represent the measurement model, illustrating the relationship between latent variables and corresponding indicators.

In the context of material structure-property analysis, different categories of microstructure descriptors can be either pre-defined based on experience [12] or identified as the exogenous latent variables ξi for microstructure descriptors in the proposed Structural Equation Modeling structure after going through the EFA process. Latent variables are often not directly measured. For instance, dispersion can be a latent variable (exogenous variable ξi) but there is no explicit mathematical definition, while dispersion descriptors, such as nearest center distances and nearest boundary distances [7], can be viewed as indicators, represented by x’s. Different indicators (microstructure descriptors in this case) provide measurements of certain features of the microstructure. The error term, δi, in the general model can effectively take into account the errors introduced by the approximations in measurement. Considering measurement errors is another strength of the Structural Equation Modeling approach compared to other methods. Rather than assuming the different categories of descriptors are independent, the correlation between them can also be analyzed by studying the relationship among latent factors in the Structural Equation model.

Depending on the data available, endogenous latent variables ηi at the output side are related to material properties or statistical representations of microstructure (e.g., 2-point CF) in this study. If the microstructure 2-point CF is treated as an exogenous latent variable, then the indicators yi can be the L2 norm ‖S(r)‖2 of the 2-point CF [21] and the fitting parameters of the CF. The Debye exponential fitting function [37] shown in Eq. (8) is used in this work to represent the 2-point CF:

$$ S(r)= exp\left(-\frac{r}{a}\right) $$
(8)

where a is a fitting parameter that describes the shape of CF.

The structural error ζi describes unmodeled factors that may influence the endogenous variables ηi. If the exogenous variables ξi in the structured model cannot explain the endogenous variables ηi well, then a large structural error ζ may exist in the final model, which indicates that additional descriptors may need to be included.

Several different approaches are widely used to solve a structural equation. The first is covariance-based Structural Equation Modeling [38]. The other approach is the Partial Least Squares (PLS) algorithm [39], which is a soft modeling approach to Structural Equation Modeling with no restriction on the normality of data [23]. The PLS algorithm is especially effective for cases when a small number of samples are available [40] and is used in our study. The PLS algorithm estimates the coefficients of both measurement and structural models by an iterative process. A brief diagram of the process is shown in Fig. 7 and the whole PLS algorithm is implemented using the software WarpPLS [41].

Fig. 7
figure 7

Diagram of PLS algorithm to solve structural equation modeling

Full size image

As a result of applying Structural Equation Modeling analysis, key microstructure descriptors are chosen as material design variables. Ideally, for each identified significant latent factor, we want to pick one descriptor as the best indicator (or microstructural design variable). The choice of multiple descriptors within one latent factor will lead to redundancy as multiple descriptors are often correlated.

Constructing structure-property relationship for microstructure design

With the identified set of descriptors, the Optimal Latin Hypercube Sampling (OLHS) [42] and the descriptor-based reconstruction algorithm can be used to generate a set of sample microstructures over the microstructure design space. Corresponding property data are obtained through finite element simulations and the descriptor-property model can be constructed using metamodeling techniques such as Kriging [43]. Figure 8 shows the general procedure to achieve optimal microstructure design using surrogate descriptor-property models. The procedure has been demonstrated in nanocomposite tire material design [12].

Fig. 8
figure 8

Procedure of nanodielectric material design

Full size image

Nanodielectrics are widely used in energy storage applications, where the total energy depends on both permittivity and breakdown strength. For the simple case consisting of two parallel conductive plates separated by a dielectric with permittivity, ε, the total energy is determined from the following equation

$$ E=\frac{1}{2}\varepsilon Ad{U}_d^2 $$
(9)

where ε is the dielectric constant, A and d are both geometric parameters of the capacitor, and Ud is the breakdown strength of the dielectric material. In order to improve the total energy storage, we need a high dielectric constant, ε, and high break down strength Ud. The breakdown of dielectric materials is a dynamic process, which makes it difficult to develop accurate simulation models.

In this study, we focus on the dielectric constant as the property of interest. For lossy materials, the dielectric constant is a complex value, which follows the form:

$$ \varepsilon =\varepsilon \hbox{'}-j\varepsilon \hbox{'}\hbox{'}, $$
(10)

where the real part ε ' represents the ability for energy storage and the imaginary part, ε ", denotes the energy loss of the material. Loss angle, tan δ, is often used to represent the energy loss:

$$ \tan \delta =\frac{\varepsilon "}{\varepsilon \hbox{'}}, $$
(10a)

which describes the ratio of energy loss to energy storage.

As a simple illustration of microstructure design of nanodielectrics, the design objectives associated with the mechanical properties can be chosen as maximizing the real part ε ' and minimizing the energy loss, tan δ. Previous work has shown that dielectric permittivity in polymer nanocomposites can be analyzed using a Prony Series approach adapted from viscoelasticity studies. This approach incorporates explicit consideration of microstructure dispersion as well as polymer interphase between the nanofillers and matrix into the Finite Element simulation [44]. Based on experimental results of bimodal brush grafted silica nanoparticles in an epoxy matrix, finite element modeling has been used to accurately capture the dielectric permittivity and loss angle measured in experiments by superposition of frequency-dependent dielectric relaxation constants. Optimization of nanodielectric materials can be achieved following the framework described in Fig. 8 once sufficient data are collected and multiple simulation property models are built.

Results and discussion

Characterization and reconstruction

Characterization results of a sample nanodielectric microstructure using the original descriptor-based approach without applying the splitting algorithm are presented in Fig. 9a, where we find that approximating the two irregularly shaped clusters by single ellipses introduces large errors. Figure 9b shows the result after using the proposed splitting algorithm. Clusters smaller than the primary particle size are considered to be a single ellipse. For this nanodielectric system, clusters with sizes larger than two primary particles (15 nm particle diameter) are considered as candidates for splitting.

Fig. 9
figure 9

Comparison between after using touching cell splitting and without. a Direct characterization using ellipses (surface fraction = 0.006, nearest center distance = 60) and (b) characterization after ellipses splitting (surface fraction = 0.0075, nearest center distance = 40)

Full size image

As shown in Fig. 9b, the irregular clusters are each split into multiple ellipses, providing a better representation compared to the result in Fig. 9a where single ellipses are used to represent the irregular clusters. As a confirmation of improved accuracy using the splitting algorithm, we compare the interfacial area and the nearest center distance using the two methods. The interfacial area (2D boundary between the filler and matrix) in Fig. 9b is 0.0075 after using the splitting algorithm, which matches better with the real surface fraction 0.0078 of the original image, compared to 0.006 of the result in Fig. 9a without using the splitting algorithm. A similar observation is made for the characterized nearest center distance, which becomes 40 pixels after splitting versus 60 pixels before splitting. Nearest center distance reflects the local clustering behavior, and the “true” value is unknown as the evaluation depends on the way the cluster is characterized. The ellipse splitting algorithm implemented in this work is shown to be effective for splitting touching clusters and offering more accurate characterization. This splitting algorithm is utilized for all microstructure characterizations in the following sections of this paper.

After applying the splitting algorithm, the following descriptors are used to characterize the nanodielectric system for the subsequent reconstructions:

  • Volume fraction (deterministic)

  • Nearest center distance (mean and variance)

  • Aspect ratio (mean, variance, normal distribution)

  • Cluster area (mean, exponential)

Figure 10 shows two image samples chosen from the nanodielectric for reconstruction. The microstructure in sample 1 has a few small local clusters and also some large particle-free spaces with volume fraction at a level as low as 0.53 %. Sample 2 has some large aggregates, which is a very common feature over the samples collected. The physical size of the image is about 1 ×1 μ and the pixel size is 2000 × 2000.

Fig. 10
figure 10

a Sample 1 microstructure, small clusters, and (b) sample 2 microstructure, large local aggregations

Full size image

The statistical information characterized from the two original microstructures is summarized in Table 1. It is observed that the nearest center distance (both mean and variance) of sample 2 is much smaller than that of sample 1 (79 < 124), which reflects the local aggregation behavior in sample 2. Since sample 1 does not exhibit strong local aggregations, six reconstructions are generated (see Fig. 11) using the original descriptor-based approach with the split algorithm but without applying the proposed decomposition and reassembly strategy. For ease of comparison, the resolution of reconstruction is set to be exactly the same as the original, 2000 × 2000 pixels. While larger reconstruction windows always result in more accurate statistics than smaller ones, keep in mind that when the size of reconstruction increases, the computational time increases dramatically, especially for 3D reconstructions. Comparing the reconstructions of sample 1 with the original microstructure, we observe many similarities. First, the distributions of cluster sizes are identical; there are a small number of big clusters and the majority are small clusters. Second, the local clusters are captured in the reconstructions while some large particle-free spaces are observed.

Table 1 Descriptor information of the two sample microstructures (unit of length: nm)
Full size table
Fig. 11
figure 11

2-point CF comparison of reconstructions

Full size image

To evaluate the accuracy of reconstructions, the 2-point CF from reconstructions are compared to the one from the original image. The relative error in L2 norm is used to measure the deviation:

$$ \mathrm{err}=\frac{{\left\Vert {S}_2\hbox{'}(r)-{S}_2(r)\right\Vert}_2}{{\left\Vert {S}_2(r)\right\Vert}_2} $$
(11)

where S2(r) is the target 2-point CF and S2 ' (r) is the 2-point CF of reconstruction. The average error from six reconstructions is found to be 5 %, which is acceptable for this low volume fraction material system.

For sample 2, with large local clusters, the proposed decomposition and reassembly strategy using small blocks are implemented and compared using the original descriptor-based approach with the split algorithm for the whole image. It is noted that without applying the proposed decomposition and reassembly strategy, the two big clusters shown in Fig. 10b are not captured by the reconstructed microstructure. Clusters in the reconstruction shown in Fig. 12a are much more evenly dispersed than the target image, even though a few big clusters do appear in reconstruction. The difference between the 2-point CF is large and the relative error calculated with Eq. (11) is over 40 %. The result is not surprising because when the aggregates are not statistically representative over the window size, e.g., an image with a very small number of large aggregates, the reconstruction cannot reproduce the results. Figure 12b shows one reconstruction sample from using the proposed decomposition and reassembly algorithm with 64 sub-blocks. Two large clusters and more particle-free spaces are observed in the reconstruction, which is closer to the original microstructure compared to Fig. 12a.

Fig. 12
figure 12

Reconstructions for microstructure with large clusters. a Reconstruction with original algorithm for the whole window, err = 48.6 %; b reconstruction using proposed algorithm with sub-blocks, err = 14.8 %

Full size image

By comparing Fig. 12a, b, it is noted that the 2-point CF obtained using our proposed decomposition and reassembly strategy matches much more closely than using the original algorithm, especially in the short range from r = 50 to 100. The relative error achieved is 14.8 %, which is a big improvement compared to 48.6 % using the original approach. The results show that the uneven local information is maintained through the proposed strategy of using small blocks. It should be noted that when assembling the small blocks, a totally random sequence is applied in our study. Omitting the relationship between the sub-blocks is acceptable here for two reasons: (1) The large clusters are sparse in the microstructure images; therefore, it is difficult to come up with a statistical characterization that is representative for the whole image. (2) For such a low volume fraction system, it has been observed that the main differences among 2-point CF occur in the short distance range, which has been captured by the information obtained from individual small blocks. 2-point CF are usually oscillating with several peaks and valleys. The location of the first deepest drop corresponds to the size of local clusters and the peaks at longer distance relate to certain global periodical patterns. As for this case study, no obvious long distance pattern can be observed, so it is not necessary to consider the higher order block-block relationships. In real implementation, the best results will be achieved by randomly assembling the small blocks multiple times and choosing the best match for the target CF, to compensate for the lack of block-block characterization.

Identification of key descriptors from images using the Structural Equation Modeling approach

In this paper, we illustrate the use of the Structural Equation Modeling approach based on the information gathered from microstructure images only, where the CF are used as supervisory responses, and the L2 norm ‖S(r)‖2 of the 2-point CF and the fitting parameters described in Eq. (8) are used as indicators. Image-driven analysis allows us to keep the generality of the results (key descriptors), independent from the properties of interest. If Structural Equation Modeling analysis is applied by using the property as responses, different material properties may result in different key structural features. Since structure-property simulations are expensive, image-based Structural Equation Modeling analysis for identifying key structure descriptors is recommended. To start with, the full set of descriptors considered for particle-based microstructural systems are first gathered from the literature related to hard or soft materials. They are classified and marked under three categories: (1) composition, (2) dispersion, and (3) geometry [21], in Table 2. The majority of the 29 descriptors are statistical, for which two moments are used to represent the entire distributions. As training samples, 117 TEM images of low volume fraction nanodielectric materials (0.5 % to 3 %) were collected.

Table 2 Descriptor set for statistical learning. Reference are provided for those descriptors without explicit meaning
Full size table

The exploratory factor analysis (EFA) approach presented in the “Methods” section and the associated three steps are first followed to identify the proper number of latent factors and group the microstructure descriptors (indicators) based on their associations with the latent factors. When applying the EFA approach, only the data collected on microstructure descriptors from 117 images is used. Methods for choosing the number of latent factors have been well studied and three widely used criteria, K1 method (eigenvalue) [45], Non-graphical Cattell’s Scree Test (optimal coordinates and acceleration factor) [46], and Horn’s Parallel Analysis [47], are employed in Step 1 of EFA to build confidence in the result.

Based on the results shown in Fig. 13, the number of microstructure latent factors is determined to be 5 for our case study. Because the major purpose of the EFA is to group descriptors, the cross loadings of descriptors on latent factors should be minimized. Hence in Step 2 of EFA, the oblique Promax rotation method [48] is chosen to adjust orthogonal factors so that the small loadings can be made closer to 0. With the Promax rotation, we maximize the number of input variables (descriptors) that have only one high loading on a specific latent factor. The EFA results are shown in Table 3. The five latent factors (meanings explained in next paragraph) explain over 80 % of the variances of the original descriptor set. The loadings of input descriptor variables on latent factors can be found in the first five columns, and the largest loading in each row is in italics. The last two columns show the uniqueness of input variables and the complexity respectively. Uniqueness is measured by \( {U}_i^2 \) in Eq. (4), and small value of uniqueness means factors explain input variables well. In the table, if we take a look at the row of ornang1, all the loadings are very small and the uniqueness is 0.96, which is very close to 1. Thus we can conclude that the variation of ornang1 is not well explained by these latent factors in our model. Complexity [49] measures the number of relevant factors for each input variable. Higher complexity means the variable is relevant to multiple factors and cannot be represented by a single factor.

Fig. 13
figure 13

Identification of the number of microstructure latent factors. Parallel analysis and optimal coordinates provide the same estimate of five latent factors. The factors marked by stars are kept as latent factors, their eigenvalues are larger than those from parallel analysis and optimal coordinate estimation

Full size image
Table 3 Results of EFA (loading, uniqueness, and complexity). The meaning of descriptors can be found in Table 2. Indices 1 and 2 indicate the mean and variance of the corresponding descriptor, respectively, e.g., area1 stands for the mean of clusters area
Full size table

In Step 3 of the EFA procedure, based on the rule that at least half of the variance of an independent variable should be explained by a latent factor (uniqueness ≤0.5), we can identify poor factor indicators (underlined) and withdraw them from our data set. Going through steps 1 to 3 in EFA, we reduced the number of characterization parameters from 29 to 19 and associate them to five latent factors. Examining the results, we can relate each factor to a physical interpretation: Factor 1 represents the size of clusters, with 6 descriptors as indicators: cluster area (area1, area2), pore size (pores1, pores2), and equivalent radius (rc1, rc2). Factor 2 represents the distribution status, with the nearest neighbor distance such as nearest boundary distance (nbd) and nearest center distance (ncd) as the indicator. Factor 3 describes the composition information, including volume fraction (vf), interfacial fraction (intph), number of clusters (n), and local volume fraction (locvf1). Volume fraction clearly describes the composition, and the other three describe higher order composition information. Factors 4 and 5 represent two geometric characteristics: Factor 4 is associated with rectangularity (rctan1, rctan2), and tortuosity (ttst2); Factor 5 is associated with compactness (comp1) and roundness (rnds1).

With the identified associations between microstructure descriptors and latent factors, and the three parameterized CF (2-point, 2-point surface, and linear path) as responses for supervised learning, a PLS algorithm is applied to identify the structural equation model, and the final results are visualized in Fig. 14. It is observed that Factor 4 has no significant influence on all three CFs. Factor 5 only has a weak impact (−0.332) on the 2-point CF, but not on the other two CFs. The above indicates that the cluster geometry information is not critical for the microstructures of the nanodielectric system in this study. Factors 1 (size of clusters) and 3 (composition) have significant influence on CFs (large coefficients such as 0.893, 0.763 and P value <0.001). Influence from Factor 2 (distribution status) mainly goes toward the surface CF (corrs), with 0.767 as the coefficient. In addition, the R-squared for all three responses are very high (average over 0.8), indicating the latent factors in this model explain well the variation of responses (CF).

Fig. 14
figure 14

Structural Model based on supervised learning using microstructure CF. Significant relationships are shown by solid lines and corresponding coefficients are marked by “*”. “corrf” = 2-point CF, “corrs” = 2-point surface CF, “corrl” = lineal path CF

Full size image

The obtained Structural Equation Model is verified based on the physical meaning of factor coefficients. For example, Factor 1 represents the size of clusters and it is meaningful that it has a negative effect (−0.542) on the surface correlation and a strong positive effect (0.893) on the lineal path correlation. Intuitively, a larger cluster size leads to smaller surface area and larger lineal path. Based on the Structural Equation Model analysis, a potential set of material design variables are chosen by including four descriptor variables, each underlines Factor 1, Factor 2, Factor 3, and Factor 5, respectively. Based on the loadings of each descriptor with respect to each latent factor, the most significant set is identified to be area1 (0.995, average cluster area) for Factor 1, ncd1 (0.959, average nearest center distance) for Factor 2, vf (0.943, volume fraction) for Factor 3, and rnds1 (0.898, average cluster roundness) for Factor 5.

The Structural Equation Model approach provides a clear association of descriptors and factors that are identified to minimize dependency through factor analysis. In contrast, if we use the existing supervised ranking method based on the Relief algorithm [21], we will run into several issues. The first problem is there is no subjective criterion to determine how many descriptors to keep only with the ranking information. Second, the redundancy issue among the top ranked descriptors cannot be properly addressed. Specifically, the top four (4) ranked descriptors from the Relief ranking algorithm based on the contribution of individual descriptors to responses for the same test case is identified to be vf, area1, pores2, and rc2. A follow-up check of the correlations among these three descriptors as shown in Table 4 indicates strong correlations with the average above 0.9. From the Structural Equation Model analysis shown in Fig. 14, area1, rc2, and pores2 belong to the same latent category (Factor 1) and their loading factors (0.995, 0.942, 0.986) are very close to each other; therefore, choosing all three of them as key descriptors becomes redundant. Even though correlations among descriptors can be identified first before applying the Relief algorithm, selecting what descriptors to keep for data mining is still a problem [21]. Moreover, with the Relief ranking algorithm, it is very likely that we withdraw important descriptors that have more significant influence on the latent factors but are ranked relatively low in the whole list of descriptors. The Structural Equation Model-based method does not have these issues because highly correlated descriptors are reduced to a single latent factor in the EFA step and the importance of each descriptor can be reflected by factor loadings, based on which the key descriptors can be selected for each latent factor. The proposed method hence provides much more insight into the data as well as helps to understand and interpret complex relationships.

Table 4 Correlation comparison of chosen descriptors. Proposed and prior ranking algorithm, high correlation among area1 (average cluster area), pores2 (variance of pore size), and rc2 (variance of equivalent radius)
Full size table

Validation using reconstruction and property simulations

To further validate that the four identified key descriptors retain the majority of the structural information, quantitative comparisons were made between the original 2D microstructure and reconstructions using identified key descriptors, through comparing CFs and simulating the dielectric properties for the epoxy-silica system [4]. Eight representative microstructures are chosen for this validation, and three reconstructions are generated for each of the eight microstructures to account for reconstruction uncertainty. The comparison of CFs are shown in Fig. 15 for two examples, where the four identified key descriptors from the Structural Equation Modeling approach are used to reconstruct 2D microstructures. It is observed that the CFs of reconstructions match well with those of original microstructure. The property simulation results are shown in Table 5, and the differences between reconstructions and the original images are measured by a relative error in terms of the two interested dielectric properties. With an average error at level 0.44 %, the identified descriptors are proven to be capable of capturing the key structural features that affect the dielectric constant ε '. The average error of loss angle tan δ is 3.5 %, which is acceptable considering reconstruction uncertainty and simulation errors.

Fig. 15
figure 15

CF of two reconstruction examples. Reconstructions match well with original microstructure in terms of the tree chosen CF. Average relative error over all 8 samples: 2-point CF 2.9 %, lineal path CF 3.9 %, 2-point surface CF 5 %

Full size image
Table 5 Comparison of dielectric properties of the original and reconstructed images. Eight samples are chosen; properties are averaged over five reconstructions for each sample
Full size table

We also compare the capabilities of predicting material properties using these two different microstructural representations (the correlation function (CF)-based approach and the key descriptor-based approach). A linear regression model is chosen for simplicity and the analysis is based on collected nanodielectric images and simulated properties. Model fitting results are presented in Table 6. It is observed that both models have high prediction accuracy and the model using CF shows slightly better performance in predicting both dielectric constant and loss angle, which is reasonable since the key descriptors are identified based on CF. In conclusion, the identified four key descriptors capture the structural information and provide satisfactory property prediction accuracy.

Table 6 Results of linear model fitting
Full size table

The effects on material properties of each descriptor can be estimated from the standardized coefficients in the fitted linear regression model (shown in Table 5). It is interesting that even through the image-based supervised learning based on the Structural Equation Modeling approach identifies the average nearest center distance, ncd1, as one of the four key descriptors, the influence of ncd1 is not significant for both properties in this case study. This can be explained by the fact that in the studied nanodielectric system, clusters are sparsely distributed, where the interactions between clusters are very weak. In that case, the variation of the nearest distance will not strongly affect material properties. The influence of average roundness, rnds1, on the two properties of interest is much smaller compared with that of average clusters area, area1, and volume fraction, vf. Smaller cluster area and larger volume fraction lead to better dielectric performance: higher energy storage capability (high ε ') and smaller dielectric loss (small tan δ), which is visualized in Fig. 16. This observation is consistent with the findings in the literature that systems with small particles have high surface area-to-volume ratio, which is critical in determining the properties of nano-filled materials [50]. In general cases, the structure-property (s-p) relationship can be more complicated so that we may need to fit nonlinear models, such as Kriging meta-models. Our ongoing work is focused on establishing processing-structure (p-s) relationship. Once the whole processing-structure relationship is completed, we can link the p-s and s-p relationships together to achieve optimal design of the material.

Fig. 16
figure 16

Structure-property relationship. Linear relationship between dielectric properties and key descriptors, only volume fraction and cluster size are considered for visualization

Full size image

Conclusions

In this paper, new characterization, reconstruction, and key microstructure feature identification techniques are developed to support the computational design of nanodielectric systems. For design representation, a descriptor-based characterization and reconstruction method is employed and tailored for a low volume fraction nanodielectric system with uneven local aggregations and irregularly shaped clusters. To handle special microstructures with large local aggregates, we propose a new decomposition and reassembly strategy, based on which the reconstruction accuracy is greatly improved. We also incorporate a touching cell splitting algorithm into the descriptor-based method to deal with irregularly shaped clusters to achieve more realistic characterization. To simplify the material design process and minimize the redundancy among design variables, a new Structural Equation Model-based method is developed to identify key descriptors. To keep the results independent from the material properties of interest, the analysis presented in this paper is based on information from the microstructure images (CF). According to the fitted Structural Equation Model, in which descriptors are classified into five groups based on the identified latent factors, we find volume fraction, cluster size, nearest center distance, and cluster roundness to be a sufficient set of descriptors to represent the structural features of the very low volume fraction nanodielectric system in this research. The relationship between the microstructure and properties are explored based on the epoxy-silica system and a close to linear relationship is observed between dielectric permittivity and the identified key descriptors.

In a future work, more image data of nanodielectric material systems with a wider range of volume fraction will be collected and simulation models for predicting all important dielectric properties will be included. In addition, the design problem will be extended to include both permittivity and breakdown strength as objectives. To make the tradeoff between the two, the Pareto frontier will be used to first identify a set of non-dominated (best achievable) optimal solutions. In addition, the Structural Equation Model-based method can also be applied to find the relations between descriptors and certain properties, which can then be directly used as predictive models in material design. Processing conditions will be taken into consideration to establish the mapping relations across the chain of processing-structure-property to ensure the manufacturability of new nanodielectric materials.

Availability of supporting data

Data presented in this work will be made available upon request.