1 Introduction

Mathematical modeling of dynamical systems and their numerical simulations are widely studied in science and engineering. One of the useful and mostly studied approaches for generalizing the classical models uses the fractional-order operators. The fractional-order operators have a long history from local to nonlocal and from singular to nonsingular kernels. These aspects were recently highlighted in some useful articles. For details, we refer the readers to [1–4].

Fractional-order operators have recently been researched in engineering and science for modeling system dynamics. In the literature, singular and nonsingular kernels are recently well studied. It is difficult to say which one is the greatest right now, but academics always examine several operators for new applications and features. For details, we refer the researchers to [5–7].

The numerical techniques play an important role in the study of dynamical models. For the fractional-order operators, recently, some numerical techniques were developed and applied. For example, the readers can see [8–14]. Using various methodologies, a novel class of mathematical modelings based on hybrid fractional differential equations with hybrid or nonhybrid boundary value conditions has attracted the interest of numerous academics. Nonhomogeneous physical phenomena that occur in their form can be modeled and described using fractional hybrid differential equations. Hybrid differential equations are significant because they incorporate a variety of dynamical systems as special instances. The derivative of an unknown function hybrid with nonlinearity is included in this family of differential equations. In addition, hybrid differential equations can be found in several subjects of mathematics and physics, such as the deflection of a curved beam with constant or varying cross-section, a three-layer beam, electromagnetic waves, or gravity-driven flows, and so on. For details, we refer the readers to [15–25].

The general classes of the fractional-order differential equations (FDEs) were considered by experts. This area is still open for sequential fractional differential equations, hybrid FDEs, mixed fractional functional equations, and many more. Dhage [26–28] initiated hybrid FDEs and divided them into two subclasses called the linear and quadratic differential equations. More relevant studies on the hybrid FDEs can be found in [29–36]. In this paper, we present a system of hybrid sequential FDEs with two different fractional operators, the Caputo and Atangana–Baleanu operators. Our presumed system of hybrid sequential FDEs with initial and boundary conditions is

$$ \begin{aligned} &^{c}\mathcal{D}^{\alpha _{i}} \Biggl[ ^{ABC}\mathcal{D}^{\varrho _{i}} {u_{i}}(t)+ \sum _{1}^{m} \mathcal{F}_{i} \bigl(t,u_{i}(t)\bigr) \Biggr]=-\lambda _{i} \bigl(t,u_{i}(t)\bigr),\quad t\in \mathrm{I}= [0,1], \\ & {u_{i}}(0)=0,\qquad u_{i}^{*}(1)=\Delta _{i},\qquad \mathcal{F}_{i}\bigl(t,u_{i}(t) \bigr)|_{t=0}=0, \end{aligned} $$
(1)

where \(\Delta _{i}=\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} ( \sum_{i=1}^{m}\mathcal{F}_{i}(t,u_{i}(t))+\mathcal{I}^{\alpha _{i}} \lambda _{i}(t,u_{i}^{*}(t)) )|_{t=1}\),, \(0<\alpha _{i}\leq 1\), \(0\leq {\varrho _{i}}\leq 1\), the functions \({u_{i}}:\mathrm{I}\rightarrow \mathcal{R}_{e}\), \(i=1,2,\ldots ,m\), are continuous, and \(\lambda _{i}, \mathcal{F}_{i}:\mathrm{I}\times \mathcal{R}_{e} \rightarrow \mathcal{R}_{e}\), \(h_{i}:\mathrm{I}\times \mathcal{R}_{e} \rightarrow \mathcal{R}_{e}\) (\(i=1,2,\ldots ,m\)) satisfy the Carathéodory conditions and are continuous functions. The \({}^{c}\mathcal{D}^{\alpha _{i}} \) are in the Caputo sense, whereas \({}^{ABC}\mathcal{D}^{\varrho _{i}}\), \(i=1,2,\ldots ,m\), are in the ABC-sense of fractional derivatives. This sort of general sequential hybrid problems have not been studied in the literature. To know whether such problems can have solutions and applications, we consider the existence, uniqueness, stability, and applications in the dynamical systems. Dhage [26–28] and the references therein give more information to the readers on the theory and applications of the problem. We use the fixed point approach for the theoretical analysis and Euler discretization technique in application aspects. For details of the nonlinear models and their simulations, we refer the readers to [37–54].

1.1 Basic definitions of fractional calculus

The concept of a nonsingular kernel was given by Caputo and Fabrizio [55] by replacing the singular kernel by exponential function. This work was then studied for some essential properties in [56]. Later on, Atangana and Baleanu [57] modified the concept of a nonsingular kernel with the replacement of the exponential kernel by the Mittag-Leffler-kernel. They called the new fractional-order differential operator the Atangana–Baleanu fractional derivative, which was recently well studied by many authors. We refer the readers to some related work on these operators and its applications in [55–57] and the references therein.

Definition 1.1

([57])

The ABC-fractional differential operator on \(\psi \in H^{1}(a,b)\), \(b>a\), for \(\varrho _{1} \in [0,1]\) is

$$ ^{ABC} {_{a}\mathcal{D}_{\tau }^{\varrho _{1}}} \psi (\tau )= \frac{B(\varrho _{1})}{1-\varrho _{1}} \int _{a}^{\tau }\psi ^{\prime }(s)E_{ \varrho _{1}} \biggl[ \frac{-\varrho _{1} (\tau -s)^{\varrho }_{1}}{1-\varrho _{1}} \biggr]\,ds, $$
(2)

where \(B(\varrho _{1})\) is a normalizer function satisfying \(B(0)=B(1)=1\). If the function does not belong to \(H^{1}(a,b), b>a\), then the fractional-order derivative of order \(\varrho _{1} \in [0,1]\) has the form

$$ ^{ABC} {_{a}\mathcal{D}_{\tau }^{\varrho _{1}}} \psi (\tau )= \frac{\varrho _{1}B(\varrho _{1})}{1-\varrho _{1}} \int _{a}^{\tau }\bigl( \psi (\tau )-\psi (s) \bigr)E_{\varrho _{1}} \biggl[ \frac{-\varrho _{1} (\tau -s)^{\varrho _{1}}}{1-\varrho _{1}} \biggr]\,ds, $$
(3)

where \(H^{1}(a,b)\) is the set of functions with continuous first derivatives.

Definition 1.2

([57])

For \(\psi \in H^{1}(a,b)\), \(b>a\), \(\varrho _{1} \in [0,1]\), the ABR-fractional derivative is

$$ ^{ABR} {_{a}\mathcal{D}_{\tau }^{\varrho _{1}}} \psi (\tau )= \frac{B(\varrho _{1})}{1-{\varrho _{1}}}\,\frac{d}{d\tau } \int _{a}^{ \tau }\psi (s)E_{\varrho _{1}} \biggl[ \frac{-\varrho _{1} (\tau -s)^{\varrho _{1}}}{1-\varrho _{1}} \biggr]\,ds. $$
(4)

Definition 1.3

([57])

The AB-integral of \(\psi \in H^{1}(a,b)\), \(b>a\), \(0<\varrho _{1}<1 \), is given by

$$ ^{AB} {_{a}\mathcal{I}_{\tau }^{\varrho _{1}}} \psi (\tau )= \frac{1-\varrho _{1}}{B(\varrho _{1})}\psi (\tau )+ \frac{\varrho _{1}}{B(\varrho _{1})\Gamma (\varrho _{1})} \int _{a}^{ \tau }\psi (s) (\tau -s)^{\varrho _{1}-1}\,ds. $$
(5)

The ABC and ABR are related to each other by the following relation.

Theorem 1.4

([57])

Let \(\psi \in H^{1}(a,b)\), \(b>a\). Then for a fractional-order \(\varrho _{1}\in [0,1]\), we have

$$ ^{ABC}_{0}\mathcal{D}^{\varrho _{1}}_{t} \psi (t)=^{ABR}_{0} \mathcal{D}^{\varrho _{1}}_{t} \psi (t)+H(t). $$
(6)

In our results, we will need to the following result.

Lemma 1.5

([58])

The AB fractional derivative and AB fractional integral of the function ψ satisfy the Newton–Leibniz formula

$$ ^{AB}{_{a}\mathcal{I}_{\tau }^{\varrho _{1}}} \bigl( ^{ABC}{_{a} \mathcal{D}_{\tau }^{\varrho _{1}}} \psi (\tau ) \bigr)=\psi (\tau )- \psi (a). $$
(7)

2 Existence of solution

In this section, we obtain the existence of a solution for the suggested hybrid FDE (1) with the help of fixed point technique.

Lemma 2.1

The solution of the sequential hybrid system (1) is

$$\begin{aligned} u_{i} =&-\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum _{1}^{m} \mathcal{F}_{i} \bigl(t,{u_{i}}(t)\bigr)+\mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t)\bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{i}}(s)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{i}(s)\bigr)\,ds \Biggr), \end{aligned}$$
(8)

where

$$\begin{aligned}& \mathcal{G}_{i}(t,s)=\frac{1}{\Gamma ({\varrho _{i}})} \textstyle\begin{cases} (1-s)^{\varrho _{i}-1} ,& t\leq s, \\ (1-s)^{\varrho _{i}-1}-(t-s)^{\varrho _{i}-1},& t\geq s,\end{cases}\displaystyle \end{aligned}$$
(9)
$$\begin{aligned}& \mathcal{H}_{i}(t,s)=\frac{1}{\Gamma ({\varrho _{i}}+\alpha _{i})} \textstyle\begin{cases} (1-s)^{\varrho _{i}+\alpha _{i}-1} ,& t\leq s, \\ (1-s)^{\varrho _{i}+\alpha _{i}-1}-(t-s)^{\varrho _{i}+\alpha _{i}-1},& t\geq s,\end{cases}\displaystyle \end{aligned}$$
(10)

for \(i=1,2,\ldots ,m\).

Proof

Applying (\(I^{\alpha _{i}}\)) to system (1), we have

$$ ^{ABC}\mathcal{D}^{\varrho _{i}} {u_{i}}(t)+\sum _{i=1}^{m} \mathcal{F}_{i} \bigl(t,{u_{i}}(t)\bigr)=-I^{\alpha _{i}}\lambda _{i} \bigl(t,{u_{i}}(t)\bigr)+C_{1,i} $$
(11)

for \(i=1,2,\ldots ,m\). Using the initial conditions \(u_{i}(0)=0\), for \(i=1,2,\ldots ,m\), we have \(C_{1,i}=0\). This implies

$$ \begin{aligned} ^{ABC}\mathcal{D}^{\varrho _{i}} {u_{i}}(t)=&-\mathcal{I}^{\alpha _{i}} \lambda _{i} \bigl(t,{u_{i}}(t)\bigr)-\sum_{i=1}^{m} \mathcal{F}_{i}\bigl(t,{u_{i}}(t)\bigr) \quad \text{for } i=1,2,\ldots ,m. \end{aligned} $$
(12)

With the help of ABC-fractional calculus and (12) we have

$$\begin{aligned} u_{i}(t) =&-\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl( \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t) \bigr)+\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{i}}(t)\bigr) \Biggr) \\ &{}-\mathcal{B}(\varrho _{i})\mathcal{I}^{\varrho _{i}} \Biggl(\sum _{1}^{m} \mathcal{F}_{i} \bigl(t,{u_{i}}(t)\bigr)+\mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t)\bigr) \Biggr)+C_{2,i}. \end{aligned}$$
(13)

Since of \(u_{i}(1)=0\), by (13) we have \(C_{2,i}=\mathcal{B}(\varrho _{i})I^{\varrho _{i}} (\sum_{1}^{m} \mathcal{F}_{i}(t,{u_{i}}(t))+I^{\alpha _{i}+\varrho _{i}}\lambda _{i}(t,{u_{i}}(t)) )|_{t=1}\) for \(i=1,2,\ldots ,m\). This leads to the following equivalent integral system:

$$\begin{aligned} u_{i}(t) =&-\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl( \sum _{1}^{m} \mathcal{F}_{i} \bigl(t,{u_{i}}(t)\bigr)+\mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t)\bigr) \Biggr) \\ &{}-\mathcal{B}(\varrho _{i})\mathcal{I}^{\varrho _{i}} \Biggl(\sum _{1}^{m} \mathcal{F}_{i} \bigl(t,{u_{i}}(t)\bigr)+\mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t)\bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i})I^{\varrho _{i}} \Biggl(\sum _{1}^{m} \mathcal{F}_{i} \bigl(t,{u_{i}}(t)\bigr)+I^{\alpha _{i}}\lambda _{i} \bigl(t,{u_{i}}(t)\bigr) \Biggr)\biggm|_{t=1} \\ =&-\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{i}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t) \bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \bigl( {} _{0}I^{\varrho _{i}+\alpha _{i}}_{1}- _{0}I^{\varrho _{i}+\alpha _{i}}_{t} \bigr)\lambda _{i}\bigl(t,{u_{i}}(t)\bigr)+ \bigl({} _{0}I^{\varrho _{i}}_{1}- _{0}I^{\varrho _{i}}_{t} \bigr)\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{i}}(t)\bigr) \Biggr) \\ =&\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1} \bigl( (1-s)^{\varrho _{i}-1}- (t-s)^{\varrho _{i}-1} \bigr)\sum_{1}^{m} \mathcal{F}_{i}\bigl(s,{u_{i}}(s)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \bigl( (1-s)^{ \varrho _{i}-1+\alpha _{i}}- (t-s)^{\varrho _{i}-1+\alpha _{i}} \bigr) \lambda _{i}\bigl(s,u_{i}(s) \bigr)\,ds \Biggr) \\ &{}-\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{i}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t) \bigr) \Biggr) \\ =&-\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{i}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t) \bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{i}}(s)\bigr)\,ds \\ &{} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{i}(s)\bigr)\,ds \Biggr) \end{aligned}$$
(14)

for \(i=1,2,\ldots ,m\). The \(\mathcal{G}_{i}(t,s)\) and \(\mathcal{H}_{i}(t,s)\), \(i=1,2,\ldots ,m\), are defined in (9) and (10), respectively. □

In this paper, we consider the Banach space \(\mathcal{B}=\{u_{i}(t): u_{i}(t)\in \mathcal{C}([0,1],\mathcal{R}_{e}) \text{ for }t\in [0,1]\}\) with norm \(\|u_{i}\|=\max_{t\in [0,1]}|u_{i}(t)|\), \(i=1,2,\ldots ,m\).

Let \(\mathcal{T}_{i}:\mathcal{C}([0,1],\mathcal{R}_{e})\rightarrow \mathcal{C}([0,1],\mathbb{R})\), \(i=1,2,\ldots ,m\), be the operators defined by

$$\begin{aligned} \mathcal{T}_{i}u_{i}(t) =&- \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{i}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t) \bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{i=1}^{m} \mathcal{F}_{i} \bigl(s,{u_{i}}(s)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\alpha _{i}+\varrho _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{i}(s)\bigr)\,ds \Biggr). \end{aligned}$$
(15)

The \(\mathcal{G}_{i}(t,s)\) and \(\mathcal{H}_{i}(t,s)\), \(i=1,2,\ldots ,m\), are given in (9) and (10), respectively. By (15) the fixed points of the operators \(\mathcal{T}_{i}\) give the solutions of the hybrid system (1). By (9) and (10) the functions \(\mathcal{G}_{i}(s,t)\) and \(\mathcal{H}_{i}(s,t)\) are clearly positive operators for both \(t\leq s\) and \(t\geq s\), for \(t,s\in (0,1]\) and \(i=1,2,\ldots , m\).

Lemma 2.2

Assume that for some \(\zeta _{i}^{1},\zeta _{i}^{2}\in \mathcal{R}_{e}\) and \(u_{i}, u_{i}^{*}\in \mathcal{C}\), \(t\in [0,k]\), we have

$$\begin{aligned}& \bigl\vert \lambda _{i}(t,u_{i})-\lambda _{i}(t,\bar{u}_{i}) \bigr\vert \leq \zeta _{i}^{1} \vert u_{i}- \bar{u}_{i} \vert , \end{aligned}$$
(16)
$$\begin{aligned}& \bigl\vert \mathcal{F}_{i}(t,u_{i})- \mathcal{F}_{i}(t,\bar{u}_{i}) \bigr\vert \leq \zeta _{i}^{2} \vert u_{i}- \bar{u}_{i} \vert , \end{aligned}$$
(17)

and

$$\begin{aligned} \eta _{i} =&\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl( \zeta _{i}^{2}\eta _{i}+\wp _{2}\bigr)+\frac{1}{\Gamma (\alpha _{i}+1)} \bigl( \zeta _{i}^{1} \eta _{i}+\wp _{1}\bigr) \biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \frac{2k^{\varrho _{i}}}{\Gamma (\varrho +1)} m\bigl( \zeta _{i}^{2}\eta _{i}+ \wp _{2}\bigr) \\ &{} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \frac{2k^{\varrho _{i}+\alpha _{i}}}{\Gamma (\varrho +\alpha _{i}+1)}\bigl( \zeta _{i}^{1}\eta _{i}+\wp _{1}\bigr) \biggr) \end{aligned}$$
(18)

for \(\eta _{i}<1\), \(i=1,2,\ldots ,m\). Then (1) has a unique solution.

Proof

In this proof, the subscripts \(i=1,2,\ldots ,n\). Assume that \(\sup_{t\in [0,k]}|\lambda _{i}(t,0)|=\wp _{1}<\infty \), \(\sup_{t\in [0,k]}|\mathcal{F}_{i}(t,0)|=\wp _{2}<\infty \), \(\mathcal{S}_{\eta _{i}}=\{u_{i}\in \mathcal{C}([0,k],\mathcal{R}_{e}): \|u_{i}\|<\eta _{i}\}\), and \(k\geq 1\). For \(u_{i}\in \mathcal{S}_{\eta _{i}}\) and \(t\in [0,k]\), we have

$$\begin{aligned} \bigl\vert \lambda _{i}\bigl(t,u_{i}(t) \bigr) \bigr\vert =& \bigl\vert \lambda _{i} \bigl(t,u_{i}(t)\bigr)-\lambda _{i}(t,0)+ \lambda _{i}(t,0) \bigr\vert \\ \leq & \bigl\vert \lambda _{i}\bigl(t,u_{i}(t) \bigr)-\lambda _{i}(t,0) \bigr\vert + \bigl\vert \lambda _{i}(t,0) \bigr\vert \\ \leq &\zeta _{i}^{1} \bigl\vert u_{i}(t) \bigr\vert + \bigl\vert \lambda _{i}(t,0) \bigr\vert \\ \leq &\zeta _{i}^{1}\eta _{i}+\wp _{1}. \end{aligned}$$
(19)

Similarly, for \(v_{i}\in \mathcal{S}_{\eta _{i}}\) and \(t\in [0,k]\), we have

$$\begin{aligned} \bigl\vert \mathcal{F}_{i}\bigl(t,v_{i}(t) \bigr) \bigr\vert =& \bigl\vert \mathcal{F}_{i} \bigl(t,v_{i}(t)\bigr)- \mathcal{F}_{i}(t,0)+ \mathcal{F}_{i}(t,0) \bigr\vert \\ \leq & \bigl\vert \mathcal{F}_{i}\bigl(t,v_{i}(t) \bigr)-\mathcal{F}_{i}(t,0) \bigr\vert + \bigl\vert \mathcal{F}_{i}(t,0) \bigr\vert \\ \leq &\zeta _{i}^{2} \bigl\vert v_{i}(t) \bigr\vert + \bigl\vert \mathcal{F}_{i}(t,0) \bigr\vert \\ \leq &\zeta _{i}^{2}\eta _{i}+\wp _{2}. \end{aligned}$$
(20)

Furthermore, for \(t\geq s\), by (9) we have

$$\begin{aligned} \int _{0}^{1} \bigl\vert \mathcal{G}_{i}(t,s) \bigr\vert \,ds =&\frac{1}{\Gamma (\varrho )} \int _{0}^{1} \bigl\vert (1-s)^{\varrho _{i}-1}-(t-s)^{\varrho _{i}-1} \bigr\vert \,ds \\ \leq & \frac{ ((1-s)^{\varrho _{i}}+(t-s)^{\varrho _{i}} )}{\Gamma (\varrho +1)} \leq \frac{2k^{\varrho _{i}}}{\Gamma (\varrho +1)}, \end{aligned}$$
(21)

and for \(t\leq s\), we have

$$\begin{aligned} \int _{0}^{1} \bigl\vert \mathcal{G}_{i}(t,s) \bigr\vert \,ds =&\frac{1}{\Gamma (\varrho )} \int _{0}^{1} \bigl\vert (1-s)^{\varrho _{i}-1} \bigr\vert \,ds \leq \frac{k^{\varrho _{i}}}{\Gamma (\varrho +1)}. \end{aligned}$$
(22)

Now, consider the Green’s functions \(\mathcal{H}_{i}(t,s)\) given by (10). For the case \(t\geq s\), we have

$$\begin{aligned} \int _{0}^{1} \bigl\vert \mathcal{H}_{i}(t,s) \bigr\vert \,ds =& \frac{1}{\Gamma (\varrho +\alpha _{i})} \int _{0}^{1} \bigl\vert (1-s)^{ \varrho _{i}+\alpha _{i}-1}-(t-s)^{\varrho _{i}+\alpha _{i}-1} \bigr\vert \,ds \\ \leq &\frac{1}{\Gamma (\varrho +\alpha _{i}+1)} \bigl((1-s)^{\varrho _{i}+ \alpha _{i}}+(t-s)^{\varrho _{i}+\alpha _{i}} \bigr) \leq \frac{2k^{\varrho _{i}+\alpha _{i}}}{\Gamma (\varrho +\alpha _{i}+1)}, \end{aligned}$$
(23)

and for \(t\leq s\), we have

$$\begin{aligned} \int _{0}^{1} \bigl\vert \mathcal{H}_{i}(t,s) \bigr\vert \,ds =& \frac{1}{\Gamma (\alpha _{i}+\varrho )} \int _{0}^{1} \bigl\vert (1-s)^{ \varrho _{i}-1+\alpha _{i}} \bigr\vert \,ds \leq \frac{k^{\alpha _{i}+\varrho _{i}}}{\Gamma (\alpha _{i}+\varrho +1)}. \end{aligned}$$
(24)

With the help of (15), for \(t\geq s\), we have

$$\begin{aligned} \bigl\vert \mathcal{T}_{i}u_{i}(t) \bigr\vert = &\Biggl\vert - \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum _{1}^{m} \mathcal{F}_{i} \bigl(t,{u_{i}}(t)\bigr)+\mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t)\bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1}\mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{i}(s)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1} \mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{i}}(s)\bigr)\,ds \Biggr) \Biggr\vert \\ \leq& \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl(\zeta _{i}^{2} \eta _{i}+\wp _{2}\bigr)+\frac{1}{\Gamma (\alpha _{i}+1)} \bigl( \zeta _{i}^{1} \eta _{i}+\wp _{1}\bigr) \biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) m \bigl( \bigl(\zeta _{i}^{2}\eta _{i}+\wp _{2}\bigr)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \bigl( \bigl(\zeta _{i}^{1}\eta _{i}+\wp _{1}\bigr)\bigr)\,ds \biggr) \\ \leq &\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl(\zeta _{i}^{2} \eta _{i}+\wp _{2}\bigr)+\frac{1}{\Gamma (1+\alpha _{i})} \bigl( \zeta _{i}^{1} \eta _{i}+\wp _{1}\bigr) \biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \frac{2k^{\varrho _{i}}}{\Gamma (\varrho +1)} m\bigl( \bigl(\zeta _{i}^{2}\eta _{i}+ \wp _{2}\bigr)\bigr) \\ &{}+ \frac{1}{\Gamma (\alpha _{i}+\varrho _{i})} \frac{2k^{\varrho _{i}+\alpha _{i}}}{\Gamma (\varrho +\alpha _{i}+1)}\bigl( \bigl(\zeta _{i}^{1}\eta _{i}+\wp _{1}\bigr)\bigr) \biggr), \end{aligned}$$
(25)

and for \(t\leq s\), we have

$$ \begin{aligned}[b] \bigl\vert \mathcal{T}_{i}u_{i}(t) \bigr\vert ={}& \Biggl\vert - \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum _{1}^{m} \mathcal{F}_{i} \bigl(t,{u_{i}}(t)\bigr)+\mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t)\bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{i}}(s)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{i}(s)\bigr)\,ds \Biggr) \Biggr\vert \\ \leq{}& \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl(\zeta _{i}^{2} \eta _{i}+\wp _{2}\bigr)+\frac{1}{\Gamma (\alpha _{i}+1)} \bigl( \zeta _{i}^{1} \eta _{i}+\wp _{1}\bigr) \biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) m \bigl( \bigl(\zeta _{i}^{2}\eta _{i}+\wp _{2}\bigr)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \bigl( \bigl(\zeta _{i}^{1}\eta _{i}+\wp _{1}\bigr)\bigr)\,ds \biggr) \\ \leq {}& \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl(\zeta _{i}^{2} \eta _{i}+\wp _{2}\bigr)+\frac{1}{\Gamma (\alpha _{i}+1)} \bigl( \zeta _{i}^{1} \eta _{i}+\wp _{1}\bigr) \biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \frac{k^{\varrho _{i}}}{\Gamma (1+\varrho )} m\bigl( \bigl(\zeta _{i}^{2}\eta _{i}+ \wp _{2}\bigr)\bigr)\\ &{} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \frac{k^{\varrho _{i}+\alpha _{i}}}{\Gamma (\varrho +\alpha _{i}+1)}\bigl( \bigl( \zeta _{i}^{1}\eta _{i}+\wp _{1}\bigr)\bigr) \biggr). \end{aligned} $$
(26)

This implies \(\mathcal{T}_{i}\mathcal{S}_{\eta _{i}}\subset \mathcal{S}_{\eta _{i}}\). Further, assuming that \(u_{l}, u_{j}\in \mathcal{C}([0,k],\mathcal{R}_{e})\) and \(k\geq 1\), for \(t\geq s\in [0,k]\), we get

$$\begin{aligned} \bigl\vert \mathcal{T}_{i}u_{l}(t)- \mathcal{T}_{i}u_{j}(t) \bigr\vert =& \Biggl\vert - \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{l}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{l}}(t) \bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{l}}(s)\bigr)\,ds \\ &{} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{l}(s)\bigr)\,ds \Biggr) \\ &{} - \Biggl[\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{j}}(s)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1}\mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{j}(s)\bigr)\,ds \Biggr) \\ &{} -\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{j}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{j}}(t) \bigr) \Biggr) \Biggr] \Biggr\vert \\ \leq &\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl(\zeta _{i}^{2} \vert u_{l}-u_{j} \vert \bigr)+ \frac{1}{\Gamma (\alpha _{i}+1)} \bigl(\zeta _{i}^{1} \vert u_{l}-u_{j} \vert \bigr) \biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) m \bigl( \bigl(\zeta _{i}^{2} \vert u_{l}-u_{j} \vert \bigr)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1}\mathcal{H}_{i}(t,s) \bigl( \bigl(\zeta _{i}^{1} \vert u_{l}-u_{j} \vert \bigr)\bigr)\,ds \biggr) \\ \leq &\biggl[\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \zeta _{i}^{2}+ \frac{1}{\Gamma (\alpha _{i}+1)} \zeta _{i}^{1} \biggr) + \mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \frac{2k^{\varrho _{i}}}{\Gamma (\varrho +1)} m\zeta _{i}^{2} \\ &{} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \frac{2k^{\varrho _{i}+\alpha _{i}}}{\Gamma (\varrho +\alpha _{i}+1)} \zeta _{i}^{1} \biggr) \biggr] \vert u_{l}-u_{j} \vert , \end{aligned}$$
(27)

and for \(t\leq s\in [0,k]\), a calculation for \(i=1,2,\ldots ,m\) leads to

$$\begin{aligned} \bigl\vert \mathcal{T}_{i}u_{l}(t)- \mathcal{T}_{i}u_{j}(t) \bigr\vert = &\Biggl\vert - \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{l}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{l}}(t) \bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{l}}(s)\bigr)\,ds \\ &{} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{l}(s)\bigr)\,ds \Biggr) \\ &{} - \Biggl[-\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{j}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{j}}(t) \bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{j}}(s)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{j}(s)\bigr)\,ds \Biggr) \Biggr] \Biggr\vert \\ \leq &\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl(\zeta _{i}^{2} \vert u_{l}-u_{j} \vert \bigr)+ \frac{1}{\Gamma (\alpha _{i}+1)} \bigl(\zeta _{i}^{1} \vert u_{l}-u_{j} \vert \bigr) \biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) m \bigl( \bigl(\zeta _{i}^{2} \vert u_{l}-u_{j} \vert \bigr)\bigr)\,ds \\ &{} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1}\mathcal{H}_{i}(t,s) \bigl( \bigl(\zeta _{i}^{1} \vert u_{l}-u_{j} \vert \bigr)\bigr)\,ds \biggr) \\ \leq &\biggl[\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \zeta _{i}^{2}+ \frac{1}{\Gamma (\alpha _{i}+1)} \zeta _{i}^{1} \biggr) + \mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \frac{k^{\varrho _{i}}}{\Gamma (\varrho +1)} m\zeta _{i}^{2} \\ &{} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \frac{k^{\varrho _{i}+\alpha _{i}}}{\Gamma (\varrho +\alpha _{i}+1)} \zeta _{i}^{1} \biggr) \biggr] \vert u_{l}-u_{j} \vert \\ \leq &\eta _{i} \vert u_{l}-u_{j} \vert . \end{aligned}$$
(28)

If \(\eta _{i}<1\), where \(\eta _{i}\) are given by (18), then \(\mathcal{T}_{i}\) are contraction operators, and by Banach’s fixed point theorem the sequential hybrid fractional-order system (1) has a unique solution, represented by the fixed points of \(\mathcal{T}_{i}\). □

Theorem 2.3

Under the assumptions of Lemma 2.2, the sequential hybrid system of FDEs (1) has a solution.

Proof

In Lemma 2.2, we proved that \(\mathcal{T}_{i}\) are bounded. Furthermore, let \(t_{1}, t_{2}\in [0,k]\) with \(t_{2}>t_{1}\) and \(k\leq 1\). In the case \(t\geq s\), we have

$$\begin{aligned}& \begin{aligned}[b] &\bigl\vert \mathcal{T}_{i}u(t_{2})- \mathcal{T}_{i}u(t_{1}) \bigr\vert \\ &\quad =\Biggl\vert - \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t_{2},u(t_{2})\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t_{2},u(t_{2}) \bigr) \Biggr)\\ &\qquad {} +\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t_{2},s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,u(s)\bigr)\,ds \\ &\qquad {}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t_{2},s) \lambda _{i}\bigl(s,u(s)\bigr)\,ds \Biggr) \\ &\qquad {}- \Biggl[- \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t_{1},u(t_{1})\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t_{1},u(t_{1}) \bigr) \Biggr) \\ &\qquad {}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t_{1},s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,u(s)\bigr)\,ds \\ &\qquad {}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1}\mathcal{H}_{i}(t_{1},s) \lambda _{i}\bigl(s,u(s)\bigr)\,ds \Biggr) \Biggr] \Biggr\vert \end{aligned} \end{aligned}$$
(29)
$$\begin{aligned}& \begin{aligned}[b] &\quad \leq \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \bigl\vert \mathcal{F}_{i}\bigl(t_{2},u(t_{2}) \bigr)-\mathcal{F}_{i}\bigl(t_{1},u(t_{1}) \bigr) \bigr\vert +\mathcal{I}^{\alpha _{i}} \bigl\vert \lambda _{i}\bigl(t_{2},u(t_{2})\bigr)- \lambda _{i}\bigl(t_{1},u(t_{1})\bigr) \bigr\vert \Biggr) \\ &\qquad {}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \biggl\vert \int _{0}^{t_{2}}(t_{2}-s)^{\varrho _{i}-1}- \int _{0}^{t_{1}}(t_{1}-s)^{ \varrho _{i}-1} \biggr\vert \sum_{1}^{m} \bigl\vert \mathcal{F}_{i}\bigl(s,u(s)\bigr) \bigr\vert \,ds \\ & \qquad {}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \biggl\vert \int _{0}^{t_{2}}(t_{2}-s)^{ \varrho _{i}+\alpha -1}- \int _{0}^{t_{1}}(t_{1}-s)^{\varrho _{i}+ \alpha -1} \biggr\vert \bigl\vert \lambda _{i}\bigl(s,u(s)\bigr) \bigr\vert \,ds \Biggr) \\ &\quad \leq \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \bigl\vert \mathcal{F}_{i}\bigl(t_{2},u(t_{2}) \bigr)-\mathcal{F}_{i}\bigl(t_{1},u(t_{1}) \bigr) \bigr\vert +\mathcal{I}^{\alpha _{i}} \bigl\vert \lambda _{i}\bigl(t_{2},u(t_{2})\bigr)- \lambda _{i}\bigl(t_{1},u(t_{1})\bigr) \bigr\vert \Biggr) \\ &\qquad {}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i}+1)} \biggl\vert t_{2}^{\varrho _{i}}-t_{1}^{\varrho _{i}}\bigl( \zeta _{i}^{2}\eta _{i}+ \wp _{2}\bigr) + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i}+1)} \biggr\vert t_{2}^{ \varrho _{i}+\alpha }\\ &\qquad {}-t_{1}^{\varrho _{i}+\alpha }|\bigl( \zeta _{i}^{1} \eta _{i}+\wp _{1}\bigr) \biggr). \end{aligned} \end{aligned}$$
(30)

This implies that \(\mathcal{T}_{i}u(t_{2})\rightarrow \mathcal{T}_{i}u(t_{1})\) as \(t_{2}\rightarrow t_{1}\). This implies \(| \mathcal{T}_{i}u_{i}(t_{2})-\mathcal{T}_{i}u_{i}(t_{1})| \rightarrow 0\) as \(t_{2}\rightarrow t_{1}\). Hence \(\mathcal{T}_{i}\) are equicontinuous operators for \(t\geq s\). The case \(t\leq s\) is similar, and thus we omit it. Next, for any \(u\in \{u\in \mathcal{C}([0,k],\mathcal{R}_{e}): u=\hbar \mathcal{T}_{i}(u), \text{ for }\hbar \in [0,1]\}\), we have

$$ \begin{aligned}[b] \Vert u \Vert ={}& \bigl\vert \mathcal{T}_{i}u_{i}(t) \bigr\vert \\ ={}& \Biggl\vert - \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{i}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t) \bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{i}}(s)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{i}(s)\bigr)\,ds \Biggr) \Biggr\vert \\ \leq {}&\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl(\zeta _{i}^{2} \eta _{i}+\wp _{2}\bigr)+\frac{1}{\Gamma (\alpha _{i}+1)} \bigl( \zeta _{i}^{1} \eta _{i}+\wp _{1}\bigr) \biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) m \bigl( \bigl(\zeta _{i}^{2}\eta _{i}+\wp _{2}\bigr)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \bigl( \bigl(\zeta _{i}^{1}\eta _{i}+\wp _{1}\bigr)\bigr)\,ds \biggr) \\ \leq {}& \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl(\zeta _{i}^{2} \eta _{i}+\wp _{2}\bigr)+\frac{1}{\Gamma (\alpha _{i}+1)} \bigl( \zeta _{i}^{1} \eta _{i}+\wp _{1}\bigr) \biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \frac{k^{\varrho _{i}}}{\Gamma (\varrho +1)} m\bigl( \bigl(\zeta _{i}^{2}\eta _{i}+ \wp _{2}\bigr)\bigr)\\ &{} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \frac{k^{\alpha _{i}+\varrho _{i}}}{\Gamma (\varrho +\alpha _{i}+1)}\bigl( \bigl( \zeta _{i}^{1}\eta _{i}+\wp _{1}\bigr)\bigr) \biggr) \\ ={}&\Lambda _{1}+\Lambda _{2} \Vert u \Vert , \end{aligned} $$
(31)

where

$$\begin{aligned} \Lambda _{i}^{1} =& \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \zeta _{i}^{2}+ \frac{1}{\Gamma (\alpha _{i}+1)} \zeta _{i}^{1} \biggr)+\mathcal{B}( \varrho _{i}) \biggl(\frac{1}{\Gamma (\varrho _{i})} \frac{k^{\varrho _{i}}}{\Gamma (\varrho +1)} m \zeta _{i}^{2} \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \frac{k^{\varrho _{i}+\alpha _{i}}}{\Gamma (\varrho +\alpha _{i}+1)} \zeta _{i}^{1} \biggr) \end{aligned}$$
(32)

and

$$\begin{aligned} \Lambda _{i}^{2} =& \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \wp _{2}+\frac{1}{\Gamma (\alpha _{i}+1)} \wp _{1} \biggr)+ \mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \frac{k^{\varrho _{i}}}{\Gamma (\varrho +1)} m\wp _{2} \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \frac{k^{\varrho _{i}+\alpha _{i}}}{\Gamma (\varrho +\alpha _{i}+1)} \wp _{1} \biggr) \end{aligned}$$
(33)

for \(i=1,2,\ldots ,m\). With the help of (31), (32), and (33) we have

$$ \Vert u \Vert \leq \frac{\Lambda _{i}^{1}}{1-\Lambda _{i}^{2}} $$
(34)

for \(i=1,2,\ldots ,m\). Hence the requirement of the Leray–Schauder alternative theorem is ensured, and therefore the system of sequential hybrid FDEs (1) has a solution. □

3 H-U-stability

Here we consider the H-U stability of system (15). The following definition plays a vital role in the stability.

Definition 3.1

The fractional-order integral system (15) is H-U-stable if for some \(\zeta _{i}>0\), there exist \(\Delta _{i}>0\), for each solution \({u_{i}}\) with

$$ \begin{aligned} \Vert {u_{i}}- \mathcal{T}_{i}{u_{i}} \Vert _{1}< \Delta _{i}, \end{aligned} $$
(35)

there are \(\bar{{u_{i}}}(t)\) of the operators system (15) with

$$ \bar{{u_{i}}}(t)=\mathcal{T}_{i} \bar{u}_{i}(t) $$
(36)

such that

$$ \Vert {u_{i}}-\bar{{u_{i}}} \Vert < \Delta _{i} \zeta _{i} $$
(37)

for all \(i=1,2,\ldots ,m\).

Theorem 3.2

With assumptions of Lemma 2.2, the integral system (15) is H-U stable, that is, the sequential hybrid system of FDEs (1) is H-U stable.

Proof

Let \({u_{i}}\in \mathcal{C}\) satisfy inequality (35), and let \(\bar{u_{i}}\in \mathcal{C}\) of system (1) satisfy (15). Also,

$$\begin{aligned} \bigl\vert \mathcal{T}_{i}u_{i}(t)- \mathcal{T}_{i}\bar{u}^{*}(t) \bigr\vert ={}& \Biggl\vert -\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{i}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t) \bigr) \Biggr) \\ &{}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{i}}(s)\bigr)\,ds \\ &{}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{i}(s)\bigr)\,ds \Biggr) \\ &{} - \Biggl[-\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{\bar{u}^{*}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{ \bar{u}^{*}}(t)\bigr) \Biggr) \\ & {}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{ \bar{u}^{*}}(s)\bigr)\,ds \\ & {} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1}\mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,\bar{u}^{*}(s)\bigr)\,ds \Biggr) \Biggr] \Biggr\vert \\ \leq{}& \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl(\zeta _{i}^{2} \bigl\vert u_{i}- \bar{u}^{*} \bigr\vert \bigr)+ \frac{1}{\Gamma (\alpha _{i}+1)} \bigl(\zeta _{i}^{1} \bigl\vert u_{i}- \bar{u}^{*} \bigr\vert \bigr) \biggr) \\ & {}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) m \bigl( \bigl(\zeta _{i}^{2} \bigl\vert u_{i}-\bar{u}^{*} \bigr\vert \bigr)\bigr)\,ds \\ & {}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \bigl( \bigl(\zeta _{i}^{1} \bigl\vert u_{i}-\bar{u}^{*} \bigr\vert \bigr)\bigr)\,ds \biggr) \\ \leq {}& \biggl[\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \zeta _{i}^{2}+ \frac{1}{\Gamma (\alpha _{i}+1)} \zeta _{i}^{1} \biggr) + \mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \frac{2k^{\varrho _{i}}}{\Gamma (\varrho +1)} m\zeta _{i}^{2} \\ & {} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \frac{2k^{\varrho _{i}+\alpha _{i}}}{\Gamma (\varrho +\alpha _{i}+1)} \zeta _{i}^{1} \biggr) \biggr] \bigl\vert u_{i}-\bar{u}^{*} \bigr\vert . \end{aligned}$$
(38)

For \(t\leq s\in [0,k]\), a calculation leads to

$$\begin{aligned}& \begin{aligned}[b]& \bigl\vert \mathcal{T}_{i}u_{i}(t)- \mathcal{T}_{i}\bar{u}^{*}(t) \bigr\vert \\ &\quad = \Biggl\vert -\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{u_{i}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{u_{i}}(t) \bigr) \Biggr) \\ &\qquad {}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{u_{i}}(s)\bigr)\,ds \\ &\qquad {}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,u_{i}(s)\bigr)\,ds \Biggr) \\ &\qquad {} - \Biggl[-\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \Biggl(\sum_{1}^{m} \mathcal{F}_{i}\bigl(t,{\bar{u}^{*}}(t)\bigr)+ \mathcal{I}^{\alpha _{i}} \lambda _{i}\bigl(t,{ \bar{u}^{*}}(t)\bigr) \Biggr) \\ &\qquad {}+\mathcal{B}(\varrho _{i}) \Biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) \sum_{1}^{m} \mathcal{F}_{i} \bigl(s,{ \bar{u}^{*}}(s)\bigr)\,ds \\ &\qquad {}+ \frac{1}{\Gamma (\alpha _{i}+\varrho _{i})} \int _{0}^{1}\mathcal{H}_{i}(t,s) \lambda _{i}\bigl(s,\bar{u}^{*}(s)\bigr)\,ds \Biggr) \Biggr] \Biggr\vert \end{aligned} \end{aligned}$$
(39)
$$\begin{aligned}& \begin{aligned}[b] & \quad \leq \frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \bigl(\zeta _{i}^{2} \bigl\vert u_{i}- \bar{u}^{*} \bigr\vert \bigr)+ \frac{1}{\Gamma (\alpha _{i}+1)} \bigl(\zeta _{i}^{1} \bigl\vert u_{i}- \bar{u}^{*} \bigr\vert \bigr) \biggr) \\ &\qquad {}+\mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \int _{0}^{1}\mathcal{G}_{i}(t,s) m \bigl( \bigl(\zeta _{i}^{2} \bigl\vert u_{i}-\bar{u}^{*} \bigr\vert \bigr)\bigr)\,ds\\ &\qquad {} + \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \int _{0}^{1} \mathcal{H}_{i}(t,s) \bigl( \bigl(\zeta _{i}^{1} \bigl\vert u_{i}-\bar{u}^{*} \bigr\vert \bigr)\bigr)\,ds \biggr) \\ & \quad \leq \biggl[\frac{1-\varrho _{i}}{\mathcal{B}(\varrho _{i})} \biggl(m \zeta _{i}^{2}+ \frac{1}{\Gamma (\alpha _{i}+1)} \zeta _{i}^{1} \biggr) + \mathcal{B}(\varrho _{i}) \biggl( \frac{1}{\Gamma (\varrho _{i})} \frac{k^{\varrho _{i}}}{\Gamma (\varrho +1)} m\zeta _{i}^{2} \\ & \qquad {}+ \frac{1}{\Gamma (\varrho _{i}+\alpha _{i})} \frac{k^{\varrho _{i}+\alpha _{i}}}{\Gamma (\varrho +\alpha _{i}+1)} \zeta _{i}^{1} \biggr) \biggr] \bigl\vert u_{i}-\bar{u}^{*} \bigr\vert \\ &\quad \leq \eta _{i} \bigl\vert u_{i}- \bar{u}^{*} \bigr\vert \end{aligned} \end{aligned}$$
(40)

Let \(\eta _{i}<1\), where \(\eta _{i}\) are defined in (18) for \(i=1,2,\ldots ,m\). With the help of (35), (36), (38), and (40) consider the norm

$$\begin{aligned} \bigl\Vert u_{i}-\bar{u}^{*}_{i} \bigr\Vert =& \bigl\Vert u_{i}-\mathcal{T}_{i}u_{i}+ \mathcal{T}_{i}u_{i}- \bar{u}^{*}_{i} \bigr\Vert \\ \leq & \Vert u_{i}-\mathcal{T}_{i}u_{i} \Vert + \bigl\Vert \mathcal{T}_{i}u_{i}- \mathcal{T}_{i}\bar{u}^{*}_{i} \bigr\Vert \\ \leq &\Delta _{i}+\eta _{i} \bigl\Vert u_{i}-\bar{u}^{*}_{i} \bigr\Vert \end{aligned}$$
(41)

for \(i=1,2,\ldots ,m\). This further implies that

$$\begin{aligned} \bigl\Vert u_{i}-\bar{u}^{*}_{i} \bigr\Vert \leq &\frac{\Delta _{i}}{1-\eta _{i}} \end{aligned}$$
(42)

with \(\zeta _{i}=\frac{1}{1-\eta _{i}}\). Therefore system (15) is H-U stable. This ultimately ensures the stability of the sequential hybrid system of FDEs (1). □

4 Application

Here we present an application of problem (1) and provide its numerical simulations. The following system of four equations is a generalization of the smoking model with relapse effect from quit smokers to the potential smoker [59]. Here \(\mathcal{P}\) is a potential smoker, \(\mathcal{L}\) is a slight smoker, \(\mathcal{S}\) is a smoker, and \(\mathcal{Q}\) is quit smokers. We have

$$\begin{aligned} \begin{gathered} {}^{ABC}\mathcal{D}^{\varrho _{1}}_{0} \mathcal{P}=\Lambda ^{*}+ \varrho \mathcal{Q}-2 \frac{\beta ^{*}\mathcal{P}\mathcal{L}}{\mathcal{P}+\mathcal{L}}-( \mu +d)\mathcal{P}, \\ {}^{ABC}\mathcal{D}^{\varrho _{2}}_{0}\mathcal{L}=2 \frac{\beta ^{*}\mathcal{P}\mathcal{L}}{\mathcal{P}+\mathcal{L}}-( \xi +\mu +d)\mathcal{L}, \\ {}^{ABC}\mathcal{D}^{\varrho _{3}}_{0}\mathcal{S}= \xi \mathcal{L} -( \xi +\mu +\delta )\mathcal{S}, \\ {}^{ABC}\mathcal{D}^{\varrho _{4}}_{0}\mathcal{Q}= \delta \mathcal{S} -( \xi +\mu +\gamma )\mathcal{Q}. \end{gathered} \end{aligned}$$
(43)

Here \(\varrho _{i}\in (0,1]\), \(i=1,2,\ldots ,6\), \((u_{1},u_{2},u_{3},u_{4})=(\mathcal{P},\mathcal{L}_{1},\mathcal{S}_{2}, \mathcal{Q})\), \(\mathcal{G}_{1}(t,\mathcal{P})=\Lambda ^{*}+\varrho \mathcal{Q}-2 \frac{\beta ^{*}\mathcal{P}\mathcal{L}}{\mathcal{P}+\mathcal{L}}-( \mu +d)\mathcal{P}\), \(\mathcal{G}_{2}(t,\mathcal{L})=2 \frac{\beta ^{*}\mathcal{P}\mathcal{L}}{\mathcal{P}+\mathcal{L}}-( \xi +\mu +d)\mathcal{L}\), \(\mathcal{G}_{3}(t,\mathcal{S})=\xi \mathcal{L} -(\xi +\mu +\delta ) \mathcal{S}\), and \(\mathcal{G}_{4}(t,\mathcal{Q})= \delta \mathcal{S} -(\xi +\mu + \gamma )\mathcal{Q}\).

4.1 Numerical scheme

Let us consider

$$ {}^{ABC}{}_{0}D^{\varrho _{1},\varrho _{2}}_{t} \mathcal{P}(t)= \mathcal{H}\bigl(t, \mathcal{P}(t)\bigr),$$

where \(\mathcal{P}(0)=\mathcal{P}_{0}\). Applying the AB fractional integral, we get

$$ \mathcal{P}(t)=\mathcal{P}(0)+\frac{1-\varrho _{1}}{AB(\varrho _{1})} \mathcal{H}\bigl(t, \mathcal{P}(t)\bigr)+ \frac{\varrho _{1}}{AB(\varrho _{1})\Gamma \varrho _{1}} \int _{0}^{t} \zeta ^{\varrho _{2}-1}(t-\zeta )^{\varrho _{1}-1}\mathcal{H}\bigl(\zeta , \mathcal{P}(\zeta )\bigr)\,d\zeta .$$

Replacing \((t)\) by \(t_{n+1}\), we have

$$\begin{aligned} \mathcal{P}_{n+1} =&\mathcal{P}(0)+ \frac{1-\varrho _{1}}{AB(\varrho _{1})}\mathcal{H}\bigl(t_{n}, \mathcal{P}(t_{n}) \bigr)\\ &{}+ \frac{\varrho _{1}}{AB(\varrho _{1})\Gamma \varrho _{1}} \int _{0}^{t_{n+1}} \zeta ^{\varrho _{2}-1}(t_{n+1}- \zeta )^{\varrho _{1}-1}\mathcal{H}\bigl( \zeta , \mathcal{P}(\zeta )\bigr)\,d\zeta \end{aligned}$$

and

$$\begin{aligned} H\bigl(t, \mathcal{P}(t)\bigr) =& \frac{H(t_{k}, \mathcal{P}(t_{k})(y-t_{k-1})}{t_{k}-t_{k-1}}- \frac{H(t_{k-1}, \mathcal{P}(t_{k-1}))(y-t_{k})}{t_{k}-t_{k-1}} \\ =&\frac{H(t_{k}, \mathcal{P}_{k})(y-t_{k-1})}{h}- \frac{H(t_{k-1}, \mathcal{P}_{k-1})(y-t_{k})}{h}. \end{aligned}$$

By applying the Lagrange polynomial we further have

$$\begin{aligned} \mathcal{P}_{n+1} =&\mathcal{P}(0)+ \frac{1-\varrho _{1}}{AB(\varrho _{1})}\mathcal{H} \bigl(t_{n}, \mathcal{P}(t_{n})\bigr) \\ &{}+ \frac{\varrho _{1}}{AB(\varrho _{1})\Gamma \varrho _{1}}\sum_{i=1}^{n} \biggl[\frac{\mathcal{H}(t_{i}, \mathcal{P}(t_{i}))}{h} \int _{t_{k}}^{t_{k+1}} (\zeta -t_{i-1}) (t_{n+1}-\zeta )^{\varrho _{1}-1}\,d\zeta \\ &{}-\frac{\mathcal{H}(t_{i-1}, \mathcal{P}(t_{i-1}))}{h} \int _{t_{k}}^{t_{n+1}} (\zeta -t_{i}) (t_{n+1}-\zeta )^{\varrho _{1}-1}\,d\zeta \biggr]. \end{aligned}$$

Now solving the integrals, we get

$$\begin{aligned} \mathcal{P}_{n+1} =&\mathcal{P}(0)+ \frac{1-\varrho _{1}}{AB(\varrho _{1})}\mathcal{H} \bigl(t_{n}, \mathcal{P}(t_{n})\bigr) \\ &{}+\frac{\varrho _{1} h^{\varrho _{1}}}{\Gamma (\varrho _{1}+2)} \sum_{i=1}^{n} \bigl[{\mathcal{H}\bigl(t_{i}, \mathcal{P}(t_{i}) \bigr)} \bigl((n-i+1)^{ \varrho _{1}}(n+2-i+\varrho _{1})\\ &{}-(n-i)^{\varrho _{1}}(n+2-i+2 \varrho _{1}) \bigr) \\ &{}-\mathcal{H}(t_{i-1}, \mathcal{P}_{i-1}) \bigl((n-i+1)^{\varrho _{1}+1}-(n-i+1+ \varrho _{1}) (n-i)^{\varrho _{1}} \bigr) \bigr]. \end{aligned}$$

Replacing the value of \(\mathcal{H}(t, \mathcal{P}(t))\) by the functions, we obtain the following numerical scheme:

$$\begin{aligned}& \begin{aligned} \mathbb{P}_{n+1}={}&\mathbb{P}(0)+\varrho _{2} t^{\varrho _{2}-1} \frac{1-\varrho _{1}}{AB(\varrho _{1})}{\mathcal{G}_{1}} \bigl(t_{n}, \mathbb{P}(t_{n})\bigr)+\varrho _{2} t^{\varrho _{2}-1} \frac{\varrho _{2} h^{\varrho _{1}}}{\Gamma (\varrho _{1}+2)} \\ &{}\times \sum_{i=1}^{n} \bigl[{{ \mathcal{G}_{1}}\bigl(t_{i}, \mathbb{P}(t_{i}) \bigr)} \bigl((n-i+1)^{\varrho _{1}}(\varrho _{1}+n+2-i)-(n-i)^{\varrho _{1}}(-i+2 \varrho _{1}+n+2) \bigr) \\ &{}-{\mathcal{G}_{1}}(t_{i-1}, \mathbb{P}_{i-1}) \bigl((n+1-i)^{ \varrho _{1}+1}-(n+\varrho _{1}-i+1) (n-i)^{\varrho _{1}} \bigr) \bigr], \end{aligned} \\& \begin{aligned} \mathbb{L}_{n+1}={}&\mathbb{L}(0)+\varrho _{2} t^{\varrho _{2}-1} \frac{1-\varrho _{1}}{AB(\varrho _{1})}{\mathcal{G}_{2}}(t_{n}, \mathbb{L}_{n})+\varrho _{2} t^{\varrho _{2}-1} \frac{\varrho _{2} h^{\varrho _{1}}}{\Gamma (\varrho _{1}+2)} \\ &{}\times \sum_{i=1}^{n} \bigl[{{ \mathcal{G}_{2}}(t_{i}, \mathbb{L}_{i})} \bigl((n-i+1)^{\varrho _{1}}(n+2-i+\varrho _{1})-(n-i)^{\varrho _{1}}(n+2 \varrho _{1}+2-i) \bigr) \\ &{}-{\mathcal{G}_{2}}(t_{i-1}, \mathbb{L}_{i-1}) \bigl((-i+n+1)^{ \varrho _{1}+1}-(n-i+\varrho _{1}+1) (n-i)^{\varrho _{1}} \bigr) \bigr], \end{aligned} \\& \begin{aligned} \mathbb{S}_{n+1}={}&\mathbb{S}(0)+\varrho _{2} t^{\varrho _{2}-1} \frac{1-\varrho _{1}}{AB(\varrho _{1})}{\mathcal{G}_{3}}(t_{n}, \mathbb{S}_{n})+\varrho _{2} t^{\varrho _{2}-1} \frac{\varrho _{2} h^{\varrho _{1}}}{\Gamma (\varrho _{1}+2)} \\ &{}\times \sum_{i=1}^{n} \bigl[{{ \mathcal{G}_{3}}(t_{i}, \mathbb{S}_{i})} \bigl((n-i+1)^{\varrho _{1}}(n+\varrho _{1}+2-i)-(n-i)^{\varrho _{1}}(n+2 \varrho _{1}+2-i) \bigr) \\ &{}-{\mathcal{G}_{3}}(t_{i-1}, \mathbb{S}_{i-1}) \bigl((n-i+1)^{1+ \varrho _{1}}-(n-i+1+\varrho _{1}) (n-i)^{\varrho _{1}} \bigr) \bigr], \end{aligned} \\& \begin{aligned} \mathbb{Q}_{n+1}={}&\mathbb{Q}(0)+\varrho _{2} t^{\varrho _{2}-1} \frac{1-\varrho _{1}}{AB(\varrho _{1})}{\mathcal{G}_{4}}(t_{n}, \mathbb{Q}_{n})+\varrho _{2} t^{\varrho _{2}-1} \frac{\varrho _{2} h^{\varrho _{1}}}{\Gamma (\varrho _{1}+2)} \\ &{}\times \sum_{i=1}^{n} \bigl[{{ \mathcal{G}_{4}}(t_{i}, \mathbb{Q}_{i})} \bigl((n-i+1)^{\varrho _{1}}(n+2-i+\varrho _{1})-(n-i)^{\varrho _{1}}(n+2-i+2 \varrho _{1}) \bigr) \\ &{}-{\mathcal{G}_{4}}(t_{i-1}, \mathbb{Q}_{i-1}) \bigl((n+1-i)^{ \varrho _{1}+1}-(n+\varrho _{1}-i+1) (n-i)^{\varrho _{1}} \bigr) \bigr], \end{aligned} \end{aligned}$$

Here the numerical scheme is applied to a particular case with the initial values \(\mathcal{P}(0)=100\), \(\mathcal{L}=30\), \(\mathcal{S}=10\), \(\mathcal{Q}=20\). \(A=10.25\), \(\beta =0.038\), \(\delta =0.000274\), \(\mu =0.0111\), \(d=0.0019\), \(\xi =0.021\), and \(\gamma =0.006\).

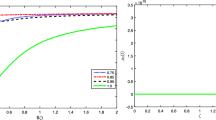
In Fig. 1, we present a graphical representation of the simulation of the potential smokers \(\mathcal{P}(t)\) in (43) for the fractional orders 1.0, 0.99, 0.98, 0.97. They increase up to 100 days and then decrease to a certain value. Comparing the results of fractional orders with integer orders, we see that the fractional-order results get closer to the classical results on values of the fractional orders closer to 1. Figures 2 and 3 show the computational results for the light \(\mathcal{L}\) and smokers \(\mathcal{S}\).

Figure 1
figure 1

Potential smokers \(\mathcal{P}(t)\) for orders 1.0, 0.99, 0.98, 0.97

Full size image
Figure 2
figure 2

Light smokers for the orders 1.0, 0.99, 0.98, 0.97

Full size image
Figure 3
figure 3

Smokers \(\mathcal{S}\) for the orders 1.0, 0.99, 0.98, 0.97

Full size image

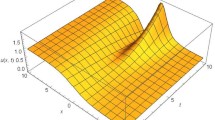
In Fig. 4, a comparative analysis is given for the numerical simulations of the \(\mathcal{Q}\) class of the smoking model (43). The final Fig. 5 shows a join solution of the model for order 1.

Figure 4
figure 4

Quit smokers \(S(t)\) for orders 1.0, 0.99, 0.98, 0.97

Full size image
Figure 5
figure 5

Joint solution for the model at 1.0

Full size image

5 Conclusions

We considered a general class of fractional-order differential equations (FDEs). This area is still open for consideration of the sequential fractional differential equations, hybrid FDEs, mixed fractional functional equations, and many more. The hybrid FDEs consist of two subclasses called the linear and quadratic differential equations. In this paper, we aimed to present a system of hybrid sequential FDEs with two different fractional operators, the Caputo and Atangana–Baleanu operators. We studied the existence and uniqueness of a solution. We have observed that some essential conditions are required for the existence of a solution of the fractional-order hybrid problem (1). There are two basic reasons for the importance. We have studied in the literature that the sequential hybrid class of FDS have not been considered for the presumed class for the existence of solution and stability analysis. Among them, one is a combination of the fractional derivative operators (the Caputo fractional differential operator and the Atangana–Baleanu fractional operator), whereas the second importance of the problem is the coupling of n FDEs with complex boundary conditions. This can further motivate the readers to the combination of other operators and make more research problems for the initial and boundary conditions. The problem is converted into its equivalent integral form using Green’s functions. Then the H-U stability is illustrated. Mathematical modeling of dynamical systems and their numerical simulations are considered as an application of the work. This aspect of the paper consists of a fractional-order smoking model studied for the numerical analysis. The numerical results are illustrated by some graphics based on our numerical scheme for model (43).