Abstract
In the current study, we conduct an investigation into the Hyers–Ulam stability of linear fractional differential equation using the Riemann–Liouville derivatives based on fractional Fourier transform. In addition, some new results on stability conditions with respect to delay differential equation of fractional order are obtained. We establish the Hyers–Ulam–Rassias stability results as well as examine their existence and uniqueness of solutions pertaining to nonlinear problems. We provide examples that indicate the usefulness of the results presented.
Similar content being viewed by others
1 Introduction
In recent years, the area related to fractional differential and integral equations has received much attention from numerous mathematicians and specialists. The derivatives of fractional order portray physical models of multiple phenomena in different fields such as biology, physics, mechanics, dynamical systems, and so on (see [1–8] and the references therein).
The possibility of fractional calculus was presented in 1695, when the notation \(\frac{d^{\nu }}{dt^{\nu }}h(x)\) was introduced to indicate the νth order derivative of function \(h(x)\). Specifically, Leibniz composed a letter to L’Hospital in which he posed an enquiry on the derivative of order \(\nu = \frac{1}{2}\), which led to the establishment of fractional calculus. Later on, fractional derivative was presented by Lacroix [9]. Perhaps the most utilized fractional derivatives are Riemann–Liouville (R–L) and Caputo derivatives, which assume an immodest role in fractional order differential equation(FRDE).
One of the best examination regions in FRDE, which receives vast considerations by analysts, entails the existence theory of solution. This is a rapidly moving topic of investigation. For details with respect to the present hypothesis, see [10–15]. Finding an exact solution of FRDE is exceptionally troublesome, and the type of exact solution is regularly so complicated that it is not convenient for numerical computation. Considering this, it is important to study an approximate solution with a relatively simple form and examine how close both the approximate and exact solutions are. By and large, we state that a FRDE is said to be Hyers–Ulam (H–U) stable if, for every solution of the FRDE, there exists an approximate solution of the concerned equation that is close to it.
Ulam [16] formulated the stability of a functional equation, which was solved by Hyers [17] using an additive function defined on the Banach space. This result led Rassias [18] to study and generalize the stability concept, establishing the Hyers–Ulam–Rassias stability. An integral transform (introduced by Fourier) involves a trigonometric form of the Mittag-Leffler function to identify an analytic solution with respect to a differential equation of fractional order. The Fourier transforms, Mittag-Leffler function, and fractional trigonometric function constitute an effective tool for analytic expression pertaining to the solution of differential equation of noninteger order. Indeed, the Fourier transform has become popular in view of recent developments in differential applications. It is also seen as the easiest and most effective way among many other transforms. Luchko [19] defined the fractional Fourier transform (FRFT) of real order ν, \(0< \nu \le 1\), and discussed its important properties. The application of FRFT for undertaking certain types of differential equations of fractional order has also been conducted. Indeed, there are many studies on FRFT and its applications in the literature [20–23].
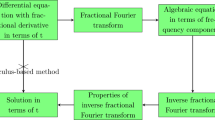
In 2017, Wang et al. [24] discussed the stability of fractional differential equation based on the right-sided Riemann–Liouville fractional derivatives with respect to a continuous function space. The fixed point theorem and weighted space method were exploited. In [25], a study on the H–U stability condition was conducted, focusing on an impulsive R-L fractional neutral functional stochastic differential equation with time delays. In [26], the stability criteria pertaining to a class of fractional differential equations was investigated, in which the Krasnoselskii fixed point method was employed. Recently, Opadhyay et al. [27] discussed the R–L fractional differential equations using the Hankel transform method. At present, some remarkable results to the stability of fractional differential equation have been reported (see [28–31] and the references therein). In [32, 33], the author studied the H–U stability of linear differential equation by using Fourier transform. To the best of our knowledge, there are no results on H–U stability of fractional differential equation by fractional Fourier transform (FRFT). The flow chart of fractional fourier transform is represented in Fig. 1.
Motivated by the ongoing research in this field, we examine the H–U stability and generalized H–U stability of FRDE in this study, i.e.,
and the delay differential equation of fractional order
where \(\mathcal{D}_{\vartheta }^{\nu }\) represents R–L fractional derivative, \(\xi >0\), \(\vartheta \in \mathbb{R}\), and \(0< \nu \le 1\) with the help of FRFT. In our investigation, we exploit the fractional Fourier transform and present it in an integral form. Furthermore, using the convolution concept and properties of fractional Fourier transform, the solution pertaining to the stability conditions with respect to FRDE is established. Specifically, we analyze Hyers–Ulam–Rassias stability of the nonlinear FRDE
and use the fixed point theorems for examining the existence and uniqueness of the solution.
We organize this article as follows. The related fundamental properties, lemmas, and definitions are presented in Sect. 2. In Sect. 3, H–U and generalized H–U stability of FRDE and delay FRDE are explained. Numerical examples and conclusion are given in Sects. 4 and 5, respectively.
2 Fundamentals
Consider \(L^{1}(\mathbb{R})\) as the space pertaining to the complex-valued Lebesgue integrable function on the real line \(\mathbb{R}\) with norm
The definition of a Fourier transform with respect to a function \(h \in L^{1}(\mathbb{R})\) is
The form of the associated inverse Fourier transform is
Note that Fourier transform is useful for conversion of a function between the time and frequency domains. It adopts the principle of rotation operation on the time-frequency distribution. Given parameter ν, we can express the fractional Fourier transform of function \(h(x)\) in a one-dimensional case as follows [34]:
where kernel \(K_{\nu }(x,\omega )\) is
and n is an integer, while
As such, the form of the associated inverse fractional Fourier transform is
where
Definition 2.1
([35])
The Mittag-Leffler function in fractional order ν with respect to one parameter is denoted by \(E_{\nu }(x^{\nu })\), which is defined as
Definition 2.2
The fractional trigonometric function is denoted by
with \(\cos x^{\nu }= \sum_{K=0}^{\infty } (-1)^{k} \frac{x^{2\nu k}}{\Gamma {(1+2\nu k)}} \) and \(\sin x^{\nu }= \sum_{K=0}^{\infty } (-1)^{k} \frac{x^{(2k+1)\nu }}{\Gamma {(1+\nu (2k+1))}}\).
Luchko et al. [36] introduced a new fractional Fourier transform \(\mathcal{F}_{\nu }\) of order ν, (\(0< \nu \leq 1\)), and its definition is
where
As such, the definition of the associated inverse fractional Fourier transform is
for any \(x \in \mathbb{R}\) and \(\nu >0\). If \(\nu = 1\), then \(\widehat{\mathcal{H}}_{\nu }(\omega )\) and the classical Fourier transform (2.1) are the same. Suppose that the space of a function with rapid decrease is denoted as \(\mathcal{S}\). In other words, the following relation with respect to the space of infinity differentiable functions \(v(x)\) on \(\mathbb{R}\) is satisfied:
Given \(x \in \mathbb{R}\) and \(n,k \in \mathbb{N} \cup \{ 0 \} \). If \(v(x) \in \mathcal{S}\), then
Based on \(V(\mathbb{R})\), the following relation with respect to a set of functions \(v \in \mathcal{S}\) is satisfied:
The Lizorkin space is \(\Phi ( \mathbb{R}) \subset L^{1}(\mathbb{R})\), and it is defined as the Fourier pre-image of the space \(V(\mathbb{R})\) in the space \(\mathcal{S}\), i.e.,
The reason for using the Lizorkin space is its convenience in using the Fourier transform as well as the inverse Fourier transform with fractional integration and differentiation operators. The properties and associated details of the Lizorkin space have been discussed in many studies (see [37–39]). In our study, we use \(\mathbb{F}\) to represent the domain of either real \(\mathbb{R}\) or complex \(\mathbb{C}\). According to the definition of Lizorkin space, the orthogonality condition is satisfied by any function \(h \in \Phi (\mathbb{R})\), i.e.,
Note that the property of invariance pertaining to the Fourier transform and its inverse holds for the space \(\Phi (\mathbb{R})\). In other words, both transforms are inverse of one another, i.e.,
Definition 2.3
Given a function \(h \in \Phi (\mathbb{R})\) of order ν, where \(0< \nu \leq 1\), the definition of its fractional Fourier transform is
The inverse fractional Fourier transform for function \(h \in \Phi (\mathbb{R})\) is
for any \(x \in \mathbb{R}\) and \(\nu >0\).
Definition 2.4
The function \((h_{1}*h_{2})(x) = \int _{\mathbb{R}}h_{1}(x-\tau )h_{2}(\tau )\,d\tau \) is denoted as the convolution of both functions of \(h_{1}\) and \(h_{2}\) defined on \(\Phi (\mathbb{R})\).
Some properties of FRFT that are closely related to the solution in this study are given as follows. Let h, \(h_{1}\), and \(h_{2}\) be functions belonging to \(\Phi (\mathbb{R})\). Then
-
(1)
If \((\mathcal{F}_{\nu }h_{1} )(\omega ) = (\mathcal{F}_{ \nu }h_{2} )(\omega )\), then \(h_{1}(x) = h_{2}(x)\);
-
(2)
\(F (\mathcal{F}_{\nu }h(x-\xi ) )(\omega ) = e_{\nu }( \omega ,\xi )\widetilde{\mathcal{H}}(\omega )\);
-
(3)
\(\mathcal{F}_{\nu } ( h_{1} * h_{2} )(\omega ) = \mathcal{F}_{\nu } ( h_{1})(\omega ) ) \mathcal{F}_{\nu } ( h_{2} )(\omega )\);
-
(4)
\(\mathcal{F}_{\nu }^{-1} ( h_{1} h_{2} )(x) = \mathcal{F}_{\nu }^{-1} ( h_{1})(x) ) *\mathcal{F}_{\nu }^{-1} ( h_{2} )(x)\).
Definition 2.5
([40])
The definition of R–L fractional integral of order \(\nu > 0\) is
and
where \(\operatorname{Re}(\nu )>0\), we have \(\Gamma {\nu }= \int _{0}^{\infty } e^{-u}u^{\nu -1}\,du\).
Definition 2.6
([40])
The definition of R–L fractional derivative of order \(\nu > 0\) is
Lemma 2.1
([39])
Based on the integration by parts formula, the R–L derivative holds for any \(h,k \in \Phi (\mathbb{R})\):
Our current study considers the definition with respect to a fractional derivative operator \(\mathcal{D}_{\vartheta }^{\nu }\) of \(h \in \Phi (\mathbb{R})\), i.e.,
where \(\mathcal{D}_{-}^{\nu }\) and \(\mathcal{D}_{+}^{\nu }\) denote the left-hand and right-hand R–L fractional derivatives of order ν, in which \(0<\nu <1\).
Lemma 2.2
A function that is continuously differentiable is denoted as \(h \in \Phi (\mathbb{R})\), \(\omega \in \mathbb{R}/ \{ 0 \} \), and \(0<\nu \le 1\), and it is able to satisfy
Proof
By taking into account of the R–L fractional integral (2.7), we get
Using the variables substitution \(\eta = x-t\), we obtain
Both the integrals in the above equation can be evaluated by using the integral formula in [41]:
Substituting equation (2.15) and (2.16) in equation (2.14), we get
By the definition of R–L fractional derivative and equation (2.17), we have
Hence, the proof is completed. □
Similarly, the following lemma is formulated.
Lemma 2.3
Suppose \(\omega \in \mathbb{R}/ \{ 0 \} \) and \(0 < \nu \le 1\). As such,
Theorem 2.1
Consider a function h in the Lizorkin space \(\Phi (\mathbb{R})\), and assume \(0<\alpha \le 1\), the operational relation as follows is true:
where \(\mathcal{A}_{\nu }(\omega )\) is given by
Proof
We first get the relation
for any function h that belongs to the Lizorkin space \(\Phi (\mathbb{R})\). For \(\omega \neq 0\), the formulas (2.9), (2.12), and (2.18) are applied, and we have the following chain of equalities:
where \(\mathcal{A}_{\nu }(\omega ) = (1-2\vartheta )\cos (\nu \pi /2)-i\operatorname{sign}( \omega )\sin (\nu \pi /2) \). □
Remark 2.1
Let us take \(\mathcal{A}_{\nu _{1}}(\omega )= (1-2\vartheta )\cos (\nu \pi /2)+i \sin (\nu \pi /2) \) for \(\omega < 0\) and \(\mathcal{A}_{\nu _{2}}(\omega ) = (1-2\vartheta )\cos (\nu \pi /2)-i\operatorname{sin}( \nu \pi /2) \) for \(\omega \ge 0\).
Theorem 2.2
(Arzela–Ascoli’s theorem)
-
(1)
A family \(\mathcal{B}\) of continuous functions on \(\mathbb{I}=[a,b]\) is a uniformly bounded set if there exists \(\lambda >0\) with
$$ \Vert h \Vert = \sup \bigl\vert h(x) \bigr\vert < \lambda ,\quad \forall h \in \mathcal{B}. $$ -
(2)
\(\mathcal{B}\) is an equicontinuous set, i.e., for any \(\epsilon >0\), there exists \(\delta > 0\) such that
$$ \vert x_{1} - x_{2} \vert \le \delta \quad \Rightarrow\quad \bigl\vert h(x_{1}) - h(x_{2}) \bigr\vert \le \epsilon , \quad \forall h \in \mathcal{B}. $$
Let \(\{ h_{n} \} _{n \in N}\) be a family of continuous functions on \(\mathbb{I}=[a,b]\). If the sequence is uniformly bounded and equicontinuous, then there exists a subsequence \(\{ h_{n_{1}}(x) \} _{n_{1} \in N}\) that converges uniformly.
Theorem 2.3
(Banach fixed point theorem)
Let \(\mathcal{B}\) be a nonempty closed subset of a Banach space ψ. Then any contraction mapping Δ from ψ into itself has a unique fixed point.
Theorem 2.4
(Schaefer’s fixed point theorem)
A Banach space is denoted by ψ. Suppose that the mapping \(\Delta : \psi \rightarrow \psi \) is completely continuous. Moreover, suppose that
is a bounded set. Then Δ has at least one fixed point on ψ.
Definition 2.7
The fractional differential equation
is said to be H–U stable if the inequality \(\vert (\mathcal{D}_{\vartheta }^{\nu }h)(x) - \mathcal{G}(x) \vert \le \epsilon \) is satisfied by a continuously differentiable mapping \(h: \mathbb{R} \rightarrow \mathbb{F}\), and there exists a solution \(h_{\nu }: \mathbb{R} \rightarrow \mathbb{F}\) of differential equation (2.20) with
where \(\epsilon > 0\) and \(K>0\) is the H–U stability constant.
Definition 2.8
The fractional differential equation with delay
is H–U stable if the inequality \(\vert (\mathcal{D}_{\vartheta }^{\nu }h)(x-\xi ) - \mathcal{G}(x) \vert \le \epsilon \) is satisfied by a continuously differentiable mapping \(h:\mathbb{R} \rightarrow \mathbb{F}\), and there exists a solution \(h_{\nu }: \mathbb{R} \rightarrow \mathbb{F}\) of differential equation (2.21) with
where \(\epsilon > 0\) and \(K>0\) is the Hyers–Ulam stability (HUS) constant.
Remark 2.2
If ϵ and Kϵ are replaced with continuous functions \(\beta (x)\) and \(\Omega (x)\) in the above definition, then equation (2.20) and equation (2.21) are generalized H–U or H–U–Rassias stable.
3 Stability results of linear FRDE
Based on the fractional Fourier transform, we derive the results with respect to the H–U stability of FRDE
in the following theorem.
Theorem 3.1
Given \(\Phi (\mathbb{R})\), a real continuous function is denoted by \(\mathcal{G}(x)\), and assume \(0 < \alpha \le 1\). If a function \(h:\mathbb{R}\rightarrow \mathbb{F}\) is able to satisfy the following:
for all \(x \in \mathbb{R}\) and for some \(\epsilon > 0\), then, with respect to fractional differential equation (3.1), a solution \(h_{\nu }:\mathbb{R} \rightarrow \mathbb{F}\) exists in which
Proof
Suppose that the definition of function \(\mathcal{Y}_{1}: \mathbb{R} \rightarrow \mathbb{F}\) is
Suppose that \(h(x)\) is a continuously differentiable function satisfying inequality (3.2). We have
for each \(\epsilon > 0\). Now, taking \(\mathcal{F}_{\nu }\) (the fractional Fourier transform operator) with respect to equation (3.3) on both sides as well as using equation (2.19), we have
Set
where \(\mathcal{A}_{1}=\frac{-i}{\mathcal{A}_{\nu _{1}}} + \frac{i}{\mathcal{A}_{\nu _{2}}}\) and \(\mathcal{A}_{2}=\frac{i}{\mathcal{A}_{\nu _{1}}} + \frac{i}{\mathcal{A}_{\nu _{2}}}\).
By the definition of convolution, we obtain
By equation (2.19) and equation (3.6) and simple computation, we obtain
Since \(\mathcal{F}_{\nu }\) is one-to-one, it follows that \((\mathcal{D}_{\vartheta }^{\nu }h_{\nu })(x) = \mathcal{G}(x)\), so \(h_{\nu }(x)\) is a solution of equation (3.1). Consequently, from equation (3.4) and equation (3.6), we obtain
Now, taking modulus with respect to equation (3.7) on both sides gives
(where \(C= \vert \frac{1}{\mathcal{A}_{\nu _{1}}}E_{\nu }(i\operatorname{sign}(x-\tau )(\nu \pi /2))+ \frac{1}{\mathcal{A}_{\nu _{2}}} E_{\nu }(-i\operatorname{sign}(x-\tau )( \nu \pi /2)) \vert \in \mathbb{R}\))
where \(K=C\int _{\mathbb{R}} \vert x-\tau \vert ^{\nu -1}\,d\tau \). Hence, FRDE (3.1) is H–U stable. □
Similarly, we can prove that FRDE (3.1) is H–U–Rassias stable with the help of FRFT.
Corollary 3.1
Given \(\Phi (\mathbb{R})\), a real continuous function is \(\mathcal{G}(x)\), and suppose \(0 < \nu \le 1\), the following inequality is satisfied subject to the existence of a continuous function \(\phi (x)\) whereby \(h:\mathbb{R} \rightarrow \mathbb{F}\) is a continuously differentiable function
for all \(x \in \mathbb{R}\). As such, a solution \(h_{\nu }:\mathcal{R} \rightarrow \mathcal{F}\) of fractional differential equation (3.1) exists whereby
where \(\Omega (x) =C \beta (x)\int _{\mathbb{R}} \vert x-\tau \vert ^{ \nu -1}\,d\tau \) for any \(x \in \mathbb{R}\).
Theorem 3.2
Consider the delay FRDE
where \(\mathcal{G}(x) \in \Phi (\mathbb{R})\), then a constant K having the following property exists, i.e., for every \(h\in \Phi (\mathbb{R})\) and given \(\epsilon >0\) satisfying
\(0 < \nu \le 1\), then there exists a solution \(h_{\nu } \in \Phi (\mathbb{R})\) of equation (3.8) such that
Proof
Let \(h \in \Phi (\mathbb{R})\) satisfy inequality (3.9) and define
for each \(x \in \mathbb{R}\). We have
By taking into account the formula and the property of FRFT and from equation (3.12), we can derive
Set
where \(\mathcal{A}_{1}=\frac{-i}{\mathcal{A}_{\nu _{1}}} + \frac{i}{\mathcal{A}_{\nu _{2}}}\) and \(\mathcal{A}_{2}=\frac{i}{\mathcal{A}_{\nu _{1}}} + \frac{i}{\mathcal{A}_{\nu _{2}}}\).
Applying the formula of convolution, we obtain
By equation (3.12) and simple computation, we obtain
Since \(\mathcal{F}_{\nu }\) is one-to-one, it follows that \((\mathcal{D}_{\vartheta }^{\nu }h_{\nu })(x-\xi ) = g(x)\). So, \(h_{\nu }(x)\) is a solution of equation (3.8).
From equation (3.11) and equation (3.12), we obtain
Now, taking modulus with respect to equation (3.13) on both sides gives
where \(K=C\int _{\mathbb{R}} \vert x+\xi -\tau \vert ^{\nu -1}\,d\tau \) for any value of x and \(\xi >0\). Consequently, the fractional differential equation with delay equation (3.8) is H–U stable. □
Similarly, we can prove that FRDE (3.8) is generalized H–U stable with the help of FRFT.
Corollary 3.2
For every function \(h\in \Phi (\mathbb{R})\) satisfying
\(0 < \alpha \le 1\) and \(\mathcal{G}(x)\) is a continuous function on \(\Phi (\mathbb{R})\), there exists a solution \(h_{\nu } \in \Phi (\mathbb{R}) \) of equation (3.8) whereby
4 Existence and stability results of nonlinear FRDE
The current section is concerned with establishing the existence and H–U–Rassias stability to the nonlinear FRDE
- \([\mathcal{D}_{1}]\):
-
\(\mathcal{G}:[-X,X] \times \mathbb{R} \rightarrow \mathbb{F}\) is continuous;
- \([\mathcal{D}_{2}]\):
-
For \(x \in [-X,X]\), constant \(0 < \mathbb{L} < 1\) exists whereby
$$ \bigl\vert \mathcal{G}(x, h_{1})-\mathcal{G}(x, h_{2}) \bigr\vert \le \mathbb{L} \vert h_{1}- h_{2} \vert , \quad \forall h_{1}, h_{2} \in \mathbb{R}; $$ - \([\mathcal{D}_{3}]\):
-
There exists a constant \(\mathbb{L}_{h}> 0\) whereby
$$ \bigl\vert \mathcal{G}(x, h) \bigr\vert \le \mathbb{L}_{h} \bigl(1+ \vert h \vert \bigr), \quad \forall h \in \mathbb{R}. $$
Denote \(\psi = \mathcal{C}(\mathbb{R}, \mathbb{F})\) as the Banach space which contains all continuous functions from \(\mathbb{R}\) in \(\mathbb{F}\) and its norm is
Theorem 4.1
Consider that hypotheses \([\mathcal{D}_{1}]\) and \([\mathcal{D}_{2}]\) are valid. As such, if \(\mathbb{L}C\frac{(2X)^{\nu }\Gamma {(1-\nu )}}{2 \pi \nu }<1\), then there exists a unique solution in ψ for (4.1).
Proof
The definition of an operator \(\Delta : \psi \rightarrow \psi \) is
for any \(x \in [-X,X]\). As such, Δ is well defined because of \([\mathcal{D}_{1}]\).
We obtain the following for any \(h_{1}, h_{2} \in \psi \) and given \(x \in [-X, X]\):
From the condition \(\mathbb{L}C\frac{(2X)^{\nu }\Gamma {(1-\nu )}}{2 \pi \nu } < 1\), Δ takes the form of a contraction mapping. As a result, we are able to establish that Δ has a unique fixed point in accordance with the Banach contraction principle, and it is a unique solution with respect to FRDE (4.1). □
Theorem 4.2
Operator Δ is compact based on hypotheses \([\mathcal{D}_{1}]\)–\([\mathcal{D}_{3}]\).
Proof
Consider the definition in equation (4.2) for the operator Δ.
Step (1): We assume that \(h_{n}\) whereby \(h_{n} \rightarrow h\) as \(n \rightarrow \infty \) in ψ. As such, we have the following given all \(x \in [-X, X]\):
We have the following with respect to \([\mathcal{D}_{2}]\):
Consequently,
Note that \(h_{n} \rightarrow h\) as \(n \rightarrow \infty \) for every \(x \in [-X,X]\), and based on the Lebesgue dominated convergence theorem,
hence
Therefore, Δ is continuous.
Step (2): Here, Δ maps a bounded set in ψ is established. For this, we just have to prove that, for any \(\kappa ^{*} > 0\), there exists \(\rho > 0\) whereby given any
we have
In fact, for any \(x \in [-X,X]\), from equation (4.2), we have
where \(\mathcal{G} \in \psi \). Based on \([\mathcal{D}_{3}]\), we have
Consequently, we have
Hence \(\Delta (E^{*})\) is bounded.
Step (3): We prove that the operator Δ is equicontinuous in ψ. Suppose \(x_{1}, x_{2} \in [-X,X]\) with \(0 \le x_{1} \le x_{2} \le X\), as \(E^{*}\) is a bounded set in ψ, and assume \(h \in E^{*}\).
Now, by \([\mathcal{D}_{3}]\), we have
Note that as \(x_{1} \rightarrow x_{2}\), and consider the above inequality, its right-hand side approximates zero, and this indicates that Δ is equicontinuous. Based on steps (1) to step (3), it is concluded that Δ is completely continuous. Therefore, operator Δ is compact as in agreement with the Arzela–Ascoli theorem. □
Next, by exploiting the fixed point theorem of Schaefer, we are able to show that the solution for equation (4.1) exists.
Theorem 4.3
Suppose that hypothesis \([\mathcal{D}_{3}]\) holds. Given \(C<1\), at least one solution in ψ exists for FRDE (4.1).
Proof
Now, a set \(\mathcal{B} \subset \psi \) is considered, and its definition is
Let \(h \in \mathcal{B}\), in which
The following is obtained for every \(x \in [-X,X]\):
For simplicity, let \(N = C \mathbb{L}_{h} \frac{(2X)^{\nu }}{\nu }\). So, (4.5) becomes
Therefore, \(\mathcal{B}\) is bounded. According to Theorems 2.2 and 4.2, at least one fixed point exists with respect to operator Δ. Therefore, the considered FODE (4.1) has at least one solution in ψ. □
The following inequality is used for further analysis:
Based on the following condition, we examine the generalized H–U stability.
- [\(\mathcal{D}_{4}\)]:
-
A function \(\mathcal{G} \in \psi \) is considered, and there exists \(\lambda _{\kappa }>0\) whereby
$$\begin{aligned} \int _{-x}^{x} & \bigl(\mathcal{A}_{1} \cos (\nu \pi /2)-i\mathcal{A}_{2}\operatorname{sign}(x- \tau )\sin ( \nu \pi /2) \bigr) \vert x-\tau \vert ^{\nu -1} \mathcal{G}(\tau )\,d\tau \le \lambda _{\kappa }\kappa (x). \end{aligned}$$
Theorem 4.4
Suppose that hypotheses \([\mathcal{D}_{1}]\), \([\mathcal{D}_{2}]\), and \([\mathcal{D}_{4}]\) hold. If \(\frac{LC\Gamma {(1-\nu )}}{2\pi }<1\), then (4.1) is H–U–Rassias stable pertaining to κ.
Proof
A unique solution with respect to FRDE (4.1) exists, i.e.,
Integrating inequality (4.6) from −x to x and using condition \([\mathcal{D}_{4}]\), we obtain
Thus,
By taking modulus on both sides, we have
By Grownwall’s inequality, we obtain
where \(W^{*} = (\frac{1}{2\pi }\Gamma {(1-\nu )} ) \exp ( \frac{LC}{2\pi }\Gamma {(1-\nu )}) \).
Equation (4.1) is stable in the sense of H–U–Rassias pertaining to κ on \((-x,x)\). □
5 Simulations
Example 5.1
Consider
with \(\nu = \frac{1}{2}\), \(\vartheta =0\), \(g(x)=\frac{8}{3}(\frac{1}{\sqrt{\pi }}x^{\frac{3}{2}}+\frac{3}{16}e^{-x}-1)\).
Let \(h_{1}(x)=x^{2}\), and from [40] we have
Note that \(h_{1}(x)=x^{2}\) satisfies
From (3.5), we obtain the exact solution of equation (5.1), i.e.,
Equation (5.1) has a solution as in agreement with Theorem 3.1. Therefore, it is H–U stable, whereby
where \(K=\frac{2\sqrt{x}}{\sqrt{\pi }}\). Hence, our result can be applied to equation (5.1).
Example 5.2
Consider
with \(\nu = \frac{3}{2}\), \(\vartheta =0\), \(\xi = 0.3\), \(g(x)=4(\frac{1}{\sqrt{\pi }} x^{\frac{1}{2}}+\frac{1}{12}e^{-x}-1)\).
Let \(h_{1}(x+0.3)=(x+0.3)^{2}\), and from [40] we have
Note that \(h_{1}(x+0.3)=(x+0.3)^{2}\) satisfies
The exact solution of equation (5.2) is
By Theorem 3.1, we get
where \(K=\frac{2\sqrt{x+0.3}}{\sqrt{\pi }}\). Therefore, we can ascertain that (5.2) is stable in the sense of H–U.
6 Conclusion
In this paper, the analysis of our results indicates that fractional Fourier transform constitutes a useful method for tackling linear and nonlinear FRDE in \(\Phi (\mathbb{R})\). In addition, our study has established the stability and existence of solution of such equations using FRFT. The effectiveness of our results has been positively shown by using two illustrative examples. Further work will focus on the application of our results to various scientific and engineering problems.
References
Bazhlekova, E., Bazhlekov, I.: Viscoelastic flows with fractional derivative models: computational approach by convolutional calculus of Dimovski. Fract. Calc. Appl. Anal. 17(4), 954–976 (2014)
Podlubny, I.: Fractional Differential Equations. Mathematics in Science and Engineering, vol. 198. Academic Press, San Diego (1999)
Machado, J.T., Kiryakova, V., Mainardi, F.: Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 16(3), 1140–1153 (2011)
Liu, F., Burrage, K.: Novel techniques in parameter estimation for fractional dynamical models arising from biological systems. Comput. Math. Appl. 62(3), 822–833 (2011)
Baleanu, D., Jajarmi, A., Mohammadi, H., Rezapour, S.: A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 134, 109705 (2020)
Baleanu, D., Etemad, S., Rezapour, S.: A hybrid Caputo fractional modeling for thermostat with hybrid boundary value conditions. Bound. Value Probl. 2020(1), 1 (2020)
Rashid, S., Aslam Noor, M., Nisar, K., Baleanu, D., Rahman, G.: A new dynamic scheme via fractional operators on time scale. Front. Phys. 8, 165 (2020). https://doi.org/10.3389/fphy
El-Nabulsi, A.: Fractional derivatives generalization of Einstein’s field equations. Indian J. Phys. 87(2), 195–200 (2013)
Lacroix, S., Traite, D.: Cacul: Differential et du Calcul Integral, 2nd. Vol. 3 Paris Courcier, 409–410 (1819)
Ali, A., Samet, B., Shah, K., Khan, R.A.: Existence and stability of solution to a toppled systems of differential equations of non-integer order. Bound. Value Probl. 2017(1), 16 (2017)
Sher, M., Shah, K., Fečkan, M., Khan, R.A.: Qualitative analysis of multi-terms fractional order delay differential equations via the topological degree theory. Mathematics 8(2), 218 (2020)
Shah, K., Hussain, W.: Investigating a class of nonlinear fractional differential equations and its Hyers–Ulam stability by means of topological degree theory. Numer. Funct. Anal. Optim. 40(12), 1355–1372 (2019)
Baleanu, D., Mousalou, A., Rezapour, S.: On the existence of solutions for some infinite coefficient-symmetric Caputo–Fabrizio fractional integro-differential equations. Bound. Value Probl. 2017(1), 1 (2017)
Baleanu, D., Agarwal, R.P., Mohammadi, H., Rezapour, S.: Some existence results for a nonlinear fractional differential equation on partially ordered Banach spaces. Bound. Value Probl. 2013(1), 112 (2013)
Baleanu, D., Rezapour, S., Mohammadi, H.: Some existence results on nonlinear fractional differential equations. Philos. Trans. R. Soc. A, Math. Phys. Eng. Sci. 371(1990), 20120144 (2013)
Ulam, S.M.: A collection of mathematical problems. New York 29 (1960)
Hyers, D.H.: On the stability of the linear functional equation. Proc. Natl. Acad. Sci. USA 27(4), 222–224 (1941)
Rassias, T.M.: On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 72(2), 297–300 (1978)
Luchko, Y., Rodrigues, M.M.: Some new properties and applications of a fractional Fourier transform. J. Inequal. Spec. Funct. 8(1), 13–27 (2017)
Ozaktas, H.M., Kutay, M.A.: The fractional Fourier transform. In: 2001 European Control Conference (ECC), pp. 1477–1483. IEEE Press, New York (2001)
Wiener, N.: Hermitian polynomials and Fourier analysis. J. Math. Phys. 8(1–4), 70–73 (1929)
Liu, K., Wang, J., Zhou, Y., O’Regan, D.: Hyers–Ulam stability and existence of solutions for fractional differential equations with Mittag-Leffler kernel. Chaos Solitons Fractals 132, 109534 (2020)
Vu, H., An, T.V., Van Hoa, N.: Ulam–Hyers stability of uncertain functional differential equation in fuzzy setting with Caputo–Hadamard fractional derivative concept. J. Intell. Fuzzy Syst. 38(2), 2245–2259 (2020)
Wang, C., Xu, T.-Z.: Stability of the nonlinear fractional differential equations with the right-sided Riemann–Liouville fractional derivative. Discrete Contin. Dyn. Syst. 10(3), 505–521 (2017)
Guo, Y., Shu, X.-B., Li, Y., Xu, F.: The existence and Hyers–Ulam stability of solution for an impulsive Riemann–Liouville fractional neutral functional stochastic differential equation with infinite delay of order \(1<\beta<2\). Bound. Value Probl. 2019(1), 1 (2019)
Dai, Q., Gao, R., Li, Z., Wang, C.: Stability of Ulam–Hyers and Ulam–Hyers–Rassias for a class of fractional differential equations. Adv. Differ. Equ. 2020(1), 1 (2020)
Upadhyay, S., Khatterwani, K.: Characterizations of certain Hankel transform involving Riemann–Liouville fractional derivatives. Comput. Appl. Math. 38(1), 24 (2019)
Baleanu, D., Rezapour, S., Saberpour, Z.: On fractional integro-differential inclusions via the extended fractional Caputo–Fabrizio derivation. Bound. Value Probl. 2019(1), 79 (2019)
Aydogan, M.S., Baleanu, D., Mousalou, A., Rezapour, S.: On high order fractional integro-differential equations including the Caputo–Fabrizio derivative. Bound. Value Probl. 2018(1), 90 (2018)
Rashid, S., Hammouch, Z., Baleanu, D., Chu, Y.-M.: New generalizations in the sense of the weighted non-singular fractional integral operator. Fractals (2020)
Khan, A., Syam, M.I., Zada, A., Khan, H.: Stability analysis of nonlinear fractional differential equations with Caputo and Riemann–Liouville derivatives. Eur. Phys. J. Plus 133(7), 1–9 (2018)
Mohanapriya, A., Ganesh, A., Gunasekaran, N.: The Fourier transform approach to Hyers–Ulam stability of differential equation of second order. J. Phys. Conf. Ser. 2020(1), 12–27 (2020)
Mohanapriya, A., Park, C., Ganesh, A., Govindan, V.: Mittag-Leffler–Hyers–Ulam stability of differential equation using Fourier transform. Adv. Differ. Equ. 2020(1), 1 (2020)
Zayed, A.I.: Fractional Fourier transform of generalized functions. Integral Transforms Spec. Funct. 7(3–4), 299–312 (1998)
Yang, X., Kang, Z., Liu, C.: Local fractional Fourier’s transform based on the local fractional calculus. In: 2010 International Conference on Electrical and Control Engineering, pp. 1242–1245. IEEE Comput. Soc., Los Alamitos (2010)
Luchko, Y.F., Martinez, H., Trujillo, J.J.: Fractional Fourier transform and some of its applications. Fract. Calc. Appl. Anal. 11(4), 457–470 (2008)
Lizorkin, P.I.: Generalized Liouville differentiation and the functional spaces \(L_{p}^{r}(E_{n})\). Imbedding theorems. Mat. Sb. 102(3), 325–353 (1963)
Lizorkin, P.I.: Generalized Liouville differentiation and the method of multiplicators in imbedding theory for function classes. Math. Notes Acad. Sci. USSR 4(4), 771–779 (1968)
Samko, S.: Densencess of the spaces \(\Phi(V)\) of Lizorkin type in the mixed \(L_{p}(R_{n})\)-spaces. Stud. Math. 3(113), 199–210 (1995)
Kilbas, A., Trujillo, J.: Differential equations of fractional order: methods results and problem – I. Appl. Anal. 78(1–2), 153–192 (2001)
Prudnikov, A., Brychkov, Y.A., Marichev, O.I.: Integrals and Series, Vol. 1: Elementary Functions. Gordon & Breach, New York (1986)
Acknowledgements
This research is made possible through financial support from the Phuket Rajabhat University, Thailand, and the Thailand Research Fund (RSA6280004). The authors are grateful to the Phuket Rajabhat University, Thailand, and the Thailand Research Fund (RSA6280004) for supporting this research.
Availability of data and materials
Not applicable.
Funding
The research is supported by the Phuket Rajabhat University, Thailand, and the Thailand Research Fund (RSA6280004).
Author information
Authors and Affiliations
Contributions
Funding acquisition, GR and BA; Conceptualization, GR and BA; Software, GR; Formal analysis, GR and BA; Methodology, GR and BA; Supervision, CPL, VG, and NG; Writing–original draft, GR and BA; Validation, GR; Writing– review and editing, GR. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Unyong, B., Mohanapriya, A., Ganesh, A. et al. Fractional Fourier transform and stability of fractional differential equation on Lizorkin space. Adv Differ Equ 2020, 578 (2020). https://doi.org/10.1186/s13662-020-03046-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03046-5