Abstract
There are often many kinds of rumors spreading in new media after emergencies; however, the existing studies have focused on the rumors with competition, and little attention has been paid to those with mutual promotion. Therefore the mutual promotion between two rumors and the state transition rules between different groups are first analyzed. Then a 3SI3R model, extending the classical 2SI2R model, and mean-field equations of the proposed model are given. Further, the stability and influence of the mutual promotion on the final size of two rumors in the proposed model are derived. Finally, numerical simulations are carried out to investigate the influence of factors, that is, the mutual promotion, occurrence time differences, and the forgetting rate, on the propagation of two rumors. The results show that the enhancement of the mutual promotion can accelerate propagation of two rumors and enlarge their final size; the increase of forgetting rate helps to decrease the final size of two rumors; the decrease in occurrence time differences can result in a small increase in the final size of the later rumor, and the overall situation of two rumors becomes more difficult to control.
Similar content being viewed by others
1 Introduction
In recent years, with rapid development of Internet technologies, the propagation of rumors has become more and more complicated [1]. On the one hand, the number of mobile users has obviously increased in new media. According to the statistics released by the China Internet Network Information Center, the number of Chinese Internet users has reached 829 million, and the proportion of mobile users has reached 98.6% by December 2018. Besides, mobile social applications such as Weibo, WeChat, and QQ help individuals to receive the latest rumors and publish their opinions on the Internet anytime and anywhere. On the other hand, multiple rumors often spread widely after emergencies, which will not only lead to public panics, but also endanger the public life and property. For example, during the 2018 bus crash in Chongqing, China, a rumor of “female drivers’ retrograde leading to the accident” propagated widely on the Internet, causing many Internet users to condemn the driver. After that, a rumor of “the accident is resulted from the driver’s fatigue caused by going to karaoke” spread quickly and exacerbated the public panics. Therefore the propagation of multiple rumors in new media has deeply affected the public life and social stability, and relevant research is of great significance.
The existing studies have made important breakthroughs in the propagation of single rumor on the Internet. On the one hand, the propagation model has been paid much attention. Pan et al. [2] and Zhao et al. [3] proposed a novel rumor-truth propagation model to investigate how suppress the spread of rumors effectively with truth, meanwhile the optimal control theory is often adopted to study the optimal control strategy of rumors [4–6]. Huo et al. [7] introduced an I2SR model to study the influence of different activity of nodes on rumor propagation. Hu et al. [8] constructed an SHAR model to investigate the impact of individual with different attitudes on rumor dissemination. Shin et al. [9] applied a text analysis method to study the evolution of misinformation on Twitter. Furthermore, the classical SIR model is often modified considering different types of individuals, including the ILSCR model [10], SIQR model [11], \(\mathrm{SI}_{\mathrm{b}}\mathrm{I}_{\mathrm{n}}\mathrm{I}_{\mathrm{u}}\) model [12], and SIRaRu model [13]. On the other hand, the identification of influential factors of a single rumor has obtained great progress. The impact of incubation on rumor propagation was analyzed in [14]. Huo and Ma [15] proposed that short pulses or long incubation was beneficial to eliminate rumors. Wang et al. [16] and Sahafizadeh et al. [17] investigated the potential impact of group propagation on the evolution of the rumor. Ma and Zhu [18] proposed the diversity of individual characteristics could decrease the evolution of the rumor. In addition, stochastic SIR model was adopted to study the influence of environmental noise [19], expert intervention [20], and network structure [21] on rumor propagation. Moreover, the studies on disease spread in complex network [22–26] and its control measures [27–30] can provide reference for the investigations on rumor propagation and control.
Different from single-rumor propagation, multiple rumors may compete with each other in the process of dissemination. Zan [31] constructed the DSIR model to study the propagation of two irrelevant rumors with different occurrence time. Liu et al. [32] suggested that the state transformation probability of dual competitive information had important impact on evolution results. Meanwhile, the influence of individual’s characteristics such as behavioral differences [33] and group psychology [34] on the dissemination of dual competitive information was investigated. Zhu et al. [35] constructed a novel DMCU model to study the competitive dissemination between original false information and updated information. Zhang and Zhu [36] constructed I2S2R rumor propagation model and analyzed its stability in homogeneous and heterogeneous networks. Trpevski et al. [37] proposed that the nodes always give priority to spreading more attractive rumors. Jie et al. [38] proposed that two rumors can accelerate or inhibit the propagation of each other under certain conditions. Vosoughi et al. [39] suggested that false information could disseminate faster.
However, there are often two rumors which promote each other in real cases, and their widespread spread is an important factor for the emergence of secondary crisis. For example, in the 2019 explosion at Xiangshui Chemical Plant in Jiangsu Province, China, rumors of “toxic chemical explosives polluting air and water” and “eighteen firefighters died from inhaling carcinogenic gases” dominated the spread of public panics, and individuals were more likely to believe the other one if they believed one of these rumors. Different from the complete competition between two rumors [31–37], Myers and Leskovec [40] studied the interaction of multiinformation with both competition and cooperation based on statistical models. Zhuang et al. [41] studied the cooperative and competitive dissemination of two informations based on SIR model; Zhang et al. [42] combines the Lotka–Volterra competition model with the cooperation model to study the coexistence conditions of multiinformation. Moreover, the work [40] mainly investigated how the interaction between multiinformation affected the spreading probability of spreaders with real data from Twitter, and the states of Internet users were limited between “uninfected” and “infected”. The competition from the work [41] was depicted as the information 1 and information 2 competing for the attention of ignorants, but the spreaders had no interaction in this situation; in contrast, the spreaders exchanged each other according to their personal interests when information 1 cooperated with information 2. The model of [42] only studied the stability and coexistence conditions of multiinformation. Different from the works [40–42], individuals may believe or disseminate two rumors that are highly similar in content. Our motivation is to explore the influence of mutual promotion between two rumors on its evolution. We proposed a 3SI3R model, in which individuals could spread two rumors simultaneously to study the influence of mutual promotion on the propagation dynamics of two rumors. Besides, our model assumes that the spreaders of one rumor are more likely to propagate another rumor than ignorants. Therefore we introduced the mutual promotion coefficient for the transmission probability between ignorants and different spreaders, which leads to some different properties that have not been studied by former researchers.
The rest of this paper is arranged as follows. The problem description is provided in Sect. 2. In Sect. 3, we propose a 3SI3R model to investigate the dissemination dynamics of two rumors with mutual promotion. Then, in Sect. 4, we derive the stability and the influence of the mutual promotion on the final size of two rumors in the proposed model. In Sect. 5, by numerical simulations we investigate the impact of factors, that is, the mutual promotion, occurrence time differences, and the forgetting rate, on the propagation of the two rumors. Finally, conclusions are given in Sect. 6.
2 Problem description
The development trend of Internet users in China can be obtained through collecting the authoritative statistics released by the China Internet Network Information Center (CNNIC) from 2008 to 2018, as shown in Fig. 1. We find that the total number of Internet users in China increases year by year, and the proportion of mobile users also shows an obvious growth, namely, mobile users have gradually played a dominant role in public opinion. Information is easy to be modified and shared on mobile social applications and results in a variety of information spreading in social network. Rumors are no exception. A variety of rumors often spread widely after emergencies, such as the 2018 bus crash in Chongqing, China, and the 2019 explosion at Xiangshui Chemical Plant in Jiangsu Province, China, described above. In view of this, the propagation law of rumors has been paid much attention. The papers related to the dissemination of two rumors during 2010 to 2019 are obtained from Web of Science, as shown in Fig. 2. It is obvious that the research trend of two-rumor propagation is increasing year by year.
In recent years, mobile Internet has gradually become the most popular medium of rumor propagation. The new characteristics of rumor propagation in new media are demonstrated as follows. (1) Diversity. Taking into account the differences of individual’s cognition and education, different individuals often hold different opinions and attitudes toward emergencies, which results in the diversity of rumor content [32]. (2) Directivity. The public opinions often demonstrate the phenomenon of “one-sided” or “hostile” in new media. Therefore many kinds of rumors may promote or compete with each other [38]. (3) Rapid dissemination [43]. The propagation of rumors has broken through the limitations of time and space with the widespread popularity of mobile applications, causing its influence to exacerbate infinitely in a short time. (4) Occurrence time differences [31]. In the early period after emergencies, information about the event is relatively scarce, and thus various rumors emerge rapidly. With the publication of official investigation results, new rumors continue to emerge. (5) Easy to be forgotten. Compared with the traditional media, the public is exposed to more information in new media. As a result, they are more likely to forget or shift their focus [43]. Different from the traditional media, the propagation of rumors in new media is more complex and leads to the public opinion crisis more difficult to be controlled. Therefore it is necessary to study the dissemination law of rumors in new media.
The propagation of two rumors with competition has been extensively studied [31–37]. However, the propagation of two rumors with mutual promotion is beneficial to aggravate the public opinion crisis. As is mentioned before, the widespread dissemination of two rumors with mutual promotion exacerbated the public panics in the 2019 explosion at Xiangshui Chemical Plant in Jiangsu Province, China. The mutual promotion between two diseases could be interpreted that individuals infected with one disease are more susceptible to another virus than susceptible individuals, and individuals can be infected with two diseases [44]. According to [45], the whole population of disease infection had been divided into three states, including “uninfected”, “infected”, and “immune”. The uninfected individuals may turn into infected individuals due to contact, and the infected individuals may change into immune individuals because of contacting with immune individuals and receiving relevant treatment. Similarly, the whole population of rumor propagation could be divided into ignorants, spreaders, and stiflers. Ignorants may become spreaders when they hear a rumor, and spreaders may turn into stiflers due to contact. Considering the similarity between rumor propagation and disease infection, the mutual promotion between two rumors can be interpreted so that individuals may disseminate both of two rumors. Specifically, for two rumors that are highly relevant in content and easy to trigger the same psychological reaction or the similar behavior of the public, individuals who spread one rumor are more likely to disseminate another rumor than ignorants. On such a basis, behaviors of different individuals are demonstrated in Fig. 3. Individuals are exposed to more rumors because of their more convenient contact with each other in new media, causing the state transmission between them, as shown in Fig. 4.
To sum up, the problem to be solved is demonstrated as follows: What is the propagation law of two rumors with mutual promotion? What are the effects of important factors, that is, the mutual promotion, occurrence time differences, and the forgetting rate, on the propagation of two rumors in new media?
3 The 3SI3R model
Considering the characteristics of rumors propagation in new media, the diversity is described with many kinds of rumors [36], and the directivity is demonstrated with the interaction between different rumors [38]. Compared with the traditional media, people are more closely related, and the average degree of social network increases in new media, which is conducive to accelerating rumor propagation. Therefore the average degree of social network is used to characterize the rapid dissemination of rumors [43]. The initial number of spreaders of earlier rumor is over the later rumor, and the occurrence time differences of rumors are depicted with the initial proportion of spreaders [46]. The forgetting rate of individuals indicates that rumors are easy to be forgotten [43].
3.1 Model assumptions
There are often a variety of rumors spreading in new media. Considering the complexity of rumors propagation, some assumptions are introduced as follows:
Assumption 1
According to the content differences of rumors, many kinds of rumors can be clustered into two rumors with mutual promotion, namely rumor 1 and rumor 2.
Considering the mutual promotion between rumor 1 and rumor 2, when a spreader of rumor 1 contacts a spreader of rumor 2, the former one is likely to disseminate both rumor 1 and rumor 2, and vice versa. Individuals will be skeptical about another rumor if the government effectively clarifies one of the two rumors. For example, in the 2019 explosion at Xiangshui Chemical Plant in Jiangsu Province, China, the local government declared that water was not polluted and air pollution was within the allowable range. As one of two rumors was clarified, individuals naturally became skeptical about another rumor. Thus Assumptions 2–3 are given as follows.
Assumption 2
The spreaders of rumors can simultaneously propagate rumor 1 and rumor 2 in new media, and they will be skeptical about another rumor and turn into hesitate state if they understand the falsity of one rumor.
Assumption 3
According to the individual’s reaction to rumor 1 and rumor 2, the whole population is divided into seven groups with ignorant (I), spreader 1 (\(S_{1}\)), spreader 2 (\(S_{2}\)), spreader 3 (\(S_{3}\)), stifler 1 (\(R_{1}\)), stifler 2 (\(R_{2}\)), and stifler 3 (\(R_{3}\)).
Ignorants are composed of individuals who have never heard of rumors. Spreaders 1 and spreaders 2 comprise individuals who only propagate rumor 1 or rumor 2, respectively. However, spreaders 3 are those who simultaneously disseminate rumor 1 and rumor 2. Stiflers 1 consist of individuals who have heard of rumor 1 but only no longer spread it, which is similar to stiflers 2. Stiflers 3 are those who have heard of both rumor 1 and rumor 2 but will not spread them anymore. The proportion of ignorants, spreaders 1, spreaders 2, spreaders 3, stiflers 1, stiflers 2, and stiflers 3 at time t must satisfy the normalization condition \(I + S_{1} + S_{2} + S_{3} + R_{1} + R_{2} + R_{3} = 1\).
Assumption 4
The interaction of two rumors occurs in an open social system, a is the inflow rate of ignorants due to birth, μ indicate the outflow rate of each of the seven groups due to disease and death. There are often no birth policy changes or major disasters during rumors propagation, and thus the inflow and outflow rates can be regarded as equal, namely \(a = \mu\), \(a,\mu \in [ 0,1 ]\) [46].
3.2 Model formulation
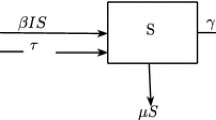
The propagation rules of two rumors with mutual promotion are demonstrated as follows according to those with competition in [36]. When an ignorant contacts spreaders 1 (spreaders 2 or spreaders 3), the former one may become a spreader 1 (spreader 2 or spreader 3) with certain probability. The spreaders 1 may become stiflers 1 due to forgetting mechanism, and the spreader 1 may turn into stifler 1 with certain probability when a spreader 1 contacts a stifler 1. The relationship between spreaders 2 and stiflers 2 is similar. In addition, the spreader 3 may become a stifler 1 with some probability and turn into hesitant to rumor 2 when a spreader 3 contacts a stifler 1. The relationship between spreaders 3 and stiflers 2 is similar. Moreover, the spreaders 3 may turn into stiflers 3 due to forgetting mechanism, and when a spreader 3 contacts a stifler 3, the spreader 3 may become stifler 3 with certain probability. Spreaders 1 may turn into stiflers 3 with certain probability when spreaders 1 contact with stiflers 3. The relationship between spreaders 2 and stiflers 3 is similar. Stiflers 1 and stiflers 2 may turn into stiflers 3 due to government interventions. Finally, spreaders 1 may become spreaders 3 with certain probability when spreaders 1 contact the spreaders of rumor 2 (the sum of spreaders 2 and spreaders 3). The relationship between spreaders 2 and the spreaders of rumor 1 is similar (the sum of spreaders 1 and spreaders 3).
Therefore we propose a 3SI3R model of two rumors with mutual promotion according to the 2SI2R model [46], as shown in Fig. 5, where the involved parameters are shown in Table 1, and the range of values of all parameters is \([ 0,1 ]\). Considering the mutual promotion between two rumors, spreaders 1 are more likely to disseminate rumor 2 than ignorants, and vice versa. According to the infection of two diseases in [44], we set \(\beta_{1} = \varepsilon \lambda_{2}\) and \(\beta_{2} = \varepsilon \lambda_{1}\), where \(\varepsilon>1\) is determined as the mutual promotion coefficient. This means that individuals who believe one rumor are less likely to believe another rumor than ignorants if \(0 < \varepsilon \le 1\), that is, the two rumors are competitive. Two rumors spread independently without interference if \(\varepsilon = 0\). Further, Myers [40] proposed that individuals are more likely to adopt and share the information if they receive multiple information that is highly relevant in content. Therefore, compared with the transmission probability between ignorants and single-rumor spreaders, the transmission probability has to satisfy the condition \(\lambda_{1},\lambda_{2} < \lambda_{3}\) when ignorants contact with spreaders 3. The transmission probability is used to characterize the attraction of rumor [47]. On such a basis, the attraction of two highly similar rumors to ignorants is at least \(\max \{ \lambda_{1},\lambda_{2} \}\) when the attraction of rumor 1 and rumor 2 is demonstrated by \(\lambda_{1}\) and \(\lambda_{2}\), respectively. Considering that the direct transformation of \(I \to S_{3}\) is equivalent to the superposition of the mutual promoted propagation of \(I \to S_{1} \to S_{3}\) and \(I \to S_{2} \to S_{3}\), and thus \(\lambda_{3} = \varepsilon^{2} \cdot \max \{ \lambda_{1},\lambda_{2} \} = \varepsilon^{2} [ \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ] / 2\). The repeated dissemination of similar information can make the individual’s memories more memorable according to the memory manipulation model [48]. Therefore the forgetting rate of spreaders 3 is smaller than that of spreaders 1 and spreaders 2, that is, \(\delta_{3} < \delta_{1},\delta_{2}\).
Based on the previous analysis, mean-field equations in homogeneous network are described as follows:
where μI is the proportion of ignorants removed as a result of disease or death, and the meanings of \(\mu S_{1}\), \(\mu S_{2}\), \(\mu S_{3}\), \(\mu R_{1}\), \(\mu R_{2}\), and \(\mu R_{3}\) are analogous; \(\lambda_{1}IS_{1}\overline{k}\) denotes the proportion of ignorants turning into spreaders 1 due to contact in homogenous network, and the meanings of \(\lambda_{2}IS_{2}\overline{k}\) and \(\lambda_{3}IS_{3}\overline{k}\) are analogous. Formula (1) has the initial conditions \(I(0) > 0\), \(S_{1}(0) \ge 0\), \(S_{2}(0) \ge 0\), \(S_{3}(0) \ge 0\), \(R_{1}(0) \ge 0\), \(R_{2}(0) \ge 0\), and \(R_{3}(0) \ge 0\), and according to [7, 12], its solution exists in the closed positive octant \(\varOmega = [(I,S_{1},S_{2},S_{3},R_{1},R_{2},R_{3}) \in \mathbb{R}_{ +}^{6}; I + S_{1} + S_{2} + S_{3} + R_{1} + R_{2} + R_{3} = 1]\) since its right side is Lipschitz continuous in Ω.
4 Stability analysis
Let the right end of formula (1) equal zero. Then the rumor-free equilibrium point \(E_{0} ( 1,0,0,0,0,0,0 )\) is obtained. Further, the propagation threshold \(R_{0}\) is an important parameter for determining whether or not the rumor can be diffused [49]. According to [50, 51], we define \(X = ( S_{1},S_{2},S_{3},I,R_{1},R_{2},R_{3} )\) to calculate \(R_{0}\). Let \(\bar{F} ( X )\) be the probability of appearance of new spreaders in each state, and let \(\bar{V} ( X )\) be the transmission probability of individuals into each state. Thus formula (1) can be expressed as \(dX / dt = \bar{F} ( X ) - \bar{V} ( X )\), where
Then the Jacobian matrices corresponding to \(\bar{F} ( X )\) and \(\bar{V} ( X )\) at \(E_{0}\) are calculated as
where
Thus
Theorem 1
If\(1 < \varepsilon \le \sqrt{2 ( \delta_{3} + \mu ) / \bar{k} [ \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ]}\), then\(E_{0} ( 1,0,0,0,0,0,0 )\)is locally asymptotically stable, and if\(\varepsilon > \sqrt{2 ( \delta_{3} + \mu ) / \bar{k} [ \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ]}\), then\(E_{0} ( 1,0,0,0,0,0,0 )\)is unstable.
Proof
The Jacobian matrix of Eq. (1) at \(E_{0} ( 1,0,0,0,0,0,0 )\) is
where \(\Delta_{1} = \delta_{1} + \mu\), \(\Delta_{2} = \delta_{2} + \mu\), \(\Delta_{3} = \delta_{3} + \mu\).
Further, the characteristic equation of the matrix \(J ( E_{0} )\) is
Thus the characteristic roots are \(q_{1} = q_{2} = - \mu\), \(q_{3} = - \eta_{1} - \mu\), \(q_{4} = - \eta_{2} - \mu\), \(q_{5} = \lambda_{1}\overline{k} - \Delta_{1}\), \(q_{6} = \lambda_{2}\overline{k} - \Delta_{2}\), and \(q_{7} = \lambda_{3}\overline{k} - \Delta_{3}\). According to the Routh–Hurwitz stability criterion [52], the characteristic roots are negative, and \(E_{0} ( 1,0,0,0,0,0,0 )\) is locally asymptotically stable if \(R_{0} \le 1\), that is, \(1 < \varepsilon \le \sqrt{2 ( \delta_{3} + \mu ) / \bar{k} [ \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ]}\). However, some of the characteristic roots are positive, and \(E_{0} ( 1,0,0,0,0,0,0 )\) is unstable if \(R_{0} > 1\), that is, \(\varepsilon > \sqrt{2 ( \delta_{3} + \mu ) / \bar{k} [ \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ]}\). □
Theorem 2
If\(1 < \varepsilon \le \sqrt{2 ( \delta_{3} + \mu ) / \bar{k} [ \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ]}\), then\(E_{0} ( 1,0,0,0,0,0,0 )\)is globally asymptotically stable.
Proof
Let us consider the Lyapunov function \(L ( t ) = k_{1}S_{1} ( t ) + k_{2}S_{2} ( t ) + k_{3}S_{3} ( t )\), where \(k_{1} = k_{2} = M / \Delta_{1}\Delta_{2}\Delta_{3}\), \(k_{3} = 1 / \Delta_{1}\Delta_{2}\Delta_{3}\), and \(M \ge 1\) is a large enough positive integer. Further, we can illustrate the function of \(L' ( t )\) as follows:
Therefore, for all \(0 \le S_{1} ( t ),S_{2} ( t ),S_{3} ( t ),R_{1} ( t ),R_{2} ( t ),R_{3} ( t ) \le 1\), \(R_{0} \le 1\), and \(\lambda_{3}\overline{k} \le \Delta_{3}\) if \(1 < \varepsilon \le \sqrt{2 ( \delta_{3} + \mu ) / \bar{k} [ \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ]}\), then the third term on the right end of the inequality is less than or equal to 0. Since \(\lambda_{1},\lambda_{2} < \lambda_{3}\) and \(\delta_{1},\delta_{2} > \delta_{3}\), we have \(\Delta_{1},\Delta_{2} > \Delta_{3}\) and \(\lambda_{1}\overline{k} < \Delta_{1}\), \(\lambda_{2}\overline{k} < \Delta_{2}\). Thus the first and second terms on the right end of the inequality are less than 0. If \(M \ge 1\) is a sufficiently large positive integer, then the last three terms of the right end of the inequality are also less than or equal to 0, and thus we derive \(L' ( t ) \le 0\). According to the LaSalle invariance principle [53], \(E_{0} ( 1,0,0,0,0,0,0 )\) is globally asymptotically stable. □
Theorem 3
If\(\varepsilon > 1\), then the final sizes of two rumors are\(R ( \infty ) = 1 - I ( 0 )e^{ - C}\)and\(dR ( \infty ) / d\varepsilon > 0\), where\(C = \frac{\varepsilon^{2}\bar{k} ( I ( 0 ) - I ( \infty ) + I ( 0 )S_{3} ( 0 ) ) [ \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ]}{2I ( 0 ) ( \delta_{3} + \mu )} + \frac{\lambda_{1}\bar{k}}{\delta_{1} + \mu} S_{1} ( 0 ) + \frac{\lambda_{2}\bar{k}}{\delta_{2} + \mu} S_{2} ( 0 )\).
Proof
Rumors will eventually die out during the propagation process [51], that is, \(S_{1} ( \infty ) = S_{2} ( \infty ) = S_{3} ( \infty ) = 0\). The propagation of two rumors reaches stable state with I, \(R_{1}\), \(R_{2}\), and \(R_{3}\) left. The final size of two rumors is \(R ( \infty ) = R_{1} ( \infty ) + R_{2} ( \infty ) + R_{3} ( \infty ) = 1 - I ( \infty )\), which demonstrates the overall situation of rumors. The final size of ignorants involves \(R_{0}\) and the matrix V [54], and thus
Let \(C = \frac{\varepsilon^{2}\bar{k} ( I ( 0 ) - I ( \infty ) + I ( 0 )S_{3} ( 0 ) ) [ \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ]}{2I ( 0 ) ( \delta_{3} + \mu )} + \frac{\lambda_{1}\bar{k}}{\delta_{1} + \mu} S_{1} ( 0 ) + \frac{\lambda_{2}\bar{k}}{\delta_{2} + \mu} S_{2} ( 0 )\). Then \(R ( \infty ) = 1 - I ( 0 )e^{ - C}\), and the relationship between \(R ( \infty )\) and ε is calculated as
Therefore the final size of two rumors is positively related to the mutual promotion. □
Theorem 4
If\(0 < \varepsilon \le 1\), then the final size of two rumors is\(\tilde{R} ( \infty ) = 1 - I ( 0 )e^{ - N}\), where\(N = \tilde{R}_{0}\frac{I ( 0 ) - I ( \infty )}{I ( 0 )} + \frac{\lambda_{1}\bar{k}}{\delta_{1} + \mu} S_{1} ( 0 ) + \frac{\lambda_{2}\bar{k}}{\delta_{2} + \mu} S_{2} ( 0 ) + \frac{\varepsilon^{2}\bar{k} [ - \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ]}{2 ( \delta_{3} + \mu )}S_{3} ( 0 )\).
Proof
The propagation threshold of the 3SI3R model with two competitive rumors is \(\tilde{R}_{0} = \max \{ \lambda_{1}\bar{k} / ( \delta_{1} + \mu ),\lambda_{2}\bar{k} / ( \delta_{2} + \mu ),\lambda_{3}\bar{k} / ( \delta_{3} + \mu ) \}\). The attraction of rumor 1 and rumor 2 is demonstrated by \(\lambda_{1}\) and \(\lambda_{2}\), respectively [38]. Then the attraction of two rumors with competition to ignorants is at most \(\min \{ \lambda_{1},\lambda_{2} \}\). Considering that the direct transformation of \(I \to S_{3}\) is equivalent to the superposition of the competitive propagation of \(I \to S_{1} \to S_{3}\) and \(I \to S_{2} \to S_{3}\), and thus \(\lambda_{3} = \varepsilon^{2} \cdot \min \{ \lambda_{1},\lambda_{2} \} = \varepsilon^{2} [ - \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ] / 2\). The propagation threshold is \(\tilde{R}_{0} = \max \{ \lambda_{1}\bar{k} / ( \delta_{1} + \mu ),\lambda_{2}\bar{k} / ( \delta_{2} + \mu ),\varepsilon^{2}\bar{k} [ - \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ] / 2 ( \delta_{3} + \mu ) \}\). The final size of ignorants involves \(\tilde{R}_{0}\) and the matrix Ṽ [54], where \(\tilde{V} = V\), and thus
Let \(N = \tilde{R}_{0}\frac{I ( 0 ) - I ( \infty )}{I ( 0 )} + \frac{\lambda_{1}\bar{k}}{\delta_{1} + \mu} S_{1} ( 0 ) + \frac{\lambda_{2}\bar{k}}{\delta_{2} + \mu} S_{2} ( 0 ) + \frac{\varepsilon^{2}\bar{k} [ - \vert \lambda_{1} - \lambda_{2} \vert + ( \lambda_{1} + \lambda_{2} ) ]}{2 ( \delta_{3} + \mu )}S_{3} ( 0 )\). Then \(\tilde{R} ( \infty ) = 1 - I ( 0 )e^{ - N}\). □
Theorem 5
If\(\varepsilon = 0\), then the final size of two rumors is\(\overset{\frown}{R} ( \infty ) = 1 - I ( 0 )e^{ - D}\), where\(D = \max \{ \frac{\lambda_{1}\bar{k}}{\delta_{1} + \mu},\frac{\lambda_{2}\bar{k}}{\delta_{2} + \mu} \} \cdot \frac{I ( 0 ) - I ( \infty )}{I ( 0 )} + \frac{\lambda_{1}\bar{k}}{\delta_{1} + \mu} S_{1} ( 0 ) + \frac{\lambda_{2}\bar{k}}{\delta_{2} + \mu} S_{2} ( 0 )\).
Proof
The propagation threshold of the 3SI3R model is \(\overset{\frown}{R}_{0} = \max \{ \lambda_{1}\bar{k} / ( \delta_{1} + \mu ), \lambda_{2}\bar{k} / ( \delta_{2} + \mu ) \}\) when two rumors spread independently. The final size of ignorants involves \(\overset{\frown}{R}_{0}\) and the matrix \(\overset{\frown}{V}\) [54], where
and thus
Let \(D = \max \{ \frac{\lambda_{1}\bar{k}}{\delta_{1} + \mu},\frac{\lambda_{2}\bar{k}}{\delta_{2} + \mu} \} \cdot \frac{I ( 0 ) - I ( \infty )}{I ( 0 )} + \frac{\lambda_{1}\bar{k}}{\delta_{1} + \mu} S_{1} ( 0 ) + \frac{\lambda_{2}\bar{k}}{\delta_{2} + \mu} S_{2} ( 0 )\). Then \(\overset{\frown}{R} ( \infty ) = 1 - I ( 0 )e^{ - D}\). □
Theorem 6
The final size of two rumors\(R ( \infty ) > \tilde{R} ( \infty ) \ge \overset{\frown}{R} ( \infty )\).
Proof
Suppose \(\varepsilon_{1} > 1\) and \(0 < \varepsilon_{2} \le 1\), and let \(\hat{\Delta}_{1} = R ( \infty ) - \tilde{R} ( \infty ) = I ( 0 ) ( e^{ - N} - e^{ - C} )\). Since
and
we have \(e^{ - N} > e^{ - C}\), and thus \(\hat{\Delta}_{1} > 0\) and \(R ( \infty ) > \tilde{R} ( \infty )\). Therefore the final size of two rumors with mutual promotion is over the final size of two rumors with competition.
Further, let \(\hat{\Delta}_{2} = \tilde{R} ( \infty ) - \overset{\frown}{R} ( \infty ) = I ( 0 ) ( e^{ - D} - e^{ - N} )\). Since
and
we have \(e^{ - D} \ge e^{ - N}\), and thus \(\hat{\Delta}_{2} \ge 0\) and \(\tilde{R} ( \infty ) \ge \overset{\frown}{R} ( \infty )\). Therefore the final size of two rumors \(R ( \infty ) > \tilde{R} ( \infty ) \ge \overset{\frown}{R} ( \infty )\). □
5 Numerical simulations
Considering that two rumors spread concurrently, it is advisable to set rumor 1 appear earlier than rumor 2. Thus the initial proportion of spreaders 1 is greater than that of spreaders 2, that is, \(S_{1} ( 0 ) > S_{2} ( 0 )\). Individuals will simultaneously spread rumor 1 and rumor 2 when spreaders 1 contact spreaders 2, and therefore spreaders 3 are converted from spreaders 1 or spreaders 2 due to contact and \(S_{3} ( 0 ) = 0\). The initial proportion of each group in the proposed model is set as \(I ( 0 ) = 0.990\), \(S_{1} ( 0 ) = 0.009\), \(S_{2} ( 0 ) = 0.001\), \(S_{3} ( 0 ) = 0\), \(R_{1} ( 0 ) = 0\), \(R_{2} ( 0 ) = 0\), \(R_{3} ( 0 ) = 0\). The parameters of the proposed model are derived from [46] in order to compare with the results of two competitive rumors: \(a = \mu = 0.0001\), \(\lambda_{1} = \lambda_{2} = 0.02\), \(\gamma_{1} = \gamma_{2} = 0.02\), \(\alpha_{1} = \alpha_{2} = \alpha_{3} = 0.02\), \(\sigma_{1} = \sigma_{2} = 0.02\), and \(\overline{k} = 20\). Considering the efforts of the government to clean up the online environment, we set \(\eta_{1} = \eta_{2} = 0.1\). Based on the above parameters, six different scenarios are proposed to investigate the influence of factors, that is, the mutual promotion, occurrence time differences, and forgetting rate, on the propagation of two rumors. The relevant parameters in different scenarios are shown in Table 2, and the weak promotion between two rumors is set as the basic scenario.
(1) The influence of the mutual promotion between two rumors.
The variation trend of the proportion of spreaders and stiflers in different mutual promotion are shown in Fig. 6. (1) Rumor 1 and rumor 2 propagate independently in scenario 1. The peak of the spreaders of rumor 1 is higher and the descent rate to fall back to zero is larger, while the peak of the spreaders of rumor 2 is lower but the descent rate to fall back to zero is smaller. (2) The increase in the competition between two rumors results in an obvious increase in the peak of the spreaders of more competitive rumor and a decrease in the peak of the spreaders of less competitive rumor [46]. Different from the propagation of two competitive rumors, the increase in the mutual promotion coefficient helps to enhance the growth rate and the peak of the spreaders of rumor 1 and rumor 2 simultaneously and decrease the differences between their peaks. (3) The stiflers of rumor 1 and rumor 2 continue to increase until it reaches a steady state. Compared with scenario 1, the final size of the stiflers of rumor 1 and rumor 2 in the basic scenario and scenario 2 is larger, and the time to reach the steady state has an obvious advance. (4) The increase in competition between two rumors helps to increase the final size of the stiflers of more competitive rumors and decrease the final size of the stiflers of less competitive rumors. However, the increase in the mutual promotion coefficient results in an obvious enlargement in the final size of the stiflers of rumor 1 and rumor 2 in scenario 1 and scenario 2. Therefore the mutual promotion between two rumors not only accelerates the propagation of rumors, but also enlarges the final size of two rumors, and thus the government and official media should promptly take interventions and weaken the mutual promotion between rumors.
(2) The influence of the forgetting rate.
The variation trend of the proportion of spreaders and stiflers in different forgetting rates is shown in Fig. 7. (1) The increase in forgetting rate can result in a decrease in the peaks of the spreaders of rumor 1 and rumor 2. (2) The increase in forgetting rate helps to decrease the final size of the stiflers of rumor 1 and rumor 2, and the time to reach the steady state has a small advance. However, with the increase of forgetting rate, the time for stiflers to reach the steady state when two rumors compete with each other [35] is shortened more than that of two rumors with mutual promotion, which is because the repeated transmission of two rumors with mutual promotion deepens the public memory and results in forgetting rate less than that of two competitive rumors. Therefore the increase in forgetting rate helps to decrease the final size of two rumors. Decision makers can release effective information to clarify the rumors and promote the increase in forgetting rate, thereby decreasing the impact of rumors.
(3) The influence of occurrence time differences.
The variation trend of the proportion of spreaders and stiflers in different occurrence time differences are shown in Fig. 8. (1) As the occurrence time differences between two rumors decreases, the peak of the spreaders of rumor 1 has a small increase, whereas the peak of rumor 2 increases obviously, and the arrival time of the peak has a small advance. Rumor 2 dies out faster with the decrease of occurrence time differences when two rumors compete with each other [46]. However, the decrease in occurrence time difference results in the widespread dissemination of rumor 1 and rumor 2 in this paper. (2) With the decrease of occurrence time differences, the final size of the stiflers of rumor 1 has no obvious change, whereas the final size of the stiflers of rumor 2 has a small increase. Namely, the decrease of occurrence time differences can result in a small increase in the final size of later rumor, and the overall situation of two rumors becomes more difficult to control. Therefore the decision makers should formulate emergency plans in advance to prevent the widespread propagation of rumors, which is caused by the continuous emergence of various rumors with mutual promotion.
6 Conclusion
In this paper, we study the propagation of two rumors with mutual promotion in new media. The mutual promotion between two rumors is first analyzed in emergency. Then a 3SI3R model is constructed according to 2SI2R model, and the equilibrium point, its stability, and the influence of the mutual promotion on the final size of two rumors in the model are derived. Finally, numerical simulations are carried out to investigate the influence of factors, that is, the mutual promotion, occurrence time differences, and the forgetting rate, on the propagation of two rumors. The significant results can be illustrated as follows. (1) The enhancement of mutual promotion between two rumors can not only accelerate the propagation of two rumors, but also enlarge their final size. (2) The increase in forgetting rate results in a decrease in the final size of two rumors. (3) The decrease of the occurrence time differences between two rumors may lead to a small increase in the final size of the later rumor, and the overall situation of two rumors becomes more difficult to be controlled.
The contributions of our work are as follows. (1) Considering that individuals may believe or spread two similar rumors, a novel 3SI3R model is proposed to research the propagation law of two rumors with mutual promotion. (2) The influence of the mutual promotion on the final size of two rumors is derived. (3) Compared with the propagation of two rumors with competition, the influence of factors, that is, the mutual promotion, occurrence time differences, and the forgetting rate, on the propagation of two rumors are analyzed considering the new characteristics, namely diversity, directivity, rapid dissemination, occurrence time differences, and forgetting rate, of the propagation of rumors in new media.
In fact, our work can be extended in several directions. On the one hand, it is natural to extend our study to multiple routes of rumors spread in heterogeneous networks. According to [55], the whole spreaders of two rumors with mutual promotion are regarded as an external virtual node that has connections with every other individual. The degree distribution of heterogeneous networks should be considered in 3SI3R model. On the other hand, we can further investigate the optimal control of the propagation of two rumors with mutual promotion and put forward the best time for government intervention. The dynamics of a variety of rumors (more than two) is also worthy of further exploration. Meanwhile, considering the spatial effects on disease spread [56–60], the spatial dynamics of rumor spread also deserves further study.
References
Zhu, L., Liu, M., Li, Y.: The dynamics analysis of a rumor propagation model in online social networks. Physica A 520, 118–137 (2019)
Pan, C., Yang, L., Yang, X., et al.: An effective rumor-containing strategy. Physica A 500, 80–91 (2018)
Zhao, J., Yang, L., Zhong, X., et al.: Minimizing the impact of a rumor via isolation and conversion. Physica A 526, 1–11 (2019)
Huo, L., Wang, L., Zhao, X.: Stability analysis and optimal control of a rumor spreading model with media report. Physica A 517, 551–562 (2019)
Xu, D., Xu, X., Xie, Y., et al.: Optimal control of an SIVRS epidemic spreading model with virus variation based on complex networks. Commun. Nonlinear Sci. Numer. Simul. 48, 200–210 (2017)
Kandhway, K., Kuri, J.: Optimal control of information epidemics modeled as Maki Thompson rumors. Commun. Nonlinear Sci. Numer. Simul. 19(12), 4135–4147 (2014)
Huo, L., Wang, L., Song, N., et al.: Rumor spreading model considering the activity of spreaders in the homogeneous network. Physica A 468, 855–865 (2017)
Hu, Y., Pan, Q., Hou, W., et al.: Rumor spreading model with the different attitudes towards rumors. Physica A 502, 331–344 (2018)
Shin, J., Jian, L., Driscoll, K., et al.: The diffusion of misinformation on social media: temporal pattern, message, and source. Comput. Hum. Behav. 83, 278–287 (2018)
Chen, G.: ILSCR rumor spreading model to discuss the control of rumor spreading in emergency. Physica A 522, 88–97 (2019)
Li, T., Wang, S., Li, B.: Research on suppression strategy of social network information based on effective isolation. Proc. Comput. Sci. 131, 131–138 (2018)
Huo, L., Ding, F., Cheng, Y.: Dynamic analysis of a \(\mathrm{SI}_{\mathrm{b}}\mathrm{I}_{\mathrm{n}}\mathrm{I}_{\mathrm{u}}\), rumor spreading model in complex social network. Physica A 523, 924–932 (2019)
Wang, J., Zhao, L., Huang, R.: SIRaRu rumor spreading model in complex networks. Physica A 398, 43–55 (2014)
Jia, J., Wu, W.: A rumor transmission model with incubation in social networks. Physica A 491, 453–462 (2018)
Huo, L., Ma, C.: Dynamical analysis of rumor spreading model with impulse vaccination and time delay. Physica A 471, 653–665 (2017)
Wang, Q., Yang, X., Xi, W.: Effects of group arguments on rumor belief and transmission in online communities: an information cascade and group polarization perspective. Inf. Manag. 55, 441–449 (2018)
Sahafizadeh, E., Ladani, B.: The impact of group propagation on rumor spreading in mobile social networks. Physica A 506, 412–423 (2018)
Ma, J., Zhu, H.: Rumor diffusion in heterogeneous networks by considering the individuals’ subjective judgment and diverse characteristics. Physica A 499, 276–287 (2018)
Jia, F., Lv, G.: Dynamic analysis of a stochastic rumor propagation model. Physica A 490, 613–623 (2018)
Jain, A., Dhar, J., Gupta, V.: Stochastic model of rumor propagation dynamics on homogeneous social network with expert interaction and fluctuations in contact transmissions. Physica A 519, 227–236 (2019)
Isham, V., Harden, S., Nekovee, M.: Stochastic epidemics and rumours on finite random networks. Physica A 389(3), 561–576 (2010)
Wang, Y., Cao, J., Li, M., et al.: Global behavior of a two-stage contact process on complex networks. J. Franklin Inst. 356(6), 3571–3589 (2019)
Li, L., Zhang, J., Liu, C., et al.: Analysis of transmission dynamics for Zika virus on networks. Appl. Math. Comput. 347, 566–577 (2019)
Zhan, X., Liu, C., Zhou, G., et al.: Coupling dynamics of epidemic spreading and information diffusion on complex networks. Appl. Math. Comput. 332, 437–448 (2018)
Wang, Y., Ma, J., Cao, J., et al.: Edge-based epidemic spreading in degree-correlated complex networks. J. Theor. Biol. 454, 164–181 (2018)
Pastor-Satorras, R., Vespignani, A.: Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86(14), 3200–3203 (2001)
Reluga, T., Smith, R., Hughes, D.: Dynamic and game theory of infectious disease stigmas. J. Theor. Biol. 476, 95–107 (2019)
Li, L., Wang, C., Wang, S., et al.: Hemorrhagic fever with renal syndrome in China: mechanisms on two distinct annual peaks and control measures. Int. J. Biomath. 11(2), 1–22 (2018)
Xing, Y., Song, L., Sun, G., et al.: Assessing reappearance factors of H7N9 avian influenza in China. Appl. Math. Comput. 309, 192–204 (2017)
Sun, G., Xie, J., Huang, S., et al.: Transmission dynamics of cholera: mathematical modeling and control strategies. Commun. Nonlinear Sci. Numer. Simul. 45, 235–244 (2017)
Zan, Y.: DSIR double-rumors spreading model in complex networks. Chaos Solitons Fractals 110, 191–202 (2018)
Liu, Y., Diao, S., Zhu, Y., et al.: SHIR competitive information diffusion model for online social media. Physica A 461, 543–553 (2016)
Wen, S., Haghighi, M., Chen, C., et al.: A sword with two edges: propagation studies on both positive and negative information in online social networks. IEEE Trans. Comput. 64(3), 640–653 (2015)
Yan, X., Jiang, P.: Effect of the dynamics of human behavior on the competitive spreading of information. Comput. Hum. Behav. 89, 1–7 (2018)
Zhu, H., Wu, H., Cao, J., et al.: Information dissemination model for social media with constant updates. Physica A 502, 469–482 (2018)
Zhang, Y., Zhu, J.: Stability analysis of I2S2R rumor spreading model in complex networks. Physica A 503, 862–881 (2018)
Trpevski, D., Tang, W., Kocarev, L.: Model for rumor spreading over networks. Phys. Rev. E 81(5), Article ID 056102 (2010)
Jie, R., Qiao, J., Xu, G., et al.: A study on the interaction between two rumors in homogeneous complex networks under symmetric conditions. Physica A 454, 129–142 (2016)
Vosoughi, S., Roy, D., Aral, S.: The spread of true and false news online. Science 359(6380), 1146–1151 (2018)
Myers, S., Leskovec, J.: Clash of the contagions: cooperation and competition in information diffusion. In: 2012 IEEE 12th International Conference on Data Mining, Brussels, Belgium, pp. 539–548 (2012)
Zhuang, Y., Chen, J., Li, Z.: Modeling the cooperative and competitive contagions in online social networks. Physica A 484, 141–151 (2017)
Zhang, Y., Tang, C., Li, C.: Cooperative and competitive dynamics model for information propagation in online social networks. J. Appl. Math. 2014(2), Article ID 610382 (2014)
Zhao, L., Cui, H., Qiu, X., et al.: SIR rumor spreading model in the new media age. Physica A 392, 995–1003 (2013)
Beutel, A., Prakash, B., Rosenfeld, R., et al.: Interacting viruses in networks: can both survive? In: Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, pp. 426–434 (2012)
Daley, D., Kendall, D.: Epidemics and rumours. Nature 204(4963), 1118 (1964)
Wang, J., Zhao, L., Huang, R.: 2SI2R rumor spreading model in homogeneous networks. Physica A 413, 153–161 (2014)
Qiu, X., Zhao, L., Wang, J., et al.: Effects of time-dependent diffusion behaviors on the rumor spreading in social networks. Phys. Lett. A 380(24), 2054–2063 (2016)
Sarafidis, Y.: What have you done for me lately? Release of information and strategic manipulation of memories. Econ. J. 117(518), 307–326 (2007)
Gromov, D., Bulla, I., Romero-Severson, E.: Systematic evaluation of the population-level effects of alternative treatment strategies on the basic reproduction number. J. Theor. Biol. 462, 381–390 (2019)
van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1–2), 29–48 (2002)
Zhang, Y., Su, Y., Weigang, L., et al.: Interacting model of rumor propagation and behavior spreading in multiplex networks. Chaos Solitons Fractals 121, 168–177 (2019)
Al-Azzawi, S.: Stability and bifurcation of pan chaotic system by using Routh–Hurwitz and Gardan methods. Appl. Math. Comput. 219(3), 1144–1152 (2012)
LaSalle, J.P.: The Stability of Dynamical Systems. CBMS–NSF Region Conference Series in Applied Mathematics, vol. 25. SIAM, Philadelphia (1976)
Arino, J., Brauer, F., van den Driessche, P., et al.: A final size relation for epidemic models. Math. Biosci. Eng. 4(2), 159–175 (2007)
Wang, Y., Cao, J., Li, X., et al.: Edge-based epidemic dynamics with multiple routes of transmission on random networks. Nonlinear Dyn. 91(1), 403–420 (2018)
Zhao, J., Tian, J.: Spatial model for oncolytic virotherapy with lytic cycle delay. Bull. Math. Biol. 81(7), 2396–2427 (2019)
Bai, Z., Peng, R., Zhao, X.: A reaction–diffusion malaria model with seasonality and incubation period. J. Math. Biol. 77(1), 201–228 (2018)
Sun, G.-Q, Jusup, M., Jin, Z., et al.: Pattern transitions in spatial epidemics: mechanisms and emergent properties. Phys. Life Rev. 19, 43–73 (2016)
Li, L.: Patch invasion in a spatial epidemic model. Appl. Math. Comput. 258, 342–349 (2015)
Robinson, M., Stilianakis, N., Drossinos, Y.: Spatial dynamics of airborne infectious diseases. J. Theor. Biol. 297, 116–126 (2012)
Acknowledgements
The authors sincerely appreciate the editor and anonymous referees for their pertinent comments and enlightening suggestions.
Availability of data and materials
The data and material used to support the findings of this study are included within this paper. It is also available from the corresponding author upon request.
Funding
This work was jointly supported by the National Natural Science Foundation of China (Project nos. 71704001 and 71601002), the Natural Science Foundation in Anhui Province (Project no. 1808085QG224), the Humanities and Social Science Key Project of Anhui Provincial Education Department (Project no. SK2019A0075), the Planning Funds of Philosophy and Social Science in Anhui Province (Project nos. AHSKY2018D13 and AHSKQ2016D19), and the Humanities and Social Sciences Foundation of Ministry of Education of China (Project no. 18YJC630249).
Author information
Authors and Affiliations
Contributions
ZW conceived the idea of the study; JL performed the simulation experiments; HN and HZ interpreted the results and collected the cases; all authors contributed to the writing and revisions. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors have declared that no competing interests exist.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Z., Liang, J., Nie, H. et al. A 3SI3R model for the propagation of two rumors with mutual promotion. Adv Differ Equ 2020, 109 (2020). https://doi.org/10.1186/s13662-020-02552-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02552-w