A modified analytical approach with existence and uniqueness for fractional Cauchy reaction–diffusion equations

Abstract

This article mainly explores and applies a modified form of the analytical method, namely the homotopy analysis transform method (HATM) for solving time-fractional Cauchy reaction–diffusion equations (TFCRDEs). Then mainly we address the error norms $L_{2}$ and $L_{\infty }$ for a convergence study of the proposed method. We also find existence, uniqueness and convergence in the analysis for TFCRDEs. The projected method is illustrated by solving some numerical examples. The obtained numerical solutions by the HATM method show that it is simple to employ. An excellent conformity obtained between the solution got by the HATM method and the various well-known results available in the current literature. Also the existence and uniqueness of the solution have been demonstrated.

1 Introduction

The beginning of fractional calculus is considered as 30 September 1695 when the derivative of arbitrary order was described by Leibniz [1]. After that many renowned mathematicians have studied the application of the fractional derivative and fractional differential equations (FDEs); some of them were Liouville, Grunwald, Letnikov and Riemann [2]. A lot of significant phenomena are well described by FDEs in electromagnetics, acoustics, viscoelasticity, electro chemistry and material science [3]. Moreover, some basic results associated to solving FDEs may be found in [4–7].

Cauchy reaction–diffusion equations (CRDEs) explain a large multiplicity of nonlinear systems in physics, chemistry, ecology, biology and engineering [8–12]. CRDEs are broadly used in application models for spatial effects in ecology. The different types of CRDEs in physics have been solved [13–15] by using a variety of kinds of analytical methods. In recent times, Yildirim [16] used a homotopy perturbation method to find the solutions of the CRDEs. In this paper, we consider the one-dimensional TFCRDEs as follows:

$$ \frac{\partial^{\lambda}w(x,t)}{\partial t^{\lambda}}=D \frac{\partial ^{2}w(x,t)}{\partial x^{2}}+r(x,t)w(x,t), \quad0 < \lambda\le1, (x,t) \in\varOmega\subset\mathbb{R}^{2}, $$

(1.1)

subject to the initial or boundary conditions

$$ w(x,0)=g(x),\qquad w(0,t)=f_{0}(t),\qquad \frac{\partial w(0,t)}{\partial x}=f_{1}(t),\quad x,t \in\mathbb{R} , $$

(1.2)

where w is the concentration, r is the reaction parameter and $D>0$ is the diffusion coefficient. The fractional derivative λ considered in this paper is in the sense of Caputo.

In this paper, we have applied HATM for solving linear and nonlinear TFCRDEs. The HATM method provides excellent agreement between two powerful methods, one is the most popular and useful homotopy analysis method (HAM) and the other one is the Laplace transform method. The HAM was first proposed and applied by Liao in [17] to solve lots of nonlinear problems. The HAM has been successfully applied by many researchers for solving linear and nonlinear partial differential equations [18, 19].

But presently, concentration of diverse researchers is on finding the solution behavior of different nonlinear equations by means of different methods jointed with Laplace transform, among them the variation iteration transform method [20] and the homotopy analysis transform method [21, 22]. The advantage of HATM over HAM is that it gives rapidly convergent series solution only by taking a small number of terms and hence HATM is very powerful and efficient in finding approximate solutions as well as analytical solutions of many fractional physical models. Moreover, the analytical method of using the Laplace transform and its inverse is shown in [23–25]. The other work related to this can be found in [26–34]. The plan of this article is to find approximate analytical solutions of TFCRDEs with the time derivative λ ($0 < \lambda\le1$).

2 Existence and uniqueness

In this section, we establish the existence and uniqueness of a solution of differential equation (1.1). We first present a few necessary definitions.

The Mittag-Leffler function is defined by

$$ E_{\lambda}(t)= \sum ^{\infty}_{k=0}{\frac{t^{k\lambda}}{\varGamma (1+\lambda k)}}. $$

(2.1)

The Riemann–Liouville fractional integral of order $\lambda>0$ is defined by

$$ I^{\lambda}f(t)=\frac{1}{\varGamma(\lambda)} \int_{0}^{t}(t-s)^{\lambda-1}f(s)\,ds, $$

(2.2)

the fractional derivative of the function f of order $\lambda>0$ is defined by

$$\begin{aligned} D_{t}^{\lambda}f(t)= \frac{1}{\varGamma(n-\lambda)}\frac{d^{n}}{dt^{n}} \int _{0}^{t}(t-s)^{n-\lambda-1}f(s)\,ds, \end{aligned}$$

(2.3)

where $\varGamma(\lambda)$ is the Gamma function.

The Laplace transform of the Riemann–Liouville fractional integral is defined as [1]

$$\begin{aligned} L \bigl[I^{\lambda}f(t) \bigr](s)=s^{-\lambda}\mathcal{F}(s). \end{aligned}$$

(2.4)

The Caputo fractional derivative of the function f of order $\lambda >0$ is defined by

$$\begin{aligned} D^{\lambda}_{t} f(t) = \frac{1}{\varGamma(n-\lambda)} \int_{0}^{t} t^{n-\lambda-1} \frac{d^{n}}{dt^{n}}f(t) \,dt. \end{aligned}$$

(2.5)

The Laplace transform of the Caputo fractional derivative is defined as [1]

$$\begin{aligned} L \bigl[D_{t}^{\lambda}f(t) \bigr] (s)=s^{\lambda}\mathcal{F}(s)-\sum_{k=0}^{n-1}s^{\lambda-k-1}f^{k}(0), \quad n-1< \lambda\le n, n \in \mathbb{N}. \end{aligned}$$

(2.6)

Define an operator $A=D\frac{\partial^{2}}{\partial x^{2}}$, with $D(A)=\{v \in H^{1}_{0}(0,1) \cap H^{2}(0,1): v^{\prime\prime} \in L^{2}(0,1)\}$. The operator A is the infinitesimal generator of an analytic semigroup $\{ T(t) : t \ge0\}$ and is self-adjoint [35]. By introducing $v(t)x = w(x, t)$ and $\gamma(t)x=r(x,t)$, Eq. (1.1) can be written as

$$\begin{aligned} D^{\lambda}_{t} v = A v + \gamma(t)v. \end{aligned}$$

(2.7)

By a mild solution v of the above problem we mean that

$$\begin{aligned} v(t)=v_{0}+\frac{1}{\varGamma(\lambda)} A \int_{0}^{t} \frac {v(s)}{(t-s)^{1-\lambda}}\,ds+\frac{1}{\varGamma(\lambda)} \int_{0}^{t} \frac {\gamma(s)v(s)}{(t-s)^{1-\lambda}}\,ds, \end{aligned}$$

(2.8)

provided $\int_{0}^{t} \frac{v(s)}{(t-s)^{1-\lambda}}\,ds \in\mathcal{D}$. The notation $\mathcal{D}$ is for the domain of the operator A equipped with the graph norm $\|v\|_{\mathcal{D}}=\|v\|+\|Av\|$. It is not difficult to check that $f(t,v)=\gamma(t)v$ satisfies the Lipschitz condition. For any $v_{1}, v_{2} \in D(A)$, we have

$$\bigl\Vert f(t,v_{1})-f(t,v_{2}) \bigr\Vert \le \bigl\vert \gamma(t) \bigr\vert \Vert v_{1}-v_{2} \Vert \le \gamma^{*} \Vert v_{1}-v_{2} \Vert , $$

where $\gamma^{*}$ is the supremum of $\gamma(t)$. So we need $\gamma(t)$ to be continuous and bounded.

The spectrum of the operator A is discrete with eigenvalues $\mu _{n}=-n^{2}D$, $n\in\mathbb{N,}$ and the eigenfunctions are of the form $\psi _{n}(z)= (\frac{2}{\pi} )^{\frac{1}{2}} \sin n z$. Moreover, $\{\psi_{n} : n \in\mathbb{N}\}$ is an orthonormal basis for X, and

$$T(t)v=\sum_{n=1}^{\infty}e^{-n^{2}D t}\langle v, \psi_{n}\rangle\psi_{n}, \quad v \in X, t > 0. $$

The above expression implies that $\{T(t), t\ge0\}$ is a uniformly bounded compact semigroup and $R(\mu, A) = (\mu I - A)^{-1}$ is a compact operator for all $\mu\in\rho(A)$. The integral equation

$$v(t)=\frac{1}{\varGamma(\lambda)} \int_{0}^{t} \frac{Av(s)}{(t-s)^{1-\lambda }}\,ds, \quad t \ge0, $$

has an associated resolvent operator $\{S _{\lambda}(t), t\ge0 \}$ on the space $X=L^{2}(0,1)$. The resolvent operator is given by

$$S_{\lambda}(t)=\frac{1}{2 \pi i} \int_{\gamma_{\theta}}e^{\mu t} \bigl(\mu ^{\lambda}-A \bigr)^{-1}\,d\mu,\quad t >0 , $$

and $S(0)=I$. We have the parameter θ with $\frac{\pi}{2}<\theta< \pi$ and the curve $\gamma_{\theta}=\{re^{i\theta}: r \ge0\} \cup\{re^{-i\theta : r \ge0}\}$.

Because $(\mu I-A)^{-1}$ is compact, from the above representation one can deduce that $\{S_{\lambda}(t): t >0\}$ is a compact operator.

Theorem 2.1

Let $\gamma\in L^{p}([0,T]:\mathbb{R}^{+})$for $p =\frac{1}{\lambda}$. If $\frac{1}{\varGamma\lambda} \sup_{s \in[0,T]} (\int_{0}^{s} \frac{\gamma (t)}{(s-t)^{1-\alpha}}\,dt ) <1$, then the abstract Cauchy problem has a unique mild solution.

The proof is similar to Theorem 2.1 of [36].

3 Fundamental scheme of HATM

The fundamental scheme of HATM is discussed through the following TFCRDEs:

$$\begin{aligned} \begin{gathered} D^{ \lambda}_{t} w(x,t)= D D_{xx}w(x,t)+ r(x,t) w(x,t), \\ 0< \lambda\leq1,\qquad (x,t)\in\varOmega\subset R^{2}.\end{gathered} \end{aligned}$$

(3.1)

By a new methodology discussed in [21], applied to Eq. (3.1), we get the mth-order deformation equation $w_{m}(x,t)$ and for $m \ge1$, at Mth order, we have

$$ w(x,t)=\sum_{m=0}^{M} w_{m}(x,t), $$

(3.2)

for $M \rightarrow\infty$, we get a precise approximation of the actual equation (3.1).

In this section, we study the convergence of HATM through the following theorem.

Theorem 3.1

As long as the series solution

$$ w(x,t)=w_{0}(x,t)+\sum_{m=1}^{\infty} w_{m}(x,t) $$

(3.3)

converges, where $w_{m}(x,t)$is governed by Eq. (3.1), it must be the exact solution of the TFCRDEs in (3.1).

Proof

If the series (3.3) converges, we can write

$$ T(x,t)=\sum_{m=0}^{\infty} w_{m}(x,t) $$

(3.4)

and

$$ \lim_{m\rightarrow\infty}w_{m}(x,t)=0. $$

(3.5)

We can verify that

$$ \sum_{m=1}^{n} \bigl[w_{m}(x,s)- \xi_{m}w_{m-1}(x,s) \bigr] = \lim_{m\rightarrow\infty}w_{m}(x,s)=0. $$

(3.6)

Taking the linear operator $\mathcal{L}$ on both sides in Eq. (3.6), we get

$$ \sum_{m=1}^{\infty} \mathcal{L} \bigl[w_{m}(x,s)-\xi_{m}w_{m-1}(x,s) \bigr] = \mathcal {L} \Biggl[\sum_{m=1}^{\infty}w_{m}(x,s)- \xi_{m}w_{m-1}(x,s) \Biggr]=0. $$

(3.7)

Along this line, we obtain

$$ \sum_{m=1}^{\infty}\mathcal{L} \bigl[w_{m}(x,s)-\xi_{m}w_{m-1}(x,s) \bigr] =\hbar H(x,s)\sum_{m=1}^{\infty} R_{m} ( \vec{w}_{m-1},x, s)=0, $$

(3.8)

since $\hbar\neq0$ and $H(x,s)\neq0$, from Eq. (3.8) we have

$$\begin{aligned}& \sum_{m=1}^{\infty} R_{m}( \vec{w}_{m-1},x,s)=0, \\& \begin{aligned} \sum_{m=1}^{\infty} R_{m}( \vec{w}_{m-1},x,s) & = \sum_{m=1}^{\infty} \Biggl[s^{\lambda} L[w_{m-1}](s)-(1-\xi _{m})\sum _{k=0}^{n-1} s^{\lambda-k-1}w_{m-1}^{k}(x,0) \\ & \quad - L[ D D_{xx}w_{m-1}+ r w_{m-1}](s) \Biggr] \\ & = s^{\lambda} L \Biggl[\sum_{m=1}^{\infty} w_{m-1} \Biggr](s)-\sum_{k=0}^{n-1} s^{\lambda-k-1}w_{m-1}^{k}(x,0) \\ & \quad - L \Biggl[ D D_{xx}{\sum_{m=1}^{\infty}w_{m-1}}+ r {\sum_{m=1}^{\infty}w_{m-1}} \Biggr](s) \\ & = s^{\lambda} L \bigl[T(x,t) \bigr](s)-\sum _{k=0}^{n-1} s^{\lambda -k-1}T^{k}(x,0) \\ & \quad -L \bigl[ D D_{xx} \bigl[T(x,t) \bigr]+ r(x,t) \bigl[T(x,t) \bigr] \bigr](s) \\ & = L \bigl[D^{ \lambda}_{t} T(x,t) \bigr](s)-L \bigl[ D D_{xx}T(x,t)+ r(x,t) T(x,t) \bigr](s). \end{aligned} \end{aligned}$$

(3.9)

Now from Eq. (3.9) we have

$$ L \bigl[D^{ \lambda}_{t} T(x,t) \bigr](s)- L \bigl[ D D_{xx}T(x,t)+ r(x,t) T(x,t) \bigr](s)=0. $$

(3.10)

By taking the inverse Laplace transform in Eq. (3.10), we get the exact solution $T(x,t)$. □

4 Function of HATM and mathematical results

Four examples of TFCRDEs are solved to exhibit the HATM method. In the whole article, MATHEMATICA 7 software package has been used for the figures’ computational processes.

Example 1

For the constant value of $D=1$ and $r=-1$, Eq. (1.1) can be recast as the Kolmogorov–Piskunov (KP) equation [16] as follows:

$$ \frac{\partial^{\lambda}w(x,t)}{\partial t^{\lambda}} = \frac{\partial ^{2}w(x,t)}{\partial x^{2}}-w(x,t), \quad0 < \lambda \le1, (x,t) \in \varOmega\subset\mathbb{R}^{2}, $$

(4.1)

subject to the initial or boundary conditions

$$\begin{gathered}w(x,0)=e^{-x}+x=g(x),\quad\quad w(0,t)=1=f_{0}(t),\\ \frac{\partial w(0,t)}{\partial x}= E_{\lambda} \bigl(-t^{\lambda} \bigr)-1=f_{1}(t),\quad x, t \in\mathbb{R}.\end{gathered} $$

By a new methodology discussed in [21], applied to Eq. (4.1) we get the mth-order deformation equation for $w_{m}(x,t)$

$$ w_{m}(x,t) =(\xi_{m}+\hbar) w_{m-1}-\hbar(1- \xi_{m}) \bigl(e^{-x}+x \bigr)-\hbar L^{-1} \bigl[s^{-\lambda} L[D_{xx} w_{m-1} -w_{m-1}](s) \bigr](t). $$

(4.2)

At last,

$$w(x,t)=w_{0}(x,t)+\sum_{m=0}^{\infty}w_{m}(x,t). $$

Next, the successive iterative values are

$$\begin{aligned}& w_{1}(x,t)=\frac{\hbar x t^{\lambda}}{\varGamma(\lambda+1)}, \\& w_{2}(x,t)=\frac{\hbar(1+\hbar) x t^{\lambda}}{\varGamma(\lambda+1)}+\frac {\hbar^{2} x t^{2\lambda}}{\varGamma(2\lambda+1)}, \\& w_{3}(x,t)=\frac{\hbar(1+\hbar)^{2} x t^{\lambda}}{\varGamma(\lambda +1)}+\frac{2\hbar^{2}(1+\hbar) x t^{2\lambda}}{\varGamma(2\lambda+1)}+\frac {\hbar^{3} x t^{3\lambda}}{\varGamma(3\lambda+1)}, \\& w_{4}(x,t)=\frac{\hbar(1+\hbar)^{3} x t^{\lambda}}{\varGamma(\lambda +1)}+\frac{3h^{2}(1+\hbar)^{2} x t^{2\lambda}}{\varGamma(2\lambda+1)}+\frac {3\hbar^{3}(1+\hbar) x t^{3\lambda}}{\varGamma(3\lambda+1)} +\frac{\hbar^{4} x t^{4\lambda}}{\varGamma(4\lambda+1)}+\cdots. \end{aligned}$$

In a similar fashion, the remaining terms of $w_{m}(x,t)$ for $m \ge5$ can be entirely obtained.

Therefore, the solution of Eq. (4.1) is

$$ w(x,t)=\sum_{k=0}^{\infty} w_{k}(x,t). $$

(4.3)

If we select $\hbar=-1$, then the solution is reduced to

$$\begin{aligned} w(x,t) =& e^{-x}+x \biggl(1+\frac{(-t^{\lambda})}{\varGamma(\lambda+1)}+\frac {(-t^{\lambda})^{2}}{\varGamma(2\lambda+1)}+ \frac{(-t^{\lambda})^{3}}{\varGamma(3\lambda+1)}+\frac{(-t^{\lambda })^{4}}{\varGamma(4\lambda+1)}+\cdots \biggr) \\ =&e^{-x}+x\sum_{k=0}^{\infty} \frac{(-t^{\lambda})^{k}}{\varGamma(k\lambda+1)} \\ =&e^{-x}+x E_{\lambda} \bigl(-t^{\lambda} \bigr). \end{aligned}$$

(4.4)

Again if we take the standard value of $\lambda=1$, then the series solution is reduced to $e^{-x}+ x e^{-t}$, this is an exact solution of standard CRDEs and hence the result is absolutely in conformity with the homotopy perturbation given by Yildirim [16] and the Adomian decomposition method by Lesnic [13].

Figure 1 demonstrates the comparisons of the exact solution and the approximate solutions with different Brownian motions. The picture of subfigures (a), (b), (c) and (d) for Fig. 1 shows that the approximate solution obtained by the current method and the exact solution are very much identical for the Cauchy problem with the constant term $D=1$.

Figure 1

The surface graph of the exact solution $u(x,t)$ and the seventh-order approximate solution $u_{7}(x,t)$ of Eq. (4.1): (a) $u(x,t)$ when $\lambda=1$, (b) $u_{7}(x,t)$ when $\lambda=1$, (c) $u_{7}(x,t)$ when $\lambda=0.75$, (d) $u_{7}(x,t)$ when $\lambda=0.5$

At the same time, in order to judge the significance and the correctness of the HATM method the absolute error curve is drawn in Fig. 2. It is to be noted that the approximate solution converges quickly towards the exact one.

Figure 2

Plot of absolute error $E_{7}(w)= \vert w(x,t)-w_{7}(x,t) \vert$ using HATM when $\lambda=1$

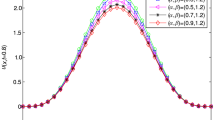
Figure 3 indicates the performance of the approximate solution for different fractional Brownian motions, $\lambda=0.7, 0.8,0.9$, and for standard motion i.e. at $\lambda=1$.

Figure 3

Plot of $u(x,t)$ verses x time for different values of λ at $t=1$ and $\hbar=-1$

Figure 4 reflects the ħ curve of Eq. (4.1). As pointed out by Liao [17], we can choose any values of ħ, where $\hbar\in(\hbar_{1}, \hbar_{2} )$ and $\hbar_{1} \approx-1.80$, $\hbar_{2} \approx-0.2$. In the particular case if $\hbar=-1$ the speed of convergence is most advantageous.

Figure 4

Plot of ħ curve for different values of λ at $x=0.5$ and $t=0.01$

In order to convergence study of the proposed method we present the absolute errors in Table 1, simultaneously the error norms $L_{2}$ and $L_{\infty}$ are presented in Table 2.

Table 1 $E_{7}$ in the solution of TFCRDEs using HATM for $\lambda=1$

Table 2 $L_{2}$ and $L_{\infty}$ error norms for TFCRDEs by HATM for $\lambda=1$

At the mth order of approximation, also we can define the exact square residual error for equation, where

$$\Delta_{m}= \int_{0}^{1} \int_{0}^{1} \Biggl(N \Biggl[\sum _{i=0}^{m} w_{i}(x,t) \Biggr] \Biggr)^{2}\,dx\,dt,$$

where

$$N \bigl[w(x,t) \bigr]= \frac{d^{\lambda}w(x,t)}{dt^{\alpha }}- \frac{d^{2} w(x,t)}{dx^{2}}+w(x,t). $$

In order to make things computationally easy we also introduced here the so-called averaged residual error defined by

$$E_{m}=\frac{1}{25} \sum_{j=1}^{5} \sum_{k=1}^{5} \Biggl( N \Biggl[\sum _{i=0}^{m} u_{i} \biggl( \frac{j}{10}, \frac{k}{10} \biggr) \Biggr] \Biggr)^{2}. $$

The optimal value of ħ can be found by solving nonlinear algebraic equation $\frac{dE_{m}}{d\hbar}=0$ [37]. The numerical results are elaborated in Tables 3 and 4.

Table 3 Optimal value of ħ for $\lambda=1$

Table 4 Optimal value of ħ for $\lambda=0.9$

It is clear from Tables 3 and 4 that the optimal value of ħ are −0.826476, −0.939232, −0.964903 and −0.79381, −0.918672, −0.950037, respectively, in the case of different orders of approximations.

Example 2

We take the following TFCRDEs [16] for $D=1$ and $r(x,t)=-1-4x^{2}$:

$$ \frac{\partial^{\lambda}w(x,t)}{\partial t^{\lambda}}= \frac{\partial ^{2}w(x,t)}{\partial x^{2}}- \bigl(1+4x^{2} \bigr)w(x,t), \quad0 < \lambda\le1, (x,t) \in\varOmega\subset\mathbb{R}^{2}, $$

(4.5)

subject to the initial or boundary conditions

$$w(x,0)=e^{x^{2}}=g(x),\qquad w(0,t)= E_{\lambda} \bigl(t^{\lambda} \bigr)=f_{0}(t), \qquad\frac {\partial w(0,t)}{\partial x}=0=f_{1}(t),\quad x, t \in \mathbb{R}. $$

Now similar to Example 1, the mth-order deformation equation (4.5) is

$$\begin{aligned}[b] w_{m}(x,t)&=(\xi_{m}+\hbar) w_{m-1}-\hbar(1- \xi_{m})e^{x^{2}}-\hbar L^{-1} \bigl[s^{-\lambda} L \bigl[D_{xx} w_{m-1} \\ &\quad- \bigl(4x^{2}+1 \bigr)w_{m-1} \bigr](s) \bigr](t).\end{aligned} $$

(4.6)

At last, we get

$$w(x,t)=w_{0}(x,t)+\sum_{m=0}^{\infty}w_{m}(x,t). $$

By taking $w_{0}(x,t)=w(x,0)=e^{x^{2}}$ and the system (4.6), we get the subsequent values as follows:

$$\begin{aligned}& w_{1}(x,t)=-\frac{\hbar e^{x^{2}} t^{\lambda}}{\varGamma(\lambda+1)}, \\& w_{2}(x,t)=-\frac{\hbar(1+\hbar) e^{x^{2}} t^{\lambda}}{\varGamma(\lambda +1)}+\frac{\hbar^{2} e^{x^{2}} t^{2\lambda}}{\varGamma(2\lambda+1)}, \\& w_{3}(x,t)=-\frac{\hbar(1+\hbar)^{2} e^{x^{2}} t^{\lambda}}{\varGamma(\lambda +1)}+\frac{2\hbar^{2}(1+\hbar) e^{x^{2}} t^{2\lambda}}{\varGamma(2\lambda +1)}- \frac{\hbar^{3} e^{x^{2}} t^{3\lambda}}{\varGamma(3\lambda+1)}, \\& w_{4}(x,t)=-\frac{\hbar(1+\hbar)^{3} e^{x^{2}} t^{\lambda}}{\varGamma(\lambda +1)}+\frac{3\hbar^{2}(1+\hbar)^{2} e^{x^{2}} t^{2\lambda}}{\varGamma(2\lambda +1)}- \frac{3\hbar^{3}(1+\hbar) e^{x^{2}} t^{3\lambda}}{\varGamma(3\lambda+1)} +\frac{\hbar^{4} e^{x^{2}} t^{4\lambda}}{\varGamma(4\lambda+1)}+\cdots. \end{aligned}$$

The solution of Eq. (4.5) for $\hbar=-1$ is given as

$$\begin{aligned} w(x,t) =& e^{x^{2}} \biggl(1+\frac{t^{\lambda}}{\varGamma(\lambda+1)}+\frac {t^{2\lambda}}{\varGamma(2\lambda+1)}+ \frac{t^{3\lambda}}{\varGamma(3\lambda+1)}+\frac{t^{4\lambda}}{\varGamma (4\lambda+1)}+\cdots \biggr) \\ =&e^{x^{2}}\sum_{k=0}^{\infty} \frac{t^{k\lambda}}{\varGamma(k\lambda+1)} \\ =&e^{x^{2}}E_{\lambda} \bigl(t^{\lambda} \bigr). \end{aligned}$$

(4.7)

Next for the standard value of $\lambda=1$, the above series solution reduced to $e^{-x}+ x e^{-t}$, this is an exact solution of standard CRDEs and hence the result is absolutely conformity with that the homotopy perturbation given by Yildirim [16] and the Adomian decomposition method by Lesnic [13].

Figure 5 shows the comparison between the exact and the approximate solution for Example 2 obtained by HATM for different values of λ.

Figure 5

The surface graph of the exact solution $u(x,t)$ and the seventh-order approximate solution $u_{7}(x,t)$ of Eq. (4.5): (a) $u(x,t)$ when $\lambda=1$, (b) $u_{7}(x,t)$ when $\lambda=1$, (c) $u_{7}(x,t)$ when $\lambda=0.75$, (d) $u_{7}(x,t)$ when $\lambda=0.5$

Again, the convergence of the above method for Eq. (4.5) is shown by drawing the absolute error curve.

Figure 6 represents the absolute error between exact and obtained solution.

Figure 6

Plot of absolute error $E_{7}(w)= \vert w(x,t)-w_{7}(x,t) \vert$ using HATM when $\lambda=1$

Figure 7 reveals the performance of the estimated solution $w(x,t)$ for Example 2.

Figure 7

Plot of $u(x,t)$ verses x time for different values of λ at $t=1$ and $\hbar=-1$

In Fig. 8 the ħ curve for Eq. (4.5) is shown. It is clear from Fig. 8 that the perfect range of ħ is from −1.60 to −0.3.

Figure 8

Plot of ħ curve for different values of λ at $x=0.5$ and $t=0.01$

Table 5 lists the absolute error $E_{7}= \vert w(x,t)-w_{7}(x,t) \vert$ obtained for different values of x and t by using the seventh-order approximate solution. Again, to show the validity and exactness of the proposed method the error norms $L_{2}$ and $L_{\infty}$ are presented in Table 6.

Table 5 $E_{7}$ in the solution of TFCRDEs by HATM for $\lambda=1$

Table 6 The error norm in the solution of TFCRDEs by HATM for $\lambda=1$

Example 3

We consider the following TFCRDEs [14] for $D=1$ and $r(x,t)= -1+ \operatorname{cos}x-\operatorname{sin}^{2} x$:

$$ \frac{\partial^{\lambda}w(x,t)}{\partial t^{\lambda}}= \frac{\partial ^{2}w(x,t)}{\partial x^{2}}- \bigl(-1+ \operatorname{cos}x-\operatorname{sin}^{2} x \bigr) w(x,t), \quad0 < \lambda\le1, (x,t) \in\varOmega\subset\mathbb{R}^{2}, $$

(4.8)

subject to the initial or boundary conditions

$$\begin{gathered} w(x,0)= \frac{1}{10} e^{\operatorname{cos}x-11} =g(x),\qquad w(0,t)= \frac {1}{10} e^{-10} E_{\lambda} \bigl(t^{-\alpha} \bigr) = f_{0}(t), \\\frac{\partial w(0,t)}{\partial x}= 0 =f_{1}(t).\end{gathered} $$

The exact solution $w(x,t)=\frac{1}{10} e^{\operatorname{cos}x-t-11}$ for $\lambda=1$.

By using the aforementioned techniques, in this case the solution of the mth-order deformation equations is as follows:

$$\begin{aligned} w_{m}(x,t)&=(\xi_{m}+\hbar) w_{m-1}-\hbar(1-\xi_{m})e^{x^{2}}-\hbar L^{-1} \bigl[s^{-\lambda}L \bigl[D_{xx} w_{m-1} \\ &\quad - \bigl(-1+ \operatorname{cos}x-\operatorname{sin}^{2} x \bigr) w_{m-1} \bigr](s) \bigr](t). \end{aligned}$$

(4.9)

By taking $w_{0}(x,t)=w(x,0)=\frac{1}{10} e^{\operatorname{cos}x-10}$ and the system (4.6), we get the subsequent values as follows:

$$\begin{aligned} w_{1}(x,t) =&\frac{\hbar e^{-11+ \operatorname{cos}x} t^{\lambda}}{10 \varGamma(\lambda+1)}, \\ w_{2}(x,t) =& \frac{\hbar(1+\hbar) e^{-11+ \operatorname{cos}x} t^{\lambda}}{10 \varGamma(\lambda+1)} + \frac{\hbar^{2} e^{-11+ \operatorname{cos}x} t^{2\lambda}}{10 \varGamma(2\lambda+1)}, \\ w_{3}(x,t) =& \frac{\hbar(1+\hbar)^{2} e^{-11+ \operatorname{cos}x} t^{\lambda}}{10 \varGamma(\lambda+1)} + \frac{\hbar^{2} (1+\hbar) e^{-11+ \operatorname{cos}x} t^{2\lambda}}{5 \varGamma(2\lambda+1)} + \frac{\hbar ^{3} e^{-11+ \operatorname{cos}x} t^{3\lambda}}{10 \varGamma(3\lambda+1)}. \end{aligned}$$

If we select $\hbar=-1$, then

$$\begin{aligned} w(x,t)&= \frac{1}{10} e^{\operatorname{cos}x-11}- \frac{e^{\operatorname {cos}x-11} t^{\lambda}}{10 \varGamma(\lambda+1)}+ \frac{e^{\operatorname {cos}x-11} t^{2\lambda}}{10 \varGamma(2\lambda+1)}+\frac{e^{\operatorname {cos}x-11} t^{3\lambda}}{11 \varGamma(3\lambda+1)}+\cdots \\ & = \frac{1}{10} e^{\operatorname{cos}x-11} \biggl[1-\frac {t^{\lambda}}{\varGamma(\lambda+1)} + \frac{t^{2\lambda}}{\varGamma(2\lambda +1)}+ \frac{t^{3\lambda}}{\varGamma(3\lambda+1)}+\cdots \biggr] \\ & = \frac{1}{10} e^{\operatorname{cos}x-11} \sum ^{\infty }_{k=0}{\frac{(-t)^{k}}{\varGamma(k\lambda+1)}} \\ & = \frac{1}{10} e^{\operatorname{cos}x-11} E_{\lambda} \bigl(-t^{\alpha} \bigr). \end{aligned}$$

(4.10)

For $\lambda=1$, this series is reduced to the closed form $\frac {1}{10} e^{\operatorname{cos}x-t-11}$, which is an exact solution of the classical CRDEs and hence the result is absolutely in conformity with the variation iteration method given by Dehghan [14].

Figure 9 shows the assessment among the exact and estimated solution. To ensure the exactness of the HATM method the absolute error curve is given in Fig. 10. Again, Fig. 11 shows the performance of the $u_{7}(x,t)$ for diverse term of λ.

Figure 9

The surface graph of the exact solution $u(x,t)$ and the seventh-order approximate solution $u_{7}(x,t)$ of Eq. (4.8): (a) $u(x,t)$ when $\lambda=1$, (b) $u_{7}(x,t)$ when $\lambda=1$, (c) $u_{7}(x,t)$ when $\lambda=0.75$, (d) $u_{7}(x,t)$ when $\lambda=0.5$

Figure 10

Plot of absolute error $E_{7}(w)= \vert w(x,t)-w_{7}(x,t) \vert$ using HATM when $\lambda=1$

Figure 11

Plot of $u(x,t)$ verses x time for different values of λ at $t=1$ and $\hbar=-1$

Figure 12 shows the ħ curve. Here we can choose any values of ħ, where $\hbar\in(\hbar_{1}, \hbar_{2} )$ and $\hbar_{1} \approx-1.70$, $\hbar_{2} \approx-0.5$.

Figure 12

Plot of ħ curve for different values of λ at $x=0.5$ and $t=0.01$

Example 4

Here we have taken the following TFCRDEs [38]:

$$ \frac{\partial^{\lambda}w(x,t)}{\partial t^{\lambda}}= \frac{\partial }{\partial x} \biggl(w\frac{\partial w}{\partial x} \biggr) + w-w^{2}, \quad 0 < \lambda\le1, x, t \geq0, $$

(4.11)

subject to the initial or boundary conditions

$$\begin{gathered} w(x,0)= 1- e^{\frac{-x}{\sqrt{2}}} =g(x),\qquad w(0,t)= 1- E_{\lambda } \bigl(-t^{\frac{\lambda}{2}} \bigr) =f_{0}(t),\\ \frac{\partial w(0,t)}{\partial x}= \frac{1}{\sqrt{2}} E_{\lambda} \bigl(-t^{\frac{\lambda}{2}} \bigr) =f_{1}(t).\end{gathered} $$

The exact solution $w(x,t)= 1- e^{\frac{-x}{\sqrt{2}} -\frac{t}{2}}$ for $\lambda=1$.

By using the aforementioned techniques, in this case the solution of the mth-order deformation equations is as follows:

$$ \begin{aligned}[b]w_{m}(x,t)&=(\xi_{m}+\hbar) w_{m-1}-\hbar(1-\xi_{m}) \bigl(1- e^{\frac{-x}{\sqrt {2}}} \bigr)- \hbar L^{-1} \Biggl[s^{-\lambda}L \Biggl[\sum ^{\infty}_{k=0}{ \bigl(w_{m-1-k}(w_{k})_{x} \bigr)_{x}} \\ &\quad + w_{m-1}- \sum^{\infty}_{k=0}{w_{m-1-k} (w_{k})} \Biggr](s) \Biggr](t).\end{aligned} $$

(4.12)

By taking $w_{0}(x,t)=w(x,0)=1- e^{\frac{-x}{\sqrt{2}}}$ and the system (4.6), we get the subsequent values as follows:

$$\begin{aligned}& w_{1}(x,t)=\frac{-\hbar e^{\frac{-x}{\sqrt{2}}} t^{\lambda}}{2 \varGamma (\lambda+1)}, \\& w_{2}(x,t)= \frac{-\hbar(1+\hbar) e^{\frac{-x}{\sqrt{2}}} t^{\lambda }}{2 \varGamma(\lambda+1)}-\frac{\hbar^{2} e^{\frac{-x}{\sqrt{2}}} t^{\lambda}}{4 \varGamma(2\lambda+1)}, \\& w_{3}(x,t)= \frac{-\hbar(1+\hbar)^{2} e^{\frac{-x}{\sqrt{2}}} t^{\lambda }}{2 \varGamma(\lambda+1)}-\frac{\hbar^{2}(1+\hbar) e^{\frac{-x}{\sqrt {2}}} t^{2\lambda}}{2 \varGamma(2\lambda+1)} - \frac{\hbar^{3} e^{\frac {-x}{\sqrt{2}}} t^{3\lambda}}{8 \varGamma(3\lambda+1)}. \end{aligned}$$

Figure 13 shows the comparison between the exact and approximate solution obtained by HATM method. The absolute error curve is presented in Fig. 14.

Figure 13

The surface graph of the exact solution $u(x,t)$ and the seventh-order approximate solution $u_{7}(x,t)$ of Eq. (4.11): (a) $u(x,t)$ when $\lambda=1$, (b) $u_{7}(x,t)$ when $\lambda=1$, (c) $u_{7}(x,t)$ when $\lambda=0.75$, (d) $u_{7}(x,t)$ when $\lambda=0.5$

Figure 14

Plot of absolute error $E_{7}(w)= \vert w(x,t)-w_{7}(x,t) \vert$ using HATM when $\lambda=1$