A fast numerical method for fractional partial differential equations

Abstract

In this paper, we use operational matrices of Chebyshev polynomials to solve fractional partial differential equations (FPDEs). We approximate the second partial derivative of the solution of linear FPDEs by operational matrices of shifted Chebyshev polynomials. We apply the operational matrix of integration and fractional integration to obtain approximations of (fractional) partial derivatives of the solution and the approximation of the solution. Then we substitute the operational matrix approximations in the FPDEs to obtain a system of linear algebraic equations. Finally, solving this system, we obtain the approximate solution. Numerical experiments show an exponential rate of convergence and hence the efficiency and effectiveness of the method.

1 Introduction

We consider a fractional partial differential equation (FPDE) of the form

$$ \rho _{1}\frac{\partial ^{\alpha }u(x,y)}{\partial x^{\alpha }}+\rho _{2}\frac{\partial ^{\beta }u(x,y)}{\partial y^{\beta }}+\rho _{3} \frac{ \partial u(x,y)}{\partial x}+\rho _{4}\frac{\partial u(x,y)}{\partial y}+\rho _{5} u(x,y)=f(x,y), $$

(1)

on $(x,y)\in [0,1]\times [0,1]$, with initial conditions:

$$ u(0,y)=g(y), u(x,0)=h(x) \quad\bigl(\text{with consistency condition } h(0)=g(0)=h_{0} \bigr), $$

where $\rho _{i}$ for $i=1, \ldots, 5$ are constants real numbers, f, g and h are known continuous functions and u is unknown functions with $0\leq \alpha,\beta \leq 1$. Here, $\frac{ \partial ^{\alpha }u(x,y)}{\partial x^{\alpha }}$ and $\frac{ \partial ^{\beta }u(x,y)}{\partial y^{\beta }}$ are fractional derivatives in Caputo sense, defined by

$$ \frac{\partial ^{\alpha }u(x,y)}{\partial x^{\alpha }}:=\frac{1}{ \varGamma (1-\alpha )} \int _{0}^{x}\frac{u_{x}(\tau,y)}{(x-\tau )^{ \alpha }}\,d\tau $$

and

$$ \frac{\partial ^{\beta }u(x,y)}{\partial y^{\beta }}:=\frac{1}{\varGamma (1-\beta )} \int _{0}^{y}\frac{u_{y}(x,\tau )}{(y-\tau )^{\beta }}\,d \tau. $$

The study of FPDE (1) motivated us with many applications. We study in this paper two instances of these applications. First, we generalize the advection equation to include the dissipating of energy due to the friction and other possible factors that may not be considered in their model easily. Second, we solve the Lighthill–Whitham–Richards equation [1] arose in vehicular traffic flow on a finite-length highway. This equation is a particular case of Eq. (1) and is obtained by putting $\rho _{3}=\rho _{4}=\rho _{5}=0$, $\rho _{1}=1$ and $f=0$ in Eq. (1).

The memory terms in FPDEs make them completely different from integer order partial differential equations (PDEs) and solving FPDEs numerically or analytically is more challenging than PDEs. However, the memory term in the integral form has its advantages and is useful in the modeling of a physical or chemical phenomenon in which the recent data depends completely on the data of the whole past time. In this respect, for example, the fractional model of the Ambartsumian equation was generalized for describing the surface brightness of the Milky Way [2]. Other recent advantages for these types of applications can be found in [3,4,5,6,7,8,9,10,11]. Therefore, it is of paramount importance to find efficient methods for solving FPDEs [12,13,14,15].

Recently, new methods for solving FPDEs have been developed in the literature. These methods include the variational iteration method [16], the Laplace transform method [17], the wavelet operational method [18,19,20,21], the Haar wavelet method [22], the Adomian decomposition method [23], the homotopy analysis method [24], the Legendre base method [25], Bernstein polynomials [26] and converting to a system of fractional differential equations [27]. The finite-difference methods are mostly studied for the numerical solution of partial differential equations [28, 29]. The advantage of these methods over other methods is that it can be used for nonlinear type of equations. However, for linear equations, the spectral methods are highly recommended because of the simplicity and efficiency [30]. Clearly, the finite-difference methods introduced in [28, 29] can be generalized for solving nonlinear fractional differential equations, but they cannot be essential for linear equations.

The spectral methods using Chebyshev polynomials are well known for ordinary and partial differential equations with rapid convergence property [30,31,32,33,34,35,36,37,38,39,40]. An important advantage of these methods over finite-difference methods is that computing the coefficient of the approximation completely determines the solution at any point of the desired interval. Therefore, in this paper, we introduce an operational matrix spectral method using Chebyshev polynomials for solving FPDEs.

Orthogonal polynomials play important roles in the spectral methods for fractional differential equations. A novel spectral approximation for the two-dimensional fractional sub-diffusion problems has been studied in [41]. New recursive approximations for variable-order fractional operators with applications can be found in [42]. Recovery of a high order accuracy in Jacobi spectral collocation methods for fractional terminal value problems with non-smooth solutions can be found in [43]. Highly accurate numerical schemes for multi-dimensional space variable-order fractional Schrödinger equations are in [44]. Operational matrices were adapted for solving several kinds of fractional differential equations. The use of numerical techniques in conjunction with operational matrices of some orthogonal polynomials for the solution of FDEs produced highly accurate solutions for such equations [45,46,47,48,49].

The discrete orthogonality properties of the Chebyshev polynomials are its advantages over other orthogonal polynomials like Legendre polynomials. Also, the zeros of the Chebyshev polynomials are known analytically. These properties lead to the Clenshaw–Curtis formula which makes integration easy. We use this formula to obtain the operational matrix of the fractional integration.

The main aim of this paper is to obtain a numerical solution of general FPDEs (1) by Chebyshev polynomials. To this end, we first approximate second partial derivatives of the unknown solution of the FPDEs (1) by Chebyshev polynomials. Then we obtain the operational matrices corresponding to fractional partial derivatives, partial derivatives, and an approximate solution. Substituting these operational formulas into FPDEs (1), we obtain a system of linear algebraic equations. Finally, by solving this system of linear algebraic equations we can find the desired approximate solution. We show also that this procedure is equivalent to applying the Chebyshev operational matrix method to a multivariable Volterra integral equation. Based on this equivalency, we obtain an error analysis.

The major difference of the introduced method in this paper with other methods with operational matrix is that we have avoided to use the differential operation. Indeed, we have approximated the second partial derivative of the solution by Chebyshev polynomials and then we have used the integral operations to obtain the approximate solution.

The structure of this paper is as follows. In Sect. 2, we review important formula and definitions of the fractional calculus and the Chebyshev polynomials. In Sect. 3, we introduce the approximations of multivariable functions in terms of the shifted Chebyshev polynomials. In Sect. 4, we obtain the operational matrix for approximating the integral and fractional integral operators. In Sect. 5, we propose a spectral method based on operational matrix for solving FPDEs of the form (1). In Sect. 6, we provide the related error analysis. In Sect. 7, some numerical examples are provided to show the efficiency of the introduced method and in Sect. 8, some applications of FPDE (1) in modeling of the advection equation and the Lighthill–Whitham–Richards equation are studied.

2 Preliminaries and notations

In this section we review some definitions and theorems for the topics of Chebyshev polynomials and fractional calculus.

2.1 Fractional calculus

In order to define the Caputo-fractional derivative, we first define the Riemann–Liouville fractional integral.

Definition 2.1

([3])

A real function $f(t)$, on $(0,\infty )$ is said to be in the space $\mathcal{C}_{\mu }$, $\mu \in \mathrm{R}$ if there exists a real number $p>\mu$ such that $f(t)=t^{p}f_{1}(t)$, where $f_{1}\in \mathcal{C}([0,\infty ])$, and it is said to be in the space $\mathcal{C}_{\mu }^{n}$ if $f^{(n)}\in \mathcal{C}_{\mu }, n\in \mathcal{N}$.

Definition 2.2

([3])

The Riemann–Liouville fractional integral of order $\alpha \geq 0$ of a function $f\in \mathcal{C}_{\alpha }$, $\alpha \geq -1$, is defined as

$$\begin{aligned} \begin{aligned} &{}_{t_{0}}I_{t}^{\alpha }f(t) =\frac{1}{\varGamma (\alpha )} \int _{t_{0}} ^{t}\frac{f(x)}{(t-x)^{1-\alpha }}\,dx,\quad \alpha >0, t>0, \\ & {}_{t_{0}}I_{t}^{0}f(t) =f(t). \end{aligned} \end{aligned}$$

(2)

Therefore, the fractional integral of $(t-t_{0})^{\beta }$ is

$$ _{t_{0}}I_{t}^{\alpha }(t-t_{0})^{\beta }= \frac{\varGamma (\beta +1)}{ \varGamma (\alpha +\beta +1)}(t-t_{0})^{\beta +\alpha },\quad \beta >-1, \alpha >0. $$

Definition 2.3

([3])

Let $f\in \mathcal{C}_{-1}^{m}$, $m\in \mathcal{N}$. Then the Caputo-fractional derivative of f is defined as

$$ _{t_{0}}D_{t}^{\alpha } f(t)= \textstyle\begin{cases} _{t_{0}}I^{m-\alpha } f^{(m)}(t),& m-1 < \alpha < m, \\ \frac{d^{m}}{dx^{m}} f(t), & \alpha =m. \end{cases} $$

(3)

Thus, for $0<\alpha <1$, we have

$$ _{t_{0}}D_{t}^{\alpha } f(t)= \frac{1}{\varGamma (1-\alpha )} \int _{t_{0}} ^{t}\frac{f'(x)}{(t-x)^{\alpha }}\,dx. $$

(4)

Some important properties of Caputo-fractional derivative are [3]

$$\begin{aligned} &{}_{t_{0}}D_{t}^{\alpha } C =0, \\ &{}_{t_{0}}D_{t}^{\alpha } (t-t_{0})^{\beta } =0,\quad \beta < \lfloor \alpha \rfloor, \\ &{}_{t_{0}}D_{t}^{\alpha } (t-t_{0})^{\beta } =\frac{\varGamma (\beta +1)}{ \varGamma (\beta +1-\alpha )}(t-t_{0})^{\beta -\alpha },\quad \beta \geq \lfloor \alpha \rfloor. \end{aligned}$$

Here, $\lfloor \alpha \rfloor$ and $\lceil \alpha \rceil$ are the floor and the ceiling of α, respectively. Furthermore, it is straightforward to show that, for every $m\in \mathcal{R}^{+}$ and $n\in \mathcal{N}$, we have ${}_{t_{0}}D_{t}^{m+n}f(t)= {_{t_{0}}D_{t} ^{m}}({_{t_{0}}D_{t}^{n}}f(t))$, [3]. Moreover, for $0\leq \alpha \leq 1$, we have

$$ _{t_{0}}I_{t}^{\alpha } {_{t_{0}}D_{t}^{\alpha }}f(t)=f(t)-f \bigl(0^{+} \bigr) $$

(5)

and

$$ {_{t_{0}}D_{t}^{\alpha }} {_{t_{0}}I_{t}^{\alpha }} f(t)=f(t). $$

(6)

2.2 Chebyshev polynomials

Definition 2.4

Let $x=\cos (\theta )$. Then the Chebyshev polynomial $T_{n}(x)$, $n\in \mathbb{N}\cup \{0\}$, over the interval $[-1,1]$, is defined by the relation

$$ T_{n}(x)=\cos (n\theta ). $$

(7)

The Chebyshev polynomials are orthogonal with respect to the weight function $w(x)=\frac{1}{\sqrt{1-x^{2}}}$ and the corresponding inner product is

$$ \langle f,g\rangle = \int _{-1}^{1}w(x)g(x)f(x)\,dx, \quad\text{for } f,g\in \mathcal{L}_{2}[-1,1]. $$

(8)

The well-known recursive formula

$$ T_{n+1}(x)=2xT_{n}(x)-T_{n-1}(x),\quad n\in \mathcal{N}, $$

(9)

with $T_{0}(x)=1$ and $T_{1}(x)=x$ is important for computing these polynomials, whereas we may use

$$ T_{n}(x)=\sum_{k=0}^{[n/2]}(-1)^{k}2^{n-2k-1} \frac{n}{n-k}\begin{pmatrix} n-k \\ k \end{pmatrix} x^{n-2k},\quad n>0, $$

(10)

to compute Chebyshev polynomials in analysis. Since the range of the problem (1) is $[0,1]$, we use the shifted Chebyshev polynomials $T^{*}_{n}(x)$ defined by

$$ T^{*}_{n}(x)=T_{n}(2x-1) $$

with corresponding weight function $w^{*}(x)=w(2x-1)$. Using, $T_{n}^{*}(x)=T_{2n}(\sqrt{x})$, (see [40], Sect. 1.3) we could compute the shifted Chebyshev polynomials by

$$ T_{n}^{*}(x)=\sum _{k=0}^{n}(-1)^{k}2^{2n-2k-1} \frac{2n}{2n-k}\begin{pmatrix} 2n-k \\ k \end{pmatrix} x^{n-k},\quad n>0. $$

(11)

The discrete orthogonality of Chebyshev polynomials leads to the Clenshaw–Curtis formula [40]:

$$ \int _{-1}^{1}w(x)f(x)\,dx\simeq \frac{\pi }{N+1}\sum_{k=1}^{N+1}f(x_{k}), $$

(12)

where $x_{k}$ for $k=1,\ldots, N+1$ are zeros of $T_{N+1}(x)$. Also, the norm of $T^{*}_{i}(x)$,

$$ \gamma _{n}:= \bigl\Vert T_{n}^{*}(x) \bigr\Vert ^{2}=\bigl\langle T_{n}^{*}(x), T_{n}^{*}(x)\bigr\rangle = \int _{0}^{1}w^{*}(x) \bigl(T_{n}^{*} \bigr)^{2}(x)\,dx= \textstyle\begin{cases} \frac{\pi }{4}, &n>0, \\ \frac{\pi }{2}, &n=0, \end{cases} $$

will be of importance below.

3 Function approximation

A function f defined over the interval $[0,1]$, may be expanded as

$$ f(x)\simeq \sum_{m=0}^{N}c_{m}T^{*}_{m}(x)=C^{T} \varPsi (x),\quad N\in \mathcal{N}, $$

(13)

where C and Ψ are the matrices of size $(N+1)\times 1$,

$$\begin{aligned} \begin{aligned} &C^{T} =[c_{0},\ldots,c_{N}], \\ &\varPsi ^{T}(x)= \bigl[T^{*}_{0}(x), \ldots,T^{*}_{N}(x) \bigr], \end{aligned} \end{aligned}$$

(14)

and

$$\begin{aligned} c_{i}&=\frac{1}{\gamma _{i}} \int _{0}^{1}w^{*}(x)f(x)T^{*}_{i}(x) \,dx \\ &=\frac{1}{\gamma _{i}} \int _{0}^{1}w(2x-1)f(x)T_{i}(2x-1) \,dx \\ &=\frac{1}{2\gamma _{i}} \int _{-1}^{1}w(t)f \biggl(\frac{t+1}{2} \biggr)T_{i}(t)\,dt \\ &\simeq \frac{\pi }{2\gamma _{i}(N+1)}\sum_{k=1}^{N+1}f \biggl( \frac{x_{k}+1}{2} \biggr)T_{i}(x_{k}),\quad i=0, \ldots, N. \end{aligned}$$

(15)

The following error estimate for an infinitely differentiable function f shows that the Chebyshev expansion of f converges with exponential rate.

Theorem 3.1

([40] Theorem 5.7)

Let $g\in \mathbb{C}[0,T]$ and g satisfy the Dini–Lipschitz condition, i.e.,

$$ \omega (\delta )\log (\delta )\rightarrow 0 \quad\textit{as } \delta \rightarrow 0, $$

where ω is modulus of continuity. Then $\Vert g-p_{n}g \Vert _{\infty }\rightarrow 0$ as $n\rightarrow \infty$.

A similar error estimate exists for the Clenshaw–Curtis quadrature.

Theorem 3.2

Let the hypotheses of Theorem 3.1 be satisfied. Then

$$ \bigl\vert I(f)- I_{N}(f) \bigr\vert < 4 \bigl\Vert f- p_{N}(f) \bigr\Vert _{ \infty }, $$

where $I(f)=\int _{-1}^{1}w(x)f(x)\,dx$ and $I_{N}(f)=\frac{\pi }{N+1} \sum_{k=1}^{N+1}f(x_{k})$.

Proof

It is clear from Theorem 1 of [50, 51]. □

Let $u(x,y)$ be a bivariate function defined on $[0,1]\times [0,1]$. Then it can similarly be expanded using Chebyshev polynomials as follows:

$$ u(x,y)\simeq \sum_{n=0}^{N} \sum_{m=0}^{N}u_{n,m}T^{*}_{n}(x)T^{*}_{m}(y)= \varPsi (x)^{T}U\varPsi (y), \quad N\in \mathcal{N}, $$

(16)

where $U=(u_{i,j})$ is a matrix of size $(N+1)\times (N+1)$ with the elements

$$\begin{aligned} u_{i,j} &=\frac{1}{\gamma _{i}\gamma _{j}} \int _{0}^{1} \int _{0}^{1}w^{*}(x)w ^{*}(y)u(x,y)T_{i}^{*}(x)T_{j}^{*}(y) \,dx\,dy \\ &=\frac{1}{4\gamma _{i}\gamma _{j}} \int _{-1}^{1} \int _{-1}^{1}w(x)w(y)u \biggl( \frac{x+1}{2},\frac{y+1}{2} \biggr)T_{i}(x)T_{j}(y) \,dx\,dy \\ &\simeq \frac{\pi ^{2}}{4\gamma _{i}\gamma _{j}(N+1)^{2}}\sum_{r=1}^{N+1} \sum_{s=1}^{N+1}u \biggl( \frac{x_{r}+1}{2},\frac{x_{s}+1}{2} \biggr)T_{i}(x_{r})T _{j}(x_{s}). \end{aligned}$$

(17)

4 Operational matrices

Theorem 4.1

Let $\varPsi (x)$ be the vector of shifted Chebyshev polynomials defined by (14). Then

$$ \int _{0}^{x}\varPsi (\tau )\,d\tau \simeq P \varPsi (x), $$

(18)

where the operational matrix P can be defined by

$$\begin{aligned} P= \left( \textstyle\begin{array}{@{}c@{\quad }c@{\quad}c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{}} \frac{1}{2} & \frac{1}{2} & 0 & 0 & \ldots & 0 & 0 & 0 & \ldots & 0 & 0 \\ - \frac{1}{8} & 0 & \frac{1}{8} & 0 & \ldots & 0 & 0 & 0 & \ldots & 0 & 0 \\ - \frac{1}{6} & - \frac{1}{4} & 0 & \frac{1}{4*3} & \ldots & 0 & 0 & 0 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ - \frac{(-1)^{n}}{2(n+1)(n-1)} & 0 & 0 & 0 & \ldots & - \frac{1}{4(n-1)} & 0 & \frac{1}{4(n+1)} & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ - \frac{(-1)^{N-1}}{2N(N-2)} & 0 & 0 & 0 & \ldots & 0 & 0 & 0 & \ldots & 0 & \frac{1}{4N} \\ - \frac{(-1)^{N}}{2(N+1)(N-1)} & 0 & 0 & 0 & \ldots & 0 & 0 & 0 & \ldots & - \frac{1}{4(N-1)} & 0 \end{array}\displaystyle \right). \end{aligned}$$

Proof

An easy computation shows that

$$ \int _{0}^{x} T^{*}_{0}( \tau )\,d\tau =x=\frac{1}{2}T^{*}_{1}(x)+ \frac{1}{2}T^{*}_{0}(x) $$

and

$$ \int _{0}^{x} T^{*}_{1}( \tau )\,d\tau =x^{2}-x=\frac{1}{8}T^{*}_{2}(x)- \frac{1}{8}T^{*}_{0}(x), $$

which can be used to obtain the first and the second rows of the matrix P, respectively. For $n>1$, we can use

$$ \int T_{n}(x)\,dx= \textstyle\begin{cases} \frac{1}{2}(\frac{T_{n+1}(x)}{n+1}-\frac{T_{|n-1|}(x)}{n-1}), & n \neq 1, \\ \frac{1}{4}T_{2}(x), & n=1, \end{cases} $$

to obtain

$$ \int _{0}^{x} T^{*}_{n}( \tau )\,d\tau =\frac{1}{4} \biggl(\frac{T^{*}_{n+1}(x)}{n+1}- \frac{T ^{*}_{n-1}(x)}{n-1} \biggr)-\frac{(-1)^{n}T^{*}_{0}(x)}{2(n+1)(n-1)}, $$

which shows the structure of the other rows of the matrix P. □

Theorem 4.2

Let $0<\alpha <1$. Then there exists $r>1$ such that

$$ \frac{1}{\varGamma (1-\alpha )} \int _{0}^{x}\frac{\varPsi (\tau )}{(x-\tau )^{ \alpha }}\,d\tau \simeq D_{\alpha }\varPsi (x); $$

(19)

$D_{\alpha }=(d_{n,r})$ is the operational matrix and its elements can be approximated by

$$ (D_{\alpha })_{0,r}\simeq \frac{\pi 2^{\alpha -2}}{\gamma _{r}(N+1) \varGamma (2-\alpha )}\sum _{j=1}^{N+1} (x_{j}+1 )^{1-\alpha }T _{r}(x_{j}), $$

for $r=1, \ldots, N$, and

$$ (D_{\alpha })_{n,r}\simeq \sum_{k=0}^{n} \sum_{j=1}^{N+1}(-1)^{k} \frac{n 2^{n-k-2+\alpha }}{2n-k}\binom{2n-k}{k}\frac{\varGamma (n-k+1)}{\varGamma (2- \alpha +n-k)} \frac{\pi ({x_{j}+1})^{n-k+1-\alpha }}{\gamma _{r}(N+1)} T _{r}(x_{j}) $$

for $n=1, \ldots, N$ and $r=0, \ldots, N$.

Proof

From (11), we get

$$\begin{aligned} &\frac{1}{\varGamma (1-\alpha )} \int _{0}^{x}\frac{T_{n}^{*}(\tau )}{(x- \tau )^{\alpha }}\,d\tau \\ &\quad=\frac{1}{\varGamma (1-\alpha )}\sum_{k=0}^{n}(-1)^{k}2^{2n-2k-1} \frac{2n}{2n-k} \binom{2n-k}{k} \int _{0}^{x}\frac{\tau ^{n-k}}{(x- \tau )^{\alpha }}\,d\tau \\ &\quad=\sum_{k=0}^{n}(-1)^{k}2^{2n-2k-1} \frac{2n}{2n-k}\binom{2n-k}{k} { _{0}I_{t}^{1-\alpha }} \bigl(x^{n-k} \bigr) \\ &\quad=\sum_{k=0}^{n}(-1)^{k}2^{2n-2k-1} \frac{2n}{2n-k}\binom{2n-k}{k}\frac{ \varGamma (n-k+1)}{\varGamma (2-\alpha +n-k)}x^{n-k+1-\alpha }, \end{aligned}$$

(20)

for $n>0$, and

$$ \frac{1}{\varGamma (1-\alpha )} \int _{0}^{x}\frac{T_{0}^{*}(\tau )}{(x- \tau )^{\alpha }}\,d\tau = \frac{x^{1-\alpha }}{\varGamma (2-\alpha )}, $$

(21)

for $n=0$. Applying (13) to $f(x)=x^{n-k+1-\alpha }$, we obtain

$$ x^{n-k+1-\alpha }\simeq \sum_{r=0}^{N} \frac{\pi }{2\gamma _{r}(N+1)} \sum_{j=1}^{N+1} \biggl(\frac{x_{j}+1}{2} \biggr)^{n-k+1-\alpha }T_{r}(x _{j})T^{*}_{r}(x) . $$

(22)

Now, by substituting the $x^{n-k+1-\alpha }$ from (22) into (20) and (21) we obtain the desired result. □

Remark 4.3

For $f\in C[-1,1]$, the maximum error of Clenshaw–Curtis formula is less than $4 \Vert f-p_{N}f \Vert _{\infty }$, [50]. Hence, the Clenshaw–Curtis formula for $x^{n-k+\alpha }$ in the proof of Theorem 4.2 shows convergence and the approximation is exact when $N\rightarrow \infty$.

5 Implementation

Considering $\varPsi (y)^{T}U\varPsi (x)$ as an approximation to $u(x,y)$, we will need to compute partial derivatives of this approximation. But this type of differentiation leads to a reduction of the order of convergence. Therefore, by considering some regularity conditions, we change our strategy and we apply the approximation of the form

$$ u_{xy}\simeq \varPsi (x)^{T} \mathbf{U}\varPsi (y), $$

(23)

where U is an unknown matrix. To this end, we suppose the regularity condition

$$ u_{xy}(x,y)=u_{yx}(x,y). $$

(24)

Remark 5.1

Schwarz’s theorem (or Clairaut’s theorem) is a well-known result that asserts that $u\in C^{2}$ is a sufficient condition for (24) to hold.

Now we can obtain the other operators of $u_{xy}$ by using appropriate operational matrices. From (23) and (24), we have, using initial conditions,

$$\begin{aligned} u_{x}(x,y)\simeq {}& \varPsi ^{T}(x) \mathbf{U} \int _{0}^{y}\varPsi (\tau )\,d \tau +u_{x}(x,0) \\ = {}&\varPsi ^{T}(x) \mathbf{U} \int _{0}^{y}\varPsi (\tau )\,d\tau +h'(x) \\ \simeq {}&\varPsi ^{T}(x) \mathbf{U} P \varPsi (y)+h'(x), \end{aligned}$$

(25)

$$\begin{aligned} u_{y}(x,y)\simeq{} & \int _{0}^{x}\varPsi ^{T}(\tau )\,d \tau \mathbf{U} \varPsi (y)+u _{y}(0,y) \\ = {}& \int _{0}^{x}\varPsi ^{T}(\tau )\,d \tau \mathbf{U} \varPsi (y)+g'(y) \\ \simeq {}&\varPsi ^{T}(x)P^{T}\mathbf{U}\varPsi (y)+g'(y), \end{aligned}$$

(26)

and

$$\begin{aligned} u(x,y) &\simeq \int _{0}^{x} \varPsi ^{T}(\tau ) \,d\tau \mathbf{U} \int _{0} ^{y}\varPsi (\tau )\,d\tau +h(x)+g(y)-h_{0} \\ &\simeq \varPsi ^{T}(x)P^{T}\mathbf{U}P\varPsi (y)+h(x)+g(y)-h_{0}. \end{aligned}$$

(27)

Consequently, we have

$$\begin{aligned} \frac{\partial ^{\alpha }u(x,y)}{\partial x^{\alpha }} &\simeq \frac{1}{ \varGamma (1-\alpha )} \int _{0}^{x}\frac{\varPsi ^{T}(\tau ) \mathbf{U} P \varPsi (y)+h'(\tau )}{(x-\tau )^{\alpha }}\,d\tau \\ &\simeq \varPsi ^{T}(x) D_{\alpha }^{T} \mathbf{U} P \varPsi (y)+\frac{d ^{\alpha }h(x)}{dx^{\alpha }} \end{aligned}$$

(28)

and

$$\begin{aligned} \frac{\partial ^{\beta }u(x,y)}{\partial y^{\beta }} &\simeq \frac{1}{ \varGamma (1-\beta )} \int _{0}^{y}\frac{\varPsi ^{T}(x)P^{T}\mathbf{U}\varPsi ( \tau )+g'(\tau )}{(y-\tau )^{\beta }}\,d\tau \\ &\simeq \varPsi ^{T}(x)P^{T}\mathbf{U} D_{\beta }\varPsi (y)+\frac{d^{ \beta }g(y)}{dx^{\beta }}. \end{aligned}$$

(29)

Substituting from (25)–(29) into (1), we obtain

$$\begin{aligned} \varPsi ^{T}(x)K\varPsi (y)= {}&\rho _{1} \varPsi ^{T}(x) D_{\alpha }^{T} \mathbf{U} P \varPsi (y)+\rho _{2}\varPsi ^{T}(x)P^{T} \mathbf{U} D_{\beta }\varPsi (y) \\ &{}+\rho _{3} \varPsi ^{T}(x) \mathbf{U} P \varPsi (y)+ \rho _{4}\varPsi ^{T}(x)P ^{T}\mathbf{U} \varPsi (y) \\ &{}+\rho _{5}\varPsi ^{T}(x)P^{T} \mathbf{U}P\varPsi (y), \end{aligned}$$

(30)

where

$$ k(x,y)=f(x,y)-\rho _{1}\frac{d^{\alpha }h(x)}{dx^{\alpha }}-\rho _{2} \frac{d ^{\beta }g(y)}{dx^{\beta }}-\rho _{3} h'(x)+\rho _{4} g'(y)-\rho _{5} \bigl(h(x)+g(y)-h _{0} \bigr) $$

(31)

is approximated by $k(x,y)\simeq \varPsi ^{T}(x)K\varPsi (y)$, using (16). Taking the orthogonality properties of $\varPsi ^{T}(x)$ and $\varPsi (y)$ into account, we can drop $\varPsi (x)$ and $\varPsi (y)$ to obtain the following system of algebraic equations:

$$\begin{aligned} K= \rho _{1}D_{\alpha }^{T} \mathbf{U} P +\rho _{2}P^{T}\mathbf{U} D _{\beta }+\rho _{3} \mathbf{U} P +\rho _{4}P^{T} \mathbf{U}+\rho _{5} P ^{T}\mathbf{U}P. \end{aligned}$$

(32)

Finally, the approximate solution can be computed using (27):

$$ u_{N}(x,y)=\varPsi ^{T}(x)P^{T} \mathbf{U}P\varPsi (y)+h(x)+g(y)-h_{0}, $$

(33)

where $u_{N}$ stands for approximate solution to distinguish it from the exact solution u.

6 Error analysis

Suppose that $u\in C^{2}$ is a unique solution of system (1), and set $z:=u_{xy}$. Then an easy computation shows that

$$ \begin{aligned}& u_{x}(x,y)= \int _{0}^{y} z(x,\tau )\,d\tau +h'(x), \\ &u_{y}(x,y)= \int _{0}^{x} z(\tau,y)\,d\tau +g'(y), \\ &u(x,y)= \int _{0}^{y} \int _{0}^{x} z(\tau,t)\,d\tau \,dt+g(y)+h(x)-h _{0}, \\ &\frac{\partial ^{\alpha }u(x,y)}{\partial x^{\alpha }}=\frac{1}{ \varGamma (1-\alpha )} \int _{0}^{x} \int _{0}^{y}\frac{ z(\tau,t)}{(x- \tau )^{\alpha }}\,dt\,d\tau + \frac{d^{\alpha }h(x)}{d x^{\alpha }}, \end{aligned} $$

(34)

and

$$ \frac{\partial ^{\beta }u(x,y)}{\partial y^{\beta }} =\frac{1}{\varGamma (1-\beta )} \int _{0}^{y} \int _{0}^{x}\frac{ z(t,\tau )}{(y-\tau )^{ \beta }}\,dt\,d\tau + \frac{d^{\beta }g(y)}{d y^{\beta }}. $$

(35)

Substituting from (34) and (35) into (1), we obtain

$$\begin{aligned} &\frac{\rho _{1}}{\varGamma (1-\alpha )} \int _{0}^{x} \int _{0}^{y}\frac{ z( \tau,t)}{(x-\tau )^{\alpha }}\,dt\,d\tau + \frac{\rho _{2}}{\varGamma (1- \beta )} \int _{0}^{y} \int _{0}^{x} \frac{ z(t,\tau )}{(y-\tau )^{\beta }}\,dt\,d\tau \\ &\quad{}+\rho _{3} \int _{0}^{y} z(x,\tau )\,d\tau +\rho _{4} \int _{0}^{x} z( \tau,y)\,d\tau \\ &\quad{}+\rho _{5} \int _{0}^{y} \int _{0}^{x} z(\tau,t)\,d\tau \,dt=k(x,y). \end{aligned}$$

(36)

Introducing, the operator $L:C_{L}[0,1]\rightarrow C_{L}[0,1]$ by

$$ L \bigl(z(x,y) \bigr):= \bigl(\rho _{1} I_{x}^{\alpha }I_{y} +\rho _{2} I_{y}^{ \beta }I_{x} +\rho _{3}I_{y} +\rho _{4}I_{x} +\rho _{5} I_{y} I_{x} \bigr) \bigl(z(x,y) \bigr) $$

we can write Eq. (36) in the operator form

$$ L \bigl(z(x,y) \bigr)=k(x,y). $$

(37)

Here, $C_{L}$ stands for continuous functions satisfying the Dini–Lipschitz condition. Suppose that

$$\begin{aligned} &e_{z}(x,y):=z(x,y)-\varPsi (x)^{T} \mathbf{Z}\varPsi (y), \end{aligned}$$

(38)

$$\begin{aligned} &e_{k}(x,z):=k(x,y)-\varPsi (x)^{T}K \varPsi (y), \end{aligned}$$

(39)

$$\begin{aligned} & \varepsilon (x,z):=L \bigl(\varPsi (x)^{T} \mathbf{Z}\varPsi (y) \bigr)-L_{N}(Z), \end{aligned}$$

(40)

where the operator $L_{N}$ is defined by

$$ L_{N}(Z):=\varPsi (x)^{T} \bigl(\rho _{1}D_{\alpha }^{T} Z P +\rho _{2}P ^{T}Z D_{\beta }+\rho _{3} Z P +\rho _{4}P^{T}Z+\rho _{5} P^{T}ZP \bigr) \varPsi (y). $$

Substituting $z(x,y)$ and $k(x,y)$ from (38) and (39) into (37) we obtain

$$ L \bigl(\varPsi (x)^{T}\mathbf{Z}\varPsi (y) \bigr)+L \bigl(e_{z}(x,y) \bigr)=\varPsi (x)^{T}K\varPsi (y)+e _{k}(x,z). $$

Using (40) and the fact that L and $L_{N}$ are linear operators we obtain

$$ L_{N}(Z)+\varepsilon (x,z)+L \bigl(e_{z}(x,y) \bigr)= \varPsi (x)^{T}K\varPsi (y)+e_{k}(x,z). $$

Taking into account that

$$ L_{N}(U)=\varPsi (x)^{T}K\varPsi (y) $$

and denoting by $E=Z-U$ the error function, we obtain

$$ L_{N}(E)=e_{k}(x,z)-\varepsilon (x,z)-L \bigl(e_{z}(x,y) \bigr). $$

If $L_{N}$ is an invertible operator, we obtain

$$ E_{N}=L_{N}^{-1} \bigl(e_{k}(x,z)-\varepsilon (x,z)-L \bigl(e_{z}(x,y) \bigr) \bigr). $$

(41)

Supposing $L_{N}^{-1}$ and L are continuous operators we obtain

$$ \Vert E \Vert _{\infty }\leq c \bigl( \bigl\Vert e_{k}(x,z) \bigr\Vert _{\infty }- \bigl\Vert \varepsilon (x,z) \bigr\Vert _{\infty }- \bigl\Vert e_{z}(x,y) \bigr\Vert _{\infty } \bigr), $$

(42)

where $c>0$ is constant number not depending on N. We note that by Remark 4.3, $\Vert \varepsilon (x,z) \Vert _{\infty }\rightarrow 0$ and by Theorem 3.1

$$ \bigl\Vert e_{k}(x,z) \bigr\Vert _{\infty }\rightarrow 0 $$

and

$$ \bigl\Vert e_{z}(x,y) \bigr\Vert _{\infty }\rightarrow 0 $$

as $N\rightarrow \infty$. Since $\Vert z-u_{N} \Vert _{\infty }\leq c \Vert E \Vert _{\infty }$, the convergence of the approximate solution is evident. This analysis also shows that the convergence rate depends on the convergence rate of the Chebyshev polynomials.

Remark 6.1

Since Z is not available, usually in most of the literature, the perturbed term

$$ R(x,z)=L \bigl(\varPsi (x)^{T}\mathbf{U}\varPsi (y) \bigr)-L_{N}(U) $$

can be introduced to obtain

$$\begin{aligned} R(x,z)&=L \bigl(\varPsi (x)^{T}\mathbf{U}\varPsi (y) \bigr)-\varPsi (x)^{T}K\varPsi (y) \\ &=L \bigl(\varPsi (x)^{T}\mathbf{U}\varPsi (y) \bigr)-k(x,z)+k(x,z)- \varPsi (x)^{T}K \varPsi (y) \\ &=L (u_{N})-L(z)+e_{k}(x,z) \\ &=L(u_{N}-z)+e_{k}(x,z) \end{aligned}$$

(43)

for error estimation. By solving

$$ L(u_{N}-z)=R(x,z)-e_{k}(x,z) $$

with the given numerical method, an error estimation is obtained.

7 Numerical examples

In this section, we apply the proposed method introduced in the previous sections to obtain numerical solutions to some FPDEs. The maximum errors are computed using

$$ E(N)=\max_{(x,y)\in D_{100}} \bigl|u(x,y)-u_{N}(x,y)\bigr|, $$

where $D_{M}=\{(x_{i},y_{j})| x_{i}=ih, y_{j}=jh, i,j=0, \ldots , M, h=\frac{1}{M}\}$.

Example 7.1

We consider the class of FPDEs

$$\begin{aligned} \frac{\partial ^{\alpha }u(x,y)}{\partial x^{\alpha }}+\frac{ \partial ^{\beta }u(x,y)}{\partial y^{\beta }} ={}& \frac{\varGamma (n+1)}{ \varGamma (n+1-\alpha )}x^{n-\alpha } \\ &{}+\frac{\varGamma (m+1)}{\varGamma (m+1-\beta )}y^{m-\beta }, \end{aligned}$$

(44)

subjected to the initial conditions

$$ h(x)=x^{n},\qquad g(y)=y^{m}, \qquad h_{0}=0, $$

with free parameters m, n, α and β. Using (31) we obtain $h\equiv 0$ and hence, $U=0_{N+1}$ (zero matrix of dimension $N+1$), and the approximate solution using (27) is $u(x,y)=h(x)+g(y)-h_{0}=x^{n}+y^{m}$. Therefore, as we expected the proposed method leads to an exact solution.

Example 7.2

We consider the class of FPDEs

$$\begin{aligned} \frac{\partial ^{\alpha }u(x,y)}{\partial x^{\alpha }}+\frac{ \partial ^{\beta }u(x,y)}{\partial y^{\beta }} ={}& \frac{\varGamma (n+1)}{ \varGamma (n+1-\alpha )}x^{n-\alpha }y^{m} \\ &{}+\frac{\varGamma (m+1)}{\varGamma (m+1-\beta )}y^{m-\beta }x^{n}, \end{aligned}$$

(45)

subjected to the initial conditions

$$ h(x)=0, \qquad g(y)=0,\qquad h_{0}=0, $$

with free parameters $m\geq 1$, $n\geq 1$, α and β. We could examine the numerical solutions with changing these parameters. The exact solution is $u(x,y)=x^{n}y^{m}$. In Table 1, the maximum error $E(N)$ is reported for $N=1,\ldots, 6$, $\alpha =0.5$, $\beta =2/3$ and different parameters of n and m. For $m=n=1$ the approximate solution is exact and the truncated error is observed only. For $m=n=2$ the approximate solution is exact when $N\geq 2$. This pattern is observed for other parameters of n and m, and the method gives the exact solution whenever $N\geq \max \{n,m\}$. Finally, we choose $m=n=12$ to find the well-known exponential rate of convergence for Chebyshev spectral methods.

Table 1 The maximum error for $N=1,\ldots, 6$, and different parameters of Example 7.2

Example 7.3

Consider the class of FPDEs of the form

$$\begin{aligned} &\frac{\partial ^{\alpha }u(x,y)}{\partial x^{\alpha }}-\frac{ \partial ^{\beta }u(x,y)}{\partial y^{\beta }}+u(x,y) \\ &\quad=\lambda _{1} x ^{1-\alpha }E_{1,2-\alpha }(\lambda _{1} x)e^{\lambda _{2}y} \\ &\qquad{}-\lambda _{2} y^{1-\beta }E_{1,2-\beta }(\lambda _{2} y)e^{\lambda _{1}x}+e^{\lambda _{1} x+\lambda _{2}y}, \end{aligned}$$

(46)

subjected to the initial conditions

$$ h(x)=e^{\lambda _{1} x},\qquad g(y)=e^{\lambda _{2} y},\qquad h_{0}=1, $$

with free parameters $\lambda _{1}$, $\lambda _{2}$, α and β. Here, $E_{n,m}(Z)$ is the two-parameter function of Mittag-Leffler type [52, 53]. The exact solution is $e^{\lambda _{1} x+\lambda _{2}y}$. In Table 2, the maximum error $E(N)$ is reported for $N=1,\ldots, 6$, $\lambda _{1}=0.5$, $\lambda _{2}=0.5$ $\beta =0.5$ and $\alpha =0.1, 0.3, 0.5, 0.7, 0.9$. It shows the exponential rate of convergence for all values of the α. To illustrate this point we plotted the logarithm of maximum error in Fig. 1. Table 3 shows the maximum error $E(N)$ for negative parameters $\lambda _{1}=-0.5$, $\lambda _{2}=-0.5$.

Figure 1

The logarithm of maximum error versus N, for Example 7.3

Table 2 The maximum error for $N=1,\ldots, 6$, $\lambda _{1}=0.5$, $\lambda _{2}=0.5$, $\beta =0.5$ and different values of the parameter α in Example 7.3

Table 3 The maximum error for $N=1,\ldots, 6$, $\lambda _{1}=-0.5$, $\lambda _{2}=-0.5$, $\beta =0.5$ and different values of the parameter α in Example 7.3

Example 7.4

Let us consider a class of FPDEs of the form

$$\begin{aligned} &\frac{\partial ^{\alpha }u(x,y)}{\partial x^{\alpha }}+\nu \frac{ \partial u(x,y)}{\partial y}+u(x,y) \\ &\quad = -\lambda _{1}^{2} x^{2-\alpha }E _{2,3-\alpha } \bigl(- \lambda _{1}^{2} x^{2} \bigr)\sin (\lambda _{2} y) \\ &\qquad{}+\cos (\lambda _{1} x) \bigl( \lambda _{2} \cos ( \lambda _{2} y)+ \sin (\lambda _{2} y) \bigr) \end{aligned}$$

(47)

subjected to the initial conditions

$$ h(x)=0,\qquad g(y)=\sin (\lambda _{2} y),\qquad h_{0}=0, $$

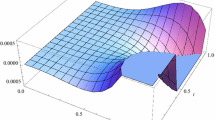
with free parameters $\lambda _{1}$, $\lambda _{2}$, and α. This time the exact solution is the sinusoid $u(x,y)=\sin (\lambda _{1} x) \cos (\lambda _{2} y)$. Table 4 shows the maximum error for $\alpha =0.2, 0.4, 06, 0.8, 1$ and $\lambda _{1}=\lambda _{2}=\pi$, and Table 5 shows these values for $\lambda _{1}=\lambda _{2}=2 \pi$. Though these tables show that increasing the frequency $f=\frac{\lambda }{2\pi }$ increase the absolute maximum error, the logarithm of maximum error plotted in Figs. 2 and 3 shows that both experiments of this example are of exponential rate. To show the effectiveness of the method we also illustrated a numerical solution in Figs. 4 and 5.

Figure 2

The logarithm of maximum error versus N, for $\lambda _{1}= \lambda _{2}=\pi$, in Example 7.4

Figure 3

The logarithm of maximum error versus N, for $\lambda _{1}= \lambda _{2}=2\pi$, in Example 7.4

Figure 4

The approximate solution for $\lambda _{1}=\lambda _{2}= \pi$, in Example 7.4

Figure 5

The approximate solution for $\lambda _{1}=\lambda _{2}=2 \pi$, in Example 7.4

Table 4 The maximum error for $N=1,\ldots, 12$, $\lambda _{1}= \pi$, $\lambda _{2}=\pi$, and different values of the parameter α in Example 7.4

Table 5 The maximum error for $N=1,\ldots, 12$, $\lambda _{1}=2 \pi$, $\lambda _{2}=2\pi$, and different values of the parameter α in Example 7.4

8 Applications

Example 8.1

The advection is the transport of a substance by bulk motion. The model has been obtained by many restrictions such as neglecting friction and other parameters which dissipate energy. The dynamics of this phenomenon is described by

$$ \frac{\partial u(x,t)}{\partial t}+\nu \frac{\partial u(x,t)}{\partial x}=f(x,t), $$

(48)

where ν is a nonzero constant velocity, f is a source function and u is a particle density. There is much literature showing how advection–dispersion equations are generalized by fractional differential equations (see for examples [54, 55]). Therefore, it is reasonable to add a term containing a fractional derivative for dissipating energy in the advection equations and we have

$$ \frac{\partial u(x,t)}{\partial t}+\nu \frac{\partial u(x,t)}{\partial x}+\eta \frac{\partial ^{\alpha } u(x,t)}{\partial x^{\alpha }}=f(x,t), $$

(49)

where η is a constant and $0 <\alpha \leq 1$.

Now we consider a source function of the form $f(x,t)=\sin (\lambda x+ \omega t)$, with $\lambda =\pi$ and $\omega =1$. We set $\eta =1$ and $\nu =1$, and solve the problem with $N=10$. We compare the results without fractional term $\eta =0$ and with the fractional term $\eta =1$, $\alpha =0.7$. Figure 6 shows the density of the substance in x direction at various times. This figure is plotted by solving Eq. (49) with fractional term (blue lines) and (48) without fractional term (red lines). In this figure, we observe that blue lines are more accumulated than the red lines with passing time. This can be interpreted as that the density of the substance in the presence of the fractional term decreases. This reduction in the density of particles can be explained by considering the dissipating of energy by friction and other physical parameters which we included by adding fractional terms.

Figure 6

Approximate solutions of the advection equation: the red line shows the approximate solutions without fractional term and the blue line shows the approximate solutions with a fractional term

Example 8.2

Lighthill–Whitham–Richards (LWR) equation. The equation

$$ \frac{\partial ^{\beta }u(x,y)}{\partial x^{\beta }}+\lambda \frac{ \partial ^{\beta }u(x,y)}{\partial y^{\beta }} =0 $$

(50)

has been extensively studied for describing a vehicular traffic flow on a finite-length highway by using local fractional directive [1]. Here, the parameters λ and $0<\beta \leq 1$ are known real numbers. Let us consider an example of this model with parameters $\lambda =1$ and $\beta =0.5$ subjected to the initial conditions $h(x)=\sinh _{\beta }(x^{\beta })$, $g(y)=- \sinh _{\beta }(y^{\beta })$ and $h_{0}=0$. We recall that

$$ \sinh _{\beta }(x):=\frac{x}{\varGamma (\beta +1)}+\frac{x^{3}}{\varGamma (3 \beta +1)}+ \cdots $$

and

$$ \cosh _{\beta }(x):=1+\frac{x^{2}}{\varGamma (2\beta +1)}+\frac{x^{4}}{ \varGamma (4\beta +1)}+ \cdots $$

are fractional generalizations of hyperbolic functions.

Kumar et al. [1] have obtained the general solution of Eq. (50) with local fractional derivatives as follows:

$$ u(x,y)=\sinh _{\beta } \bigl(x^{\beta } \bigr) \cosh _{\beta } \bigl(x^{\beta } \bigr)-\cosh _{ \beta } \bigl(x^{\beta } \bigr)\sinh _{\beta } \bigl(x^{\beta } \bigr). $$

(51)

Now, we solve this equation with fractional derivatives in the Caputo sense by our proposed method. We observe that this solution shows a similar behavior to the solution obtained in (51) despite the differences in their definitions of fractional derivatives. In Fig. 7, the scaled solutions of Eq. (50) with Caputo-fractional derivatives and local fractional derivatives are depicted. This comparison shows that we can also use the Caputo-fractional derivatives for describing a vehicular traffic flow in the Lighthill–Whitham–Richards model.

Figure 7

The scaled solution of Lighthill–Whitham–Richards equation with Caputo-fractional derivatives (markers with blue color) and local fractional derivatives (lines with red color) with $\beta =0.5$ and $\lambda =1$

9 Conclusion

An operational matrix method based on shifted Chebyshev polynomials was introduced for solving fractional partial differential equations. We avoided differentiation in the introduced method by using some smooth condition and approximating of the higher partial derivatives of the solution. We transformed the fractional partial differential equation into a singular Volterra integral equation. Then we addressed the approximate solution obtained by solving an algebraic equation. The numerical examples show that the introduced method gives the exact solution whenever the solution is a polynomial and the approximate solution converges very rapidly with an exponential rate for other examples.

A generalization of our introduced method for nonlinear equations is more challenging than the linear case. Parallel to this work, it seems that the finite-difference methods also can efficiently be generalized and studied for linear and nonlinear equations. Therefore, we consider these topics for future studies and investigations.