Abstract
In this article, an accurate and efficient numerical method is presented for solving the space-fractional order diffusion equation (SFDE). Jacobi polynomials are used to approximate the solution of the equation as a base of the tau spectral method which is based on the Jacobi operational matrices of fractional derivative and integration. The main advantage of this method is based upon reducing the nonlinear partial differential equation into a system of algebraic equations in the expansion coefficient of the solution. In order to test the accuracy and efficiency of our method, the solutions of the examples presented are introduced in the form of tables to make a comparison with those obtained by other methods and with the exact solutions easy.
Similar content being viewed by others
1 Introduction
Due to their accuracy, fractional partial differential equations (PDEs) in the description of nonlinear phenomena in engineering, physics, viscoelasticity, fluid mechanics, biology, and other areas of science have got a lot of attention in recent years [1–3]. There are many advantages of fractional derivatives, one of them is that it can be seen as a set of ordinary derivatives that give the fractional derivatives the ability to describe what integer-order derivatives cannot [4]. One may refer for the historical development of fractional operators to [5, 6].
The tau spectral method is one of the most important methods that have been used to find numerical solutions of differential equations. Expressing the solution as an expansion of certain orthogonal polynomials and then choosing the coefficients in the expansion in order to satisfy the differential equation as accurately as possible is the main idea of the spectral methods.
In a lot of papers there have been proposals for solving the multi-term fractional differential equations such as the Haar wavelet [7, 8], the homotopy analysis method [9, 10], the Legendre wavelet method [11], the homotopy-perturbation method [12, 13], and the variational iteration method [14]. Spectral methods have been used to introduce approximate solutions for the fractional differential equations based on collocation and tau methods, see [15, 16]. Moreover, spectral methods are applied with the help of the operational matrix of fractional derivatives for numerical approximations of the linear and nonlinear FDEs [17–19], not only the operational matrices of fractional derivatives, but those of fractional integrations are used with the help of the tau and pseudospectral methods to solve some types of FDEs [20–22].
The use of general Jacobi polynomials has the advantage of obtaining the solutions in terms of the Jacobi parameters α and β. Hence to generalize and instead of developing approximation results for each particular pair of indices, it would be very useful to carry out a systematic study on Jacobi polynomials () with general indices, which can then be directly applied to other applications. It is with this motivation that we introduce in this paper a family of Jacobi polynomials with indices .
The operational matrix was presented for fractional derivatives of shifted Jacobi polynomials by Doha et al. [23] and used with the help of the spectral tau method to introduce numerical solutions of FDEs. Recently, spectral methods are used together with the shifted Jacobi polynomials for investigating numerical approximations of linear and nonlinear FDEs with constant and variable coefficients in [24].
During the past few decades fractional order partial differential equations began to play a key role especially in the study and modeling of anomalies and complex systems [2, 25–29]. SFDEs model phenomena exhibiting anomalous diffusion that cannot be modeled accurately by the classical diffusion equations. Because of the nonlocal property of fractional differential operators, the numerical methods for SFDEs often generate dense or even full coefficient matrices. Numerical approaches to different types of fractional diffusion models have been increasingly appearing in the literature [30–35]. Spectral methods are applied together with the finite difference method [36] in order to find an approximate solution of SFDEs; see [30]. Bhrawy and Baleanu [37] proposed the Legendre-Gauss-Lobatto collocation scheme for solving the SFDEs with variable coefficients. Recently, Saadatmandi and Dehghan [38] and Doha et al. [39] applied the operational matrix of fractional derivatives with the help of tau approximations based on Legendre polynomials and Chebyshev polynomials for numerical solutions of SFDEs, respectively.
In this paper we are concerned with the direct solution techniques for the numerical solution of SFDEs, using the Jacobi tau approximations. Developing an efficient algorithm using the tau method together with operational matrices of a fractional derivative and integration of shifted Jacobi polynomials is our main aim. The shifted Jacobi tau method based on Jacobi operational matrices reduces SFDEs to a system of algebraic equations, which simplifies the problem. We note that the improved operational matrix techniques based on the Legendre tau method [38], the Chebyshev tau method [39], and some other interesting methods can be obtained directly as special cases from our proposed shifted Jacobi operational matrices with Jacobi tau approximations.
The article is arranged in the following way: In Section 2, some properties of Jacobi polynomials and some necessary definitions are introduced. In Section 3, we apply our algorithm for the solution of SFDEs. The error estimate is given in Section 4. In Section 5 several examples have been applied. Also, a conclusion is presented in the final section.
2 Basic ideas and definitions
2.1 Fractional derivation and integration
The Riemann-Liouville and Caputo fractional definitions are the two most used definitions of fractional calculus.
Definition 2.1 The integral of order (fractional) according to Riemann-Liouville is given by
where
is the gamma function.
The operator satisfies the following properties:
Definition 2.2 The Caputo fractional derivatives of order ν is defined as
where m is the ceiling function of ν.
The operator satisfies the following properties:
2.2 SFDE
Consider a one-dimensional SFDE considered as
with initial and boundary conditions
and
respectively, where represents the solute concentration, is the source term and is the initial solute concentration but and are the boundary solute concentrations.
2.3 Properties of shifted Jacobi polynomials
The Jacobi polynomials are orthogonal with Jacobi weight function over , namely
where is the Kronecker function and
One can generate Jacobi polynomials from the recurrence relation:
where
By introducing the variable , Jacobi polynomials can be used in the interval that will be called shifted Jacobi polynomials. Let the shifted Jacobi polynomials be denoted by . Then the shifted Jacobi polynomials are orthogonal with respect to the weight function over , namely
where
The analytic form of the shifted Jacobi polynomials of degree i is given by
where
A function , square integrable in , can be expressed in terms of shifted Jacobi polynomials as
where the coefficients are given by
In practice, only the first terms of shifted Jacobi polynomials are considered. Hence we can write
where the shifted Jacobi coefficient vector C and the shifted Jacobi vector are given by
Similarly a function of two independent variables defined for and may be expanded in terms of the double shifted Jacobi polynomials as
where the shifted Jacobi vectors and are defined similarly to (12); also the shifted Jacobi coefficient matrix A is given by
where
The first integration of can be expressed as
where is an operational matrix of integration of order one in the Riemann-Liouville sense and is defined as follows:
where
(see [40] for a proof).
The fractional derivative of order of can be expressed as
where is the Jacobi operational matrix of derivatives of order ν in the Caputo sense and is defined as follows:
where
Note that in , the first rows are all zero (see [23] for a proof).
3 The numerical scheme
In this section, we apply the spectral tau method together with the shifted Jacobi operational matrix to solve SFDE (5) with initial conditions (6) and boundary conditions (7).
First, we approximate , , , and by the shifted Jacobi polynomials as
where A is an unknown matrix, but , Q and F are known matrices which can be written as
where and are given as in (10) but the are given as in (14).
By getting the integrated form of (5) from 0 to t and using (6), we have
Using (15), (17), and (20) it is easy to obtain
Let
where H is a matrix. To illustrate H, (24) can be written as
Multiplying both sides of the above equation by , and integrating the result from 0 to L, we obtain
By using (25) and making use of (8) we have
Employing (24), (23) can be written as
Also using (15) and (20) we get
Applying (20), (27), and (28) the residual for (22) can be written as
where
As in a typical tau method, see [41], we generate linear algebraic equations using the following algebraic equations:
Also, substituting (20) in (7) we obtain
respectively. Equations (31) and (32) are collocated at points. For suitable collocation points we use the shifted Jacobi roots , of . The number of unknown coefficients is equal to and can be obtained from (30)-(32). Consequently given in (20) can be calculated.
4 Numerical results
Example 1 Let us consider (5) with initial condition , , and boundary conditions and , with and ; see [31].
The exact solution of the problem is of the form .
Consider and , the exact and approximated solutions, respectively. Then the error is defined by
where is the norm.
Regarding this problem we study four different choices of ν, △x and △t with .
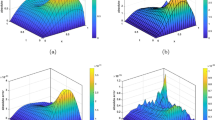
In Tables 1 and 2, we compare errors using the proposed method, at with different choices of ν, △x, α, β and △t, and that obtained by Sousa [31]. Also, in Figure 1, we plot the error function at , , and , while in Figure 2, we show the logarithmic graphs of the maximum absolute errors (MAEs) (Log10error) at , , and various choices of N (); by using our algorithm. From these figures, it is shown that the numerical errors decay rapidly as N increased. This confirms that the proposed method has an exponential rate of convergence.
In [31], Sousa implemented the Crank-Nicolson discretization in time together with the spline approximations for introducing a solution of this problem and the results are shown in Tables 1 and 2. It is clear from Tables 1 and 2 that the presented method is more accurate than the spline method. Moreover, numerical results that have been obtained in the case of are entirely consistent with the results presented by Doha et al. [39].
Example 2 Consider the following problem:
where
with initial condition
and boundary conditions
where the exact solution of this problem is
This problem was also investigated by Khader using the Chebyshev collocation method, see [30], but in [38] the authors introduced a tau approach based on shifted Legendre polynomials for solving it. In Table 3 we introduce the absolute errors at with , and various choices of α and β, while in Figure 3, we plot the error function at and . For the sake of comparison, the results obtained by Khader [30] are also introduced in the second column of Table 3. Table 3 confirms that this method is more accurate than the Chebyshev collocation method [30] (see Table 1 in [30]). Results that have been obtained in the case of , are entirely consistent with the results presented by Saadatmandi and Dehghan [38].
In the case where an exact solution is not known, one follows a similar method. The difference is that one calculates the residual errors only, since comparison to an exact solution is not possible.
Example 3 Consider (5) with the coefficient function, , and the source function, , with initial condition , , and boundary conditions and .
The exact solution of the problem is of the form .
Table 4 lists the absolute errors using the Jacobi tau spectral method based on the Jacobi operational matrix at with and different choices of α, and β. Also in Figure 4, we show the logarithmic graphs of the MAEs at , , and various choices of N (); by using our algorithm.
Results that have been obtained in the case of are entirely consistent with the results presented by Doha et al. [39].
5 Conclusion
The fundamental objective of the paper is to introduce a new method for solving the SFDE (5)-(7). Using the tau spectral method based on shifted Jacobi polynomials together with the operational matrix of fractional derivatives this objective has been achieved. The fractional derivatives are described in the Caputo sense. By adding more terms of the shifted Jacobi polynomial from (13), the errors will be smaller. In order to illustrate the accuracy of the method, we compared our approximate solutions of the problems with their exact and with the approximate solutions presented by other methods. According to the numerical results given in the previous section, the proposed method may be extended to solve several types of two-sided space-fractional partial FDEs subject to nonhomogeneous conditions.
References
Kilbas AA, Srivastava HM, Trujillo JJ North-Holland Math. Stud. 204. In Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam; 2006.
Podlubny I Math. Sci. Eng. In Fractional Differential Equations. Academic Press, New York; 1999.
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives, Theory and Applications. Gordon & Breach, Yverdon; 1993.
Su L, Wang W, Xu Q: Finite difference methods for fractional dispersion equations. Appl. Math. Comput. 2010, 216: 3329-3334. 10.1016/j.amc.2010.04.060
Miller K, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York; 1993.
Oldham KB, Spanier J: The Fractional Calculus. Academic Press, New York; 1974.
Chen Y, Yi M, Yu C: Error analysis for numerical solution of fractional differential equation by Haar wavelets method. J. Comput. Sci. 2012. 10.1016/j.jocs.2012.04.008
Li YL: Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Comput. 2010, 216: 2276-2285. 10.1016/j.amc.2010.03.063
Hashim I, Abdulaziz O, Momani S: Homotopy analysis method for fractional IVPs. Commun. Nonlinear Sci. Numer. Simul. 2009, 14: 674-684. 10.1016/j.cnsns.2007.09.014
Odibat Z, Momani S, Xu H: A reliable algorithm of homotopy analysis method for solving nonlinear fractional differential equations. Appl. Math. Model. 2010, 34: 593-600. 10.1016/j.apm.2009.06.025
Jafari H, Yousefi SA: Application of Legendre wavelets for solving fractional differential equations. Comput. Math. Appl. 2011, 62: 1038-1045. 10.1016/j.camwa.2011.04.024
Abdulaziz O, Hashim I, Momani S: Application of homotopy-perturbation method to fractional IVPs. J. Comput. Appl. Math. 2008, 216: 574-584. 10.1016/j.cam.2007.06.010
Odibat Z, Momani S: Modified homotopy perturbation method: application to quadratic Riccati differential equation of fractional order. Chaos Solitons Fractals 2008, 36: 167-174. 10.1016/j.chaos.2006.06.041
Yanga S, Xiao A, Su H: Convergence of the variational iteration method for solving multi-order fractional differential equations. Comput. Math. Appl. 2010, 60: 2871-2879. 10.1016/j.camwa.2010.09.044
Doha EH, Bhrawy AH, Ezz-Eldien SS: Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations. Appl. Math. Model. 2011, 35: 5662-5672. 10.1016/j.apm.2011.05.011
Bhrawy AH, Alofi AS, Ezz-Eldien SS: A quadrature tau method for variable coefficients fractional differential equations. Appl. Math. Lett. 2011, 24: 2146-2152. 10.1016/j.aml.2011.06.016
Doha EH, Bhrawy AH, Ezz-Eldien SS: A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order. Comput. Math. Appl. 2011, 62: 2364-2373. 10.1016/j.camwa.2011.07.024
Kayedi-Bardeh A, Eslahchi MR, Dehghan M: A method for obtaining the operational matrix of the fractional Jacobi functions and applications. J. Vib. Control 2012. 10.1177/1077546312467049
Saadatmandi A, Dehghan M: A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl. 2010, 59: 1326-1336. 10.1016/j.camwa.2009.07.006
Bhrawy AH, Alofi AS: The operational matrix of fractional integration for shifted Chebyshev polynomials. Appl. Math. Lett. 2013, 26: 25-31. 10.1016/j.aml.2012.01.027
Bhrawy AH, Alghamdi MA, Taha TM: A new modified generalized Laguerre operational matrix of fractional integration for solving fractional differential equations on the half line. Adv. Differ. Equ. 2012. 10.1186/1687-1847-2012-179
Bhrawy AH, Doha EH, Baleanu D, Ezz-Eldien SS: A spectral tau algorithm based on Jacobi operational matrix for numerical solution of time fractional diffusion-wave equations. J. Comput. Phys. 2014. 10.1016/j.jcp.2014.03.039
Doha EH, Bhrawy AH, Ezz-Eldien SS: A new Jacobi operational matrix: an application for solving fractional differential equations. Appl. Math. Model. 2012, 36: 4931-4943. 10.1016/j.apm.2011.12.031
Doha EH, Bhrawy AH, Baleanu D, Ezz-Eldien SS: On shifted Jacobi spectral approximations for solving fractional differential equations. Appl. Math. Comput. 2013, 219: 8042-8056. 10.1016/j.amc.2013.01.051
Chechkin AV, Gorenflo R, Sokolov IM: Fractional diffusion in inhomogeneous media. J. Phys. A 2005, 38: 679-684. 10.1088/0305-4470/38/42/L03
Dal F: Application of variational iteration method to fractional hyperbolic partial differential equations. Math. Probl. Eng. 2009. 10.1155/2009/824385
Dalir M, Bashour M: Applications of fractional calculus. Appl. Math. Sci. 2010, 4: 1021-1032.
Dubbeldam JLA, Milchev A, Rostiashvili VG, Vilgis TA: Polymer translocation through a nanopore: a showcase of anomalous diffusion. Phys. Rev. E 2007., 76: Article ID 010801
Metzler R, Klafter J: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 2000, 339: 1-77. 10.1016/S0370-1573(00)00070-3
Khader MM: On the numerical solutions for the fractional diffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16: 2535-2542. 10.1016/j.cnsns.2010.09.007
Sousa E: Numerical approximations for fractional diffusion equations via splines. Comput. Math. Appl. 2011, 62: 938-944. 10.1016/j.camwa.2011.04.015
Tadjeran C, Meerschaert MM, Scheffler H-P: A second-order accurate numerical approximation for the fractional diffusion equation. J. Comp. Physiol. 2006, 213: 205-213. 10.1016/j.jcp.2005.08.008
Yuste SB: Weighted average finite difference methods for fractional diffusion equations. J. Comp. Physiol. 2006, 216: 264-274. 10.1016/j.jcp.2005.12.006
Zheng Y, Li C, Zhao Z: A note on the finite element method for the space-fractional advection diffusion equation. Comput. Math. Appl. 2010, 59: 1718-1726. 10.1016/j.camwa.2009.08.071
Su L, Wang W, Yang Z: Finite difference approximations for the fractional advection diffusion equation. Phys. Lett. A 2009, 373: 4405-4408. 10.1016/j.physleta.2009.10.004
Dehghan M: Finite difference procedures for solving a problem arising in modeling and design of certain optoelectronic devices. Math. Comput. Simul. 2006, 71: 16-30. 10.1016/j.matcom.2005.10.001
Bhrawy AH, Baleanu D: A spectral Legendre-Gauss-Lobatto collocation method for a space-fractional advection diffusion equations with variable coefficients. Rep. Math. Phys. 2013, 72: 219-233. 10.1016/S0034-4877(14)60015-X
Saadatmandi A, Dehghan M: A tau approach for solution of the space fractional diffusion equation. Comput. Math. Appl. 2011, 62: 1135-1142. 10.1016/j.camwa.2011.04.014
Doha EH, Bhrawy AH, Ezz-Eldien SS: Numerical approximations for fractional diffusion equations via a Chebyshev spectral-tau method. Cent. Eur. J. Phys. 2013, 11(10):1494-1503. 10.2478/s11534-013-0264-7
Bhrawy, AH, Tharwat, MM, Alghamdi, MA: A new operational matrix of fractional integration for shifted Jacobi polynomials. Bull. Malays. Math. Soc. (2013, accepted)
Canuto C, Hussaini MY, Quarteroni A, Zang TA: Spectral Methods in Fluid Dynamics. Springer, New York; 1988.
Acknowledgements
This paper was funded by the Deanship of Scientific Research DSR, King Abdulaziz University, Jeddah. The authors, therefore, acknowledge with thanks DSR technical and financial support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors have equal contributions to each part of this paper. All the authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Doha, E.H., Bhrawy, A.H., Baleanu, D. et al. The operational matrix formulation of the Jacobi tau approximation for space fractional diffusion equation. Adv Differ Equ 2014, 231 (2014). https://doi.org/10.1186/1687-1847-2014-231
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-231