1 Introduction

Stationary wave solutions for nonlinear equations play an important role in understanding many mathematical models arising in physics and applied sciences. These solutions were developed and categorized to fit many physical learned aspects (see [1]). For example, the authors of [2,3,4] used rogue soliton-waves to study the coupled variable-coefficient fourth-order nonlinear Schrödinger equations in an inhomogeneous optical fiber and coupled Sasa–Satsuma equations. Hu et al. in [5] explored the mixed lump–kink and rogue wave–kink solutions for a \((3+1)\)-dimensional B-type Kadomtsev–Petviashvili equation in fluid mechanics. Further, many interesting soliton-type solutions for physical applications that arise in plasma, surface waves of finite depth, and optical fiber were studied by researchers in, e.g., [6,7,8,9].

In this work, we present a new interesting two-wave version of the generalized fifth-order KdV equation which was discussed in [10, 11]. The standard fifth-order KdV equation has the form

$$ w_{t}+a_{1} w^{2} w_{x}+a_{2} w_{x} w_{xx}+a_{3} w w_{xxx}+ w_{xxxxx}=0, $$
(1.1)

where \(w=w(x,t)\) and \(a_{1}\), \(a_{2}\), \(a_{3}\) are some arbitrary constants. The fifth-order KdV equation (1.1) is a hybrid mathematical model with wide applications to surface and internal waves in fluids [11], as well as to waves in other media [12,13,14]. Special cases of (1.1) are widely used in different branches of sciences such as fluid physics, plasma physics, and quantum theory. For instance, when \(a_{1}=\frac{3}{10} a_{3}^{2}\), \(a_{2}=2 a _{3}\), \(a_{3}=10\), equation (1.1), called Lax equation, was studied in [15]. Also, when \(a_{1}=\frac{2}{5} a_{3}^{2}\), \(a_{2}=a _{3}\), \(a_{3}=5\), this equation is called Sawada–Kotera equation and was solved in [16]. In addition, the authors of [17] obtained the solution to (1.1) for \(a_{1}= \frac{1}{5}a_{3}^{2}\), \(a_{2}=a_{3}\), \(a_{3}=10\), which is known as the Kaup–Kupershmidt equation. Later on, under the assumption \(a_{1}=\frac{2}{9}a_{3}^{2}\), \(a_{2}=2a_{3}\), \(a_{3}=3\), the Ito equation was investigated in [18]. For the case \(a_{1}=45\), \(a_{2}=- \frac{75}{2}\), \(a_{3}=-15\), it is called Kaup–Kupershmidt–Parker–Dye equation [19]. The solution to Caudrey–Dodd–Gibbon equation was found in [20] provided that \(a_{1}=180\), \(a_{2}=30\), \(a _{3}=30\). Finally, for \(a_{1}=45\), \(a_{2}=-15\), \(a_{3}=-15\), (1.1) is called Sawada–Kotera–Parker–Dye equation, which was explored in [21].

The purpose of listing the aforementioned classifications of (1.1) is to highlight the importance and merit of studying new versions of the model, and also to explore its physical features. Now, we proceed to present for the first time the two-waves’ version of (1.1) by applying the operators

$$ \begin{aligned} &N = \frac{\partial }{\partial t}-\alpha s \frac{\partial }{\partial x}, \\ &L = \frac{\partial }{\partial t}-\beta s \frac{\partial }{\partial x}, \end{aligned} $$
(1.2)

respectively, on the expressions \(a_{1} w^{2} w_{x}+a_{2} w_{x} w_{xx}+a _{3} w w_{xxx}\) and \(w_{xxxxx}\) and extending the term \(w_{t}\) into the expression \(w_{tt}-s^{2} w_{xx}\). Therefore, the two-wave fifth-order KdV (TWfKdV) is

$$\begin{aligned}& w_{tt}-s^{2} w_{xx}+ \biggl(\frac{\partial }{\partial t}+ \alpha s \frac{ \partial }{\partial x} \biggr)\bigl\{ a_{1} u^{2} u_{x}+a_{2} w_{x} w_{xx}+a _{3} w w_{xxx}\bigr\} \\& \quad {}+ \biggl(\frac{\partial }{\partial t}-\beta s \frac{ \partial }{\partial x} \biggr) \{w_{xxxxx}\}=0, \end{aligned}$$
(1.3)

where α, β, and s are the nonlinearity, dispersion, and phase velocity, respectively, with \(|\alpha | \leq 1\), \(|\beta | \leq 1\), and \(s \geq 0\). If we set \(s=0\) in (1.3) and integrate once with respect to time t, the TWfKdV equation is reduced to the fifth-order KdV equation (1.2) for the description of a single-wave propagating in one direction only. To learn about constructing two-mode equations, the reader is advised to read [22,23,24,25,26,27,28,29,30,31].

The two-wave equation (1.3) describes the spread of moving two-waves under the influence of dispersion, nonlinearity, and phase velocity factors. We aim to seek possible solutions for (1.3) by implementing two techniques, the Kudryashov-expansion method and sine–cosine function method. Also, we study the effect of phase velocity on the motion of the obtained solutions. Both techniques require converting (1.3) by means of the new variable \(\zeta =x-c t\) into the differential equation

$$ \bigl(c^{2}-s^{2}\bigr)w'-(c+ \alpha s) \bigl(a_{1} w^{2} w'+a_{2} w' w'' +a _{3} w w''' \bigr)-(c+\beta s) \bigl( w^{(5)}\bigr)=0, $$
(1.4)

where \(w=w(\zeta )\).

2 Kudryashov solutions of TMfKdV

The Kudryashov-expansion technique [32,33,34,35] proposes the solution of (1.4) as a polynomial of the variable Z, namely

$$ w(Z)=\sum_{i=0}^{n} A_{i} Z^{i},\quad Z=Z(\zeta ), $$
(2.1)

where variable Z satisfies the differential equation

$$ Z'=\mu Z(Z-1). $$
(2.2)

Solving (2.2) gives

$$ Z(\zeta )=\frac{1}{1+d e^{\mu \zeta }}, $$
(2.3)

where d is a nonzero free constant. The index n is to be determined by applying the order-balance procedure of the linear term \(w^{(5)}\) against the nonlinear term \(w^{2} w'\), which gives that \(n=2\). Therefore, we can write (2.1) as

$$ w(\zeta ) = A_{0} +A_{1} Z +A_{2} Z^{2}. $$
(2.4)

Differentiating both (2.2) and (2.4) implicitly leads to

$$ \begin{aligned} &Z'' = \mu ^{2} Z(Z-1) (2Z-1), \\ &Z''' = \mu ^{3} Z(Z-1) \bigl(6Z^{2}-6Z+1\bigr), \\ &Z^{(4)} = \mu ^{4} Z(Z-1) \bigl(24 Z^{3}-36 Z^{2}+14 Z-1\bigr), \\ &Z^{(5)} = \mu ^{5} Z(Z-1) \bigl(120 Z^{4}-240 Z^{3}+150 Z^{2}-30 Z+1\bigr), \end{aligned} $$
(2.5)

and

$$ \begin{aligned} &w'(\zeta ) = A_{1} Z' +2 A_{2} Z Z', \\ &w''(\zeta ) = A_{1} Z'' +2 A_{2} \bigl(Z Z''+\bigl(Z' \bigr)^{2}\bigr), \\ &w'''(\zeta ) = A_{1} Z''' +2 A_{2} \bigl(Z Z'''+3Z' Z'' \bigr), \\ &w^{(4)}(\zeta ) = A_{1} Z^{(4)} +2 A_{2} \bigl(Z Z^{(4)}+4 Z' Z'''+3 \bigl(Z''\bigr)^{2}\bigr), \\ &w^{(5)}(\zeta ) = A_{1} Z^{(5)} +2 A_{2} \bigl(Z Z^{(5)}+5 Z' Z^{(4)}+10 Z'' Z'''\bigr). \end{aligned} $$
(2.6)

Now, we insert (2.2) through (2.6) into (1.4) to get a finite polynomial in Z. By setting each coefficient of \(Z^{i}\) to zero, a nonlinear algebraic system with unknowns \(A_{0}\), \(A_{1}\), \(A _{2}\), μ, c is obtained. We cannot solve the resulting system unless we consider some restrictions on the coefficients \(a_{0}\), \(a _{1}\), \(a_{2}\) and the parameters α, β.

2.1 Kudryashov-Case I

The first solution for the TMfKdV (1.3) exists when the coefficients are assigned as

$$ a_{1}=\frac{6 \mu ^{2} a_{3}}{A_{1}},\qquad a_{2}=\frac{60 \mu ^{2}-A_{1} a_{3}}{A_{1}}, \qquad a_{3}= \mathtt{free}; $$

and the two-mode parameters have the relation

$$ \alpha =\beta . $$

Hence,

$$ \begin{aligned} &A_{2} = - A_{1}, \\ &A_{0} = 0, \\ &A_{1} = \mathtt{free} \neq 0, \\ &c = \frac{1}{2} \bigl(\mu ^{4} \mp \sqrt{4 s^{2} +4 s \beta \mu ^{4}+ \mu ^{8}} \bigr). \end{aligned} $$
(2.7)

Therefore, the first obtained solution is

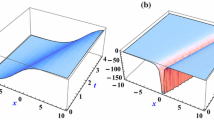
$$ u(x,t)=\frac{A_{1} d e^{\mu (x-\frac{1}{2}t (\mu ^{4} \mp \sqrt{4 s^{2} +4 2 \beta \mu ^{4}+\mu ^{8}} ) )}}{ (1+d e^{\mu (x-\frac{t}{2} (\mu ^{4} \mp \sqrt{4 s ^{2} +4 s \beta \mu ^{4}+\mu ^{8}} ) )} )^{2}}. $$
(2.8)

Figure 1 presents 3D plots of the two-waves depicted in (2.8) upon increasing the phase velocity s. Figure 2 is a 2D plot of (2.8) when coordinate x is fixed. It can be seen that these two waves can be regarded as left–right waves (having opposite directions).

Figure 1
figure 1

Shapes of the two-waves depicted in (2.8) by increasing the phase velocity: \(s=1, 3, 5\), respectively, and the other assigned values are \(\beta =0.1\), \(d= \mu =A_{1}=1\)

Full size image
Figure 2
figure 2

2D plot of (2.8) when \(x=1\), \(s=5\) and the other assigned values are \(\beta =0.1\), \(d= \mu =A_{1}=1\)

Full size image

2.2 Kudryashov-Case II

When we take the coefficients

$$ a_{1}=\frac{(183- 7\sqrt{849}) \mu ^{4}}{8 A_{0}^{2}},\qquad a_{2}=\frac{(443- 7\sqrt{849}) \mu ^{2}}{8 A_{0}}, \qquad a_{3}= \frac{-13 \mu ^{2}}{A_{0}} , $$

and the two-wave parameters satisfy \(\alpha =\beta \), then the second solution for (1.3) is reached. Accordingly,

$$ \begin{aligned} &A_{0} = \mathtt{free} \neq 0, \\ &A_{1} = 0, \\ &A_{2} = - \frac{3}{26}(41+ \sqrt{849})A_{0}, \\ &c = \frac{1}{16} \bigl(-7(15+\sqrt{849})\mu ^{4} \\ &\hphantom{c ={}}{}\mp \sqrt{256 s ^{2} -224(15+\sqrt{849})s \beta \mu ^{4}+294(179+5 \sqrt{849})\mu ^{8}} \bigr). \end{aligned} $$
(2.9)

Thus, the second obtained solution is

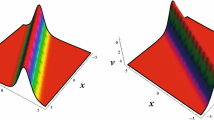
$$ u(x,t)=A0-\frac{3(41+ \sqrt{849})A_{0}}{26 (1+d e^{\mu (x- \frac{t}{16} (-7(15+\sqrt{849})\mu ^{4} \mp \sqrt{256 s^{2} -224(15+ \sqrt{849})s \beta \mu ^{4}+294(179+5\sqrt{849})\mu ^{8}} ) )} ) ^{2}}. $$
(2.10)

Figure 3 presents the 3D plot of the two-waves depicted in (2.10).

Figure 3
figure 3

The two-waves depicted in (2.10) with \(\beta =0.1\), \(s=d= \mu =A_{0}=1\)

Full size image

2.3 Kudryashov-Case III

It is worth mentioning that when the two-waves’ parameters satisfy \(\alpha =\beta =\pm 1\), the third solution for TWfKdV (1.3) (with no restrictions on the coefficients \(a_{1}\), \(a_{2}\), \(a_{3}\)) is obtained. So,

$$ \begin{aligned} &A_{0} = \mathtt{free}, \\ &A_{1} = \mathtt{free} \neq 0, \\ &A_{2} = 0, \\ &c = \pm s, \end{aligned} $$
(2.11)

which gives that the third obtained solution is

$$ u(x,t)=A_{0} +\frac{A_{1}}{1+d e^{\mu (x\pm s t)}}. $$
(2.12)

Figure 4 presents 3D plots of the two-waves depicted in (2.12) upon increasing the interaction phase velocity s.

Figure 4
figure 4

Shapes of the two-waves depicted in (2.12) by increasing the phase velocity: \(s=5, 10, 15\), respectively, and the other assigned values are \(d= \mu =A_{0}=A_{1}=1\)

Full size image

3 Sine–cosine solution of TMfKdV

The goal of this section is to find periodic solutions of TWfKdV by means of sine–cosine function method (see [36,37,38]). This scheme propose the solution of (1.4) in the form

$$ w(\zeta )=A \sin ^{p}(\mu \zeta ), $$
(3.1)

or

$$ w(\zeta )=A \cos ^{p}(\mu \zeta ). $$
(3.2)

To determine the values of A, p, μ and c, we substitute (3.1) or (3.2) in (1.4), and then collect the coefficients of same powers of \(\sin ^{i}\) or \(\cos ^{i}\) and set each to zero. In fact, we have an algebraic system with \(\alpha =\beta \), namely

$$ \begin{aligned} &\bigl\{ \sin ^{p-5},\cos ^{p-5} \bigr\} \mbox{:}\quad -A p \bigl(24 - 50 p + 35 p^{2} - 10 p^{3} + p^{4}\bigr) (c + s \beta ) \mu ^{5}, \\ &\bigl\{ \sin ^{p-3},\cos ^{p-3}\bigr\} \mbox{:}\quad 2 A p \bigl(4 - 10 p + 10 p^{2} - 5 p^{3} + p ^{4}\bigr) (c + s \beta ) \mu ^{5}, \\ &\bigl\{ \sin ^{p-1},\cos ^{p-1}\bigr\} \mbox{:}\quad -A p \mu \bigl(-c^{2} + c p^{4} \mu ^{4} + s \bigl(s + p^{4} \beta \mu ^{4}\bigr)\bigr), \\ &\bigl\{ \sin ^{2p-3},\cos ^{2p-3}\bigr\} \mbox{:}\quad -A^{2} (-1 + p) p \bigl(a3 (-2 + p) + a2 p\bigr) (c + s \alpha ) \mu ^{3}, \\ &\bigl\{ \sin ^{2p-1},\cos ^{2p-1}\bigr\} \mbox{:}\quad A^{2} (a2 + a3) p^{3} (c + s \alpha ) \mu ^{3}, \\ &\bigl\{ \sin ^{3p-1},\cos ^{3p-1}\bigr\} \mbox{:}\quad -A^{3} a1 p (c + s \alpha ) \mu . \end{aligned} $$
(3.3)

Solving (3.3) requires \(p=-2\), and the TWfKdV’s coefficients are

$$ \begin{aligned} &a_{1} = -\frac{6 a_{3} \mu ^{2}}{A}, \\ &a_{2} = -\frac{A a_{3} +60 \mu ^{2}}{A}. \end{aligned} $$
(3.4)

So, we deduce that the wave speed c is

$$ c=8 \mu ^{4}\mp \sqrt{s^{2}+16 s \beta \mu ^{4}+64 \mu ^{8}}. $$
(3.5)

Therefore, two periodic-type solutions are

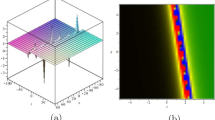
$$ \begin{aligned} &w(x,t) = A \csc ^{2}\bigl(\mu \bigl(x- \bigl(8 \mu ^{4}\mp \sqrt{s^{2}+16 s \beta \mu ^{4}+64 \mu ^{8}}\bigr)t\bigr)\bigr), \\ &w(x,t) = A \sec ^{2}\bigl(\mu \bigl(x-\bigl(8 \mu ^{4}\mp \sqrt{s^{2}+16 s \beta \mu ^{4}+64 \mu ^{8}}\bigr)t \bigr)\bigr). \end{aligned} $$
(3.6)

Figure 5 presents plots of the two-waves obtained in (3.6) upon increasing the phase velocity s.

Figure 5
figure 5

Shapes of the two-waves depicted in (3.6) by increasing the phase velocity: \(s=1, 5, 10\), respectively, and the other assigned values are \(A=\mu =\beta =1\)

Full size image

4 Conclusion

A new two-wave version of the generalized fifth-order KdV problem is established. This new model possesses two directional waves with interacting phase velocity. We obtained different solutions of this new model under particular choices of the coefficients \(a_{1}\), \(a_{2}\), \(a _{3}\), and the constraint condition \(\alpha =\beta =d\) with \(|d|<1\). Also, we studied the impact of increasing the phase velocity on the shape of spreading its two-waves. The following findings are recorded:

  • For \(a_{1}=\frac{6 \mu ^{2} a_{3}}{A_{1}}\), \(a_{2}=\frac{60 \mu ^{2}-A _{1} a_{3}}{A_{1}}\), \(a_{3}= \mathtt{free}\), and \(\alpha =\beta \), the TWfKdV is a soliton-type.

  • For \(a_{1}=\frac{(183- 7\sqrt{849}) \mu ^{4}}{8 A_{0}^{2}}\), \(a _{2}=\frac{(443- 7\sqrt{849}) \mu ^{2}}{8 A_{0}}\), \(a_{3}= \frac{-13 \mu ^{2}}{A_{0}}\), and \(\alpha =\beta \), the TWfKdV is a kink-type.

  • For arbitrary \(a_{1}\), \(a_{2}\), \(a_{3}\) and \(\alpha =\beta =\pm 1\), the TWfKdV is a kink-type.

  • For \(a_{1}=-\frac{6 a_{3} \mu ^{2}}{A}\), \(a_{2}=-\frac{A a_{3} +60 \mu ^{2}}{A}\) and \(\alpha =\beta \), the TWfKdV is a singular periodic-type.

We may say that these two-waves could be useful in many physical and engineering applications, for example, they can be used as barrier waves to strengthen the transmission of different signals’ data. Also, if a large amount of data is difficult to pass on to a single router, it can be distributed on two routers.