1 Introduction

Dual-mode type is a new family of nonlinear partial differential equations which fall in the following form: [1, 2]

$$ y_{tt}-s^{2}y_{xx}+\biggl( \frac{\partial}{\partial t}-\alpha s \frac{\partial}{\partial x}\biggr)N(y,y_{x},\ldots)+ \biggl(\frac{\partial}{\partial t}-\beta s \frac{\partial}{\partial x}\biggr)L(y_{kx})=0, $$
(1.1)

where \(N(y,y_{x},\ldots)\) and \(L(y_{kx}) : k\geq2\) are the nonlinear and linear terms involved in the equation. \(y(x,t)\) is the unknown field-function, \(s>0\) is the phase velocity, \(\vert \beta \vert \leq1\), \(\vert \alpha \vert \leq1\), β is the dispersion parameter, and α is the parameter of nonlinearity. With \(s=0\) and integrating with respect to t, the dual-mode problem is reduced to a partial differential equation of the first order in time t.

A few dual-mode models have been established and studied. In [3,4,5,6,7,8], authors extracted abundant soliton solutions for the second-order KdV. [9, 10] established the dual-mode Burgers and fourth-order Burgers and obtained multiple soliton solutions by means of the simplified Hirota technique. In [11,12,13], the tanh technique and Hirota method were implemented to seek possible solutions of the two-mode coupled Burgers equation, coupled m-KdV, and coupled KdV. Finally, the dual-mode perturbed Burgers, Ostrovsky, and Schrodinger equations were established in [14, 15].

1.1 Structure of dual-mode \((2+1)\)-dimensional Kadomtsev–Petviashvili

The Kadomtsev–Petviashvili (KP) equation reads [16, 17]

$$ \frac{\partial}{\partial x} (W_{t}-6 W W_{x}+W_{xxx} )+3\sigma W_{yy}=0, $$
(1.2)

where \(W=W(x,y,t)\). It models three connected aspects: weakly dispersive, longer wave length compared with its wave amplitude, and slower variation in y-coordinate compared with its propagation in x-coordinate. σ gives the strength of the surface tension, strong with \(\sigma>0\) and weak if \(\sigma<0\).

To derive the dual-mode version of KP, we apply the operator \(N=(\frac{\partial}{\partial t}-\alpha_{1} s \frac{\partial }{\partial x}-\alpha_{2} s \frac{\partial}{\partial y})\) to the nonlinear terms of (1.2) and the operator \(L=(\frac{\partial}{\partial t}-\beta_{1} s \frac{\partial}{\partial x}-\beta_{2} s \frac{\partial}{\partial y})\) to the linear terms, i.e.,

$$ \begin{aligned}[b] 0={}&\frac{\partial}{\partial x} \biggl(W_{tt}-s^{2} W_{xx}-s^{2} W_{yy}-6 \biggl(\frac{\partial}{\partial t}- \alpha_{1} s \frac{\partial}{\partial x}-\alpha_{2} s \frac{\partial}{\partial y} \biggr) (W W_{x})\\ &+\biggl(\frac{\partial}{\partial t}-\beta_{1} s \frac{\partial }{\partial x}-\beta_{2} s \frac{\partial}{\partial y}\biggr) (W_{xxx}) \biggr) \\ &+3\sigma\biggl(\frac{\partial}{\partial t}-\beta_{1} s \frac{\partial}{\partial x}- \beta_{2} s \frac{\partial}{\partial y}\biggr) (W_{yy}),\end{aligned} $$
(1.3)

\(\alpha_{1}\), \(\alpha_{2}\) are the nonlinearity parameters, \(\beta_{1}\), \(\beta_{2}\) are the dispersive parameters, and s is the phase velocity.

We aim in this work to seek possible soliton solutions for (1.3) and study graphically the effects of the aforementioned parameters on the propagations of the obtained dual waves such model possesses.

2 Solutions of DMKP by tanh-expansion technique

First, we use the new variable \(z=a x+ b y -c t\) to convert (1.3) into the following reduced differential equation:

$$ \begin{aligned}[b] 0={}& \bigl(a\bigl(c^{2}-\bigl(a^{2}+b^{2} \bigr)s^{2}\bigr) -3\sigma b^{2}(c+\beta_{1} a s+ \beta_{2} b s) \bigr)W+3a^{2} (c+\alpha_{1} a s+ \alpha_{2} b s) W^{2} \\ &-a^{4} (c+\beta_{1} a s+\beta_{2} b s) W'',\end{aligned} $$
(2.1)

where \(W=W(z)\). Balancing \(W^{2}\) with \(W''\) in tanh technique sense [18, 19], the solution of (2.1) is

$$ W(z)=A_{1}+A_{2} \tanh(z)+A_{3} \tanh^{2}(z). $$
(2.2)

To determine the values of \(A_{1}\), \(A_{2}\), \(A_{3}\), a, b, and c, we substitute (2.2) in (2.1) and apply the identity \(\operatorname {sech}^{2}(z)=1-\tanh^{2}(z)\) to get a polynomial of tanh function. Setting the coefficient of the same power of tanh to zero, we obtain the following non-algebraic system:

$$\begin{aligned}& \begin{aligned}0={}&3 a^{2} A_{1}^{2} c - 2 a^{4} A_{3} c + a A_{1} c^{2} - a^{3} A_{1} s^{2} - a A_{1} b^{2} s^{2} + 3 a^{3} A_{1}^{2} s \alpha_{1} + 3 a^{2} A_{1}^{2} b s \alpha_{2} \\ &- 2 a^{5} A_{3} s \beta_{1}- 2 a^{4} A_{3} b s \beta_{2} - 3 A_{1} b^{2} c \sigma- 3 a A_{1} b^{2} s \beta_{1} \sigma- 3 A_{1} b^{3} s \beta_{2} \sigma,\end{aligned} \\& \begin{aligned}0={}& 2 a^{4} A_{2} c + 6 a^{2} A_{1} A_{2} c + a A_{2} c^{2} - a^{3} A_{2} s^{2} - a A_{2} b^{2} s^{2} + 6 a^{3} A_{1} A_{2} s \alpha_{1} + 6 a^{2} A_{1} A_{2} b s \alpha_{2} \\ &+ 2 a^{5} A_{2} s \beta_{1}+ 2 a^{4} A_{2} b s \beta_{2} - 3 A_{2} b^{2} c \sigma- 3 a A_{2} b^{2} s \beta_{1} \sigma- 3 A_{2} b^{3} s \beta_{2} \sigma,\end{aligned} \\& 0= 3 a^{2} A_{2}^{2} c + 8 a^{4} A_{3} c + 6 a^{2} A_{1} A_{3} c + a A_{3} c^{2} - a^{3} A_{3} s^{2} - a A_{3} b^{2} s^{2} + 3 a^{3} A_{2}^{2} s \alpha_{1} \\& \phantom{0=}{} + 6 a^{3} A_{1} A_{3} s \alpha_{1}+ 3 a^{2} A_{2}^{2} b s \alpha_{2} + 6 a^{2} A_{1} A_{3} b s \alpha_{2} + 8 a^{5} A_{3} s \beta_{1} + 8 a^{4} A_{3} b s \beta_{2} \\& \phantom{0=}{} - 3 A_{3} b^{2} c \sigma- 3 a A_{3} b^{2} s \beta_{1} \sigma- 3 A_{3} b^{3} s \beta_{2} \sigma, \\& 0= -2 a^{4} A_{2} c + 6 a^{2} A_{2} A_{3} c + 6 a^{3} A_{2} A_{3} s \alpha_{1} + 6 a^{2} A_{2} A_{3} b s \alpha_{2} - 2 a^{5} A_{2} s \beta_{1} - 2 a^{4} A_{2} b s \beta_{2}, \\& 0=-6 a^{4} A_{3} c + 3 a^{2} A_{3}^{2} c + 3 a^{3} A_{3}^{2} s \alpha_{1} + 3 a^{2} A_{3}^{2} b s \alpha_{2} - 6 a^{5} A_{3} s \beta_{1} - 6 a^{4} A_{3} b s \beta_{2}. \end{aligned}$$
(2.3)

We study the solution of the above system via compatible constraint relations:

For \(\alpha_{1}=\alpha_{2}=\beta_{1}=\beta_{2}=\gamma\) with \(|\gamma|<1\), we get two solution sets.

2.1 The first solution set

$$ \begin{gathered} a= \text{free constant},\qquad A_{1}= \text{free constant},\qquad A_{2}= 0, \\ A_{3}=2 a^{2}, \\ c=\frac{s \gamma(a\pm\sqrt{a^{2}(2\gamma^{2}-1)})}{\gamma^{2}-1},\qquad b= \frac{ a \gamma^{2} \pm\sqrt{a^{2}(2\gamma^{2}-1)}}{1-\gamma^{2}}.\end{gathered} $$
(2.4)

Therefore, the resulting dual-wave solution of DMKP (1.3) is

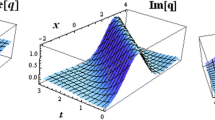
$$ W(x,y,t)=A_{1}+3 a^{2} \tanh^{2} \biggl(a x +\frac{ a \gamma^{2} \pm \sqrt{a^{2}(2\gamma^{2}-1)}}{1-\gamma^{2}} y-\frac{s \gamma(a\pm \sqrt{a^{2}(2\gamma^{2}-1)})}{\gamma^{2}-1} t \biggr), $$
(2.5)

where \(\frac{1}{\sqrt{2}}< | \gamma|<1\). Figure 1 shows the proximity of the two waves with increasing the phase velocity s and fixing γ. Figure 2 shows the extent of convergence and spacing of the two waves by the sign of γ and fixing s.

Figure 1
figure 1

3D plots of the dual waves \(W(x,y,t)\) and the impact of phase velocity s on its propagating

Full size image
Figure 2
figure 2

3D plots of the dual waves \(W(x,y,t)\) and the impact of linearity-dispersive parameter γ on its propagating

Full size image

2.2 The second solution set

$$ \begin{gathered}a= \text{free constant},\qquad A_{1}= 0,\qquad A_{2}= \text{free constant}, \\ A_{3}=2 a^{2}, \\ c=-(a+b)s \gamma,\qquad b= \frac{ a \gamma^{2} \pm\sqrt{a^{2}(2\gamma^{2}-1)}}{1-\gamma^{2}}.\end{gathered} $$
(2.6)

Therefore, the resulting dual-wave solution of DMKP (1.3) is

$$ \begin{aligned}[b] W(x,y,t)={}&A_{2} \tanh \biggl(a x +\frac{ a \gamma^{2} \pm \sqrt{a^{2}(2\gamma^{2}-1)}}{1-\gamma^{2}} y\\&- \biggl(a+\frac{ (a \gamma^{2} \pm\sqrt{a^{2}(2\gamma^{2}-1)}}{1-\gamma^{2}} \biggr)s \gamma t \biggr) \\ &+2 a^{2} \tanh^{2} \biggl(a x +\frac{ a \gamma^{2} \pm \sqrt{a^{2}(2\gamma^{2}-1)}}{1-\gamma^{2}} y\\ &- \biggl(a+\frac{ (a \gamma^{2} \pm\sqrt{a^{2}(2\gamma^{2}-1)}}{1-\gamma^{2}} \biggr)s \gamma t \biggr),\end{aligned} $$
(2.7)

where \(\frac{1}{\sqrt{2}}< | \gamma| <1\). Figure 3 shows the shape of the obtained solution described in (2.7).

Figure 3
figure 3

3D plots of the first wave, second wave, and dual waves for \(W(x,y,t)\) given in (2.7)

Full size image

3 Solutions of DMKP by Kudryashov expansion technique

It is to be noted that the tanh solution obtained in the preceding section is σ-independent and, therefore, using another method to study the solution of DMKP is needed. We use here the Kudryashov technique where the solution takes the following form [20, 21]:

$$ W(x,y,t)=W(z)=\sum_{i=0}^{n} \lambda_{i} Y^{i},\quad Y=Y(z), z=a x+b y-c t. $$
(3.1)

The variable Y satisfies the differential equation

$$ Y'=Y(Y-1)\ln(k). $$
(3.2)

Solving (3.2) gives

$$ Y(z)=\frac{1}{1+d k^{z}}. $$
(3.3)

The index n to be determined by applying order-balance procedure between \(W^{2}\) and \(W''\) appears in (2.1). Thus, \(n=2\) and accordingly we write (3.1) as

$$ W(z)= \lambda_{0} +\lambda_{1} Y + \lambda_{2} Y^{2}. $$
(3.4)

Differentiating both (3.2) and (3.4) implicitly leads to

$$ Y''=Y(Y-1) (2Y-1)\ln^{2}(k) $$
(3.5)

and

$$ \begin{gathered} W'(z)=\lambda_{1} Y' +2 \lambda_{2} Y Y', \\ W''(z)=\lambda_{1} Y'' +2 \lambda_{2} \bigl(Y Y''+ \bigl(Y'\bigr)^{2}\bigr).\end{gathered} $$
(3.6)

Now, we insert (3.2) through (3.6) in (2.1) to get a polynomial in Y. By setting each coefficient of \(Y^{i}\) to zero, a nonlinear algebraic system is obtained. Seeking a solution to this system, we get

$$ \begin{gathered}\alpha_{1} =\alpha_{2} = \beta_{1}= \beta_{2}= \gamma, \qquad \vert \gamma \vert < 1, \\ \lambda_{0}=0, \\ \lambda_{1}=-2 a^{2} \ln^{2}(k) , \\ \lambda_{2}=-\lambda_{1}, \\ \begin{aligned} c={}&\bigl(3 b^{2} \sigma+ a^{4} \ln^{2}(k)\\& \pm\sqrt{(3 b^{2} \sigma+ a^{4}\ln^{2}(k))^{2} +4 a s (a^{3} s + 3 b^{3} \gamma\sigma+ a b^{2} (s + 3 \gamma\sigma) + a^{4} (a + b) \gamma\ln^{2}(k))}\bigr)\\&/(2 a).\end{aligned}\end{gathered} $$
(3.7)

Therefore, a new solution of DMKP (1.3) is

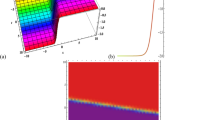
$$ W(x,y,t)= -\frac{2 a^{2} d \ln^{2}(k) k^{c t + a x + b y}(2 + \ln(k))}{ (k^{c t} + d k^{a x + b y})^{2}}. $$
(3.8)

Figures 4 and 5 provide 3D plots of the Kudryashov solutions when \(\sigma> 0\) and \(\sigma<0\), respectively.

Figure 4
figure 4

3D soliton solution of \(W(x,y,t)\) given in (3.8) when \(\sigma=2\) and respectively \(t=1\) and \(t=2\). The other assigned values are \(a=b=d=1\), \(k=e\), \(\gamma=\frac{1}{2}\)

Full size image
Figure 5
figure 5

3D soliton solution of \(W(x,y,t)\) given in (3.8) when \(\sigma=-2\) and respectively \(t=1\) and \(t=2\). The other assigned values are \(a=b=d=1\), \(k=e\), \(\gamma=\frac{1}{2}\)

Full size image

4 Conclusion

A new dual-mode Kadomtsev–Petviashvili (DMKP) equation is introduced. This model describes the spread of two simultaneously directional waves. We have studied possible solutions for DMKP and obtained the following findings:

  • σ-independent tanh soliton solution is obtained for the DMKP.

  • σ-dependent Kudryashov soliton solution is obtained for the DMKP.

  • The above two solutions exist when \(\alpha_{1}=\alpha_{2}=\beta_{1}=\beta_{2}=\gamma\) with \(\frac{1}{\sqrt{2}} < |\gamma|< 1\).

Also, a graphical analysis is provided to show the impact of both linearity-dispersive parameter γ and the phase velocity s on the spread of the obtained dual waves for DMKP.