Abstract
A new approximate technique is introduced to find a solution of FVFIDE with mixed boundary conditions. This paper started from the meaning of Caputo fractional differential operator. The fractional derivatives are replaced by the Caputo operator, and the solution is demonstrated by the hybrid orthonormal Bernstein and block-pulse functions wavelet method (HOBW). We demonstrate the convergence analysis for this technique to emphasize its reliability. The applicability of the HOBW is demonstrated using three examples. The approximate results of this technique are compared with the correct solutions, which shows that this technique has approval with the correct solutions to the problems.
Similar content being viewed by others
1 Introduction
The applications of fractional calculus can be observed in many fields of physics and engineering such as fluid dynamic traffic [1] and signal processing [2]. Due to the invaluable contribution of fractional calculus in various fields of engineering, the researchers have shown high interest in studying fractional calculus. In this regard as in many cases, it is very difficult to find the correct analytical solutions of fractional differential and integral equations. The approximate methods have gained importance to prevent this difficulty. Initially the authors used different approximate techniques to find the approximate solution of fractional differential and integral equations such as spline collocation method (SCM) [3], fractional transform method (FTM) [4], homotopy perturbation method (HPM) [5], operational Tau method (OTM) [6], rationalized Haar functions method (RHFM) [7], reproducing kernel Hilbert space method (RKHSM) [8], Adomian decomposition method (ADM) [9], and B-spline method [10].
In this paper, we derive the approximate solution of FVFIDE using HOBW. The approximate consequence found by the introduced method is compared with the correct solution of the problem, showing the greatest degree of accuracy.
2 Preliminaries of fractional calculus
In this segment, we first survey some fundamental definitions of the fractional calculus theory which are required for building up our outcomes. The broadly utilized definitions of fractional integral and fractional derivative are the definitions of Riemann–Liouville and Caputo [11,12,13,14].
Definition 2.1
A real function \(y(x), x>0\), is said to be in the space \(C_{\sigma}\), \(\sigma \in R\), if there is a genuine number ρ with \(\rho> \sigma\) to such an extent that \(y(x)= x^{\rho} y_{0} (x), y_{0} ( x ) \in C [ 0, \infty )\), and \(y ( x ) \in C_{\sigma}^{n}\) if \(y^{n} ( x ) \in C_{\sigma}, n \in N\).
Definition 2.2
([15])
The Riemann fractional integral of order \(\alpha >0\) of a function f is given by
This integral operator J has the following properties:
-
(a)
\(J^{\alpha} J^{\beta} = J^{\beta} J^{\alpha}\);
-
(b)
\(J^{\alpha} J^{\beta} = J^{\alpha+\beta}\);
-
(c)
\(J^{\alpha} (t-a)^{\xi} = \frac{\varGamma ( \xi +1)}{\varGamma ( \xi +\alpha+1)} (t-a)^{\alpha+ \xi},\alpha,\beta>0, \xi >-1\).
Definition 2.3
The Riemann–Liouville fractional derivative is defined by [16]
In fact \(D_{*}^{\alpha} J^{\alpha} f ( t ) = D^{m} J^{m-\alpha} J^{\alpha} f ( t ) = D^{m} J^{m} f ( t ) =f ( t )\). The effect of the operator \(D^{\alpha}\) on the power functions:
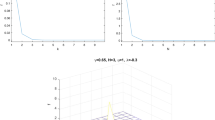
where the fractional derivative \(D_{*}^{\alpha} f ( t )\) is not zero for constant function when \(\alpha\notin N\), from (2.3) when \(\gamma=0\), then \(D_{*}^{\alpha} 1= \frac{t^{-\alpha}}{\varGamma ( -1+\alpha )}\), but \(D_{*}^{\alpha} t^{\alpha-j} =0, j:1 ( 1 ) m\). Figure 1 shows the effect of Riemann–Liouville fractional derivative (\(D^{\alpha}\)) on \(t^{\gamma}\). It is illustrated that when \(\gamma=0\), the Riemann–Liouville derivative is not zero and it is zero when \(\gamma=-0.5\). Therefore, this definition does not agree with the principles of integer order calculus.
Definition 2.4
The fractional derivative of \({f}({t})\) in the Caputo sense is given by [16]
We demonstrate the following form of FVFIDE that we will solve by the HOBW technique.
with MBC: \(\sum_{j=1}^{d} [a_{i,j} y^{(j-1)} (0) + b_{i,j} y^{ ( j-1 )} (1)]= r_{i}, i=1,2,\dots,d\), where \(y: [ 0,1 ]\rightarrow \mathbb{R}, i=1,2\), are continuous functions. \(g: [ 0,1 ]\rightarrow \mathbb{R}\) and \(k_{i}: [ 0,1 ] \times [ 0,1 ]\rightarrow \mathbb{R}, i=1,2\), are continuous functions. \(F_{i}: [ 0,1 ] \times \mathbb{R}\rightarrow \mathbb{R}, i=1,2\), are nonlinear terms and Lipschitz continuous functions. Here \(D^{\alpha}\) is understood as Caputo fractional derivative. Using HOBW this FVFIDE is converted into a system of algebraic equations that can be disbanded by Newton’s method. We applied the Gauss–Legendre quadrature technique for calculating the integration on nonlinear terms. The obtained consequence is compared with that by the Nystrom method.
3 The HOBW method and the operational matrix of the integration
3.1 Wavelets and the HOBW methods
Wavelets constitute a group of functions constructed from dilation and translation of a single function \(\psi (x)\) called the mother wavelet, in which the parameter of dilation a and the parameter of translation b vary continuously:
By letting a and b be discrete values such as \(a = a_{0}^{ - k},b = n b_{0} a_{0}^{ - k}, a_{0} > 1\), \(b_{0} > 0\), where n and k are positive integers, we attain the family of discrete wavelets:
Then \(\psi_{k,n}(t)\) shape a wavelet basis for \(L^{2}(R)\). In particular, when \(a_{0} = 2\), \(b_{0} = 1\), then \(\psi_{k,n}(t)\) shape an orthonormal basis. Here, \(\mathrm{HOBW}_{i,j}(t) = \mathrm{HOBW}(k,i,j,t)\) involves four arguments, \(i = 1,\ldots,2^{k - 1}\), k is any positive integer, j is the degree of Bernstein polynomials, and t is the normalized time. \(\mathrm{HOBW}_{i,j}(t)\) are defined on [0, 1) as in [17]:
where \(i = 1,2,\ldots, 2^{k - 1}\), \(j = 0,1,\ldots, M - 1\) and k is a positive integer. Thus, we attain our new basis as \(\{ \mathrm{HOBW}_{1,0},\mathrm{HOBW}_{1,1},\ldots,\mathrm{HOBW}_{2^{k - 1},M - 1}\}\) and any function is truncated with them.
The HOBW are orthonormal basis that is given by
where \((\cdot,\cdot)\) is called the inner product in \(L^{2}[0,1)\). The HOBW has compact support \([\frac{i - 1}{2^{k - 1}},\frac{i}{2^{k - 1}}], i = 1,\ldots,2^{k - 1}\).
3.2 Function approximation by the HOBW functions
Any function \(y(t)\), which is integrable in \([0, 1)\), is truncated by the HOBW method as follows:
where the HOBW coefficients \(c_{ij}\) can be calculated as given below:
We approximate \(y(t)\) by a truncated series as follows:
where \(\mathrm{HOBW}(t)\) and C are \(2^{k - 1}M \times 1\) vectors given by
and
4 Solution of FVFIDE via the HOBW method
Consider the nonlinear FVFIDE with MBC given in Eq. (2.5), and we approximate the unknown function \(y(x) \in [0, 1] \) by the HOBW method as \(y ( x ) = C^{T} \mathrm{HOBW}(x)\).
We assume
we approximate \(u_{i} (x)\) and \(v_{i} ( x )\) as:
where A and B are like C.
First, applying J to both sides of Eq. (2.5) and using the approximation above, we have
\(y_{i} ( x )\) of Eq. (4.3) is replaced with the approximate solution \(C_{i}^{T} \mathrm{HOBW} ( x )\) as follows:
We collocate Eq. (4.4) in \(2^{k-1} M\) nodal points of Newton–Cotes as \(x_{i} = \frac{2i-1}{2^{k} M}\). We have
Applying the Gauss–Legendre quadrature method for evaluating the integrals in Eq. (4.5), we change the domain of integration from \([0, x_{i}]\) to \([ -1,1 ]\). Using the transformation \(\tau= \frac{x_{i}}{2} (s+1)\) and then applying the Gauss–Legendre method yields
where \(M_{1}\) and \(M_{2}\) are the orders of Bernstein polynomial used in the Gauss–Legendre quadrature rule
From (4.6) give a system of \(2^{k-1} M\times 2^{k-1} M\) nonlinear algebraic equations with the same number of unknowns in the vectors C, A, and B. Numerically disbanding this system by Newton’s technique, we get the solutions for the unknown vectors C, A, and B.
5 Existence and uniqueness
Consider FVIDE (2.5) that can be rewritten in the operator form as follows:
where
Applying \(J^{\alpha}\) to both sides of Eq. (5.1), we have
where \(h_{i} ( x ) = \sum_{k=0}^{n-1} \frac{t^{k}}{k!} y_{i}^{k} ( 0+ ), n-1<\alpha<n\), \(n\in N\). Equation (5.3) is written in a form of fixed point equation \(\mathcal{A} y_{i} = y_{i}\), where \(\mathcal{A}\) is defined as
Let (\(C [ 0,1 ], \Vert \cdot \Vert _{\infty} \)) be the Banach space of all continuous functions with the norm \(\Vert f \Vert _{\infty} = \operatorname{max}_{t} \vert f(t) \vert \). Also, the operators \(\mathcal {F}_{1i}\) and \(\mathcal {F}_{2i}\) satisfy the Lipschitz condition on [0, 1] as follows:
where \(L_{1}\) and \(L_{2}\) are Lipschitz constants. So, we achieve the uniqueness of the solution of Eq. (2.5).
Theorem 5.1
If \(L_{1} \Vert \mathcal {K}_{1i} \Vert _{\infty} + L_{1} \Vert \mathcal {K}_{2i} \Vert _{\infty} <\varGamma ( \alpha+1 )\), then problem (2.5) has a unique solution \(y\in [ 0,1 ]\).
Proof
Let \({A}: C [ 0,1 ] \rightarrow C [ 0,1 ]\) such that
Let \(\tilde{y}_{i}, y_{i} \in {C}[0,1]\) and
Then for \(x>0\), we have
Therefore,
Since \(\varOmega_{L_{1}, L_{2},{K}_{1},{K}_{2}, \alpha} <1\) by contraction mapping theorem, problem (2.5) has a unique solution in \(C [ 0,1 ]\). □
6 Convergence analysis
Theorem 6.1
Let \(y(x) \) be a function defined on [0, 1) and \(\vert y(x) \vert \leq M_{y}\), then the sum of absolute values of HOBW coefficients of \(y(x) \) defined in Eq. (10) converges absolutely on the interval [0, 1] if \(\vert c_{n,m} \vert \leq 2^{\frac{1-k}{2}} M_{y}\).
Proof
Any function \(y ( x ) \in L^{2} [0,1]\) can be approximated by HOBW as follows:
where the coefficients \(c_{m,n}\) can be determined as follows:
At \(m\geq0\),
By putting the variable \(2^{k} x-2n+1=t\), we have
Applying Holder’s inequality,
This proves that
Hence,
This means that the series \(\sum_{{i}=1}^{{M}} \sum_{{j}=0}^{{n}} {c}_{{ij}} \mathrm{HOBW} ({x})\) is convergent as \({k}\rightarrow \infty\). □
Theorem 6.2
If the sum of absolute values of the HOBW coefficients of a continuous function \({y}({x})\) shape convergent series, then the HOBW expansion \(\sum_{{i}=1}^{{M}} \sum_{{j}=0}^{{n}} {c}_{{ij}} \mathrm{HOBW} ({x})\) converges with respect to \({L}^{2}\)-norm on \([0, 1]\).
Proof
Let \({L}^{2} (R)\) be the Hilbert space and
where \(c_{n,m} = \langle \tilde{y} ( x ),\mathrm{HOB W}_{n,m} (x) \rangle \) for fixed n.
Let us denote \(\mathrm{HOB W}_{n,m} (x)= \chi_{l}\) and let \(\alpha_{l} = \langle \tilde{y} ( x ),\chi_{l} (x) \rangle\).
We define the sequence of partial sums \(\{S_{n} \}\), where
For every \(\varepsilon>0\), there exists a positive number \(N ( \varepsilon )\) such that, for every \(n>m>N ( \varepsilon )\),
From Theorem 5.1, \(\sum_{k=0}^{\infty} \vert \alpha_{k} \vert ^{2}\) is absolutely convergent.
According to the Cauchy criterion, for every \(\varepsilon>0\), there exists a positive number such that
whenever \(n>m>N ( \varepsilon )\).
Hence \(\Vert S_{n} (x)- S_{m} (x) \Vert _{2}^{2} < \sum_{k=m+1}^{n} \vert \alpha_{k} \vert ^{2} <\varepsilon\).
This implies that \(\Vert S_{n} (x)- S_{m} (x) \Vert _{2} \leq \sqrt{\varepsilon} <\varepsilon\).
So, the sequence of a partial sum of the series converges with respect to \(L^{2}\)-norm and hence it completes the proof. □
7 Numerical examples
Example 7.1
Consider the following fractional nonlinear Volterra integro-differential equation:
with mixed conditions
\(y ( x ) =-1-x- e^{x}\) is the exact solution at \(\alpha=1\).
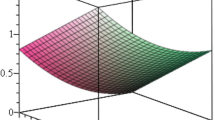
Table 1 demonstrates the absolute errors acquired by the present strategy for different estimations of \(k, M\) at \(\alpha=1\). The examination of numerical results for \(\alpha=0.75\), \(\alpha=0.85\), \(\alpha=0.95\), \(\alpha=1 \) and the exact solution for \(\alpha=1 \) is shown in Fig. 2. It is clear from Fig. 2 that as α is near to 1, the related numerical solution converges to the exact solution.
Numerical and exact solutions for different a for Example 7.1
Example 7.2
We consider the nonlinear FVFIDE
with the MBC
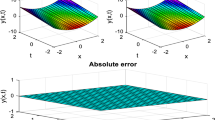
with the correct solution \({y} ( {x} ) ={x}\). This problem has been disbanded by HOBW for \(M = 4, k = 3\), which reduces the integral equation to a system of algebraic equations that is disbanded by Newton’s method. The consequence obtained by the introduced method is compared with that by the Nystrom method (for \(N = 20\)). The approximate solutions and absolute errors (Abs. Error) for Example 7.2 are introduced in Table 2.
Example 7.3
We consider the nonlinear FVFIDE
where \({}_{1} {F}_{1} [0.3,1.3;-{x}]\) is the Kummer confluent hypergeometric function defined as
with \(({a})_{{n}} ={a} ( {a}+1 ) ( {a}+2 ) \cdots(a+n-1)\) and \(({a})_{0} =1\), subject to the MBC \(y ( 0 ) =1, y ( 1 ) =e\).
The correct solution to this problem is given as \({y} ( {x} ) ={e}\). This problem is disbanded by HOBW at \({M}=4\), \(k=3\), which reduces the integral equation to a system of algebraic equations that is disbanded by Newton’s method. The consequence obtained by the introduced method is compared with that by the Nystrom method (for \(N = 20\)). The numerical solutions and Abs. Errors for Example 7.3 are introduced in Table 3.
Example 7.4
Let us consider the nonlinear FVFIDE
with boundary conditions \({y} ( 0 ) =1, {y} ( 1 ) ={e}\).
The correct solution is \({y} ( {x} ) = x^{2} +x\).
This problem is disbanded by HOBW which reduces the integral equation to a system of algebraic equations that is disbanded by Newton’s method. The consequence obtained by the method is compared with that by the Nystrom method [18]. The numerical consequence and Abs. Error for Example 7.4 are introduced in Table 4.
Maximum absolute errors at different values of M and k have been presented in Table 5.
8 Conclusion
In this work, we have fully attempted to find the numerical solution of the fractional system of Volterra integro differential equations by using the HOBW method. The numerical procedure and methodology are done in a very straightforward and effective manner. The numerical accuracy is also a point of interest. Through the numerical calculation, we confirmed that the HOBW method has the highest degree of accuracy. On the basis of this work, the researchers can extend this technique to some other fractional systems of ordinary and partial differential equations.
References
He, J.H.: Some applications of nonlinear fractional differential equations and their approximations. Bull. Sci. Technol. Soc. 15(2), 86–90 (1999)
Panda, R., Dash, M.: Fractional generalized splines and signal processing. Signal Process. 86, 2340–2350 (2006)
Peedas, A., Tamme, E.: Spline collocation method for integro-differential equations with weakly singular kernels. J. Comput. Appl. Math. 197, 253–269 (2006)
Nazari, D., Shahmorad, S.: Application of the fractional differential transform method to fractional-order integro-differential equations with nonlocal boundary conditions. J. Comput. Appl. Math. 234, 883–891 (2010)
Ghazanfari, B., Ghazanfari, A.G., Veisi, F.: Homotopy perturbation method for nonlinear fractional integro-differential equations. Aust. J. Basic Appl. Sci. 12(4), 5823–5829 (2010)
Karimi Vanani, S., Aminataei, A.: Operational Tau approximation for a general class of fractional integro-differential equations. Comput. Appl. Math. 3(30), 655–674 (2011)
Ordokhani, Y., Rahimi, N.: Numerical solution of fractional Volterra integro-differential equations via the rationalized Haar functions. J. Sci. Kharazmi Univ. 14(3) 211–224 (2014)
Bushnaq, S., Maayah, B., Momani, S., Alsaedi, A.: A reproducing kernel Hilbert space method for solving systems of fractional integrodifferential equations. Abstr. Appl. Anal. 2014, Article ID 103016 (2014) https://doi.org/10.1155/2014/103016
Jafari, H., Daftardar-Gejji, V.: Solving a system of nonlinear fractional differential equations using Adomian decomposition. J. Comput. Appl. Math. 196(2), 644–651 (2006)
Al-Marashi, A.A.: Approximate solution of the system of linear fractional integro-differential equations of Volterra using B-spline method. J. Am. Res. Math. Stat. 3(2), 39–47 (2015)
Zhou, F., Xu, X.: The third kind Chebyshev wavelets collocation method for solving the time-fractional convection diffusion equations with variable coefficients. Appl. Math. Comput. 280, 11–29 (2016)
Wang, Y., Fan, Q.: The second kind Chebyshev wavelet method for solving fractional differential equations. Appl. Math. Comput. 218, 8592–8601 (2012)
Jian, R.L., Chang, P., Isah, A.: New operational matrix via Genocchi polynomials for solving Fredholm–Volterra fractional integro-differential equations. Adv. Math. Phys. 2017, 1–12 (2017)
Nazari Susahab, D., Jahanshahi, M.: Numerical solution of nonlinear fractional Volterra–Fredholm integro-differential equations with mixed boundary conditions. Int. J. Ind. Math. 7, 63–69 (2015)
Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, vol. 198. Academic Press, San Diego (1998)
Mainardi, F., Goreno, R.: On Mittag-Leffler-type functions in fractional evolution processes. J. Comput. Appl. Math. 118, 283–299 (2000)
Mohamed, R.A., Hadhoud, A.R.: Hybrid orthonormal Bernstein and block-pulse functions wavelet scheme for solving the 2D Bratu problem. Results Phys. 12, 525–530 (2019)
Nazari Susahab, D., Jahanshahi, M.: Numerical solution of nonlinear fractional Volterra–Fredholm integro-differential equations with mixed boundary conditions. Int. J. Ind. Math. 7(1), 63–69 (2015)
Acknowledgements
We are thankful to the reviewers for their useful suggestions and corrections.
Funding
This research work is not supported by any funding agencies.
Author information
Authors and Affiliations
Contributions
All authors equally contributed to this manuscript and approved the final version.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ali, M.R., Hadhoud, A.R. & Srivastava, H.M. Solution of fractional Volterra–Fredholm integro-differential equations under mixed boundary conditions by using the HOBW method. Adv Differ Equ 2019, 115 (2019). https://doi.org/10.1186/s13662-019-2044-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2044-1