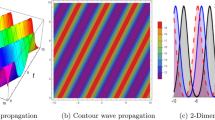
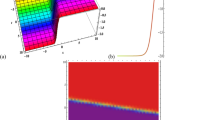
Abstract
The goal of this study is to offer an exclusive functional conversion to produce \((n+1)\)-dimensional dual-mode nonlinear equations. This transformation has been implemented and new \((3+1)\)-dimensional dual-mode Gradner-type and KdV-type have been established. Finally, the simplified bilinear method is used to tell the necessary conditions on these new models to have multiple singular-solitons.
Similar content being viewed by others
1 Introduction
The main upstream of understanding the physical nature of mathematical models arising in different disciplines of science is to extract their traveling wave solutions. Seeking for possible reliable solutions require suggesting and developing mathematical methods with supportive geometric analysis such as conservation laws and symmetry analysis [1,2,3,4,5,6,7,8,9,10].
Traveling wave solutions have different types which give a complete understanding of the dynamics of a particular physical model. Solitons, kinks, and periodics are the most popular types that propagate as single-moving-waves as in KdV, mKdV, and Burgers’. But, in the case of Boussinesq equation, its traveling wave solutions propagate as dual-waves with interaction phase velocity.
The phenomenon of dual-waves has been adopted by Korsunsky and developed by Wazwaz [11, 12] when they considered the KdV equation of second order in time which reads
where \(\phi =\phi (x,t)\) is a field function, s is the interaction phase velocity, α is the nonlinearity factor, and β is the dispersive factor with \(s\geq 0\), \(|\alpha | \leq 1\), \(|\beta | \leq 1\), and we refer to equation (1.1) as the two-mode KdV equation (TMKdV). The equation given in (1.1) was revisited by Alquran and Jarrah, and new Jacobi elliptic sine-cosine solutions were obtained [13].
Inspired by the form of TMKdV, many new two-mode or dual-mode models have been established. Two-mode Burgers equation (TMBE) and two-mode fifth-order KdV equations (TMFKdV) [14, 15], the two-mode higher-order Boussinesq–Burger system [16], two-mode coupled Burgers equation [17], two-mode coupled modified Korteweg–de Vries [18], two-mode coupled Korteweg–de Vries [19], two-mode Korteweg–de Vries–Burgers equation [20], the weak-dissipative two-mode perturbed Burgers and Ostrovsky models [21], two-mode Kuramoto–Sivashinsky [22], the dual-mode nonlinear Schrodinger’s equation and Kerr-law nonlinearity [23], the two-mode second- and third-order dispersive Fisher [24, 25] and the dual-mode Kadomtsev–Petviashvili model with strong-weak surface tension [26]. Single and multiple soliton/kink solutions have been obtained for the aforementioned models by using a simplified bilinear method, tanh method, sine-cosine method, Kudryashov method, and the \((G'/G)\)-expansion method.
The motivation of this work is to introduce for the first time a formulation of \((n+1)\)-dimensional dual-mode equations and to establish new \((3+1)\)-dimensional dual-mode equations of type Gardner and KdV. Also, we aim to find the necessary constraint conditions that enable such equations possess soliton solutions, singular soliton solutions, multiple soliton solutions, and multiple singular soliton solutions by using the simplified bilinear method.
The forms of single-mode \((3+1)\)-dimensional Gardner and KdV-type equations are, respectively, read as
and
The above two equations are widely used in physics and its applications such as quantum field theory, plasma physics, and fluid physics. Also, different types of solutions have been obtained by using many methods such as Hirota’s direct method, the Casorati and Grammian determinant solutions, and the inverse scattering method [27,28,29,30].
2 Formulation of \((n+1)\)-dimensional dual-mode equations
Wazwaz and Korsunsky [11, 12, 14, 15] established the \((1+1)\)-dimensional two-mode equation in a scaled form as
where \(m\geq 2\), \(L(v_{kx})\) is a linear term, \(N(v,v_{x},\ldots)\) is a nonlinear term, \(c>0\) is the phase velocities, \(x \in (-\infty , \infty )\), \(t>0\), \(\vert b \vert \leq 1\), and \(\vert d \vert \leq 1\).
In this study we propose a new scale for the \((n+1)\)-dimensional dual-mode equations in the variables \(t,x_{1},x_{2},x_{3},\ldots ,x _{n} \). The new scale is suggested to have the following form:
where L and N are, respectively, linear and nonlinear, \(\vert a_{i} \vert \leq 1\), and \(\vert b_{i} \vert \leq 1\), \(i=1,2,\ldots,n\). Note that when \(c=0\) and integrating once with respect to t, (2.2) is reduced to the standard single-mode \((n+1)\)-dimensional equation.
3 Analysis of the method
In this section, we give a brief description of the simplified bilinear method to find N-soliton solutions for nonlinear partial differential equations (NPDEs) as follows:
First, we substitute
where
in the problem under consideration, to find the relation among \(l_{j_{i}}\) and \(\lambda _{i}\). To find the soliton solutions, we use an appropriate transformation formula. We often use one of the following formulas:
For one-soliton solutions, we use the auxiliary function
For two-soliton solutions, we use the auxiliary function
For three-soliton solutions, we use the auxiliary function
provided that three-soliton solutions exist if \(\nu _{123}=\nu _{12}\nu _{13}\nu _{23}\). Moreover, for any nonlinear PDEs that have three-soliton solutions, they also have N-soliton solutions for \(N\geq 4\).
4 Applications
The purposes of this section is to apply the above described method to solve new \((3+1)\)-dimensional dual-mode nonlinear PDEs.
4.1 Soliton solutions for \((3+1)\)-dimensional dual-mode Gardner equation
Applying the suggested prescribed scale (2.2) on (1.2), the \((3+1)\)-dimensional dual-mode Gardner equation will have the following form:
We aim to find the needed necessary conditions in order to obtain multiple soliton and multiple singular-soliton solutions by using a simplified bilinear method [31,32,33,34,35,36,37,38,39,40,41]. To drop the presence of the operator \(\partial _{x}^{-1}\), we use the transformation
Accordingly, a new equivalent version of \((3+1)\)-TMGE (4.1) is given by
Inserting
with
into the linear terms of (4.2), we get the dispersion relations
where
Now, we consider the Cole–Hopf transformation
which leads to
provided that R is a constant and \(f(x,y,z,t)\) is an auxiliary function. For the one-soliton solution, we consider
where \(c_{1}=\pm 1\). Following (4.3), inserting (4.6) and (4.7) into (4.2) and solving for R, the one soliton solution of (4.2) exists if
By the Cole–Hopf transformation (4.6), we conclude the one-soliton solution of (4.2) as
and then,
In the case \(c_{1}=1\), we get the single-soliton solution as follows:
For the case \(c_{1}=-1\), we get the singular single-soliton solution as follows:
where
For the two-soliton solutions, we set the auxiliary function
where \(c_{i}=\pm 1\) and \(i=1,2\). Inserting (4.6), (4.8), and (4.9) in (4.2), the two-soliton solution of (4.2) exists if
where a is any real number.
Combining (4.9)–(4.14) and (4.6), the two-soliton solution is
and thus,
By setting \(c_{1}=c_{2}=1\) in (4.15), the two-soliton solution is
and the singular two-soliton solution by substituting \(c_{1}=c_{2}=-1\) is
For the three-soliton solution, we use the auxiliary function
where \(c_{i}=\pm 1\), \(i=1,2,3\). Accordingly, the three-soliton solution is
and then,
By setting \(c_{i}=1\) for \(i=1,2,3\), we obtain the three-soliton solution
Setting \(c_{i}=-1\) for \(i=1,2,3\), the singular three-soliton solution is
Remark
For a finite N, where \(N\geq 4\) and under the conditions \(a_{1}=a_{2}=a_{3}=b_{1}=b_{2}=b_{3}=\pm 1\) and \(\beta _{i}=\frac{2\alpha _{i}l-k\alpha _{i}^{2}-hk\zeta _{i}}{hk}\), \(\zeta _{i}=a\alpha _{i}\), \(i=1,2,\ldots,N\), (4.2) has N-soliton solutions and singular N-soliton solutions given by [31, 32]
and
4.2 Soliton solutions for \((3+1)\)-dimensional dual-mode KdV-type
Applying the new formulation (2.2), the new \((3+1)\)-dimensional dual-mode KdV equation (\((3+1)\)-TMKdV) has the following form:
Inserting
with
into the linear terms of (4.22), we get the dispersion relations
where
Now, we consider the Cole–Hopf transformation
and the auxiliary function
Using (4.23), inserting (4.24) and (4.25) into the \((3+1)\)-TMGE (4.22) and solving for R, the one-soliton solution of (4.22) exists if
Therefore, the one-soliton solution of the \((3+1)\)-TMGE is
In case \(c_{1}=1\), we get the single-soliton solution
and for the case \(c_{1}=-1\), we get the singular single-soliton solution
For the two-soliton solutions, we use the auxiliary function
where \(c_{i}=\pm 1\) and \(i=1,2\). Inserting (4.23), (4.24), and (4.26) in (4.22), the two-soliton solution of (4.22) exists if
Therefore, the two-soliton solution of the \((3+1)\)-TMKDVE is given by
In case \(c_{1}=1\), we get the two-soliton solution
and for the case \(c_{1}=-1\), we get the singular two-soliton solution
We should remark here that we cannot find three or more soliton solutions for (4.22) because this type of KdV equation is not integrable.
5 Conclusions
In this work, we proposed a functional conversion that produces \((n+1)\)-dimensional dual-mode equations of the form
These types of equations describe the spreading of dual-waves moving simultaneously with interaction phase velocity. The simplified bilinear method with the aid of some Cole–Hopf transformations is used to study \((3+1)\)-dimensional dual-mode Gardner-type and KdV-type. We concluded the following results:
-
Kink solutions and singular kink solutions for \((3+1)\)-TMGE exist only if \(a_{1}=a_{2}=a_{3}=b_{1}=b_{2} =b_{3}\) and \(\beta _{1}=\frac{2 \alpha _{1}l-k\alpha _{1}^{2}-hk\zeta _{1}}{hk}\), while the N-soliton and singular N-soliton solutions exist only if \(a_{1}=a_{2}=a_{3}=b_{1}=b _{2} =b_{3}=\pm 1\), \(\zeta _{i}=a\alpha _{i} \) and \(\beta _{i}=\frac{2 \alpha _{i}l-k\alpha _{i}^{2}-hk\zeta _{i}}{hk}\), \(i=1,2,\ldots, N\).
-
One-soliton solutions for \((3+1)\)-TMKdV exist only if \(a_{1}=a_{2}=a _{3}=b_{2}=b_{2}=b_{3}\) and two-soliton solutions exist if \(a_{1}=a _{2}=a_{3}=b_{2}=b_{2}=b_{3}=\pm 1\). This equation is non-integrable, it possesses no k-soliton solutions for \(k=3, 4, \ldots \) .
As future work, we may consider a fractional version of dual-mode equations and conduct the same analysis as that used in [42,43,44,45,46,47].
References
Abdel-Gawad, H.I., Tantawy, M., Inc, M., Yusuf, A.: On multi-fusion solitons induced by inelastic collision for quasi-periodic propagation with nonlinear refractive index and stability analysis. Mod. Phys. Lett. B 32(29), 1850353 (2018)
Yusuf, A., Inc, M., Aliyu, A.I., Baleanu, D.: Conservation laws, soliton-like and stability analysis for the time fractional dispersive long-wave equation. Adv. Differ. Equ. 2018, 319 (2018)
Baleanu, D., Inc, M., Yusuf, A., Aliyu, A.I.: Lie symmetry analysis and conservation laws for the time fractional simplified modified Kawahara equation. Open Phys. 16, 302–310 (2018)
Baleanu, D., Inc, M., Yusuf, A., Aliyu, A.I.: Optimal system, nonlinear self-adjointness and conservation laws for generalized shallow water wave equation. Open Phys. 16, 364–370 (2018)
Inc, M., Yusuf, A., Aliyu, A.I., Baleanu, D.: Lie symmetry analysis and explicit solutions for the time fractional generalized Burgers–Huxley equation. Opt. Quantum Electron. 50(2), 94 (2018)
Inc, M., Aliyu, A.I., Yusuf, A., Baleanu, D.: Optical solitons for complex Ginzburg–Landau model in nonlinear optics. Optik 158, 368–375 (2018)
Baleanu, D., Inc, M., Yusuf, A., Aliyu, A.I.: Traveling wave solutions and conservation laws for nonlinear evolution equation. J. Math. Phys. 59(2), 023506 (2018)
Inc, M., Aliyu, A.I., Yusuf, A., Baleanu, D.: Optical solitons for Biswas–Milovic model in nonlinear optics by Sine–Gordon equation method. Optik 157, 267–274 (2018)
Inc, M., Yusuf, A., Aliyu, A.I., Hashemi, M.S.: Soliton solutions, stability analysis and conservation laws for the Brusselator reaction diffusion model with time- and constant-dependent coefficients. Eur. Phys. J. Plus 133(5), 168 (2018)
Inc, M., Yusuf, A., Aliyu, A.I., Baleanu, D.: Soliton solutions and stability analysis for some conformable nonlinear partial differential equations in mathematical physics. Opt. Quantum Electron. 50(4), 190 (2018)
Korsunsky, S.V.: Soliton solutions for a second-order KdV equation. Phys. Lett. A 185, 174–176 (1994)
Wazwaz, A.M.: Multiple soliton solutions and other exact solutions for a two-mode KdV equation. Math. Methods Appl. Sci. 40(6), 1277–1283 (2017)
Alquran, M., Jarrah, A.: Jacobi elliptic function solutions for a two-mode KdV equation. J. King Saud Univ., Sci. (2017). https://doi.org/10.1016/j.jksus.2017.06.010
Wazwaz, A.M.: A two-mode Burgers equation of weak shock waves in a fluid: multiple kink solutions and other exact solutions. Int. J. Appl. Comput. Math. 3(4), 3977–3985 (2017)
Wazwaz, A.M.: Two-mode fifth-order KdV equations: necessary conditions for multiple-soliton solutions to exist. Nonlinear Dyn. 87(3), 1685–1891 (2017)
Jaradat, A., Noorani, M.S.M., Alquran, A., Jaradat, H.M.: Construction and solitary wave solutions of two-mode higher-order Boussinesq–Burger system. Adv. Differ. Equ. 2017, 376 (2017)
Jaradat, H.M.: Two-mode coupled Burgers equation: multiple-kink solutions and other exact solutions. Alex. Eng. J. 57(3), 2151–2155 (2018)
Syam, M., Jaradat, H.M., Alquran, M.: A study on the two-mode coupled modified Korteweg–de Vries using the simplified bilinear and the trigonometric-function methods. Nonlinear Dyn. 90(2), 1363–1371 (2017)
Jaradat, H.M., Syam, M., Alquran, M.: A two-mode coupled Korteweg–de Vries: multiple-soliton solutions and other exact solutions. Nonlinear Dyn. 90(1), 371–377 (2017)
Alquran, M., Jaradat, H.M., Syam, M.: A modified approach for a reliable study of new nonlinear equation: two-mode Korteweg–de Vries–Burgers equation. Nonlinear Dyn. 91(3), 1619–1626 (2018)
Jaradat, I., Alquran, M., Ali, M.: A numerical study on weak-dissipative two-mode perturbed Burgers’ and Ostrovsky models: right-left moving waves. Eur. Phys. J. Plus 133, 164 (2018)
Jaradat, H.M., Alquran, M., Syam, M.: A reliable study of new nonlinear equation: two-mode Kuramoto–Sivashinsky. Int. J. Appl. Comput. Math. 4, 64 (2018)
Jaradat, I., Alquran, M., Momani, S., Biswas, A.: Dark and singular optical solutions with dual-mode nonlinear Schrodinger’s equation and Kerr-law nonlinearity. Optik 172, 822–825 (2018)
Alquran, M., Yassin, O.: Dynamism of two-mode’s parameters on the field function for third-order dispersive Fisher: application for fibre optics. Opt. Quantum Electron. 50(9), 354 (2018)
Yassin, O., Alquran, M.: Constructing new solutions for some types of two-mode nonlinear equations. Appl. Math. Inf. Sci. 12(2), 361–367 (2018)
Abu Irwaq, I., Alquran, M., Jaradat, I., Baleanu, D.: New dual-mode Kadomtsev–Petviashvili model with strong-weak surface tension: analysis and application. Adv. Differ. Equ. 2018, 433 (2018)
Konopelchenko, B.G.: Inverse spectral transform for the \((2+1)\)-dimensional Gardner equation. Inverse Probl. 7, 739–753 (1991)
Yu, G.F., Tam, H.W.: On the \((2+1)\)-dimensional Gardner equation: determinant solutions and pfaffianization. J. Math. Anal. Appl. 330, 989–1001 (2007)
Wazwaz, A.M.: Multiple kink solutions for the \((2+1)\)-dimensional integrable Gardner equation. Proc. Rom. Acad., Ser. A: Math. Phys. Tech. Sci. Inf. Sci. 15, 241–246 (2014)
Alomari, A.K., Awawdeh, F., Tahat, N., Bani Ahmad, F., Shatanaw, W.: Multiple solutions for fractional differential equations: analytic approach. Appl. Math. Comput. 219(17), 8893–8903 (2013)
Hirota, R.: Exact solution of the Korteweg–de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 27, 1192–1194 (1971)
Hirota, R.: Exact solution of the modified Korteweg–de Vries equation for multiple collisions of solitons. J. Phys. Soc. Jpn. 33, 1456–1458 (1972)
Wazwaz, A.M.: Multiple kink solutions and multiple singular kink solutions for two systems of coupled Burgers’ type equations. Commun. Nonlinear Sci. Numer. Simul. 14, 2962–2970 (2009)
Wazwaz, A.M.: Kinks and travelling wave solutions for Burgers-like equations. Appl. Math. Lett. 38, 174–179 (2014)
Wazwaz, A.M.: Gaussian solitary wave solutions for nonlinear evolution equations with logarithmic nonlinearities. Nonlinear Dyn. 83, 591–596 (2016)
Hirota, R.: Exact N-soliton solutions of a nonlinear wave equation. J. Math. Phys. 14, 805–809 (1973)
Jaradat, H.M., Awawdeh, F., Al-Shara’, S., Alquran, M., Momani, S.: Controllable dynamical behaviors and the analysis of fractal Burgers hierarchy with the full effects of inhomogeneities of media. Rom. J. Phys. 60(3–4), 324–343 (2015)
Awawdeh, F., Al-Shara’, S., Jaradat, H.M., Alomari, A.K., Alshorman, R.: Symbolic computation on soliton solutions for variable coefficient quantum Zakharov–Kuznetsov equation in magnetized dense plasmas. Int. J. Nonlinear Sci. Numer. Simul. 15(1), 35–45 (2014)
Jaradat, H.M.: New solitary wave and multiple soliton solutions for the time-space fractional Boussinesq equation. Ital. J. Pure Appl. Math. 36, 367–376 (2016)
Jaradat, H.M.: Dynamic behavior of traveling wave solutions for a class for the time-space coupled fractional kdV system with time-dependent coefficients. Ital. J. Pure Appl. Math. 36, 945–958 (2016)
Alquran, M., Jaradat, H.M., Al-Shara’, S., Awawdeh, F.: A new simplified bilinear method for the N-soliton solutions for a generalized FmKdV equation with time-dependent variable coefficients. Int. J. Nonlinear Sci. Numer. Simul. 16, 259–269 (2015)
Ullah, A., Shah, K.: Numerical analysis of Lane Emden–Fowler equations. J. Taibah Univ. Sci. 12(2), 180–185 (2018)
Khan, T., Shah, K., Khan, A., Khan, R.A.: Solution of fractional order heat equation via triple Laplace transform in two dimensions. Math. Methods Appl. Sci. 41(2), 818–825 (2018)
Khan, H., Khan, A., Chen, W., Shah, K.: Stability analysis and a numerical scheme for fractional Klein Gordon equations. Math. Methods Appl. Sci. 42(2), 723–732 (2019)
Ali, S., Bushnaq, S., Shah, K., Arif, M.: Numerical treatment of fractional order Cauchy reaction diffusion equations. Chaos Solitons Fractals 103, 578–587 (2017)
Alquran, M., Jaradat, I.: A novel scheme for solving Caputo time-fractional nonlinear equations: theory and application. Nonlinear Dyn. 91(4), 2389–2395 (2018)
Jaradat, I., Al-Dolat, M., Al-Zoubi, K., Alquran, M.: Theory and applications of a more general form for fractional power series expansion. Chaos Solitons Fractals 108, 107–110 (2018)
Acknowledgements
Authors would like to thank the editor and the anonymous referees for their in-depth reading and insightful comments on an earlier version of this paper.
Availability of data and materials
Not applicable.
Funding
This work is financially supported by UKM Grant: DIP-2017-011 and Ministry of Education Malaysia Grant FRGS/1/2017/STG06/UKM/01/1.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and read and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that there is no conflict of interests regarding the publication of this manuscript. The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jaradat, A., Jaradat, M.M.M., Noorani, M.S.M. et al. Construction of \((n+1)\)-dimensional dual-mode nonlinear equations: multiple shock wave solutions for \((3+1)\)-dimensional dual-mode Gardner-type and KdV-type. Adv Differ Equ 2019, 19 (2019). https://doi.org/10.1186/s13662-019-1960-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-1960-4