1 Introduction

Nonlinear evolution equations have been used as the models to describe a variety of engineering phenomena and science such as optical fibers, chemical kinetics, fluid dynamics, mathematical biology, chemical reactions, plasma waves and others [1–4]. The study of nonlinear equations is an interesting topic in solitary waves theory. Many methods are established to find exact solutions for nonlinear partial differential equations (PDEs) such as Lie symmetries method, truncated Painleve expansion method, the inverse scattering method, Hirota’s bilinear method, Darboux transformation, Backlund transformation, simplified Hirota’s method, trigonometric-function series method, modified mapping method, modified (\(G'/G\))-expansion method, tanh-coth expansion method, Jacobi elliptic function expansion method, first integral method and others (see [5–30] and [31–40]). Also, important developments for searching for analytical solitary wave solutions for PDEs can be found in [41–50].

The most integrable systems describe unidirectional waves such as the KP equation, Burgers, KdV, mKdV equations and a higher-order Boussinesq-Burgers equation, where these equations are first order PDE in time and model only the right-moving in the positive x-direction. However, the Boussinesq equation models both left- and right-going waves and second-order in time. The two-mode equations are analogous to the two-mode Boussinesq equation and hence are represented by a new nonlinear partial differential equation of second-order in time.

A higher-order Boussinesq-Burgers equation was introduced by Jin-Ming and Yao-Ming (2011) [2] in the form

$$ \begin{gathered} v_{t}-3av^{2}v_{x}+\frac{3}{2}a(vw)_{x}-\frac{1}{4}av_{xxx}=0,\\ w_{t}+\frac{3}{2}aww_{x}-3a(v^{2}w)_{x}+3av_{x}v_{xx}+\frac{3}{2}avv_{xxx}-\frac{1}{4}aw_{xxx}=0, \end{gathered} $$
(1)

where a is a non-zero arbitrary constant.

Wazwaz [51–53] and Korsunsky [54] proposed the scaled form of the two-mode equation as follows:

$$ u_{tt}-c^{2}u_{xx}+\biggl(\frac{\partial}{\partial t}-a_{1}c \frac{\partial }{\partial x}\biggr)N(u,u_{x},\ldots)+\biggl(\frac{\partial}{\partial t}-a_{2}c \frac{\partial }{\partial x}\biggr)L(u_{kx})=0, $$
(2)

where \(c>0\) is the phase velocities, \(\vert a_{1} \vert \leq1\), \(\vert a_{2} \vert \leq1\), \(a_{2}\) is the dispersion parameter, \(a_{1}\) is the parameter of nonlinearity, \(N(u,u_{x},\ldots)\) is the nonlinear term and \(L(u_{kx})\) is the linear term in the equation, \(k\geq2\). Based on this argument, Jaradat et al. [55–57] used the same sense as Korsunsky [54] and Wazwaz [51–53] to establish the two-mode coupled system of n equations

$$\begin{aligned}[b] 0 ={}&(u_{i})_{tt}-c^{2}(u_{i})_{xx}+ \biggl(\frac{\partial}{\partial t}-a_{1} c\frac{\partial}{\partial x} \biggr)N_{i}\bigl(u_{1},\ldots,u_{n},(u_{1})_{x},\ldots,(u_{n})_{x},\ldots \bigr) \\ & +\biggl(\frac{\partial}{\partial t}-a_{2}c\frac{\partial}{\partial x}\biggr)L_{i}\bigl((u_{i})_{kx}\bigr),\quad i=2,3,\ldots,n.\end{aligned} $$
(3)

To establish the two-mode higher-order Boussinesq-Burgers equation (TM-ho-BBE) (1), we have

$$\begin{gathered} N_{1}(v,w,v_{x},w_{x},\ldots) =-3av^{2}v_{x}+\frac {3}{2}a(vw)_{x}, \\ L_{1}(v_{kx}) =-\frac{1}{4}av_{xxx}, \\ N_{2}(v,w,v_{x},w_{x},\ldots) = \frac{3}{2}aww_{x}-3a\bigl(v^{2}w\bigr)_{x}+3av_{x} v_{xx}+\frac{3}{2}avv_{xxx}, \\ L_{2}(v_{kx}) =-\frac{1}{4}aw_{xxx}.\end{gathered} $$

Thus, using equation (3), (TM-ho-BBE) will have the form

$$ \begin{gathered}0 =v_{tt}-c^{2}v_{xx}- \frac{1}{4}a\biggl(\frac{\partial }{\partial t}-a_{2}c\frac{\partial}{\partial x} \biggr)v_{xxx}+\biggl(\frac{\partial }{\partial t}-a_{1}c \frac{\partial}{\partial x}\biggr) \biggl\{ -3av^{2}v_{x}+ \frac{3}{2}a(vw)_{x} \biggr\} , \\ \begin{aligned}0 ={}&w_{tt}-c^{2}w_{xx}-\frac{1}{4}a\biggl( \frac{\partial}{\partial t}-a_{2}c\frac{\partial}{\partial x} \biggr)w_{xxx} \\ & +\biggl(\frac{\partial}{\partial t}-a_{1}c\frac{\partial}{\partial x}\biggr) \biggl\{ \frac{3}{2}aww_{x}-3a\bigl(v^{2}w\bigr)_{x}+3av_{x}v_{xx}+ \frac {3}{2}avv_{xxx} \biggr\} .\end{aligned}\end{gathered} $$
(4)

Note that when \(c=0\) and integrating with respect to t, the two-mode higher-order Boussinesq-Burgers equation (TM-ho-BBE) (4) is reduced to the standard higher-order Boussinesq-Burgers equation (1).

The aim of this study is to find the necessary conditions needed for multiple-soliton solutions and singular multiple-soliton solutions to exist for (TM-ho-BBE) by using the simplified form of Hirota’s method. Moreover, we determine more exact solutions to this new system by using the Tanh method.

2 Multiple soliton solutions and singular multiple soliton solutions

In this section, we used the simplified bilinear method to find the necessary conditions needed to produce single soliton solutions, singular soliton solutions, multiple soliton solutions and singular multiple soliton solutions of (TM-ho-BBE).

Substituting

$$v(x,t)=w(x,t)=e^{\lambda_{i}(x,t)},\quad \lambda_{i}(x,t)=r_{i}x-d_{i}t, $$

into the linear terms of equation (4) and solving the resulting equation gives

$$d_{i}=\frac{-ar_{i}^{3}\pm r_{i}\sqrt{a^{2}r_{i}^{4}-16aa_{2}cr_{i}^{2}+64c^{2}}}{8}.$$

As a result, \(\lambda_{i}(x,t)\) becomes

$$ \lambda_{i}(x,t)=r_{i}x-\frac{-ar_{i}^{3}\pm r_{i}\sqrt{a^{2}r_{i}^{4}-16aa_{2}cr_{i}^{2}+64c^{2}}}{8}t,\quad i=1,2,\ldots. $$
(5)

Now, we propose the solutions to (TM-ho-BBE) (4) in the form

$$\begin{aligned}& v(x,t) =C_{1}\frac{\partial}{\partial x}\bigl(\ln h(x,t)\bigr), \end{aligned}$$
(6)
$$\begin{aligned}& w(x,t) =C_{2}\frac{\partial^{2}}{\partial x^{2}}\bigl(\ln h(x,t)\bigr), \end{aligned}$$
(7)

where \(C_{1}\) and \(C_{2}\) are constants. To find the one-soliton solution, we assume the auxiliary function \(h(x,t)\) to be

$$ h(x,t)=1+\alpha_{1}e^{\lambda_{1}(x,t)}=1+\alpha_{1}e^{r_{1} x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt {a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }, $$
(8)

where \(\alpha_{1}=\pm1\). Substitute (6), (7) and (8) into (TM-ho-BBE) (4). Then, solving for numerical values \(C_{1}\) and \(C_{2}\), we find that the one-soliton solution of (TM-ho-BBE) (4) exists only if \(a_{1}=a_{2}\). Therefore, two sets of solutions are obtained

$$\begin{aligned}& C_{1} =\frac{\pm1}{2}, \end{aligned}$$
(9)
$$\begin{aligned}& C_{2} =\frac{-1}{2}. \end{aligned}$$
(10)

Then the one-soliton solution of (TM-ho-BBE) (4) is given by

$$\begin{aligned}& v(x,t) =\frac{\pm1}{2}\frac{\alpha_{1}r_{1}e^{r_{1}x-\frac {-ar_{1}^{3}\pm r_{1}\sqrt{a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }}{1+\alpha_{1}e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt{a^{2}r_{1}^{4} -16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }}, \\& \begin{aligned}w(x,t) ={}&\frac{-1}{2} \biggl( \frac{\alpha_{1}r_{1}^{2}e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt {a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }}{1+\alpha_{1}e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt{a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }} \biggr) \\ & +\frac{1}{2} \biggl( \frac{\alpha_{1}r_{1}e^{r_{1}x-\frac {-ar_{1}^{3}\pm r_{1}\sqrt{a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }}{1+\alpha_{1}e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt{a^{2}r_{1}^{4} -16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }} \biggr) ^{2},\end{aligned} \end{aligned}$$

where

$$\lambda_{1}(x,t)=r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt{a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t. $$

For \(\alpha_{1}=1\), the single soliton solution is

$$\begin{aligned}& \begin{aligned}[b] v(x,t) & =\frac{\pm1}{2}\frac{r_{1}e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt{a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }}{1+e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt {a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }} \\ & =\frac{\pm1}{4}r_{1} \biggl(1+\tanh \biggl( \frac{\lambda _{1}(x,t)}{2} \biggr) \biggr),\end{aligned} \end{aligned}$$
(11)
$$\begin{aligned}& \begin{aligned}[b]w(x,t) ={}& \frac{-1}{2} \biggl( \frac{r_{1}^{2}e^{r_{1}x-\frac {-ar_{1}^{3}\pm r_{1}\sqrt{a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }}{1+e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt {a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }} \biggr) \\ & +\frac{1}{2} \biggl( \frac{r_{1}e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1} \sqrt{a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }}{1+e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt {a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }} \biggr) ^{2} \\ ={}&\frac{-1}{8}r_{1}^{2}\operatorname {sech}^{2}\hspace {0.03in} \biggl( \frac{\lambda_{1}(x,t)}{2} \biggr).\end{aligned} \end{aligned}$$
(12)

For \(\alpha_{1}=-1\), the singular single soliton solution is

$$\begin{aligned}& \begin{aligned}[b] v(x,t) & =\frac{\mp1}{2}\frac{r_{1}e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt{a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }}{1-e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt {a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }} \\ & =\frac{\pm1}{4}r_{1} \biggl(1+\coth \biggl( \frac{\lambda _{1}(x,t)}{2} \biggr) \biggr),\end{aligned} \end{aligned}$$
(13)
$$\begin{aligned}& \begin{aligned}[b]w(x,t) ={}&\frac{1}{2} \biggl( \frac{r_{1}^{2}e^{r_{1}x-\frac {-ar_{1}^{3}\pm r_{1}\sqrt{a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }}{1-e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt {a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }} \biggr) \\ & +\frac{1}{2} \biggl( \frac{r_{1}e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1} \sqrt{a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }}{1-e^{r_{1}x-\frac{-ar_{1}^{3}\pm r_{1}\sqrt {a^{2}r_{1}^{4}-16aa_{2}cr_{1}^{2}+64c^{2}}}{8}t }} \biggr) ^{2} \\ ={}&\frac{1}{8}r_{1}^{2} \operatorname {csch}^{2}\hspace {0.03in} \biggl( \frac{\lambda_{1}(x,t)}{2} \biggr) .\end{aligned} \end{aligned}$$
(14)

To find the two-wave solutions, we assume

$$ h(x,t)=1+\alpha_{1}e^{\lambda_{1}(x,t)}+\alpha_{2}e^{\lambda _{2}(x,t)}+c_{12} \alpha_{1}\alpha_{2}e^{\lambda_{1}(x,t)+\lambda_{2}(x,t)}. $$
(15)

Insert (9), (10) and (15) in (4) and solve for \(c_{12}\). Then two-soliton solutions exist only if \(a_{1}=a_{2}=\pm1\) and

$$ c_{12}=0. $$
(16)

This can be generalized to

$$ c_{ij}=0,\quad 1\leq i< j\leq3. $$
(17)

Also, inserting (16), (15), (9), (10) in (6) and (7) and under the constraint condition \(a_{1}=a_{2}=\pm1\), we obtain the following two-soliton solutions:

$$\begin{gathered} v(x,t) =\frac{\pm1}{2}\frac{r_{1}\alpha_{1}e^{\lambda _{1}}+r_{2}\alpha _{2}e^{\lambda_{2}}}{1+\alpha_{1}e^{\lambda_{1}}+\alpha _{2}e^{\lambda _{2}}}, \\ w(x,t) =\frac{-1}{2} \biggl( \frac{\alpha_{1}r_{1}^{2}e^{\lambda _{1}}+\alpha_{2}r_{2}^{2}e^{\lambda_{2}}}{1+\alpha_{1}e^{\lambda _{1}}+\alpha _{2}e^{\lambda_{2}}}- \biggl( \frac{\alpha_{1}r_{1}e^{\lambda _{1}}+r_{2}\alpha_{2}e^{\lambda_{2}}}{1+\alpha_{1}e^{\lambda_{1}}+\alpha_{2}e^{\lambda_{2}}} \biggr) ^{2} \biggr),\end{gathered} $$

where

$$\begin{gathered} \lambda_{1} =r_{1}x-\frac{-ar_{1}^{3}\pm(ar_{1}^{3}\pm 8cr_{1})}{8}t, \\ \lambda_{2} =r_{2}x-\frac{-ar_{2}^{3}\pm(ar_{2}^{3}\pm8cr_{2})}{8}t.\end{gathered} $$

For \(\alpha_{1}=\alpha_{2}=1\), the two-soliton solution is

$$\begin{gathered} v(x,t) =\frac{\pm1}{2}\frac{r_{1}e^{\lambda_{1}}+r_{2}e^{\lambda _{2}}}{1+e^{\lambda_{1}}+e^{\lambda_{2}}}, \\ w(x,t) =\frac{-1}{2} \biggl( \frac{r_{1}^{2}e^{\lambda_{1}}+r_{2}^{2}e^{\lambda_{2}}}{1+e^{\lambda_{1}}+e^{\lambda_{2}}}- \biggl( \frac {r_{1}e^{\lambda_{1}}+r_{2}e^{\lambda_{2}}}{1+e^{\lambda _{1}}+e^{\lambda _{2}}} \biggr) ^{2} \biggr).\end{gathered} $$

For \(\alpha_{1}=\alpha_{2}=-1\), the two-singular-soliton solution is

$$\begin{gathered} v(x,t) =\frac{\mp1}{2}\frac{r_{1}e^{\lambda_{1}}+r_{2}e^{\lambda _{2}}}{1-e^{\lambda_{1}}-e^{\lambda_{2}}}, \\ w(x,t) =\frac{1}{2} \biggl( \frac{r_{1}^{2}e^{\lambda_{1}}+r_{2}^{2}e^{\lambda_{2}}}{1-e^{\lambda_{1}}-e^{\lambda_{2}}}+ \biggl( \frac {r_{1}e^{\lambda_{1}}+r_{2}e^{\lambda_{2}}}{1-e^{\lambda _{1}}-e^{\lambda _{2}}} \biggr) ^{2} \biggr).\end{gathered} $$

To find three-soliton solutions, we assume

$$ h(x,t)=1+\alpha_{1}e^{\lambda_{1}(x,t)}+\alpha_{2}e^{\lambda _{2}(x,t)}+ \alpha_{3}e^{\lambda_{3}(x,t)}+c_{123}\alpha_{1} \alpha_{2}\alpha _{3}e^{\lambda_{1}(x,t)+\lambda_{2}(x,t)+\lambda_{3}(x,t)}, $$
(18)

where

$$\lambda_{i}=r_{i}x-\frac{-ar_{i}^{3}\pm(ar_{i}^{3}\pm8cr_{i})}{8}t,\quad i=1,2,3. $$

Substituting (6), (7) and (18) into (4) and solving for \(c_{123}\), we find

$$c_{123}=0. $$

Accordingly, we obtain the following three-wave solutions:

$$\begin{gathered} v(x,t) =\frac{\pm1}{2}\frac{\alpha_{1}r_{1}e^{\lambda _{1}}+r_{2}\alpha _{2}e^{\lambda_{2}}+r_{3}\alpha_{3}e^{\lambda_{3}}}{1+\alpha _{1}e^{\lambda _{1}}+\alpha_{2}e^{\lambda_{2}}+\alpha_{3}e^{\lambda_{3}}}, \\ w(x,t) =\frac{-1}{2} \biggl( \frac{r_{1}^{2}\alpha_{1}e^{\lambda _{1}}+r_{2}^{2}\alpha_{2}e^{\lambda_{2}}+r_{3}^{2}\alpha_{3}e^{\lambda _{3}}}{1+\alpha_{1}e^{\lambda_{1}}+\alpha_{2}e^{\lambda_{2}}+\alpha_{3}e^{\lambda_{3}}}- \biggl( \frac{r_{1}\alpha_{1}e^{\lambda_{1}}+r_{2}\alpha _{2}e^{\lambda_{2}}+r_{3}\alpha_{3}e^{\lambda_{3}}}{1+\alpha _{1}e^{\lambda _{1}}+\alpha_{2}e^{\lambda_{2}}+\alpha_{3}e^{\lambda_{3}}} \biggr) ^{2} \biggr).\end{gathered} $$

For \(\alpha_{1}=\alpha_{2}=\alpha_{3}=1\), the three-wave solution is

$$\begin{gathered} v(x,t) =\frac{\pm1}{2}\frac{r_{1}e^{\lambda_{1}}+r_{2}e^{\lambda _{2}}+r_{3}e^{\lambda_{3}}}{1+e^{\lambda_{1}}+e^{\lambda_{2}}+e^{\lambda _{3}}}, \\ w(x,t) =\frac{-1}{2} \biggl( \frac{r_{1}^{2}e^{\lambda_{1}}+r_{2}^{2}e^{\lambda_{2}}+r_{3}^{2}e^{\lambda_{3}}}{1+e^{\lambda _{1}}+e^{\lambda _{2}}+e^{\lambda_{3}}}- \biggl( \frac{r_{1}e^{\lambda _{1}}+r_{2}e^{\lambda _{2}}+r_{3}e^{\lambda_{3}}}{1+e^{\lambda_{1}}+e^{\lambda_{2}}+e^{\lambda _{3}}} \biggr)^{2} \biggr).\end{gathered} $$

For \(\alpha_{1}=\alpha_{2}=\alpha_{3}=-1\), the singular three-soliton solution is

$$\begin{gathered} v(x,t) =\frac{\mp1}{2}\frac{r_{1}e^{\lambda_{1}}-r_{2}e^{\lambda _{2}}-r_{3}e^{\lambda_{3}}}{1-e^{\lambda_{1}}-e^{\lambda_{2}}-e^{\lambda _{3}}}, \\ w(x,t) =\frac{1}{2} \biggl( \frac{r_{1}^{2}e^{\lambda_{1}}+r_{2}^{2}e^{\lambda_{2}}+r_{3}^{2}e^{\lambda_{3}}}{1-e^{\lambda _{1}}-e^{\lambda _{2}}-e^{\lambda_{3}}}+ \biggl( \frac{r_{1}e^{\lambda _{1}}+r_{2}e^{\lambda _{2}}+r_{3}e^{\lambda_{3}}}{1-e^{\lambda_{1}}-e^{\lambda_{2}}-e^{\lambda _{3}}} \biggr) ^{2} \biggr).\end{gathered} $$

Finally, we reach the fact that (TM-ho-BBE) has N-soliton solutions under the necessary condition \(a_{1}=a_{2}=\pm1\), where \(N\geq1\) [16, 58]. They are given by

$$\begin{gathered} v(x,t) =\frac{\pm1}{2}\frac{{ \sum_{k=1}^{N}} r_{k}e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }}{1+{ \sum_{k=1}^{N}} e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }}, \\ w(x,t) =\frac{-1}{2} \biggl( \frac{{ \sum_{k=1}^{N}} r_{k}^{2}e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }}{1+ { \sum_{k=1}^{N}} e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }}- \biggl( \frac{{ \sum_{k=1}^{N}} r_{k}e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }}{1+{ \sum_{k=1}^{N}} e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }} \biggr) ^{2} \biggr).\end{gathered} $$

Also, the singular N-soliton solutions under the same condition are given by

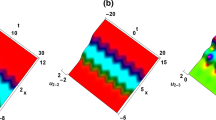
$$\begin{gathered} v(x,t) =\frac{\mp1}{2}\frac{{ \sum_{k=1}^{N}} r_{k}e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }}{1-{ \sum_{k=1}^{N}} e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }}, \\ w(x,t) =\frac{1}{2} \biggl( \frac{{ \sum_{k=1}^{N}} r_{k}^{2}e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }}{1- { \sum_{k=1}^{N}} e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }}+ \biggl( \frac{{ \sum_{k=1}^{N}} r_{k}e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }}{1-{ \sum_{k=1}^{N}} e^{r_{k}x-\frac{-ar_{k}^{3}\pm(ar_{k}^{3}\pm8cr_{k})}{8}t }} \biggr) ^{2} \biggr) .\end{gathered} $$

Finally, we would like to present two plots of the obtained solutions of (TM-ho-BBE). Figure 1 is the one-soliton solution and Figure 2 is the two-soliton solution.

Figure 1
figure 1

The one-soliton solution of \(\pmb{u_{1}}\) when \(\pmb{{r_{1}=3}}\) , \(\pmb{a=-2}\) , \(\pmb{c=1}\) , \(\pmb{a_{1}=a_{2}=1.5}\) , \(\pmb{C_{1}=0.5}\) , \(\pmb{{C_{2}=-0.5}}\) .

Full size image
Figure 2
figure 2

The two-soliton solution of \(\pmb{u_{2}}\) when \(\pmb{{r_{1}=2.5}}\) , \(\pmb{r_{2}=1.5}\) , \(\pmb{a=-1}\) , \(\pmb{c=a_{1}=a_{2}=1}\) , \(\pmb{C_{1}=0.5}\) , \(\pmb{C_{2}=-0.5}\) .

Full size image

3 Alternative method: hyperbolic tangent expansion

In this section, we aim to validate the necessary conditions that guarantee the existence of solutions to (TM-ho-BBE). To achieve this goal, we propose an alternative method, the hyperbolic tangent expansion [59–63], to construct solitary wave solutions of problem (4). We first consider the wave transform \(z=x- \lambda t\) to reduce (4) into the following ordinary differential equations:

$$ \begin{gathered} 0 =\bigl(\lambda^{2}-c^{2}\bigr)v+ \frac{1}{4}a (\lambda+a_{2} c)v^{\prime\prime}+3a( \lambda+a_{1} c) \biggl( \frac {1}{3}v^{3}- \frac{1}{2}v w \biggr) , \\ \begin{aligned}0 ={}&\bigl(\lambda^{2}-c^{2}\bigr)w^{\prime}+ \frac{1}{4}a (\lambda+a_{2} c)w^{\prime\prime\prime} \\ & +3a(\lambda+a_{1} c) \biggl( \bigl(v^{2} w \bigr)^{\prime}-\frac{1}{2}w w^{\prime }-v^{\prime}v^{\prime\prime}- \frac{1}{2}v v^{\prime\prime\prime } \biggr) ,\end{aligned}\end{gathered} $$
(19)

where \(v=v(z)\) and \(w=w(z)\).

Finite polynomials in terms of hyperbolic functions are to be considered as favorable suggested solutions of (19). Thus, we assume that

$$ \begin{gathered} v(z) =\sum_{i=0}^{n_{1}}c_{i}Y^{i}, \\ w(z) =\sum_{j=0}^{n_{2}}d_{j}Y^{j},\end{gathered} $$
(20)

where

$$ Y=Y(z)=\tanh(\mu z). $$
(21)

Balancing the behavior of Y in the highest derivative against its counterpart within the nonlinear terms appearing in (19) leads to \(n_{1}+2=3 n_{1}=n_{1}+n_{2}\) or \(n_{2}+3=2n_{1}+3=2n_{2}+1=2n_{1}+n_{2}+1\). Thus, \(n_{1}=1\), \(n_{2}=2\). Accordingly, the solution of (19) in deterministic form is

$$ \begin{gathered}v(z) =c_{0} + c_{1} Y, \\ w(z) =d_{0} + d_{1} Y + d_{2} Y^{2}.\end{gathered} $$
(22)

The task now is to determine the values of the parameters \(c_{0}\), \(c_{1}\), \(d_{0}\), \(d_{1}\), \(d_{2}\) and λ, μ. To achieve this, we first substitute (22) in (19), then we collect all coefficients of powers of Y in the resulting equations and set them to zero. Finally, we solve the prescribed algebraic system to retrieve the values of the required parameters. The algebraic calculations have been executed by Mathematica and the following obtained solutions have been verified as well. The first solution of (4) is

$$ \begin{gathered}v(x,t) =\mp\mu\tanh\bigl(\mu(x-\lambda_{1} t)\bigr), \\ w(x,t) =-\mu^{2} + \mu^{2} \tanh^{2}\bigl(\mu(x- \lambda_{1} t)\bigr),\end{gathered} $$
(23)

where \(\lambda_{1}=\frac{1}{2} ( -a \mu^{2} \mp\sqrt{4c^{2}-4a a_{2} c \mu^{2}+a^{2} \mu^{4}} ) \).

The second solution is

$$ \begin{gathered}v(x,t) =\mp\frac{\mu}{2} \tanh\bigl(\mu(x- \lambda_{2} t)\bigr), \\ w(x,t) =-\frac{\mu^{2}}{2} + \frac{\mu^{2}}{2} \tanh^{2}\bigl(\mu (x-\lambda_{2} t)\bigr),\end{gathered} $$
(24)

where \(\lambda_{2}=\frac{1}{8} ( -a \mu^{2} - \sqrt{64c^{2}-16 a a_{2} c \mu^{2}+a^{2} \mu^{4}} ) \).

The third solution is

$$ \begin{gathered}v(x,t) =\mp\frac{\mu}{2}\mp\frac{\mu}{2} \tanh \bigl( \mu(x-\lambda_{k} t)\bigr), \\ w(x,t) =-\frac{\mu^{2}}{2} + \frac{\mu^{2}}{2} \tanh^{2}\bigl(\mu (x-\lambda_{k} t)\bigr),\quad k=3, 4,\end{gathered} $$
(25)

where

$$\begin{gathered} \lambda_{3} =\frac{1}{2} \bigl( -a \mu^{2} - \sqrt{4c^{2}-4a a_{2} c \mu^{2}+a^{2} \mu^{4}} \bigr) , \\ \lambda_{4} =\frac{1}{2} \bigl( -a \mu^{2} + \sqrt{4c^{2}-4a a_{2} c \mu^{2}+a^{2} \mu^{4}} \bigr) .\end{gathered} $$

4 Conclusion

In this paper, we established a new nonlinear two-mode higher-order Boussinesq-Burgers equation (TM-ho-BBE). By using a simplified form of Hirota’s method we reached the following two facts:

  • Single soliton and singular soliton solutions exist for (TM-ho-BBE) if \(a_{1}=a_{2}\).

  • Multiple soliton and multiple singular soliton solutions exist only under the condition \(a_{1}=a_{2}=\mp1\).

Also, we applied an alternative method called hyperbolic tangent expansion to validate the necessary conditions needed for solitary solutions to exist.