Rumor spreading of a SEIR model in complex social networks with hesitating mechanism

Abstract

In the process of rumor spreading, controlling and killing rumor problem is of great importance on social networks. In this paper, we present a new SEIR (susceptible-exposed-infected-removed) rumor spreading model with hesitating mechanism. By using mean-field theory, the equilibrium of the model and the basic reproduction number $R_{0}$ are obtained. The global stability of the rumor-free equilibrium and the permanence are proved in detail, and the global attractivity of the rumor-prevailing equilibrium is proved by using a monotone iterative technique. Furthermore, the modified model with feedback mechanism on social networks is introduced. The feedback mechanism cannot change the basic reproductive number but it can reduce the continuous level and the spread of rumor. Numerical simulations confirm the analytical results.

1 Introduction

Rumors are usually defined as unconfirmed elaborations or annotations of public things, events, or issues that are fabricated and propagated through various means [1, 2], which can cause unnecessary public anxiety and economic loss to affected countries [3–5]. What’s worse, with the development of network communications, rumor has propagated more quickly and widely [6–8]. Therefore, the study of rumor spreading model is of dramatic importance, which plays a significant role in managing and controlling the spread of rumor.

Rumor spreading in complex social networks has recently attracted an increasing amount of attention from researchers [9–12]. They describe the dynamics of the models by deriving corresponding mean-field equations to formulate the characteristics and analyze the critical threshold of rumor spreading in the complex networks. In 1965, Daley and Kendall put forward the first classical DK rumor spreading model [13]. Some researchers applied a mathematical model to study the rumors and developed another classical model [14–17]. Early classical representations of rumor spreading dynamics assumed that all individuals have the homogeneous probability of connection [18–20]. Obviously, these simple models can not completely reflect the realistic feature of the spread of rumor, which is subsequently extended in ways to make them more realistic in recent years. Such extensions are combining with spreading mode that the online networks platform could affect the topology of rumor spreading network. Another direction to research rumor spreading model is to focus on the complex topology of social interactions. In the field of social network, the scale-free property is the fundamental characteristic, and the nodes stand for individuals and the edges stand for various interactions of people. Therefore, it makes more sense to study spreading dynamics on scale-free networks [21–26]. For further understanding of the rumor spreading dynamic in the real world, the counterattack and self-resistance mechanisms, trust mechanism, latent mechanism, rumor-killer mechanism, and information pushing mechanism [27–33] have been taken into account. These models more accurately reflect the spread of rumors and also give a lot of control strategies for rumors.

Undeniably, the influences of hesitating mechanisms also play an important role in the process of rumor spreading. Recently, in order to investigate the influence of heterogeneity of the underlying complex networks and hesitating mechanisms on rumor spreading, Liu et al. proposed a SEIR rumor propagation model on the heterogeneous networks [34]. They found that the spreading threshold significantly depends on the topology of the complex networks and analyzed globally dynamic behaviors of the rumor. Wan et al. presented a SEIR rumor spreading model with demographics on scale-free networks [35]. They proved the global asymptotic stability of rumor-free equilibrium and the permanence of the rumor, but the simulation of the experiment was not given, and the direct immunization of rumor spreading was not considered. However, in real life, some wise people or functional departments which realize the information is rumor will take appropriate measures to prevent its continued spreading in the early days when rumors begin to spread, i.e., direct immunization [36]. Furthermore, the initiative response of individual is not considered when rumors spreading prevail, i.e., feedback mechanism. In fact, once people know the harm of rumor, they will question and further verify the rumor, and thus reduce the trust and the spread of rumor. Obviously, the feedback mechanism can change the network topology structure [37, 38]. In this paper, considering the direct immunization, we focus on a SEIR rumor model in social networks, we comprehensively prove the permanence of the rumor spreading in detail. Meanwhile, the modified model with feedback mechanism in social networks is introduced.

The rest of the paper is organized as follows: in Sect. 2, we present a new SEIR model in social networks. In Sect. 3, the dynamical behaviors of rumor spreading are analyzed in detail. Section 4 gives theoretical analysis to the stability of the equilibrium. In Sect. 5, the modified model feedback mechanism in social networks is introduced. In Sect. 6, numerical simulations are given to illustrate the main results. Finally, the conclusions are given in Sect. 7.

2 Model formulation

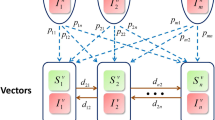
In this paper, we consider the whole population $N_{k}(t)$ to be located in a relevant social network. Users can be regarded as nodes and direct relationships between users can be considered as edges. Our model is based on dividing the whole population into four states: S, E, I, and R. At each time step, each individual adopts one of four states S, E, I, or R, which respectively stand for the people who have never contacted with rumor (susceptible), the people who have been infected, the people who have been in hesitate state and do not spread rumor (exposed), the people who are actively spreading it (infected), and the people who have known the rumor but never believed and spread it (removed). Taking the heterogeneity induced by the presence of nodes with different connectivities into account, we let $S_{k}(t)$, $E_{k}(t)$, $I_{k}(t)$, and $R_{k}(t)$ be the relative densities of susceptible, infected, and recovered nodes of degree k at time t, respectively. The process of SEIR rumor spreading is shown in Fig. 1.

Figure 1

Transfer diagram for rumor spreading model

In the process of rumor spreading, the spreading among these four states is governed by the following rules: we assume that $\lambda (k) > 0$ is the degree-dependent infected rate, and it denotes the acceptability of k degree nodes for rumors. The susceptible nodes know the rumor but do not trust at rate γ if it connects to an infected one, the exposed node is infected with probability β, h represents the attractiveness of rumor itself on the complex social network, and the corresponding repellant of rumor is $1 - h$. The fuzziness of rumor is $m\ (0 \le m \le 1)$ and the corresponding clarity of rumor is $1 - m$. The forgetting rate is δ. Due to trust and interest in the rumor, the exposed node becomes an infected node with probability βh, and with probability $\beta (1 - h)$, it becomes a recover node. Because of the fuzziness of the rumor, the parameters δm and $\delta (1 - m)$ represent that the infected node has become susceptible and removed, respectively. The degree-dependent parameter $b(k) > 0$ represents the number of newly immigrated individuals with degree k per unit time, and each newly immigrated individual is susceptible, the reconnection of these nodes follows the above propagation rules. This type of rewiring preserves the network mean degree (the total number of links remains constant) but changes the mean degree of susceptible and infected nodes [39–41]. The emigration is proportional to the node size with probability μ. The parameters are all nonnegative. The model can be described by the following system of ordinary differential equations:

$$ \textstyle\begin{cases} \frac{dS_{k}(t)}{dt} = b(k) - \lambda (k)\varTheta(t)S_{k}(t) - \gamma k\varTheta (t)S_{k}(t) - \mu S_{k}(t) + \delta mI_{k}(t), \\ \frac{dE_{k}(t)}{dt} = \lambda (k)\varTheta (t)S_{k}(t) - \mu E_{k}(t) - \beta E_{k}(t), \\ \frac{dI_{k}(t)}{dt} = \beta hE_{k}(t) - \delta I_{k}(t) - \mu I_{k}(t), \\ \frac{dR_{k}(t)}{dt} = \gamma k\varTheta (t)S_{k}(t) + \beta (1 - h)E_{k}(t) + \delta (1 - m)I_{k}(t) - \mu R_{k}(t), \end{cases} $$

(2.1)

$\varTheta (t)$ denotes the probability of ignoramus contacts with a sharer at time t, which satisfies the relation

$$ \varTheta (t) = \sum_{i = 1}^{n} \frac{\varphi (i)}{i}P(i|k)\frac{I_{i}(t)}{N_{i}(t)}, $$

(2.2)

where $P(i|k)$ denotes the conditional probability that a node with degree k is connected to a node with degree i. Considering the uncorrelated network [42], in this paper, $P(i|k) = iP(i)/ \langle k \rangle$. Here, $P(k)$ is the probability that a randomly chosen node has degree k, thus $\sum_{k = 1}^{n} P(k) = 1$, $\langle k \rangle = \sum_{k = 1}^{n} kP(k)$ denotes the average degree, and $\varphi (k)$ is a function that represents the infectivity of a node with degree k; the factor $1/i$ stands for the probability that one of the infected neighbors of a node, with degree i, will contact this node at the present time step. Summing the four equations in (2.1), we can obtain

$$\begin{aligned} &\frac{dN_{k}(t)}{dt} = b(k) - \mu N_{k}(t), \quad\mbox{then } N_{k}(t) = N_{k}(0)e^{ - \mu t} + \frac{b(k)}{\mu} \bigl(1 - e^{ - \mu t}\bigr),\\ & \lim_{t \to \infty} N_{k}(t) = \frac{b(k)}{\mu}. \end{aligned}$$

We suppose that $N_{k}(0) = S_{k}(0) + E_{k}(0) + I_{k}(0) + R_{k}(0) = \frac{b(k)}{\mu}$ in order to have a population of constant size, namely $S_{k}(t) + E_{k}(t) + I_{k}(t) + R_{k}(t) = N_{k}(t) \equiv \eta_{k}$, where $\eta_{k} = b(k)/\mu$. So we can obtain

$$ \varTheta (t) = \frac{1}{ \langle k \rangle} \sum_{i = 1}^{n} \frac{\varphi (k)}{\eta_{k}}P(k)I_{k}(t). $$

(2.3)

Furthermore, $S(t) = \sum_{k = 1}^{n} P(k)S_{k}(t)$, $E(t) = \sum_{k = 1}^{n} P(k)E_{k}(t)$, $I(t) = \sum_{k = 1}^{n} P(k)I_{k}(t)$, $R(t) = \sum_{k = 1}^{n} P(k)R_{k}(t)$ are the average densities of the four individual states, respectively. The initial conditions for system can be given as follows: $S_{k}(0) = \eta_{k} - E_{k}(0) - I_{k}(0) - R_{k}(0) > 0, E_{k}(0) \ge 0,I_{k}(0) \ge 0,R_{k}(0) \ge 0$, and $\varTheta (0) > 0$.

3 The basic reproduction number and existence of equilibriums

In this section, we present an analytic solution to the deterministic equations describing the dynamics of the SEIR rumor spreading process in social networks.

Theorem 1

Consider system (2.1), let $R_{0} = \frac{ \langle \varphi (k)\lambda (k) \rangle \beta h}{ \langle k \rangle (\delta + \mu )(\beta + \mu )}$. There always exists a rumor-free equilibrium $E_{0}(b(k) / \mu,0,0,0)$ when $R_{0} < 1$. When $R_{0} > 1$, system (2.1) has a rumor-prevailing equilibrium $E_{ +} (S_{k}^{ *},E_{k}^{ *},I_{k}^{ *},R_{k}^{ *} )$.

Proof

To get the rumor-prevailing equilibrium solution $E_{ +} (S_{k}^{ *},E_{k}^{ *},I_{k}^{ *},R_{k}^{ *} )$, we need to make the right-hand side of the system equal to zero, it should satisfy

$$ \textstyle\begin{cases}b(k) + \delta mI_{k}^{ *} - \mu S_{k}^{ *} - \lambda (k)\varTheta^{ *} S_{k}^{ *} - \gamma k\varTheta^{ *} S_{k}^{ *} = 0, \\ \lambda (k)\varTheta^{ *} S_{k}^{ *} - \mu E_{k}^{ *} - \beta E_{k}^{ *} = 0, \\ \beta hE_{k}^{ *} - \delta I_{k}^{ *} - \mu I_{k}^{ *} = 0, \\ \gamma k\varTheta^{ *} S_{k}^{ *} + \delta (1 - m)I_{k}^{ *} + \beta (1 - h)E_{k}^{ *} - \mu R_{k}^{ *} = 0, \\ S_{k}^{ *} + E_{k}^{ *} + I_{k}^{ *} + R_{k}^{ *} = \eta_{k}, \end{cases}$$

(3.1)

where $\varTheta^{ *} = \frac{1}{ \langle k \rangle} \sum_{i = 1}^{n} \frac{\varphi (k)}{\eta_{k}}P(k)I_{k}^{ *} (t)$. One has

$$ \textstyle\begin{cases} S_{k}^{ *} = \frac{(\mu + \delta )(\beta + \mu )}{\lambda (k)\beta h\varTheta^{ *}} I_{k}^{ *}, \\ E_{k}^{ *} = \frac{\mu + \delta}{\beta h}I_{k}^{ *}, \\ R_{k}^{ *} = \frac{\gamma k(\beta + \mu )(\delta + \mu ) + \beta \lambda (k)[(\delta + \mu ) - h(\mu + \delta m)]}{\lambda (k)\mu \beta h}I_{k}^{ *}. \end{cases}$$

(3.2)

Considering the following normalization condition $S_{k}(t) + E_{k}(t) + I_{k}(t) + R_{k}(t) = \eta_{k}$ for all k, we obtain

$$ I_{k}^{ *} = \frac{\mu \lambda (k)\varTheta^{ *} \beta h\eta_{k}}{(\mu + \gamma k\varTheta^{ *} )(\beta + \mu )(\delta + \mu ) + \lambda (k)\varTheta^{ *} ( (\beta + \mu )(\delta + \mu ) - \beta h\delta m )}. $$

(3.3)

Inserting into (2.2), we obtain that

$$ \varTheta^{ *} = \frac{1}{ \langle k \rangle} \sum_{i = 1} \frac{\varphi (k)}{\eta_{k}}P(k)I_{k}^{ *}. $$

(3.4)

For simplification, we substitute Θ for $\varTheta^{ *}$, then from (3.4) we have the self-consistency equation:

$$\begin{aligned} \varTheta &= \frac{1}{ \langle k \rangle} \sum_{i = 1} \frac{\varphi (k)}{\eta_{k}}P(k)\frac{\lambda (k)\beta h\varTheta \mu \eta_{k}}{(\mu + \gamma k\varTheta )(\beta + \mu )(\delta + \mu ) + \lambda (k)\varTheta ( (\beta + \mu )(\delta + \mu ) - \beta h\delta m )} \\ &=:f(\varTheta ). \end{aligned}$$

(3.5)

Clearly, $\varTheta = 0$ is the solution of (3.5), i.e., $f(0) \le 0$. The conditions under a nontrivial solution to (3.5) exist.

To ensure that the equation has a nontrivial solution $\varTheta (\varTheta \in (0,1))$, the following condition should be satisfied:

$$\begin{aligned} \frac{df(\varTheta )}{d\varTheta} \Big\vert _{\varTheta = 0} > 1, \end{aligned}$$

(3.6)

which indicates that $\frac{ \langle \varphi (k)\lambda (k) \rangle}{ \langle k \rangle} \frac{\beta h}{(\delta + \mu )(\beta + \mu )} > 1$, we can obtain the basic reproductive number

$$ R_{0} = \frac{ \langle \varphi (k)\lambda (k) \rangle}{ \langle k \rangle} \frac{\beta h}{(\delta + \mu )(\beta + \mu )}. $$

(3.7)

So, a nontrivial solution exists if and only if $R_{0} > 1$.

Inserting the nontrivial solution of (3.4) into Eq. (3.3), we can obtain $I_{k}^{ *}$. By (3.2) and (3.3) we can easily get $0 < S_{k}^{ *} < \eta_{k}$, $0 < E_{k}^{ *} < \eta_{k}$, $0 < I_{k}^{ *} < \eta_{k}$, $0 < R_{k}^{ *} < \eta_{k}$.

Thus, the equilibrium $E_{ +} (S_{k}^{ *},E_{k}^{ *},I_{k}^{ *},R_{k}^{ *} )$ is well-defined. Hence, when $R_{0} > 1$, only one positive equilibrium $E_{ +} (S_{k}^{ *},E_{k}^{ *},I_{k}^{ *},R_{k}^{ *} )$ of system (2.1) exists. The proof is completed. □

Remark

• (1) The basic reproductive number $R_{0}$ is obtained by Eq. (3.7), it determines the existence of the endemic equilibrium. The details will be further verified in the next section. It can also be interpreted as the average number of secondary infections generated by an infected node during its infection time [43].

• (2) The basic reproductive number $R_{0}$ depends on some parameters and the fluctuation of the degree distribution. Interestingly, $R_{0}$ has no correlation with the degree-dependent new immigrate $b(k)$ and the recovered rate γ. It seems that the attractive parameter h and the infected rate β have the same effects, because their increase will make $R_{0}$ increase. In Sect. 6, their effects will be explored by the detailed numerical calculation.

• (3) If $\lambda (k) = \lambda k,\varphi (k) = k,b(k) = 0$, and $\mu = 0$, then system (2.1) becomes the network-based SEIRS model without demographics, and $R_{0} > 1$ is simplified to $\lambda > \lambda_{c}$, where $\lambda_{c} = \frac{\delta \langle k \rangle}{\beta \langle k^{2} \rangle}$. It is clear that, in the infinite size network, the total number of nodes $N_{k}(t)$ grows to infinity, i.e., $N_{k}(t) \to \infty$, then $\langle k^{2} \rangle \to \infty$, thus the absence of the spreading threshold, i.e., $\lambda_{c} \to 0$, is observed.

4 Stability analysis of the equilibrium

Theorem 2

If $R_{0} < 1$, the rumor-free equilibrium $E_{0}$ of system (2.1) is locally asymptotically stable, and it is unstable when $R_{0} > 1$.

Proof

For $S_{k}(t) + E_{k}(t) + I_{k}(t) + R_{k}(t) = \eta_{k}$, i.e., if the values of $E_{k}(t), I_{k}(t)$, and $R_{k}(t)$ are fixed, there is only one corresponding $S_{k}(t)$, therefore, it will be sufficient for us to discuss the last three equations of (2.1):

$$ \textstyle\begin{cases} \frac{dE_{k}(t)}{dt} = \lambda (k)\varTheta (t)S_{k}(t) - \mu E_{k}(t) - \beta E_{k}(t), \\ \frac{dI_{k}(t)}{dt} = \beta hE_{k}(t) - \delta I_{k}(t) - \mu I_{k}(t), \\ \frac{dR_{k}(t)}{dt} = \gamma k\varTheta (t)S_{k}(t) + \beta (1 - h)E_{k}(t) + \delta (1 - m)I_{k}(t) - \mu R_{k}(t), \end{cases} $$

(4.1)

where the Jacobian matrix of the rumor-free equilibrium $E_{0}$ of system (4.1) is

$$\begin{array}{rl}& J={\left[\begin{array}{cccc}{A}_{11}& A_{12}& \cdots & A_{1n}\\ A_{21}& A_{22}& \cdots & A_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ A_{n1}& A_{n2}& \cdots & A_{nn}\end{array}\right]}_{3n\times 3n}\text{where }{A}_{ij}=\left(\begin{array}{ccc}0& \frac{\lambda (j)\phi (j)P(j)}{〈k〉}& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),\\ & A_{nn}=\left(\begin{array}{ccc}-(\beta +\mu )& -\frac{\lambda (j)\phi (j)P(j)}{〈k〉}& 0\\ \beta h& -(\delta +\mu )& 0\\ \beta (1-h)& \delta (1-m)-\frac{\lambda (j)\phi (j)P(j)}{〈k〉}& \mu \end{array}\right)(i,j=1,2,\dots ,n).\end{array}$$

By using the mathematical induction method, the characteristic equation can be calculated as follows:

$$ (x + \mu )^{n}(x + \beta + \mu )^{n - 1}(x + \delta + \mu )^{n - 1} \biggl\{ (x + \beta + \mu ) (x + \delta + \mu ) - \beta h \frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} \biggr\} = 0, $$

(4.2)

where $\sum_{i = 1}^{n} \lambda (i)\varphi (i)P(i) = \lambda (1)\varphi (1)P(1) + \lambda (2)\varphi (2)P(2) + \cdots + \lambda (n)\varphi (n)P(n) = \langle \lambda (k)\varphi (k) \rangle$.

This equation has a negative root −μ with multiplicity n, a negative root $- \mu - \beta$ with multiplicity $n - 1$, and a negative root $- \mu - \delta$ with multiplicity $n - 1$. The stability of $E_{0}$ is only dependent on

$$ x^{2} + (\beta + \delta + 2\mu )x + (\delta + \mu ) (\beta + \mu ) - \beta h\frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} = 0. $$

(4.3)

According to equation (4.3), if $R_{0} > 1$, we can easily get $(\delta + \mu )(\beta + \mu ) - \beta h\frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} > 0$, that is, $x < 0$. If $x = R_{0} < 1$, then $x < 0$, and if $x = R_{0} > 1$, then $x > 0$. Thus, $E_{0}$ is locally asymptotically stable when $R_{0} > 1$. The proof is completed. □

In the following, we consider global asymptotic stability of $E_{0}$ and the global attractivity of $E^{ *}$, which is one of the most important topics in the study of rumor spreading.

Lemma 4.1

([44])

If $a > 0$, $b > 0$, and $\frac{dx(t)}{dt} \ge b - ax$, when $t \ge 0$ and $x(0) \ge 0$, we have $\lim_{t \to \infty} \sup x(t) \le \frac{b}{a}$, if $a > 0$, $b > 0$, and $\frac{dx(t)}{dt} \le b - ax$, when $t \ge 0$ and $x(0) \ge 0$, we have $\lim_{t \to \infty} \sup x(t) \le \frac{b}{a}$.

Theorem 3

If $R_{0} < 1$, the rumor-free equilibrium $E_{0}$ of system (2.1) is globally asymptotically stable.

Proof

First, we define a Lyapunov function $V(t)$ as follows:

$$ V(t) = \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k) E_{k}(t) + \frac{(\beta + \mu )}{\beta h}\sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k) I_{k}(t). $$

(4.4)

Then, according to a calculation of the derivative of $V(t)$ along the solution of system (2.1), we get

$$\begin{aligned} \mathop{V} ^{\cdot}(t) ={}& \sum \frac{\varphi (k)}{\eta_{k}}P(k) \bigl( \lambda (k)\varTheta (t)S_{k}(t) - \mu E_{k}(t) - \beta E_{k}(t) \bigr) \\ &{}+ \sum \frac{(\beta + \mu )}{\beta h} \frac{\varphi (k)}{\eta_{k}} \bigl( \beta hE_{k}(t) - \delta I_{k}(t) - \mu I_{k}(t) \bigr) \\ ={}& \sum \frac{\varphi (k)}{\eta_{k}}P(k)\lambda (k)\varTheta (t)S_{k}(t) + \sum \frac{(\beta + \mu )}{\beta h} \frac{\varphi (k)}{\eta_{k}} \bigl( - \delta I_{k}(t) - \mu I_{k}(t) \bigr) \\ \le{}& \sum \frac{\varphi (k)}{\eta_{k}}P(k) \biggl[ \lambda (k)\varTheta (t) \eta_{k} + \frac{ - (\beta + \mu )(\delta + \mu )}{\beta h}I_{k}(t) \biggr] \\ = {}& \varTheta (t)\frac{1}{\beta h} \bigl( (\beta + \mu ) (\delta + \mu ) \bigr) (R_{0} - 1). \end{aligned}$$

(4.5)

When $R_{0} < 1$, we can obtain $V(t) \le 0$ for all $t \ge 0$, and that $V(t) = 0$ only if $\varTheta (t) = 0$, that is, $I_{k}^{ *} = 0$. Combining with the second equation of system (4.1), it obviously follows that $E_{k}^{ *} = 0$ as $t \to + \infty$ for $k = 1,2, \ldots,n$.

Due to $I_{k}^{ *} = 0$ and $E_{k}^{ *} = 0$, from the first equation for system (2.1), it follows that

$$\frac{dS_{k}(t)}{dt} = b(k) + \delta mI_{k}(t) - \lambda (k)\varTheta (t)S_{k}(t) - \gamma k\varTheta (t)S_{k}(t) - \mu S_{k}(t). $$

By Lemma 4.1, we derive that

$$ \lim_{t \to \infty} \sup S_{k}(t) \le \frac{b(k)}{\mu} =:S_{k}^{0}. $$

(4.6)

For arbitrarily enough small $\varepsilon_{2} > 0$, there exists $t_{2} > 0$ such that $0 \le E_{k}(t) \le \varepsilon_{2},0 \le I_{k}(t) \le \varepsilon_{2}$ for $t > t_{2}$. From the first equation (4.1), we have

$$ \frac{dS_{k}(t)}{dt} \ge b(k) + \delta m\varepsilon_{2} - \lambda (k)S_{k}(t)M\varepsilon_{2} - \gamma kS_{k}(t)M \varepsilon_{2} - \mu S_{k}(t), $$

(4.7)

where $M = \frac{1}{ \langle k \rangle} \sum_{i = 1}^{n} kP(k)$, by Lemma 4.1, we have $\lim_{t \to + \infty} S_{k}(t) \ge \frac{b(k) + \delta m\varepsilon_{2}}{\mu + (\lambda (k) + \gamma k)M\varepsilon_{2}}$. Setting $\varepsilon_{2} \to 0$, it follows that $\lim_{t \to + \infty} S_{k}(t) \ge \frac{b(k)}{\mu} = S_{k}^{0}$.

From (4.4) and (4.7), it is clear that $\lim_{t \to + \infty} S_{k}(t) = S_{k}^{0} = \frac{b(k)}{\mu} = \eta (k)$. This proves that the rumor-free equilibrium $E_{0}$ of system (4.1) is globally asymptotically stable when $R_{0} < 1$. The proof is completed. □

Next, the global attractivity of the rumor-prevailing equilibrium is discussed. The main result is given in the following theorem.

Theorem 4

Suppose that $( S_{k}(t),E_{k}(t),I_{k}(t) )$ is a solution of system (4.1) satisfying initial conditions $E_{k}(t) > 0$ or $I_{k}(t) > 0$. If $R_{0} > 1$, then $\lim_{t \to \infty} ( S_{k}(t),E_{k}(t),I_{k}(t) ) = ( S_{k}^{ *} (t),E_{k}^{ *} (t),I_{k}^{ *} (t) )$, where $( S_{k}^{ *} (t),E_{k}^{ *} (t),I_{k}^{ *} (t) )$ is the information-prevailing equilibrium of (4.1) satisfying (3.2) for $k = 1,2, \ldots,n$.

Proof

In the following, k is fixed to be any integer in ($1,2, \ldots,n$). By Theorem 4, there exists a sufficiently small constant $\xi\ (0 < \xi < 1)$ and a larger enough constant $T > 0$ such that $I_{i_{0}}(t) \ge \xi$ for $t > T$, therefore $\varTheta (t) > \xi \varTheta$ for $t > T$. Thus

$$\varTheta = \frac{1}{ \langle k \rangle} \sum_{i = 1} \frac{\varphi (i)}{\eta_{i}}P(i)I_{i}(t) \ge \frac{\varphi (i_{0})P(i_{0})}{\eta_{i_{0}} \langle k \rangle} \xi = \phi \xi > 0, $$

where $\phi = \frac{\varphi (i_{0})P(i_{0})}{\eta_{i_{0}} \langle k \rangle}$. Submitting this into the equation of (4.1) gives

$$ S_{{k}}'(t) \le b(k) + \delta m\bigl(\eta_{k} - S_{k}(t)\bigr) - \bigl(\lambda (k) + \gamma k\bigr)\phi \xi S_{k}(t) - \mu S_{k}(t),\quad t > T. $$

(4.8)

By Lemma 4.1, we derive that $\lim \sup_{t \to \infty} S_{k}(t) \le \frac{b(k) + \delta m\eta_{k}}{ ( \lambda (k) + \gamma k )\phi \xi + \mu + \delta m}$, thus, for any given constant $0 < \xi_{1} < \frac{ ( \lambda (k) + \gamma k )\phi \xi \eta_{k}}{2 ( \mu + \delta m + ( \lambda (k) + \gamma k )\phi \xi )}$, there exists $t_{1} > T$ such that $S_{k}(t) \le A_{k}^{(1)} - \xi_{1}$ for $t > t_{1}$, where

$$A_{k}^{(1)} = \frac{b(k) + \delta m\eta_{k}}{ ( \lambda (k) + \gamma k )\phi \xi + \mu} + 2\xi_{1} < \eta_{k}. $$

Since $\varTheta \le \frac{1}{ \langle k \rangle} \sum_{i = 1} \varphi (i)P(i) =:\varPhi$, we obtain from the second equation of system (4.1) that

$$\begin{aligned} E_{k}'(t) &\le \lambda (k) \bigl( \eta_{k} - E_{k}(t) - I_{k}(t) - R_{k}(t) \bigr) - (\beta + \mu )E_{k}(t) \\ &\le \lambda (k)\varPhi \bigl( \eta_{k} - E_{k}(t) \bigr) - ( \beta + \mu )E_{k}(t) \\ &= \eta_{k}\lambda (k)\varPhi - E_{k}(t) \bigl( \lambda (k) \varPhi + \beta + \mu \bigr),\quad t > t_{1}. \end{aligned}$$

(4.9)

Hence, for any given constant $0 < \xi_{2} < \min \{ 1/2,\xi_{1},(\mu + \beta )\eta_{k}[2 ( \lambda (k)\varPhi + \mu + \beta )]^{ - 1}\}$, there exists $t_{2} > t_{1}$ such that $E_{k}(t) \le B_{k}^{(1)} - \xi_{2}$ for $t > t_{2}$, where

$$B_{k}^{(1)} = \frac{\lambda (k)\varPhi \eta_{k}}{\lambda (k)\varPhi + \mu + \beta} + 2\xi_{2} < \eta_{k}. $$

Then it follows from the third equation of (4.1) that

$$ I_{k}'(t) \le \beta h\bigl(\eta_{k} - I_{k}(t)\bigr) - (\mu + \delta )I_{k}(t) = \beta h \eta_{k} - ( \mu + \delta + \beta h )I_{k}(t),\quad t > t_{2}. $$

(4.10)

Similarly, for any given constant $0 < \xi_{3} < \min \{ 1/3,\xi_{2},(\mu + \beta h)\eta_{k}[2(\mu + \delta + \beta h)]^{ - 1}\}$, there exists $t_{3} > t_{2}$ such that $I_{k}(t) \le C_{k}^{(1)} - \xi_{3}$ for $t > t_{3}$, where

$$C_{k}^{(1)} = \frac{\delta \eta_{k}}{\mu + \delta + \beta h} + 2\xi_{3} < \eta_{k}. $$

On the other hand, we substitute this into the first equation of (4.1)

$$ S_{{k}}'(t) \ge b(k) + \delta m\eta_{k} - \bigl( \lambda (k) + \gamma k \bigr)\varPhi S_{k}(t) - \mu S_{k}(t) - \delta mS_{k}(t), \quad t > T. $$

(4.11)

So, for any given enough small constant $0 < \xi_{4} < \min \{ 1/4,\xi_{3},(b(k) + \delta m\eta_{k})[2((\lambda (k) + \gamma k)\varPhi + \mu + \delta m)]^{ - 1}\}$, there exists $t_{4} > t_{3}$ such that $S_{k}(t) \ge a_{k}^{(1)} + \xi_{4}$ for $t > t_{4}$, where

$$a_{k}^{(1)} = \frac{b(k) + \delta m\eta_{k}}{(\lambda (k) + \gamma k)\varPhi + \mu + \delta m} - 2\xi_{4} > 0. $$

It follows that

$$ E_{k}'(t) \ge \lambda (k)\phi \xi a_{k}^{(1)} - (\beta + \mu )E_{k}(t),\quad t > t_{4}. $$

(4.12)

So, for any given enough small constant $0 < \xi_{5} < \min \{ 1/5,\xi_{4},(\lambda (k)\phi \xi a_{k}^{(1)})[2(\mu + \beta )]^{ - 1}\}$, there exists $t_{5} > t_{4}$ such that $E_{k}(t) \ge b_{k}^{(1)} + \xi_{5}$ for $t > t_{5}$, where

$$b_{k}^{(1)} = \bigl(\lambda (k)\phi \xi a_{k}^{(1)} \bigr) (\mu + \beta )^{ - 1} - 2\xi_{5} > 0. $$

The third equation of (2.1) implies that

$$ I_{k}'(t) \ge \beta hb_{k}^{(1)} - ( \mu + \delta )I_{k}(t),\quad t > t_{5}. $$

(4.13)

So, for any given enough small constant $0 < \xi_{6} < \min \{ 1/6,\xi_{5},(\beta hb_{k}^{(1)})(2(\mu + \delta ))^{ - 1}\}$, there exists $t_{6} > t_{5}$ such that $I_{k}(t) \ge c_{k}^{(1)} + \xi_{6}$ for $t > t_{6}$, where $c_{k}^{(1)} = \beta hb_{k}^{(1)}(\mu + \delta )^{ - 1} - 2\xi_{6} > 0$.

Due to ξ being a small positive constant, we can derive that $0 < a_{k}^{(1)} < A_{k}^{(1)} < 1$, $0 < b_{k}^{(1)} < B_{k}^{(1)} < 1$, and $0 < c_{k}^{(1)} < C_{k}^{(1)} < 1$. Let

$$ q^{(j)} = \frac{1}{ \langle k \rangle} \sum_{j = 1}^{n} iP(i) c_{i}^{(j)},\qquad Q^{(j)}\frac{1}{ \langle k \rangle} \sum _{j = 1}^{n} iP(i) C_{i}^{(j)},\quad j = 1,2, \ldots. $$

(4.14)

We can easily get $0 < q^{(j)} \le \varTheta (t) \le Q^{(j)} < \varPhi$, $t > t_{4}$.

Again, from the first equation of (4.1), we have

$$ S_{{k}}'(t) \le b(k) + \delta m\eta_{k} - \bigl(\lambda (k) + \gamma k\bigr)q^{(1)}S_{k}(t) - \mu S_{k}(t) - \delta mS_{k}(t), \quad t > t_{4}. $$

(4.15)

Hence, for any given constant $0 < \xi_{7} < \min \{ 1/7,\xi_{6}\}$, there exists $t_{7} > t_{6}$ such that

$$S_{{k}}'(t) \le A_{k}^{(2)} \triangleq \min \bigl\{ A_{k}^{(1)} - \xi_{1}, \bigl(b(k) + \delta m\eta_{k}\bigr)\bigl[\bigl(\lambda (k) + \gamma k \bigr)q^{(1)} + \mu + \delta m\bigr]^{ - 1} + \xi_{7} \bigr\} ,\quad t > t_{7}. $$

Then, from the second equation of (4.1), we have

$$ E_{k}'(t) \ge \lambda (k)Q^{(1)}A_{k}^{(2)} - (\mu + \beta )E_{k}(t),\quad t > t_{7}. $$

(4.16)

So, for any given constant $0 < \xi_{8} < \min \{ 1/8,\xi_{7}\}$, there exists $t_{8} > t_{7}$ such that

$$E_{k}'(t) \le B_{k}^{(2)} \triangleq\min \bigl\{ B_{k}^{(1)} - \xi_{2}, \bigl( \lambda (k)Q^{(1)}A_{k}^{(2)} \bigr) (\mu + \beta )^{ - 1} + \xi_{8}\bigr\} , \quad t > t_{8}. $$

Consequently, from the third equation of (4.1), we have

$$ I_{k}'(t) \le \beta hB_{k}^{(2)} - ( \mu + \delta )I_{k}(t),\quad t > t_{8}. $$

(4.17)

Hence, for any given constant $0 < \xi_{9} < \min \{ 1/9,\xi_{8}\}$, there exists $t_{9} > t_{8}$ such that

$$I_{k}'(t) \le C_{k}^{(2)}\triangleq\min \bigl\{ C_{k}^{(1)} - \xi_{3}, \bigl(\beta hB_{k}^{(2)}\bigr) (\delta + \mu )^{ - 1} + \xi_{9}\bigr\} ,\quad t_{9} > t_{8}. $$

Turning back, one has

$$ S_{{k}}'(t) \ge b(k) + \delta m\eta_{k} - \bigl(\lambda (k) + \gamma k\bigr)Q^{(2)}S_{k}(t) - \mu S_{k}(t) - \delta mS_{k}(t), \quad t > t_{9}. $$

(4.18)

So, for any given enough small constant $0 < \xi_{10} < \min \{ 1/10,\xi_{9},(b(k) + \delta m\eta_{k})[2(\lambda (k) + \gamma k)Q^{(2)} + \mu + \delta m]^{ - 1}\}$, there exists $t_{10} > t_{9}$ such that $S_{k}(t) \ge a_{k}^{(2)} + \xi_{10}$ for $t > t_{10}$, where

$$a_{k}^{(2)} = \max \bigl\{ a_{k}^{(1)} + \xi_{4},\bigl(b(k) + \delta m\eta_{k}\bigr) \bigl( \lambda (k) + \gamma k\bigr)Q^{(2)} + \mu + \delta m )^{ - 1} - 2 \xi_{10}\bigr\} . $$

It follows that

$$ E_{k}'(t) \ge \lambda (k)q^{(1)}a_{k}^{(2)} - (\beta + \mu )E_{k}(t), \quad t > t_{10}. $$

(4.19)

So, for any given enough small constant $0 < \xi_{11} < \min \{ 1/11,\xi_{10},\lambda (k)q^{(1)}a_{k}^{(2)} + [2(\mu + \beta )]^{ - 1}\}$, there exists $t_{11} > t_{10}$ such that $E_{k}(t) \ge b_{k}^{(2)} + \xi_{11}$ for $t > t_{10}$, where

$$b_{k}^{(2)} = \max \bigl\{ b_{k}^{(1)} + \xi_{5},\lambda (k)q^{(1)}a_{k}^{(2)} + \bigl[2(\mu + \beta )\bigr]^{ - 1} - 2\xi_{11}\bigr\} . $$

The third equation of (4.1) implies that

$$ I_{k}'(t) \ge \beta hb_{k}^{(2)} - ( \mu + \delta )I_{k}(t),\quad t > t_{11}. $$

(4.20)

So, for any given enough small constant $0 < \xi_{12} < \min \{ 1/12,\xi_{11},[\beta hb_{k}^{(2)}](2(\mu + \delta ))^{ - 1}\}$, there exists $t_{12} > t_{11}$ such that $I_{k}(t) \ge c_{k}^{(2)} + \xi_{12}$ for $t > t_{12}$, where

$$c_{k}^{(2)} = \max \bigl\{ \bigl[c_{k}^{(1)} + \xi_{6},\beta hb_{k}^{(2)}\bigr](\mu + \delta )^{ - 1} - 2\xi_{12}\bigr\} . $$

Repeating the above analyses and calculations, we get six sequences $A_{k}^{(i)},B_{k}^{(i)},C_{k}^{(i)},a_{k}^{(i)},b_{k}^{(i)}, c_{k}^{(i)},i = 1,2 ,\ldots$ . Due to the first three being monotone decreasing sequences and the last three being monotone increasing ones, there exists a sufficiently large positive integer $L \ge 2$ such that $l \ge L$:

$$\begin{aligned} \begin{aligned} &A_{k}^{(l)} = \frac{b(k) + \delta m\eta_{k}}{(\lambda (k) + \gamma k)q^{(l - 1)} + \mu + \delta m} + \xi_{6l - 5},\qquad B_{k}^{(l)} = \frac{\lambda (k)Q^{(l - 1)}A_{k}^{(l)}}{\mu + \beta} + \xi_{6l - 4}, \\ &C_{k}^{(l)} = \frac{\beta hB_{k}^{(l)}}{\delta + \mu} + \xi_{6l - 3},\qquad a_{k}^{(l)} = \frac{b(k) + \delta m\eta_{k}}{(\lambda (k) + \gamma k)Q^{(l)} + \mu + \delta m} + \xi_{6l - 2},\ \\ &b_{k}^{(l)} = \frac{\lambda (k)q^{(l - 1)}a_{k}^{(l)}}{\mu + \beta} + \xi_{6l - 1},\qquad c_{k}^{(l)} = \frac{\beta hb_{k}^{(l)}}{\delta + \mu} + \xi_{6l}. \end{aligned} \end{aligned}$$

(4.21)

We can easily get that

$$ a_{k}^{(l)} \le S_{k}(t) \le A_{k}^{(l)},\qquad b_{k}^{(l)} \le E_{k}(t) \le B_{k}^{(l)},\qquad \mathrm{c}_{k}^{(l)} \le I_{k}(t) \le C_{k}^{(l)}, \quad t > t_{6l}. $$

(4.22)

Since the sequential limits of (4.21) exist, let $\lim_{l \to \infty} \Delta_{k}^{(l)} = \Delta_{k}$, where $\Delta_{k}^{(l)} \in \{ A_{k}^{(l)},B_{k}^{(l)},C_{k}^{(l)}, a_{k}^{(l)},b_{k}^{(l)},c_{k}^{(l)},Q_{k}^{(l)},q_{k}^{(l)}\}$ and $\Delta_{k} \in \{ A_{k},B_{k},C_{k},a_{k},b_{k},c_{k},Q_{k},q_{k}\}$.

Noting that $0 < \xi_{1} < 1/l$, one has $\xi_{1} \to 0$ as $l \to \infty$. In the six sequences of (4.21), by taking $l \to \infty$, it follows from (4.21) that

$$\begin{aligned} \begin{aligned} & A_{k} = \frac{b(k) + \delta m\eta_{k}}{(\lambda (k) + \gamma k)q + \mu + \delta m},\qquad B_{k} = \frac{\lambda (k)QA_{k}}{\mu + \beta},\qquad C_{k} = \frac{\beta hB_{k}}{\delta + \mu}, \\ &a_{k} = \frac{b(k) + \delta m\eta_{k}}{(\lambda (k) + \gamma k)Q + \mu + \delta m},\qquad b_{k} = \frac{\lambda (k)qa_{k}}{\mu + \beta},\qquad c_{k} = \frac{\beta hb_{k}}{\delta + \mu}, \end{aligned} \end{aligned}$$

(4.23)

where

$$ q = \frac{1}{ \langle k \rangle} \sum_{i = 1}^{n} iP(i) c_{i},\qquad Q = \frac{1}{ \langle k \rangle} \sum_{i = 1}^{n} iP(i) C_{i}. $$

(4.24)

Further,

$$\begin{aligned} \begin{aligned} &C_{k}^{(l)} = \frac{\beta h\lambda (k)Q(b(k) + \delta m\eta_{k})}{(\delta + \mu )(\mu + \beta ) ( (\lambda (k) + \gamma k)q + \mu + \delta m )}, \\ &c_{k}^{(l)} = \frac{\beta h\lambda (k)q(b(k) + \delta m\eta_{k})}{(\delta + \mu )(\mu + \beta ) ( (\lambda (k) + \gamma k)Q + \mu + \delta m )}. \end{aligned} \end{aligned}$$

(4.25)

Substituting (4.24) into q and Q, respectively, one has

$$\begin{aligned} &1 = \frac{\beta h(\mu + \delta m)}{ \langle k \rangle (\delta + \mu )(\mu + \beta )}\sum_{i = 1}^{n} \frac{\varphi (k)P(k)\lambda (k)}{ ( (\lambda (k) + \gamma k)Q + \mu + \delta m )}, \\ &1 = \frac{\beta h(\mu + \delta m)}{ \langle k \rangle (\delta + \mu )(\mu + \beta )}\sum_{i = 1}^{n} \frac{\varphi (k)P(k)\lambda (k)}{ ( (\lambda (k) + \gamma k)q + \mu + \delta m )}. \end{aligned}$$

By subtracting the above two equations, we arrive at

$$ 0 = \frac{\beta h(\mu + \delta m)(Q - q)}{ \langle k \rangle (\delta + \mu )(\mu + \beta )}\sum_{i = 1}^{n} \frac{\varphi (k)P(k)\lambda (k)(\lambda (k) + \gamma k)}{ ( (\lambda (k) + \gamma k)Q + \mu + \delta m ) ( (\lambda (k) + \gamma k)q + \mu + \delta m )}. $$

(4.26)

It is obvious that $q = Q$, so $\frac{1}{ \langle k \rangle} \sum_{i = 1}^{n} \frac{\varphi (k)}{\eta_{k}}P(k) (C_{k} - c_{k}) = 0$, which sees that $C_{k} = c_{k}$ for $i = 1,2, \ldots,n$. From (4.24) and (4.25), it follows that

$$\lim_{t \to \infty} S_{k}(t) = A_{k} = a_{k},\qquad \lim_{t \to \infty} E_{k}(t) = B_{k} = b_{k},\qquad \lim_{t \to \infty} I_{k}(t) = C_{k} = c_{k}. $$

Finally, substituting $q = Q$ into (4.22), in view of (3.2) and (4.23), we obtain $S_{k} = S_{k}^{ *}$, $E_{k} = E_{k}^{ *}$, and $I_{k} = I_{k}^{ *}$. The proof is completed. □

5 The modified SEIR model with feedback mechanism

Rumor has a sudden and fast spreading speed, it has bad influence on the normal social stability. Due to the fact that the internet rumors are difficult to identify and bewitch, it is easy to cause serious social problems and even cause social unrest and political instability. However, due to the rapid development of network technology, the information spreading on the network will be further verified, which will weaken the spread of rumors, and this can be described as a feedback mechanism. Based on the above observations and model (2.1), we present the modified model with feedback mechanism in social networks:

$$ \textstyle\begin{cases} \frac{dS_{k}(t)}{dt} = b(k) + \delta mI_{k}(t) - \lambda (k)\varTheta (t)(1 - \alpha \varTheta (t))S_{k}(t) \\ \phantom{\frac{dS_{k}(t)}{dt} =}{}- \gamma k\varTheta (t)(1 - \alpha \varTheta (t))S_{k}(t) - \mu S_{k}(t), \\ \frac{dE_{k}(t)}{dt} = \lambda (k)\varTheta (t)(1 - \alpha \varTheta (t))S_{k}(t) - \mu E_{k}(t) - \beta E_{k}(t), \\ \frac{dI_{k}(t)}{dt} = \beta hE_{k}(t) - \delta I_{k}(t) - \mu I_{k}(t), \\ \frac{dR_{k}(t)}{dt} = \gamma k\varTheta (t)(1 - \alpha \varTheta (t))S_{k}(t) + \delta (1 - m)I_{k}(t) + \beta (1 - h)E_{k}(t) - \mu R_{k}(t), \end{cases} $$

(5.1)

where α is the positive parameter called ‘fear factor’, which is determined by the fear degree of people to the rumor spreading. $\varTheta (t)$ denotes the probability of a susceptible contacting an infected at time t, which satisfies the relation

$$ \varTheta (t) = \frac{1}{ \langle k \rangle} \sum_{i = 1}^{n} \frac{\varphi (k)}{\eta_{k}}P(k)I_{k}(t). $$

(5.2)

Here, $P( i | k) = iP(k)/ \langle k \rangle, \lambda (k)(1 - \alpha \varTheta (t))S_{k}(t)\varTheta (t)$ represents the proportion of individuals who having acquired infection became exposed individuals. The spreading speed will decrease when α becomes lower, which is consistent with the actual prevalence law of rumor spreading.

Theorem 5

Consider model (5.1), define $R_{1} = \frac{ \langle \varphi (k)\lambda (k) \rangle \beta h}{ \langle k \rangle (\delta + \mu )(\beta + \mu )}$, then the following statements hold:

• (1) If $R_{1} < 1$, there always exists a rumor-free equilibrium $E_{1}(\eta_{k},0,0,0)$.

• (2) There is a rumor-prevailing equilibrium $E_{1 +} (S_{k}^{ *},E_{k}^{ *},I_{k}^{ *},R_{k}^{ *} )$ if $R_{1} > 1$.

Proof

To get the rumor-prevailing equilibrium solution $E_{1 +} (S_{k}^{ *},E_{k}^{ *},I_{k}^{ *},R_{k}^{ *} )$, we need to make the right-hand side of system (5.1) equal to zero, it should satisfy

$$ \textstyle\begin{cases} b(k) + \delta mI_{k}^{ *} - \lambda (k)\varTheta^{ *} (1 - \alpha \varTheta^{ *} )S_{k}^{ *} - \gamma k\varTheta^{ *} (1 - \alpha \varTheta^{ *} )S_{k}^{ *} - \mu S_{k}^{ *} = 0, \\ \lambda (k)\varTheta^{ *} (1 - \alpha \varTheta^{ *} )S_{k}^{ *} - \mu E_{k}^{ *} - \beta E_{k}^{ *} = 0, \\ \beta hE_{k}^{ *} - \delta I_{k}^{ *} - \mu I_{k}^{ *} = 0, \\ \gamma k\varTheta^{ *} (1 - \alpha \varTheta^{ *} )S_{k}^{ *} + \delta (1 - m)I_{k}^{ *} + \beta (1 - h)E_{k}^{ *} - \mu R_{k}^{ *} = 0, \\ S_{k}^{ *} + E_{k}^{ *} + I_{k}^{ *} + R_{k}^{ *} = \eta_{k}, \end{cases} $$

(5.3)

where $\varTheta^{ *} = \frac{1}{ \langle k \rangle} \sum_{i = 1}^{n} \frac{\varphi (k)}{\eta_{k}}p(k)I_{k}^{ *} (t)$. One has

$$ \textstyle\begin{cases} S_{k}^{ *} = \frac{(\mu + \delta )(\beta + \mu )}{\lambda (k)\beta h\varTheta^{ *} (1 - \alpha \varTheta^{ *} )}I_{k}^{ *}, \\ E_{k}^{ *} = \frac{\mu + \delta}{\beta h}I_{k}^{ *}, \\ R_{k}^{ *} = \frac{\gamma k(\beta + \mu )(\mu + \delta ) + \lambda (k)\beta ( (\mu + \delta ) - h(\mu + \delta m) )}{\lambda (k)\beta h\mu} I_{k}^{ *}. \end{cases} $$

(5.4)

Considering the following normalization condition $S_{k}(t) + E_{k}(t) + I_{k}(t) + R_{k}(t) = \eta_{k}$ for all k, we obtain

$$ I_{k}^{ *} = \frac{\mu \lambda (k)\varTheta^{ *} (1 - \alpha \varTheta^{ *} )\beta h\eta_{k}}{(\mu + \gamma k\varTheta^{ *} (1 - \alpha \varTheta^{ *} ))(\beta + \mu )(\delta + \mu ) + \lambda (k)\varTheta^{ *} (1 - \alpha \varTheta^{ *} ) ( (\beta + \mu )(\delta + \mu ) - \beta h\delta m )}. $$

(5.5)

Inserting (5.5) into (5.2), we have the self-consistency equation

$$\begin{aligned} \varTheta^{ *} ={}& \frac{1}{ \langle k \rangle} \sum_{i = 1} \varphi (k)P(k) \\ &{}\times \frac{\varTheta^{ *} (1 - \alpha \varTheta^{ *} )\lambda (k)\beta h}{ ( \gamma k\varTheta^{ *} (1 - \alpha \varTheta^{ *} ) + \mu )(\beta + \mu )(\delta + \mu ) + \lambda (k)\varTheta^{ *} (1 - \alpha \varTheta^{ *} ) ( (\beta + \mu )(\delta + \mu ) - \beta h\delta m )} \\ =:{}&f\bigl(\varTheta^{ *} \bigr). \end{aligned}$$

(5.6)

Clearly, $\varTheta^{ *} = 0$ is the solution of (5.6). To ensure that (5.6) has a nontrivial solution, i.e., $0 < \varTheta^{ *} \le 1$, the following conditions must be satisfied:

$$ \frac{df(\varTheta^{ *} )}{d\varTheta^{ *}}\Big|_{\varTheta^{ *} = 0} > 1 \quad\mbox{and}\quad f(1) \le 1, $$

(5.7)

which indicates that $\frac{ \langle \varphi (k)\lambda (k) \rangle}{ \langle k \rangle} \frac{\beta h}{(\delta + \mu )(\beta + \mu )} > 1$, so we can get the basic reproductive number

$$ R_{1} = \frac{\beta h}{(\delta + \mu )(\beta + \mu )}\frac{ \langle \varphi (k)\lambda (k) \rangle}{ \langle k \rangle}. $$

(5.8)

So, a nontrivial solution exists if and only if $R_{1} > 1$. □

Remark

The feedback mechanism parameter α cannot change the basic reproductive number, but it can reduce the prevailing level and weaken the rumor spreading.

Theorem 6

When $R_{1} < 1$, the rumor-free equilibrium is globally asymptotically stable; when $R_{1} > 1$, system (5.1) is permanent, there exists $\varepsilon > 0$ such that

$$\lim \inf_{x \to \infty} \bigl\{ S_{k}(t),E_{k}(t),I_{k}(t) \bigr\} _{k = 1}^{n} \ge \varepsilon, $$

where $( S_{k}(t),E_{k}(t),I_{k}(t) )$ is any solution of (5.3) satisfying (5.1) and $E_{k}(0) > 0$ or $I_{k}(0) > 0$.

Proof

Let $S_{k}(t) = \eta_{k} + x_{k}(t),E_{k}(t) = y_{k}(t),I_{k}(t) = z_{k}(t),k = 1,2, \ldots,n$, where ($x_{k}(t),y_{k}(t),z_{k}(t)$) is a small perturbation of $E_{1}$. Now we consider the linearized system at $E_{1}$:

$$\textstyle\begin{cases} \frac{dx_{k}(t)}{dt} = - \mu x_{k}(t) + \delta mz_{k}(t) - (\lambda (k) + \gamma k)\frac{1}{ \langle k \rangle} \sum \varphi (k)P(k)z_{i}(t), \\ \frac{dy_{k}(t)}{dt} = \gamma k\frac{1}{ \langle k \rangle} \sum \varphi (k)P(k)z_{i}(t) - \mu y_{k}(t) - \beta y_{k}(t), \\ \frac{dz_{k}(t)}{dt} = \beta hy_{k}(t) - \delta z_{k}(t) - \mu z_{k}(t) \end{cases} $$

which can be written as

$$\frac{d}{dt}=\left(\begin{array}{c}{x}_1\\ y_1\\ z_1\\ x_2\\ y_2\\ z_2\\ ⋮\\ x_n\\ y_n\\ z_n\end{array}\right)=Q\left(\begin{array}{c}{x}_1\\ y_1\\ z_1\\ x_2\\ y_2\\ z_2\\ ⋮\\ x_n\\ y_n\\ z_n\end{array}\right),$$

where matrix Q is

$$\left(\begin{array}{cccccccccc}-\mu & 0& \delta m-A_1{l}_1& 0& 0& -A_1{l}_2& \cdots & 0& 0& -A_1{l}_n\\ 0& -\mu -\beta & B_1{l}_1& 0& 0& B_1{l}_2& \cdots & 0& 0& B_1{l}_n\\ 0& \beta h& -\delta -\mu & 0& 0& 0& \cdots & 0& 0& 0\\ 0& 0& -A_2{l}_1& -\mu & 0& \delta m-A_2{l}_2& \cdots & 0& 0& -A_2{l}_n\\ 0& 0& B_2{l}_1& 0& -\mu -\beta & B_2{l}_2& \cdots & 0& 0& B_2{l}_n\\ 0& 0& 0& 0& \beta h& -\delta -\mu & \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& -A_n{l}_1& 0& 0& -A_n{l}_2& \cdots & -\mu & 0& \delta m-A_n{l}_n\\ 0& 0& B_n{l}_1& 0& 0& B_n{l}_2& \cdots & 0& -\mu -\beta & B_n{l}_n\\ 0& 0& 0& 0& 0& 0& \cdots & 0& \beta h& -\delta -\mu \end{array}\right).$$

To simplify the matrix, we rewrite it as follows:

$$Q=\left(\begin{array}{ccc}{N}_{11}& \cdots & N_{1n}\\ ⋮& \ddots & ⋮\\ N_{n1}& \cdots & N_{nn}\end{array}\right),$$

where

$$\begin{array}{rl}& N_{11}=\left(\begin{array}{ccc}-\mu & 0& \delta m-A_1{l}_1\\ 0& -\mu -\beta & B_1{l}_1\\ 0& \beta h& -\delta -\mu \end{array}\right),\\ & N_{1n}=\left(\begin{array}{ccc}0& 0& A_1{l}_n\\ 0& 0& B_1{l}_n\\ 0& 0& 0\end{array}\right),\\ & N_{n1}=\left(\begin{array}{ccc}0& 0& A_n{l}_1\\ 0& 0& B_n{l}_1\\ 0& 0& 0\end{array}\right),\\ & N_{nn}=\left(\begin{array}{ccc}-\mu & 0& \delta m-A_n{l}_n\\ 0& -\mu -\beta & B_n{l}_n\\ 0& \beta h& -\delta -\mu \end{array}\right),\end{array}$$

in which $A_{k} = \frac{\lambda (k) + \gamma k}{ \langle k \rangle},B_{k} = \frac{\lambda (k)}{ \langle k \rangle},l_{k} = \varphi (k)P(k)$. A direct calculation leads to the characteristic polynomial of the rumor-free equilibrium in the following form:

$$(x + \mu )^{n}\bigl(x + (\mu + \beta )\bigr)^{n - 1}\bigl(x + ( \mu + \delta )\bigr)^{n - 1}\bigl(x^{2} + px + q\bigr) = 0, $$

where $p = 2\mu + \delta + \beta,q = (\beta + \mu )(\delta + \mu ) - \beta h\sum_{i = 1}^{n} \varphi (i) P(i)$.

It is obvious that $p > 0$ and $R_{1} < 1$ is equivalent to $q > 0$. Therefore, there exists a unique positive eigenvalue x of Q if and only if $R_{1} > 1$; otherwise, if $R_{1} < 1$, all real-valued eigenvalues of Q are negative. By the Perron–Frobenius theorem, this implies that the maximal real part of all eigenvalues of Q is positive if and only if $R_{1} > 1$. Then a theorem of Lajmanovich and York [45] yields the results of this theorem. The proof is completed. □

Conjecture

Suppose that $( S_{k}(t),E_{k}(t),I_{k}(t) )$ is a solution of (5.3) with $S_{k}(0) > 0$, $E_{k}(0) > 0$ and $I_{k}(0) > 0$. If $R_{1} > 1$, then $\lim \inf_{x \to \infty} \{ S_{k}(t),E_{k}(t),I_{k}(t) \} = (S_{k}^{ *},E_{k}^{ *},I_{k}^{ *} )$, where ($S_{k}^{ *},E_{k}^{ *},I_{k}^{ *}$) is the unique alcoholism equilibrium of (5.3).

Remark

We have great difficulty in proving the global stability of $E_{1 +}$. Then we only carry out simulations to test our conjecture (Fig. 9). It is still an open problem to prove the global stability of $E_{1 +}$.

6 Simulation results and analysis

First, we perform some sensitivity analysis of the basic reproduction number $R_{0}$ in terms of the model parameters on social networks. Obviously,

$$\begin{aligned} &\frac{\partial R_{0}}{\partial h} = \frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} \frac{\beta}{[(\delta + \mu )(\beta + \mu )]^{2}}, \qquad \frac{\partial R_{0}}{\partial \delta} = \frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} \frac{ - \beta h(\beta + \mu )}{[(\delta + \mu )(\beta + \mu )]^{2}}, \\ &\frac{\partial R_{0}}{\partial \beta} = \frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} \frac{\mu h(\delta + \mu )}{[(\delta + \mu )(\beta + \mu )]^{2}}, \qquad\frac{\partial R_{0}}{\partial \mu} = \frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} \frac{ - (\delta + 2\mu + \mu )}{[(\delta + \mu )(\beta + \mu )]^{2}}. \end{aligned}$$

We can find some interesting results, which have been showed in Fig. 2. In Fig. 2(a) and (b), it can be seen that big β or h can lead to large $R_{0}$. That is to say, the larger infected or the higher attractiveness of rumor can increase the chance of rumor spreading. From Fig. 2(c) and (d), $R_{0}$ increases as δ or μ decreases. At the same time, variance of degree distribution $\langle \varphi (k)\lambda (k) \rangle$ manifests the diversity in contact patterns. Particularly, the ratio $\langle \varphi (k)\lambda (k) \rangle / \langle k \rangle$ is the parameter defining the level of heterogeneity of the network [26].

Figure 2

The relationship between the basic reproduction number $R_{0}$ and the parameters on social networks

Next, we carry out Runge–Kutta method simulations to investigate the dynamics of model (2.1) on both artificial and real networks. We take the degree distribution to be $P(k) = ck^{ - l}\ (2 < l \le 3)$, in which $l = 3$ and c satisfies $\sum_{k = 1}^{n} P(k) = 1$, $n = 1000$. We choose $\lambda (k) = \lambda k,\varphi (k) = k,b(k) = b/n$.

In Fig. 3(a), the parameters are chosen as $b = 0.1,\lambda = 0.15,\gamma = 0.1,\delta = 0.2,\beta = 0.25,m = 0.1,h = 0.4$, thus the basic reproduction number $R_{0} = 0.65$. It is shown that when $R_{0} < 1$, the rumor spreading will disappear, even for a large fraction of the infected nodes at the beginning. And we can also see $I_{k} \to 0$ as $t \to \infty$. It suggests that the rumor-free equilibrium is globally asymptotically stable when $R_{0} < 1$, in agreement with Theorem 2. In Fig. 3(b), the parameters are chosen as $b = 0.04,\lambda = 0.35,\gamma = 0.1,\delta = 0.2,\beta = 0.3,m = 0.2,h = 0.6$, the basic reproduction number is $R_{0} = 3.51$. It is shown that when $R_{0} > 1$, even for a small fraction of the infected nodes at the beginning, the rumor is permanent on the network, in accord with Theorem 2.

Figure 3

Each compartment population changes over time when $R_{0} < 1$ (a) and $R_{0} > 1$ (b)

Figure 4 shows the dynamical behavior of $I_{100}$ in $R_{0} < 1$ (a) and $R_{0} > 1$ (b) with different degree. We find that the larger degree leads to a larger value of the spreading level.

Figure 4

Dynamic behavior of $I_{k}$ in rumor-free equilibrium (a) and rumor-prevailing equilibrium (b) with different degree

Figure 5 shows the effect of attractive parameter h to $I_{150}$ and $R_{150}$. We choose the parameters $h = 0.1$ in Fig. 5(a) and $h = 0.4$ in Fig. 5(b). We can find that the greater attraction of the rumor, the greater people who spread rumor and the fewer people who recover rumor.

Figure 5

Density of $I_{150}$ and $R_{150}$ versus varying over different attractive parameter h

Figures 6 and 7 show the effect of forget rate δ and fuzzy parameter m to each population. One can see that both forget rate δ and fuzzy parameter m have great influence on $S_{k}$ and $R_{k}$. In Fig. 6, we choose $\delta = 0.1$ in (a) and $\delta = 0.05$ in (a), it shows that the forget rate δ has a positive effect on $S_{k}$ and $R_{k}$. In Fig. 7, we choose $m = 0.15$ in (a) and $m = 0.4$ in (a), we find that increasing fuzzy parameter m can decrease the level of recovered. In the real world, the fuzzier the rumor is, the more curious people will be. This fact causes a secondary rumor diffusion. Thus, if we want to reduce the final rumor size, the authoritative organizations or media should give precise and clear information.

Figure 6

Each compartment population changes over time with different forget rate δ

Figure 7

Each compartment population changes over time with different fuzzy parameter m

In Fig. 8(a), the prevalence $I_{100}$ versus t corresponding to different infected rates β, which are chosen as $0.1,0.4,0.7,0.9$ from bottom to top, is shown. We can see that $I_{100}$ increases significantly as β increases. In Fig. 8(b), the prevalence $R_{100}$ versus t corresponding to different infected rates γ, which are chosen as $0.1,0.4,0.7,0.9$ from bottom to top, is illustrated. We can easily find that the density of the removed population increases as γ increases.

Figure 8

Density of $I_{100}$ versus t varying over different infected rate β in (a) and the density of $R_{100}$ versus t varying over different direct immunization rate γ in (b)

In Fig. 9(a), the parameters are chosen as in Fig. 3(a) and the parameters in Fig. 5(b) are chosen as in Fig. 3(b). We can see that $I_{100}$ corresponding decreases significantly as the feedback parameter α increases, i.e., a larger feedback parameter can reduce the rumor spreading level.

Figure 9

Density of $I_{100}$ versus t with $R_{1} < 1$ (a) and $R_{1} > 1$ (b) to a different feedback parameter

7 Conclusion

This paper is mainly focused on the dynamics of rumor spreading on the complex social networks. A detailed SEIR rumor spreading model with hesitating mechanism has been presented and simulated. By using mean-field theory, we obtained the basic reproduction number $R_{0}$ and the equilibrium. As the results indicate, the basic reproduction number in society networks is virtually correlated with the fluctuations of the degree distribution. Interestingly, $R_{0}$ bears no relation to the degree-dependent immigration $b(k)$. The global stability of equilibrium and the permanence have been proved in detail. We get the conclusion that higher attractiveness and fuzziness of rumor contribute to rumor spreading. Furthermore, increasing feedback parameters can result in the weakness of rumor spreading and the decrease of the population finally is infected. The study may give us valuable guidance to prevent the rumor spreading.