1 Introduction

With the development of online social networks, rumor has propagated more quickly and widely, coming within people’s horizons [1–3]. Rumor propagation may have tremendous negative effects on human lives, such as reputation damage, social panic and so on [4–7]. In order to investigate the mechanism of rumor propagation and effectively control the rumor, lots of rumor spreading models have been studied and analyzed in detail. In 1965, Daley and Kendal first proposed the classical DK model to study the rumor propagation [5]. They divided the population into three disjoint categories, namely, those who who never heard the rumor, those knowing and spreading the rumor, and finally those knowing the rumor but never spreading it. From then on, most rumor propagation studies were based on the DK model [8–14].

In the early stages, most rumor spreading models were established on homogeneous networks [15–18]. However, it is well known that a significant characteristic of social networks is their scale-free property. In networks, the nodes stand for individuals and the contacts stand for various interactions among those individuals. Scale-free networks can be characterized by degree distribution which follows a power-law distribution \(P(k)\sim k^{ - \gamma}\) (\(2 < \gamma \le 3\)) [19]. Recently, some scholars have studied a variety of rumor spreading models and found that the heterogeneity of the underlying network had a major influence on the dynamic mechanism of rumor spreading [18, 20–26].

It is noteworthy that the influence of hesitation plays a crucial role in process of rumor spreading. Lately, there were a few researchers who have studied the effects of hesitation. For instance, Xia et al. [27] proposed a novel SEIR rumor spreading model with hesitating mechanism by adding a new exposed group (E) in the classical SIR model. Liu et al. [28] presented a SEIR rumor propagation model on the heterogeneous network. They calculated the basic reproduction number \(R_{0}\) by using the next generation method, and they found that the basic reproduction number \(R_{0}\) depends on the fluctuations of the degree distribution. However, in most of the research work mentioned above, the immigration and emigration are not considered when rumor breaks out. Although references [27, 28] proposed a SEIR model with hesitating mechanism, neither could serve as a strict proof of globally asymptotically stability of rumor-free equilibrium and the permanence of the rumor. In this paper, considering the immigration and emigration rate, we study and analyze a new SEIR model with hesitating mechanism on heterogeneous networks and comprehensively prove the globally asymptotical stability of rumor-free equilibrium and the permanence of rumor in detail.

The rest of this paper is organized as follows. In Section 2, we present a new SEIR spreading model with hesitating mechanism on scale-free networks. In Section 3, the basic reproduction number and the two equilibria of the proposed model are obtained. In Section 4, we analyze the globally asymptotic stability of equilibria. Finally, we conclude the paper in Section 5.

2 Modeling

Consider the whole population as a relevant online network. The SEIR rumor spreading model is based on dividing the whole population into four groups, namely: the susceptible, referring to those who have never contacted with the rumor, denoted by S; the exposed, referring to those who have been infected, in a hesitate state not spreading the rumor, denoted by E; the infected, referring to those who have accepted and spread the rumor, denoted by I; the recovered, referring to those who know the rumor but have ceased to spread it, denoted by R. During the period of rumor spreading, we suppose that the individuals with the same number of contacts are dynamically equivalent and belong to the same group in this paper. Let \(S_{k}(t)\), \(E_{k}(t)\), \(I_{k}(t)\) and \(R_{k}(t)\) be the densities of the above-mentioned nodes with the connectivity degree k at time t. Then the aggregate number of population at time is \(N(t)\), and the density of the whole population with degree k satisfies

$$ N_{k}(t) = S_{k}(t) + E_{k}(t) + I_{k}(t) + R_{k}(t). $$
(2.1)

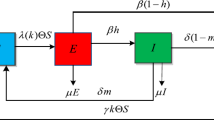
The transfer diagram for the SEIR rumor propagation model is shown in Figure 1. In this paper, we assume that the degree-dependent parameter \(b(k) > 0\) denotes the number of new immigration individuals with degree k per unit time, and each new immigration individual is susceptible. The emigration rate of all individuals is μ. Exposed individuals turn into infected individuals with probability βh due to believing and spreading the rumor. They recover from the rumor with probability \(\beta (1 - h)\). The infected individuals become exposed individuals with probability δm. They recover from the rumor with probability \(\delta (1 - m)\).

Figure 1
figure 1

Transfer diagram for SEIR rumor propagation model.

Full size image

Based on the above hypotheses and notation, the dynamic mean-field reaction rate equations described by

$$ \left \{ \textstyle\begin{array}{l} \frac{dS_{k}(t)}{dt} = b(k) - \lambda (k)\Theta (t)S_{k}(t) - \mu S_{k}(t), \\ \frac{dE_{k}(t)}{dt} = \lambda (k)\Theta (t)S_{k}(t) - \beta E_{k}(t) + \delta mI_{k}(t) - \mu E_{k}(t), \\ \frac{dI_{k}(t)}{dt} = \beta hE_{k}(t) - \delta I_{k}(t) - \mu I_{k}(t), \\ \frac{dR_{k}(t)}{dt} = \beta (1 - h)E_{k}(t) + \delta (1 - m)I_{k}(t) - \mu R_{k}(t), \end{array}\displaystyle \right . $$
(2.2)

where \(\lambda (k) > 0\) is the degree of acceptability of k for individuals for the rumor, and the probability \(\Theta (t)\) denotes a link to an infected individual, satisfying

$$ \Theta (t) = \frac{1}{ \langle k \rangle} \sum_{i} \frac{\varphi (i)}{i}P(i|k)\frac{I_{i}(t)}{N_{i}(t)}. $$
(2.3)

Here, \(1 / i\) represents the probability that one of the infected neighbors of an individual, with degree i, will contact this individual at the present time step; \(P(i|k)\) is the probability that an individual of degree k is connected to an individual with degree i. In this paper, we focus on degree uncorrelated networks. Thus, \(P(i|k) = iP(i) / \langle k \rangle\), where \(\langle k\rangle = \sum_{i} iP(i)\) is the average degree of the network. For a general function \(f(k)\), it is defined as \(\langle f(k)\rangle = \sum_{i} f(i)P(i)\). The function \(\varphi (k)\) is the infectivity of an individual with degree k.

Adding the four equations of system (2.2), we have \(\frac{dN_{k}(t)}{dt} = b(k) - \mu N_{k}(t)\). Then we can obtain \(N_{k}(t) = \frac{b(k)}{\mu} (1 - e^{ - \mu t}) + N_{k}(0)e^{ - \mu t}\), where \(N_{k}(0)\) represents the initial density of the whole population with degree k. Hence, \(\lim \sup_{t \to \infty} N_{k}(t) = b(k) / \mu\), then \(N_{k}(t) = S_{k}(t) + E_{k}(t) + I_{k}(t) + R_{k}(t) \le b(k) / \mu\) for all \(t > 0\). In order to have a population of constant size, we suppose that \(S_{k}(t) + E_{k}(t) + I_{k}(t) + R_{k}(t) = N_{k}(t) = \eta_{k}\), where \(\eta_{k} = b(k) / \mu\). Thus, we have

$$ \Theta (t) = \frac{1}{ \langle k \rangle} \sum_{k = 1} \frac{\varphi (k)}{\eta_{k}}P(k)I_{k}(t). $$
(2.4)

Furthermore,

$$\begin{gathered} S(t) = \sum_{k} P(k)S_{k}(t),\qquad E(t) = \sum_{k} P(k)E_{k}(t), \\ I(t) = \sum_{k} P(k)I_{k}(t), \quad \mbox{and}\quad R(t) = \sum_{k} P(k)R_{k}(t) \end{gathered} $$

are the global average densities of the four rumor groups, respectively. From a practical perspective, we only need to consider the case of \(P(k) > 0\) for \(k = 1, 2, \ldots\) . The initial conditions for system (2.2) satisfy

$$ \begin{gathered} 0 \le S_{k}(0), E_{k}(0), I_{k}(0), R_{k}(0) \le \eta_{k}, \\ S_{k}(0) + E_{k}(0) + I_{k}(0) + R_{k}(0) = \eta_{k},\qquad \Theta (0) > 0. \end{gathered} $$
(2.5)

3 The basic reproduction number and equilibria

In this section, we reveal some properties of the solutions and obtain the equilibria of system (2.2).

Theorem 1

Define the basic reproduction number \(R_{0} = \frac{\beta h}{(\beta + \mu )(\delta + \mu ) - \beta h\delta m}\frac{ \langle \varphi (k)\lambda (k) \rangle}{ \langle k \rangle} \), then there always exists a rumor-free equilibrium \(E_{0}(\eta_{k},0,0,0)\). And if \(R_{0} > 1\), system (2.2) has a unique rumor-prevailing equilibrium \(E_{ +} (S_{k}^{\infty},E_{k}^{\infty},I_{k}^{\infty},R_{k}^{\infty} )\).

Proof

We can easily see that the rumor-free equilibrium \(E_{0}(\eta_{k},0,0,0)\) of system (2.2) is always existent. To obtain the equilibrium solution \(E_{ +} (S_{k}^{\infty},E_{k}^{\infty},I_{k}^{\infty},R_{k}^{\infty} )\), we let the right side of system (2.2) be equal to zero. Thus, we have

$$\left \{ \textstyle\begin{array}{l} b(k) - \lambda (k)\Theta^{\infty} S_{k}^{\infty} - \mu S_{k}^{\infty} = 0, \\ \lambda (k)\Theta^{\infty} S_{k}^{\infty} - \beta E_{k}^{\infty} + \delta mI_{k}^{\infty} - \mu E_{k}^{\infty} = 0, \\ \beta hE_{k}^{\infty} - \delta I_{k}^{\infty} - \mu I_{k}^{\infty} = 0, \\ \beta (1 - h)E_{k}^{\infty} + \delta (1 - m)I_{k}^{\infty} - \mu R_{k}^{\infty} = 0, \end{array}\displaystyle \right . $$

where \(\Theta^{\infty} = \frac{1}{ \langle k \rangle} \sum_{k = 1} \frac{\varphi (k)}{\eta_{k}}P(k)I_{k}^{\infty} \). One has

$$ \left \{ \textstyle\begin{array}{l} E_{k}^{\infty} = \frac{(\delta + \mu )}{\beta h}I_{k}^{\infty}, \\ S_{k}^{\infty} = \frac{(\beta + \mu )(\delta + \mu ) - \beta h\delta m}{\beta h\lambda (k)\Theta^{\infty}} I_{k}^{\infty}, \\ R_{k}^{\infty} = \frac{(\delta + \mu )(1 - h) + h\delta (1 - m)}{h\mu} I_{k}^{\infty}. \end{array}\displaystyle \right . $$
(3.1)

According to \(S_{k}^{\infty} + E_{k}^{\infty} + I_{k}^{\infty} + R_{k}^{\infty} = \eta_{k}\) for all k, we have

$$ I_{k}^{\infty} = \frac{\mu \beta h\lambda (k)\Theta^{\infty} \eta_{k}}{\mu (\beta + \mu )(\delta + \mu ) - \mu \beta h\delta m + \lambda (k)\Theta^{\infty} [ (\beta + \mu )(\delta + \mu ) - m\beta h\delta ]}. $$
(3.2)

Inserting equation (3.2) into equation (2.4), we can obtain the self-consistency equation:

$$ \begin{aligned}[b] \Theta^{\infty} ={}& \frac{1}{ \langle k \rangle} \sum _{k = 1} \frac{\varphi (k)}{\eta_{k}} \\ &\times P(k)\frac{\mu \beta h\lambda (k)\Theta^{\infty} \eta_{k}}{\mu (\beta + \mu )(\delta + \mu ) - \mu \beta h\delta m + \lambda (k)\Theta^{\infty} [ (\beta + \mu )(\delta + \mu ) - m\beta h\delta ]} \\ \triangleq{} & f\bigl(\Theta^{\infty} \bigr). \end{aligned} $$
(3.3)

Obviously, \(\Theta^{\infty} = 0\) is a solution of (3.3), then \(S_{k}^{\infty} = \eta_{k}\) and \(E_{k}^{\infty} = I_{k}^{\infty} = R_{k}^{\infty} = 0\), which is a rumor-free equilibrium of system (2.2). In order to ensure equation (3.3) has a nontrivial solution, i.e., \(0 < \Theta^{\infty} \le 1\), the following conditions must be fulfilled:

$$\frac{df(\Theta^{\infty} )}{d\Theta^{\infty}} \bigg|_{\Theta^{\infty} = 0} > 1\quad \mbox{and} \quad f(1) \le 1. $$

Thus, we can obtain

$$\frac{\beta h}{(\beta + \mu )(\delta + \mu ) - \beta h\delta m}\frac{ \langle \varphi (k)\lambda (k) \rangle}{ \langle k \rangle} > 1. $$

Let the base reproduction number as follows:

$$ R_{0} = \frac{\beta h}{(\beta + \mu )(\delta + \mu ) - \beta h\delta m}\frac{ \langle \varphi (k)\lambda (k) \rangle}{ \langle k \rangle}. $$
(3.4)

System (2.2) admits a unique rumor equilibrium \(E_{ +} (S_{k}^{\infty},E_{k}^{\infty},I_{k}^{\infty},R_{k}^{\infty} )\) satisfying equation (3.1) if and only if \(R_{0} > 1\). The proof is completed. □

Remark 1

The basic reproductive number \(R_{0}\) is obtained by equation (3.4), which depends on some model parameters and the fluctuations of the degree distribution. Interestingly, the basic reproductive number \(R_{0}\) has no correlation with the degree-dependent immigration \(b(k)\). According to the form of \(R_{0}\), we see that increase of the emigration rate μ will make \(R_{0}\) decrease. If \(b(k) = 0\) and \(\mu = 0\), then system (2.2) become the network-based SEIR model without demographics, and \(R_{0} = \frac{h}{\delta (1 - hm)}\frac{ \langle \varphi (k)\lambda (k) \rangle}{ \langle k \rangle} \), which is in consistence with reference [28].

4 Discussion

4.1 The stability of the rumor-free equilibrium

Theorem 2

The rumor-free equilibrium \(E_{0}\) of SEIR system (2.2) is locally asymptotically stable if \(R_{0} < 1\), and it is unstable if \(R_{0} > 1\).

Proof

Let \(S_{k}(t) = \eta_{k} - E_{k}(t) - I_{k}(t) - R_{k}(t)\), where \(\eta_{k} = b(k) / \mu\). Therefore, system (2.2) can be rewritten as

$$ \left \{ \textstyle\begin{array}{l} \frac{dE_{k}(t)}{dt} = \lambda (k)\Theta (t) ( \eta_{k} - E_{k}(t) - I_{k}(t) - R_{k}(t) ) - (\beta + \mu )E_{k}(t) + \delta mI_{k}(t), \\ \frac{dI_{k}(t)}{dt} = \beta hE_{k}(t) - (\delta + \mu )I_{k}(t), \\ \frac{dR_{k}(t)}{dt} = \beta (1 - h)E_{k}(t) + \delta (1 - m)I_{k}(t) - \mu R_{k}(t). \end{array}\displaystyle \right . $$
(4.1)

Then the Jacobian matrix of system (4.1) at \(( 0, 0, 0 )\) is a \(3k_{\max} *3k_{\max} \) as follows:

$$ J = \begin{bmatrix} A_{1} & B_{12} & B_{13} & \cdots & B_{1k_{\max}} \\ B_{21} & A_{2} & B_{23} & \cdots & B_{2k_{\max}} \\ \vdots & \vdots & \ddots & & \vdots \\ B_{{k_{\max} 1}} & B_{{k_{\max} 2}} & B_{k_{\max} 3} & \cdots & A_{k_{\max}} \end{bmatrix} , $$

where

$$ A_{j} = \begin{pmatrix} - (\beta + \mu ) & \delta m + \frac{\lambda (j)\varphi (j)P(j)}{ \langle k \rangle} & 0 \\ \beta h & - (\delta + \mu ) & 0 \\ \beta (1 - h) & \delta (1 - m) & - \mu \end{pmatrix} , \qquad B_{ij} = \begin{pmatrix} 0 & \frac{\lambda (j)\varphi (j)P(j)}{ \langle k \rangle} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} . $$

By using mathematical induction, the characteristic equation can be calculated as follows:

$$\begin{gathered} ( z + \mu )^{k_{\max}} ( z + \beta + \mu )^{k_{\max} - 1} ( z + \delta + \mu )^{k_{\max} - 1} \\ \quad{}\times \biggl( ( z + \beta + \mu ) ( z + \delta + \mu ) - \beta h\delta m - \beta h\frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} \biggr) = 0, \end{gathered} $$

where

$$\bigl\langle \lambda (k)\varphi (k) \bigr\rangle = \lambda (1)\varphi (1)P(1) + \lambda (2)\varphi (2)P(2) + \cdots +\lambda (k_{\max} )\varphi (k_{\max} )P(k_{\max} ). $$

The stability of \(E_{0}\) is only dependent on

$$ ( z + \beta + \mu ) ( z + \delta + \mu ) - \beta h\delta m - \beta h \frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} = 0. $$
(4.2)

Then we have

$$ z^{2} + ( \beta + \delta + 2\mu )z + ( \beta + \mu ) ( \delta + \mu ) - \beta h\delta m - \beta h\frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} = 0. $$
(4.3)

According to equation (4.3), if \(R_{0} < 1\), we can easily get \(( \beta + \mu ) ( \delta + \mu ) - \beta h\delta m - \beta h\frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} > 0\), i.e., \(z < 0\). Hence, \(E_{0}\) is locally asymptotically stable if \(R_{0} < 1\) and unstable if \(R_{0} > 1\). The proof is completed. □

Theorem 3

The rumor-free equilibrium \(E_{0}\) of SEIR system (2.2) is globally asymptotically stable if \(R_{0} < 1\).

Proof

First, we define a Lyapunov function \(V(t)\) as follows:

$$ V(t) = \sum_{k} \frac{\varphi (k)}{\eta_{k}} \biggl[ P(k)E_{k}(t) + \frac{(\beta + \mu )}{\beta h}I_{k}(t) \biggr]. $$
(4.4)

Then, according to a calculation of the derivative of \(V(t)\) along the solution of system (2.2), we have

$$\begin{aligned} V(t) ={}& \sum_{k} \frac{\varphi (k)P(k)}{\eta_{k}} \biggl[ E_{k}(t) + \frac{(\beta + \mu )}{\beta h}I_{k}(t) \biggr] \\ ={}& \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k)\biggl[ \lambda (k)\Theta (t)S_{k}(t) - (\beta + \mu )E_{k}(t) + \delta mI_{k}(t)\\ & + \frac{(\beta + \mu )}{\beta h} \bigl( \beta hE_{k}(t) - (\delta + \mu )I_{k}(t) \bigr) \biggr] \\ \le{}& \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k) \biggl[ \lambda (k)\Theta (t)\eta_{k} + \frac{\delta m\beta h - (\beta + \mu )(\delta + \mu )}{\beta h}I_{k}(t) \biggr] \\ ={}& \Theta (t)\sum_{k} \varphi (k)P(k)\lambda (k) + \frac{\delta m\beta h - (\beta + \mu )(\delta + \mu )}{\beta h}\sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k)I_{k}(t) \\ ={}& \Theta (t) \bigl\langle \varphi (k)\lambda (k) \bigr\rangle + \frac{\delta m\beta h - (\beta + \mu )(\delta + \mu )}{\beta h} \langle k \rangle \Theta (t) \\ ={}& \Theta (t)\frac{1}{\beta h} \bigl[ \beta h \bigl\langle \varphi (k)\lambda (k) \bigr\rangle + \bigl[ \delta m\beta h - (\beta + \mu ) (\delta + \mu ) \bigr] \langle k \rangle \bigr] \\ ={}& \Theta (t) \langle k \rangle \frac{ [ (\beta + \mu )(\delta + \mu ) - \beta h\delta m ]}{\beta h}(R_{0} - 1). \end{aligned} $$

When \(R_{0} < 1\), we can easily find that \(V(t) \le 0\) for all \(V(t) \ge 0\), and that \(V(t) = 0\) only if \(\Theta (t) = 0\), i.e., \(I_{k}(t) = 0\). Thus, by the LaSalle invariance principle [29], this implies the rumor-free equilibrium \(E_{0}\) of system (2.2) is globally attractive. Therefore, when \(R_{0} < 1\), the rumor-free equilibrium \(E_{0}\) of SEIR system (2.2) is globally asymptotically stable. The proof is completed. □

4.2 The global attractivity of the rumor-prevailing equilibrium

In this section, the permanent of rumor and the global attractivity of the rumor-prevailing equilibrium are discussed.

Theorem 4

When \(R_{0} > 1\), the rumor is permanent on the network, i.e., there exists a positive constant \(\varsigma > 0\), such that \(\lim \inf I(t)_{t \to \infty} = \lim \inf_{t \to \infty} \sum_{k} P(k)I_{k}(t) > \varsigma\).

Proof

We desire to use the condition stated in Theorem 4.6 in [30]. Define

$$\begin{gathered} \begin{aligned}X ={}&\bigl\{ (S_{1},E_{1},I_{1},R_{1}, \ldots,S_{k_{\max}},E_{k_{\max}},I_{k_{\max}},R_{k_{\max}} ):\\&S_{k},E_{k},I_{k},R_{k} \ge 0 \mbox{ and } S_{k} + E_{k} + I_{k} + R_{k} = \eta,k = 1, \ldots,k_{\max} \bigr\} ,\end{aligned} \\ X_{0} = \biggl\{ (S_{1},E_{1},I_{1},R_{1}, \ldots,S_{k_{\max}},E_{k_{\max}},I_{k_{\max}},R_{k_{\max}} ) \in X: \sum_{k} P(k)I_{k} > 0\biggr\} , \\ \partial X_{0} = X\setminus X_{0}. \end{gathered} $$

In the following, we will explain that system (2.2) is uniformly persistent with respect to \((X_{0},\partial X_{0})\).

Clearly, X is positively and bounded with respect to system (2.2). Assume that \(\Theta (0) = \frac{1}{ \langle k \rangle} \sum_{k = 1} \frac{\varphi (k)}{\eta_{k}}P(k)I_{k}(0) > 0\), then we have \(I_{k}(0) > 0\) for some k. Thus, \(I(0) = \sum_{k = 1} P(k)I_{k}(0) > 0\). For \(I'(t) = \sum_{k} P(k)I_{k}'(t) \ge - (\delta + \mu )\sum_{k} P(k)I_{k}(t) = - (\delta + \mu )I(t)\), we have \(I(t) \ge I(0)e^{ - (\delta + \mu )t} > 0\). Therefore, \(X_{0}\) is also positively invariant. Furthermore, there exists a compact set B, in which all solutions of system (2.2) initiated in X ultimately enter and remain forever after. The compactness condition (C4.2) of Theorem 4.6 in reference [30] is easily verified for this set B.

Denote

$$\begin{aligned} M_{\partial} ={}& \bigl\{ \bigl(S_{1}(0),E_{1}(0),I_{1}(0),R_{1}(0), \ldots,S_{k_{\max}} (0),E_{k_{\max}} (0),I_{k_{\max}} (0),R_{k_{\max}} (0)\bigr):\\& \bigl(S_{1}(t),E_{1}(t),I_{1}(t),R_{1}(t), \ldots, S_{k_{\max}} (t),E_{k_{\max}} (t),I_{k_{\max}} (t),R_{k_{\max}} (t)\bigr) \in \partial X_{0},t \ge 0 \bigr\} , \end{aligned} $$

and

$$\begin{aligned} \Omega ={}& \bigcup \bigl\{ \omega \bigl(S_{1}(0),E_{1}(0),I_{1}(0),R_{1}(0), \ldots,S_{k_{\max}} (0),E_{k_{\max}} (0),I_{k_{\max}} (0),R_{k_{\max}} (0)\bigr):\\&\bigl(S_{1}(0),E_{1}(0),I_{1}(0),R_{1}(0), \ldots, S_{k_{\max}} (0),E_{k_{\max}} (0),I_{k_{\max}} (0),R_{k_{\max}} (0)\bigr) \in X \bigr\} , \end{aligned} $$

where \(\omega (S_{1}(0),E_{1}(0),I_{1}(0),R_{1}(0), \ldots,S_{k_{\max}} (0),E_{k_{\max}} (0),I_{k_{\max}} (0),R_{k_{\max}} (0))\) is the omega limit set of the solutions of system (2.2) starting in \((S_{1}(0),E_{1}(0),I_{1}(0),R_{1}(0), \ldots,S_{k_{\max}} (0),E_{k_{\max}} (0), I_{k_{\max}} (0),R_{k_{\max}} (0))\). Restricting system (2.2) on \(M_{\partial} \), we can obtain

$$ \left \{ \textstyle\begin{array}{l} \frac{dS_{k}(t)}{dt} = b(k) - \mu S_{k}(t), \\ \frac{dE_{k}(t)}{dt} = - (\beta + \mu )E_{k}(t), \\ \frac{dI_{k}(t)}{dt} = - (\delta + \mu )I_{k}(t) ,\\ \frac{dR_{k}(t)}{dt} = \beta (1 - h)E_{k}(t) - \mu R_{k}(t). \end{array}\displaystyle \right . $$
(4.5)

Obviously, system (4.5) has a unique equilibrium \(E_{0}\) in X. Thus, \(E_{0}\) is the unique equilibrium of system (2.2) in \(M_{\partial} \). We can easily find that \(E_{0}\) is locally asymptotically stable. For system (4.5) is a linear system; this indicates that \(E_{0}\) is globally asymptotically stable. Hence \(\Omega = \{ E_{0}\} \). And \(E_{0}\) is a covering of X, which is isolated and acyclic (because there exists no nontrivial solution in \(M_{\partial} \) which links \(E_{0}\) to itself). Finally, the proof of theorem will be completed if it is shown that \(E_{0}\) is a weak repeller for \(X_{0}\), i.e.,

$$\lim \sup_{t \to \infty} \operatorname{dist}\bigl(\bigl(S_{1}(t),E_{1}(t),I_{1}(t),R_{1}(t), \ldots,S_{k_{\max}} (t),E_{k_{\max}} (t),I_{k_{\max}} (t),R_{k_{\max}} (t)\bigr),E_{0}\bigr) > 0, $$

where \((S_{1}(t),E_{1}(t),I_{1}(t),R_{1}(t), \ldots,S_{k_{\max}} (t),E_{k_{\max}} (t),I_{k_{\max}} (t),R_{k_{\max}} (t))\) is an arbitrary solution with initial value in \(X_{0}\). In order to use the method of Leenheer and Smith [31], we need only to prove \(W^{s}(E_{0}) \cap X_{0} = \emptyset\), where \(W^{s}(E_{0})\) is the stable manifold of \(E_{0}\). Assume it is not sure, then there exists a solution \((S_{1}(t),E_{1}(t),I_{1}(t),R_{1}(t), \ldots,S_{k_{\max}} (t),E_{k_{\max}} (t), I_{k_{\max}} (t),R_{k_{\max}} (t))\) in \(X_{0}\), such that

$$ S_{k}(t) \to \eta_{k},\qquad E_{k}(t) \to 0 , \qquad I_{k}(t) \to 0,\qquad R_{k}(t) \to 0\quad \mbox{as } t \to \infty. $$
(4.6)

According to \(R_{0} = \frac{b\beta}{\mu [ (\gamma + \varepsilon + \mu )(\beta + \delta + \mu ) - \beta \varepsilon ]}\frac{ \langle \lambda (k)\varphi (k) \rangle}{ \langle k \rangle} > 1\), we have

$$\sum_{k} \frac{\lambda (k)\varphi (k)P(k)}{ \langle k \rangle \eta_{k}}\eta_{k} > \frac{\mu [ (\gamma + \varepsilon + \mu )(\beta + \delta + \mu ) - \beta \varepsilon ]}{b\beta}. $$

Then we can choose sufficiently small \(\xi > 0\) such that

$$ \biggl\langle \frac{\lambda (k)\varphi (k)}{ \langle k \rangle \eta_{k}}(\eta_{k} - \xi ) \biggr\rangle > \frac{\mu [ (\gamma + \varepsilon + \mu )(\beta + \delta + \mu ) - \beta \varepsilon ]}{b\beta}. $$
(4.7)

Since \(\xi > 0\), by (4.6) there exists a constant \(T > 0\) such that

$$ \frac{b}{\mu} - \xi < S_{k}(t) < \frac{b}{\mu} + \xi,\qquad 0 < E_{k}(t) < \xi,\qquad 0 < I_{k}(t) < \xi,\qquad 0 < R_{k}(t) < \xi $$
(4.8)

for all \(t \ge T\) and \(k = 1, 2, \ldots, k_{\max} \).

The derivative of \(V(t) = \sum_{k} \frac{\varphi (k)}{\eta_{k}} [ P(k)E_{k}(t) + \frac{(\beta + \mu )}{\beta h}I_{k}(t) ]\) along the solution of system (2.2) is given by

$$\begin{aligned} V'(t) ={}& \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k) \biggl( E'_{k}(t) + \frac{(\beta + \mu )}{\beta h}I'_{k}(t) \biggr) \\ ={}& \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k) \biggl( \lambda (k)\Theta (t)S_{k}(t) + \delta mI_{k}(t) - \frac{(\beta + \mu )(\delta + \mu )}{\beta h}I_{k}(t) \biggr) \\ ={}& \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k) \biggl( \lambda (k)\Theta (t)S_{k}(t) + \frac{\delta m\beta h - (\beta + \mu )(\delta + \mu )}{\beta h}I_{k}(t) \biggr) \\ >{}& \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k) \biggl( \lambda (k)\Theta (t) ( \eta_{k} - \xi ) + \frac{\delta m\beta h - (\beta + \mu )(\delta + \mu )}{\beta h}I_{k}(t) \biggr) \\ ={}& \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k) \biggl( \frac{\lambda (k) ( \eta_{k} - \xi )}{ \langle k \rangle} \sum_{i} \frac{\varphi (i)}{\eta_{i}}P(i)I_{i}(t) \biggr) \\ &+ \frac{\delta m\beta h - (\beta + \mu )(\delta + \mu )}{\beta h}\sum_{i} \frac{\varphi (i)}{\eta_{i}}P(i)I_{i}(t) \\ ={}& \biggl\langle \frac{\varphi (k)\lambda (k)}{\eta_{k} \langle k \rangle} ( \eta_{k} - \xi ) \biggr\rangle \sum_{i = 1} \frac{\varphi (i)}{\eta_{i}}P(i)I_{i}(t) + \frac{\delta m\beta h - (\beta + \mu )(\delta + \mu )}{\beta h}\sum_{i} \frac{\varphi (i)}{\eta_{i}}P(i)I_{i}(t) \\ ={}& \sum_{i = 1} \biggl[ \biggl\langle \frac{\varphi (k)\lambda (k)}{\eta_{k} \langle k \rangle} ( \eta_{k} - \xi ) \biggr\rangle - \frac{(\beta + \mu )(\delta + \mu ) - \beta h\delta m}{\beta h} \biggr]\frac{\varphi (i)}{\eta_{i}}P(i)I_{i}(t) \\ >{}& 0. \end{aligned}$$

Consequently, \(V(t) \to \infty\) as \(t \to \infty\), which apparently contradicts the boundedness of \(V(t)\). This completes the proof. □

Lemma 1

[32]

If \(a > 0\), \(b > 0\) and \(\frac{dx(t)}{dt} \ge b - ax\), when \(t \ge 0\) and \(x(0) \ge 0\), we can obtain \(\lim \inf_{t \to + \infty} x(t) \ge \frac{b}{a}\). If \(a > 0, b > 0\) and \(\frac{dx(t)}{dt} \le b - ax\), when \(t \ge 0\) and \(x(0) \ge 0\), we can obtain \(\lim \sup_{t \to + \infty} x(t) \le \frac{b}{a}\).

Next, by using a novel monotone iterative technique in reference [33], we discuss the global attractivity of the rumor-prevailing equilibrium.

Theorem 5

Suppose that \(( S_{k}(t),E_{k}(t),I_{k}(t),R_{k}(t) )\) is a solution of system (2.2), satisfying the initial condition equation (2.5). When \(R_{0} > 1\), then \(\lim_{t \to \infty} ( S_{k}(t),E_{k}(t),I_{k}(t),R_{k}(t) ) = ( S_{k}^{\infty},E_{k}^{\infty},I_{k}^{\infty},R_{k}^{\infty} )\), where \(( S_{k}^{\infty},E_{k}^{\infty},I_{k}^{\infty},R_{k}^{\infty} )\) is the unique positive rumor equilibrium of system (2.2) satisfying (3.1) for \(k = 1, 2, \ldots,n\).

Proof

Since the first three equations in system (2.2) are independent of the fourth one, it suffices to consider the following system:

$$ \left \{ \textstyle\begin{array}{l} \frac{dS_{k}(t)}{dt} = b(k) - \lambda (k)\Theta (t)S_{k}(t) - \mu S_{k}(t), \\ \frac{dE_{k}(t)}{dt} = \lambda (k)\Theta (t)S_{k}(t) - (\beta + \mu )E_{k}(t) + \delta mI_{k}(t), \\ \frac{dI_{k}(t)}{dt} = \beta hE_{k}(t) - (\delta + \mu )I_{k}(t). \end{array}\displaystyle \right . $$
(4.9)

We assume that k is fixed to be any integer in \(\{ 1, 2, \ldots,n \}\). By Theorem 4, there exist a positive constant \(0 < \varepsilon < 1 / 3\) and a large enough constant \(T > 0\) such that \(I_{k}(t) \ge \varepsilon\) for \(t > T\). Hence,

$$\Theta (t) = \frac{1}{ \langle k \rangle} \sum_{i = 1} \frac{\varphi (i)}{\eta_{i}}P(i)I_{i}(t) \ge \frac{1}{ \langle k \rangle} \frac{\varphi (i_{0})P(i_{0})}{\eta_{i_{0}}} \varepsilon = \vartheta \varepsilon > 0, $$

where \(\vartheta = \frac{1}{ \langle k \rangle} \frac{\varphi (i_{0})P(i_{0})}{\eta_{i_{0}}}\). From the first equation of system (4.9), we have

$$\frac{dS_{k}(t)}{dt} \le b(k) - \lambda (k)\vartheta \varepsilon S_{k}(t) - \mu S_{k}(t),\quad t > T. $$

By Lemma 1, we derive that \(\lim \sup_{t \to + \infty} S_{k}(t) \le \frac{\mu \eta_{k}}{\lambda (k)\vartheta \varepsilon + \mu} \). Then, for arbitrarily given positive constant \(0 < \varepsilon_{1} < \frac{\lambda (k)\vartheta \varepsilon \eta_{k}}{2 ( \lambda (k)\vartheta \varepsilon + \mu )}\), there exists a \(t_{1} > T\) such that \(S_{k}(t) \le X_{k}^{(1)} - \varepsilon_{1}\) for \(t > t_{1}\), where

$$X_{k}^{(1)} = \frac{\mu \eta_{k}}{\lambda (k)\vartheta \varepsilon + \mu} + 2\varepsilon_{1} < \eta_{k}. $$

For \(\Theta (t) \le \frac{1}{ \langle k \rangle} \sum_{i = 1} \varphi (i)P(i) = M\), from the second equation of system (4.9) for \(t > t_{1}\), we can get

$$\begin{aligned} \frac{dE_{k}(t)}{dt} \le{}& \lambda (k)M\bigl(\eta_{k} - E_{k}(k) - I_{k}(k) - R_{k}(k)\bigr) - (\beta + \mu )E_{k}(t) \\ & + \delta m\bigl(\eta_{k} - E_{k}(k) - S_{k}(k) - R_{k}(k)\bigr) \\ \le{}& \lambda (k)M\bigl(\eta_{k} - E_{k}(k)\bigr) - ( \beta + \mu )E_{k}(t) + \delta m\bigl(\eta_{k} - E_{k}(k)\bigr) \\ ={}& \eta_{k} \bigl[ \lambda (k)M + \delta m \bigr] - E_{k}(k) \bigl[ \lambda (k)M + \delta m + \beta + \mu \bigr]. \end{aligned} $$

Similarly, for arbitrary given positive constant \(0 < \varepsilon_{2} < \min \{ 1 / 2,\varepsilon_{1},\frac{ ( \delta m + \beta + \mu )\eta_{k}}{2 ( \lambda (k)M + \delta m + \beta + \mu )} \}\), there exists a \(t_{2} > t_{1}\), such that \(E_{k}(t) \le Y_{k}^{(1)} - \varepsilon_{2}\) for \(t > t_{2}\), where

$$Y_{k}^{(1)} = \frac{\lambda (k)M\eta_{k}}{\lambda (k)M + \delta m + \beta + \mu} + 2\varepsilon_{2} < \eta_{k}. $$

From the third equation of system (4.9), we have

$$\frac{dI_{k}(t)}{dt} \le \beta h\bigl(\eta_{k} - I_{k}(t) \bigr) - (\delta + \mu )I_{k}(t) = \beta h\eta_{k} - (\delta + \mu + \beta h)I_{k}(t),\quad t > t_{2}. $$

Thus, for arbitrary given positive constant \(0 < \varepsilon_{3} < \min \{ 1 / 3,\varepsilon_{2},\frac{(\mu + \beta h)\eta_{k}}{2 ( \delta + \mu + \beta h )} \}\), there exists a \(t_{3} > t_{2}\), such that \(I_{k}(t) \le Z_{k}^{(1)} - \varepsilon_{3}\) for \(t > t_{3}\), where

$$Z_{k}^{(1)} = \frac{\delta \eta_{k}}{ ( \delta + \mu + \beta h )} + 2\varepsilon_{3} < \eta_{k}. $$

On the other hand, from the first equation of system (4.9), we can get

$$\frac{dS_{k}(t)}{dt} \ge b(k) - \lambda (k)MS_{k}(t) - \mu S_{k}(t),\quad t > T. $$

By Lemma 1, we derive that \(\lim \inf_{t \to + \infty} S_{k}(t) \ge \frac{b(k)}{\lambda (k)M + \mu} \). Then, for arbitrary given positive constant \(0 < \varepsilon_{4} < \min \{ 1 / 4,\varepsilon_{3},\frac{b(k)}{2 [ \lambda (k)M + \mu ]} \}\), there exists a \(t_{4} > t_{3}\), such that \(S_{k}(t) \ge x_{k}^{(1)} + \varepsilon_{4}\), for \(t > t_{4}\), where

$$x_{k}^{(1)} = \frac{b(k)}{\lambda (k)M + \mu} - 2\varepsilon_{4} > 0. $$

It follows that

$$\frac{dE_{k}(t)}{dt} \ge \lambda (k)\vartheta \varepsilon x_{k}^{(1)} + \delta m\eta_{k} - (\beta + \mu + \delta m)E_{k}(t),\quad t > t_{4}. $$

Hence, for arbitrary given positive constant \(0 < \varepsilon_{5} < \min \{ 1 / 5,\varepsilon_{4},\frac{\lambda (k)\vartheta \varepsilon x_{k}^{(1)} + \delta m\eta_{k}}{2(\beta + \mu + \delta m)} \}\), there exists a \(t_{5} > t_{4}\), such that \(E_{k}(t) \ge y_{k}^{(1)} + \varepsilon_{5}\) for \(t > t_{5}\), where

$$y_{k}^{(1)} = \frac{\lambda (k)\vartheta \varepsilon x_{k}^{(1)} + \delta m\eta_{k}}{(\beta + \mu + \delta m)} - 2\varepsilon_{5} > 0. $$

Then

$$\frac{dI_{k}(t)}{dt} \ge \beta hy_{k}^{(1)} - (\delta + \mu )I_{k}(t),\quad t > t_{5}. $$

Hence, for arbitrary given positive constant \(0 < \varepsilon_{6} < \min \{ 1 / 6,\varepsilon_{5},\frac{\beta hy_{k}^{(1)}}{2(\delta + \mu )} \}\), there exists a \(t_{6} > t_{5}\), such that \(I_{k}(t) \ge z_{k}^{(1)} + \varepsilon_{6}\) for \(t > t_{6}\), where

$$z_{k}^{(1)} = \frac{\beta hy_{k}^{(1)}}{(\delta + \mu )} - 2\varepsilon_{6} > 0. $$

Since ε is a small positive constant, we have \(0 < x_{k}^{(1)} < X_{k}^{(1)} < \eta_{k}\), \(0 < y_{k}^{(1)} < Y_{k}^{(1)} < \eta_{k}\) and \(0 < z_{k}^{(1)} < Z_{k}^{(1)} < \eta_{k}\). Let

$$w^{(j)} = \frac{1}{ \langle k \rangle} \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k)z_{k}^{j}(t),\qquad W^{(j)} = \frac{1}{ \langle k \rangle} \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k)Z_{k}^{j}(t), \quad j = 1,2 \ldots. $$

From the above discussion, we found that

$$0 < w^{(1)} \le \Theta (t) \le W^{(1)} < M,\quad t > t_{6}. $$

Again, by system (4.9), we have

$$\frac{dS_{k}(t)}{dt} \le b(k) - \lambda (k)w^{(1)}S_{k}(t) - \mu S_{k}(t),\quad t > t_{6}. $$

Hence, for arbitrary given positive constant \(0 < \varepsilon_{7} < \min \{ 1 / 7,\varepsilon_{6} \}\), there exists a \(t_{7} > t_{6}\) such that

$$S_{k}(t) \le X_{k}^{(2)} \triangleq \min \biggl\{ X_{k}^{(1)} - \varepsilon_{1},\frac{b(k)}{\lambda (k)w^{(1)} + \mu} + \varepsilon_{7} \biggr\} ,\quad t > t_{7}. $$

Thus,

$$\frac{dE_{k}(t)}{dt} \le \lambda (k)W^{(1)}X_{k}^{(2)} + \delta mZ_{k}^{(1)} - (\beta + \mu )E_{k}(t), \quad t > t_{7}. $$

Therefore, for arbitrary given positive constant \(0 < \varepsilon_{8} < \min \{ 1 / 8,\varepsilon_{7} \}\), there exists a \({t_{8} > t_{7}}\), such that

$$E_{k}(t) \le Y_{k}^{(2)} \triangleq \min \biggl\{ Y_{k}^{(1)} - \varepsilon_{2},\frac{\lambda (k)W^{(1)}X_{k}^{(2)} + \delta mZ_{k}^{(1)}}{(\beta + \mu )} + \varepsilon_{8} \biggr\} . $$

It follows that

$$\frac{dI_{k}(t)}{dt} \le \beta hY_{k}^{(2)} - (\delta + \mu )I_{k}(t),\quad t > t_{8}. $$

So, for arbitrary given positive constant \(0 < \varepsilon_{9} < \min \{ 1 / 9,\varepsilon_{8} \}\), there exists a \(t_{9} > t_{8}\), such that

$$I_{k}(t) \le Z_{k}^{(2)} \triangleq \min \biggl\{ Z_{k}^{(1)} - \varepsilon_{3},\frac{\beta hY_{k}^{(2)}}{(\delta + \mu )} + \varepsilon_{9} \biggr\} ,\quad t > t_{9}. $$

Turning back to system (4.9), we have

$$\frac{dS_{k}(t)}{dt} \ge b(k) - \lambda (k)W^{(2)}S_{k}(t) - \mu S_{k}(t),\quad t > t_{9}. $$

Hence, for arbitrary given positive constant \(0 < \varepsilon_{10} < \min \{ 1 / 10,\varepsilon_{9},\frac{b(k)}{2 ( \lambda (k)W^{(2)} + \mu )} \}\), there exists a \(t_{10} > t_{9}\), such that \(S_{k}(t) \ge x_{k}^{(2)} + \varepsilon_{10}\) for \(t > t_{10}\), where

$$x_{k}^{(2)} = \max \biggl\{ x_{k}^{(1)} + \varepsilon_{4},\frac{b(k)}{\lambda (k)W^{(2)} + \mu} - 2\varepsilon_{10} \biggr\} . $$

Accordingly, one obtains

$$\frac{dE_{k}(t)}{dt} \ge \lambda (k)w^{(1)}x_{k}^{(2)} + \delta mz_{k}^{(1)} - (\beta + \mu )E_{k}(t), \quad t > t_{10}. $$

Hence, for arbitrary given positive constant \(0 < \varepsilon_{11} < \min \{ 1 / 11,\varepsilon_{10},\frac{\lambda (k)w^{(1)}x_{k}^{(2)} + \delta mz_{k}^{(1)}}{2(\beta + \mu )} \}\), there exists a \(t_{11} > t_{10}\), such that \(E_{k}(t) \ge y_{k}^{(2)} + \varepsilon_{11}\) for \(t > t_{11}\), where

$$y_{k}^{(2)} = \max \biggl\{ y_{k}^{(1)} + \varepsilon_{5},\frac{\lambda (k)w^{(1)}x_{k}^{(2)} + \delta mz_{k}^{(1)}}{(\beta + \mu )} - 2\varepsilon_{11} \biggr\} . $$

Thus,

$$\frac{dI_{k}(t)}{dt} \ge \beta hy_{k}^{(2)} - (\delta + \mu )I_{k}(t),\quad t > t_{11}. $$

Hence, for arbitrary given positive constant \(0 < \varepsilon_{12} < \min \{ 1 / 12,\varepsilon_{11},\frac{\beta hy_{k}^{(2)}}{2(\delta + \mu )} \}\), there exists a \(t_{12} > t_{11}\), such that \(I_{k}(t) \ge z_{k}^{(2)} + \varepsilon_{12}\) for \(t > t_{12}\), where

$$z_{k}^{(2)} = \max \biggl\{ z_{k}^{(1)} + \varepsilon_{6},\frac{\beta hy_{k}^{(2)}}{(\delta + \mu )} - 2\varepsilon_{12} \biggr\} . $$

In the same way, we can carry out step h (\(h = 3,4, \ldots \)) of the calculation and get six sequences: \(\{ X_{k}^{(h)} \}\), \(\{ Y_{k}^{(h)} \}\), \(\{ Z_{k}^{(h)} \}\), \(\{ x_{k}^{(h)} \}\), \(\{ y_{k}^{(h)} \}\) and \(\{ z_{k}^{(h)} \}\). We found that the first three sequences are monotone increasing and the last three sequences are strictly monotone decreasing, and there exists a large positive integer N so that for \(h \ge \mathrm{N}\)

$$ \begin{gathered} X_{k}^{(h)} = \frac{b(k)}{\lambda (k)w^{(h - 1)} + \mu} + \varepsilon_{6h - 5}, \\ Y_{k}^{(h)} = \frac{\lambda (k)W^{(h - 1)}X_{k}^{(h)} + \delta mZ_{k}^{(h - 1)}}{(\beta + \mu )} + \varepsilon_{6h - 4}, \\ Z_{k}^{(h)} = \frac{\beta hY_{k}^{(h)}}{(\delta + \mu )} + \varepsilon_{6h - 3}, \\ x_{k}^{(h)} = \frac{b(k)}{\lambda (k)W^{(h)} + \mu} - 2\varepsilon_{6h - 2}, \\ y_{k}^{(h)} = \frac{\lambda (k)w^{(h - 1)}x_{k}^{(h)} + \delta mz_{k}^{(1 - 1)}}{(\beta + \mu )} - 2\varepsilon_{6h - 1}, \\ z_{k}^{(h)} = \frac{\beta hy_{k}^{(h)}}{(\delta + \mu )} - 2\varepsilon_{6h}. \end{gathered} $$
(4.10)

Clearly, we found that

$$ x_{k}^{(h)} \le S_{k}(t) \le X_{k}^{(h)}, \qquad y_{k}^{(h)} \le E_{k}(t) \le Y_{k}^{(h)},\qquad z_{k}^{(h)} \le I_{k}(t) \le Z_{k}^{(h)},\quad t > t_{6h}. $$
(4.11)

Owing to the existence of sequential limits of equation (4.10), let \(\lim_{t \to \infty} \Omega_{k}^{(h)} = \Omega_{k}\), where \(\Omega_{k}^{(h)} \in \{ X_{k}^{(h)},Y_{k}^{(h)},Z_{k}^{(h)},x_{k}^{(h)},y_{k}^{(h)},z_{k}^{(h)},W_{k}^{(h)},w_{k}^{(h)} \}\) and \(\Omega_{k} \in \{ X_{k},Y_{k},Z_{k},x_{k},y_{k},z_{k},W_{k},w_{k} \}\).

For \(0 < \varepsilon_{h} < 1 / h\), one has \(\varepsilon_{h} \to 0\) as \(h \to \infty\). Taking \(h \to \infty\), by calculating the six sequences of equation (4.10), we can obtain the following form

$$ \begin{gathered} X_{k} = \frac{b(k)}{\lambda (k)w + \mu},\qquad Y_{k} = \frac{\lambda (k)WX_{k} + \delta mZ_{k}}{(\beta + \mu )},\qquad Z_{k} = \frac{\beta hY_{k}}{(\delta + \mu )}, \\ x_{k} = \frac{b(k)}{\lambda (k)W + \mu},\qquad y_{k} = \frac{\lambda (k)wx_{k} + \delta mz_{k}}{(\beta + \mu )},\qquad z_{k} = \frac{\beta hy_{k}}{(\delta + \mu )}. \end{gathered} $$
(4.12)

From equation (4.12), a direct computation leads to

$$ \begin{gathered} Z_{k} = \frac{\beta h\lambda (k)W}{ [ (\delta + \mu )(\beta + \mu ) - \beta h\delta m ]}\frac{b(k)}{\lambda (k)w + \mu}, \\ z_{k} = \frac{\beta h\lambda (k)w}{ [ (\delta + \mu )(\beta + \mu ) - \beta h\delta m ]}\frac{b(k)}{\lambda (k)W + \mu}, \end{gathered} $$
(4.13)

where \(w = \frac{1}{ \langle k \rangle} \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k)z_{k}\), \(W = \frac{1}{ \langle k \rangle} \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k)Z_{k}\).

Further, substituting equation (4.13) into w and W, respectively, we can obtain

$$ \begin{gathered} 1 = \frac{1}{ \langle k \rangle} \frac{\beta h}{ [ (\delta + \mu )(\beta + \mu ) - \beta h\delta m ]}\sum _{k} \frac{\varphi (k)}{\eta_{k}}\frac{P(k)\lambda (k)b(k)}{\lambda (k)W + \mu}, \\ 1 = \frac{1}{ \langle k \rangle} \frac{\beta h}{ [ (\delta + \mu )(\beta + \mu ) - \beta h\delta m ]}\sum_{k} \frac{\varphi (k)}{\eta_{k}}\frac{P(k)\lambda (k)b(k)}{\lambda (k)w + \mu}. \end{gathered} $$
(4.14)

Subtracting the above two equations, a direct computation leads to

$$0 = (w - W)\frac{1}{ \langle k \rangle} \frac{\beta h}{ [ (\delta + \mu )(\beta + \mu ) - \beta h\delta m ]}\sum _{k} \frac{\varphi (k)}{\eta_{k}}\frac{P(k)\lambda (k)b(k)\lambda (k)}{(\lambda (k)W + \mu )(\lambda (k)w + \mu )}. $$

Obviously, it implies that \(w = W\). So, \(\frac{1}{ \langle k \rangle} \sum_{k} \frac{\varphi (k)}{\eta_{k}}P(k) ( Z_{k} - z_{k} ) = 0\), which is equivalent to \(z_{k} = Z_{k}\) for \(1 \le k \le n\). Then, from equation (4.12) and equation (4.13), it follows that

$$\lim_{t \to 0}S_{k}(t) = X_{k} = x_{k},\qquad \lim_{t \to 0}E_{k}(t) = Y_{k} = y_{k},\qquad \lim_{t \to 0}I_{k}(t) = Z_{k} = z_{k}. $$

Finally, by substituting \(w = W\) into equation (4.13), in view of equation (3.1) and equation (4.12), it is found that \(X_{k} = S_{k}^{\infty} \), \(Y_{k} = E_{k}^{\infty} \), \(Z_{k} = R_{k}^{\infty} \). This completes the proof. □

5 Conclusions

In this paper, a new SEIR rumor spreading model with demographics on scale-free networks is presented. Through the mean-field theory analysis, we obtained the basic reproduction number \(R_{0}\) and the equilibria. The basic reproduction number \(R_{0}\) determines the existence of the rumor-prevailing equilibrium, and it depends on the topology of the underlying networks and some model parameters. Interestingly, \(R_{0}\) bears no relation to the degree-dependent immigration \(b(k)\). When \(R_{0} < 1\), the rumor-free equilibrium \(E_{0}\) is globally asymptotically stable, i.e., the infected individuals will eventually disappear. When \(R_{0} > 1\), there exists a unique rumor-prevailing \(E_{ +} \), and the rumor is permanent, i.e., the infected individuals will persist and we have convergence to a uniquely prevailing equilibrium level. The study may provide a reliable tactic basis for preventing the rumor spreading.