Abstract
In this paper, based on gauge transformation of Lax pairs, we construct an N-fold Darboux transformation for the discrete Ragnisco–Tu equation which is a typical member in the Ragnisco–Tu hierarchy. By using the N-fold Darboux transformation, new multi-soliton solutions of the discrete Ragnisco–Tu equation can be directly constructed starting from a seed solution.
Similar content being viewed by others
1 Introduction
It is well known that constructing explicit solutions for an integrable system, whether continuous or discrete, plays an important role in describing and explaining nonlinear phenomena such as nonlinear optics effect, fusion reaction in plasma physics, superconduction phenomenon, magnetohydrodynamic phenomenology, etc. Furthermore, the investigation of integrable discrete systems and their related properties has always been important and has become a focus of recent research. In recent years, a great deal of progress has been made on the theory of discrete integrable systems. Lots of important nonlinear integrable differential-difference equations have been obtained [1–12]. In particular, constructing exact solutions for a differential-difference equation is one of the most fundamental and significant topics. There are some methods to construct solutions such as the inverse scattering transform method [13], the bilinear transformation method of Hirota [14], the Bäcklund and Darboux transformation techniques [15, 16], the Fokas unified approach [17], the long-time asymptotics approach [18], and so on. Among them, the Darboux transformation is the most effective technique to find explicit solutions of the integrable differential-difference equations [10, 11, 17–26]. This method based on Lax pairs has been proven to be one of the most fruitful algorithmic procedures to get explicit solutions of nonlinear evolution equations. In this paper, we construct an N-Fold Darboux transformation of Lax pair of the discrete Ragnisco–Tu equation, new multi-soliton solutions can be directly constructed starting from a seed solution.
The main purpose of the present paper is to construct the N-fold Darboux transformation of the following discrete Ragnisco–Tu equation [27, 28]:
where \(u_{n}\), \(v_{n}\) are two potentials. System (1) is a member of the Ragnisco–Tu hierarchy and admits the following Lax pair:
where the shift operator E is defined as
and λ is the spectral parameter and \(\lambda_{t} = 0\). System (1) can be obtained from the following discrete zero-curvature equation:
Therefore, in this paper, we construct the N-fold Darboux transformation for Eq. (1). Outline of this paper is organized as follows. In Sect. 2, based on its Lax pairs, the N-fold Darboux transformation is constructed for Eq. (1). In Sect. 3, as one of the applications of the N-fold Darboux transformation, we give some exact solutions of Eq. (1). Conclusions are made in the last section.
2 N-Fold DT of Ragnisco–Tu system
At present, much work has been done on a single Darboux transformation (DT) of the Lax integrable nonlinear integrable systems [29–32]. Here we would like to construct an N-fold DT for the Ragnisco–Tu system (1). For this purpose, we search for the following gauge transformation:
which can change the Lax pair (2) and (3) into
with
To make \(\widetilde{U}_{n}\), \(\widetilde{V}_{n}\) and \(U_{n}\), \(V_{n}\) have the same form respectively, we take \(\phi_{n}=(\phi_{1n},\phi_{2n})^{T}\), \(\varphi_{n}=(\varphi_{1n},\varphi_{2n})^{T}\) as two basic solutions of the Lax pair (2) and (3) and define a \(2\times2\) matrix \(T_{n}\) by
where \(T_{11}\), \(T_{12}\), \(T_{21}\), \(T_{22}\) depend on variables n and t:
and \(T_{i}^{11}(n)\), \(T_{i}^{12}\), \(T_{i}^{21}(n)\), \(T_{i}^{22}(n)\) can be determined by the following linear algebraic system:
with
\(\lambda_{j}\) and \(\gamma_{j}\) (\(\lambda_{j}\neq\lambda_{k}\), \(\gamma_{j}\neq\gamma _{k}\), as \({k}\neq{j}\)) are some parameters suitably chosen such that the determinants of coefficients for system (8) are nonzero.
From (7)–(9), it is easy to see that
where \(\operatorname{det}T_{n}\) is a \((2N)\)th-degree polynomial in λ.
On the other hand, from (8) we have
Therefore,
which implies that \(\lambda_{j}\) (\(1\leq j \leq2N\)) are 2N roots of \(\operatorname{det}T_{n}\), that is,
By using the above fact, we can prove the following proposition.
Proposition 1
The matrix \(\widetilde{U}_{n}\) defined by (5) has the same form as \(U_{n}\), that is,
in which the transformation formulae between old and new potentials are defined by
the transformation \((\psi_{n},u_{n},v_{n})\rightarrow(\tilde{\psi}_{n},\tilde{u}_{n},\tilde{v}_{n})\) is usually called a DT of the spectral problem (2).
Proof
Let \(T_{n}^{-1}=T_{n}^{*}/\operatorname{det}T_{n}\) and
It is easy to see that \(f_{11}(\lambda,n)\) and \(f_{22}(\lambda,n)\) are \((2N+1)\)th-degree polynomials in λ, \(f_{12}(\lambda,n)\) and \(f_{21}(\lambda,n)\) are 2Nth-degree polynomials in λ, respectively. From (2) and (9), we can find that
where \(\mu_{j}(n)=v_{n}+\alpha_{j}(n)\), \(\nu_{j}(n)=\lambda_{j}+u_{n}v_{n}+u_{n}\alpha _{j}(n)\) (\(j=1,2,\ldots,2N\)).
By virtue of (11) and (13), it can be verified that \(\lambda_{j}\) (\(j=1,2,\ldots,2N\)) are roots of \(f_{k,l}(\lambda ,n)\) (\(k,l=1,2\)). Again noticing (8), we can conclude that
Therefore, we have
where \(p_{ij}^{(l)}\) (\(i,j=1,2\); \(l=0,1\)) are independent of λ. At the same time, the above equation can be rewritten as
By comparing the coefficients of \(\lambda^{N+1}\), \(\lambda^{N}\) in (14), we obtain
Thus we complete the proof. □
Proposition 2
Under transformation (4), the matrix \(\tilde{V}_{n}\) defined by (5) has the same form as \(V_{n}\), that is,
the old potentials \(u_{n}\) and \(v_{n}\) are mapped into new \(\tilde{u}_{n}\) and \(\tilde{v}_{n}\) according to the same DT Eq. (4).
Proof
Let \(T_{n}^{-1}=T_{n}^{*}/\operatorname{det}T_{n}\) and
With a direct calculation we know that \(g_{11}(\lambda ,n)\), \(g_{22}(\lambda,n)\) or \(g_{12}(\lambda,n)\), \(g_{21}(\lambda,n)\) are \((2N+1)\)th or 2Nth polynomials in λ, respectively. It can be checked that \(\lambda _{j}\) (\(j=1,2,\ldots,2N\)) are roots of \(g_{k,l}(\lambda,n)\) (\(k,l=1,2\)). And the matrix \((T_{nt}+T_{n}V_{n})T_{n}^{*}\) is written as
namely
where \(r_{ij}^{l}\) (\(i,j=1,2\); \(l=0,1\)) are independent of λ. Comparing the coefficients of \(\lambda^{i}\) (\(i=N+1,N,N-1\)) in Eq. (15), we gain the following formulas:
The proof is thus completed. □
From the fact of equivalence between differential-difference Eq. (5) and the discrete zero-curvature equation \(\tilde{U}_{nt}-\tilde{V}_{n+1}\tilde{U}_{n}+\tilde{U}_{n}\tilde{V}_{n}=0\), with the help of Proposition 1 and Proposition 2, we obtain the following proposition.
Theorem 1
The solutions \((u_{n},v_{n})\) of the Ragnisco–Tu system (1) are mapped into new solutions \((\tilde{u}_{n},\tilde{v}_{n})\) under the N-fold DT (4) and (12): \((\psi_{n},u_{n},v_{n})\rightarrow(\tilde{\psi}_{n},\tilde{u}_{n},\tilde{v}_{n})\).
3 Applications of DT and exact solutions
In this section, we will give some exact solutions of the Ragnisco–Tu system (1) via transformations (4) and (12). Substituting the trivial solution \(u_{n}=1\), \(v_{n}=1\) into the Lax pair (2) and (3), we can give two real basic solutions as follows:
According to (9), we have
where \(\triangledown_{i}=\frac{(\lambda_{i}+2+\sqrt{\lambda _{i}^{2}+4})^{2n}}{(4\lambda_{i})^{n}}\operatorname{exp}(\sqrt{\lambda_{i}^{2}+4}t)\), \(i=1,2,\ldots,2N\).
Solving the linear algebraic system (8) by using Cramer’s rule, we have
with
and \(\Delta T_{N-i}^{11}(n)\) is produced from \(\Delta_{1}\) by replacing its ith column with \((-\lambda_{1}^{N},-\lambda_{2}^{N},\ldots,-\lambda _{2N}^{N})\), \(\Delta T_{N-i}^{12}(n)\) is produced from \(\Delta_{1}\) by replacing its \((N+i)\)th column with \((-\lambda_{1}^{N},-\lambda_{2}^{N},\ldots ,-\lambda_{2N}^{N})\) where \(i=1,2,\ldots,N\). Similarly, we have
with
and \(\Delta T_{N-i}^{21}(n)\) is produced from \(\Delta_{2}\) by replacing its ith column with \((-\alpha_{1}\lambda_{1}^{N},-\alpha_{2}\lambda _{2}^{N},\ldots, -\alpha_{2N}\lambda_{2N}^{N})\), \(\Delta T_{N-i}^{22}(n)\) is produced from \(\Delta_{2}\) by replacing its \((N+i)\)th column with \((-\alpha_{1}\lambda_{1}^{N}, -\alpha_{2}\lambda_{2}^{N},\ldots,-\alpha_{2N}\lambda _{2N}^{N})\), where \(i=1,2,\ldots,N\).
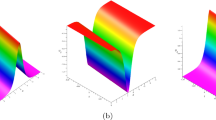
On the basis of (19) and (20), we can derive a new solution to system (1), here we discus three cases when \(N=1, 2, 3\).
(I) When \(N=1\), let \(\lambda=\lambda_{i}\) (\(i=1,2\)). Solving the linear system (8) leads to
with
Hence, an explicit solution of Eq. (1) is obtained as follows:
where
and
where
(II) When \(N=2\), let \(\lambda=\lambda_{i}\) (\(i=1,2,3,4\)). Solving the linear system (8) leads to
with
Therefore, an explicit solution of Eq. (1) is obtained as follows:
and
(III) When \(N=3\), let \(\lambda=\lambda_{i}\) (\(i=1,2,3,4,5,6\)). Solving the linear system (8) leads to
with
Therefore, an explicit solution of Eq. (1) is obtained as follows:
and
4 Conclusions and remarks
In this paper, we have constructed the N-fold Darboux transformation for the discrete Ragnisco–Tu system. As an application of the N-fold Darboux transformation, we provide three explicit cases of the forms of the exact solutions when \(N=1\), \(N=2\), and \(N=3\). Moreover, if these resulting solutions are taken as new starting points, we may make a Darboux transformation once again and obtain another set of new explicit solutions. This process can be done continuously, and multi-soliton solutions will usually be obtained.
References
Ablowitz, M.J., Ladik, J.F.: On the solution of a class of nonlinear partial difference equation. Stud. Appl. Math. 57, 1–12 (1977)
Tu, G.Z.: A trace identity and its applications to the theory of discrete integrable systems. J. Phys. A, Math. Gen. 23, 3903–3922 (1990)
Ma, W.X.: Conservation laws by symmetries and adjoint symmetries. Discrete Contin. Dyn. Syst. 11, 707–721 (2018)
Ma, W.X., Zhou, Y.: Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J. Differ. Equ. 264, 2633–2659 (2018)
Wang, H.: Lump and interaction solutions to the \((2+1)\)-dimensional Burgers equation. Appl. Math. Lett. 85, 27–34 (2018)
Fu, C., Lu, C.N., Yang, H.W.: Time-space fractional \((2+1)\) dimensional nonlinear Schrödinger equation for envelope gravity waves in baroclinic atmosphere and conservation laws as well as exact solutions. Adv. Differ. Equ. 2018, 56 (2018)
Guo, M., Zhang, Y., Wang, M., Chen, Y.D., Yang, H.W.: A new ZK-ILW equation for algebraic gravity solitary waves in finite depth stratified atmosphere and the research of squall lines formation mechanism. Comput. Math. Appl. 75, 3589–3603 (2018)
Guo, M., Fu, C., Zhang, Y., Liu, J.X., Yang H.W.: Study of ion-acoustic solitary waves in a magnetized plasma using the three-dimensional time-space fractional Schamel-KdV equation. Complexity 2018, Article ID 6852548 (2018)
Tao, M.S., Dong, H.H.: Algebro-geometric solutions for a discrete integrable equation. Discrete Dyn. Nat. Soc. 2017, 1–9 (2017)
Chen, J.C., Ma, Z.Y., Hu, Y.H.: Nonlocal symmetry, Darboux transformation and soliton-cnoidal wave interaction solution for the shallow water wave equation. J. Math. Anal. Appl. 460, 987–1003 (2018)
Li, X.Y., Zhao, Q.L.: A new integrable symplectic map by the binary nonlinearization to the super AKNS system. J. Geom. Phys. 121, 123–137 (2017)
Zhao, Q.L., Li, X.Y.: A Bargmann system and the involutive solutions associated with a new 4-order lattice hierarchy. Anal. Math. Phys. 6(3), 237–254 (2016)
Ablowitz, M., Clarkson, P.: Solitons, Nonlinear Evolutions and Inverse Scattering. Cambridge University Press, Cambridge (1991)
Wang, D.S., Chen, F., Wen, X.Y.: Darboux transformation of the general Hirota equation: multisoliton solutions, breather solutions, and rogue wave solutions. Adv. Differ. Equ. 2016, 67 (2016)
Zhu, S.D., Song, J.F.: Residual symmetries, nth Bäcklund transformation and interaction solutions for \((2+1)\)-dimensional generalized Broer–Kaup equations. Appl. Math. Lett. 83, 33–39 (2018)
Wang, D.S., Yin, Y.B.: Symmetry analysis and reductions of the two-dimensional generalized Benney system via geometric approach. Comput. Math. Appl. 71, 748–757 (2016)
Zhang, N., Xia, T.C., Hu, B.B.: A Riemann–Hilbert approach to complex Sharma–Olver equation on half line. Commun. Theor. Phys. 68, 580–594 (2017)
Wang, D.S., Wang, X.L.: Long-time asymptotics and the bright N-soliton solutions of the Kundu–Eckhaus equation via the Riemann–Hilbert approach. Nonlinear Anal., Real World Appl. 41, 334–361 (2018)
Zhao, Q.L., Li, X.Y., Liu, F.S.: Two integrable lattice hierarchies and their respective Darboux transformations. Appl. Math. Comput. 219, 5693–5705 (2013)
Zhang, Y., Dong, H.H., Zhang, X.E., Yang, H.W.: Rational solutions and lump solutions to the generalized \((3 + 1)\)-dimensional shallow water-like equation. Comput. Math. Appl. 73, 246–252 (2017)
Yang, H.W., Xu, Z.H., Yang, D.Z., Feng, X.R., Yin, B.S., Dong, H.H.: ZK-Burgers equation for three-dimensional Rossby solitary waves and its solutions as well as chirp effect. Adv. Differ. Equ. 2016, 167 (2016)
Zhang, N., Xia, T.C.: A hierarchy of lattice soliton equations associated with a new discrete eigenvalue problem and Darboux transformations. Int. J. Nonlinear Sci. Numer. Simul. 16, 301–306 (2015)
Fan, E.G.: N-Fold Darboux transformation and soliton solutions for a nonlinear Dirac system. J. Phys. A 38, 1063–1069 (2005)
Fan, E.G.: Solving Kadomtsev–Petviashvili equation via a new decomposition and Darboux transformation. Commun. Theor. Phys. 37, 145–148 (2002)
Dong, H.H., Chen, T.T., Chen, L.F., Zhang, Y.: A new integrable symplectic map and the lie point symmetry associated with nonlinear lattice equations. J. Nonlinear Sci. Appl. 9, 5107–5118 (2016)
Xu, X.X., Sun, Y.P.: An integrable coupling hierarchy of Dirac integrable hierarchy, its Liouville integrability and Darboux transformation. J. Nonlinear Sci. Appl. 10, 3328–3343 (2017)
Xu, X.X., Sun, Y.P.: Two symmetry constraints for a generalized Dirac integrable hierarchy. J. Math. Anal. Appl. 458, 1073–1090 (2018)
Xu, X.X.: Solving an integrable coupling system of Merola–Ragnisco–Tu lattice equation by Darboux transformation of Lax pair. Commun. Nonlinear Sci. Numer. Simul. 23, 192–201 (2015)
Zhang, N., Xia, T.C.: A new negative discrete hierarchy and its N-fold Darboux transformation. Commun. Theor. Phys. 68(6), 687–692 (2017)
Zhang, W., Bai, Z.B., Sun, S.J.: Extremal solutions for some periodic fractional differential equations. Adv. Differ. Equ. 2016, 179 (2016)
Xu, X.X.: A deformed reduced semi-discrete Kaup–Newell equation, the related integrable family and Darboux transformation. Appl. Math. Comput. 251, 275–283 (2015)
Li, Q., Wang, D.S., Wen, X.Y., Zhuang, J.H.: An integrable lattice hierarchy based on Suris system: N-fold Darboux transformation and conservation laws. Nonlinear Dyn. 91, 625–639 (2018)
Funding
This work was supported by the Natural Science Foundation of China (Nos. 11271008; 61072147), the SDUST Research Fund (No.2018TDJH101), and the Natural Science Foundation of Shandong Province (Nos.ZR2018MA017; ZR2016AL04; ZR2016FL05; ZR2017MF039).
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, N., Xia, T. & Jin, Q. N-Fold Darboux transformation of the discrete Ragnisco–Tu system. Adv Differ Equ 2018, 302 (2018). https://doi.org/10.1186/s13662-018-1751-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1751-3