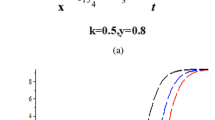1 Introduction

It is well known that envelope gravity waves play an important role in atmospheric dynamics [1–5], the troposphere is excited by convection, topography and other excitation processes to transfer energy and momentum from the source (e.g., mountains, thermal forcing) to the middle and upper atmosphere [6–9]. Atmospheric parameters, such as density and temperature, oscillate with fluctuations due to the influence of envelope gravity waves at the middle and upper atmosphere. In addition, the atmosphere is further achieved through the wave process of envelope gravity waves in actual atmospheric movement. Envelope gravity waves closely relate to the changes in the troposphere weather and climate, such as topographic precipitation, deep convection and typhoon rainstorms [10, 11].

The problem of propagation of nonlinear wave in plasma and fluid can be described by differential equations such as the KDV equation, the mKDV equation, the NLS equation, and the Boussinesq equation [12–20]. The NLS equation describes the time–space evolution of slow-changing envelopes, it has high theoretical value in quantum matters and has been extensively used in various branches of physics, such as optics, envelope gravity waves etc. [21, 22]. However, most of these studies are based on the integer-order model and the research on the fractional model is still relatively small. Fractional calculus is one of the best tools to investigate various scientific, engineering and mathematical models [23–25]. Numerous marine processes exhibit fractional dynamics, which are fractional systems. The use of fractional model can better reveal the nature of the phenomenon and behavior. Fractional calculus is the promotion of integral calculus. The study of fractional systems [26–31] has a more universal meaning. Thus we discuss the influence of fractional order for the propagation of envelope gravity waves by constructing the time–space fractional \((2+1)\) NLS equation.

Conservation laws are very important for the study of nonlinear physical phenomena, symmetry and conservation laws [32–35] provide much information as regards systems simulated by differential equations. Only a few scholars discuss the conservation laws of fractional partial differential equation, for example, the generalizations of Noether’s theorem [36], the new conservation theorem [37], the fractional generalized Noether operator [38], therefore, the conservation laws of the time–space nonlinear FPDES need further research. Moreover, there are many ways to solve differential equations such as the trial function method [39], the subequation method [40], the function variable method [41], the first integral method [42], etc. We can also get many other kinds of solutions, such as lump-soliton solutions [43–46], which are also very important.

The organization of the article is as follows: in Section 2, the integer-order model is derived by using the multiple-scale, perturbation method [47]. In Section 3, the fractional-order model is obtained by employing the semi-inverse method, Euler–Lagrange equation and Agrawal’s method [48, 49]. In Section 4, with the help of Lie group analysis method [50–52], the conservation laws of time–space FNLS equation will be discussed. In Section 5, we get the exact solutions to the above equation by using the \(\exp(-\phi(\xi))\) method [53]. In Section 6, some brief conclusions can be drawn.

2 Derivation of \((2+1)\) dimensional NLS equation

Starting with the basic dynamic equations of atmospheric motion, they can be written in the form

$$ \left\{ \textstyle\begin{array}{l} \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v \frac {\partial u}{\partial y}+w\frac{\partial u}{\partial z}=-\frac{1}{\rho _{0}}\frac{\partial p}{\partial x}+fv, \\ \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac {\partial v}{\partial y}+w \frac{\partial v}{\partial z}=-\frac{1}{\rho _{0}}\frac{\partial p}{\partial y}-fu, \\ \frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac {\partial w}{\partial y}+w \frac{\partial w}{\partial z}=-\frac{1}{\rho _{0}}\frac{\partial p}{\partial z}+\frac{g \theta}{\theta_{0}}, \\ \frac{\partial\theta}{\partial t}+u\frac{\partial\theta}{\partial x}+v\frac{\partial\theta}{\partial y}+\sigma w=0, \\ \frac{\partial\rho_{0} u}{\partial x}+\frac{\partial\rho_{0} v}{\partial y}+\frac{\partial\rho_{0} w}{\partial z}=0, \end{array}\displaystyle \right . $$
(1)

where \(\rho_{0}\) denotes the density; \(\theta_{0}\) is the temperature of the environmental flow field; \(\sigma=\frac{\partial\theta _{0}}{\partial z}\).

Introducing the dimensionless quantities

$$ \begin{gathered} t=f^{-1}\bigl(t^{*}\bigr),\qquad (x,y)=L \bigl(X^{*},Y^{*}\bigr),\qquad Z=D\bigl(z^{*}\bigr), \\ (u,v)=U\bigl(u^{*},v^{*}\bigr),\qquad w=\frac{U}{L}D\bigl(w^{*}\bigr),\qquad \rho_{0}=\frac {P}{gH}(\rho_{s}), \\ \theta=\delta\theta\bigl(\theta^{*}\bigr),\qquad\delta p_{x,y}= \frac {P}{gH}fLU\bigl(p^{*}\bigr),\qquad\delta p_{z}= \frac{P}{\theta_{0} H}\delta\theta \bigl(p^{*}\bigr), \end{gathered} $$
(2)

where the quantities with asterisk mean they are dimensionless.

Assuming \(D\sim H\), \(\frac{U}{fL} \sim o(1)\), \(\delta\theta=\frac {\delta UD}{fL} \) and substituting Eqs. (2) into Eqs. (1) yields

$$ \left\{ \textstyle\begin{array}{l} \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v \frac {\partial u}{\partial y}+w\frac{\partial u}{\partial z}=-\frac{1}{\rho _{s}}\frac{\partial p}{\partial x}+v, \\ \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac {\partial v}{\partial y}+w \frac{\partial v}{\partial z}=-\frac{1}{\rho _{s}}\frac{\partial p}{\partial y}-u, \\ \frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac {\partial w}{\partial y}+w\frac{\partial w}{\partial z}= \epsilon ^{-1}(-\frac{1}{\rho_{s}}\frac{\partial p}{\partial z}+\theta ), \\ \frac{\partial\theta}{\partial t}+u\frac{\partial\theta}{\partial x}+v\frac{\partial\theta}{\partial y}+ w=0, \\ \frac{\partial\rho_{s} u}{\partial x}+\frac{\partial\rho_{s} v}{\partial y}+\frac{\partial\rho_{s} w}{\partial z}=0, \end{array}\displaystyle \right . $$
(3)

where we omit the subscript asterisks for simplicity, \(\epsilon=\frac {f^{2}}{N^{2}}\) and \(N^{2}=\frac{g\theta}{\theta_{0}}\) are the new parameters.

We suppose that the solution of Eq. (3) has the following form:

$$ \left\{ \textstyle\begin{array}{l} u=U(y,z)+\epsilon(u_{0}+\epsilon u_{1}+\epsilon^{2} u_{2})+\cdots, \\ v=V(y,z)+\epsilon(v_{0}+\epsilon v_{1}+ \epsilon^{2} v_{2})+\cdots, \\ w=\epsilon(w_{0}+\epsilon w_{1}+\epsilon^{2} w_{2})+\cdots, \\ \theta=\Theta(y,z)+\epsilon(\theta_{0}+\epsilon \theta_{1}+\epsilon^{2} \theta_{2})+\cdots, \\ p=P(y,z)+\epsilon(p_{0}+\epsilon p_{1}+ \epsilon^{2} p_{2})+\cdots, \end{array}\displaystyle \right . $$
(4)

where U represents the speed of the basic flow, Θ indicates the temperature field and P denotes the air pressure.

We introduce the slow time and space scales for the purpose of addressing the effects of nonlinearity and amplitude modulation of space,

$$ T_{1}=\epsilon t,\qquad T_{2}=\epsilon^{2} t,\qquad X_{1}=\epsilon x,\qquad X_{2}=\epsilon^{2} x,\qquad Y=\epsilon y. $$
(5)

We introduce a new set of variables,

$$ \rho_{s}u_{n}=u_{n},\qquad\rho_{s}v_{n}=v_{n}, \qquad\rho_{s}w_{n}=w_{n},\qquad\rho_{s} \theta _{n}=\theta_{n},\quad n=0,1,2. $$
(6)

Substituting Eqs. (4), (5) and (6) into Eqs. (1) one acquires the lowest-order approximate equations of ϵ,

$$ \varepsilon^{0}: \left\{ \textstyle\begin{array}{l} -\frac{1}{\rho_{s}} \frac{\partial P}{\partial y}-U=0, \\ -\frac{1}{\rho_{s}}\frac{\partial P}{\partial z}+\Theta=0, \end{array}\displaystyle \right . $$
(7)

obviously, we will get

$$ \frac{\partial U}{\partial z}=-\frac{\partial\Theta}{\partial y}. $$
(8)

Further, the first-order approximate equations of ϵ will be obtained,

$$ \varepsilon^{1}: \left\{ \textstyle\begin{array}{l} \frac{\partial u_{0}}{\partial t}+U \frac{\partial u_{0}}{\partial x}+V\frac {\partial u_{0}}{\partial y}+(U_{y}-1)v_{0}+U_{z}w_{0}+ \frac{\partial p_{0}}{\partial x}=0, \\ \frac{\partial v_{0}}{\partial t}+U\frac{\partial v_{0}}{\partial x}+V\frac {\partial v_{0}}{\partial y}+ \frac{\partial p_{0}}{\partial y}+u_{0}=0, \\ \frac{\partial p_{0}}{\partial z}-\theta_{0}=0, \\ \frac{\partial\theta_{0}}{\partial t}+U\frac{\partial\theta _{0}}{\partial x}+V\frac{\partial\theta_{0}}{\partial y}+\Theta _{y}v_{0}+w_{0}=0, \\ \frac{\partial u_{0}}{\partial x}+\frac{\partial v_{0}}{\partial y}+\frac {\partial w_{0}}{\partial z}=0. \end{array}\displaystyle \right . $$
(9)

Eliminating the other variables except for \(p_{0}\) in Eqs. (9) yields the following equation:

$$ M\biggl(\frac{\partial p_{0}}{\partial x}\biggr)=0, $$
(10)

where

$$ \begin{gathered} M=\frac{\partial^{2}}{\partial y^{2}}-(U_{y}-1) \frac{\partial^{2}}{\partial z^{2}}+2U_{z}\frac{\partial^{2}}{\partial y\, \partial z}+\biggl[U_{zz}- \frac{\Psi _{y}}{\Psi}-U_{z}\frac{\Psi_{z}}{\Psi}\biggr]\frac{\partial}{\partial y} \\ \phantom{M=} +\biggl[(U_{y}-1)\frac{\Psi_{z}}{\Psi}-U_{z} \frac{\Psi_{y}}{\Psi}\biggr]\frac{\partial }{\partial z}-\frac{1}{U} \biggl[U_{z}z-\frac{\Psi_{y}}{\Psi}-U_{z}\frac{\Psi_{z}}{\Psi } \biggr], \\ \Psi=U_{y}-1+U^{2}_{z},\qquad\Psi_{y}= \frac{\partial\Psi}{\partial y},\qquad\Psi =\frac{\partial\Psi}{\partial y}. \end{gathered} $$
(11)

Suppose Eq. (10) has the following solution in the form of separate variables:

$$ p_{0}=p^{*}_{0}(y,z)A(T_{1},T_{2},X_{1},X_{2},Y) \exp\bigl[i(kx-\omega t)\bigr], $$
(12)

where k represents the zonal wave number, ω indicates the frequency of the envelope gravity waves and A denotes a slowly varying envelope complex amplitude.

Therefore, other solutions to Eqs. (9) are also given

$$ \left\{ \textstyle\begin{array}{l} u_{0}=u^{*}_{0}(y,z)A(T_{1},T_{2},X_{1},X_{2},Y) \exp[i(kx-\omega t)], \\ v_{0}=v^{*}_{0}(y,z)A(T_{1},T_{2},X_{1},X_{2},Y) \exp[i(kx-\omega t)], \\ w_{0}=w^{*}_{0}(y,z)A(T_{1},T_{2},X_{1},X_{2},Y) \exp[i(kx-\omega t)], \\ \theta_{0}=\theta^{*}_{0}(y,z)A(T_{1},T_{2},X_{1},X_{2},Y) \exp[i(kx-\omega t)]. \end{array}\displaystyle \right . $$
(13)

Next, the second-order approximate equations of ϵ will be given,

$$ \varepsilon^{2}: \left\{ \textstyle\begin{array}{l} \frac{\partial u_{1}}{\partial t}+U \frac{\partial u_{1}}{\partial x}+V\frac {\partial u_{1}}{\partial y}+(U_{y}-1)v_{1}+U_{z}w_{1}+ \frac{\partial p_{1}}{\partial x} \\ \quad=-[\frac{\partial u_{0}}{\partial T_{1}}+U\frac{\partial u_{0}}{\partial X_{1}}+V\frac{\partial u_{0}}{\partial Y}+ \frac{1}{\rho _{s}}(u_{0}\frac{\partial u_{0}}{\partial x}+v_{0} \frac{\partial u_{0}}{\partial y}+w_{0}\frac{\partial u_{0}}{\partial z})+\frac{\partial p_{0}}{\partial X_{1}} ]\equiv\Psi_{u_{1}}, \\ \frac{\partial v_{1}}{\partial t}+U\frac{\partial v_{1}}{\partial x}+V\frac {\partial v_{1}}{\partial y}+ \frac{\partial p_{1}}{\partial y}+u_{1}+V_{y}v_{1}+V_{z}w_{1} \\ \quad=-[\frac{\partial v_{0}}{\partial T_{1}}+U\frac{\partial v_{0}}{\partial X_{1}}+V\frac{\partial v_{0}}{\partial Y}+ \frac{1}{\rho _{s}}(u_{0}\frac{\partial v_{0}}{\partial x}+v_{0} \frac{\partial v_{0}}{\partial y}+w_{0}\frac{\partial v_{0}}{\partial z})+\frac{\partial p_{0}}{\partial Y} ]\equiv\Psi_{v_{1}}, \\ \frac{\partial p_{1}}{\partial z}-\theta_{1}=-(\frac{\partial w_{0}}{\partial t}+U \frac{\partial w_{0}}{\partial x}+V\frac{\partial w_{0}}{\partial y})\equiv\Psi_{w_{1}} , \\ \frac{\partial\theta_{1}}{\partial t}+U\frac{\partial\theta _{1}}{\partial x}+V\frac{\partial\theta_{1}}{\partial y}+ \Theta_{y}v_{1}+w_{1} \\ \quad=-[\frac{\partial\theta_{0}}{\partial T_{1}}+U\frac{\partial\theta _{0}}{\partial X_{1}}+V\frac{\partial\theta_{0}}{\partial Y}+ \frac{1}{\rho _{s}}(u_{0}\frac{\partial\theta_{0}}{\partial x}+v_{0} \frac{\partial\theta _{0}}{\partial y})]\equiv\Psi_{\theta_{1}}, \\ \frac{\partial u_{1}}{\partial x}+\frac{\partial v_{1}}{\partial y}+\frac {\partial w_{1}}{\partial z}=-( \frac{\partial u_{0}}{\partial X_{1}}+\frac {\partial v_{0}}{\partial Y})\equiv\Psi_{p_{1}}. \end{array}\displaystyle \right . $$
(14)

Substituting Eqs. (12) and (13) into Eqs. (14) one acquires

$$ \left\{ \textstyle\begin{array}{l} \phi_{u1}=-[u^{*}_{0}A_{T_{1}}+ (Uu^{*}_{0}+p^{*}_{0})A_{X_{1}}+Vu^{*}_{0}A_{Y} ]\exp [i(kx-\omega t)] \\ \phantom{ \phi_{u1}=}-\frac{1}{\rho_{s}}(ik(u^{*}_{0})^{2}+v^{*}_{0}u^{*}_{0y}+w^{*}_{0}u^{*}_{0z} )|A|^{2}\exp [2i(kx-\omega t)], \\ \phi_{v1}=-[v^{*}_{0}A_{T_{1}}+Uv^{*}_{0}A_{X_{1}}+ (Vv^{*}_{0}+p^{*}_{0})A_{Y}]\exp [i(kx-\omega t)] \\ \phantom{\phi_{v1}=}-\frac{1}{\rho_{s}}(iku^{*}_{0}v^{*}_{0}++v^{*}_{0}v^{*}_{0y}+w^{*}_{0}v^{*}_{0z} )|A|^{2}\exp [2i(kx-\omega t)], \\ \phi_{w1}=[iw^{*}_{0}(\omega-kU)-Vw^{*}_{0y} ]A\exp[i(kx-\omega t)], \\ \phi_{\theta_{1}}=-[\theta^{*}_{0}A_{T_{1}}+U \theta^{*}_{0}A_{X_{1}}+V\theta ^{*}_{0}A_{Y} ]\exp[i(kx-\omega t)] \\ \phantom{\phi_{\theta_{1}}=}-\frac{1}{\rho_{s}}(iku^{*}_{0}\theta^{*}_{0}+v^{*}_{0} \theta^{*}_{0y})|A|^{2}\exp [2i(kx-\omega t)], \\ \phi_{p_{1}}=-(u^{*}_{0}A_{X_{1}}+v^{*}_{0}A_{Y} )\exp[i(kx-\omega t)]. \end{array}\displaystyle \right . $$
(15)

Similarly, eliminating the other variables except for \(p_{1}\) in Eqs. (14) leads to the following equation:

$$ M\biggl(\frac{\partial p_{1}}{\partial x}\biggr)=M_{1}(\phi_{u_{1}})+M_{2}( \phi _{v_{1}})+M_{3}(\phi_{w_{1}})+M_{4}( \phi_{\theta_{1}}), $$
(16)

where

$$ \left\{ \textstyle\begin{array}{l} M_{1}=\frac{\partial}{\partial y}+U_{zz}+U_{z} \frac{\partial}{\partial z}+\frac{1}{U}+\frac{1}{\Psi}(\Psi_{y}+U_{z} \Psi_{z}), \\ M_{2}=-\frac{1}{U}[\frac{\partial}{\partial y}+U_{z}z+U_{z} \frac{\partial }{\partial z}-\frac{1}{\Psi}(\Psi_{y}+U_{y} \Psi_{z})], \\ M_{3}=\frac{1}{U}[U_{z}\frac{\partial}{\partial y}-(U_{y}-1) \frac{\partial }{\partial z}-\frac{1}{\Psi}(U_{y}-1)\Psi_{z} ], \\ M_{4}=U_{z}\frac{\partial}{\partial y}+\frac{U_{z}}{U}-(U_{y}-1) \frac{\partial }{\partial z}-\frac{\Psi_{y}}{\Psi}U_{z}-\frac{(U_{y}-1)}{U} \frac{\Psi_{z}}{\Psi}. \end{array}\displaystyle \right . $$
(17)

In addition, for Eq. (16) the following solution in the form of separate variables exists by analysis and assumptions:

$$ p_{1}=p^{*}_{1}(y,z)\bigl[A\exp\bigl[i(kx-\omega t) \bigr]+|A|^{2}\exp\bigl[2i(kx-\omega t)\bigr]\bigr]. $$
(18)

Thus, other solutions to Eqs. (9) are also obtained

$$ \left\{ \textstyle\begin{array}{l} u_{1}=u^{*}_{1}(y,z) [A_{X_{1}}\exp[i(kx-\omega t)]+|A|^{2}\exp [2i(kx-\omega t)]], \\ v_{1}=v^{*}_{1}(y,z)[A_{Y}\exp[i(kx- \omega t)]+|A|^{2}\exp[2i(kx-\omega t)]], \\ w_{1}=w^{*}_{1}(y,z)[A_{Y}\exp[i(kx- \omega t)]+|A|^{2}\exp[2i(kx-\omega t)]], \\ \theta_{1}=\theta^{*}_{1}(y,z)[A_{X_{1}}\exp [i(kx-\omega t)]+|A|^{2}\exp [2i(kx-\omega t)] ], \end{array}\displaystyle \right . $$
(19)

and the third-order approximate equations of ϵ will be written as

$$ \varepsilon^{3}: \left\{ \textstyle\begin{array}{l} \frac{\partial u_{2}}{\partial t}+U \frac{\partial u_{2}}{\partial x}+V\frac {\partial u_{2}}{\partial y}+(U_{y}-1)v_{2}+U_{z}w_{2}+ \frac{\partial p_{2}}{\partial x} \\ \quad=-[\frac{\partial u_{0}}{\partial T_{2}}+U\frac{\partial u_{0}}{\partial X_{2}}+U\frac{\partial u_{1}}{\partial X_{1}}+V \frac{\partial u_{1}}{\partial Y}+\frac{\partial u_{1}}{\partial T_{1}}+\frac{1}{\rho _{s}}(u_{0} \frac{\partial u_{0}}{\partial X_{1}}+v_{0}\frac{\partial u_{0}}{\partial Y}+u_{1} \frac{\partial u_{0}}{\partial x} \\ \quad\quad{}+v_{1}\frac{\partial u_{0}}{\partial y}+w_{1}\frac{\partial u_{0}}{\partial z}+u_{0} \frac{\partial u_{1}}{\partial x}+v_{0}\frac{\partial u_{1}}{\partial y}+w_{0} \frac{\partial u_{1}}{\partial z})+\frac{\partial p_{0}}{\partial X_{2}}+\frac{\partial p_{1}}{\partial X_{1}}]\\ \quad\equiv \Psi _{u_{2}}, \\ \frac{\partial v_{2}}{\partial t}+U\frac{\partial v_{2}}{\partial x}+V\frac {\partial v_{2}}{\partial y}+ \frac{\partial p_{2}}{\partial y}+u_{2}+V_{y}v_{2}+V_{z}w_{2} \\ \quad=-[\frac{\partial v_{0}}{\partial T_{2}}+U\frac{\partial v_{0}}{\partial X_{2}}+U\frac{\partial v_{1}}{\partial X_{1}}+V \frac{\partial v_{1}}{\partial Y}+\frac{\partial v_{1}}{\partial T_{1}}+\frac{1}{\rho _{s}}(u_{0} \frac{\partial v_{0}}{\partial X_{1}}+v_{0}\frac{\partial v_{0}}{\partial Y}+u_{1} \frac{\partial v_{0}}{\partial x} \\ \quad\quad{}+v_{1}\frac{\partial v_{0}}{\partial y}+w_{1} \frac{\partial v_{0}}{\partial z}+u_{0}\frac{\partial v_{1}}{\partial x}+v_{0} \frac{\partial v_{1}}{\partial y}+w_{0}\frac{\partial v_{1}}{\partial z})+\frac{\partial p_{1}}{\partial Y} ]\\ \quad\equiv\Psi_{v_{2}}, \\ \frac{\partial p_{2}}{\partial z}-\theta_{2}=-[\frac{\partial w_{0}}{\partial t_{1}}+U \frac{\partial w_{0}}{\partial X_{1}}+V\frac{\partial w_{0}}{\partial Y}+U\frac{\partial w_{1}}{\partial x}+\frac{1}{\rho _{s}} (u_{0}\frac{\partial w_{1}}{\partial x}+v_{0}\frac{\partial w_{1}}{\partial y} \\ \phantom{\frac{\partial p_{2}}{\partial z}-\theta_{2}=}+w_{0}\frac{\partial w_{1}}{\partial z})+\frac{\partial w_{1}}{\partial t}] \\ \phantom{\frac{\partial p_{2}}{\partial z}-\theta_{2}}\equiv\Psi_{w_{2}} , \\ \frac{\partial\theta_{2}}{\partial t}+U\frac{\partial\theta _{2}}{\partial x}+V\frac{\partial\theta_{2}}{\partial y}+ \Theta_{y}v_{2}+w_{2} \\ \quad=-[\frac{\partial\theta_{0}}{\partial T_{2}}+U\frac{\partial\theta _{0}}{\partial X_{2}}+U\frac{\partial\theta_{1}}{\partial X_{1}}+V \frac {\partial\theta_{1}}{\partial Y}+\frac{\partial\theta_{1}}{\partial T_{1}}+\frac{1}{\rho_{s}}(u_{0} \frac{\partial\theta_{0}}{\partial X_{1}}+v_{0}\frac {\partial\theta_{0}}{\partial Y}+u_{1} \frac{\partial\theta_{0}}{\partial x} \\ \quad\quad{}+v_{1}\frac{\partial\theta_{0}}{\partial y}+w_{1} \frac{\partial \theta_{0}}{\partial z}+u_{0}\frac{\partial\theta_{1}}{\partial x}+v_{0} \frac {\partial\theta_{1}}{\partial y}+w_{0}\frac{\partial\theta_{1}}{\partial z})+\frac{\partial p_{1}}{\partial Y} ]\\ \quad\equiv\Psi_{\theta_{2}}, \\ \frac{\partial u_{2}}{\partial x}+\frac{\partial v_{2}}{\partial y}+\frac {\partial w_{2}}{\partial z}=-( \frac{\partial u_{1}}{\partial X_{1}}+\frac {\partial u_{0}}{\partial X_{2} }+\frac{\partial v_{1}}{\partial Y})\equiv \Psi_{p_{2}}. \end{array}\displaystyle \right . $$
(20)

Then substitute Eqs. (18) and (19) into Eq. (20) and we can get the following forms by means of the secular-producing terms proportional to \(\exp[i(kx-\omega t)]\):

$$ \left\{ \textstyle\begin{array}{l} \phi_{u2}=u^{*}_{0}(A_{T_{2}}+UA_{X_{2}})+Uu^{*}_{1}A_{X_{1}X_{1}}\\ \phantom{\phi_{u2}=}+ \frac{1}{\rho _{s}}(3iku^{*}_{o}u^{*}_{1}+u^{*}_{oy}u^{*}_{1y}+u^{*}_{0z}w^{*}_{1}+v^{*}_{0}u^{*}_{1y}+w^{*}_{0}u^{*}_{1z} )|A|^{2}A, \\ \phi_{v2}=v^{*}_{0}(A_{T_{2}}+UA_{X_{2}})+Vv^{*}_{1}A_{YY}\\ \phantom{\phi_{v2}=}+ \frac{1}{\rho _{s}}(iku^{*}_{1}v^{*}_{0}+v^{*}_{1}v^{*}_{oy}+w^{*}_{1}v^{*}_{0z}+2iku^{*}_{0}v^{*}_{1}+v^{*}_{0}v^{*}_{1y}+w^{*}_{0}v^{*}_{1z} )|A|^{2}A, \\ \phi_{w2}=w^{*}_{0}(A_{T_{1}}+UA_{X_{1}})+Vw^{*}_{1}A_{YY}, \\ \phi_{\theta_{2}}=\theta^{*}_{0}(A_{T_{2}}+UA_{X_{2}})+U \theta ^{*}_{1}A_{X_{1}X_{1}}+\frac{1}{\rho_{s}}(iku^{*}_{1} \theta^{*}_{0}+v^{*}_{1}\theta ^{*}_{0y}+2iku^{*}_{0} \theta^{*}_{1}+v^{*}_{0}\theta^{*}_{1y} )|A|^{2}A, \\ \phi_{p_{2}}=u^{*}_{0}A_{X_{2}}+u^{*}_{1}A_{X_{1}X_{1}}+v^{*}_{1}A_{YY}. \end{array}\displaystyle \right . $$
(21)

Meanwhile, eliminating the other variables except for \(p_{1}\) in Eq. (14) one obtains the following equation:

$$ M\biggl(\frac{\partial p_{2}}{\partial x}\biggr)=M_{1}(\phi_{u2})+M_{2}( \phi _{v2})+M_{3}(\phi_{w2})+M_{4}( \phi_{\theta_{2}}). $$
(22)

We adopt the following variable transformations:

$$ X=\frac{1}{U}X_{1}=\frac{1}{U}X_{2},\qquad t=T_{1}=T_{2}, $$
(23)

and the \((2+1)\) NLS equation will be obtained,

$$ i\biggl(\frac{\partial A}{\partial t}+\frac{\partial A}{\partial X}\biggr)+a_{1} \frac {\partial^{2} A}{\partial X^{2}}-a_{2}\frac{\partial^{2} A}{\partial y^{2}}+a_{3}|A|^{2}A=0, $$
(24)

where the coefficients are expressed as

$$ \left\{ \textstyle\begin{array}{l} a_{1}=-i(Uu^{*}_{1}+u^{*}_{1} ), \\ a_{2}=i(Vv^{*}_{1}+Vw^{*}_{1}+v^{*}_{1} ), \\ a3=\frac{1}{\rho _{s}}[3ku^{*}_{0}u^{*}_{1}+ku^{*}_{1}v^{*}_{0}+2ku^{*}_{0}v^{*}_{1}-i (u^{*}_{0y}v^{*}_{1}+u^{*}_{0z}w^{*}_{1} \\ \phantom{a3=}+v^{*}_{0}u^{*}_{1y}+w^{*}_{0}u^{*}_{1z}+v^{*}_{0y}v^{*}_{1}+w^{*}_{1}v^{*}_{0z}+v^{*}_{0}v^{*}_{1y} )]. \end{array}\displaystyle \right . $$
(25)

According to [9], the corresponding transformation can be defined

$$ x=X-t, $$
(26)

so Eq. (24) is rewritten as follows:

$$ i\frac{\partial A}{\partial t}+a_{1}\frac{\partial^{2} A}{\partial x^{2}}-a_{2} \frac{\partial^{2} A}{\partial y^{2}}+a_{3}|A|^{2}A=0. $$
(27)

3 Formulation of time–space fractional \((2+1)\) dimensional NLS equation

The semi-inverse method and the fractional variational principle are used to get the time–space fractional \((2+1)\) dimensional NLS equation as follows:

Defining a potential equation \(A(x,y,t)=u(x,y,t)+iv(x,y,t)\), where \(u(x,y,t)\) and \(v(x,y,t)\) indicate real functions of x, y and t, and the potential equation of the classical \((2+1)\) dimensional NLS equation (27) will be given,

$$ -v_{t}+a_{1}u_{xx}-a_{2}u_{yy}+a_{3}u \bigl(u^{2}+v^{2}\bigr)+i\bigl[u_{t}+a_{1}v_{xx}-a_{2}v_{yy}+a_{3}v \bigl(u^{2}+v^{2}\bigr)\bigr]=0. $$
(28)

Further, the system of two second-order equations can be represented in the following form:

$$\begin{aligned}& -v_{t}+a_{1}u_{xx}-a_{2}u_{yy}+a_{3}u \bigl(u^{2}+v^{2}\bigr)=0, \end{aligned}$$
(29)
$$\begin{aligned}& u_{t}+a_{1}v_{xx}-a_{2}v_{yy}+a_{3}v \bigl(u^{2}+v^{2}\bigr)=0. \end{aligned}$$
(30)

We will construct a trial-functional with the help of the semi-inverse method for getting a variational principle for systems (29) and (30). Further, the system of two second-order equations can be represented in the following form:

$$ J(u,v)= \int\biggl[u_{t}v-\frac{a_{1}}{2}v^{2}_{x}+ \frac{a_{2}}{2}v^{2}_{y}+\frac {a_{3}}{4} \bigl(2u^{2}v^{2}+v^{4}\bigr)+H(u)\biggr]\,d\Omega, $$
(31)

where \(d\Omega=dx\,dy\,dt\) and \(H(u)\) is an unknown function consisting of the derivatives of u and u.

Considering the variation in Eq. (31) for u and we can get the Euler–Lagrange equation

$$ -v_{t}+a_{3}uv^{2}+\frac{\delta H}{\delta u}=0, $$
(32)

where \(\frac{\delta H}{\delta u}\) means He’s variational differential [48] for u,

$$ \begin{aligned}[b] \frac{\delta H}{\delta u}={}&\frac{\partial H}{\partial u}-\frac{\partial }{\partial t}\biggl( \frac{\partial H}{\partial u_{t}}\biggr)-\frac{\partial}{\partial x}\biggl(\frac{\partial H}{\partial u_{x}}\biggr)- \frac{\partial}{\partial y}\biggl(\frac {\partial H}{\partial u_{y}}\biggr)\\ &+\frac{\partial^{2}}{\partial t^{2}}\biggl( \frac {\partial H}{\partial u_{tt}}\biggr)+\frac{\partial^{2}}{\partial x^{2}}\biggl(\frac {\partial H}{\partial u_{xx}}\biggr)+ \cdots.\end{aligned} $$
(33)

In order to make equation (32) satisfy equation (29), we set

$$ \frac{\delta H}{\delta u}=v_{t}-a_{3}uv^{2}=a_{1}u_{xx}-a_{2}u_{yy}+a_{3}u^{3}, $$
(34)

and H can also be defined as follows:

$$ H=-\frac{a_{1}}{2}u^{2}_{x}+\frac{a_{2}}{2}u^{2}_{y}+ \frac{a_{3}}{4}u^{4}. $$
(35)

Further, we will obtain the final variational principle

$$ J(u,v)= \int\biggl[u_{t}v-\frac{a_{1}}{2}\bigl(u^{2}_{x}+v^{2}_{x} \bigr)+\frac {a_{2}}{2}\bigl(u^{2}_{y}+v^{2}_{y} \bigr)+\frac{a_{3}}{4}\bigl(u^{2}+v^{2} \bigr)^{2}\biggr]\,d\Omega. $$
(36)

Substituting \(u=\frac{A+A^{*}}{2}\), \(v=i\frac{A-A^{*}}{2}\), where \(A^{*}\) expresses the complex conjugate of A and \(A^{*}=u-iv\), and we will obtain the following variational principle:

$$ \begin{aligned}[b] J(A)={}& \int\biggl[\frac{i}{4}\bigl(A^{*}-A\bigr) \biggl( \frac{\partial A}{\partial t}+\frac {\partial A^{*}}{\partial t}\biggr)\\&-\frac{a_{1}}{2}\biggl( \frac{\partial A}{\partial x}\frac{\partial A^{*}}{\partial x}\biggr)+\frac{a_{2}}{2}\biggl( \frac{\partial A}{\partial y}\frac{\partial A^{*}}{\partial y}\biggr)+\frac{a_{3}}{4}\bigl(AA^{*} \bigr)^{2}\biggr]\, d\Omega,\end{aligned} $$
(37)

from which we can identify the Lagrangian of \((2+1)\) dimensional NLS equation,

$$ L=\frac{i}{4}\bigl(A^{*}-A\bigr) \biggl(\frac{\partial A}{\partial t}+ \frac{\partial A^{*}}{\partial t}\biggr)-\frac{a_{1}}{2}\biggl(\frac{\partial A}{\partial x} \frac {\partial A^{*}}{\partial x}\biggr)+\frac{a_{2}}{2}\biggl(\frac{\partial A}{\partial y} \frac{\partial A^{*}}{\partial y}\biggr)+\frac{a_{3}}{4}\bigl(AA^{*}\bigr)^{2}. $$
(38)

Similarly, the Lagrangian of the time–space fractional \((2+1)\) dimensional NLS equation is written as

$$ F=\frac{i}{4}\bigl(A^{*}-A\bigr) \bigl(D^{\alpha}_{t}A+D^{\alpha}_{t}A^{*} \bigr)-\frac{a_{1}}{2}\bigl(D^{\beta}_{x}AD^{\beta}_{x}A^{*} \bigr)+\frac{a_{2}}{2}\bigl(D^{\gamma}_{y}AD^{\gamma}_{y}A^{*} \bigr)+\frac{a_{3}}{4}\bigl(AA^{*}\bigr)^{2}, $$
(39)

here the fractional derivative \(D^{\alpha}_{t}A\) shows the \(mRL\) fractional derivative defined in [54]

$$ D^{\alpha}_{z}f(z)=\frac{1}{\Gamma(1-\alpha)}\frac{d}{d_{z}}{ \int^{z}_{a} d\zeta \frac{[f(\zeta)-f(a)]}{(z-\zeta)^{\alpha}}},\quad0\leq \alpha< 1. $$
(40)

Next, the functional of the time–space fractional \((2+1)\) dimensional NLS equation can take the form

$$ J\bigl(A^{*}\bigr)= \int_{X}(dx)^{\beta}\int_{Y}(dy)^{\gamma}\int_{T}(dt)^{\alpha}F\bigl(A^{*},D^{\alpha}_{t}A^{*},D^{\beta}_{x}A^{*},D^{\gamma}_{y}A^{*} \bigr). $$
(41)

Moreover, we have the following definition [54, 55]:

$$ \int^{t}_{a} (dt)^{\alpha}=\alpha \int^{t}_{a} d\tau(t-\tau)^{\alpha}f(\tau). $$
(42)

Integrating by parts according to the above relation [54, 55],

$$ \begin{aligned}[b] \int^{b}_{a}(dz)^{\alpha}f(z)D^{\alpha}_{z} g(z)={}&\Gamma(1+\alpha) \bigl[g(z)f(z) \bigr]\big|^{b}_{a}\\&- \int^{b}_{a}(dz)^{\alpha}g(z)D^{\alpha}_{z}f(z), \quad f(z),g(z)\in[a,b].\end{aligned} $$
(43)

Further, by optimizing the variation of the functional \(\delta J_{F}(A^{*})=0\), the Euler–Lagrange equation of the time–space fractional \((2+1)\) dimensional NLS equation can be written

$$ \frac{\partial F}{\partial A^{*}}-D^{\alpha}_{t}\biggl(\frac{\partial F}{\partial D^{\alpha}_{t}A^{*}} \biggr)-D^{\beta}_{x}\biggl(\frac{\partial F}{\partial D^{\beta}_{x}A^{*}} \biggr)-D^{\gamma}_{y}\biggl(\frac{\partial F}{\partial D^{\gamma}_{y}A^{*}}\biggr)=0. $$
(44)

Finally, substituting the Lagrange defined by Eq. (5) into the Euler–Lagrange formula, we can obtain the time–space fractional \((2+1)\) dimensional NLS equation

$$ iD^{\alpha}_{t}A+a_{1}D^{2\beta}_{x}A-a_{2}D^{2\gamma}_{y}A+a_{3}A|A|^{2}=0. $$
(45)

4 Conservation laws of time–space fractional \((2+1)\) dimensional NLS equation

In the section, we present a time–space FPDE with three independent variables,

$$ G\bigl(x,y,t,A,D^{\alpha}_{t}A,D^{2\beta}_{x}A,D^{2\gamma}_{y}A, \ldots\bigr)=0,\quad\alpha >0, \beta>0, \gamma>0. $$
(46)

Introducing an one-parameter Lie group for infinitesimal transformations,

$$ \begin{gathered} \overline{x} \rightarrow x+\epsilon\xi(x,y,t,A)+o \bigl(\epsilon^{2}\bigr), \\ \overline{y} \rightarrow y+\epsilon\zeta(x,y,t,A)+o\bigl(\epsilon^{2} \bigr), \\ \overline{t} \rightarrow t+\epsilon\tau(x,y,t,A)+o\bigl(\epsilon^{2} \bigr), \\ \overline{A} \rightarrow A+\epsilon\eta(x,y,t,A)+o\bigl(\epsilon^{2} \bigr), \\ D^{\alpha}_{t}\overline{A} \rightarrow D^{\alpha}_{t}A+ \epsilon\eta^{\alpha}_{t}(x,y,t,A)+o\bigl(\epsilon^{2} \bigr), \\ D^{2\beta}_{x}\overline{A} \rightarrow D^{2\beta}_{x}A+ \epsilon\eta^{2\beta }_{x}(x,y,t,A)+o\bigl(\epsilon^{2} \bigr), \\ D^{2\gamma}_{y}\overline{A} \rightarrow D^{2\gamma}_{y}A+ \epsilon\eta ^{2\gamma}_{y}(x,y,t,A)+o\bigl(\epsilon^{2} \bigr), \\ \cdots \end{gathered} $$
(47)

where ξ, ζ, τ and η indicate infinitesimals and \(\epsilon\ll1\) means a group parameter.

The extended infinitesimals [56] can be written

$$ \begin{gathered} \eta^{\alpha}_{t}=D^{\alpha}_{t}( \eta)+\xi D^{\alpha}_{t}(A_{x})-D^{\alpha}_{t}( \xi A_{x})+\zeta D^{\alpha}_{t}(A_{y})-D^{\alpha}_{t}( \zeta A_{y})+D^{\alpha}_{t}\bigl(D_{t}(\tau )A\bigr) \\ \phantom{\eta^{\alpha}_{t}=}-D^{\alpha+1}_{t}(\tau A)+\tau D^{\alpha+1}_{t}(A), \\ \eta^{2\beta}_{x}=D^{2\beta}_{x}( \eta)+D^{\beta}_{x}\bigl(\tau D^{\beta}_{x}(A_{t})\bigr)-D^{2\beta}_{x}(\tau A_{t})+D^{\beta}_{x}\bigl(\zeta D^{\beta}_{x}(A_{y})\bigr) \\ \phantom{\eta^{2\beta}_{x}=}-D^{2\beta}_{x}(\zeta A_{y})+D^{2\beta}_{x}\bigl(D_{x}(\xi)A \bigr)-D^{2\beta+1}_{x}(\xi A)+D^{\beta}_{x}\bigl( \xi D^{\beta+1}_{x}(A)\bigr)\\ \phantom{\eta^{2\beta}_{x}=}+\xi D^{2\beta }_{x}(A_{x})+ \tau D^{2\beta}_{x}(A_{t})+\zeta D^{2\beta}_{x}(A_{y}), \\ \eta^{2\gamma}_{y}=D^{2\gamma}_{y}( \eta)+D^{\gamma}_{y}\bigl(\tau D^{\gamma}_{y}(A_{t})\bigr)-D^{2\gamma}_{y}(\tau A_{t})+D^{\gamma}_{y}\bigl(\xi D^{\gamma}_{y}(A_{x})\bigr)\\ \phantom{\eta^{2\gamma}_{y}=}-D^{2\gamma}_{y}(\xi A_{x})+D^{2\gamma}_{y}\bigl(D_{y}(\zeta)A \bigr) -D^{2\gamma+1}_{y}(\zeta A)+D^{\gamma}_{y} \bigl(\zeta D^{\gamma+1}_{y}(A)\bigr)\\ \phantom{\eta^{2\gamma}_{y}=}+\xi D^{2\gamma}_{y}(A_{x})+ \tau D^{2\gamma}_{y}(A_{t})+\zeta D^{2\gamma}_{y}(A_{y}), \end{gathered} $$
(48)

where \(D_{t}\), \(D_{x}\) and \(D_{y}\) represent the total derivative operator defined in the following form:

$$ D_{x_{j}}=\frac{\partial}{\partial x_{j}}+A_{j}\frac{\partial}{\partial A}+A_{jk} \frac{\partial}{\partial A_{k}}+\cdots, \quad j,k=1,2,3,\ldots. $$
(49)

Obviously, \(x_{1}=t\), \(x_{2}=x\), \(x_{3}=y\), \(A_{j}=\frac{\partial A}{\partial x_{j}}\) and \(A_{jk}=\frac{\partial^{2}}{\partial x_{j}\, \partial x_{k}}\).

On the basis of the generalized Leibnitz rule [57] and the generalization of the chain rule [58], we can get the expression of the extended symmetry operator \(\eta^{\alpha}_{t}\),

$$ \begin{aligned}[b] \eta^{\alpha}_{t}={}&D^{\alpha}_{t} \eta+\bigl(\eta_{A}-\alpha D_{t}(\tau)\bigr)D^{\alpha}_{t}A-AD^{\alpha}_{t}\eta_{A}+ \mu_{l}\\ &+\sum^{\infty}_{n=1}\left[ \begin{pmatrix} \alpha\\ n \end{pmatrix} D^{\alpha}_{t} \eta_{A}- \begin{pmatrix} \alpha\\ n+1 \end{pmatrix} D^{n+1}_{t}( \tau)\right] D^{\alpha-n}_{t}(A)\\ &-\sum^{\infty}_{n=1} \begin{pmatrix} \alpha\\ n \end{pmatrix} D^{n}_{t}( \xi)D^{\alpha-n}_{t}A_{x}-\sum ^{\infty}_{n=1} \begin{pmatrix} \alpha\\ n \end{pmatrix} D^{n}_{t}(\zeta)D^{\alpha-n}_{t}A_{y}, \end{aligned} $$
(50)

where

$$ \begin{aligned}[b] \mu_{l}={}&\sum^{\infty}_{n=2} \sum^{n}_{m=2}\sum ^{m}_{k=2}\sum^{k-1}_{r=0} \begin{pmatrix} l \\ n \end{pmatrix} \begin{pmatrix} n \\ m \end{pmatrix} \begin{pmatrix} k \\ r \end{pmatrix} \\&\times\frac{1}{r!}\frac{t^{n-l}}{\Gamma(n+1-l)}[-A]^{r} \frac{\partial ^{m}}{\partial t^{m}}\bigl[A^{k-r}\bigr]\frac{\partial^{n-m+k}\eta}{\partial t^{n-m}\, \partial A^{k}}, \quad l=\alpha, \beta,\gamma. \end{aligned} $$
(51)

In the same way, the extended infinitesimal \(\eta^{2\beta}_{x}\) and \(\eta ^{2\gamma}_{y}\) can also be defined as

$$\begin{aligned}& \begin{aligned}[b] \eta^{2\beta}_{x}={}&D^{2\beta}_{x} \eta+\bigl(\eta_{A}-\beta D_{x}(\xi)\bigr)D^{2\beta }_{x}A-AD^{2\beta}_{x} \eta_{A}+\mu_{\beta}\\&+\sum^{\infty}_{n=1} \left[ \begin{pmatrix} 2\beta\\ n \end{pmatrix} D^{n}_{x} \eta_{A}- \begin{pmatrix} 2\beta\\ n+1 \end{pmatrix} D^{n+1}_{x}( \xi) + \begin{pmatrix} \beta\\ n+1 \end{pmatrix} D^{n}_{x}( \xi)\right]D^{2\beta-n}_{x}A\\ &+\sum^{\infty}_{n=1} \left[ \begin{pmatrix} \beta\\ n \end{pmatrix} - \begin{pmatrix} 2\beta\\ n \end{pmatrix} \right]D^{n}_{x}( \tau)D^{2\beta-n}_{x}(A_{t})+\sum ^{\infty}_{n=1}\left[ \begin{pmatrix} \beta\\ n \end{pmatrix} - \begin{pmatrix} 2\beta\\ n \end{pmatrix} \right] D^{n}_{x}(\zeta)D^{2\beta-n}_{x}(A_{y}) \\ &+ \xi D^{2\beta}_{x}(A_{x})+\tau D^{2\beta}_{x}(A_{t})+ \zeta D^{2\beta}_{x}(A_{y}), \end{aligned} \end{aligned}$$
(52)
$$\begin{aligned}& \begin{aligned}[b] \eta^{2\gamma}_{y}={}&D^{2\gamma}_{y} \eta+\bigl(\eta_{A}-\gamma D_{y}(\zeta)\bigr)D^{2\gamma }_{y}A-AD^{2\gamma}_{y} \eta_{A}+\mu_{\gamma}\\ &+\sum^{\infty}_{n=1} \left[ \begin{pmatrix} 2\gamma\\ n \end{pmatrix} D^{n}_{y} \eta_{A}- \begin{pmatrix} 2\gamma\\ n+1 \end{pmatrix} D^{n+1}_{y}( \zeta) + \begin{pmatrix} \gamma\\ n+1 \end{pmatrix} D^{n}_{y}( \zeta)\right]D^{2\gamma-n}_{y}A\\ &+\sum^{\infty}_{n=1} \left[ \begin{pmatrix} \gamma\\ n \end{pmatrix} - \begin{pmatrix} 2\gamma\\ n \end{pmatrix} \right]D^{n}_{y}( \tau)D^{2\gamma-n}_{y}(A_{t})+\sum ^{\infty}_{n=1}\left[ \begin{pmatrix} \gamma\\ n \end{pmatrix} - \begin{pmatrix} 2\gamma\\ n \end{pmatrix} \right] D^{n}_{y}(\xi)D^{2\gamma-n}_{y}(A_{x}) \\&+ \xi D^{2\gamma}_{y}(A_{x})+\tau D^{2\gamma}_{y}(A_{t})+ \zeta D^{2\gamma}_{y}(A_{y}). \end{aligned} \end{aligned}$$
(53)

By the Lie symmetry theory, we will obtain the infinitesimal generator

$$ X=\xi(x,y,t,A)\frac{\partial}{\partial x}+\zeta(x,y,t,A)\frac{\partial }{\partial y}+ \tau(x,y,t,A)\frac{\partial}{\partial t}+\eta (x,y,t,A)\frac{\partial}{\partial A}. $$
(54)

The invariance criterion of system (46) can be given as follows:

$$ P^{(n)}_{r}V(\Delta)\big|_{\Delta=0}=0,\quad n=1,2,\ldots, $$
(55)

where \(\Delta=G(x,y,t,A,D^{\alpha}_{t}A,D^{2\beta}_{x}A,D^{\gamma}_{y}A,\ldots)\).

The invariance condition leads to

$$ \tau(x,y,t,A)\big|_{t=0}=0. $$
(56)

Using the second prolongation to Eq. (45), the following invariance criterion is obtained:

$$ i\eta^{\alpha}_{t}+a_{1}\eta^{2\beta}_{x}-a_{2} \eta^{2\gamma}_{y}+2a_{3}A^{*}A\eta=0. $$
(57)

Substituting (50), (52) and (53) into Eq. (57) yields the determining equations, from which we identify

$$ \begin{gathered} X_{1}=\frac{\partial}{\partial x},\qquad X_{2}=\frac{\partial}{\partial y},\qquad X_{3}=\frac{\partial}{\partial t}, \\ X_{4}=\beta y\frac{\partial}{\partial x}-\gamma x\frac{\partial }{\partial y},\qquad X_{5}=\frac{x}{\beta}\frac{\partial}{\partial x}+\frac {y}{\gamma} \frac{\partial}{\partial y}+\frac{2t}{\alpha}\frac{\partial }{\partial t}-A\frac{\partial}{\partial A}. \end{gathered} $$
(58)

With the help of Lie group analysis, we acquire the conservation laws of Eq. (45) defined by the following form:

$$ D_{t}(C_{t})+D_{x}(C_{x})+D_{y}(C_{y})=0, $$
(59)

where \(C_{t}\), \(C_{x}\) and \(C_{y}\) denote the conserved vectors.

A formal Lagrangian [59] for Eq. (45) is written as

$$ \mathcal{L}=\omega(x,y,t) \bigl(i D^{\alpha}_{t}A+a_{1}D^{2\beta}_{x}A-a_{2}D^{2\gamma }_{y}A+a_{3}A^{2}A^{*} \bigr), $$
(60)

where \(\omega(x,y,t)\) indicates a new dependent variable.

The adjoint equation of Eq. (45) is given by

$$ Q^{*}=\frac{\delta\mathcal{L}}{\delta A}, $$
(61)

where the expression of the Euler–Lagrange operator \(\frac{\delta }{\delta A}\) is defined as

$$ \begin{aligned}[b] \frac{\delta}{\delta A}={}&\frac{\partial}{\partial A}+ \bigl(D^{\alpha}_{t}\bigr)^{*}\frac {\partial}{\partial(D^{\alpha}_{t} A)}+ \bigl(D^{\beta}_{x}\bigr)^{*}\frac{\partial}{\partial (D^{\beta}_{x} A)}+ \bigl(D^{\gamma}_{y}\bigr)^{*}\frac{\partial}{\partial(D^{\gamma}_{y} A)} \\ & +\sum^{\infty}_{k=1}(-1)^{k}D_{i1}D_{i2} \cdots D_{ik}\frac{\partial }{\partial A_{i1i2\cdots ik}}. \end{aligned} $$
(62)

Here \((D^{\alpha}_{t})^{*}\) means the adjoint operator of \(D^{\alpha}_{t}\).

In addition, \(W=\eta-\tau A_{t}-\xi A_{x}-\zeta A_{y}\) is the Lie characteristic functions, we get

$$ \begin{gathered} W_{1}=-A_{x},\qquad W_{2}=-A_{y},\qquad W_{3}=-A_{t}, \\ W_{4}=-\beta yA_{x}+\gamma xA_{y},\qquad W_{5}=-A-\frac{x}{\beta}A_{x}-\frac {y}{\gamma}A_{y}- \frac{2t}{\alpha}A_{t}. \end{gathered} $$
(63)

According to the fractional generalizations of the Noether operators [38], the component of the conserved vector has the form

$$ C_{\psi}=\xi_{\psi}\mathcal{L}+\sum ^{n-1}_{k=0}(-1)^{k}D^{l-1-k}_{\psi}(W)D^{k}_{\psi}\frac{\partial\mathcal{L}}{\partial D^{l}_{\psi}A}-(-1)^{n}J \biggl(W,D^{n}_{\psi}\frac{\partial\mathcal{L} }{\partial D^{l}_{\psi}A}\biggr), $$
(64)

where \(J(\cdot)\) expresses the integral

$$ J(f,g)=\frac{1}{\Gamma(n-\alpha)} \int^{t}_{0} \int^{T}_{t}\frac{f(\tau,x,y)g(\mu ,x,y)}{(\mu-\tau)^{\alpha+1-n}}\,d\mu\, d\tau. $$
(65)

Let us take \(W_{5}\) as an example to calculate the conservation laws of Eq. (45) by using the preceding formula,

$$\begin{aligned}& \begin{aligned}[b] C_{t}&=\tau\mathcal{L}+D^{\alpha-1}_{t}(W_{5}) \frac{\partial\mathcal {L}}{\partial D^{\alpha}_{t} A}+J\biggl(W,D_{t}\frac{\partial\mathcal{L}}{\partial D^{\alpha}_{t} A}\biggr) \\ & =i\omega D^{\alpha-1}_{t}\biggl(-A-\frac{x}{\beta}A_{x}- \frac{y}{\gamma }A_{y}-\frac{2t}{\alpha}A_{t}\biggr)+J \biggl[\biggl(-A-\frac{x}{\beta}A_{x}-\frac{y}{\gamma }A_{y}- \frac{2t}{\alpha}A_{t}\biggr),i\omega_{t}\biggr], \end{aligned} \end{aligned}$$
(66)
$$\begin{aligned}& \begin{aligned}[b]C_{x}={}&\xi\mathcal{L}+D^{2\beta-1}_{x}(W_{5}) \frac{\partial\mathcal {L}}{\partial D^{2\beta}_{x} A}+J\biggl(w,D_{x}\frac{\partial\mathcal {L}}{\partial D^{2\beta}_{x} A}\biggr) \\ ={}&a_{1}\omega D^{2\beta-1}_{x}\biggl(-A- \frac{x}{\beta}A_{x}-\frac{y}{\gamma }A_{y}- \frac{2t}{\alpha}A_{t}\biggr)\\&+J\biggl[\biggl(-A-\frac{x}{\beta}A_{x}- \frac{y}{\gamma }A_{y}-\frac{2t}{\alpha}A_{t} \biggr),a_{1}\omega_{x}\biggr], \end{aligned} \end{aligned}$$
(67)
$$\begin{aligned}& \begin{aligned}[b] C_{y}={}&\zeta\mathcal{L}+D^{2\gamma-1}_{y}(W_{5}) \frac{\partial\mathcal {L}}{\partial D^{2\gamma}_{y} A}+J\biggl(w,D_{y}\frac{\partial\mathcal {L}}{\partial D^{2\gamma}_{y} A}\biggr) \\ ={}&{-}a_{2}\omega D^{2\gamma-1}_{y}\biggl(-A- \frac{x}{\beta}A_{x}-\frac{y}{\gamma }A_{y}- \frac{2t}{\alpha}A_{t}\biggr)\\&+J\biggl[\biggl(-A-\frac{x}{\beta}A_{x}- \frac{y}{\gamma }A_{y}-\frac{2t}{\alpha}A_{t} \biggr),-a_{2}\omega_{y}\biggr]. \end{aligned} \end{aligned}$$
(68)

5 Exact solutions of time–space fractional \((2+1)\) dimensional NLS equation

In this part, the \(\exp(-\phi(\xi))\) method will be applied to obtain the exact solutions to Eq. (45), as follows.

To begin with, consider the following fractional complex transformation:

$$ A(x,y,t)=A(\xi),\quad\xi=\frac{b_{1}x^{\beta}}{\Gamma(\beta+1)}+\frac {b_{2}y^{\gamma}}{\Gamma(\gamma+1)}+ \frac{b_{3}t^{\alpha}}{\Gamma(\alpha+1)}, $$
(69)

where \(b_{1}\), \(b_{2}\) and \(b_{3}\) indicate constants defined later.

Thus, Eq. (45) can be transformed into the following differential equation [60]:

$$ ib_{3}A_{\xi}+b^{2}_{1}a_{1}A_{\xi\xi}-b^{2}_{2}a_{2}A_{\xi\xi}+a_{3}A|A|^{2}=0, $$
(70)

and the complex function A can be given,

$$ A(\xi)=\frac{ib_{3}}{\exp[2(a_{2}b^{2}_{2}-a_{1}b^{2}_{1})]}\xi U(\xi), $$
(71)

where \(U(\xi)\) denotes the real function, we can get the following equation:

$$ c_{1}U+c_{2}U^{3}+c_{3}U_{\xi\xi}=0, $$
(72)

here \(c_{1}=b^{2}_{3}\), \(c_{2}=4a_{3}(a_{1}b^{2}_{1}-a_{2}b^{2}_{2})\), \(c_{3}=-4(a_{1}b^{2}_{1}-a_{2}b^{2}_{2})\).

For the purpose of balancing the highest-order derivative term and the nonlinear term of Eq. (45), it can be determined that \(n=1\), and the solutions of Eq. (72) are written

$$ U(\xi)=d_{0}+d_{1}\exp\bigl(-\phi(\xi)\bigr), $$
(73)

where \(d_{1}\) and \(d_{2}\) are constants and \(\exp(-\phi(\xi))\) satisfies the following equation:

$$ \phi'(\xi)=\exp\bigl(-\phi(\xi)\bigr)+\mu\exp\bigl(\phi(\xi) \bigr)+\lambda. $$
(74)

Substituting Eq. (73) and Eq. (74) into Eq. (70) and extracting all the same power terms of \([\exp(-\phi(\xi))]^{j}\), \(j=-3,\ldots,0\), dividing the coefficients into zero one acquires a set of algebraic equations,

$$ \begin{gathered} \phi^{3\xi}:d_{0}c_{1}+d^{3}_{0}c_{2}+c_{3}d_{1} \mu\lambda=0, \\ \phi^{2\xi}:d_{1}c_{1}+3d^{2}_{0}d_{1}c_{2}+2d_{1}c_{3} \mu+d_{1}\lambda^{2}c_{3}=0, \\ \phi^{1\xi}:3c_{2}d_{0}d^{2}_{1}+3d_{1}c_{3} \lambda=0, \\ \phi^{0\xi}:d^{3}_{1}c_{2}+2d_{1}c_{3}=0. \end{gathered} $$
(75)

Further solving the above algebraic equations (75), we will get

$$ d_{0}=\pm i\frac{\sqrt{c_{3}}\lambda}{\sqrt{2c_{2}}},\qquad d_{1}=\pm i \frac {\sqrt{2c_{3}}}{\sqrt{(}c_{2})},\qquad c_{1}=\frac{1}{2}\bigl(c_{3} \lambda^{2}+4c_{3}\mu\bigr). $$
(76)

Substituting Eq. (76) into Eq. (73) leads to

$$ U(\xi)=\pm i\frac{\sqrt{c_{3}}\lambda}{\sqrt{2c_{2}}}+\pm i\frac{\sqrt {2c_{3}}}{\sqrt{c_{2}}}\exp\bigl(-\phi(\xi) \bigr). $$
(77)

Finally, based on the above results, we can discuss solutions of different cases.

  1. (I)

    When \(\lambda^{2}-4\mu<0\) and \(\mu\neq0\), the trigonometric function solutions are written

    $$ \begin{aligned}[b] A_{2}(x,y,t)={}&{\pm}\frac{\sqrt{\lambda^{2}+4\mu}c_{3}}{\exp [2(a_{2}b^{2}_{2}-a_{1}b^{2}_{1})]}\\&\times\xi\biggl(\frac{\lambda}{2\sqrt{c_{2}}}+ \frac{1}{\sqrt {c_{2}}}\frac{2\mu}{\sqrt{4\mu-\lambda^{2}}\tan(\frac{\sqrt{4\mu-\lambda ^{2}}}{2}(\xi+C))-\lambda}\biggr).\end{aligned} $$
    (78)
  2. (II)

    When \(\lambda^{2}-4\mu>0\) and \(\mu\neq0\), the hyperbolic function solutions are written

    $$ \begin{aligned}[b] A_{1}(x,y,t)={}&{\pm}\frac{\sqrt{\lambda^{2}+4\mu}c_{3}}{\exp [2(a_{2}b^{2}_{2}-a_{1}b^{2}_{1})]}\\&\times\xi\biggl(\frac{\lambda}{2\sqrt{c_{2}}}- \frac{1}{\sqrt {c_{2}}}\frac{2\mu}{\sqrt{\lambda^{2}-4\mu}\tanh(\frac{\sqrt{\lambda^{2}-4\mu }}{2}(\xi+C))+\lambda}\biggr).\end{aligned} $$
    (79)
  3. (III)

    When \(\lambda^{2}-4\mu>0\) and \(\mu =0\), \(\lambda\neq0\), the hyperbolic function solutions are written

    $$ \begin{aligned}[b] A_{3}(x,y,t)={}&{\pm}\frac{\sqrt{\lambda^{2}+4\mu}c_{3}}{\exp [2(a_{2}b^{2}_{2}-a_{1}b^{2}_{1})]}\\&\times\xi\biggl(\frac{\lambda}{2\sqrt{c_{2}}}+ \frac{1}{\sqrt {c_{2}}}\frac{\lambda}{\cosh(\lambda(\xi+C))+\sinh(\lambda(\xi+C))-1}\biggr).\end{aligned} $$
    (80)
  4. (IV)

    When \(\lambda^{2}-4\mu=0\) and \(\mu\neq0\), \(\lambda\neq0\), the rational function solutions are written

    $$ A_{4}(x,y,t)=\pm\frac{\sqrt{\lambda^{2}+4\mu}c_{3}}{\exp [2(a_{2}b^{2}_{2}-a_{1}b^{2}_{1})]}\xi\biggl(\frac{\lambda}{2\sqrt{c_{2}}}- \frac{1}{\sqrt {c_{2}}}\frac{\lambda^{2}(\xi+C)}{2(\lambda(\xi+C)+2)}\biggr). $$
    (81)
  5. (V)

    When \(\lambda^{2}-4\mu=0\) and \(\mu=0\), \(\lambda=0\), the function solutions are written

    $$ A_{5}(x,y,t)=\pm\frac{\sqrt{\lambda^{2}+4\mu}c_{3}}{\exp [2(a_{2}b^{2}_{2}-a_{1}b^{2}_{1})]}\xi\biggl(-\frac{1}{\sqrt{c_{2}}} \frac{1}{\xi+C}\biggr). $$
    (82)

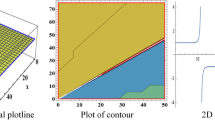
Adopting the \(\exp(-\phi(\xi))\) method, we get the exact solutions to the time–space fractional \((2+1)\) dimensional NLS equation. Based on Eq. (78), the following graphics are given (see Figures 1–7).

Figure 1
figure 1

(a) The exact solution represented by Eq. (78), \(t=2\), \(\alpha=1\), \(\beta=1\), \(\gamma=1\). (b) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=1\), \(\beta=1\), \(\gamma =1\)

Full size image
Figure 2
figure 2

(a) The exact solution represented by Eq. (78), \(t=2\), \(\alpha=0.5\), \(\beta=1\), \(\gamma=1\). (b) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=0.5\), \(\beta=1\), \(\gamma=1\)

Full size image
Figure 3
figure 3

(a) The exact solution represented by Eq. (78), \(t=2\), \(\alpha=0.75\), \(\beta=1\), \(\gamma=1\). (b) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=0.75\), \(\beta=1\), \(\gamma=1\)

Full size image
Figure 4
figure 4

(a) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=1\), \(\beta=0.25\), \(\gamma=1\). (b) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=1\), \(\beta=1\), \(\gamma =0.25\)

Full size image
Figure 5
figure 5

(a) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=1\), \(\beta=0.5\), \(\gamma=1\). (b) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=1\), \(\beta=1\), \(\gamma =0.5\)

Full size image
Figure 6
figure 6

(a) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=1\), \(\beta=0.75\), \(\gamma=1\). (b) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=1\), \(\beta=1\), \(\gamma =0.75\)

Full size image
Figure 7
figure 7

(a) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=0.25\), \(\beta=0.25\), \(\gamma=0.25\). (b) The exact solution represented by Eq. (78), \(t=3\), \(\alpha=0.5\), \(\beta =0.5\), \(\gamma=0.5\)

Full size image

In the present numerical simulation, we draw some three-dimensional graphs of the exact solution (78). First we compare the effect of the fractional order on the solution at two different moments, \(t=2\) and \(t=3\), and At a certain moment \(t=3\), the change of solution is considered in the case of changing the fractional order of time and space. The behavior shows that the change of fractional order changes the nature of the solution and has a huge influence on the nonlinear propagation of the envelope gravity waves.

6 Conclusion

In this work, we first obtain the \((2+1)\) dimensional NLS equation for envelope gravity waves by using multiple-scale, perturbation method. The semi-inverse method is applied to get the Lagrangian of the \((2+1)\) dimensional NLS equation. Then the fractional Euler–Lagrange equation with the fractional variational principle is derived. Based on the modified Riemann–Liouville fractional derivative, we can have the time–space fractional \((2+1)\) dimensional NLS equation, which can better reflect the propagation characteristics of the envelope gravity wave and capture the nonlinear phenomenon in actual atmospheric movement. Using the Lie group analysis method, the conservation laws of the time–space fractional \((2+1)\) dimensional NLS equation are discussed in depth. By adopting the \(\exp(-\phi(\xi))\) method, we list the exact solutions to different cases. Taking one of the solutions as an example, we compare the effects of fractional order for the solution. After further research, we find that the fractional model is more practical and is a pioneering effort to find help for the study of actual atmospheric and ocean movement.