1 Introduction

When nonlinearity and dispersion are exactly matched in a dispersive wave system, a kind of the stable waves of permanent form, or the solitary waves, may arise. Russell observed a solitary wave firstly in 1834. Since then, the research on solitary waves has become an advanced subject in the fields of mechanics, physics, applied mathematics, and atmospheric and oceanic sciences and attracted more and more attention [1–12]. Rossby waves as the main research object of the present paper are an important branch of solitary waves.

Rossby waves exist widely in the real world, for example, the great red spot in the atmosphere of Jupiter, eddy motion of ocean current in the Gulf of Mexico, blocking highs of the atmosphere in the earth, and so on. Rossby waves have an important effect on the propagation of energy and form and keep the western boundary current in the ocean, such as Kuroshio, East Australia current. Meanwhile, they related to many natural phenomena such as Nino phenomenon and north Atlantic interannual oscillation. The research on Rossby waves has great theoretical meaning and application value.

As we know, solitary waves such as Rossby solitary waves can be modeled by nonlinear partial differential equations. The Korteweg-de Vries (KdV) equation

$$ u_{t}+\mu uu_{x}+\delta u_{xxx}=0 $$
(1)

as the pioneer relevant equation describes the generation and evolution of Rossby solitary waves [13] and admits the two-dimensional solitary wave solution

$$ u=a \operatorname{sech}^{2}k(x-vt). $$
(2)

With the development of Rossby solitary wave theories, aiming at the stratified field, Wadati [14] derived the modified KdV equation

$$ u_{t}+\mu u^{2}u_{x}+\delta u_{xxx}=0 $$
(3)

to describe the amplitude of Rossby solitary waves. This modified KdV equation [15] possesses a two-dimensional solitary wave solution of a similar ‘sech2’ form, but its nonlinearity is stronger than that of the KdV equation and can be used to reflect the dynamics of Rossby solitary wave when the initial disturbance is stronger. Besides of the two kinds of equations, for other initial disturbance, employing a different time and space stretching transform, Meng and Lv [16] and the authors of the paper [17] also derived the Boussinesq equation

$$ u_{tt}+a_{1}u_{xx}+a_{2}u^{2}_{xx}+a_{3}u_{xxxx}=0 $$
(4)

to show Rossby solitary waves.

Looking at the researches mentioned, we can find that these researches were finished by some two-dimensional solitary wave equations. These two-dimensional solitary wave equations can describe the propagation of Rossby solitary waves in a line. However, for the general theory and real problems, such as the propagation of Rossby solitary waves on the real ridges in the ocean and the real mountains in the atmosphere, two-dimensional models are not enough to explain the dynamics of Rossby solitary waves, and three-dimensional models must be considered. In fact, although three-dimensional equations such as the Kadomtsev-Petviashvili (KP) equation [18] have already been derived to describe the interaction of internal solitary waves, for three-dimensional Rossby solitary waves, commonly referred to as ‘lumps’, have received far less attention than the two-dimensional Rossby solitary waves. In this paper, the three-dimensional Rossby solitary waves fall into our research thesis.

On the other hand, the construction of the solutions of solitary wave models has been extensively investigated in the past decade, and many methods have been proposed to solve the soliton equation [19–24]. For the above-mentioned model, similar solutions of the ‘sech2’ form are presented, and the solitary waves owning this type solutions are called classical solitary waves. With the development of solitary wave theory, the integro-differential equation

$$ u_{t}+a_{1}uu_{x}+a_{2}H(u_{xx})=0 $$

is also derived to describe Rossby solitary waves and is called the BO equation, where H denotes the well-known Hilbert transformation. In the equation, the integral term \(H(u_{xx})\) expresses the dispersive effect. The solution of the BO equation is the rational function

$$ u(x,t)=\frac{\delta}{1+\delta^{2}(x-\delta t)^{2}}, $$

and therefore the solitary waves expressed by the BO model are called algebraic solitary waves [25, 26]. Recently, professor Ma and his cooperates investigated the rational solutions of the soliton equations by the Hirota method and Maple software in [27, 28], which motivated us to use the Hirota method for rational solutions of our three-dimension solitary wave model.

The concept of ‘chirp effect’ [29] is put forward to reflect frequency modulation effect in the fiber soliton communication. Because of the interaction between nonlinearity and dispersive, the excursion of the center wave happens, which can result in the occurrence of chirp effect. For the fiber soliton, the different parts of the pulse produce different frequencies, so the chirp effect occurs during the propagation. Motivated by the chirp effect in fiber soliton communication, we discuss the chirp effect that happens during the propagation of Rossby solitary waves in the atmosphere and ocean. This paper is little involved in the past research. Particularly, we note that dissipation effect plays an important role during the propagation of Rossby solitary waves in the real ocean and atmosphere, so that the dissipation effect on the three-dimensional Rossby solitary waves also falls into our research scope.

The main purpose of the present work is to establish a model of three-dimensional Rossby solitary waves and to revel the effect of dissipation and chirp on the three-dimensional Rossby solitary waves during propagation. The plan of the paper is as follows. In Section 2, by adopting new three-dimensional time and space stretching transform, we derive a new ZK-Burgers equation to describe the evolution of three-dimensional Rossby solitary waves from the quasi-geostrophic vorticity equation. Based on the ZK-Burgers equation, the conservation laws of three-dimensional Rossby solitary waves are discussed and given in Section 3. In Section 4, we give the classical solitary wave solutions of the ZK-Burgers equation by using the sine-cosine method and the rational solutions by using the Hirota method. The rational solutions of ZK equation are obtained firstly in this paper. Based on these analytical solutions, the dissipation and chirp effect is discussed. Finally, some conclusions are given in Section 5.

2 ZK-Burgers equation

The theoretical basis of this study is the nondimensional barotrophic and quasi-geostrophic potential vorticity equation including turbulent dissipation on a β-plane channel, written as

$$ \biggl(\frac{\partial}{\partial t}+\frac{\partial\psi}{\partial x}\frac {\partial}{\partial y}- \frac{\partial\psi}{\partial y}\frac{\partial }{\partial x} \biggr) \bigl(\nabla^{2}\psi+\beta y \bigr)=-\mu_{0} \nabla^{2}\psi+Q, $$
(5)

where \(\nabla^{2}\) is the Laplace operator, φ is a geostrophic stream function, \(\nabla^{2}\psi\) denotes the vorticity dissipation caused by the Ekman boundary layer, \(0\leq\mu_{0}\ll1\) expresses the dissipative coefficient, and Q denotes the heating function to be given later.

Lateral boundary conditions is a nondimensional rigid wall boundary condition are taken as

$$ \frac{\partial\psi}{\partial x}=0, \qquad y=0, 1. $$
(6)

Here \(y=0\) and \(y=1\) denote the south and north boundaries of zonal flow, respectively.

We assume that the stream function is the sum of zonal flow and disturbance stream function of the form

$$ \psi=- \int_{0}^{y}\bigl[u(s)-c+\epsilon^{2} \alpha\bigr]\,ds+\epsilon^{2}\psi', $$
(7)

where the small parameter ϵ is much less than 1, α is called the detuning parameter and reflects the proximity of the system to a resonate state, and the Rossby waves phase speed c is taken as a constant.

Substituting (7) into (5) and (6) and dropping the apostrophe for simplicity, we obtain the following nonlinear equation and boundary conditions for the disturbance stream function:

$$\begin{aligned}& \frac{\partial}{\partial t}\nabla^{2}\psi+\bigl(u(y)-c+ \epsilon^{2}\alpha\bigr)\frac {\partial}{\partial x}\nabla^{2}\psi+ \bigl[\beta-u''(y)\bigr] \frac{\partial\psi}{\partial x} + \epsilon^{2}J\bigl(\psi,\nabla^{2}\psi\bigr) =- \mu_{0}\nabla^{2}\psi, \end{aligned}$$
(8)
$$\begin{aligned}& \frac{\partial\psi}{\partial x}=0,\qquad y=0, 1. \end{aligned}$$
(9)

We introduce the time and space stretching transform as follows:

$$ X=\epsilon x,\qquad Y=\epsilon y,\qquad T=\epsilon^{3}t. $$
(10)

We note that this transform is different from the two-dimensional transform in [13]. Meanwhile, in order to balance the dissipation and nonlinearity, we assume that

$$ \mu_{0}=\epsilon^{3}\mu,\qquad Q=- \mu_{0}\frac{du}{dy}. $$
(11)

Substituting (10) and (11) into (8) and (9), we have

$$\begin{aligned}& \biggl[\epsilon^{3}\frac{\partial}{\partial T}+\epsilon\bigl(u-c+ \epsilon^{2} \alpha \bigr)\frac{\partial}{\partial X}+\epsilon^{3}\mu \biggr]\biggl(\epsilon^{2}\frac{\partial ^{2}\psi}{\partial X^{2}} +\epsilon^{2} \frac{\partial^{2}\psi}{\partial Y^{2}}+2\epsilon\frac{\partial ^{2}\psi}{\partial Y \partial y}+\frac{\partial^{2}\psi}{\partial y^{2}}\biggr) \\& \quad {}+\epsilon \bigl(\beta-u''\bigr)\frac{\partial\psi}{\partial X} +\epsilon^{3}\frac{\partial\psi}{\partial X}\biggl(\epsilon^{3} \frac{\partial ^{3}\psi}{\partial Y^{3}}+3\epsilon\frac{\partial^{3}\psi}{ \partial y^{2}\, \partial Y}+3\epsilon^{2} \frac{\partial^{3}\psi}{\partial y\, \partial Y^{2}}+\frac{\partial^{3}\psi}{\partial y^{3}}\biggr) \\& \quad {}-\epsilon^{3}\biggl( \frac {\partial\psi}{\partial y}+\epsilon\frac{\partial\psi}{\partial Y}\biggr) \biggl(\epsilon^{2} \frac{\partial^{3}\psi}{\partial Y^{2}\, \partial X}+\frac {\partial^{3}\psi}{\partial y^{2}\, \partial X} +2\epsilon\frac{\partial^{3}\psi}{ \partial y\, \partial Y\, \partial X}\biggr) \\& \quad {}+\epsilon^{5} \frac{\partial\psi }{\partial X}\frac{\partial^{3}\psi}{ \partial y\, \partial X^{2}}+\epsilon^{6}\frac{\partial\psi}{\partial X} \frac {\partial^{3}\psi}{ \partial Y\, \partial X^{2}}-\epsilon^{5}\frac{\partial\psi}{\partial y}\frac {\partial^{3}\psi}{ \partial X^{3}}- \epsilon^{6}\frac{\partial\psi}{\partial Y}\frac{\partial ^{3}\psi}{ \partial X^{3}}=0, \end{aligned}$$
(12)
$$\begin{aligned}& \frac{\partial\psi}{\partial X}=0, \qquad y=0, 1. \end{aligned}$$
(13)

Expanding the disturbance stream function in powers of ϵ according the WKB method

$$ \psi=\psi_{0}+\epsilon\psi_{1}+ \epsilon^{2}\psi_{2}+\cdots $$
(14)

and then substituting (14) into (12) and (13), we obtain

$$ \epsilon^{1}\mbox{: } \textstyle\begin{cases} (u-c)\frac{\partial}{\partial X}\frac{\partial^{2}\psi_{0}}{\partial y^{2}}+ [\beta-u''(y)]\frac{\partial\psi_{0}}{\partial X}=0, \\ \frac{\partial\psi_{0}}{\partial X}=0,\qquad y=0,1. \end{cases} $$
(15)

Assuming that \(\psi_{0}\) has a separable solution of the form

$$ \psi_{0}=A(X,Y,T)\phi_{0}(y), $$
(16)

substituting (16) into (15), and assuming that \(u\neq c\), we have

$$ \textstyle\begin{cases} \frac{d^{2}\phi_{0}}{dy^{2}}+\frac{\beta-u''(y)}{u(y)-c}\phi_{0}=0, \\ \phi_{0}(y)=0,\qquad y=0,1. \end{cases} $$
(17)

In order to obtain the governing model of Rossby waves, we continue by solving the higher-order problem

$$ \epsilon^{2}\mbox{: }\textstyle\begin{cases} (u-c)\frac{\partial}{\partial X}\frac{\partial^{2}\psi_{1}}{\partial y^{2}}+ [\beta-u''(y)]\frac{\partial\psi_{1}}{\partial X}=-2(u-c)\frac{\partial ^{3}\psi_{0}}{\partial X\, \partial Y\, \partial y}, \\ \frac{\partial\psi_{1}}{\partial X}=0, \qquad y=0,1. \end{cases} $$
(18)

By analysis we find that it is reasonable to assume that the solution \(\psi_{1}\) has the following form:

$$ \psi_{1}=A_{Y}(X,Y,T)\phi_{1}(y). $$
(19)

In a similar way, substituting (19) into (18) leads to

$$ \textstyle\begin{cases} \frac{d^{2}\phi_{1}}{dy^{2}}+\frac{\beta-u''(y)}{u-c}\phi_{1}=-2(u-c)\frac {\partial\phi_{0}}{\partial y}, \\ \phi_{1}(y)=0,\qquad y=0,1. \end{cases} $$
(20)

We find that the governing model of Rossby solitary waves cannot be derived in order to \(O(\epsilon^{2})\), so that we need to proceed to the higher-order equation

$$ \epsilon^{3}\mbox{:}\quad \textstyle\begin{cases} (u-c)\frac{\partial}{\partial X}\frac{\partial^{2}\psi_{2}}{\partial y^{2}}+ [\beta-u''(y)]\frac{\partial\psi_{2}}{\partial X}=-2(u-c)\frac{\partial ^{3}\psi_{1}}{\partial X\, \partial Y\, \partial y}-\frac{\partial}{\partial T} \frac{\partial^{2}\psi_{0}}{\partial y^{2}}-\mu\frac{\partial^{2}\psi _{0}}{\partial y^{2}} \\ \quad {}-\alpha\frac{\partial}{\partial X}\frac{\partial^{2}\psi_{0}}{\partial y^{2}} -(u-c)\frac{\partial^{3}\psi_{0}}{\partial X^{3}}-(u-c)\frac{\partial^{3}\psi _{0}}{\partial X\, \partial Y^{2}} +\frac{\partial\psi_{0}}{\partial y}\frac{\partial^{3}\psi_{0}}{\partial X\, \partial y^{2}}- \frac{\partial\psi_{0}}{\partial X}\frac{\partial^{3}\psi_{0}}{\partial y^{3}}, \\ \frac{\partial\psi_{2}}{\partial X}=0, \qquad y=0,1. \end{cases} $$
(21)

Substituting (16) and (19) into (21), we have

$$\begin{aligned} \frac{\partial}{\partial X}\biggl(\frac{\partial^{2}\psi_{2}}{\partial y^{2}}+ \frac{\beta-u''}{u-c} \psi_{2}\biggr) =&-2\frac{\partial^{3}A}{\partial X\, \partial Y^{2}}\phi_{1y}+\biggl( \frac{\partial A}{\partial T}+\alpha\frac{\partial A}{\partial X}+\mu A\biggr)\frac{\beta-u''}{(u-c)^{2}} \phi_{0}-\frac{\partial ^{3}A}{\partial X^{3}}\phi_{0} \\ &{}-\frac{\partial^{3}A}{\partial X\, \partial Y^{2}}\phi_{0} +\frac{1}{u-c}( \phi_{0y}\phi_{0yy}-\phi_{0}\phi_{0yyy})A \frac{\partial A}{\partial X}. \end{aligned}$$
(22)

Multiplying both sides of Eq. (22) by \(\phi_{0}\) and integrating it over y from 0 to 1, by virtue of (17) and (20) and the identical relation

$$ \phi_{0}\frac{\partial^{2}\psi_{2}}{\partial y^{2}}=\frac{\partial}{\partial y}\biggl( \phi_{0}\frac{\partial\psi_{2}}{\partial y}\biggr)-\frac{\partial}{\partial y}\biggl( \psi_{2}\frac{d \psi_{0}}{dy}\biggr)+\psi_{2}\frac{d^{2}\phi_{0}}{dy^{2}}, $$
(23)

we get

$$ A_{T}+\alpha A_{X}+a_{0}AA_{X}+a_{1}A_{XXX}+ \mu A+a_{2}A_{XYY}=0, $$
(24)

where the coefficients satisfy

$$ \textstyle\begin{cases} a_{0}=\int_{0}^{1}\frac{\phi_{0}}{u-c}(\phi_{0y}\phi_{0yy}-\phi_{0}\phi _{0yyy})\, dy/\sigma,\qquad a_{1}=-\int_{0}^{1}\phi_{0}^{2}\, dy/\sigma, \\ a_{2}=-\int_{0}^{1}(\phi_{0}^{2}+2\phi_{0}\phi_{1y})\, dy/\sigma,\quad \sigma=\int_{0}^{1}\frac{\beta-u''}{(u-c)^{2}}\phi_{0}^{2}\, dy. \end{cases} $$
(25)

Equation (24) is three-dimensional. When \(a_{2}=0\), Eq. (24) reduces to the KdV-Burgers equation, which has been derived to describe two-dimensional Rossby solitary waves; when the dissipation is absent, that is, \(\mu=0\), Eq. (24) becomes a high-dimensional KdV equation, the ZK equation, so we call it the ZK-Burgers equation.

3 Conservation laws of three-dimensional Rossby solitary waves

A conservation law [30] is an important concept to describe the conservation of fundamental physical quantity and plays an important role in analyzing unsteady problems of waves during propagation. In this section, we discuss the conservation laws of three-dimensional Rossby solitary waves.

In what follows, we make the following assumption:

$$ A, A_{X}, A_{XX}, A_{XY} \rightarrow0\quad \mbox{as } |X|, |Y|\rightarrow \infty. $$
(26)

Equation (24) can be rewritten as

$$ \frac{\partial}{\partial T}A+\frac{\partial}{\partial X}\biggl(\alpha A+ \frac {a_{0}}{2}A^{2}+a_{1}A_{XX}+a_{2}A_{YY} \biggr)+\mu A=0. $$
(27)

First, integrating Eq. (27) with respect to X and Y from −∞ to +∞, by (26) we get

$$ C_{1}= \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}A\, dX\, dY=\exp(-\mu T) \int_{-\infty}^{+\infty}A(X,Y,0)\, dX\, dY. $$
(28)

It is easy to find that when dissipation is absent, that is, \(\mu=0\), \(C_{1}\) is a time-invariant quantity and denotes the conservative mass of three-dimensional Rossby solitary waves. Furthermore, from (28) we can also find that the mass of the three-dimensional Rossby solitary waves decreases exponentially with the increasing of time T and the dissipative coefficient in the presence of dissipation.

Second, multiplying Eq. (24) by 2A, we get

$$\begin{aligned} \begin{aligned}[b] &\frac{\partial}{\partial T}\bigl(A^{2}\bigr)+\frac{\partial}{\partial X} \biggl(\alpha A^{2}+\frac{2a_{0}}{3}A^{3}+2a_{1}AA_{XX}-a_{1}A_{X}^{2}+2a_{2}AA_{YY}+a_{2}A_{Y}^{2} \biggr) \\ &\quad {}-\frac {\partial}{\partial Y} (2a_{2}A_{X}A_{Y})+ \mu A^{2}=0. \end{aligned} \end{aligned}$$
(29)

In a similar way, integrating Eq. (29) with respect to X and Y from −∞ to +∞, by (26) we get

$$ C_{2}= \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}A^{2}\, dX\, dY=\exp (-2\mu T) \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}A^{2}(X,Y,0)\, dX\, dY. $$
(30)

Here \(C_{2}\) also is a time-invariant quantity and regarded as the momentum of three-dimensional Rossby solitary waves. Without dissipation, the momentum of three-dimensional Rossby solitary waves is conserved; with dissipation, it decreases exponentially with the increasing of time T and the dissipative coefficient; moreover, it decreases more quickly than the mass.

Third, multiplying both sides of Eq. (24) by \(3A^{2}\), we obtain the first equation; taking the derivative of Eq. (24) with respect to X and then multiplying by \(-6a_{1}A_{X}/a_{0}\) lead to the second equation; taking the derivative of Eq. (24) with respect to Y and then multiplying \(-6a_{2}A_{Y}/a_{0}\) lead to the third equation. Summing the above three equations and neglecting dissipation and then integrating the obtained equation with respect to X and Y from −∞ to +∞, we find that

$$ C_{3}= \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}\biggl(A^{3}- \frac {3a_{1}}{a_{0}}A_{X}^{2}-\frac{3a_{2}}{a_{0}}A_{Y}^{2} \biggr)\, dX\, dY $$
(31)

is also a time-invariant quantity and shows the conservative energy of three-dimensional Rossby solitary waves. After tedious calculation (which we omit here), we also find that the energy of three-dimensional Rossby solitary waves decreases with the increasing of time T and dissipative coefficient μ.

Besides to the above three conservation laws, let us finally construct the new quantity

$$ \widetilde{C}_{4}=\frac{d}{dT} \int_{-\infty}^{+\infty} \int_{-\infty }^{+\infty}(X+Y)A\, dX\, dY, $$
(32)

which is related to the phase of the three-dimensional Rossby solitary waves. Neglecting dissipation and using (26), (28), and (30), we easily find that \(\widetilde{C}_{4}\) is a time-invariant quantity, that is, \(\frac{d\widetilde{C}_{4}}{dT}=0\). We are more interested in the quantity

$$ C_{4}=\frac{\widetilde{C}_{4}}{C_{1}}, $$
(33)

which can be used to express the velocity of the center of gravity for the ensemble of such three-dimensional Rossby solitary waves. Because \(C_{1}\) and \(\widetilde{C}_{4}\) are both time-invariant quantities, we easily obtain that \(C_{4}\) is also a time-invariant quantities; in other words, the velocity of the center of gravity of three-dimensional Rossby solitary waves is conserved.

4 The analytical solutions of ZK equation

As a well-known soliton equation, the KdV equation plays a key role in the development of soliton theory. However, the KdV equation is considered a \((1+1)\)-dimensional model (one spatial and one time dimensions). The best known two-dimensional generalizations of the KdV equation are the KP and ZK equations. For the ZK equation, there were many researches discussing the analytical solutions of the ZK equation in different conditions with different methods [30–40], such as the ansatz method, the modified F-expansion method, and so on, some important results were obtained. Equation (24) we obtain in the paper is different from the common ZK equation due to the presence of dissipation effect. Because of the relation between KdV and ZK equation, it is reasonable to consider the classical solitary wave solutions of the ‘sech2’ form; on the other hand, motivated by the research about rational solutions of soliton equation by professor Ma, we have to think deeply whether rational solutions of the ZK equation exist. So this section is be divided into two subsections: one is devoted to seeking classical solitary wave solutions of the ZK equation by the sine-cosine method, and the other one is devoted to exploring the rational solutions of the ZK equation.

4.1 Classical solitary wave solutions

Assuming that

$$ \xi=X+Y-(C+\alpha)T, $$
(34)

where C denotes the speed of wave, we have the following transform form:

$$ \begin{aligned} &\frac{\partial}{\partial T}=-(C+\alpha)\frac{d}{d\xi}, \qquad \frac{\partial }{\partial X}=\frac{d}{d\xi}, \qquad \frac{\partial}{\partial Y}= \frac{d}{d\xi}, \\ &\frac{\partial^{2}}{\partial X^{2}}=\frac{d^{2}}{d\xi^{2}},\qquad \frac{\partial ^{2}}{\partial Y^{2}}=\frac{d^{2}}{d\xi^{2}}. \end{aligned} $$
(35)

Substituting (35) into Eq. (24) and neglecting dissipation (i.e., \(\mu=0\)), Eq. (24) can be rewritten as

$$ -CA_{\xi}+\frac{a_{0}}{2}\bigl(A^{2} \bigr)_{\xi}+a_{1}A_{\xi\xi\xi}+a_{2}A_{\xi\xi\xi}=0. $$
(36)

Integrating Eq. (39) with respect to ξ and taking the integrable constant as zero lead to

$$ -CA+\frac{a_{0}}{2}A^{2}+(a_{1}+a_{2})A_{\xi\xi}=0. $$
(37)

Suppose that Eq. (24) has solutions of the following form:

$$ A(X,Y,T)=\bigl[\lambda\cos^{\tau}(\gamma\xi)\bigr],\quad | \xi|\leq\frac{\pi}{2\gamma}, $$
(38)

or

$$ A(X,Y,T)=\bigl[\lambda\sin^{\tau}(\gamma\xi)\bigr],\quad | \xi|\leq\frac{\pi}{2\gamma}, $$
(39)

where λ, τ, and γ are undetermined parameters; γ shows the wave number. Based on this assumption, we have

$$ \begin{aligned} &A(\xi)=\lambda\cos^{\tau}(\gamma \xi),\qquad A^{2}(\xi)=\lambda^{2}\cos^{2\tau}(\gamma\xi), \\ &A_{\xi\xi}=-\gamma^{2}\tau^{2}\lambda \cos^{\tau}(\gamma\xi)+\gamma^{2}\lambda \tau(\tau-1) \cos^{\tau-2}(\gamma\xi) \end{aligned} $$
(40)

and

$$ \begin{aligned} &A(\xi)=\lambda\sin^{\tau}(\gamma \xi),\qquad A^{2}(\xi)=\lambda^{2}\sin^{2\tau }(\gamma\xi), \\ &A_{\xi\xi}=-\gamma^{2}\tau^{2}\lambda \sin^{\tau}(\gamma\xi)+\gamma^{2}\lambda \tau(\tau-1) \sin^{\tau-2}(\gamma\xi). \end{aligned} $$
(41)

Substituting (40) and (41) into Eq. (37), we have

$$ -C\cos^{\tau}(\gamma\xi)+\frac{a_{0}}{2} \lambda^{2}\cos^{2\tau}(\gamma\xi )-(a_{1}+a_{2}) \gamma^{2}\tau\lambda\cos^{\tau-2}(\gamma\xi) \bigl(\tau \sin^{2}(\gamma\xi)-1\bigr)=0 $$
(42)

and

$$ -C\sin^{\tau}(\gamma\xi)+\frac{a_{0}}{2} \lambda^{2}\sin^{2\tau}(\gamma\xi )-(a_{1}+a_{2}) \gamma^{2}\tau\lambda\sin^{\tau-2}(\gamma\xi) \bigl(\tau \cos^{2}(\gamma\xi)-1\bigr)=0. $$
(43)

In order to make these two equations hold, the following algebraic equations must be satisfied:

$$ \textstyle\begin{cases} \tau-1\neq0, \\ \tau-2=2\tau, \\ (a_{1}+a_{2})\gamma^{2}\tau^{2}=-C, \\ (a_{1}+a_{2})\gamma^{2}\lambda\tau(\tau-1)=-\frac{a_{0}}{2}\lambda^{2}. \end{cases} $$
(44)

By a direct calculation we get

$$ \tau=-2,\qquad \gamma=\frac{1}{2}\sqrt{\frac{-C}{a_{1}+a_{2}}}, \qquad \lambda=\frac{3C}{a_{0}}. $$
(45)

If \(\frac{C}{a_{1}+a_{2}}<0\), then it is easy to obtain periodic wave solutions of Eq. (24) of the following form:

$$ A(X,Y,T)=\frac{3C}{a_{0}}\csc^{2}\biggl( \frac{1}{2}\sqrt{\frac {-C}{a_{1}+a_{2}}}\bigl[X+Y-(C+\alpha) T\bigr]\biggr), \quad \frac{C}{a_{1}+a_{2}}< 0 $$
(46)

and

$$ A(X,Y,T)=\frac{3C}{a_{0}}\sec^{2}\biggl( \frac{1}{2}\sqrt{\frac {-C}{a_{1}+a_{2}}}\bigl[X+Y-(C+\alpha)T\bigr]\biggr), \quad \frac{C}{a_{1}+a_{2}}< 0. $$
(47)

Meanwhile, if \(\frac{C}{a_{1}+a_{2}}>0\), we can obtain solitary wave solutions of Eq. (24) of the following form:

$$ A(X,Y,T)=\frac{-3C}{a_{0}}\operatorname{csch}^{2} \biggl(\frac{1}{2}\sqrt{\frac {C}{a_{1}+a_{2}}}\bigl[X+Y-(C+\alpha)T\bigr] \biggr), \quad \frac{C}{a_{1}+a_{2}}>0 $$
(48)

and

$$ A(X,Y,T)=\frac{-3C}{a_{0}}\operatorname{sech}^{2} \biggl(\frac{1}{2}\sqrt{\frac {C}{a_{1}+a_{2}}}\bigl[X+Y-(C+\alpha) T\bigr] \biggr),\quad \frac{C}{a_{1}+a_{2}}>0, $$
(49)

4.2 Rational solutions

In the same way, neglecting dissipation effect and assuming that \(\alpha =0\) and \(\mu=0\), Eq. (24) can be rewritten as

$$ A_{T}+a_{0} AA_{X}+a_{1} A_{XXX}+a_{2} A_{XYY}=0. $$
(50)

For convenience, we normalize the coefficients in Eq. (50) and adopt the following transformation:

$$ A=\frac{6\sqrt[3]{a_{1}}A^{\prime}}{\sqrt[3]{3}a_{0}},\qquad X=\sqrt[3]{\frac {3}{a_{1}}}X', \qquad Y=\frac{6\sqrt[3]{9a_{1}}}{\sqrt[3]{a_{2}}}Y'. $$
(51)

Omitting the apostrophes, Eq. (50) becomes

$$ A_{T}+6AA_{X}+3A_{XXX}+3A_{XYY}=0. $$
(52)

Introducing the variable substitution \(A(X,Y,T)=v(\xi,t)\), \(\xi=l_{1} X+l_{2} Y\), letting \(6l_{1}=\gamma_{1}\) and \(3l_{1}^{2}+3l_{1} l_{2}^{2}=\gamma_{2}\), adopting the bilinear transform

$$ v=\frac{12\gamma_{2}}{\gamma_{1}}(\ln\tau)_{\xi\xi},\qquad f= \frac{g}{\tau}, $$
(53)

and letting \(v=w_{\xi}={(\frac{12\gamma_{2}\tau_{\xi}}{\gamma_{1}\tau})}_{\xi }\), after direct calculation, we have

$$\begin{aligned}& \frac{12\gamma_{2}}{\gamma_{1}}\biggl(\frac{\tau_{\xi t}}{\tau}-\frac{\tau_{\xi} \tau_{t}}{\tau^{2}} \biggr)+ \frac{\gamma_{1}}{2}\frac{12\gamma_{2}}{\gamma_{1}}^{2}\biggl( \frac{\tau_{\xi\xi }^{2}}{\tau^{2}}-\frac{2\tau_{\xi\xi}\tau_{\xi}}{\tau^{3}}+\frac{\tau_{\xi }^{4}}{\tau^{4}}\biggr) \\& \quad {}+\frac{12\gamma_{2}}{\gamma_{1}}\biggl(\frac{\tau_{\xi\xi\xi\xi}}{\tau}-\frac {4\tau_{\xi\xi\xi} \tau_{\xi}}{\tau^{2}}- \frac{3\tau_{\xi\xi}^{2}}{\tau^{2}} +\frac{12\tau_{\xi\xi}\tau_{\xi}^{2}}{\tau^{3}}-\frac{6\tau_{\xi}^{4}}{\tau^{4}}\biggr)=0. \end{aligned}$$
(54)

Then based on Eq. (54), we obtain the bilinear form of Eq. (52):

$$ D_{\xi}\bigl(D_{t}+\gamma_{2} D_{\xi}^{3}\bigr)\tau\cdot\tau=0. $$
(55)

The definition of the generalized bilinear D operator is

$$\begin{aligned} D_{p,\xi}^{m}D_{p,t}^{n} F\cdot F&=\biggl( \frac{\partial}{\partial\xi}+\alpha _{p}\frac{\partial}{\partial\xi'}\biggr)^{m} \biggl(\frac{\partial}{\partial t}+\alpha _{p}\frac{\partial}{\partial t'} \biggr)^{n} F(\xi, t)F\bigl(\xi', t'\bigr) \bigg|_{\xi'=\xi, t'=t} \\ &=\sum_{i=0}^{m}\sum _{j=0}^{n} \binom{m}{i} \binom{n}{j} \alpha_{p}^{i}\alpha_{p}^{j} \frac{\partial^{m-i}}{\partial\xi^{m-i}}\frac {\partial^{i}}{\partial\xi^{\prime i}} \frac{\partial^{n-j}}{\partial t^{n-j}}\frac{\partial^{j}}{\partial t^{\prime j}}F(\xi, t)F\bigl(\xi', t'\bigr) \bigg|_{\xi'=\xi, t'=t} \\ &=\sum_{i=0}^{m}\sum _{j=0}^{n} \binom{m}{i} \binom{n}{j} \alpha_{p}^{i}\alpha_{p}^{j} \frac{\partial^{m+n-i-j}F(\xi, t)}{\partial\xi ^{m-i}\partial t^{n-j}}\frac{\partial^{i+j} F(\xi, t)}{\partial\xi ^{i}\partial t^{j}}, \quad m, n\geq0, \end{aligned}$$

where \(\alpha_{p}^{s}\) is calculated as follows:

$$\begin{aligned}& \alpha_{p}^{s}=(-1)^{r_{p}(s)},\qquad s=r_{p}(s) \bmod p, \\& D_{2,t}D_{2,\xi} F \cdot F=2F_{\xi, t}F-2F_{t}F_{\xi}, \qquad D_{2, \xi}^{4} F\cdot F=2F_{4\xi}F-8F_{3\xi}F_{\xi}+6F_{2\xi}^{2}. \end{aligned}$$

Consequently, the linear combination of Eq. (55) yields the ZK equation

$$ D_{\xi}\bigl(D_{t}+\beta D_{\xi}^{3} \bigr)F\cdot F=2F_{\xi, t}F-2F_{t}F_{\xi}+2\beta F_{4\xi}F-8\beta F_{3\xi}F_{\xi}+6\beta F_{2\xi}^{2}. $$
(56)

We use the symbolic computation with Maple and obtain polynomial solutions of degrees of x and t less than eight to the generalized bilinear ZK equation,

$$ F= \sum_{i=0}^{8} \sum _{j=0}^{8}c_{ij} \xi^{i}t^{j}, $$
(57)

where the \(c_{ij}\) are constants, and acquire 25 classes of polynomial solutions to the Eq. (56). Among the 25 classes of solutions, we enumerate four classes of solutions as follows:

$$\begin{aligned}& {\frac{c_{{2,7}}c_{{3,2}}{\xi}^{2}{t}^{2}}{c_{{3,7}}}}+{\frac{c_{{2,7} }c_{{3,1}}{\xi}^{2}t}{c_{{3,7}}}}+{\frac{c_{{2,7}}c_{{3,4}}{\xi}^{2}{t}^{ 4}}{c_{{3,7}}}}+{ \frac{c_{{2,7}}c_{{3,6}}{\xi}^{2}{t}^{6}}{c_{{3,7}}}}+ {\frac{c_{{2,7}}c_{{3,3}}{\xi}^{2}{t}^{3}}{c_{{3,7}}}} \\& \quad {}+{\frac{c_{{2,7} }c_{{3,5}}{\xi}^{2}{t}^{5}}{c_{{3,7}}}}+c_{{0,7}}{t}^{7}+{\frac{c_{{2,7}}^{2}c_{{3,1}}\xi t}{3c_{{3,7}}^{2}}} +{\frac{c_{{2,7}}^{2}c_{{3,5}}\xi{t}^{5}}{3c_{{3,7}}^{2}}}+{ \frac{c_{{2,7}}^{2}c_{{3,2}}\xi{t}^{2}}{3c_{{3,7}}^{2}}} \\& \quad {}+{ \frac{c_{{2,7}}^{2}c_{{3,4}}\xi{t}^{4}}{3c_{{3,7}}^{2}}}+{ \frac{c_{{2,7}}^{2}c_{{3,3}}\xi{t}^{3}}{3c_{{3,7}}^{2}}}+{ \frac{c_{{2,7}}^{2}c_{{3,6}}\xi{t}^{6}}{3c_{{3,7}}^{2}}}+c_{{3,0}}{\xi}^{3}+c_{{3,1}}{ \xi}^{3}t \\& \quad {}+c_{{3,4}}{\xi }^{3}{t}^{4}+c_{{3,2}}{ \xi}^{3}{t}^{2}+c_{{2,7}}{\xi}^{2 }{t}^{7}+c_{{3,3}}{ \xi}^{3}{t}^{3}+c_{{3,6}}{\xi }^{3}{t}^{6}+c_{{3,7}}{ \xi}^{3}{t}^{7}+c_{{3,5}}{\xi}^{3}{t}^{5} \\& \quad {}+{\frac{ ( 12 \gamma_{2} c_{{3,5}}c_{{3 ,7}}-12 \gamma_{2}c_{{3,6}}^{2}+c_{{0,7}}c_{{3,6}} ) {t}^{6}}{c_{{3,7} }}}+{\frac{ ( 12 \gamma_{2} c_{{3,1}}c_{{3,7}}-12 \gamma_{2} c_{{3,2}}c_{{3,6}}+c_{{0,7}}c_{{3,2}} ) {t}^{2}}{c_{{3,7}}}} \\& \quad {}+{\frac{ ( 12 \gamma_{2} c_{ {3,2}}c_{{3,7}}-12 \gamma_{2} c_{{3,3}}c_{{3,6}}+c_{{0,7}}c_{{3,3}} ) {t} ^{3}}{c_{{3,7}}}}+{\frac{ ( 12 \gamma_{2} c_{{3,0}}c_{{3,7}}-12 \gamma_{2} c_{{3,1 }}c_{{3,6}}+c_{{0,7}}c_{{3,1}} ) t}{c_{{3,7}}}} \\& \quad {}+{\frac{ ( 12 \gamma_{2} c_{{3,4}}c_{{3,7}}-12 \gamma_{2} c_{{3,5}}c_{{3,6}}+c_{{0,7}}c_{{3,5}} ) {t}^{5}}{c_{{3,7}}}}+{\frac{ ( 12 \gamma_{2} c_{{3,3}}c_{{3,7}}- 12 \gamma_{2} c_{{3,4}}c_{{3,6}}+c_{{0,7}}c_{{3,4}} ) {t}^{4}}{c_{{3,7}}} } \\& \quad {}+12 \gamma_{2} c_{{3,7}}{t}^{8}-{ \frac{c_{{3,0}} ( 12 \gamma_{2} c_{{3,6}}-c_{{0,7}} ) }{c_{{3,7} }}}+{\frac{c_{{2,7}}c_{{3,0}}{\xi}^{2}}{c_{{3,7}}}}+{\frac{c_{{2 ,7}}^{2}\xi{t}^{7}}{3c_{{3,7}}}}+{ \frac{c_{{2,7}}^{2}c_{{3,0}}\xi }{3c_{{3,7}}^{2}}}, \end{aligned}$$
(58)
$$\begin{aligned}& c_{{3,0}}{\xi}^{3}+{\frac{c_{{2,6}}^{2}c_{{3,1}}\xi t}{3c_{{3,6}}^{2}}}+{ \frac{c_{{2,6}}^{2}c_{{3,5}}\xi{t}^{5}}{3c_{{3,6}}^{2}}} +{\frac{c_{{2,6}}^{2}c_{{3,2}}\xi{t}^{2}}{3c_{{3,6}}^{2}}}+c_{{ 3,1}}{ \xi}^{3}t+c_{{3,4}}{\xi}^{3}{t}^{4}+c_{{3,2}}{ \xi}^{3}{t}^{2} \\& \quad {}+c_{{3,3} }{\xi}^{3}{t}^{3}+c_{{3,6}}{\xi}^{3}{t}^{6}+c_{{3,5}}{ \xi}^{3}{t}^{5}+{ \frac{c_{{2,6}}c_{{3,2}}{\xi}^{2}{t}^{2}}{c_{{3,6}}}}+{ \frac{c_{{2,6}} c_{{3,1}}{\xi}^{2}t}{c_{{3,6}}}}+{\frac{c_{{2,6}}c_{{3,4}}{\xi}^{2}{t}^{4 }}{c_{{3,6}}}} \\& \quad {}+{\frac{c_{{2,6}}c_{{3,3}}{\xi}^{2}{t}^{3}}{c_{{3,6}}}}+{ \frac{c_{{2,6}}c_{{3,5}}{\xi}^{2}{t}^{5}}{c_{{3,6}}}}+{\frac{ ( 12 \gamma_{2} c_{{3,4}}c_{{3,6}}-12 \gamma_{2}c_{{3,5}}^{2}+c_{{0,6}}c_{{3,5}} ) {t}^{5}}{c_{{3,6}}}} \\& \quad {}+{\frac{ ( 12 \gamma_{2} c_{{3,3}}c_{{3,6}}- 12 \gamma_{2} c_{{3,4}}c_{{3,5}}+c_{{0,6}}c_{{3,4}} ) {t}^{4}}{c_{{3,6}}} }+{\frac{c_{{2,6 }}^{2}c_{{3,0}}\xi}{3c_{{3,6}}^{2}}}+{\frac{c_{{2,6}}^{2}\xi{t}^{6}}{3c_{{3,6}}}} \\& \quad {}-{\frac{c_{{3,0}} ( 12 \gamma_{2} c_{{3,5}}-c_{{0,6}} ) }{c_{{3,6}}}}+{ \frac{ ( 12 \gamma_{2} c_{{3, 1}}c_{{3,6}}-12 \gamma_{2} c_{{3,2}}c_{{3,5}}+c_{{0,6}}c_{{3,2}} ) {t}^{2 }}{c_{{3,6}}}} \\& \quad {}+{\frac{ ( 12 \gamma_{2} c_{{3,2}}c_{{3,6}}-12 \gamma_{2} c_{{3,3}}c _{{3,5}}+c_{{0,6}}c_{{3,3}} ) {t}^{3}}{c_{{3,6}}}}+{\frac{ ( 12 \gamma_{2} c_{{3,0}}c_{{3,6}}-12 \gamma_{2} c_{{3,1}}c_{{3,5}}+c_{{0,6}}c_{{3 ,1}} ) t}{c_{{3,6}}}} \\& \quad {}+{\frac{c_{{2,6}}^{2}c_{{3,3}}\xi{t}^{3}}{3c_{{3,6}}^{2}}}+{ \frac{c_{{2,6}}^{2}c_{{3,4}}\xi{t}^{4}}{3c_{{3,6}}^{2}}}+{\frac {c_{{2,6}}c_{{3,0}}{\xi}^{2}}{c_{{3,6}}}}+c_{{0,6}}{t}^{6} +c_{{2,6}}{\xi}^{2}{t}^{6}+12 \gamma_{2} c_{{3,6}}{t}^{7}, \end{aligned}$$
(59)
$$\begin{aligned}& -{\frac{ ( 1\text{,}866\text{,}240 {\gamma}_{2}^{2}c_{{6,0}}^{2}c_{{6,1}}^{4}-62\text{,}208 \gamma_{2} c_{{3,1}}c_{{6,0}}c_{{6,1}}^{4}+6\text{,}480 \gamma _{2}c_{{5,1}}^{3} c_{{6,0}}c_{{6,1}}^{2}-432 c_{{1,1}}c_{{5,1}}c_{{6,1}}^{4} ) }{2\text{,}592 c_{{6,1}}^{6}c_{{6,0}}^{-1}}} \\& \quad {}-{\frac{c_{{6,0}} (5\text{,}184 c_{{3,1}}^{2}c_{{6,1}}^{4}-720 c_{{3,1}}c_{{5,1}}^{3}c_{{6,1 }}^{2}+25 c_{{5,1}}^{6} ) }{25\text{,}920 c_{{6,1}}^{6}}}+c_{{1,1}}xt+c_{{3,1}}{x}^{3}t+30 \gamma_{2} c_{{5,1}}{\xi}^{2}{t}^{2} \\& \quad {}+{\frac{c_{{5,1}} ( 72 c_{ {3,1}}c_{{6,1}}^{2}-5 c_{{5,1}}^{3} ) {\xi}^{2}t}{144 c_{{6 ,1}}^{3}}}+{\frac{c_{{5,1}}c_{{6,0}}{\xi}^{5}}{c_{{6,1}}}}+{ \frac{\gamma_{2} ( 1\text{,}440 \gamma_{2} c_{{6,0}}c_{{6,1}}^{2}-48 c_{{3,1}}c_{{6,1} }^{2}+5 c_{{5,1}}^{3} ) {t}^{2}}{2c_{{6,1}}^{2}}} \\& \quad {}-{\frac{c _{{5,1}}c_{{6,0}} ( 4\text{,}320 \gamma_{2} c_{{6,0}}c_{{6,1}}^{2}-72 c_{{3,1}} c_{{6,1}}^{2}+5 c_{{5,1}}^{3} ) {\xi}^{2}}{144 c_{{6,1}}^{ 4}}}+60 \gamma_{2} c_{{6,1}}{ \xi}^{3}{t}^{2}-720 {\gamma} _{2}^{2}c_{{6,1}}{t}^{3} \\& \quad {}+{\frac { ( 18\text{,}662\text{,}400 {\gamma}_{2}^{2}c_{{6,0}}^{2}c_{{6,1}}^{4}+4\text{,}320 c_{{1,1 }}c_{{5,1}}c_{{6,1}}^{4}-5\text{,}184 c_{{3,1}}^{2}c_{{6,1}}^{4}+720 c _{{3,1}}c_{{5,1}}^{3}c_{{6,1}}^{2}-25 c_{{5,1}}^{6} ) t}{ 25\text{,}920 c_{{6,1}}^{5}}} \\& \quad {}+{\frac{5\beta c_{{5,1}}^{2}\xi {t}^{2}}{c_{{6,1}}}}-{\frac{c_{{6,0}} ( 60 \gamma_{2} c _{{6,0}}-c_{{3,1}} ) {\xi}^{3}}{c_{{6,1}}}}+{\frac{5 c_{{5,1}} ^{2}c_{{6,0}}{\xi}^{4}}{12 c_{{6,1}}^{2}}}-{ \frac{c_{{6,0}} ( 5 \gamma_{2}c_{{5,1}}^{2}c_{{6,0}}-c_{{1 ,1}}c_{{6,1}}^{2} ) \xi}{c_{{6,1}}^{3}}} \\& \quad {}+{\frac{5 c_{{5,1}}^{2} {\xi}^{4}t}{12 c_{{6,1}}}}+c_{{6,1}}{\xi}^{6}t+c_{{5,1}}{ \xi }^{5}t+c_{{6,0}}{\xi}^{6}, \end{aligned}$$
(60)
$$\begin{aligned}& {\frac{4\text{,}320 c_{{1,0}}c_{{5,0}}c_{{6,0}}^{4}-5\text{,}184 c_{{3,0}}^{2} c_{{6,0}}^{4}+720 c_{{3,0}}c_{{5,0}}^{3}c_{{6,0}}^{2}-25 c_{{5 ,0}}^{6}}{25\text{,}920 c_{{6,0}}^{5}}}+ {\frac{5\gamma_{2}c_{{5,0}} ^{2}\xi t}{c_{{6,0}}}}+c_{{5,0}}{ \xi}^{5} \\& \quad {}-720 {\gamma} _{2}^{2}c_{{6,0}}{t}^{2}+{ \frac{c_{{5,0}} ( 72 c_{{3,0}}c_{{6,0}}^{2}-5 c_{{5,0}}^{3} ) {\xi}^{2}}{144 c _{{6,0}}^{3}}}-{\frac{\gamma_{2} ( 48 c_{{3,0}}{c_{{6,0}}}^{2}-5 {c_{{5,0}}}^{3} ) t}{2{c_{{6,0}}}^{2}}} \\& \quad {}+c_{{6,0}}{\xi}^{6}+c_{{3,0} }{ \xi}^{3}+{\frac{5 c_{{5,0}}^{2}{\xi}^{4}}{12 c_{{6,0}}}}+c_{{1,0}}\xi+60 \gamma_{2} c_{{6,0}}{\xi}^{3}t+30 \gamma_{2} c_{{5,0}}{\xi}^{2}t, \end{aligned}$$
(61)

where the involved constants \(c_{ij}\) are arbitrary, provided that the solutions are meaningful. We can confirm that there are two distinct classes of rational solutions generated from (57) to the ZK equation by considering the transformation of the coefficient \(c_{ij}\):

$$\begin{aligned} u =& ( 3 xc_{{3,7}}+c_{{2,7}} ) \bigl( 3 {x}^{3} c_{{3,7}}^{2}+36 \beta tc_{{3,7}}^{2}+3 {x}^{2}c_{{2,7}}c_{{3,7}}-36 \beta c_{{3,6}}c_{{3,7}}+xc_{{2,7}}^{2}+3 c_{{0,7}}c_{{3,7}} \bigr)^{-2} \\ &{}\times \bigl( -9 {x}^{3}c_{{3,7}}^{3}+216 \beta tc_{{3,7}}^{3}-9 { x}^{2}c_{{2,7}}c_{{3,7}}^{2}-216 \beta c_{{3,6}}c_{{3,7}}^{2} \\ &{}-3 xc_{ {2,7}}^{2}c_{{3,7}}+18 c_{{0,7}}c_{{3,7}}^{2}-c_{{2,7}}^{3} \bigr) \end{aligned}$$
(62)

and

$$\begin{aligned}& u=-360\frac{p}{q}, \\& p= 11\text{,}197\text{,}440 {x}^{10}c_{{6,0}}^{10}+18 \text{,}662\text{,}400 {x} ^{9}c_{{5,0}}c_{{6,0}}^{9}+60 \text{,}466\text{,}176\text{,}000 {\beta}^{2}{t}^{2}{x}^{4}c_{{6,0 }}^{10} \\& \hphantom{p={}}{}+13 \text{,}996\text{,}800 {x}^{8}c_{{5,0}}^{2}c_{{6,0}}^{8}+483\text{,}729\text{,}408\text{,}000 {\beta}^{3}{t}^{3}xc_{{6,0}}^{10} \\& \hphantom{p={}}{}+40 \text{,}310\text{,}784\text{,}000 {\beta }^{2}{t}^{2}{x}^{3}c_{{5,0}}c_{{6,0}}^{9} +6 \text{,}220\text{,}800 {x}^{7}c_{{5,0}}^{3}c_{{6,0}}^{7} \\& \hphantom{p={}}{}+80\text{,}621\text{,}568\text{,}000 {\beta }^{3}{t}^{3}c_{{5,0}}c_{{6,0}}^{9} +10 \text{,}077\text{,}696\text{,}000 {\beta}^{ 2}{t}^{2}{x}^{2}c_{{5,0}}^{2}c_{{6,0}}^{8} \\& \hphantom{p={}}{}+2 \text{,}015\text{,}539\text{,}200 \beta t{x}^{4}c_{{3,0}}c_{{6,0}}^{9} -186\text{,}624\text{,}000 \beta t{x}^{4}c_{{5,0}}^{3}c_{{6,0}}^{7}+1 \text{,}814\text{,}400 {x}^{6}c_{{5,0}}^{4}c_{{6,0}}^{6} \\& \hphantom{p={}}{}+24 \text{,}186\text{,}470\text{,}400 {\beta}^{2 }{t}^{2}xc_{{3,0}}c_{{6,0}}^{9} -1\text{,}119\text{,}744\text{,}000 {\beta}^{2}{t}^{2}xc_{{5,0} }^{3}c_{{6,0}}^{7} \\& \hphantom{p={}}{}+1 \text{,}343\text{,}692\text{,}800 \beta t{x}^{3}c_{{3,0}}c_{{5,0}}c_{{6,0} }^{8} -124 \text{,}416\text{,}000 \beta t{x}^{3}c_{{5,0}}^{4}c_{{6,0}}^{6} \\& \hphantom{p={}}{}-33\text{,}592\text{,}320 {x}^{5}c_{{1,0}}c_{{6,0}}^{9}+2 \text{,}799\text{,}360 {x}^{5}c_{{3,0}}c_{{5,0}}^{2} c_{{6,0}}^{7}+129\text{,}600 {x}^{5}c_{{5,0}}^{5}c_{{6,0}}^{5} \\& \hphantom{p={}}{}+ 4\text{,}031\text{,}078\text{,}400 {\beta}^{2} {t}^{2}c_{{3,0}}c_{{5,0}}c_{{6,0}}^{8} -326\text{,}592\text{,}000 {\beta}^{2}{t}^{2}c_{{5,0}}^{4}c_{{6,0}}^{6} \\& \hphantom{p={}}{}+335\text{,}923\text{,}200 \beta t{x}^{2}c_{ {3,0}}c_{{5,0}}^{2}c_{{6,0}}^{7} -31\text{,}104\text{,}000 \beta t {x}^{2}c_{{5,0}}^{5 }c_{{6,0}}^{5}-27 \text{,}993\text{,}600 {x}^{4}c_{{1,0}}c_{{5,0}}c_{{6,0}}^{8} \\& \hphantom{p={}}{}+ 16\text{,}796\text{,}160 {x}^{4}c_{{3,0}}^{2}c_{{6,0}}^{8}-777 \text{,}600 {x}^{4}c_{{3,0 }}c_{{5,0}}^{3}c_{{6,0}}^{6} +403\text{,}107\text{,}840 \beta txc_{{3,0}}^{2}c_{{6,0 }}^{8} \\& \hphantom{p={}}{}-37 \text{,}324\text{,}800 \beta txc_{{3,0}}c_{{5,0}}^{3}c_{{6,0}}^{6}-9 \text{,}331\text{,}200 {x}^{3}c_{{1,0}}c_{{5,0}}^{2}c_{{6,0}}^{7} +11\text{,}197\text{,}440 {x}^{3}c_{{3 ,0}}^{2}c_{{5,0}}c_{{6,0}}^{7} \\& \hphantom{p={}}{}-1 \text{,}296\text{,}000 {x}^{3}c_{{3,0}}c_{{5,0}} ^{4}c_{{6,0}}^{5}+36\text{,}000 {x}^{3}c_{{5,0}}^{7}c_{{6,0}}^{3} + 67\text{,}184\text{,}640 \beta tc_{{3,0}}^{2} c_{{5,0}}c_{{6,0}}^{7} \\& \hphantom{p={}}{}-10\text{,}886\text{,}400 \beta tc_{{3,0 }}c_{{5,0}}^{4}c_{{6,0}}^{5}+432 \text{,}000 \beta tc_{{5,0}}^{7}c_{{6,0}}^{3}-1 \text{,}555\text{,}200 {x}^{2}c_{{1,0}}c_{{5,0}}^{3}c_{{6,0}}^{6} \\& \hphantom{p={}}{}+2\text{,}799\text{,}360 {x}^{2}c_{{3,0}}^{2}c_{{5,0}}^{2}c_{{6,0}}^{6}-388 \text{,}800 {x}^{2}c_{ {3,0}}c_{{5,0}}^{5}c_{{6,0}}^{4}+13 \text{,}500 {x}^{2}c_{{5,0}}^{8}c_{ {6,0}}^{2} \\& \hphantom{p={}}{}-129\text{,}600 x c_{{1,0}}c_{{5,0}}^{4}c_{{6,0}}^{5}+2 \text{,}239\text{,}488 xc_{{3,0}}^{3}c_{{6,0}}^{7}-311 \text{,}040 xc_{{3,0}}^{2}c_{{5,0}}^{3 }c_{{6,0}}^{5} \\& \hphantom{p={}}{}+10 \text{,}800 xc_{{3,0}}c_{{5,0}}^{6}c_{{6,0}}^{3} +1\text{,}866\text{,}240 c_{{1,0}}^{2}c_{{6,0}}^{8}-311 \text{,}040 c_{{1,0}}c_{{3,0}}c_{ {5,0}}^{2}c_{{6,0}}^{6} \\& \hphantom{p={}}{}+21 \text{,}600 c_{{1,0}}c_{{5,0}}^{5}c_{{6,0}}^{4}+373 \text{,}248 c_{{3,0}}^{3}c_{{5,0}}c_{{6,0}}^{6} -77\text{,}760 c_{{3,0}} ^{2}c_{{5,0}}^{4}c_{{6,0}}^{4} \\& \hphantom{p={}}{}+5 \text{,}400 c_{{3,0}}c_{{5,0}}^{7}c_{{ 6,0}}^{2}-125 c_{{5,0}}^{10}c_{{6,0}}^{2}, \\& q= \bigl( -25\text{,}920 {x}^{6}c_{{6,0}}^{6}-1 \text{,}555\text{,}200 \beta t{x}^{3}c_{{6,0}}^{6}-25 \text{,}920 {x}^{5}c_{{5,0}}c_{{6,0}}^{5}+18 \text{,}662\text{,}400 {\beta }^{2}{t}^{2}c_{{6,0}}^{6} \\& \hphantom{q={}}{}-777\text{,}600 \beta t{x}^{2}c_{{5,0}}c_{{6,0}}^{5}-10\text{,}800 {x}^{4}c_{{5,0}} ^{2}c_{{6,0}}^{4}-129\text{,}600 \beta txc_{{5,0}}^{2}c_{{6,0}}^{4}-25\text{,}920 {x}^{3}c_{{3,0}}c_{{6,0}}^{5} \\& \hphantom{q={}}{}+622\text{,}080\beta tc_{{3,0}}c_{{6,0}}^{5}- 64\text{,}800 \beta tc_{{5,0}}^{3}c_{{6,0}}^{3}-12 \text{,}960 {x}^{2}c_{{3,0}}c_{{5,0 }}c_{{6,0}}^{4}+900 {x}^{2}c_{{5,0}}^{4}c_{{6,0}}^{2} \\& \hphantom{q={}}{}-25 \text{,}920 xc_{{1,0}}c_{{6,0}}^{5}-4\text{,}320 c_{{1,0}}c_{{5,0}}c_{{6,0}}^{4}+5 \text{,}184 c_{{3,0}}^{2}c_{{6,0}}^{4}-720 c_{{3,0}}c_{{5,0}}^{3}c_{{6,0} }^{2}+25 c_{{5,0}}^{6} \bigr) ^{2}. \end{aligned}$$
(63)

In fact, the polynomial solutions in the first group of (58)-(59) and the second group of (60)-(61) change into (62) and (63), respectively.

The first class of solutions in (62) reduces to

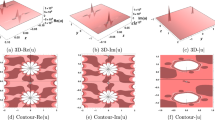
$$\begin{aligned}& u=\frac{p}{q}, \\& p=\bigl(-0.11979\cdot10^{-7}x^{3}+0.287496 \cdot10^{-9}t-0.1089\cdot 10^{-7}x^{2}+0.1616264 \cdot10^{-7} \\& \hphantom{p={}}{}-0.33\cdot10^{-8}x\bigr) \bigl(0.33\cdot 10-2x+0.1 \cdot10^{-2}\bigr), \\& q=\bigl(0.363\cdot10^{-5}x^{3}+0.4356\cdot10^{-7}t+0.33 \cdot 10^{-5}x^{2}+0.26004\cdot10^{-5}+0.1 \cdot10^{-5}x\bigr)^{2}, \end{aligned}$$
(64)

when \(c_{3,7}=0.0011\), \(c_{2,7}=0.001\), \(c_{3,6}=0.001\), \(c_{0,7}=0.0008\), \(\beta=0.001\). The picture of the solution (64) is presented in Figure 1.

Figure 1
figure 1

The solution ( 64 ).

Full size image

From the second class of solutions in (63) we obtain

$$\begin{aligned}& u=\frac{p}{q}, \\& p= -0.17640\cdot10^{-5}\bigl(0.4404601350\cdot10^{-38}t+0.9501485144 \cdot 10^{-36}x \\& \hphantom{p={}}{}+0.5079242590\cdot10^{-40}t^{2} +0.1952022642\cdot10^{-42}t^{3}+0.3162999652 \cdot 10^{-34}x^{10} \\& \hphantom{p={}}{}+0.4518570932\cdot10^{-34}x^{9} -0.4663481371\cdot10^{-35}x^{4}+0.2904795599 \cdot10^{-34}x^{8} \\& \hphantom{p={}}{}+0.1106588800\cdot10^{-34}x^{7} +0.2766471999\cdot10^{-35}x^{6}-0.2362228335 \cdot10^{-34}x^{5} \\& \hphantom{p={}}{}+0.8273408826\cdot 10^{-36}x^{2} +0.2225160652\cdot10^{-35}x^{3} +0.4658120333\cdot10^{-36} \\& \hphantom{p={}}{}+0.1708019812\cdot10^{-38}t^{2} x^{4}+0.1366415850\cdot10^{-41}t^{3} x +0.9760113212\cdot10^{-39}t^{2} x^{3} \\& \hphantom{p={}}{}+0.2091452831\cdot10^{-39}t^{2} x^{2}+0.2921394431\cdot10^{-36}t x^{4} +0.3704859301\cdot10^{-39}t^{2} x \\& \hphantom{p={}}{}+0.1669368246\cdot10^{-36}t x^{3}+0.3577217671 \cdot10^{-37}t x^{2} +0.3338736493\cdot10^{-37}t x\bigr), \\& q= \bigl(-0.3049462080\cdot10^{-20}x^{6}-0.1829677248 \cdot10^{-22}t x^{3}-0.2613824640\cdot10^{-20}x^{5} \\& \hphantom{q={}}{} +0.2195612698\cdot10^{-25}t^{2}-0.7841473920 \cdot10^{-23}t x^{2}-0.933508800\cdot10^{-21}x^{4} \\& \hphantom{q={}}{}-0.1120210560\cdot10^{-23}t x-0.1742549760\cdot 10^{-20}x^{3}+0.3702029184\cdot10^{-23}t \\& \hphantom{q={}}{} -0.689653440\cdot10^{-21}x^{2}-0.871274880 \cdot10^{-21}x+0.45365184\cdot 10^{-22}\bigr)^{2}, \end{aligned}$$
(65)

when \(c_{6,0}=0.00007\), \(c_{5,0}=0.00006\), \(c_{3,0}=0.00004\), \(c_{1,0}=0.00002\), \(\beta =0.0001\). The picture of the solution (65) is presented in Figure 2.

Figure 2
figure 2

The solution ( 65 ).

Full size image

Remarks

As we know, the integro-differential equations (BO, ILW) which own the rational function solutions can be used to describe the algebraic solitary waves; these rational solutions can be used to describe the fission of solitary waves and to explain the possible physical mechanism of the squall line in the real atmosphere. On the other hand, the differential equations (KdV, mKdV) can describe the classic solitary waves. Now, through the above deduction, we can learn that the ZK-Burgers equation as a differential equation has rational function solutions. Can it also describe algebraic solitary waves? It is an open problem. We will discuss it in the future.

5 Dissipation and chirp effect of three-dimensional Rossby solitary waves

In Section 4, we have derived the analytical solutions of Eq. (24) without dissipation effect. In this section, based on the solitary wave solution (49), on the one hand, we will seek an approximate analytical solution of Eq. (20) with dissipation and, furthermore, discuss the influence of dissipation on the three-dimensional Rossby solitary waves by using the obtained approximate analytical solution. On the other hand, we will study the chirp effect of three-dimensional Rossby solitary waves.

5.1 Dissipation effect of three-dimensional Rossby solitary waves

Because of \(\mu\ll1\) and \(\mu\ll a_{0}\sim a_{1}+a_{2}\), we take the new space coordinate

$$ \rho=X+Y- \int_{0}^{T}\alpha+\frac{a_{0} A_{0}}{3}\, dT. $$
(66)

Assuming that \(A_{0}=A_{0}(\mu T)\) and substituting (66) into Eq. (24), we have

$$ \frac{\partial A}{\partial T}-\frac{a_{0} A_{0}}{3}\frac{\partial A}{\partial\rho}+a_{0} A\frac{\partial A}{\partial\rho}+(a_{1}+a_{2}) \frac{\partial^{3}A}{\partial\rho^{3}}+\mu A=0. $$
(67)

Introducing two time scales

$$ \tau=T,\qquad \eta=\mu T, $$
(68)

and assuming the solution as

$$ A(\rho,T)=A_{1}(\rho,\tau,\eta)+\mu A_{2}( \rho,\tau)+\cdots, $$
(69)

we obtain the following approximate equations:

$$\begin{aligned}& \mu^{0}\mbox{: } \frac{\partial A_{1}}{\partial\tau}-\frac{a_{0} A_{0}}{3} \frac {\partial A_{1}}{\partial\rho}+a_{0} A_{1}\frac{\partial A_{1}}{\partial\rho }+(a_{1}+a_{2}) \frac{\partial^{3}A_{1}}{\partial\rho^{3}}=0, \end{aligned}$$
(70)
$$\begin{aligned}& \mu^{1}\mbox{: } \frac{\partial A_{2}}{\partial\tau}-\frac{a_{0} A_{0}}{3} \frac {\partial A_{2}}{\partial\rho}+a_{0}\biggl(A_{1}\frac{\partial A_{2}}{\partial\rho }+A_{2} \frac{\partial A_{1}}{\partial\rho}\biggr)+(a_{1}+a_{2})\frac{\partial ^{3}A_{2}}{\partial\rho^{3}}=- \frac{\partial A_{1}}{\partial\eta}-A_{1}. \end{aligned}$$
(71)

Taking

$$ \zeta=\rho+\frac{a_{0} A_{0}}{3}\tau, $$
(72)

Eqs. (70) and (71) can be rewritten as

$$\begin{aligned}& \mu^{0}\mbox{: } \frac{\partial A_{1}}{\partial\tau}+a_{0} A_{1}\frac{\partial A_{1}}{\partial\rho}+(a_{1}+a_{2}) \frac{\partial^{3}A_{1}}{\partial\rho^{3}}=0, \end{aligned}$$
(73)
$$\begin{aligned}& \mu^{1}\mbox{: }\frac{\partial A_{2}}{\partial\tau}+a_{0} \biggl(A_{1}\frac{\partial A_{2}}{\partial\rho}+A_{2}\frac{\partial A_{1}}{\partial\rho} \biggr)+(a_{1}+a_{2})\frac {\partial^{3}A_{2}}{\partial\rho^{3}}=- \frac{\partial A_{1}}{\partial\eta}-A_{1}. \end{aligned}$$
(74)

Equation (73) is the common ZK equation; without loss of generality, based on (49), we take into account its solitary wave solution as

$$ A_{1}(\zeta,\tau)=-A_{0}\operatorname{sech}^{2} \biggl\{ \biggl(\frac {A_{0}a_{0}}{12(a_{1}+a_{2})} \biggr)^{\frac{1}{2}}\biggl(\zeta- \frac{a_{0} A_{0}}{3}\tau \biggr) \biggr\} , $$
(75)

where \(A_{0}=\frac{3C}{a_{0}}\). Substituting (50) into (75), we have the following approximate solitary wave solution of Eq. (24):

$$ A_{1}(X,T)=-A_{0}\operatorname{sech}^{2} \biggl\{ \biggl(\frac{A_{0}a_{0}}{12(a_{1}+a_{2})} \biggr)^{\frac{1}{2}}\biggl(X+Y- \int_{0}^{T}(\alpha+C)\, dT\biggr) \biggr\} \frac{C}{a_{1}+a_{2}}>0. $$
(76)

Next, in order to determine the form of \(A_{0}(\mu T)\), it is necessary to solve Eq. (74). Taking

$$ A_{2}=B(I), \quad I=\zeta-C\tau, $$
(77)

and substituting (77) into Eq. (74) lead to

$$ -v\frac{dB}{dI}+a_{0}\frac{\partial}{\partial I} (A_{1}B )+(a_{1}+a_{2})\frac{\partial^{3}B}{\partial I^{3}}=M(A_{1}), $$
(78)

where \(M(A_{1})=-\frac{\partial A_{1}}{\partial\eta}-A_{1}\). The solvability condition of Eq. (78) is

$$ \int_{-\infty}^{+\infty}G(I)M(A_{1})\, dI=0, $$
(79)

where \(G(I)\) satisfies

$$ -v\frac{dG}{dI}+a_{0} A_{1} \frac{dG}{dI}+(a_{1}+a_{2})\frac{\partial ^{3}G}{\partial I^{3}}=0. $$
(80)

Obviously, if \(G(\pm\infty)=0\) is satisfied, then the solution of Eq. (64) is

$$ G=-A_{0}\operatorname{sech}^{2} \biggl\{ \biggl(\frac{A_{0}a_{0}}{12(a_{1}+a_{2})} \biggr)^{\frac{1}{2}}(\zeta-vT) \biggr\} . $$
(81)

Substituting (81) into Eq. (79), we have

$$ A_{0}=\frac{3C}{a_{0}}e^{-\frac{4\mu T}{3}}. $$
(82)

So the approximate solitary wave solution of the ZK-Burgers equation is

$$ A(X,T)=-A_{1}(T)\operatorname{sech}^{2} \biggl\{ \biggl(\frac {A_{1}(T)a_{0}}{12(a_{1}+a_{2})} \biggr)^{\frac{1}{2}}\biggl(X+Y- \int_{0}^{T}\alpha+\frac {a_{0} A_{1}(T)}{3}\, dT\biggr) \biggr\} , $$
(83)

where

$$ A_{1}(T)=\frac{3C}{a_{0}}e^{-\frac{4\mu T}{3}}. $$
(84)

In the same way, we can also obtain other approximate periodic wave and solitary wave solutions. Based on (83), it is easy to find that the propagation speed and width of three-dimensional Rossby solitary waves are as follows, respectively:

$$\begin{aligned}& c_{s}=\alpha+Ce^{-\frac{4\mu T}{3}}, \end{aligned}$$
(85)
$$\begin{aligned}& W_{s}=2\sqrt{\frac{a_{1}+a_{2}}{C}} e^{\frac{2}{3}\mu T}. \end{aligned}$$
(86)

It is obvious that the propagation speed of three-dimensional Rossby solitary waves decreases exponentially with the increasing of μ and time T; on the contrary, the width of three-dimensional Rossby solitary waves increases exponentially with the increasing of μ and time T. The figures of three-dimensional Rossby solitary waves at three different time points are as follows.

From Figures 3-5 we also find that, due to dissipation effect, the amplitude of three-dimensional Rossby solitary waves also decreases with time T.

Figure 3
figure 3

Three-dimensional Rossby solitary wave with \(\pmb{\mu =0.05}\) at \(\pmb{T=0}\) .

Full size image
Figure 4
figure 4

Three-dimensional Rossby solitary wave with \(\pmb{\mu =0.05}\) at \(\pmb{T=5}\) .

Full size image
Figure 5
figure 5

Three-dimensional Rossby solitary wave with \(\pmb{\mu =0.05}\) at \(\pmb{T=10}\) .

Full size image

5.2 Chirp effect of three-dimensional Rossby solitary waves

The Chirp effect is a concept from optical soliton communication area and is also called the frequency modulation effect. Because of the dispersion and nonlinear effect, the excursion phenomenon of the center wave occurs, and the chirp effect is caused. In this subsection, we introduce the chirp idea of optical soliton communication and analyze the dispersion and nonlinear effect during the propagation process of three-dimensional Rossby solitary waves. It is beneficial for studying the propagation feature of three-dimensional Rossby solitary waves.

For the ZK-Burgers equation (24), let us neglect dissipation effect (\(\mu=0\)) and take the detuning parameter \(\alpha= 0\), that is, the system is resonant. Then the equation can be rewritten as

$$ A_{T}+a_{0}AA_{X}+a_{1}A_{XXX}+a_{2}A_{XYY}=0, $$
(87)

where \(a_{0}\) is the nonlinear coefficient, and \(a_{1}\) and \(a_{2}\) are dispersion coefficients. Here, based on the analytical solution of the ZK equation, we take the initial wave form of three-dimensional Rossby solitary waves as

$$ A=\frac{-C}{a_{0}}\operatorname{sech}^{2}\biggl[ \frac{1}{2}\sqrt{\frac {C}{a_{1}+a_{2}}}(X+Y)\biggr], \quad \frac{C}{a_{1}+a_{2}}>0. $$
(88)

First, we discuss the nonlinear effect of three-dimensional Rossby solitary waves alone. Then Eq. (87) becomes

$$ A_{T}=-a_{0}AA_{X}. $$
(89)

Investigating the condition of time T from 0 to ΔT, where Δt is an infinitesimal variable, and introducing (88) into Eq. (89), we obtain the following approximate solution of Eq. (89):

$$\begin{aligned} A(\varDelta T, X, Y) =&\frac{C^{2}}{a_{0}^{2}}\operatorname{sech}^{2} \biggl[\frac{1}{2}\sqrt {\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr]\exp\biggl\{ \frac{-2C^{4}\varDelta T}{a_{0}^{3}} \\ &{}\times \operatorname{sech}^{2} \biggl[\frac{1}{2}\sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr]\tanh\biggl[ \frac{1}{2}\sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr]\biggr\} . \end{aligned}$$
(90)

Based on the approximate solution (90), it is easy to give the phase of the wave as follows:

$$\begin{aligned} \varphi_{N} =&\frac{-2C^{4}\varDelta T}{a_{0}^{3}}\operatorname{sech}^{2} \biggl[\frac{1}{2}\sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr] \\ &{}\times\tanh\biggl[ \frac{1}{2}\sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr]. \end{aligned}$$
(91)

Then the chirp caused by nonlinearity is

$$\begin{aligned} \varDelta \nu_{N} =&-\nabla\varphi_{N} \\ =& \frac{2C^{4}\varDelta T}{a_{0}^{3}}\sqrt{\frac {C}{a_{1}+a_{2}}}\biggl\{ 2\operatorname{sech}^{2} \biggl[\frac{1}{2}\sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr] \\ &{}\times\tanh^{2}\biggl[\frac{1}{2}\sqrt {\frac{C}{a_{1}+a_{2}}}(X+Y) \biggr]+\tanh^{4}\biggl[\frac{1}{2}\sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y) \biggr]\biggr\} . \end{aligned}$$
(92)

Second, neglecting the nonlinearity effect, let us consider the dispersion effect alone. Then Eq. (87) becomes

$$ A_{T}=-a_{1}A_{XXX}-a_{2}A_{XYY}. $$
(93)

In a similar way, we can get an approximate solution of Eq. (93),

$$\begin{aligned} A(\varDelta T, X, Y) =&\frac{C^{2}}{a_{0}^{2}}\operatorname{sech}^{2} \biggl[\frac{1}{2}\sqrt {\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr] \exp\biggl\{ - \frac{(a_{1}+a_{2})\varDelta T}{16}\biggl(\frac{C}{a_{1}+a_{2}}\biggr)^{\frac{3}{2}} \\ &{}\times\biggl[1+2\operatorname{sech}^{2}\biggl(\frac{1}{2} \sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr) \\ &{}\times\tanh\biggl(\frac{1}{2}\sqrt{ \frac {C}{a_{1}+a_{2}}}(X+Y)\biggr)\biggr]\biggr\} , \end{aligned}$$
(94)

so that the phase of the wave meets

$$\begin{aligned} \varphi_{D} =&-\frac{C^{\frac{3}{2}}\varDelta T}{16\sqrt{a_{1}+a_{2}}} \biggl\{ 1+2 \operatorname{sech}^{2}\biggl[\frac{1}{2} \sqrt{ \frac{C}{a_{1}+a_{2}}}(X+Y)\biggr] \\ &{}\times\tanh\biggl[\frac{1}{2}\sqrt{ \frac {C}{a_{1}+a_{2}}}(X+Y)\biggr]\biggr\} . \end{aligned}$$
(95)

Based on (95), we can obtain the chirp caused by the dispersion effect

$$\begin{aligned} \varDelta \nu_{D} =&-\nabla\varphi_{D} \\ =& \frac{C^{2}\varDelta T}{a_{1}+a_{2}}\biggl\{ 2 \operatorname{sech}^{2}\biggl[ \frac{1}{2}\sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr] \\ &{}\times\tanh^{2} \biggl[\frac{1}{2}\sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr]+\tanh^{4}\biggl[\frac{1}{2}\sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y) \biggr]\biggr\} . \end{aligned}$$
(96)

According to (92) and (96), the whole chirp is

$$\begin{aligned} \varDelta \nu_{S} =&\varDelta \nu_{N}+\varDelta \nu_{D} \\ =&\biggl(\frac{2C^{4}}{a^{3}_{0}}+\frac {C^{\frac{3}{2}}}{8\sqrt{a_{1}+a_{2}}}\biggr)\frac{C}{a_{1}+a_{2}}\varDelta T\biggl\{ 2 \operatorname{sech}^{2}\biggl[\frac{1}{2}\sqrt{ \frac{C}{a_{1}+a_{2}}}(X+Y)\biggr] \\ &{}\times\tanh^{2}\biggl[\frac{1}{2}\sqrt{ \frac{C}{a_{1}+a_{2}}}(X+Y)\biggr]+\tanh^{4}\biggl[\frac {1}{2} \sqrt{\frac{C}{a_{1}+a_{2}}}(X+Y)\biggr]\biggr\} . \end{aligned}$$
(97)

By employing (97) we find that when the wave speed C satisfies the formula

$$ C^{5}=\frac{a^{6}_{0}}{2^{8}(a_{1}+a_{2})}, $$
(98)

the nonlinear effect balances to the dispersion effect, that is, \(\varDelta \nu_{S}=0\); when the wave speed C satisfies

$$ C^{5}< \frac{a^{6}_{0}}{2^{8}(a_{1}+a_{2})}, $$
(99)

the dispersive effect is greater than the nonlinear effect, that is, \(|\varDelta \nu_{D}|>|\varDelta \nu_{N}|\); on the contrary, when the wave speed C satisfies

$$ C^{5}>\frac{a^{6}_{0}}{2^{8}(a_{1}+a_{2})}, $$
(100)

the dispersion effect is less than the nonlinear effect, that is, \(|\varDelta \nu_{D}|<|\varDelta \nu_{N}|\).

6 Conclusion

In this paper, the ZK-Burgers equation is constructed to describe the three-dimensional Rossby solitary waves by employing the multiscale and perturbation expansion method. By analyzing the ZK-Burgers equation we obtain four conservation laws of three-dimensional Rossby solitary waves, that is, mass, momentum, energy, velocity of the center gravity and discuss their variation trends with dissipation effect. Moreover, analytical solutions of the ZK-Burgers equation are derived based on the sine-cosine and Hirota methods. With the help of analytical solutions, the dissipation and chirp effect are studied. The results show that, due to the dissipation effect, the propagation speed and amplitude of three-dimensional Rossby solitary waves decrease exponentially, and the width of three-dimensional Rossby solitary waves increases exponentially with the increasing of μ and time T; on the other hand, the whole chirp effect is related to the zonal flow, β effect, and wave speed. When (82) is satisfied, the three-dimensional Rossby solitary waves can be spread steadily. The smaller the wave speed, the stronger the dispersive effect; the greater the wave speed, the stronger the nonlinear effect as the zonal flow and β effect is determined.