1 Introduction

In the past few decades, the fractional calculus has attracted considerable attention and interest due to its extensive applications in modeling practical scientific problems, such as heat-transfer engineering [1], anomalous relaxation models [2], solid mechanics [3], viscoelastic materials [4], continuum and statistical mechanics [5], mathematical physics [6], control system [7], chaos [8, 9], finance [10], electromagnetics [11, 12], and image processing [13]. Based on different problems, a variety of fractional diffusion equations (FDEs) need to be solved, in which the time-fractional anomalous FDE is always an important concern of many mathematicians; refer, e.g., to [14–16] and references therein.

However, some complex physical processes [17, 18] that lack temporal scaling over the whole time domain cannot be described by the time-fractional anomalous FDEs with a constant-order temporal derivative. Such processes can be modeled via the time distributed-order FDEs. The idea of distributed-order FDE was first proposed by Caputo (see [19] and references therein). Chechkin et al. [20] presented diffusion-like equations with time and space fractional derivatives of distributed order for the kinetic description of anomalous diffusion and relaxation phenomena, and showed that the time distributed-order FDE can describe the accelerating superdiffusion and retarding subdiffusion. Boundary value problems for the generalized time-FDE of distributed order over an open bounded domain were considered by Luchko [21]. Furthermore, Meerschaert et al. [22] gave explicit strong solutions and stochastic analogues to time distributed-order FDE on bounded domains, with Dirichlet boundary conditions. By employing the techniques of the Fourier and Laplace transforms, a fundamental solution to the Cauchy problem for the distributed-order time-fractional diffusion-wave equation in the transform domain was obtained by Gorenflo et al. [23]. Jiang et al. [24] derived the analytical solutions of multiterm time-space Caputo–Riesz fractional advection diffusion equations with Dirichlet nonhomogeneous boundary conditions. For more general distributed-order FDEs, the analytical solutions are not easily acquired. Therefore, numerical methods are worth considering to solve the distributed-order FDEs.

In a more general sense, the first step is to approximate the distributed integral with a finite sum based on a simple quadrature rule when solving distributed-order FDEs via numerical methods. Thus the distributed-order FDE is converted into a multiterm FDE [25], and we have to efficiently solve the approximated multiterm FDE. To our knowledge, only a few articles have considered such problem. Liu et al. [26] discussed some computationally effective numerical methods for simulating the multiterm time-fractional wave-diffusion equations and extended such numerical techniques to other kinds of multiterm fractional time-space models with fractional Laplacian operator. Morgado et al. [27] studied a numerical approximation for the time distributed-order FDE concerning the stability and convergence; they [28] also presented an implicit difference scheme for numerical approximation of the distributed-order time fractional reaction–diffusion equation with nonlinear source term. An implicit difference scheme for the time distributed-order and Riesz space FDE on bounded domains with Dirichlet boundary conditions was constructed by Ye et al. [29]. Mashayekhi et al. [30] introduced a new numerical method for solving the distributed-order FDEs, which is based upon hybrid functions approximation. Hu et al. [31] provided an implicit numerical method of a new time distributed-order and two-sided space fractional advection–dispersion equation and proved the uniqueness, stability, and convergence of the method. A numerical method of distributed-order FDEs of a general form was investigated by Katsikadelis [25], where the trapezoidal rule was employed to approximate the distributed integral, and the analog equation method was applied to solve the resultant multiterm FDE. However, the stability and convergence were only shown in the experimental examples, and there was no rigorous theoretical proof.

There should be significant interest in developing numerical schemes for solving distributed-order FDEs. However, the current studies in this area are still relatively limited, especially for the time distributed-order and space FDEs; refer to [29, 31, 32]. Moreover, most of these numerical methods have no complete theoretical analysis for both convergence and stability; see, for example, [25, 26, 33]. These motivate us to consider in particular a fast and stable numerical approach for solving the following new class of time distributed-order and space FDEs (TDFDEs) with variable coefficients and initial boundary conditions:

$$\begin{aligned} &{}D_{t}^{\omega(\alpha)}u(x,t)=d_{+}(x,t){}_{RL}D_{0,x}^{\beta }u(x,t)+d_{-}(x,t){}_{RL}D_{x,L}^{\beta}u(x,t)+f(x,t), \\ &\quad0< x< L, 0< t\leq T, \end{aligned}$$
(1.1)
$$\begin{aligned} &u(0,t)=0,\qquad u(L,t)=0,\quad0\leq t\leq T, \end{aligned}$$
(1.2)
$$\begin{aligned} &u(x,0)=\psi(x),\quad0\leq x\leq L, \end{aligned}$$
(1.3)

where \(\alpha\in[0,1]\), \(\beta\in(1,2)\), \(x\in[0,L]\), \(t\in[0,T]\), and \(f(x,t)\), \(d_{\pm}(x,t)\), and \(\psi(x)\) are given functions. Here \(f(x,t)\) is the source term, and diffusion coefficient functions \(d_{\pm }(x,t)\) are nonnegative, that is, \(d_{\pm}(x,t)\geq0\). Specifically, the time fractional derivative \({}D_{t}^{\omega(\alpha)}\) of distributed-order is denoted by [21]

$$\begin{aligned} D_{t}^{\omega(\alpha)}u(x,t)= \int_{0}^{1}\omega(\alpha){}^{C}_{0}D_{t}^{\alpha }u(x,t) \,d\alpha \end{aligned}$$

with the left-handed Caputo fractional derivative \({}^{C}_{0}D_{t}^{\alpha}\) defined as [34, 35]

$$ ^{C}_{0}D_{t}^{\alpha}u(x,t)= \textstyle\begin{cases} \frac{1}{\Gamma(1-\alpha)}\int_{0}^{t}(t-\xi)^{-\alpha}\frac{\partial {u}}{\partial\xi}(x,\xi)\,d\xi,& 0\leq\alpha< 1,\\ u_{t}(x,t),& \alpha=1, \end{cases} $$

and a continuous nonnegative weight function \(\omega(\alpha)\) on the interval \([0,1]\) such that \(\int_{0}^{1}\omega(\alpha)\,d\alpha=c_{0}>0\). Moreover, \({}_{RL}D_{0,x}^{\beta}\) and \({}_{RL}D_{x,L}^{\beta}\) are the the left- and right-handed Riemann–Liouville fractional derivatives of order \(\beta\in(1,2)\) [36, 37] defined respectively as

$$ {}_{RL}D_{0,x}^{\beta}u(x,t)=\frac{1}{\Gamma(2-\beta)} \frac{\partial ^{2}}{\partial x^{2}} \int_{0}^{x}{\frac{u(\xi,t)}{(x-\xi)^{\beta-1}}}\,d\xi $$

and

$$ {}_{RL}D_{x,L}^{\beta}u(x,t) =\frac{1}{\Gamma(2-\beta)} \frac{\partial ^{2}}{\partial x^{2}} \int_{x}^{L}{\frac{u(\xi,t)}{(\xi-x)^{\beta-1}}}\,d\xi, $$

where \(\Gamma(\cdot)\) denotes the gamma function.

Since the fractional differential operator is nonlocal [38, 39], a naive discretization of the FDE leads to traditional approaches [40] of solving FDEs, which tend to generate dense systems, whose solution with Gaussian elimination costs \(\mathcal{O}(M^{3})\) arithmetic operations and requires a storage of order \(\mathcal{O}(M^{2})\). Wang and Wang [41] found that the coefficient matrix had a Toeplitz structure in the linear system, which was generated by the discretization introduced in [42]. More precisely, this coefficient matrix can be expressed as a sum of diagonal-multiply-Toeplitz matrices. This implied that the storage requirement was \(\mathcal{O}(M)\) instead of \(\mathcal{O}(M^{2})\), and the complexity of the matrix–vector multiplication by the fast Fourier transform (FFT) [43] required only \(\mathcal{O}(M\log M)\) operations. With this advantage, Wang and Wang [44] employed the conjugate gradient normal residual (CGNR) method to solve the discretized linear systems in \(\mathcal{O}(M \log^{2} M)\) arithmetic operations. The convergence of the CGNR method can be fast when the diffusion coefficients are very small, that is, discretized systems are well-conditioned [44]. Nevertheless, if the diffusion coefficient functions are not small, the resultant systems become ill-conditioned, and hence the CGNR method converges very slowly.

To overtake this shortcoming and get a faster convergence, some Krylov subspace methods with circulant preconditioners have been studied and extended. Lei and Sun [45] developed the preconditioned CGNR (PCGNR) method with a circulant preconditioner, an extension of the Strang circulant preconditioner [46], to solve the discretized Toeplitz-like linear systems of the FDE. Pan et al. [47] introduced approximate inverse preconditioners for such systems and proved that the spectra of the preconditioned matrices are clustered around one. Thus Krylov subspace methods with the proposed preconditioner converge very fast. Donatelli et al. [48] proposed two tridiagonal structure-reserving preconditioners with CGNR and generalized minimal residual (GMRES) methods for solving the resultant Toeplitz-like linear systems. Using the short-memory principle [49] to generate a sequence of approximations for the inverse of the discretization matrix with a low computational effort, Bertaccini et al. [50] solved the mixed classical and fractional partial differential equations effectively by preconditioned Krylov iterative methods. Our recent work [51] showed that the preconditioned conjugate gradient squared (PCGS) method with suitable circulant preconditioners can efficiently solve the resultant Toeplitz-like linear systems.

In this paper, we focus on deriving a fast implicit difference scheme for solving the new problem (1.1)–(1.3). We first transform TDFDEs into multiterm time-space FDEs by applying numerical integration. Then we present an implicit difference scheme with unconditional stability and convergence that is first-order accurate in space and \((1+\frac{\sigma}{2})\)-order accurate in time. We prove these properties of the proposed scheme both theoretically and numerically. On the other hand, we show that the discretizations of TDFDEs lead to a nonsymmetric Toeplitz-like system of linear equations. The linear system can be solved efficiently by using Krylov subspace methods with suitable circulant preconditioners [52–54]. It can greatly reduce the memory and computational costs; the memory requirement and computational complexity are only \(\mathcal{O}(M)\) and \(\mathcal{O}(M\log M)\) in each iteration step, respectively. Meanwhile, it is meaningful to investigate the performance of some other preconditioned Krylov subspace solvers, such as the preconditioned biconjugate gradient stabilized (PBiCGSTAB) method [55], the preconditioned biconjugate residual stabilized (PBiCRSTAB) method [56], and the preconditioned GPBiCOR\((m, \ell)\) (PGPBiCOR\((m, \ell)\)) method [57].

The rest of this paper is organized as follows. In Sect. 2, we present an implicit difference scheme for the TDFDEs. The uniqueness, unconditional stability, and convergence of the implicit difference scheme are analyzed in Sect. 3. In Sect. 4, we show that the resultant linear system has nonsymmetric Toeplitz matrices and design fast solution techniques based on preconditioned Krylov subspace methods to solve problem (1.1)–(1.3). In Sect. 5, we present numerical experiments to show the effectiveness of the numerical method. Concluding remarks are given in Sect. 6.

2 An implicit difference scheme for TDFDEs

In this section, we present an implicit difference method for discretizing the TDFDEs defined by (1.1)–(1.3). The distributed integral term of TDFDEs is discretized by using numerical integration, and we show that the discretizations lead to multiterm time-space FDEs. Then we propose an implicit difference scheme with the shifted Grünwald–Letnikov formulae approximation to solve the mutiterm time-space FDEs.

For simplicity, but without loss of the generality, we first divide the integral interval \([0,1]\) into q-subintervals with \(0=\xi_{0}<\xi_{1}<\xi _{2}<\cdots<\xi_{q}=1\) and take \(\Delta\xi_{s}=\xi_{s}-\xi_{s-1}=\frac {1}{q}=\sigma\) (\(q\in N\)), \(\alpha_{s}=\frac{\xi_{s-1}+\xi_{s}}{2}=\frac {2s-1}{2q}\) (\(s=1,2,\ldots,q\)). The following lemma gives a complete description of the discretization in the integral term.

Lemma 2.1

(The compound midpoint quadrature rule [29])

Let \(z(\alpha)\in C^{2}[0,1]\), \(\Delta\alpha=1/q=\sigma(q\in N)\). Then we have

$$ \int_{0}^{1}z(\alpha)\,d\alpha=\sum _{s=1}^{q} z\biggl(\frac{2s-1}{2q}\biggr) \frac {1}{q}+\mathcal{O}\bigl(\sigma^{2}\bigr). $$

Considering the left side of formula (1.1), let \(z(\alpha)=\omega(\alpha){}^{C}_{0}D_{t}^{\alpha}u(x,t)\) and suppose that \(\omega(\alpha)\in C^{2}[0,1]\) and \({}^{C}_{0}D_{t}^{\alpha }u(x,t)\in C^{2}[0,1]\). Using Lemma 2.1, we obtain

$$ {}D_{t}^{\omega(\alpha)}u(x,t)=\sum _{s=1}^{q}d_{s}\bigl({}^{C}_{0}D_{t}^{\alpha _{s}}u(x,t) \bigr)+\mathcal{O}\bigl(\sigma^{2}\bigr),$$
(2.1)

where \(d_{s}=\omega(\alpha_{s})\Delta\xi_{s}\). Thus problem (1.1)–(1.3) is now transformed into the following multiterm time-space FDEs:

$$\begin{aligned} &\sum_{s=1}^{q}d_{s} \bigl({}^{C}_{0}D_{t}^{\alpha _{s}}u(x,t) \bigr)=d_{+}(x,t){}_{RL}D_{0,x}^{\beta }u(x,t)+d_{-}(x,t){}_{RL}D_{x,L}^{\beta}u(x,t)+f(x,t), \\ &\quad0< x< L, 0< t\leq T, \end{aligned}$$
(2.2)
$$\begin{aligned} &u(0,t)=0,\qquad u(L,t)=0,\quad0\leq t\leq T, \end{aligned}$$
(2.3)
$$\begin{aligned} &u(x,0)=\psi(x),\quad0\leq x\leq L. \end{aligned}$$
(2.4)

Next, we solve the multiterm time-space FDEs. We discretize the domain \([0, L]\times[0,T]\) with \(x_{i}=ih\), \(i=0,1,2,\ldots,M\), and \(t_{k}=k\tau\), \(k=0,1,2,\ldots,N\), where \(h=\frac{L}{M}\) and \(\tau=\frac{T}{N}\) are the sizes of spatial grid and time step, respectively.

The following two lemmas will be further useful in the discretizations of the multiterm time-space FDEs.

Lemma 2.2

([58])

Let \(0<\alpha<1\), and let u be absolutely continuous in t on \([0,T]\) with \(\partial^{2}u/\partial t^{2}\in C([0,L]\times[0,t_{k}])\). Then

$$ {}^{C}_{0}D_{t}^{\alpha}u(x,t_{k})= \frac{1}{\mu} \Biggl[ u(x,t_{k})-\sum _{j=1}^{k-1}\bigl(a_{k-j-1}^{\alpha }-a_{k-j}^{\alpha} \bigr)u(x,t_{j})-a_{k-1}^{\alpha}u(x,t_{0}) \Biggr]+\mathcal {O}\bigl(\tau^{2-\alpha}\bigr), $$

where \(a_{k}^{\alpha}=(k+1)^{1-\alpha}-k^{1-\alpha}\), \(\mu=\tau^{\alpha}\Gamma (2-\alpha)\), \(0\leq t_{k}\leq T\).

Lemma 2.3

([59])

For \(1<\beta<2\), suppose that \(u\in L_{1}(\mathbb{R})\cap C^{\beta +1}(\mathbb{R})\). Then the shifted Grünwald–Letnikov formulae approximate the left and right Riemann–Liouville derivatives as follows:

$$\begin{aligned} &{}_{RL}D_{0,x}^{\beta}u(x_{i},t)= \frac{1}{h^{\beta}}\sum_{j=0}^{i+1}g_{j}^{(\beta)}u_{(}x_{i-j+1},t)+ \mathcal{O}(h), \\ &{}_{RL}D_{x,L}^{\beta}u(x_{i},t)= \frac{1}{h^{\beta}}\sum_{j=0}^{M-i+1}g_{j}^{(\beta)}u_{(}x_{i+j-1},t)+ \mathcal{O}(h), \end{aligned}$$

where \(g_{j}^{(\beta)}\) is the alternating fractional binomial coefficient given as

$$ \textstyle\begin{cases} g_{0}^{(\beta)}=1,\\ g_{j}^{(\beta)}=\frac{(-1)^{j}}{j!}\beta(\beta-1)\cdots(\beta-j+1),\quad j=1,2,\ldots. \end{cases} $$

Define the grid function \(U_{i}^{k}=u(x_{i},t_{k})\) as the exact solution of the equations (1.1)–(1.3), \(f_{i}^{k}=f(x_{i},t_{k})\), \(d_{+,i}^{k}=d_{+}(x_{i},t_{k})\), \(d_{-,i}^{k}=d_{-}(x_{i},t_{k})\). Considering (2.2) at \((x_{i},t_{k+1})\), by Lemma 2.2 the Caputo time-fractional derivative for \(\alpha_{s}\in(0,1)\) can be approximated by

$$ {}^{C}_{0}D_{t}^{\alpha_{s}} U_{i}^{k+1}= \frac{1}{\mu_{s}} \Biggl[U_{i}^{k+1}- \sum_{j=1}^{k}\bigl(a_{k-j}^{\alpha _{s}}-a_{k-j+1}^{\alpha_{s}} \bigr)U_{i}^{j}-a_{k}^{\alpha_{s}}U_{i}^{0} \Biggr]+\mathcal {O}\bigl(\tau^{2-\alpha_{s}}\bigr),$$
(2.5)

where

$$ a_{k}^{\alpha_{s}}=(k+1)^{1-\alpha_{s}}-k^{1-\alpha_{s}},\qquad \mu_{s}=\tau ^{\alpha_{s}}\Gamma(2-\alpha_{s}), \quad s=1,2,\ldots,q. $$

By Lemma 2.3 the left and right Riemann–Liouville derivatives of order \(\beta\in(1,2)\) can be approximated by adopting the shifted Grünwald–Letnikov formula as follows:

$$\begin{aligned} &{}_{RL}D_{0,x}^{\beta}U_{i}^{k+1}= \frac{1}{h^{\beta}}\sum_{j=0}^{i+1}g_{j}^{(\beta)}U_{i-j+1}^{k+1}+ \mathcal{O}(h), \end{aligned}$$
(2.6)
$$\begin{aligned} &{}_{RL}D_{x,L}^{\beta}U_{i}^{k+1}= \frac{1}{h^{\beta}}\sum_{j=0}^{M-i+1}g_{j}^{(\beta)}U_{i+j-1}^{k+1}+ \mathcal{O}(h). \end{aligned}$$
(2.7)

Applying formulae (2.5)–(2.7) to equation (2.2), by (2.1) we obtain

$$\begin{aligned} &\sum_{s=1}^{q} \frac{d_{s}}{\mu_{s}} \Biggl[U_{i}^{k+1}-\sum _{j=1}^{k}\bigl(a_{k-j}^{\alpha_{s}}-a_{k-j+1}^{\alpha_{s}} \bigr)U_{i}^{j}-a_{k}^{\alpha _{s}}U_{i}^{0} \Biggr] \\ &\quad =\frac{d_{+,i}^{k+1}}{h^{\beta}}\sum_{j=0}^{i+1}g_{j}^{(\beta )}U_{i-j+1}^{k+1} +\frac{d_{-,i}^{k+1}}{h^{\beta}}\sum_{j=0}^{M-i+1}g_{j}^{(\beta)}U_{i+j-1}^{k+1} \\ &\qquad{} +f_{i}^{k+1}+p_{i}^{k+1},\quad 1\leq i\leq M-1, 0\leq k\leq N-1, \end{aligned}$$
(2.8)

where there exists a positive constant \(\kappa_{1}\) such that

$$ \bigl\vert p_{i}^{k+1} \bigr\vert = \bigl\vert \mathcal{O}\bigl(h+\tau^{1+\sigma/2}+\sigma^{2}\bigr) \bigr\vert \leq\kappa _{1}\bigl(h+\tau^{1+\frac{\sigma}{2}}+\sigma^{2} \bigr). $$
(2.9)

Let \(u_{i}^{k}\) be a numerical approximation to \(U_{i}^{k}\). By omitting the local truncation error term \(p_{i}^{k+1}\) in (2.8) and considering the discretization of the initial and boundary conditions (1.2)–(1.3) we obtain the following implicit difference scheme for TDFDEs (1.1)–(1.3):

$$\begin{aligned} &\sum_{s=1}^{q} \frac{d_{s}}{\mu_{s}} \Biggl[u_{i}^{k+1}-\sum _{j=1}^{k}\bigl(a_{k-j}^{\alpha_{s}}-a_{k-j+1}^{\alpha_{s}} \bigr)u_{i}^{j}-a_{k}^{\alpha _{s}}u_{i}^{0} \Biggr]\\ &\quad =\frac{d_{+,i}^{k+1}}{h^{\beta}}\sum_{j=0}^{i+1}g_{j}^{(\beta )}u_{i-j+1}^{k+1} +\frac{d_{-,i}^{k+1}}{h^{\beta}}\sum_{j=0}^{M-i+1}g_{j}^{(\beta)}u_{i+j-1}^{k+1} \\ &\qquad {} +f_{i}^{k+1},\quad 1\leq i\leq M-1, 0\leq k\leq N-1, \end{aligned}$$
(2.10)
$$\begin{aligned} &u_{0}^{k}=u_{M}^{k}=0,\quad0\leq k \leq N, \end{aligned}$$
(2.11)
$$\begin{aligned} &u_{i}^{0}=\psi_{i}^{0}= \psi(x_{i}),\quad0\leq i\leq M. \end{aligned}$$
(2.12)

For convenience of the following theoretical analysis, we define

$$ v=\frac{h^{-\beta}}{\sum_{r=1}^{q}(d_{r}/\mu_{r})},\qquad \bar{v}=\frac{1}{\sum_{r=1}^{q}(d_{r}/\mu_{r})},\qquad v_{s}=\frac{d_{s}}{\mu_{s}\sum_{r=1}^{q}(d_{r}/\mu_{r})}.$$
(2.13)

Thus, we rewrite the difference scheme (2.10)–(2.12) as follows:

$$\begin{aligned} &u_{i}^{k+1}-v \Biggl[d_{+,i}^{k+1} \sum_{j=0}^{i+1}g_{j}^{(\beta )}u_{i-j+1}^{k+1}+d_{-,i}^{k+1} \sum_{j=0}^{M-i+1}g_{j}^{(\beta )}u_{i+j-1}^{k+1} \Biggr] \\ &\quad=\sum_{j=1}^{k} \Biggl[ \sum_{s=1}^{q}v_{s} \bigl(a_{k-j}^{\alpha _{s}}-a_{k-j+1}^{\alpha_{s}}\bigr) \Biggr]u_{i}^{j}+\sum_{s=1}^{q}v_{s}a_{k}^{\alpha _{s}}u_{i}^{0}+ \bar{v}f_{i}^{k+1}, \\ &\qquad i=1,2,\ldots,M-1, k=0,1,\ldots,N-1, \end{aligned}$$
(2.14)
$$\begin{aligned} &u_{0}^{k}=u_{M}^{k}=0,\quad0\leq k \leq N, \end{aligned}$$
(2.15)
$$\begin{aligned} &u_{i}^{0}=\psi_{i}^{0}= \psi(x_{i}),\quad0\leq i\leq M. \end{aligned}$$
(2.16)

  Let \(u^{k}=(u_{1}^{k}, u_{2}^{k},\ldots,u_{M-1}^{k})^{T}\), \(f^{k}=(f_{1}^{k}, f_{2}^{k},\ldots,f_{M-1}^{k})^{T}\), and let I be the identity matrix of appropriate size. Then the numerical scheme (2.14) can be written in matrix form as follows:

$$ \bigl(I-vA^{k+1}\bigr)u^{k+1}=\sum _{j=1}^{k}c_{k,j}u^{j}+b_{k}u^{0}+ \bar{v}f^{k+1},\quad k=0,1,2,\ldots,N-1,$$
(2.17)

where

$$ A^{k+1}=D_{+}^{k+1}G_{\beta}+D_{-}^{k+1}G_{\beta}^{T},\qquad c_{k,j}=\sum_{s=1}^{q}v_{s} \bigl(a_{k-j}^{\alpha_{s}}-a_{k-j+1}^{\alpha_{s}}\bigr),\qquad b_{k}=\sum_{s=1}^{q}v_{s}a_{k}^{\alpha_{s}}, $$

with \(D_{\pm}^{k+1}= \operatorname{diag}(d_{\pm, 1}^{k+1},\ldots,d_{\pm , M-1}^{k+1})\) and

$$ G_{\beta}= \begin{bmatrix} {g}_{1}^{(\beta)}&{g}_{0}^{(\beta)}&0&\cdots&0&0\\ {g}_{2}^{(\beta)}&{g}_{1}^{(\beta)}&{g}_{0}^{(\beta)}&\cdots&0&0\\ {g}_{3}^{(\beta)}&{g}_{2}^{(\beta)}&{g}_{1}^{(\beta)}&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ {g}_{M-2}^{(\beta)}&{g}_{M-3}^{(\beta)}&{g}_{M-4}^{(\beta)}&\cdots &{g}_{1}^{(\beta)}&{g}_{0}^{(\beta)}\\ {g}_{M-1}^{(\beta)}&{g}_{M-2}^{(\beta)}&{g}_{M-3}^{(\beta)}&\cdots &{g}_{2}^{(\beta)}&{g}_{1}^{(\beta)} \end{bmatrix} . $$

It is obvious that \(G_{\beta}\) is a Toeplitz matrix (see [46]). Furthermore, the linear system (2.17) can be written as

$$ M^{k+1}u^{k+1}=b^{k},\quad k=0,1,2, \ldots,N-1,$$
(2.18)

where

$$ M^{k+1}=I-vA^{k+1}=I-v\bigl(D_{+}^{k+1}G_{\beta}+D_{-}^{k+1}G_{\beta}^{T} \bigr) $$

and

$$ b^{k}=\sum_{j=1}^{k}c_{k,j}u^{j}+b_{k}u^{0}+ \bar{v}f^{k+1}. $$

3 Solvability, stability, and convergence results

In this section, we analyze the unique solvability, unconditional stability, and convergence of the implicit difference scheme (2.14)–(2.16). Meanwhile, the difference scheme is proved to converge with the first-order in space and the \((1+\frac{\sigma }{2})\)-order in time.

Before proving the most important result of this section on the solvability, stability, and convergence properties, we first need to recall the following useful proposition.

Proposition 3.1

([60])

Let \(1<\beta<2\) and \(g_{j}^{(\beta)}\) be defined as in Lemma 2.3. Then we have

$$ \textstyle\begin{cases} g_{0}^{(\beta)}=1,\qquad g_{1}^{(\beta)}=-\beta< 0,\qquad g_{2}^{(\beta )}>g_{3}^{(\beta)}>\cdots>0,\\ \sum_{j=0}^{\infty}g_{j}^{(\beta)}=0,\qquad \sum_{j=0}^{m}g_{j}^{(\beta )}< 0,\quad m\geq1,\\ g_{j}^{(\beta)}=(1-\frac{\beta+1}{j})g_{j-1}^{(\beta)},\quad j=1,2,3,\ldots. \end{cases} $$

The starting point of our analysis is the following theoretical result.

Theorem 3.2

The difference scheme (2.14)–(2.16) for the TDFDEs is uniquely solvable.

Proof

Let \(m_{ij}^{k+1}\) be the \((i,j)\) entry of the \(M^{k+1}\) in (2.18). Since \(v>0\) and \(d_{\pm}(x,t)\geq0\), by Proposition 3.1 we get

$$ \begin{aligned} m_{ii}^{k+1}-\sum _{j=1,j\neq i}^{M-1} \bigl\vert m_{ij}^{k+1} \bigr\vert ={}& \bigl[1-v\bigl(d_{+,i}^{k+1}+d_{-,i}^{k+1} \bigr)g_{1}^{(\beta)} \bigr]\\ &{}-v \Biggl[d_{+,i}^{k+1} \sum_{j=0,j\neq1}^{i}g_{j}^{(\beta)}+d_{-,i}^{k+1} \sum_{j=0,j\neq1}^{M-i}g_{j}^{(\beta)} \Biggr] \\ \geq{}& \bigl[1-v\bigl(d_{+,i}^{k+1}+d_{-,i}^{k+1} \bigr)g_{1}^{(\beta)} \bigr]-v\bigl(d_{+,i}^{k+1}+d_{-,i}^{k+1} \bigr)\sum_{j=0,j\neq1}^{\infty}g_{j}^{(\beta )} \\ ={}&1-v\bigl(d_{+,i}^{k+1}+d_{-,i}^{k+1} \bigr)\sum_{j=0}^{\infty}g_{j}^{(\beta)}=1>0. \end{aligned} $$

This implies that the coefficient matrix \(M^{k+1}\) is a strictly diagonally dominant M-matrix (see [41]), and therefore it is nonsingular, so the difference scheme (2.14)–(2.16) is uniquely solvable. □

The unique solvability of the implicit difference scheme (2.14)–(2.16) has been established, and now we further show its stability.

Theorem 3.3

The difference scheme (2.14)–(2.16) for the TDFDEs is unconditionally stable, where \(1<\beta<2\).

Proof

Assume that the initial errors are \(\varepsilon_{i}^{0}\) \((i=0,1,\ldots ,M-1)\), let \(\bar{\psi}_{i}^{0}=\psi_{i}^{0}+\varepsilon_{i}^{0}\), and let \(u_{i}^{k}\) and \(\bar{u}_{i}^{k}\) be the numerical solutions of scheme (2.14) corresponding to the initial data \(\psi_{i}^{0}\) and \(\bar{\psi}_{i}^{0}\) \((i=1,2,\ldots,M-1)\), respectively. Then \(\varepsilon_{i}^{k}=u_{i}^{k}-\bar {u}_{i}^{k}\) satisfies

$$ \begin{aligned} &\varepsilon_{i}^{1}-v \Biggl[d_{+,i}^{1} \sum_{j=0}^{i+1}g_{j}^{(\beta )} \varepsilon_{i-j+1}^{1}+d_{-,i}^{1}\sum _{j=0}^{M-i+1}g_{j}^{(\beta )} \varepsilon_{i+j-1}^{1} \Biggr]\\ &\quad =\sum _{s=1}^{q}v_{s}a_{0}^{\alpha_{s}} \varepsilon_{i}^{0}=\varepsilon_{i}^{0}, \\ &\varepsilon_{i}^{k+1}-v \Biggl[d_{+,i}^{k+1}\sum_{j=0}^{i+1}g_{j}^{(\beta )} \varepsilon_{i-j+1}^{k+1}+d_{-,i}^{k+1}\sum _{j=0}^{M-i+1}g_{j}^{(\beta )} \varepsilon_{i+j-1}^{k+1} \Biggr] \\ &\quad =\sum_{j=1}^{k} \Biggl[\sum _{s=1}^{q}v_{s} \bigl(a_{k-j}^{\alpha_{s}}-a_{k-j+1}^{\alpha _{s}}\bigr) \Biggr]\varepsilon_{i}^{j}+\sum_{s=1}^{q}v_{s}a_{k}^{\alpha_{s}} \varepsilon _{i}^{0},\quad k=1,\ldots,N-1. \end{aligned} $$

Denote \(E^{k}=[\varepsilon_{1}^{k},\varepsilon_{2}^{k},\ldots,\varepsilon _{M-1}^{k}]^{T}\). The theorem will be proved if we show that

$$ \bigl\Vert E^{k+1} \bigr\Vert _{\infty}\leq \bigl\Vert E^{0} \bigr\Vert _{\infty},\quad k=0,1,2,\ldots. $$

To this end, we will use the mathematical induction.

For \(k=0\), denote \(|\varepsilon_{l}^{1}|=\max_{1\leq i\leq M-1}|\varepsilon _{i}^{1}|\). It follows from Proposition 3.1, \(v>0\), and \(d_{\pm}(x,t)\geq0\) that

$$\begin{aligned} \bigl\Vert E^{1} \bigr\Vert _{\infty} = &\bigl\vert \varepsilon_{l}^{1} \bigr\vert \\ \leq& \Biggl\{ 1-v \Biggl[ d_{+,l}^{1}\sum _{j=0}^{l+1}g_{j}^{(\beta )}+d_{-,l}^{1} \sum_{j=0}^{M-l+1}g_{j}^{(\beta)} \Biggr] \Biggr\} \bigl\vert \varepsilon _{l}^{1} \bigr\vert \\ =& \bigl\vert \varepsilon_{l}^{1} \bigr\vert -v \bigl[d_{+,l}^{1}g_{1}^{(\beta )}+d_{-,l}^{1}g_{1}^{(\beta)} \bigr] \bigl\vert \varepsilon_{l}^{1} \bigr\vert \\ &{} -v \Biggl[d_{+,l}^{1}\sum_{j=0,j\neq1}^{l+1}g_{j}^{(\beta)} \bigl\vert \varepsilon_{l}^{1} \bigr\vert +d_{-,l}^{1}\sum_{j=0,j\neq1}^{M-l+1}g_{j}^{(\beta)} \bigl\vert \varepsilon _{l}^{1} \bigr\vert \Biggr] \\ \leq& \bigl\vert \varepsilon_{l}^{1} \bigr\vert -v \bigl[d_{+,l}^{1}g_{1}^{(\beta )}+d_{-,l}^{1}g_{1}^{(\beta)} \bigr] \bigl\vert \varepsilon_{l}^{1} \bigr\vert \\ &{}-v \Biggl[d_{+,l}^{1}\sum_{j=0,j\neq1}^{l+1}g_{j}^{(\beta)} \bigl\vert \varepsilon_{l-j+1}^{1} \bigr\vert +d_{-,l}^{1}\sum_{j=0,j\neq1}^{M-l+1}g_{j}^{(\beta)} \bigl\vert \varepsilon _{l+j-1}^{1} \bigr\vert \Biggr] \\ =& \bigl\vert \varepsilon_{l}^{1} \bigr\vert -v \Biggl[d_{+,l}^{1}\sum_{j=0}^{l+1}g_{j}^{(\beta )} \bigl\vert \varepsilon_{l-j+1}^{1} \bigr\vert +d_{-,l}^{1}\sum_{j=0}^{M-l+1}g_{j}^{(\beta)} \bigl\vert \varepsilon_{l+j-1}^{1} \bigr\vert \Biggr] \\ \leq &\Biggl\vert \varepsilon_{l}^{1}-v \Biggl[d_{+,l}^{1}\sum_{j=0}^{l+1}g_{j}^{(\beta )} \varepsilon_{l-j+1}^{1} +d_{-,l}^{1}\sum _{j=0}^{M-l+1}g_{j}^{(\beta)} \varepsilon_{l+j-1}^{1} \Biggr] \Biggr\vert \\ = &\bigl\vert \varepsilon_{l}^{1} \bigr\vert = \bigl\Vert E^{0} \bigr\Vert _{\infty}. \end{aligned}$$

Now suppose that, for some integer \(k\geq0\), the result is established, that is,

$$ \bigl\Vert E^{j} \bigr\Vert _{\infty}\leq \bigl\Vert E^{0} \bigr\Vert _{\infty}\quad\mbox{for }j\leq k. $$

As we did earlier for \(k=0\), let \(|\varepsilon_{l}^{k+1}|=\max_{1\leq i\leq M-1}|\varepsilon_{i}^{k+1}|\). By Proposition 3.1, \(v>0\), and \(d_{\pm}(x,t)\geq0\) we can see that

$$\begin{aligned} \bigl\Vert E^{k+1} \bigr\Vert _{\infty} =& \bigl\vert \varepsilon_{l}^{k+1} \bigr\vert \\ \leq& \Biggl\{ 1-v \Biggl[d_{+,l}^{k+1}\sum _{j=0}^{l+1}g_{j}^{(\beta )}+d_{-,l}^{k+1} \sum_{j=0}^{M-l+1}g_{j}^{(\beta)} \Biggr] \Biggr\} \bigl\vert \varepsilon _{l}^{k+1} \bigr\vert \\ =& \bigl\vert \varepsilon_{l}^{k+1} \bigr\vert -v \bigl[d_{+,l}^{k+1}g_{1}^{(\beta )}+d_{-,l}^{k+1}g_{1}^{(\beta)} \bigr] \bigl\vert \varepsilon_{l}^{k+1} \bigr\vert \\ &{}-v \Biggl[d_{+,l}^{k+1}\sum_{j=0,j\neq1}^{l+1}g_{j}^{(\beta)} \bigl\vert \varepsilon _{l}^{k+1} \bigr\vert +d_{-,l}^{k+1}\sum_{j=0,j\neq1}^{M-l+1}g_{j}^{(\beta)} \bigl\vert \varepsilon _{l}^{k+1} \bigr\vert \Biggr] \\ \leq& \bigl\vert \varepsilon_{l}^{k+1} \bigr\vert -v \bigl[d_{+,l}^{k+1}g_{1}^{(\beta )}+d_{-,l}^{k+1}g_{1}^{(\beta)} \bigr] \bigl\vert \varepsilon_{l}^{k+1} \bigr\vert \\ &{} -v \Biggl[d_{+,l}^{k+1}\sum_{j=0,j\neq1}^{l+1}g_{j}^{(\beta)} \bigl\vert \varepsilon _{l-j+1}^{k+1} \bigr\vert +d_{-,l}^{k+1}\sum_{j=0,j\neq1}^{M-l+1}g_{j}^{(\beta)} \bigl\vert \varepsilon _{l+j-1}^{k+1} \bigr\vert \Biggr] \\ =& \bigl\vert \varepsilon_{l}^{k+1} \bigr\vert -v \Biggl[d_{+,l}^{k+1}\sum_{j=0}^{l+1}g_{j}^{(\beta )} \bigl\vert \varepsilon_{l-j+1}^{k+1} \bigr\vert +d_{-,l}^{k+1}\sum_{j=0}^{M-l+1}g_{j}^{(\beta)} \bigl\vert \varepsilon _{l+j-1}^{k+1} \bigr\vert \Biggr] \\ \leq& \Biggl\vert \varepsilon_{l}^{k+1}-v \Biggl[d_{+,l}^{k+1}\sum_{j=0}^{l+1}g_{j}^{(\beta)} \varepsilon_{l-j+1}^{k+1} +d_{-,l}^{k+1}\sum _{j=0}^{M-l+1}g_{j}^{(\beta)} \varepsilon _{l+j-1}^{k+1} \Biggr] \Biggr\vert \\ \leq&\sum_{j=1}^{k} \Biggl[\sum _{s=1}^{q}v_{s}\bigl(a_{k-j}^{\alpha _{s}}-a_{k-j+1}^{\alpha_{s}} \bigr) \Biggr] \bigl\vert \varepsilon_{l}^{j} \bigr\vert +\sum_{s=1}^{q}v_{s}a_{k}^{\alpha_{s}} \bigl\vert \varepsilon_{l}^{0} \bigr\vert \\ \leq& \Biggl\{ \sum_{j=1}^{k} \Biggl[\sum _{s=1}^{q}v_{s} \bigl(a_{k-j}^{\alpha _{s}}-a_{k-j+1}^{\alpha_{s}}\bigr) \Biggr]+\sum_{s=1}^{q}v_{s}a_{k}^{\alpha_{s}} \Biggr\} \bigl\Vert E^{0} \bigr\Vert _{\infty}\\ =&\sum_{s=1}^{q}v_{s} \bigl\Vert E^{0} \bigr\Vert _{\infty}= \bigl\Vert E^{0} \bigr\Vert _{\infty}, \end{aligned}$$

which completes the proof of Theorem 3.3. □

The next step is to analyze the convergence of the implicit method given in (2.14)–(2.16). To this end, suppose that the continuous problem (1.1)–(1.3) has a smooth solution \(u(x,t)\in C_{x,t}^{\beta+1,2}([0,L]\times [0,T])\). Recall that U denotes the exact solution of system (1.1)–(1.3); u represents the numerical solution of the implicit difference approximation (2.14)–(2.16) for \(1<\beta<2\). Let us assume that the error \(e=U-u\) at mesh points \((x_{i},t_{k})\) is defined by \(e_{i}^{k}=U_{i}^{k}-u_{i}^{k}\) (\(i=1,2,\ldots ,M-1;k=0,1,2,\ldots,N\)). Let \(R^{k}=[e_{1}^{k},e_{2}^{k},\ldots,e_{M-1}^{k}]^{T}\) and \(R^{0}=[e_{1}^{0},e_{2}^{0},\ldots,e_{M-1}^{0}]^{T}=0\).

According to (2.13), equation (2.8) can be rewritten as

$$\begin{aligned} &U_{i}^{k+1}-v \Biggl[d_{+,i}^{k+1}\sum_{j=0}^{i+1}g_{j}^{(\beta )}U_{i-j+1}^{k+1}+d_{-,i}^{k+1} \sum_{j=0}^{M-i+1}g_{j}^{(\beta )}U_{i+j-1}^{k+1} \Biggr] \\ &\quad=\sum_{j=1}^{k} \Biggl[ \sum_{s=1}^{q}v_{s} \bigl(a_{k-j}^{\alpha _{s}}-a_{k-j+1}^{\alpha_{s}}\bigr) \Biggr]U_{i}^{j}+\sum_{s=1}^{q}v_{s}a_{k}^{\alpha_{s}}U_{i}^{0} +\bar{v}f_{i}^{k+1}+\bar{v}p_{i}^{k+1}, \\ &\qquad i=1,2,\ldots,M-1,~k=0,1,\ldots,N-1. \end{aligned}$$
(3.1)

Subtracting (3.1) from (2.14), we have

$$\begin{aligned} &e_{i}^{k+1}-v \Biggl[d_{+,i}^{k+1} \sum_{j=0}^{i+1}g_{j}^{(\beta )}e_{i-j+1}^{k+1}+d_{-,i}^{k+1} \sum_{j=0}^{M-i+1}g_{j}^{(\beta )}e_{i+j-1}^{k+1} \Biggr] \\ &\quad=\sum_{j=1}^{k} \Biggl[ \sum_{s=1}^{q}v_{s} \bigl(a_{k-j}^{\alpha _{s}}-a_{k-j+1}^{\alpha_{s}}\bigr) \Biggr]e_{i}^{j}+\sum_{s=1}^{q}v_{s}a_{k}^{\alpha_{s}}e_{i}^{0} \\ &\qquad{}+\bar{v}\mathcal{O}\bigl(h+\tau^{1+\sigma/2}+\sigma^{2} \bigr),\quad k=0,1,\ldots,N-1. \end{aligned}$$
(3.2)

The bound (3.2) is an essential ingredient for the convergence analysis of this section. The following theorem shows that our implicit difference scheme is convergent with first-order accuracy in space and \((1+\frac{\sigma}{2})\)-order in time (i.e., \(\mathcal{O}(h+\tau ^{1+\sigma/2})\)).

Theorem 3.4

Suppose that the continuous problem (1.1)–(1.3) has a smooth solution \(u(x,t)\in C_{x,t}^{\beta+1,2}([0,L]\times[0,T])\), \(1<\beta<2\). Then

$$ \bigl\Vert R^{k+1} \bigr\Vert _{\infty}\leq \kappa_{1}\bigl(h+\tau^{1+\sigma/2}+\sigma^{2}\bigr) \Bigm/\sum _{s=1}^{q}\frac{d_{s}a_{k}^{\alpha_{s}}}{\mu_{s}},\quad k=0,1,2, \ldots,N-1. $$

Proof

For \(k=0\), suppose \(\|R^{1}\|_{\infty}=|e_{l}^{1}|=\max_{1\leq i\leq M-1}|e_{i}^{1}|\). By Proposition 3.1, \(v>0\), \(d_{\pm }(x,t)\geq0\), (2.9), (2.13), and (3.2) we acquire

$$\begin{aligned} \bigl\Vert R^{1} \bigr\Vert _{\infty} =& \bigl\vert e_{l}^{1} \bigr\vert \leq \Biggl\{ 1-v \Biggl[d_{+,l}^{1}\sum _{j=0}^{l+1}g_{j}^{(\beta )}+d_{-,l}^{1} \sum_{j=0}^{M-l+1}g_{j}^{(\beta)} \Biggr] \Biggr\} \bigl\vert e_{l}^{1} \bigr\vert \\ \leq& \bigl\vert e_{l}^{1} \bigr\vert -v \bigl[d_{+,l}^{1}g_{1}^{(\beta)}+d_{-,l}^{1}g_{1}^{(\beta )} \bigr] \bigl\vert e_{l}^{1} \bigr\vert \\ &{}-v \Biggl[d_{+,l}^{1}\sum_{j=0,j\neq1}^{l+1}g_{j}^{(\beta )} \bigl\vert e_{l-j+1}^{1} \bigr\vert +d_{-,l}^{1}\sum_{j=0,j\neq1}^{M-l+1}g_{j}^{(\beta)} \bigl\vert e_{l+j-1}^{1} \bigr\vert \Biggr] \\ =& \bigl\vert e_{l}^{1} \bigr\vert -v \Biggl[d_{+,l}^{1}\sum_{j=0}^{l+1}g_{j}^{(\beta)} \bigl\vert e_{l-j+1}^{1} \bigr\vert +d_{-,l}^{1} \sum_{j=0}^{M-l+1}g_{j}^{(\beta)} \bigl\vert e_{l+j-1}^{1} \bigr\vert \Biggr] \\ \leq& \Biggl\vert e_{l}^{1}-v \Biggl[d_{+,l}^{1} \sum_{j=0}^{l+1}g_{j}^{(\beta)}e_{l-j+1}^{1} +d_{-,l}^{1}\sum_{j=0}^{M-l+1}g_{j}^{(\beta)}e_{l+j-1}^{1} \Biggr] \Biggr\vert \\ =& \Biggl\vert \sum_{s=1}^{q}v_{s}a_{0}^{\alpha_{s}}e_{i}^{0}+ \bar{v}\bigl[\mathcal{O}\bigl(h+\tau ^{1+\sigma/2}+\sigma^{2}\bigr) \bigr] \Biggr\vert \\ =& \bigl\vert \bar{v}\bigl[\mathcal{O}\bigl(h+\tau^{1+\sigma/2}+ \sigma^{2}\bigr)\bigr] \bigr\vert \\ \leq& \kappa_{1}\bar{v}\bigl[h+\tau^{1+\sigma/2}+ \sigma^{2}\bigr] \\ =&\kappa_{1}\bigl(h+\tau^{1+\sigma/2}+\sigma^{2}\bigr) \Bigm/ \sum_{s=1}^{q}\frac {d_{s}a_{0}^{\alpha_{s}}}{\mu_{s}}. \end{aligned}$$

Suppose that the result is valid for some integer \(k\geq1\), that is,

$$\bigl\Vert R^{j} \bigr\Vert _{\infty}\leq \kappa_{1}\bigl(h+\tau^{1+\sigma/2}+\sigma^{2}\bigr) \Bigm/\sum _{s=1}^{q}\frac{d_{s}a_{j-1}^{\alpha_{s}}}{\mu_{s}},\quad j=1,2, \ldots,k. $$

Let \(|e_{l}^{k+1}|=\max_{1\leq i\leq M-1}|e_{i}^{k+1}|\). According to Proposition 3.1, \(v>0\), \(d_{\pm}(x,t)\geq0\), (2.9), (2.13), and (3.2), since the coefficients \(a_{j}^{\alpha_{s}}\) are decreasing for \(j=0,1,2,\ldots\) , we have

$$\begin{aligned} \bigl\Vert R^{k+1} \bigr\Vert _{\infty} =& \bigl\vert e_{l}^{k+1} \bigr\vert \leq \Biggl\vert e_{l}^{k+1}-v \Biggl[d_{+,l}^{k+1} \sum_{j=0}^{l+1}g_{j}^{(\beta )}e_{l-j+1}^{k+1} +d_{-,l}^{k+1}\sum_{j=0}^{M-l+1}g_{j}^{(\beta)}e_{l+j-1}^{k+1} \Biggr] \Biggr\vert \\ \leq&\sum_{j=1}^{k} \Biggl[\sum _{s=1}^{q}v_{s}\bigl(a_{k-j}^{\alpha _{s}}-a_{k-j+1}^{\alpha_{s}} \bigr) \Biggr] \bigl\vert e_{i}^{j} \bigr\vert + \kappa_{1}\bar{v}\bigl[h+\tau^{1+\sigma /2}+\sigma^{2}\bigr] \\ \leq&\sum_{s=1}^{q}v_{s} \Biggl[\sum_{j=1}^{k}\bigl(a_{k-j}^{\alpha _{s}}-a_{k-j+1}^{\alpha_{s}} \bigr)\kappa_{1}\bigl(h+\tau^{1+\sigma/2}+\sigma^{2}\bigr) \Biggm/ \sum_{s=1}^{q}\frac{d_{s}a_{j-1}^{\alpha_{s}}}{\mu_{s}} \Biggr] \\ &{}+\kappa_{1}\bar{v}\bigl[h+\tau^{1+\sigma/2}+\sigma^{2} \bigr] \\ \leq&\sum_{s=1}^{q}v_{s} \Biggl[\sum_{j=1}^{k}\bigl(a_{k-j}^{\alpha _{s}}-a_{k-j+1}^{\alpha_{s}} \bigr)\kappa_{1}\bigl(h+\tau^{1+\sigma/2}+\sigma^{2}\bigr) \Biggm/ \sum_{s=1}^{q}\frac{d_{s}a_{k}^{\alpha_{s}}}{\mu_{s}} \Biggr] \\ &{}+\kappa_{1}\bar{v}\bigl[h+\tau^{1+\sigma/2}+\sigma^{2} \bigr] \\ =&\kappa_{1}\bigl(h+\tau^{1+\sigma/2}+\sigma^{2}\bigr) \Biggl[\Biggl(1-\sum_{s=1}^{q}v_{s}a_{k}^{\alpha_{s}} \Biggr) \Biggm/\sum_{s=1}^{q}\frac{d_{s}a_{k}^{\alpha _{s}}}{\mu_{s}}+ \bar{v} \Biggr] \\ =&\kappa_{1}\bigl(h+\tau^{1+\sigma/2}+ \sigma^{2}\bigr) \Bigm/\sum_{s=1}^{q} \frac {d_{s}a_{k}^{\alpha_{s}}}{\mu_{s}}, \end{aligned}$$

which proves the theorem. □

4 Fast solution techniques based on preconditioned Krylov subspace solvers

In this section, we analyze both the implementation and the computational complexity of the implicit difference scheme (2.14)–(2.16) and propose an efficient implementation based on Krylov subspace solvers with suitable circulant preconditioners.

According to (2.17) and (2.18), there is a sequence of nonsymmetric Toeplitz linear system to be solved at each time level k. If a direct method is employed to solve the linear system (2.18), the LU decomposition can be reused in each time level k. This approach, however, needs the memory requirement of \(\mathcal{O}(M^{2})\) and the complexity of \(\mathcal{O}(M^{3})\) per iteration step, which is prohibitively expensive if M is large. Fortunately, since \(G_{\beta}\) is a Toeplitz matrix, it can be stored with only M entries [41]. The Krylov subspace methods with circulant preconditioners [45, 61] can be used to solve Toeplitz-like linear systems with a fast convergence rate. In this case, we also remark that the computational complexity of preconditioned Krylov subspace methods is only in \(\mathcal{O}(M\log M)\) at each iteration step for implementing the implicit difference scheme. In this study, we employ four preconditioned Krylov subspace methods, the PBiCGSTAB method, the PBiCRSTAB method, the PGPBiCOR\((m, \ell)\) method, and the PCGNR method. The numerical results show the performance of three proposed preconditioned Krylov subspace solvers over the LU decomposition and the PCGNR method, while solving (2.18), and reveal that the results of the PGPBiCOR\((m, \ell)\) method are better than others when \(m=2\), \(\ell=1\).

The PGPBiCOR(2,1) method with the preconditioner K applied to the system \(Ax=b\) is given in Algorithm 4.1.

Algorithm 4.1
figure a

PGPBiCOR(2,1) for \(A\textbf{x} = \textbf{b}\) with preconditioner K

Full size image

Now we propose a circulant preconditioner generated from the Strang circulant preconditioner [46] in the PGPBiCOR(2,1) method for solving (2.18). For a real Toeplitz matrix \(Q=[q_{j-m}]_{0\leq j,m< N}\), the Strang circulant matrix \(s(Q)=[s_{j-m}]_{0\leq j,m< N}\) is obtained by copying the central diagonals of Q to complete the circulant requirements [43]. More precisely, the diagonals of \(s(Q)\) are given by

$$\begin{aligned} s_{j}= \textstyle\begin{cases} q_{j}, &0\leq j< N/2,\\ 0, &j=N/2\mbox{ if } N\mbox{ is even},\\ q_{j-N},&N/2< j< N,\\ s_{j+N},&0< -j< N. \end{cases}\displaystyle \end{aligned}$$

Recall formula (2.18):

$$M^{k+1}=I-vA^{k+1}=I-v\bigl(D_{+}^{k+1}G_{\beta}+D_{-}^{k+1}G_{\beta}^{T} \bigr), $$

where \(D_{\pm}^{k+1}= \operatorname{diag}(d_{\pm, 1}^{k+1},\ldots,d_{\pm , M-1}^{k+1})\), and \(G_{\beta}\) is the Toeplitz matrix. Then our circulant preconditioner is defined as

$$ S^{k+1}=I-v\bigl[\bar{d}_{+}^{k+1}s(G_{\beta})+ \bar{d}_{-}^{k+1}s\bigl(G_{\beta}^{T}\bigr) \bigr], $$
(4.1)

where

$$ \bar{d}_{\pm}^{k+1}=\frac{1}{M-1}\sum _{i=1}^{M-1}d_{\pm,i}^{k+1}. $$

Specifically, the first columns of both \(s(G_{\beta})\) and \(s(G_{\beta}^{T})\) are given by

$$\left ( \textstyle\begin{array}{c} g_{1}^{(\beta)} \\ g_{2}^{(\beta)} \\ \vdots\\ g_{\lfloor\frac{M}{2}\rfloor}^{(\beta)} \\ 0 \\ \vdots\\ 0 \\ g_{0}^{(\beta)} \end{array}\displaystyle \right )\quad \mbox{and}\quad \left ( \textstyle\begin{array}{c} g_{1}^{(\beta)} \\ g_{0}^{(\beta)} \\ 0 \\ \vdots\\ 0 \\ g_{\lfloor\frac{M}{2}\rfloor}^{(\beta)} \\ \vdots\\ g_{2}^{(\beta)} \end{array}\displaystyle \right ), $$

respectively. A high efficiency of Strang’s circulant preconditioner for space FDEs with constant diffusion coefficients was demonstrated in [45]. In [45], the proposed preconditioner was invertible, and its spectrum was theoretically proven to be clustered at 1 if the diffusion coefficients were constant. In this paper, we focus the attention on the case of variable diffusion coefficients. We further show that the preconditioner \(S^{k+1}\) defined in (4.1) is also nonsingular and thus is well-defined. Before that, we need the following lemma, which is essential to prove the nonsingularity of \(S^{k+1}\) in (4.1).

Lemma 4.2

All eigenvalues of \(s(G_{\beta})\) and \(s(G_{\beta}^{T})\) fall inside the open disc

$$ \bigl\{ z\in\mathbb{C}: \vert z+\beta \vert < \beta\bigr\} . $$

Proof

All Gershgorin discs [51] of the circulant matrices \(s(G_{\beta})\) and \(s(G_{\beta}^{T})\) are centered at \(g_{1}^{(\beta )}=-\beta\) with radius

$$r_{N}=g_{0}^{(\beta)}+\sum _{j=2}^{\lfloor\frac{M }{2}\rfloor}g_{j}^{(\beta)}< \sum _{j=0,j\neq1}^{\infty}g_{j}^{(\beta )}=-g_{1}^{(\beta)}= \beta $$

by the properties of the sequence \(\{g_{j}^{(\beta)}\}\); refer to Proposition 3.1. □

Remark 4.3

It is worth mentioning that the real parts of all eigenvalues of \(s(G_{\beta})\) and \(s(G_{\beta}^{T})\) are strictly negative for all M.

As we know, a circulant matrix E can be diagonalized by the Fourier matrix F [43], that is,

$$E=F^{*}\Lambda F, $$

where the entries of F are given by

$$F_{j,m}=\frac{1}{\sqrt {N}}e^{{2\pi ijm}/{N}},\quad 0\leq j,m\leq N-1, $$

with the imaginary unit i, and Λ is a diagonal matrix holding the eigenvalues of E.

Then it follows that \(s(G_{\beta})=F^{*}\Lambda_{\beta}F\) and \(s(G_{\beta}^{T})=F^{*}\bar{\Lambda}_{\beta}F\), where \(\bar{\Lambda}_{\beta}\) is the complex conjugate of \(\Lambda_{\beta}\). Decompose the circulant matrix \(S^{k+1}=F^{*}\Lambda_{s} F\) with the diagonal matrix \(\Lambda_{s}=I-v[\bar {d}_{+}^{k+1}\Lambda_{\beta}+\bar{d}_{-}^{k+1}\bar{\Lambda}_{\beta}]\). Then \(S^{k+1}\) is invertible if all diagonal entries of \(\Lambda_{s}\) are nonzero. Moreover, we can obtain the following conclusion about the invertibility of \(S^{k+1}\) in (4.1).

Theorem 4.4

For \(1 < \beta< 2\), the preconditioner \(S^{k+1}\) defined as in (4.1) is nonsingular, and

$$\bigl\Vert \bigl(S^{k+1}\bigr)^{-1} \bigr\Vert _{2}\leq1. $$

Proof

By Remark 4.3 we have \(\operatorname{Re}([\Lambda_{\beta}]_{i,i})<0\). Noting that \(v>0\) and \(\bar{d}_{\pm}^{k+1}\geq0\), we obtain

$$\bigl\vert [\Lambda_{s}]_{i,i} \bigr\vert \geq \operatorname{Re} \bigl([\Lambda_{s}]_{i,i}\bigr)=1-v\bigl[\bar {d}_{+}^{k+1}\operatorname{Re}\bigl([\Lambda_{\beta}]_{i,i} \bigr)+\bar{d}_{-}^{k+1}\operatorname{Re}\bigl([\bar{\Lambda }_{\beta}]_{i,i}\bigr)\bigr]\geq1>0 $$

for each \(i=1,\ldots,M-1\). Therefore, \(S^{k+1}\) is nonsingular. Furthermore, we have

$$\bigl\Vert \bigl(S^{k+1}\bigr)^{-1} \bigr\Vert _{2}=\frac{1}{\min_{1\leq i\leq M-1} \vert [\Lambda _{s}]_{i,i} \vert }\leq1. $$

Hence the statements in Theorem 4.4 are proved. □

Unfortunately, when the diffusion coefficients \(d_{\pm}(x,t)\) are nonconstant functions, the preconditioned sequence \((S^{k+1})^{-1} M^{k+1}\) cannot be clustered at 1; we refer to [48] for details of the theoretical analysis. For clarity, we still give some figures to illustrate the clustering eigenvalue distributions of several specified preconditioned matrices in the next section.

5 Numerical examples

The numerical experiments presented in this section have a two-fold objective. They illustrate that the proposed finite difference scheme can indeed converge with first-order in space and \((1+\frac{\sigma }{2})\)-order in time. At the same time, they assess the computational efficiency of the fast solution techniques (Algorithm 4.1) designed in Sect. 4. The nonsymmetric linear system (2.18) is solved at each time step by the PCGNR method, the PBiCRSTAB method, the PBiCGSTAB method, the PGPBiCOR(2,1) method (Algorithm 4.1), and LU factorization of MATLAB, respectively. The numbers of iterations required for convergence and CPU times of those methods are shown further. The stopping criterion of those methods is

$$\frac{ \Vert r^{(k)} \Vert _{2}}{ \Vert r^{(0)} \Vert _{2}} < 10^{-12}, $$

where \(r^{(k)}\) is the residual vector of the linear system after k iterations, and the initial guess is chosen as a zero vector. In the following tables, setting \(e(h,\tau,\sigma)=\max_{1\leq i\leq M-1}|u(x_{i},t_{N},\sigma)-u_{i}^{N}|\), where \(u(x_{i},t_{N},\sigma)\) id the exact solution, and \(u_{i}^{N}\) is the numerical solution with step sizes h and τ at \(t_{N}=T\). The convergence order is computed by

$$\begin{aligned} &\mathit{rate}_{h}=\log_{2}\frac{e(h,\tau,\sigma)}{e(h/2,\tau,\sigma)},\\ &\mathit{rate}_{\tau}=\log_{2}\frac{e(h,\tau,\sigma)}{e(h,\tau/2,\sigma)},\\ &\mathit{rate}_{\sigma}=\log_{2}\frac{e(h,\tau,\sigma)}{e(h,\tau,\sigma/2)}. \end{aligned}$$

The number of spatial grid points is denoted by M, N denotes the number of time steps, CPU (s) denotes the total CPU time in seconds for solving the whole TDFDEs problem, and Iter denotes the average number of iterations required for solving the TDFDEs problem, that is,

$$\mathrm{Iter}=\frac{1}{N}\sum_{n=1}^{N}\mathrm{Iter}(n), $$

where Iter(n) denotes the number of iterations required for solving (2.18). For those methods, besides the proposed circulant preconditioner \(S^{k+1}\) in (4.1), we also test the T. Chan’s preconditioner [43] which can be written as

$$c\bigl(M^{k+1}\bigr)=I-v\bigl[\bar{d}_{+}^{k+1}c(G_{\beta})+ \bar{d}_{-}^{k+1}c\bigl(G_{\beta}^{T}\bigr) \bigr], $$

where \(c(Q)\) denotes Chan’s preconditioner for an arbitrary matrix Q. More specifically, the first columns of the circulant matrices \(c(G_{\beta})\) and \(c(G_{\beta}^{T})\) are given as

$$\frac{1}{M-1}\left ( \textstyle\begin{array}{c} (M-1)g_{1}^{(\beta)} \\ (M-2)g_{2}^{(\beta)} \\ \vdots\\ 2g_{M-2}^{(\beta)} \\ g_{M-1}^{(\beta)}+(M-2)g_{0}^{(\beta)} \end{array}\displaystyle \right )\quad \mbox{and}\quad \frac{1}{M-1}\left ( \textstyle\begin{array}{c} (M-1)g_{1}^{(\beta)} \\ g_{M-1}^{(\beta)}+(M-2)g_{0}^{(\beta)}\\ 2g_{M-2}^{(\beta)} \\ \vdots\\ (M-2)g_{2}^{(\beta)} \end{array}\displaystyle \right ), $$

respectively.

In all tables, the symbols “PCGNR(S)”, “PBiCRSTAB(S)”, “PBiCGSTAB(S)”, and “PGPBiCOR(S)” correspond to the PCGNR, PBiCRSTAB, PBiCGSTAB, and PGPBiCOR methods with the circulant preconditioner \(S^{k+1}\), respectively. Similarly, the symbols “PCGNR(C)”, “PBiCRSTAB(C)”, “PBiCGSTAB(C)”, and “PGPBiCOR(C)” denote Chan’s circulant preconditioner \(c(M^{k+1})\) for the PCGNR, PBiCRSTAB, PBiCGSTAB, and PGPBiCOR(2,1) methods, respectively. All numerical experiments are implemented in MATLAB (R2013a) on a desktop PC with 4 GB RAM, Inter (R) Core (TM) i3-2130 CPU, @3.40 GHz.

Example 5.1

Consider the following time distributed-order and space fractional diffusion equations with variable coefficients:

$$\textstyle\begin{cases} \int_{0}^{1}\Gamma(3-\alpha){}^{C}_{0}D_{t}^{\alpha}u(x,t)\,d\alpha\\ \quad =d_{+}(x,t){}_{RL}D_{0,x}^{\beta}u(x,t)+d_{-}(x,t){}_{RL}D_{x,L}^{\beta }u(x,t)+f(x,t),\quad 0< x< 1, 0< t\leq T,\\ u(0,t)=0,\qquad u(1,t)=0,\quad0\leq t\leq T,\\ u(x,0)=x^{2}(1-x)^{2},\quad0\leq x\leq1, \end{cases} $$

where \(1<\beta\leq2\), \(d_{+}(x,t)=(1+t)x^{0.6}\), \(d_{-}(x,t)=(1+t)(1-x)^{0.6}\), and

$$ \begin{aligned} f(x,t)={}&{-}\bigl(1-t^{2}\bigr) \biggl[ \frac{\Gamma(3)}{\Gamma(3-\beta )}\bigl(d_{+}(x,t)x^{2-\beta}+d_{-}(x,t) (1-x)^{2-\beta}\bigr) \\ &{}-2\frac{\Gamma(4)}{\Gamma(4-\beta)}\bigl(d_{+}(x,t)x^{3-\beta }+d_{-}(x,t) (1-x)^{3-\beta}\bigr) \\ &{}+\frac{\Gamma(5)}{\Gamma(5-\beta )}\bigl(d_{+}(x,t)x^{4-\beta}+d_{-}(x,t) (1-x)^{4-\beta}\bigr) \biggr] \\ &{}-2x^{2}(1-x)^{2}\bigl(t^{2}-t\bigr)/\ln t. \end{aligned} $$

The exact solution of this problem is \(u(x,t)=x^{2}(1-x)^{2}(1-t^{2})\).

The errors and convergence orders are displayed in Tables 1 and 2. We can clearly see that the convergence orders are of first-order in space and \((1+\frac{\sigma}{2})\)-order in time, which verifies the correctness of our theoretical results.

Table 1 Maximum errors and spatial convergence orders of difference scheme (2.14)–(2.16) for Example 5.1 with \(\alpha = 0.5\); \(\sigma = 0.1\); \(T = 1.5\); \(N = 800\)
Full size table
Table 2 Maximum errors and temporal convergence orders of difference scheme (2.14)–(2.16) for Example 5.1 with \(\alpha = 0.5\); \(\sigma = 0.2\); \(T = 1.5\); \(M = 2000\)
Full size table

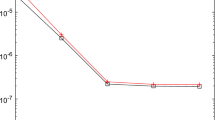
A comparison of the exact and numerical solutions for \(\beta=1.8\) with \(h=0.02\), \(\tau=0.015\), \(\alpha = 0.5\), \(\sigma=0.1\) at \(t=0.3\) (triangles), \(t=0.75\) (stars), and \(t=1.5\) (squares) is shown in Fig. 1. We can see that the numerical solution is in good conformity with the exact one.

Figure 1
figure 1

Exact solutions (lines) and numerical solutions (symbols) of Example 5.1 with \(\beta = 1.8\) at \(t = 0.3\) (rounds), \(t = 0.75\) (squares), \(t = 1.5\) (rhombus)

Full size image

In Figs. 2 and 3, the eigenvalue plots of the original matrix \(M^{k+1}\) and the preconditioned matrices \((S^{k+1})^{-1}M^{k+1}\) are plotted. These two figures confirm that the circulant preconditioning exhibits very nice clustering properties. The eigenvalues of preconditioned matrices are clustered at 1, except for a few outliers. It indicates that the vast majority of the eigenvalues are well separated away from 0. It may guarantee that our proposed preconditioners can deeply accelerate Krylov subspace methods for solving the nonsymmetric Toeplitz system. We also validate the effectiveness and robustness of the designed circulant preconditioner from the perspective of clustering spectrum distribution.

Figure 2
figure 2

Spectrum of original matrix (red) and preconditioned matrix (blue) for Example 5.1 at time level (a): \(k=0\) and (b): \(k=1\), respectively, when \(M = N = 128\), \(\alpha = 0.5\), \(q = 10\), \(\beta = 1.8\), and \(T = 0.75\)

Full size image
Figure 3
figure 3

Spectrum of original matrix (red) and preconditioned matrix (blue) for Example 5.1 at time level (a): \(k=0\) and (b): \(k=1\), respectively, when \(M = N = 256\), \(\alpha = 0.5\), \(q = 10\), \(\beta = 1.8\), and \(T = 1.5\)

Full size image

Tables 3 and 4 report the numerical results for solving Example 5.1, which show that both the average number of iterations and the CPU time of the PCGNR, PBiCRSTAB, PBiCGSTAB, PGPBiCOR(2,1) with Strang’s circulant preconditioners are much less than those with Chan’s circulant preconditioners, respectively. It also verifies that the proposed PGPBiCOR(2,1) method based on Strang’s preconditioner is more attractive than other proposed methods in aspects of the less CPU time and average number of iterations.

Table 3 Comparisons for solving Example 5.1 by the LU method and the PCGNR/PBiCRSTAB method with two circulant preconditioners, where \(\beta = 1.3, 1.5, 1.8\), \(\alpha = 0.5\), \(q = 10\), and \(T =0.75\)
Full size table
Table 4 Comparisons for solving Example 5.1 by the PBiCGSTAB/PGPBiCOR(2, 1) method with two circulant preconditioners, where \(\beta = 1.3, 1.5, 1.8\), \(\alpha = 0.5\), \(q = 10\), and \(T = 0.75\)
Full size table

Example 5.2

Consider the following equation:

$$ \textstyle\begin{cases} \int_{0}^{1}\omega(\alpha){}^{C}_{0}D_{t}^{\alpha}u(x,t)\,d\alpha\\ \quad =d_{+}(x,t){}_{RL}D_{0,x}^{\beta}u(x,t)+d_{-}(x,t){}_{RL}D_{x,L}^{\beta }u(x,t) +(1+t^{2})\sin x,\quad0< x< 1, 0< t\leq 5,\\ u(0,t)=0,\qquad u(1,t)=0,\quad0\leq t\leq5,\\ u(x,0)=10\delta(x),\quad0\leq x\leq1, \end{cases} $$

where \(1<\beta\leq2\), \(d_{+}(x,t)=(1+t)x^{0.6}\), \(d_{-}(x,t)=(1+t)(1-x)^{0.6}\).

Gorenflo et al. [23] considered the special case \(\omega(\alpha) = \delta(\alpha-\eta)\), \(0< \eta<1\), and showed that the fundamental solution of the time distributed-order fractional diffusion equation can be viewed as a probability density function in space x, evolving in time t. Hu et al. [31] also considered the solutions of the time distributed-order and two-sided space-fractional advection-dispersion equation in the special cases of the derivative weight function \(\omega(\alpha) = \delta(\alpha-0.5)\) and \(\omega(\alpha) = \tau^{\alpha}\), where τ is a positive constant.

We also take \(\omega(\alpha) = \delta(\alpha-0.5)\) and \(\omega(\alpha ) = \tau^{\alpha}\) as examples to investigate the numerical solutions of Example 5.2, respectively. Taking \(q = 15\), \(M = 50\), \(N = 20\), and \(T = 5\), Fig. 4 exhibits the numerical solutions of (2.14)–(2.16) in solving Example 5.2 with different β and \(\omega(\alpha)\). The effect of the spatial order β and these two weight functions \(\omega(\alpha)\) can be illustrated by (a), (b), (c), and (d). First, we fixed \(\omega(\alpha)\) and, increasing the number of the β, we observed a lower diffusion. Then, we can see from these four solution profiles that different diffusion phenomena occur under different weight function \(\omega(\alpha)\) conditions with fixed β. In this example, when \(\omega(\alpha) = \delta(\alpha-0.5)\), it leads to a slightly faster diffusion than that of \(\omega(\alpha) = \tau^{\alpha}\). This implies that we can model different complex dynamical process by choosing appropriate \(\omega(\alpha)\).

Figure 4
figure 4

Numerical solutions of Example 5.2 at \(\alpha = 0.5\), \(q = 15\), \(M = 50\), \(N = 20\), and \(T = 5\) with different β and \(\omega(\alpha)\). \(\omega(\alpha) = \tau^{\alpha}\) (red); \(\omega(\alpha) = \delta(\alpha-0.5)\) (blue)

Full size image

6 Conclusion

In this paper, an implicit difference scheme approximating the TDFDEs on bounded domains has been described. The implicit difference scheme is unconditionally stable and convergent based on mathematical induction. Meanwhile, the new difference scheme converges with the first-order in space and the \((1+\frac{\sigma}{2})\)-order in time for the TDFDEs. Numerical experiments confirming the obtained theoretical results are carried out. More significantly, it has also been shown that an efficient implementation of the PGPBiCOR(2,1) method with Strang’s circulant preconditioner for solving the discretized Toeplitz-like linear system requires only \(\mathcal{O}(M \log M)\) computational complexity and \(\mathcal{O}(M)\) storage cost. Extensive numerical results fully support the theoretical findings and prove the efficiency of the proposed preconditioned Krylov subspace methods.

In future work, we will focus on handling two- or more dimensional TDFDEs with fast solution techniques. Meanwhile, we will also focus on the development of other efficient preconditioners for accelerating the convergence of Krylov subspace solvers for discretized Toeplitz systems.