1 Introduction

Fractional differential equations (FDEs) are generalizations of classical differential equations of integer order. FDEs have been studied nowadays to describe several physical aspects and procedure in natural conditions [3–19]. However, fractional partial differential equations (FPDEs) having only time derivative have been analyzed via the Lie symmetry method [20–26]. Recently, the Lie method has been developed to the systems of time FPDEs [27]. More recently, the Lie method has been extended for the first time to the analysis of FPDEs having space and time derivative with fractional order and the systems of space and time FPDEs in [1, 2]. To the best of our knowledge, application of the Lie method to the space-time FPDEs and the systems of space-time FPDEs appeared only in [1, 2]. Therefore, applying this new approach to more space-time FPDEs in order to obtain lots of solutions will be remarkable contribution to the literature.

The LSA and Cls supply lots of ideas on the systems modeled by the differential equations. Lie symmetries are a very significant tool in determining exact solutions and Cls of differential equations. In spite of the significance of Cls in analyzing the integrability and internal properties and in proving the existence and uniqueness of solutions of differential equations [28–30], the Cls for PDEs having fractional-order are not investigated in detail. The generalization for investigating Cls for FDEs was presented in [31, 32]. In recent time, the fractional generalized Noether operators have been introduced [30] for FPDEs that do not have a Lagrangian in order to find Cls using a new conservation theorem [33]. Even though very few works [34–36] that have to do with Cls of FPDEs can be found, the analysis of Cls for the STFPDEs has entirely not been investigated in more detail.

In this study, we consider STFRHE given by

$$ \frac{\partial^{\alpha }u}{\partial t^{\alpha }}+u\frac{\partial^{ \beta }u}{\partial x^{\beta }}+uu_{xxx}+3u_{x}u_{xx}=0, $$
(1)

where \(0<\alpha \le 1\) and \(\beta <2\). In Eq. (1), \(\frac{ \partial^{\alpha }u}{\partial t^{\alpha }}\) and \(\frac{\partial^{ \beta }u}{\partial x^{\beta }}\) are the RL fractional derivatives of order \(\alpha,\beta >0\), respectively. If \(\beta =1\), Eq. (1) becomes

$$ \frac{\partial^{\alpha }u}{\partial t^{\alpha }}+u\frac{\partial u}{ \partial x}+uu_{xxx}+3u_{x}u_{xx}=0. $$
(2)

The invariance properties for Eq. (2) that can be used to interpret the formation of patterns in liquid drops were analyzed and investigated in [37]. If \(\alpha =1\) and \(\beta =1\), Eq. (1) becomes

$$ \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+uu_{xxx}+3u _{x}u_{xx}=0. $$
(3)

Some approximate analytical solutions for Eq. (3) were presented in [38, 39]. Many methods have been applied to reach analytical solutions for PDEs [40–47].

The aim of this study is to analyze and investigate the LSA, explicit solution via the power series technique and Cls for Eq. (1).

The outline of the paper is presented in the following way: In Section 2 we present some preliminaries; in Section 3 we present symmetry analysis and reduction; in Section 4 we analyze explicit solution for the reduced equation; in Section 5 we construct Cls for the underlying equation. Finally, concluding remarks are given in Section 6.

2 Preliminaries

Herein, we present some preliminaries. The RL fractional derivative [19, 27] is defined by

$$ D^{\alpha }f(t) = \textstyle\begin{cases} \frac{d^{n}f}{dt^{n}},&\alpha =n, \\ \frac{d}{dt^{n}}I^{n-\alpha }f(t), &0\le n-1< \alpha < n, \end{cases} $$
(4)

where n is a natural number and \(I^{\mu }f(t)\) is given by

$$\begin{aligned}& I^{\mu }f(t)=\frac{1}{\Gamma (\mu)} \int_{0}^{t}(t-s)^{\mu -1}f(s)\,ds,\quad \mu >0, \end{aligned}$$
(5)
$$\begin{aligned}& I^{\mu }f(t)=f(t), \end{aligned}$$
(6)

and \(\Gamma (z)\) represents the gamma function.

Consider the following space-time FPDEs:

$$ \bigtriangleup =F\bigl(x, t, u, \partial^{\alpha }_{t}, \partial^{\beta } _{x}, u_{xx}, u_{xxx},\ldots \bigr). $$
(7)

Suppose that a one-parameter group of transformations is given by

$$\begin{aligned}& \begin{aligned}&\bar{t}=t+\epsilon \xi^{2}(t,x,u)+O\bigl( \epsilon^{2}\bigr), \\ &\bar{x}=x+\epsilon \xi^{1}(t,x,u)+O\bigl( \epsilon^{2}\bigr), \\ &\bar{u}=u+\epsilon \eta (t,x,u)+O\bigl(\epsilon^{2} \bigr), \\ &\frac{\partial^{\alpha } \bar{u}}{\partial \bar{t}}=\frac{ \partial^{\alpha }u}{\partial t^{\alpha }}+\epsilon \eta^{\alpha,t}(t,x,u)+O \bigl( \epsilon^{2}\bigr), \\ &\frac{\partial^{\beta } \bar{u}}{\partial \bar{x}}=\frac{ \partial^{\beta }u}{\partial x^{\beta }}+\epsilon \eta^{\beta,x}(t,x,u)+O \bigl( \epsilon^{2}\bigr), \\ &\frac{\partial \bar{u}}{\partial \bar{x}}=\frac{\partial u}{\partial x}+\epsilon \eta^{x}(t,x,u)+O \bigl(\epsilon^{2}\bigr), \\ &\frac{\partial^{2} \bar{u}}{\partial \bar{x}^{2}}=\frac{\partial ^{2} u}{\partial x^{2}}+\epsilon \eta^{xx}(t,x,u)+O \bigl(\epsilon^{2}\bigr), \\ &\frac{\partial^{3} \bar{u}}{\partial \bar{x}^{3}}=\frac{\partial ^{3} u}{\partial x^{3}}+\epsilon \eta^{xxx}(t,x,u)+O \bigl(\epsilon^{2}\bigr), \end{aligned} \end{aligned}$$
(8)

where

$$\begin{aligned}& \begin{aligned}&\eta^{\alpha,t}=D^{\alpha }_{t}(\eta)+ \xi^{1} D^{\alpha }_{t}(u _{x})-D^{\alpha }_{t} \bigl(\xi^{1} u_{x}\bigr)+D^{\alpha }_{t} \bigl(u\bigl(D_{t} \xi^{2}\bigr)\bigr)-D ^{\alpha +1}_{t}( \xi u)+\xi^{2} D^{\alpha +1}_{t}(u), \\ &\eta^{\beta,t}=D^{\beta }_{x}(\eta)+D^{\beta }_{x}\bigl(u\bigl(D_{x} \xi ^{1} \bigr)\bigr)-D^{\beta +1}_{x}\bigl(\xi^{1} u\bigr)+\xi D^{\beta +1}_{x}(u)+\xi^{2} D ^{\beta }_{t}(u_{t})-D^{\beta }_{x} \bigl(\xi^{2} u_{t}\bigr), \\ &\eta^{x}=D_{x}(\eta)-u_{x} D_{x}\bigl(\xi^{1}\bigr)-u_{t} D_{t} \bigl(\xi^{2}\bigr), \\ &\eta^{xx}=D_{x}\bigl(\eta^{x} \bigr)-u_{xt} D_{x}\bigl(\xi^{1} \bigr)-u_{xx} D_{t}\bigl(\xi ^{2}\bigr), \\ &\eta^{xxx}=D_{x}\bigl(\eta^{xx} \bigr)-u_{xxt} D_{x}\bigl(\xi^{1} \bigr)-u_{xxx} D_{t}\bigl(\xi ^{2}\bigr), \\ &\ldots \end{aligned} \end{aligned}$$
(9)

In Eq. (7), \(D_{x}\) and \(D_{t}\) represent the total differential operators defined by

$$\begin{aligned}& D_{x}=\frac{\partial }{\partial x}+u_{x} \frac{\partial }{\partial u}+u_{xx} \frac{\partial }{\partial u_{x}}+\cdots , \end{aligned}$$
(10)
$$\begin{aligned}& D_{t}=\frac{\partial }{\partial t}+u_{t} \frac{\partial }{\partial u}+u_{tt} \frac{\partial }{\partial u_{t}}+\cdots . \end{aligned}$$
(11)

The corresponding Lie algebra of symmetries consists of the following vector fields:

$$ X=\xi^{1}\frac{\partial }{\partial x}+\xi^{2}\frac{\partial }{\partial t}+\eta \frac{\partial }{\partial u}. $$
(12)

The vector field Eq. (12) is a Lie point symmetry of Eq. (7) provided

$$ P^{\alpha, \beta, 3}r X(\bigtriangleup)\vert _{\bigtriangleup =0}=0. $$
(13)

Also, the invariance condition [48] yields

$$ \xi^{1}(t, x, u)\vert _{x=0}=0,\qquad \xi^{2}(t, x, u) \vert _{t=0}=0, $$
(14)

and the αth and βth extended infinitesimals with Eq. (10) are given as in [19, 27].

3 Lie symmetries and reduction for Eq. (1)

Suppose that Eq. (1) is an invariant under Eq. (8), we have that

$$ \frac{\partial^{\alpha }\bar{u}}{\partial \bar{t}^{\alpha }}+u\frac{ \partial^{\beta }\bar{u}}{\partial \bar{x}^{\beta }}+\bar{u}\bar{u} _{\bar{x}\bar{x}\bar{x}}+3 \bar{u}_{\bar{x}}\bar{u}_{\bar{x}\bar{x}}=0 $$
(15)

so that \(u=u(x,t)\) satisfies Eq. (1). Using Eq. (8) in Eq. (15), we get the invariant equation

$$ \eta^{\alpha,t}+u\eta^{\beta,x}+u_{xxx}\eta +3u_{xx} \eta^{x}+3u_{x} \eta^{xx}+u\eta^{xxx}=0. $$
(16)

Putting the values of \(\eta^{\alpha,t}\), \(\eta^{\beta,x}\), \(\eta^{x}\), \(\eta^{xx}\) and \(\eta^{xxx}\) into Eq. (16) and isolating coefficients, we have

$$\begin{aligned}& \partial^{\alpha }_{t}\eta -u\partial^{\alpha }_{t} \eta_{u}+u \partial^{\beta }_{x}\eta -u^{2} \partial^{\beta }_{x}\eta_{u}+u\eta _{xxx}=0, \\& \left( \begin{matrix} \alpha \\ n \end{matrix}\right) \partial^{n}_{t}(\eta)- \left( \begin{matrix} \alpha \\ n+1 \end{matrix}\right) D^{n+1}_{t}\bigl( \xi^{2}\bigr)=0, \quad n=1,2,\ldots, \\& \left( \begin{matrix} \beta \\ n \end{matrix}\right) \partial^{n}_{x}(\eta)- \left( \begin{matrix} \beta \\ n+1 \end{matrix}\right) D^{n+1}_{x}\bigl( \xi^{1}\bigr)=0,\quad n=1,2,\ldots, \\& \xi^{1}_{u}=\xi^{2}_{u}= \xi^{1}_{t}=\xi^{2}_{x}= \eta_{uu}=0, \\& u\beta \xi^{1}_{x}-\alpha \xi^{2}_{t}=0. \end{aligned}$$

Solving these equations, we obtain

$$\xi^{1}=c_{1}+x\alpha c_{2},\qquad \xi^{2}=t\beta c_{2},\qquad \eta =\alpha u c_{2}(3- \beta), $$

where \(c_{1}\), \(c_{2}\) represent arbitrary constants. Thus infinitesimal symmetry group for Eq. (1) is as follows:

$$ X_{1}=\frac{\partial }{\partial x},\qquad X_{2}=\alpha x \frac{\partial }{\partial x}+\beta t\frac{\partial }{ \partial t}+\alpha u(3-\beta) \frac{\partial }{\partial u}. $$
(17)

In particular, for the symmetry \(X_{2}\), we obtain the following similarity transformation and similarity variable:

$$\frac{dx}{\alpha x}=\frac{dt}{t\beta }=\frac{du}{ \alpha u(3-\beta)}. $$

Solving the above equations, we get

$$ z_{1}=xt^{-\frac{\alpha }{\beta }}, \qquad z_{2}=ut^{-\frac{\alpha (3-\beta)}{\beta }}. $$
(18)

Hence, from the symmetry \(X_{2}\), we get the group-invariant solution

$$ u=t^{\frac{\alpha (3-\beta)}{\beta }}f(\xi),\qquad \xi =xt^{-\frac{\alpha }{\beta }}, $$
(19)

where f is an arbitrary function of ξ.

Theorem

By the similarity transformation, Eq. (19) reduces Eq. (1) to the following:

$$ \bigl(P^{1-\alpha +\frac{\alpha }{\beta }(3-\beta), \alpha }_{\frac{ \beta }{\alpha }}f \bigr) (\xi)+f\xi^{-\beta } \bigl(Q^{-\beta,\beta } _{1} f \bigr) (\xi)+ff_{\xi \xi \xi }+3f_{\xi }f_{\xi \xi }=0 $$
(20)

with the left-hand-sided EK fractional differential operator [49, 50]

$$\begin{aligned}& \bigl(P^{\xi^{2}, \alpha }_{\delta }f \bigr)=\prod^{n-1}_{j=0} \biggl(\xi ^{2}+j-\frac{1}{\delta }\frac{d}{d\xi } \biggr) \bigl(K^{\xi^{2}+\alpha, n- \alpha }_{\delta }f\bigr) (\xi), \end{aligned}$$
(21)
$$\begin{aligned}& n= \textstyle\begin{cases} [\alpha ]+1, &\alpha \ne \mathbf{N}, \\ \alpha,&\alpha \in \mathbf{N}, \end{cases}\displaystyle \end{aligned}$$
(22)

where

$$ \bigl(K^{\xi^{2}, \alpha }_{\delta }f\bigr) (\xi)= \textstyle\begin{cases} \frac{1}{\Gamma (\alpha)}\int^{\infty }_{1}(u-1)^{\alpha -1}u^{-(\xi ^{2}+\alpha)}f(\xi u^{\frac{1}{\delta }})\,du, &\alpha >0, \\ f(\xi),&\alpha =0. \end{cases} $$
(23)

The right-hand-sided EK fractional differential operator is given by

$$\begin{aligned}& \bigl(Q^{\xi^{2}, \beta }_{\delta }f \bigr)=\prod^{n-1}_{j=0} \biggl(\xi ^{2}+j-\frac{1}{\delta }\frac{d}{d\xi } \biggr) \bigl(L^{\xi^{2}+\beta, n- \beta }_{\delta }f\bigr) (\xi), \end{aligned}$$
(24)
$$\begin{aligned}& n = \textstyle\begin{cases} [\beta ]+1, &\beta \ne \mathbf{N}, \\ \beta,&\beta \in \mathbf{N}, \end{cases}\displaystyle \end{aligned}$$
(25)

where

$$ \bigl(L^{\xi^{2}, \beta }_{\delta }f\bigr) (\xi)= \textstyle\begin{cases} \frac{1}{\Gamma (\beta)}\int^{1}_{0}(1-u)^{\beta -1}u^{\xi^{2}}f( \xi u^{\frac{1}{\delta }})\,du, &\beta >0, \\ f(\xi),&\beta =0. \end{cases} $$
(26)

Proof

Let \(n-1<\alpha <1\), \(n=1,2,3,\ldots\) . In accordance with the RL fractional derivative in Eq. (15), we get

$$ \frac{\partial^{\alpha }u}{\partial t^{\alpha }}=\frac{\partial^{n}}{ \partial t^{n}} \biggl[\frac{1}{\Gamma (n-\alpha)} \int^{t}_{1}(t-s)^{n- \alpha -1}s^{\frac{\alpha (3-\beta)}{\beta }}f \bigl(x s^{-(\frac{\alpha }{ \beta })}\bigr)\,ds \biggr]. $$
(27)

Let \(v=\frac{t}{s}\), \(ds=-\frac{t}{v^{2}}\,dv\). Thus, Eq. (27) becomes

$$ \frac{\partial^{\alpha }u}{\partial t^{\alpha }}=\frac{\partial^{n}}{ \partial t^{n}} \biggl[t^{n-\alpha +\frac{\alpha (3-\beta)}{\beta }}\frac{1}{ \Gamma (n-\alpha)} \int^{\infty }_{1}(v-1)^{n-\alpha -1}v^{-(n-\alpha +1+\frac{\alpha (3-\beta)}{\beta })}f \bigl(\xi v^{\frac{\alpha }{\beta }}\bigr)\,dv \biggr]. $$
(28)

Applying EK fractional integral operator Eq. (23) to Eq. (28), we get

$$ \frac{\partial^{\alpha }u}{\partial t^{\alpha }}=\frac{\partial^{n}}{ \partial t^{n}} \bigl[t^{n-\alpha +\frac{\alpha (3-\beta)}{\beta }} \bigl(K^{1+\frac{\alpha (3-\beta)}{\beta }, n-\alpha }_{\frac{\beta }{\alpha }}f \bigr) (\xi) \bigr]. $$
(29)

We simplify the right-hand side of Eq. (29). Considering \(\xi =xt^{-\frac{ \alpha }{\beta }}\), \(\phi \in (0, \infty)\), we acquire

$$ t\frac{\partial }{\partial t}\phi (\xi)=tx\biggl(-\frac{\alpha }{\beta }\biggr)t ^{-\frac{\alpha }{\beta }-1}\phi '(\xi)=-\frac{\alpha }{\beta } \xi \frac{\partial }{\partial \xi }\phi (\xi). $$
(30)

Hence,

$$\begin{aligned}& \frac{\partial^{n}}{\partial t^{n}} \bigl[t^{n-\alpha +\frac{\alpha (3- \beta)}{\beta }} \bigl(K^{1+\frac{\alpha (3-\beta)}{\beta }, n- \alpha }_{\frac{\beta }{\alpha }}f \bigr) (\xi) \bigr] \\& \quad =\frac{\partial^{n-1}}{\partial t^{n-1}} \biggl[\frac{\partial }{\partial t} \bigl(t^{n-\alpha +\frac{\alpha (3-\beta)}{\beta }} \bigl(K^{1+\frac{ \alpha (3-\beta)}{\beta }, n-\alpha }_{\frac{\beta }{\alpha }}f \bigr) (\xi) \bigr) \biggr] \\& \quad = \frac{\partial^{n-1}}{\partial t^{n-1}} \biggl[t^{n-\alpha +\frac{ \alpha (3-\beta)}{\beta }-1} \biggl(n- \frac{\alpha }{\beta }-\frac{ \alpha }{\beta }\xi \frac{\partial }{\partial \xi } \biggr) \\& \qquad {} \times \bigl(K^{1+\frac{\alpha (3-\beta)}{\beta }, n-\alpha }_{\frac{ \beta }{\alpha }}f \bigr) (\xi) \biggr]. \end{aligned}$$
(31)

Repeating \((n-1)\)-times, we have

$$\begin{aligned}& \frac{\partial^{n}}{\partial t^{n}} \bigl[t^{n-\alpha +\frac{\alpha (3- \beta)}{\beta }} \bigl(K^{1+\frac{\alpha (3-\beta)}{\beta }, n- \alpha }_{\frac{\beta }{\alpha }}f \bigr) (\xi) \bigr] \\& \quad =\frac{\partial^{n-1}}{\partial t^{n-1}} \biggl[\frac{\partial }{\partial t} \bigl(t^{n-\alpha +\frac{\alpha (3-\beta)}{\beta }} \bigl(K^{1+\frac{ \alpha (3-\beta)}{\beta }, n-\alpha }_{\frac{\beta }{\alpha }}f \bigr) (\xi) \bigr) \biggr] \end{aligned}$$
(32)
$$\begin{aligned}& \quad =\frac{\partial^{n-1}}{\partial t^{n-1}} \biggl[t^{n-\alpha +\frac{ \alpha (3-\beta)}{\beta }-1} \biggl(n- \frac{\alpha }{\beta }-\frac{ \alpha }{\beta }\xi \frac{\partial }{\partial \xi } \biggr) \\& \qquad {} \times \bigl(K^{1+\frac{\alpha (3-\beta)}{\beta }, n-\alpha }_{\frac{ \beta }{\alpha }}f \bigr) (\xi) \biggr] \\& \quad \vdots \\& \quad =t^{-\alpha +\frac{\alpha (3-\beta)}{\beta }}\prod^{n-1}_{j=0} \biggl[ \biggl(1- \alpha +\frac{\alpha (3-\beta)}{\beta }+j-\frac{\alpha }{ \beta }\xi \frac{\partial }{\partial \xi } \biggr) \\& \qquad {}\times \bigl(K^{1+\frac{\alpha (3-\beta)}{\beta }, n-\alpha }_{\frac{ \beta }{\alpha }}f \bigr) (\xi) \biggr] . \end{aligned}$$
(33)

Applying EK fractional differential operator Eq. (21) to Eq. (33), we obtain that

$$ \frac{\partial^{n}u}{\partial t^{n}} \bigl[\bigl(t^{n-\alpha +\frac{\alpha (3-\beta)}{\beta }} \bigl(K^{1+\frac{\alpha (3-\beta)}{\beta }, n- \alpha }_{\frac{\beta }{\alpha }}f \bigr) (\xi) \bigr) \bigr]=t^{-\alpha +\frac{\alpha (3-\beta)}{\beta }} \bigl(P^{1-\alpha +\frac{\alpha (3- \beta)}{\beta }, \alpha }_{\frac{\beta }{\alpha }}f \bigr) (\xi). $$
(34)

Substituting Eq. (34) into Eq. (29), we have

$$ \frac{\partial^{\alpha }u}{\partial t^{\alpha }}=t^{-\alpha +\frac{ \alpha (3-\beta)}{\beta }} \bigl(P^{{1-\alpha +\frac{\alpha (3-\beta)}{\beta }}, \alpha }_{\frac{\beta }{\alpha }}f \bigr) (\xi). $$
(35)

Comparably, βth-order with respect to x can be derived to be the following:

$$ \frac{\partial^{\beta }u}{\partial x^{\beta }}=t^{\frac{\alpha (3- \beta)}{\beta }} \xi^{-\beta } \bigl(Q^{-\beta, \beta }_{1}f \bigr) ( \xi). $$
(36)

Thus, using Eqs. (35) and (36), we obtain

$$ \bigl(P^{1-\alpha +\frac{\alpha }{\beta }(3-\beta), \alpha }_{\frac{ \beta }{\alpha }}f \bigr) (\xi)+f\xi^{-\beta } \bigl(Q^{-\beta,\beta } _{1} f \bigr) (\xi)+ff_{\xi \xi \xi }+3f_{\xi }f_{\xi \xi }=0. $$
(37)

The proof of the theorem is completed. □

4 Explicit power series solutions for Eq. (37)

We investigate the explicit solutions via the PS method [51, 52]. Let

$$ f(\xi)=\sum^{\infty }_{n=0}a_{n} \xi^{n}. $$
(38)

From Eq. (38), we can have

$$ f'=\sum^{\infty }_{n=0}na_{n} \xi^{n-1},\qquad f''=\sum ^{\infty }_{n=0}n(n-1)a_{n}\xi^{n-2},\qquad f''=\sum^{\infty }_{n=0}n(n-1) (n-2)a_{n}\xi^{n-3}. $$
(39)

Putting Eqs. (38) and (39) in Eq. (37), one obtains

$$\begin{aligned}& \sum^{\infty }_{n=0} \frac{\Gamma (2-\alpha +\frac{\alpha (3-\beta)}{ \beta }-\frac{n\alpha }{\beta })}{\Gamma (2+\frac{\alpha (3-\beta)}{ \beta }-\frac{n\alpha }{\beta })}a_{n}\xi^{n}+\sum ^{\infty }_{n=0}a _{n}\xi^{n}\sum ^{\infty }_{n=0}\frac{\Gamma (1-n)}{\Gamma (1-n+\beta)}a_{n} \xi^{n} \\& \quad {} +\sum^{\infty }_{n=0}a_{n} \xi^{n}\sum^{\infty }_{n=0}(n+3) (n+2) (n+1)a _{n+3}\xi^{n} \\& \quad {} +3\sum^{\infty }_{n=0}(n+1)a_{n+1} \xi^{n}\sum^{\infty }_{n=0}(n+2) (n+1)a _{n+2}\xi^{n}=0. \end{aligned}$$
(40)

Comparing coefficients in Eq. (40) when \(n=0\), we get

$$ a_{3}=\frac{1}{6a_{0}} \biggl(\frac{\Gamma (2-\alpha +\frac{\alpha (3- \beta)}{\beta })}{\Gamma (2+\frac{\alpha (3-\beta)}{\beta })}a_{0}+ \frac{a^{2}_{0}}{\Gamma (1+\beta)}-6a_{1} a_{2} \biggr), $$
(41)

when \(n\ge 1\), we have

$$\begin{aligned} a_{n+3} =&\frac{1}{(n+3)(n+2)(n+1)} \Biggl\{ \frac{\Gamma (2-\alpha +\frac{ \alpha (3-\beta)}{\beta }+\frac{n\alpha }{\beta })}{\Gamma (2+\frac{ \alpha (3-\beta)}{\beta }-\frac{n\alpha }{\beta })}a_{n} \\ &{}+ \sum^{n} _{k=0}\frac{\Gamma (1-n-k)}{\Gamma (1-n-k+\beta)}a_{k} a_{n-k} \end{aligned}$$
(42)
$$\begin{aligned} &{} -3\sum^{n}_{k=0}(n-k+2) (n-k+1)a_{k} a_{n-k+2} \Biggr\} . \end{aligned}$$
(43)

Thus, each coefficient \(a_{n}\) (\(n\ge 1\)) for Eq. (38) is found by the arbitrary constants \(a_{i}\) (\(i=0,1,2\)). This means that the explicit PS solution for Eq. (37) exists, and its coefficients depend on Eqs. (41) and (42). Therefore, the PS solution for Eq. (37) can be represented in the form:

$$\begin{aligned} f(\xi) =&a_{0}+a_{1}\xi +a_{2} \xi^{2}+a_{3}\xi^{3} \sum ^{\infty } _{n=1}a_{n+3}\xi^{n+3} \\ =&a_{0}+a_{1}\xi +a_{2}\xi^{2}+ \frac{1}{6a_{0}} \biggl(\frac{\Gamma (2- \alpha +\frac{\alpha (3-\beta)}{\beta })}{\Gamma (2+\frac{\alpha (3- \beta)}{\beta })}a_{0}+ \frac{a^{2}_{0}}{\Gamma (1+\beta)}-6a_{1} a _{2} \biggr)\xi^{3} \\ &{} +\sum^{\infty }_{n=1} \frac{1}{(n+3)(n+2)(n+1)} \Biggl\{ \frac{\Gamma (2- \alpha +\frac{\alpha (3-\beta)}{\beta }+\frac{n\alpha }{\beta })}{ \Gamma (2+\frac{\alpha (3-\beta)}{\beta }-\frac{n\alpha }{\beta })}a _{n} \\ &{}+\sum ^{n}_{k=0}\frac{\Gamma (1-n-k)}{\Gamma (1-n-k+\beta)}a_{k} a _{n-k} \\ &{}-3\sum^{n}_{k=0}(n-k+2) (n-k+1)a_{k} a_{n-k}a_{n-k+2} \Biggr\} \xi^{n+3}. \end{aligned}$$
(44)

Consequently, we acquire the explicit power series given by

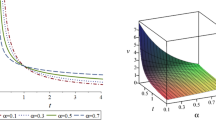
$$\begin{aligned} u(x,t) =&a_{0}t^{\frac{\alpha (3-\beta)}{\beta }}+a_{1}xt^{\frac{ \alpha (2-\beta)}{\beta }}+a_{2}xt^{\frac{\alpha (1-\beta)}{\beta }}+a _{3}xt^{-\alpha }+\sum^{\infty }_{n=1}a_{n+3}xt^{-\frac{\alpha (n+ \beta)}{\beta }} \\ =&a_{0} t^{\frac{\alpha (3-\beta)}{\beta }}+a_{1}xt^{\frac{\alpha (2- \beta)}{\beta }}+a_{2}xt^{\frac{\alpha (1-\beta)}{\beta }} \\ &{} +\frac{1}{6a_{0}} \biggl(\frac{\Gamma (2-\alpha +\frac{\alpha (3-\beta)}{\beta })}{\Gamma (2+\frac{\alpha (3-\beta)}{\beta })}a_{0}+a^{2} _{0} \xi^{-\beta }\Gamma (1-\beta)-6a_{1} a_{2} \biggr)xt^{-\alpha } \\ &{} +\sum^{\infty }_{n=1} \frac{1}{(n+3)(n+2)(n+1)} \Biggl\{ \frac{\Gamma (2- \alpha +\frac{\alpha (3-\beta)}{\beta }+\frac{n\alpha }{\beta })}{ \Gamma (2+\frac{\alpha (3-\beta)}{\beta }-\frac{n\alpha }{\beta })}a _{n} \\ &{}+\xi^{-\beta } \sum^{n}_{k=0}\frac{\Gamma (1-\beta +n-k)}{1-n-k}a _{k} a_{n-k} \\ &{} -3\sum^{n}_{k=0}(n-k+2) (n-k+1)a_{k} a_{n-k}a_{n-k+2} \Biggr\} xt^{-\frac{(n+3) \alpha }{\beta }}. \end{aligned}$$
(45)

In Figures 1-3, we have illustrated the physical features for Eq. (45) with different parameter values.

Figure 1
figure 1

Numerical simulation for the 3D plot of ( 45 ). When \(a_{0}=a_{1}=a_{2}=6\), \(a_{3}=0.5\), \(a_{4}=1.7\), \(\beta =1.9\), \(\alpha =0.5\), \(\Gamma =0.85\).

Full size image
Figure 2
figure 2

Numerical simulation for the 3D plot of ( 45 ). When \(a_{0}=a_{1}=a_{2}=2.6\), \(a_{3}=1.25\), \(a_{4}=1.7\), \(\beta =1.2\), \(\alpha =0.85\), \(\Gamma =0.5\).

Full size image
Figure 3
figure 3

Numerical simulation for the contour plot of ( 45 ). When \(a_{0}=a_{1}=a_{2}=2.6\), \(a_{3}=1.25\), \(a_{4}=1.7\), \(\beta =1.5\), \(\alpha =0.85\), \(\Gamma =0.5\).

Full size image

5 Conservation laws

More details about the description of Cls can be found in [1, 27, 33, 52]. The Lagrangian is presented by

$$ L=v(x,t) \biggl(\frac{\partial^{\alpha }u}{\partial t^{\alpha }}+u\frac{ \partial^{\beta }u}{\partial t^{\beta }}+uu_{xxx}+3u_{x}u_{xx} \biggr). $$
(46)

In Eq. (46) \(v(x, t)\) is another dependent variable. The Euler-Lagrange operator [33] is

$$\begin{aligned} \frac{\delta }{\delta u}=\frac{\partial }{\partial u}+\bigl(D^{\alpha } _{t} \bigr)^{*}\frac{\partial }{\partial D^{\alpha }_{t}u}+\bigl(D^{\beta }_{x} \bigr)^{*}\frac{ \partial }{\partial D^{\beta }_{x}u}-D_{x}\frac{\partial }{\partial u _{x}}+D^{2}_{xx} \frac{\partial }{\partial u_{xx}}-D^{3}_{xxx}\frac{ \partial }{\partial u_{xxx}}, \end{aligned}$$
(47)

where \((D^{\alpha }_{t})^{*}\) and \((D^{\beta }_{t})^{*}\) are the adjoint operators of \((D^{\alpha }_{t})\) and \((D^{\beta }_{t})\), respectively. The adjoint equation is given by [33]

$$ F^{*}=\frac{\delta L}{\delta u}=0. $$
(48)

So, we can have

$$ \bar{X}+D_{t}\bigl(\xi^{2}\bigr)l+D_{x}\bigl( \xi^{1}\bigr)l=W\frac{\delta }{\delta u}+D _{t}N^{t}+D_{x}N^{x}. $$
(49)

In Eq. (49) l represents the identity operator, \(\frac{\delta }{ \delta u}\) is the Euler-Lagrangian operator, \(N^{t}\) and \(N^{x}\) represent the Noether operators, X̄ is defined by

$$\begin{aligned} \bar{X}={}&\xi^{2} \frac{\partial }{\partial t}+\xi^{1} \frac{\partial }{ \partial x}+\eta \frac{\partial }{\partial u}+\eta^{\alpha,t}\frac{ \partial }{\partial D^{\alpha }_{t}u}+ \eta^{\beta,x}\frac{\partial }{ \partial D^{\beta }_{x}u} \\ &{}+\eta^{x}\frac{\partial }{\partial u_{x}}+ \eta^{xx}\frac{\partial }{\partial u_{xx}}+\eta^{xxx}\frac{\partial }{ \partial u_{xxx}}. \end{aligned}$$
(50)

With the help of Eqs. (46) and (48), we can write the adjoint equation to Eq. (1) as follows:

$$ F^{*}=\bigl(D^{\alpha }_{t}\bigr)^{*}v+u \bigl(D^{\beta }_{x}\bigr)^{*}v+u(v_{x} +v_{xxx})=0. $$
(51)

Next, we look for the differential substitution for nonlinear self-adjointness. Let

$$ v=\phi (x,t,u), \quad \mbox{such that }\phi (x,t,u)\ne 0. $$
(52)

Thus, taking the derivatives of Eq. (52), we have

$$\begin{aligned} \begin{aligned}&v_{x}=\phi_{x} +\phi_{u} u_{x}, \\ &v_{xx}=\phi_{xx}+2\phi_{xu}u_{x} +\phi_{u} u_{xx}+\phi_{uu}u^{2}_{x}, \\ &v_{xxx} =\phi_{xxx}+3\phi_{xxu}u_{x} +3 \phi_{xuu}u^{2}_{x} +3\phi _{xu}u_{xx}+3 \phi_{uu}u_{x}u_{xx}+\phi_{u}u_{xxx}+ \phi_{uuu}u^{3}_{x}. \end{aligned} \end{aligned}$$
(53)

Inserting Eqs. (52) and (53) into Eq. (51) and solving the results, we obtain

$$ \phi (x,t,u)=A_{1} x+A_{2}. $$
(54)

Therefore, the variable \(v(x,t)=A_{1} x+A_{2}\), and it will be used for the analysis of the Cls.

The Lie characteristic function W is given by

$$ W=\eta -\xi^{2} u_{t}-\xi^{1} u_{x}. $$
(55)

The t component of the conserved vectors is defined by [33, 52]

$$ N^{t}=\xi^{2} l+\sum^{n-1}_{k=0}(-1)^{k}oD^{\alpha -1-k}(W)D^{k}_{t} \frac{ \partial }{\partial oD^{\alpha }_{t}u}-(-1)^{n}J\biggl(W,D^{n}_{t} \frac{ \partial }{\partial oD^{\alpha }_{t}u}\biggr), $$
(56)

where \(n=[\alpha ]+1\) and J is given by

$$ J(f, g)=\frac{1}{\Gamma (n-\alpha)} \int^{t}_{0} \int^{p}_{t}\frac{f( \xi^{2}, x)g(x,\mu)}{(\mu -\xi^{2})^{\alpha +1-n}}\,d\mu \,dt. $$
(57)

Equivalently, the x component of the conserved vectors (CV) can be expressed as

$$ N^{x}=\xi^{1} l+\sum^{m-1}_{k=0}(-1)^{k}oD^{\beta -1-k}(W)D^{k}_{x} \frac{ \partial }{\partial oD^{\beta }_{x}u}-(-1)^{m}J_{1}\biggl(W,D^{m}_{x} \frac{ \partial }{\partial oD^{\beta }_{x}u}\biggr), $$
(58)

where \(m=[\beta ]+1\) and \(J_{1}\) is given by

$$ J_{1}(f, g)=\frac{1}{\Gamma (n-\beta)} \int^{x}_{0} \int^{q}_{t}\frac{f( \xi^{1}, t)g(\mu, t)}{(\mu -\xi^{1})^{\beta +1-m}}\,d\mu \,dt. $$
(59)

The invariance condition for any given generator X of Eq. (1) and its solutions reads as follows:

$$ \bigl(\bar{X}L+D_{t}\bigl(\xi^{2}\bigr)L+D_{x} \bigl(\xi^{1}\bigr)L\bigr)\vert _{\text{Eq. (1)}}=0; $$
(60)

and consequently, the Cls of Eq. (1) can be written as

$$ D_{t}\bigl(N^{t}L\bigr)+D_{x} \bigl(N^{x}L\bigr)=0. $$
(61)

Now, we present the Cls for Eq. (1) using the basic definitions presented above. Consider the following cases.

Case 1. For \(\alpha \in (0, 1)\), the t components of the CV are

$$\begin{aligned}& C^{t}_{1}= oD^{\alpha -1}_{t}(W_{i}) (A_{1} x+A_{2})+J(W_{i}, v_{t}), \\& C^{t}_{2} =W_{i} \bigl(3u_{xx}(A_{1} x+A_{2})-3D_{t} \bigl(u_{x} (A_{1} x+A _{2})\bigr)+D^{2}_{t}\bigl(u(A_{1} x+A_{2})\bigr) \bigr) \\& \hphantom{C^{t}_{2} =} +D_{t}(W_{i}) \bigl(3u_{x}-D_{t} \bigl(u(A_{1} x+A_{2})\bigr) \bigr)+D^{2}_{t} \bigl(W _{i}u(A_{1} x+A_{2})\bigr), \end{aligned}$$

where \(i=1, 2\) and the functions \(W_{i}\) are given by

$$W_{1}=u_{x},\qquad W_{2}=\alpha u(3-\beta)-\beta tu_{t}+\alpha x u _{x}. $$

Case 2. For \(\alpha \in (1, 2)\), the t components of the CV are

$$\begin{aligned}& C^{t}_{3}= oD^{\alpha -1}_{t}(W_{i}) (A_{1} x+A_{2})+J(W_{i}, v_{t})-v _{t} oD^{\alpha -2}_{t}(W_{i})-J(W_{i}, v_{tt}), \\& C^{t}_{4} =W_{i} \bigl(3u_{xx}v-3D_{t} u_{x} (A_{1} x+A_{2})+D^{2}_{t} \bigl(u(A _{1} x+A_{2})\bigr) \bigr) \\& \hphantom{C^{t}_{4} =} +D_{t}(W_{i}) \bigl(3u_{x}-D_{t}(uv) \bigr)+D^{2}_{t}(W_{i})u(A_{1} x+A _{2}), \end{aligned}$$

where \(i=1, 2\) and the functions \(W_{i}\) are given by

$$W_{1}=u_{x},\qquad W_{2}=\alpha u(3-\beta)-\beta tu_{t}+\alpha x u _{x}. $$

Case 3. For \(\beta \in (0, 1)\), the x components of the CV are

$$\begin{aligned}& C^{x}_{1}=oD^{\beta -1}_{x}(W_{i}) (A_{1} x+A_{2})+J(W_{i}, v_{t}), \\& C^{x}_{2} =W_{i} \bigl(3u_{xx}(A_{1} x+A_{2})-3D_{x} u_{x} (A_{1} x+A _{2})+D^{2}_{x}u(A_{1} x+A_{2}) \bigr) \\& \hphantom{C^{x}_{2} =} +D_{x}(W_{i}) \bigl(3u_{x}-D_{x}u(A_{1} x+A_{2}) \bigr)+D^{2}_{x}(W_{i})u(A _{1} x+A_{2}), \end{aligned}$$

where \(i=1, 2\) and the functions \(W_{i}\) are given by

$$W_{1}=u_{x},\qquad W_{2}=\alpha u(3-\beta)-\beta tu_{t}+\alpha x u _{x}. $$

Case 4. For \(\beta \in (1, 2)\), the x components of the CV are

$$\begin{aligned}& C^{x}_{3}=oD^{\beta -1}_{x}(W_{i}) (A_{1} x+A_{2})+J(W_{i}, v_{t})-v _{t} oD^{\beta -2}_{x}(W_{i})-J(W_{i}, v_{tt}), \\& C^{x}_{4} =W_{i} \bigl(3u_{xx}(A_{1} x+A_{2})-3D_{x} u_{x} (A_{1} x+A _{2})+D^{2}_{x}u(A_{1} x+A_{2}) \bigr) \\& \hphantom{C^{x}_{4} =} +D_{x}(W_{i}) \bigl(3u_{x}-D_{x}u(A_{1} x+A_{2}) \bigr)+D^{2}_{x}(W_{i})u(A _{1} x+A_{2}), \end{aligned}$$

where \(i=1, 2\) and the functions \(W_{i}\) are given by

$$W_{1}=u_{x}, \qquad W_{2}=\alpha u(3-\beta)-\beta tu_{t}+\alpha x u _{x}. $$

6 Concluding remarks

This work used the extension presented in [1, 2] to examine the LSA and Cls for the space-time fractional Rosenou-Haynam equation (RHE) with RL derivative. The space-time fractional RHE was a reduced to space-time ODE of fractional order using its Lie point symmetries with a new dependent variable. We solved the reduced space-time ODE using the power series method for the first time. Moreover, we constructed Cls for the governing equation using a new conservation theorem.