1 Introduction

Fractional calculus is an extension of classical calculus that generalizes the order of derivatives and integrals to a non-integer order. Fractional calculus was first discussed more than 300 years ago by Leibniz and L’Hôpital [1], who considered derivatives of order \(\alpha =\frac{1}{2}\). In the last few decades, fractional calculus has been widely used in many fields such as engineering [2–4], mechanics [5, 6], physics [7, 8], chemistry [9, 10], and biology [11–13]. For some dynamic phenomena, models with fractional order derivatives provide a better and more efficient description than those with classical derivatives [14]. Models with fractional order derivatives can take different forms depending on the system understudy and purpose of the model. Among them, fractional differential equations (FDEs) and fractional partial differential equations (FPDEs) are most often applied to represent continuous and deterministic systems. FDEs and FPDEs have been mathematically studied from several different perspectives, yielding methods for solving FDEs [15–19] and FPDEs [20–26] and characterization of the asymptotic behavior of solutions [27–30].

Recently, many researchers have used fractional differential equations to develop models for predator–prey interactions [31–34], atmospheric dispersion [35], pharmacokinetics [36], HIV infection [37], and bioreactors [38]. The predator–prey model has been applied to describe the relationship between two species in biological systems in which one a predator feeds on the other its prey [39]. Fractional order predator–prey models have been used by many researchers, who also discussed the stability and numerical solutions of the models [32, 33, 40, 41]. Moreover, some studies showed the conditions for existence of a Hopf bifurcation [42–44] and the appearance of a limit cycle [45].

The Kolmogorov model is a general continuous time predator–prey model, consisting of a system of first order differential equations [46]. There are many types of Kolmogorov models such as the Lotka–Volterra model [47], Gauss-type models [48], Hsu model [49], Kuang and Freedman model [50], and Huang and Merrill model [51]. Among them, the Gauss-type predator–prey models have been widely used to formulate population models [52–55]. A crucial phenomenon in biology is the decrease in per capita growth rate at low population densities [56], which was first described by Warder Clyde Allee in the 1930s [57]. Several researchers are interested in the Allee effect for multi-species systems and have included the Allee effect term in Gauss-type predator–prey models [58, 59]. In addition, many population models [60–62] are often associated with a functional response, which refers to the predation rate per predator as a function of prey density [63, 64] and predator density [65–67]. There are a variety of functional responses such as the Holling type-I–III functions [68], Holling type-IV function [69], the simplified Holling type-IV function [70], the Beddington–DeAngelis function [66], the Crowley–Martin function [71].

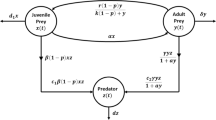
In 2010, Eduardo et al. [72] studied a Gauss-type predator–prey model with Allee effect on prey and Holling type-III functional response and examined the global behavior of this model. They identified three important assumptions as regards the interactions between prey and predator:

  • the prey population is affected by the Allee effect,

  • the functional response is Holling type-III, and

  • the predator is a generalist species; see details in Ref. [73].

The model is given by

$$ \begin{gathered} \frac{dx}{dt}=r \biggl( 1-\frac{x}{K} \biggr) (x-m)x-\frac{sx^{2}}{x^{2}+a ^{2}}y, \\ \frac{dy}{dt}= \biggl( \frac{px^{2}}{x^{2}+a^{2}}-c \biggr) y, \\ \text{with the initial conditions }x(t_{0})=x_{0} \text{ and } y(t_{0})=y_{0}, \end{gathered} $$
(1)

where \(x=x(t)\) and \(y=y(t)\) are the population sizes of prey and predator at time t, respectively; the sizes may be numbers of individuals or density. In order to represent biological populations, all parameters in model (1) are positive; that is, \(r,K,m,s,p,a,c>0\) and \(a,m< K\). The meaning of the parameters in model (1) is given as follows:

  • r is the growth rate of the prey.

  • K is the environmental capacity of the prey.

  • m is the minimum viable population.

  • s is the maximum per capita consumption rate.

  • a is the amount of prey at which predation rate is maximal.

  • p is the conversion efficiency of reduction rate of the predator.

  • c is the natural per capita death rate of the predator.

In model (1), the Allee effect is defined by the term \(r ( 1-\frac{x}{K} ) ( x-m ) x\) and the Holling type-III functional response is represented by the term \(\frac{sx^{2}}{x^{2}+a ^{2}}\). This functional response describes a behavior in which the number of prey consumed per predator initially increases quickly as the density of prey grows and levels off with further increase in prey density [74].

The most famous definitions of fractional order derivatives are the Grünwald–Letnikov [75], Riemann–Liouville [76], and Caputo [77] definitions. The Caputo definition is very useful because in this case the derivative of a constant is zero and the initial conditions for the fractional order differential equations can be provided in the same manner as for the classical integer case, which has a clear physical meaning [78]. This paper aims to construct a fractional Gauss-type predator–prey model with Allee effect and Holling type-III functional response in the Caputo sense by modifying model (1). We analyze the local stability of the equilibria for the model using the linearization method. Moreover, given a derivative order, the conditions for the existence of a Hopf bifurcation of the positive equilibrium are obtained.

This article is organized as follows: In Sect. 2, the definition of a fractional order derivative in the Caputo sense and some important theorems for fractional order systems are introduced. The model is then developed along with the existence and uniqueness of a nonnegative solution of the model in Sect. 3. In Sect. 4, we analyze the local stability of the equilibrium points and examine the conditions for the existence of a Hopf bifurcation at the positive equilibrium. Some numerical examples to support the theoretical results are shown in Sect. 5. Finally, the conclusions of this study are presented in Sect. 6.

2 Preliminaries

In this section, the definition of a fractional derivative in the Caputo sense is given. Furthermore, definitions of an equilibrium point and some important theorems of the local stability of a fractional order system are presented.

Definition 2.1

([77])

Let \(k\in \mathbb{N}\), \(f\in A^{k}[t _{0},T]\), where \(A^{k}[t_{0},T]\) is the set of all functions \(f:[t_{0},T]\longrightarrow \mathbb{R}\), such that \(f^{(k-1)}\) is absolutely continuous, and \(t\in [t_{0},T]\). Then, for \(k-1<\alpha <k\), the Caputo fractional derivative of order α is defined by

$$\begin{aligned} _{t_{0}}^{C}D_{t}^{\alpha }f(t)= \frac{1}{\Gamma (k-\alpha )} \int_{t _{0}}^{t}(t-\tau )^{k-\alpha -1}f^{(k)}( \tau )\,d\tau , \end{aligned}$$

where \(\Gamma (\cdot )\) denotes the Gamma function [79].

Theorem 2.2

([80])

The Laplace transform of the Caputo fractional derivative of order α for \(0<\alpha <1\) is

$$\begin{aligned} \mathcal{L} \bigl\lbrace _{0}^{C}D_{t}^{\alpha }f(t) \bigr\rbrace ( \mathfrak{s})=\mathfrak{s}^{\alpha }\mathcal{F}(\mathfrak{s})- \mathfrak{s}^{\alpha -1}f(0), \end{aligned}$$

where \(\mathcal{F}(\mathfrak{s})=\mathcal{L}\{f(t)\}(\mathfrak{s})\) and \(\mathfrak{s}\) is a real or complex parameter.

Theorem 2.3

([77])

Let \(\beta >0\) and \(b\in \mathbb{C}\). The Laplace transform of \(E_{\beta ,1}(-bt^{\beta })\) is

$$\begin{aligned} \mathcal{L} \bigl\lbrace E_{\beta ,1}\bigl(-bt^{\beta }\bigr) \bigr\rbrace ( \mathfrak{s})=\frac{\mathfrak{s}^{\beta -1}}{\mathfrak{s}^{\beta }+b}, \end{aligned}$$

where \(E_{\beta ,1}(\cdot )\) denotes the Mittag-Leffler function [79].

The initial value problem for the Caputo fractional differential system, consisting of n equations for \(0<\alpha <1\), is given by

$$\begin{aligned} _{t_{0}}^{C}D_{t}^{\alpha }X(t)=f \bigl(t,X(t)\bigr) \quad \text{with } X(t_{0})=X_{0}, \end{aligned}$$
(2)

where \(f:[t_{0},\infty )\times \Omega \longrightarrow \mathbb{R}^{n}\) is piecewise continuous in t and locally Lipschitz continuous in X on \([t_{0},\infty )\times \Omega , \Omega \subset \mathbb{R} ^{n}\).

An equilibrium point of system (2) and the stability of the equilibrium point are described by the following definition and theorems.

Definition 2.4

([81])

A point \(X^{*}\) is called an equilibrium point of system (2) if and only if \(f(t,X^{*})=0\).

Suppose that an equilibrium point of system (2) is \(X^{*}=0\). If \(X^{*}\neq 0\), then it can be shifted to the origin by changing a variable [82]: \(Y(t)=X(t)-X^{*}\). System (2) can be written in terms of the new variable \(Y(t)\) as

$$\begin{aligned} _{t_{0}}^{C}D_{t}^{\alpha }Y(t)={_{t_{0}}^{C}}D_{t}^{\alpha } \bigl(X(t)-X ^{*}\bigr)=f\bigl(t,X(t)\bigr)=f\bigl(t,Y(t)+X^{*} \bigr)=g\bigl(t,Y(t)\bigr), \end{aligned}$$

where \(g(t,0)=0\) and the system has equilibrium at the origin.

Theorem 2.5

([33])

Let \(J(X^{*})\) denote the Jacobian matrix of system (2) evaluated at equilibrium point \(X^{*}\). The eigenvalues of \(J(X^{*})\) are \(\lambda_{i}\), where \(i=1,\ldots,n\). Then equilibrium point \(X^{*}\) is a saddle point if some eigenvalues \(\lambda_{i}\) satisfy \(\vert \arg (\lambda_{i}) \vert >\frac{\alpha \pi }{2}\) and some others satisfy \(\vert \arg (\lambda_{i}) \vert < \frac{\alpha \pi }{2}\).

Theorem 2.6

([1, 33])

Considering the system (2),

  1. (i)

    equilibrium point \(X^{*}\) is locally asymptotically stable if and only if all eigenvalues \(\lambda_{i}\), \(i=1,\ldots,n\) of \(J(X^{*})\) satisfy \(\vert \arg (\lambda_{i}) \vert >\frac{\alpha \pi }{2}\),

  2. (ii)

    equilibrium point \(X^{*}\) is stable if and only if all eigenvalues \(\lambda_{i}\), \(i=1,\ldots,n\) of \(J(X^{*})\) satisfy \(\vert \arg (\lambda_{i}) \vert \geq \frac{\alpha \pi }{2}\) and eigenvalues with \(\vert \arg (\lambda_{i}) \vert =\frac{\alpha \pi }{2}\) have the same geometric multiplicity and algebraic multiplicity, and

  3. (iii)

    equilibrium point \(X^{*}\) is unstable if and only if there exist eigenvalues \(\lambda_{i}\) for some \(i=1,\ldots,n\) of \(J(X^{*})\) which satisfy \(\vert \arg (\lambda_{i}) \vert < \frac{\alpha \pi }{2}\).

3 Fractional order model

In this section, we construct the fractional Gauss-type predator–prey model with Allee effect and Holling type-III functional response by modifying model (1). We subsequently show the existence and uniqueness of a nonnegative solution.

Starting with model (1), we replace the first order derivatives in the model with the Caputo fractional order derivatives. Consequently, a new model with fractional differential equations can be written as:

$$ \begin{gathered} ^{C}_{t_{0}}D^{\alpha }_{t}x=r \biggl( 1-\frac{x}{K} \biggr) (x-m)x-\frac{sx ^{2}}{x^{2}+a^{2}}y, \\ ^{C}_{t_{0}}D^{\alpha }_{t}y= \biggl( \frac{px^{2}}{x^{2}+a^{2}}-c \biggr) y, \end{gathered} $$
(3)

where \(0<\alpha <1\) with initial \(x(t_{0})=x_{0}\) and \(y(t_{0})=y_{0}\).

Let

$$\begin{aligned}& X(t)=\left ( \begin{matrix} x(t) \\ y(t) \end{matrix} \right ) ,\quad\quad X_{0}=\left ( \begin{matrix} x_{0} \\ y_{0} \end{matrix} \right ) ,\quad \text{and} \\& f\bigl(X(t)\bigr)=\left ( \begin{matrix} f_{1} \\ f_{2} \end{matrix} \right ) =\left ( \begin{matrix} r ( 1-\frac{x}{K} ) (x-m)x-\frac{sx^{2}}{x^{2}+a^{2}}y \\ ( \frac{px^{2}}{x^{2}+a^{2}}-c ) y \end{matrix} \right ) . \end{aligned}$$

Then model (3) can be written as \(_{t_{0}}^{C}D_{t} ^{\alpha }X(t)=f(X(t))\) with \(X_{0}=\bigl( {\scriptsize\begin{matrix}{} x_{0} \cr y_{0} \end{matrix}} \bigr) \).

3.1 Existence and uniqueness of a nonnegative solution

Let \(\mathbb{R}^{2}_{+}=\{X=(x,y)^{T}\in \mathbb{R}^{2} \mid x \geq 0, y\geq 0\}\) be the nonnegative quadrant of the xy-plane.

From model (3), we can verify that \(f_{i}\), \(\frac{ \partial f_{i}}{\partial x}\), and \(\frac{\partial f_{i}}{\partial y} \) for \(i=1,2 \) are continuous in \(\mathbb{R}^{2}_{+}\). According to a lemma in reference [83], we find that \(f(X(t))\) satisfies a local Lipschitz condition with respect to X in \(\mathbb{R}^{2}_{+}\). Therefore, by Remark 3.8 in Ref. [82], fractional order model (3) has a unique solution in \(\mathbb{R}^{2}_{+}\).

A requirement for the biological significance of the model, that the solution is nonnegative for \(t>t_{0} \) if the initial solution of model (3) starts in \(\mathbb{R}^{2}_{+}\), will be considered in the next subsection.

3.2 Nonnegative solution

Theorem 3.1

If \(x(t_{0})\geq 0\) and \(y(t_{0})\geq 0\), then the solution \(X ( t ) \) of model (3) remains in \(\mathbb{R} ^{2}_{+}\).

Proof

This theorem is proved by contradiction.

Let \(X_{0}=\bigl( {\scriptsize\begin{matrix}{} x_{0} \cr y_{0} \end{matrix}} \bigr) \in \mathbb{R}^{2}_{+}\), and \(X(t)\) for \(t\geq t_{0}\) be the solution of model (3).

Suppose there exists a solution \(X(t)\) that moves away from \(\mathbb{R}^{2}_{+}\). Then there are two possibilities: it passes through either the x-axis or y-axis. The proof will be divided into these two cases.

Case 1: If solution \(X(t)\) passes through the x-axis, then there exists \(t^{*}\geq t_{0}\) such that \(y(t^{*})=0\) and \(x(t^{*})>0\). Moreover, there exists \(t_{1}>t^{*}\) such that \(t_{1}\) is sufficiently close to \(t^{*}\), \(y(t)<0\), and \(x(t)>0\) for all \(t\in (t^{*},t_{1}]\). From model (3), we have \({}^{C}_{t_{0}}D^{\alpha }_{t}y=\frac{px ^{2}y}{x^{2}+a^{2}}-cy\) and it follows that

$$\begin{aligned} ^{C}_{t_{0}}D^{\alpha }_{t}y> \frac{px^{2}y}{x^{2}+a^{2}} \quad \textrm{for all } t\in \big(t^{*},t_{1}\big]. \end{aligned}$$
(4)

Since \(y(t)<0\), \(p>\frac{px^{2}(t)}{x^{2}(t)+a^{2}}\), and inequality (4) holds, we obtain

$$\begin{aligned} ^{C}_{t_{0}}D^{\alpha }_{t}y>py. \end{aligned}$$
(5)

Applying the Laplace transform to both sides of inequality (5) yields

$$ \begin{gathered} \mathfrak{s}^{\alpha }Y(\mathfrak{s})-\mathfrak{s}^{\alpha -1}y(t_{0}) >pY( \mathfrak{s}), \\ \bigl(\mathfrak{s}^{\alpha }-p\bigr)Y(\mathfrak{s}) >\mathfrak{s}^{\alpha -1}y(t _{0}), \\ Y(\mathfrak{s}) >\frac{\mathfrak{s}^{\alpha -1}y(t_{0})}{ \mathfrak{s}^{\alpha }-p}, \end{gathered} $$
(6)

where \(Y(\mathfrak{s})=\mathcal{L}\{y(t)\}(\mathfrak{s})\).

Applying the inverse Laplace transform to both sides of inequality (6) gives

$$\begin{aligned} y(t)>y(t_{0})E_{\alpha ,1}\bigl(pt^{\alpha } \bigr) \quad \textrm{for all } t\in \big(t^{*},t_{1}\big]. \end{aligned}$$
(7)

Since \(y(t_{0})\geq 0\) and inequality (7) holds in this case, we have \(y(t)>0\) for all \(t\in (t^{*},t_{1}]\), which contradicts \(y(t)<0\) for all \(t\in (t^{*},t_{1}]\).

Case 2: If solution \(X(t)\) passes through the y-axis, then there exists \(t^{*}\geq t_{0}\) such that \(x(t^{*})=0\) and \(y(t^{*})>0\). Additionally, there exists \(t_{1}>t^{*}\) such that \(t_{1}\) is sufficiently close to \(t^{*}\), \(x(t)<0\), and \(y(t)>0\) for all \(t\in (t^{*},t_{1}]\). From model (3), we have \({}^{C}_{t _{0}}D^{\alpha }_{t}x=r ( 1-\frac{x}{K} ) (x-m)x-\frac{sx ^{2}}{x^{2}+a^{2}}y\), which leads to

$$ \begin{gathered} ^{C}_{t_{0}}D^{\alpha }_{t}x >- \frac{sx^{2}}{x^{2}+a^{2}}y, \\ ^{C}_{t_{0}}D^{\alpha }_{t}x >- \frac{sx^{2}}{a^{2}}y \quad \textrm{for all } t\in \big(t^{*},t_{1}\big]. \end{gathered} $$
(8)

From the second equation of model (3), we have

$$\begin{aligned} ^{C}_{t_{0}}D^{\alpha }_{t}y= \biggl( \frac{px^{2}}{x^{2}+a^{2}}-c \biggr) y< \frac{px ^{2}}{x^{2}+a^{2}}y< py. \end{aligned}$$

Taking the Laplace transform of both sides of the above inequality and then applying the inverse Laplace transform, we get

$$\begin{aligned} y(t)< y(t_{0})E_{\alpha ,1}\bigl(pt^{\alpha }\bigr) \quad \textrm{for all } t\in \big(t^{*},t_{1}\big]. \end{aligned}$$

Thus, \(y(t) < M \) for some \(M \geq 0 \) and \(t\in (t^{*},t_{1}] \). From inequality (8) and the above result, we obtain

$$\begin{aligned} ^{C}_{t_{0}}D^{\alpha }_{t}x>- \frac{sx^{2}}{a^{2}}M. \end{aligned}$$

Since \(t_{1}\) is sufficiently near \(t^{*}\), we have an \(x(t)\) that is close to 0 for all \(t\in (t^{*},t_{1}]\). Thus, \(-x^{2}(t)>x(t)\) and then

$$\begin{aligned} ^{C}_{t_{0}}D^{\alpha }_{t}x> \frac{sM}{a^{2}}x. \end{aligned}$$
(9)

Taking the Laplace transform of both sides of inequality (9) and then applying the inverse Laplace transform give

$$\begin{aligned} x(t)>x(t_{0})E_{\alpha ,1} \biggl( \frac{sM}{a^{2}}t^{\alpha } \biggr) \quad \textrm{for all } t\in \big(t^{*},t_{1}\big]. \end{aligned}$$
(10)

However, since \(x(t_{0})\geq 0\) and inequality (10) holds, \(x(t)>0\) for all \(t\in (t^{*},t_{1}]\), which contradicts \(x(t)<0\) for all \(t\in (t^{*},t_{1}]\).

Considering both Case 1 and Case 2, we conclude that the solution of model (3) remains in \(\mathbb{R}^{2}_{+}\) if the initial solution starts in this region. □

4 Main results

4.1 Equilibrium points and stability analysis

According to Definition 2.4, an equilibrium point of model (3) is obtained by solving the following equations:

$$\begin{aligned} ^{C}_{t_{0}}D^{\alpha }_{t}x=0, \quad \textrm{and}\quad ^{C}_{t_{0}}D^{\alpha }_{t}y=0, \end{aligned}$$

that is,

$$\begin{aligned}& x \biggl[ r \biggl( 1-\frac{x}{K} \biggr) (x-m)-\frac{sx}{x^{2}+a^{2}}y \biggr] =0, \\& y \biggl( \frac{px^{2}}{x^{2}+a^{2}}-c \biggr) =0. \end{aligned}$$

We have the following four equilibrium points:

  1. (i)

    the extinction equilibrium point: \(E_{0}=(0,0)\),

  2. (ii)

    the predator-free equilibrium points: \(E_{1}=(m,0)\) and \(E_{2}=(K,0)\),

  3. (iii)

    the coexistence equilibrium point: \(E_{3}=(x^{*},y^{*})\), where

    $$\begin{aligned} x^{*}=\sqrt{\frac{ca^{2}}{p-c}} \quad \textrm{and}\quad y^{*}=\frac{r}{sx^{*}} \biggl( 1-\frac{x^{*}}{K} \biggr) \bigl(x^{*}-m\bigr) \bigl(x^{*^{2}}+a ^{2}\bigr). \end{aligned}$$
    (11)

Since the populations of prey and predator are nonnegative, equilibrium point \(E_{3}=(x^{*},y^{*})\) exists whenever \({p>c}\).

Next the local stability of the equilibrium points is analyzed using the linearization method. The Jacobian matrix of model (3) evaluated at point \((x,y)\) is given by

$$ J(x,y)=\left [ \begin{matrix} G(x,y) &-\frac{sx^{2}}{x^{2}+a^{2}} \\ \frac{2pa^{2}x}{ ( x^{2}+a^{2} ) ^{2}}y&\frac{px^{2}}{x^{2}+a ^{2}}-c \end{matrix} \right ] , $$
(12)

where \(G(x,y)=x [ r ( 1-\frac{2x-m}{K} ) -\frac{s(a^{2}-x ^{2})}{(x^{2}+a^{2})^{2}}y ] + [ r ( 1-\frac{x}{K} ) (x-m)-\frac{sx}{x ^{2}+a^{2}}y ] \).

By using Theorems 2.5 and 2.6, we obtain the stabilities of the four equilibrium points, which are discussed in the following theorems.

Theorem 4.1

Equilibrium point \(E_{0}=(0,0)\) of model (3) is locally asymptotically stable.

Proof

From Eq. (12), the Jacobian matrix of model (3) evaluated at equilibrium point \(E_{0}=(0,0)\) is given by

$$\begin{aligned} J(0,0)=\left [ \begin{matrix} -rm&0 \\ 0&-c \end{matrix} \right ] . \end{aligned}$$

Hence, the eigenvalues of \(J(0,0)\) are \(\lambda_{1}=-rm<0\) and \(\lambda_{2}=-c<0\). Consequently, \(\arg (\lambda_{1})=\arg (\lambda _{2})=\pi \), which leads to \(\vert \arg (\lambda_{1}) \vert > \frac{\alpha \pi }{2}\) and \(\vert \arg (\lambda_{2}) \vert > \frac{\alpha \pi }{2}\) for \(0<\alpha <1\).

Therefore, by Theorem 2.6, we conclude that equilibrium point \(E_{0}=(0,0)\) is locally asymptotically stable. □

Theorem 4.2

Equilibrium point \(E_{1}=(m,0)\) of model (3) is unstable and is a saddle point if \(\frac{(p-c)m^{2}}{ca^{2}}<1\).

Proof

From Eq. (12), the Jacobian matrix of model (3) evaluated at equilibrium point \(E_{1}=(m,0)\) is given by

$$\begin{aligned} J(m,0)=\left [ \begin{matrix} rm ( 1-\frac{m}{K} ) &-\frac{sm^{2}}{m^{2}+a^{2}} \\ 0&\frac{pm^{2}}{m^{2}+a^{2}}-c \end{matrix} \right ] . \end{aligned}$$

Hence, the eigenvalues of \(J(m,0)\) are \(\lambda_{1}=rm ( 1- \frac{m}{K} ) \) and \(\lambda_{2}=\frac{pm^{2}}{m^{2}+a^{2}}-c\). Since \(m< K\), we have \(\lambda_{1}>0\). Then \(\arg (\lambda_{1})=0\), which satisfies the condition \(\vert \arg (\lambda_{1}) \vert <\frac{\alpha \pi }{2}\). By using Theorem 2.6, equilibrium point \(E_{1}=(m,0)\) is unstable.

If \(\frac{(p-c)m^{2}}{ca^{2}}<1\), then \(\lambda_{2}<0\). Hence, \(\arg (\lambda_{2})=\pi \), which results in \(\vert \arg (\lambda_{2}) \vert >\frac{ \alpha \pi }{2}\).

According to Theorem 2.5, equilibrium point \(E_{1}=(m,0)\) is a saddle point if \(\frac{(p-c)m^{2}}{ca^{2}}<1\). □

Theorem 4.3

Equilibrium point \(E_{2}=(K,0)\) of model (3) is a saddle point if \(\frac{(p-c)K^{2}}{ca^{2}}>1\) and is locally asymptotically stable if \(\frac{(p-c)K^{2}}{ca^{2}}<1\).

Proof

By using Eq. (12), the Jacobian matrix of model (3) evaluated at equilibrium point \(E_{2}=(K,0)\) is given by

$$\begin{aligned} J(K,0)=\left [ \begin{matrix} -r ( K-m ) &-\frac{sK^{2}}{K^{2}+a^{2}} \\ 0&\frac{pK^{2}}{K^{2}+a^{2}}-c \end{matrix} \right ] . \end{aligned}$$

Hence, the eigenvalues of \(J(K,0)\) are \(\lambda_{1}=-r ( K-m ) \) and \(\lambda_{2}=\frac{pK^{2}}{K^{2}+a^{2}}-c\). We have \(\lambda_{1}<0\) because \(m< K\). Hence, \(\arg (\lambda_{1})=\pi \) leading to \(\vert \arg ( \lambda_{1}) \vert >\frac{\alpha \pi }{2}\). If \(\frac{(p-c)K^{2}}{ca ^{2}}>1\), then \(\lambda_{2}>0\). Thus, \(\arg (\lambda_{2})=0\), which results in \(\vert \arg (\lambda_{2}) \vert <\frac{\alpha \pi }{2}\). On the other hand, if \(\frac{(p-c)K^{2}}{ca^{2}}<1\), then \(\lambda_{2}<0\). Then \(\arg (\lambda_{2})=\pi \), which satisfies \(\vert \arg (\lambda_{2}) \vert >\frac{ \alpha \pi }{2}\).

Therefore, by Theorem 2.5 and 2.6, equilibrium point \(E_{2}=(K,0)\) is a saddle point if \(\frac{(p-c)K^{2}}{ca^{2}}>1\) and is locally asymptotically stable if \(\frac{(p-c)K^{2}}{ca^{2}}<1\). □

Theorem 4.4

Equilibrium point \(E_{3}=(x^{*},y^{*})\) of model (3) is locally asymptotically stable if one of the following conditions holds:

  1. (i)

    \(\operatorname {tr}( J ( x^{*},y^{*} ) ) \leq 0\).

  2. (ii)

    \(\operatorname {tr}( J ( x^{*},y^{*} ) ) >0\), \(\operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4\det ( J ( x^{*},y^{*} ) ) <0\), and \(\vert \operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4 \det ( J ( x^{*},y^{*} ) ) \vert ^{1/2}>\operatorname {tr}( J ( x^{*},y^{*} ) ) \tan ( \frac{\alpha \pi }{2} ) \).

Proof

By using Eq. (12), the Jacobian matrix of model (3) evaluated at equilibrium point \(E_{3}=(x^{*},y^{*})\) is given by

$$\begin{aligned} J\bigl(x^{*},y^{*}\bigr)=\left [ \begin{matrix} G(x^{*},y^{*}) &-\frac{sx^{*^{2}}}{x^{*^{2}}+a^{2}} \\ \frac{2pa^{2}x^{*}}{ ( x^{*^{2}}+a^{2} ) ^{2}}y^{*}&0 \end{matrix} \right ] , \end{aligned}$$

where \(G(x^{*},y^{*})=x^{*} [ r ( 1-\frac{2x^{*}-m}{K} ) -\frac{s(a ^{2}-x^{*^{2}})}{(x^{*^{2}}+a^{2})^{2}}y^{*} ] \).

Then the determinant and trace, respectively, of the Jacobian matrix \(J(x^{*},y^{*})\) are

$$\begin{aligned} \det \bigl(J\bigl(x^{*},y^{*}\bigr)\bigr)= \biggl[ \frac{sx^{*^{2}}}{x^{*^{2}}+a^{2}} \biggr] \biggl[ \frac{2pa^{2}x^{*}}{ ( x^{*^{2}}+a^{2} ) ^{2}}y^{*} \biggr] >0 \end{aligned}$$
(13)

and

$$\begin{aligned} \operatorname {tr}\bigl(J\bigl(x^{*},y^{*}\bigr) \bigr)=x^{*} \biggl[ r \biggl( 1-\frac{2x^{*}-m}{K} \biggr) - \frac{s(a ^{2}-x^{*^{2}})}{(x^{*^{2}}+a^{2})^{2}}y^{*} \biggr] . \end{aligned}$$
(14)

Thus, the eigenvalues of \(J(x^{*},y^{*})\) are written as

$$ \begin{gathered} \lambda_{1}=\frac{1}{2} \bigl( \operatorname {tr}\bigl(J\bigl(x^{*},y^{*}\bigr)\bigr)+ \bigl[ \operatorname {tr}^{2} \bigl( J\bigl(x^{*},y^{*}\bigr) \bigr) -4 \det \bigl( J\bigl(x^{*},y^{*}\bigr) \bigr) \bigr] ^{1/2} \bigr) , \\ \lambda_{2}=\frac{1}{2} \bigl( \operatorname {tr}\bigl(J\bigl(x^{*},y^{*} \bigr)\bigr)- \bigl[ \operatorname {tr}^{2} \bigl( J\bigl(x^{*},y^{*} \bigr) \bigr) -4\det \bigl( J\bigl(x^{*},y^{*}\bigr) \bigr) \bigr] ^{1/2} \bigr) . \end{gathered} $$
(15)

(i) Assume that \(\operatorname {tr}( J ( x^{*},y^{*} ) ) \leq 0\). The proof will be divided into three cases.

Case 1: If \(\operatorname {tr}( J ( x^{*},y^{*} ) ) =0\), then, by Eq. (15), we obtain a pair of complex conjugate eigenvalues \(\lambda_{1}\) and \(\lambda_{2}=\bar{\lambda_{1}}\). Since \(\operatorname {Re}(\lambda_{1})=\operatorname {Re}(\lambda_{2})=\operatorname {tr}( J ( x^{*},y^{*} ) ) =0\), we have \(\arg (\lambda_{1})=\frac{ \pi }{2}\) and \(\arg (\lambda_{2})=\frac{-\pi }{2}\) leading to \(\vert \arg (\lambda_{1}) \vert >\frac{\alpha \pi }{2}\) and \(\vert \arg (\lambda_{2}) \vert >\frac{ \alpha \pi }{2}\).

By Theorem 2.6, equilibrium point \(E_{3}=(x^{*},y^{*})\) is locally asymptotically stable.

Case 2: If \(\operatorname {tr}( J ( x^{*},y^{*} ) ) <0\) and \(\operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4\det ( J ( x^{*},y^{*} ) ) \geq 0\), then according to Eq. (15), the eigenvalues of \(J(x^{*},y^{*})\) are \(\lambda_{1}<0\) and \(\lambda_{2}<0\). Consequently, we obtain the condition \(\vert \arg ( \lambda_{1}) \vert >\frac{\alpha \pi }{2}\) and \(\vert \arg (\lambda_{2}) \vert >\frac{ \alpha \pi }{2}\).

Hence, by Theorem 2.6, the equilibrium point \(E_{3}=(x^{*},y ^{*})\) is locally asymptotically stable.

Case 3: If \(\operatorname {tr}( J ( x^{*},y^{*} ) ) <0\) and \(\operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4\det ( J ( x^{*},y^{*} ) ) <0\), then, by Eq. (15), we obtain a pair of complex conjugate eigenvalues \(\lambda_{1}\) and \(\lambda_{2}=\bar{\lambda_{1}}\). Since \(\operatorname {tr}( J ( x^{*},y ^{*} ) ) <0\), we have \(\operatorname {Re}(\lambda_{1})= \operatorname {Re}(\lambda_{2})=\operatorname {tr}( J ( x^{*},y^{*} ) ) <0\). Thus, \(\vert \arg (\lambda_{1}) \vert >\frac{\alpha \pi }{2}\) and \(\vert \arg (\lambda _{2}) \vert >\frac{\alpha \pi }{2}\).

Therefore, by Theorem 2.6, equilibrium point \(E_{3}=(x^{*},y ^{*})\) is locally asymptotically stable.

By considering Case 1, Case 2, and Case 3, we conclude that equilibrium point \(E_{3}=(x^{*},y^{*})\) is locally asymptotically stable if \(\operatorname {tr}( J ( x^{*},y^{*} ) ) \leq 0\).

(ii) Assume that \(\operatorname {tr}( J ( x^{*},y^{*} ) ) >0\), \(\operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4\det ( J ( x^{*},y^{*} ) ) <0\) and \(\vert \operatorname {tr}^{2} ( J ( x ^{*},y^{*} ) ) -4\det ( J ( x^{*},y^{*} ) ) \vert ^{1/2}> \operatorname {tr}( J ( x^{*},y^{*} ) ) \tan ( \frac{ \alpha \pi }{2} ) \). By Eq. (15), we have a pair of complex conjugate eigenvalues \(\lambda_{1}\) and \(\lambda_{2}= \bar{\lambda_{1}}\) such that \(\operatorname {Im}(\lambda_{1})=- \operatorname {Im}(\lambda_{2})={ [ 4\det ( J(x^{*},y^{*}) ) -\operatorname {tr}^{2} ( J(x^{*},y^{*}) ) ] }^{1/2}>0\) and \(\operatorname {Re}(\lambda_{1})=\operatorname {Re}(\lambda_{2})= \operatorname {tr}( J(x^{*},y^{*}) ) >0\). From the assumptions, we obtain \(\operatorname {Im}(\lambda_{1})>\operatorname {Re}(\lambda _{1})\tan ( \frac{\alpha \pi }{2} ) \) and \(-\operatorname {Im}( \lambda_{2})>\operatorname {Re}(\lambda_{2})\tan ( \frac{\alpha \pi }{2} ) \). These imply that \(\frac{\alpha \pi }{2}<\arg ( \lambda_{1})<\frac{\pi }{2}\) and \(\frac{-\pi }{2}<\arg (\lambda_{2})<\frac{- \alpha \pi }{2}\), which satisfy the conditions \(\vert \arg (\lambda_{1}) \vert >\frac{ \alpha \pi }{2}\) and \(\vert \arg (\lambda_{2}) \vert >\frac{\alpha \pi }{2}\), respectively.

According to Theorem 2.6, equilibrium point \(E_{3}=(x^{*},y ^{*})\) is locally asymptotically stable. □

Theorem 4.5

Equilibrium point \(E_{3}=(x^{*},y^{*})\) of model (3) is unstable if one of the following conditions holds:

  1. (i)

    \(\operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4 \det ( J ( x^{*},y^{*} ) ) \geq 0\) and \(\operatorname {tr}( J ( x^{*},y^{*} ) ) >0\).

  2. (ii)

    \(\operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4 \det ( J ( x^{*},y^{*} ) ) <0\), \(\operatorname {tr}( J ( x^{*},y^{*} ) ) >0\), and \(\vert \operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4 \det ( J ( x^{*},y^{*} ) ) \vert ^{1/2}<\operatorname {tr}( J ( x^{*},y^{*} ) ) \tan ( \frac{\alpha \pi }{2} ) \).

Proof

(i) Assume that \(\operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4 \det ( J ( x^{*},y^{*} ) ) \geq 0\) and \(\operatorname {tr}( J ( x^{*},y^{*} ) ) >0\). From Eq. (13) in Theorem 4.4, we have \(\det (J(x^{*},y^{*}))>0\). Then, by Eq. (15), we obtain \(\lambda_{1}>0\) and \(\lambda _{2}>0\), which lead to \(\vert \arg (\lambda_{1}) \vert <\frac{\alpha \pi }{2}\) and \(\vert \arg (\lambda_{2}) \vert <\frac{\alpha \pi }{2}\).

Hence, by Theorem 2.6, the equilibrium point \(E_{3}=(x^{*},y ^{*})\) is unstable.

(ii) Assume that \(\operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4 \det ( J ( x^{*},y^{*} ) ) <0\), \(\operatorname {tr}( J ( x^{*},y^{*} ) ) >0\), and \(\vert \operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4\det ( J ( x^{*},y^{*} ) ) \vert ^{1/2}<\operatorname {tr}( J ( x ^{*},y^{*} ) ) \tan ( \frac{\alpha \pi }{2} ) \). From Eq. (15), we obtain a pair of complex conjugate eigenvalues \(\lambda_{1}\) and \(\lambda_{2}=\bar{\lambda_{1}}\) such that \(\operatorname {Im}(\lambda_{1})=-\operatorname {Im}(\lambda_{2})= [ 4 \det ( J(x^{*},y^{*}) ) -\operatorname {tr}^{2} ( J(x^{*}, y ^{*}) ) ] ^{1/2}>0\) and \(\operatorname {Re}(\lambda_{1})= \operatorname {Re}(\lambda_{2})=\operatorname {tr}( J(x^{*},y^{*}) ) >0\). By the assumptions, we obtain \(\operatorname {Im}(\lambda_{1})<\operatorname {Re}(\lambda_{1})\tan ( \frac{ \alpha \pi }{2} ) \) and \(-\operatorname {Im}(\lambda_{2})< \operatorname {Re}(\lambda_{2})\tan ( \frac{\alpha \pi }{2} ) \). These imply that \(0<\arg (\lambda_{1})<\frac{\alpha \pi }{2}\) and \(\frac{-\alpha \pi }{2}<\arg (\lambda_{2})<0\), then \(\vert \arg (\lambda _{1}) \vert <\frac{\alpha \pi }{2}\) and \(\vert \arg (\lambda_{2}) \vert <\frac{\alpha \pi }{2}\).

Therefore, by Theorem 2.6, equilibrium point \(E_{3}=(x^{*},y ^{*})\) is unstable. □

4.2 Existence of a Hopf bifurcation

A Hopf bifurcation occurs when a system has a pair of complex conjugate eigenvalues of the Jacobian matrix at an equilibrium point and when the stability of the equilibrium point changes from stable to unstable as a bifurcation parameter crosses a critical value [84, 85]. From the results of Sect. 4.1, we observe that the order of derivatives has an effect on the stability of model (3). Thus, we can choose the order to be the bifurcation parameter. The conditions for existence of a Hopf bifurcation in a fractional order system are different from integer order systems. There are some studies that considered the existence of Hopf bifurcations in fractional order systems [86, 87]. In this study, we use the conditions for the existence of a Hopf bifurcation which were introduced by Xiang Li and Ranchao Wu [87]. The conditions for the existence are modified for our system as given below.

Theorem 4.6

([87]; Existence of Hopf bifurcation)

When bifurcation parameter α passes through the critical value \(\alpha^{*}\in (0,1)\), fractional order system (3) undergoes a Hopf bifurcation at the equilibrium point if the following conditions hold:

  1. (a)

    the Jacobian matrix of the system (3) at the equilibrium point has a pair of complex conjugate eigenvalues \(\lambda_{1,2}=\theta \pm i\omega \), where \(\theta >0\);

  2. (b)

    \(m(\alpha^{*})=0 \), where \(m(\alpha )= \frac{\alpha \pi }{2}-\min_{1\leq i\leq 2} \vert \arg (\lambda_{i}) \vert \);

  3. (c)

    \(\frac{dm(\alpha )}{d\alpha }| _{\alpha =\alpha^{*}}\neq 0 \).

Remark 1

Condition (b) indicates that \(\alpha^{*}\) is the switching point of stability and condition (c) guarantees that \(m(\alpha )\) can change sign when the bifurcation parameter α passes through the critical value \(\alpha^{*}\) [87].

We then establish the conditions for the existence of a Hopf bifurcation at the positive equilibrium point as the order of derivatives crosses a critical value. The result is presented as the following theorem.

Theorem 4.7

Model (3) undergoes a Hopf bifurcation at equilibrium point \(E_{3}=(x^{*},y^{*})\) when bifurcation parameter α passes through the critical value \(\alpha^{*}=\frac{2}{\pi }\arctan [ ( \vert \operatorname {tr}^{2} ( J(x^{*}, y^{*}) ) -4\det ( J(x^{*},y^{*}) ) \vert ^{1/2})/( \operatorname {tr}( J(x^{*},y^{*}) ) ) ] \) if \(\operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4\det ( J ( x^{*},y^{*} ) ) <0 \) and \(\operatorname {tr}( J ( x^{*}, y^{*} ) ) >0\).

Proof

Assume that \(\operatorname {tr}^{2} ( J ( x^{*},y^{*} ) ) -4 \det ( J ( x^{*},y^{*} ) ) <0\), \(\operatorname {tr}( J ( x^{*},y^{*} ) ) >0\), and the critical value \(\alpha^{*}=\frac{2}{\pi }\arctan [ \frac{ \vert \operatorname {tr}^{2} ( J(x^{*},y^{*}) ) -4\det ( J(x^{*},y^{*}) ) \vert ^{1/2}}{ \operatorname {tr}( J(x^{*},y^{*}) ) } ] \).

Define \(\theta =\frac{1}{2}\operatorname {tr}(J(x^{*},y^{*}))\) and \(\omega =\frac{1}{2} \vert \operatorname {tr}^{2} ( J(x^{*},y^{*}) ) -4 \det ( J(x^{*},y^{*}) ) \vert ^{1/2}\). By the second assumption, we have \(\theta >0\). According to the first assumption and Eq. (15), we have a pair of complex conjugate eigenvalues \(\lambda_{1,2}=\theta \pm i\omega \), with \(\theta >0\). Hence, condition (a) in Theorem 4.6 holds.

From the second assumption and \(m(\alpha )=\frac{\alpha \pi }{2}- \min_{1\leq i\leq 2} \vert \arg (\lambda_{i}) \vert \), we obtain

$$\begin{aligned} m\bigl(\alpha^{*}\bigr) &=\frac{\alpha^{*}\pi }{2}-\min _{1\leq i\leq 2} \bigl\vert \arg ( \lambda_{i}) \bigr\vert \\ &=\frac{\alpha^{*}\pi }{2}-\arctan \biggl( \frac{\omega }{\theta } \biggr) \\ &=\arctan \biggl( \frac{\omega }{\theta } \biggr) -\arctan \biggl( \frac{ \omega }{\theta } \biggr) \\ &=0 . \end{aligned}$$

Then condition (b) in Theorem 4.6 holds.

Finally, from the definition of \(m(\alpha )\), we have

$$\begin{aligned} \frac{dm(\alpha )}{d\alpha }\bigg| _{\alpha =\alpha^{*}}=\frac{\pi }{2} \neq 0. \end{aligned}$$

This implies that condition (c) holds.

Therefore, from Theorem 4.6, model (3) undergoes a Hopf bifurcation at equilibrium point \(E_{3}=(x^{*},y^{*})\) when bifurcation parameter α passes through the critical value \(\alpha^{*}\). □

5 Numerical simulations

In this section, we present numerical examples and simulate model (3) to illustrate the results of Sect. 4. However, we only show the numerical examples for the coexistence equilibrium point. There are many numerical methods for solving nonlinear fractional differential equations such as the predictor-corrector method [15, 88], Adomian decomposition method [16], variational iteration method [17], and Adams method [89]. However, the Adams method is often used for solving nonlinear fractional differential equations [90–92] and is useful for studying the dynamic behavior (especially long time behavior) of the solutions [45]. Thus, in this study, the Adams method is used to solve model (3) by the Matlab software.

The goals of the numerical simulations are to identify the effects of different parameter values and of variations of the derivative order α on the dynamic behavior of the model (3). The discussion of these effects is divided into the two following subsections.

5.1 The effect of different parameter values

We assign three different sets of parameters. In each set, we calculate the coexistence equilibrium point \(E_{3}=(x^{*},y^{*})\) of the model by using Eq. (11). With these parameters, the determinant and trace of the Jacobian matrix \(J(x^{*},y^{*})\) are calculated by using Eqs. (13) and (14).

In Fig. 1, we set the parameters in the model as \(s=236\), \(r=4\), \(K=100\), \(m=1\), \(a=60\), \(p=4\), and \(c=2\). With these parameters, the coexistence equilibrium point is \(E_{3}=(60,48)\). We obtain \(\operatorname {tr}( J(60,48) ) =-45.6<0\), which satisfy sufficient condition (i) in Theorem 4.4. According to Theorem 4.4, equilibrium point \(E_{3}=(60,48)\) is locally asymptotically stable, which implies that a trajectory converges to equilibrium point \(E_{3}=(60,48)\) if the initial conditions start close enough to this equilibrium as shown in Fig. 1. The dynamic behaviors of interacting prey (x) and predator (y) for the order \(\alpha =0.7\) with the initial values \((x_{0},y_{0})=(50,40),(50,55),(75,55),(80,45) \) are shown in Fig. 1(a). For comparison, the relationships of the two species for \(\alpha =0.9\) with \((x_{0},y_{0})=(51,45),(53,48),(75,50),(70,47) \) are shown in Fig. 1(b).

Figure 1
figure 1

Dynamic behavior of model (3) with several initial conditions and the following parameters: \(s=236\), \(r=4\), \(K=100\), \(m=1\), \(a=60\), \(p=4\), and \(c=2\). (a) Derivative order \(\alpha =0.7\) and (b) derivative order \(\alpha =0.9\)

Full size image

In Fig. 2, we set \(s=156\), \(r=3\), \(K=100\), \(m=1\), \(a=40\), \(p=4\), and \(c=2\). The coexistence equilibrium point for these parameters is \(E_{3}=(40,36)\) and we obtain \(\det ( J(40,36) ) =140.4\) and \(\operatorname {tr}( J(40,36) ) =25.2\). The result satisfies the sufficient condition (i) in Theorem 4.5 because \(\operatorname {tr}( J(40,36) ) >0\) and \(\operatorname {tr}^{2} ( J(40,36) ) -4 \det ( J(40,36) ) =73.44>0\). Therefore, according to Theorem 4.5, equilibrium point \(E_{3}=(40,36)\) is unstable, which implies that all the trajectories diverge from this equilibrium point as shown in Fig. 2. Figure 2(a) shows the simulation for the order \(\alpha =0.4\) with the initial values \((x_{0},y_{0})=(41,35),(37,36.5),(35.5,35.5),(42,36)\). For comparison, Fig. 2(b) shows the dynamic behavior for \(\alpha =0.85\) with \((x_{0},y_{0})=(40,35) ,(40,37),(38,36),(42,36)\).

Figure 2
figure 2

Dynamic behavior of model (3) with several initial conditions and the following parameters: \(s=156\), \(r=3\), \(K=100\), \(m=1\), \(a=40\), \(p=4\), and \(c=2\). (a) Derivative order \(\alpha =0.4\) and (b) derivative order \(\alpha =0.85\)

Full size image

The simulations presented in the two figures above indicate that the stability of the equilibrium points does not depend on the order \(\alpha \in (0,1)\). This result is consistent with the theorems in the previous section.

In Fig. 3, we set \(s=102\), \(r=8\), \(K=100\), \(m=3\), \(a=51\), \(p=2\), and \(c=1\) as parameters in the model, then the coexistence equilibrium point is \(E_{3}=(51,188.16)\). We obtain \(\det ( J(51,188.16) ) =188.16\) and \(\operatorname {tr}( J(51,188.16) ) =4.08>0\), which lead to \(\operatorname {tr}^{2} ( J(51,188.16) ) -4\det ( J(51,188.16) ) =-735.99<0\). Since the order α appears in condition (ii) of Theorem 4.4 and 4.5, the stability of equilibrium point \(E_{3}=(51,188.16)\) is dependent on the value of the order \(\alpha \in (0,1)\). For order \(\alpha =0.75\), we get \(\vert \operatorname {tr}^{2} ( J ( 51,188.16 ) ) -4\det ( J ( 51,188.16 ) ) \vert ^{1/2}> \operatorname {tr}( J ( 51,188.16 ) ) \tan ( \frac{0.75 \pi }{2} ) \). According to Theorem 4.4, equilibrium point \(E_{3}=(51,188.16)\) is locally asymptotically stable as shown in Fig. 3(a). In addition, if order \(\alpha =0.95\), then \(\vert \operatorname {tr}^{2} ( J ( 51,188.16 ) ) -4\det ( J ( 51,188.16 ) ) \vert ^{1/2}< \operatorname {tr}( J ( 51,188.16 ) ) \tan ( \frac{0.95 \pi }{2} ) \). According to Theorem 4.5, equilibrium point \(E_{3}=(51,188.16)\) is unstable, which is shown in Fig. 3(b). These simulations are run with the initial values \((x_{0},y_{0})=(51,189),(51,187), (50,188.16),(52,188.16)\).

Figure 3
figure 3

Dynamic behavior of model (3) with several initial conditions and the following parameters: \(s=102\), \(r=8\), \(K=100\), \(m=3\), \(a=51\), \(p=2\), and \(c=1\). (a) Derivative order \(\alpha =0.75\) and (b) derivative order \(\alpha =0.95\)

Full size image

The simulation results in Fig. 3 indicate that the order α of model (3) has an effect on the stability of equilibrium point \(E_{3}\). Next, we demonstrate how the order α can cause a Hopf bifurcation at \(E_{3}\) for model (3).

5.2 The effect of varying the order α

We choose parameters in model (3) as \(s=0.56\), \(r=0.02\), \(K=100\), \(m=2\), \(a=30\), \(p=1\), and \(c=0.5\). By using Eq. (11) with these parameters, the coexistence equilibrium point is found to be \(E_{3}=(30,42)\). It follows from Eqs. (13) and (14) that \(\det ( J(30,42) ) =0.2\) and \(\operatorname {tr}( J(30,42) ) =0.25\), respectively. We obtain \(\operatorname {tr}^{2} ( J(30,42) ) -4\det ( J(30,42) ) =-0.72<0\) and the critical value in Theorem 4.7 is \(\alpha^{*}=\frac{2}{\pi } \arctan ( \frac{ \vert -0.72 \vert ^{1/2}}{0.25} ) =0.817\). We simulate model (3) by using the above parameters with initial values \((x_{0},y_{0})=(35,45)\) and setting the derivative order \(\alpha =0.79, 0.80, 0.83\), and 0.95. The simulation results are shown in Fig. 4.

Figure 4
figure 4

Effect of the derivative order α on the dynamic behavior of model (3) with the following parameters: \(s=0.56\), \(r=0.02\), \(K=100\), \(m=2\), \(a=30\), \(p=1\), and \(c=0.5\). (a) Derivative order \(\alpha =0.79\), (b) derivative order \(\alpha =0.80\), (c) derivative order \(\alpha =0.83\), and (d) derivative order \(\alpha =0.95\)

Full size image

In Figs. 4(a) and 4(b), numerical simulations are shown for the orders \(\alpha =0.79\) and \(\alpha =0.80\), respectively, in which both values satisfy \(\alpha <\alpha^{*}\). By using these orders and the parameters which are specified above, condition (ii) in Theorem 4.4 is satisfied. Consequently, equilibrium point \(E_{3}=(30,42)\) is locally asymptotically stable. Figures 4(a) and 4(b) show that the trajectory converges to equilibrium point \(E_{3}=(30,42)\).

However, if we use \(\alpha =0.83\) and \(\alpha =0.95\) in which both values satisfy \(\alpha >\alpha^{*}\), then, according to Theorem 4.5, equilibrium point \(E_{3}=(30,42)\) is unstable. The simulation results indicate that the trajectory diverges from equilibrium point \(E_{3}\), which is shown in Figs. 4(c) and 4(d) for the orders \(\alpha =0.83\) and \(\alpha =0.95\), respectively.

The above results indicate that equilibrium point \(E_{3}=(30,42)\) loses its stability when the order α is increased to pass through the critical value \(\alpha^{*}\), which implies that a Hopf bifurcation occurs. This result is consistent with Theorem 4.7.

In addition, Figs. 4(c) and 4(d) illustrate the appearance of an attracting limit cycle of model (3). In further simulations, we use the same set of parameters as in Fig. 4, but we change the initial values to \((x_{0},y_{0})=(28,40)\) and \((100,120)\) and the derivative orders to \(\alpha =0.9\) and 0.99. The simulations reveal that there exists an attracting limit cycle of model (3) as shown in Fig. 5(a) for \(\alpha =0.9\) and Fig. 5(b) for \(\alpha =0.99\). However, the authors of studies in Refs. [93–95] suggest that exact periodic solutions do not exist for fractional order differential equations systems. Therefore, the limit cycle appearing in Fig. 4 and Fig. 5 cannot be an exact periodic solution of model (3).

Figure 5
figure 5

Effect of the derivative order α on the dynamic behavior of model (3) with the following parameters: \(s=0.56\), \(r=0.02\), \(K=100\), \(m=2\), \(a=30\), \(p=1\), and \(c=0.5\). (a) Derivative order \(\alpha =0.9\) and (b) derivative order \(\alpha =0.99\)

Full size image

6 Conclusions

In this paper, we have studied the dynamic behavior of a fractional Gauss-type predator–prey model with Allee effect and Holling type-III functional response. The model was constructed by starting with the first order model as shown in Eq. (1). We showed the existence and uniqueness of a nonnegative solution of the model. We used the linearization method to classify the local stability of the three types of equilibrium points. In addition, we obtained the conditions and critical value \(\alpha^{*}\) for occurrence of a Hopf bifurcation at the positive equilibrium point. Finally, numerical simulations were used to show the dynamic behavior of interaction between prey and predator and to verify the validity of the theoretical results. The simulation results illustrated that the order α is a factor affecting the dynamic behavior and is responsible for a Hopf bifurcation. Moreover, the numerical results showed the appearance of an attracting limit cycle of model (3). However, this limit cycle cannot be an exact periodic solution of the model.