Abstract
This paper considers projective synchronization of fractional-order delayed neural networks. Sufficient conditions for projective synchronization of master–slave systems are achieved by constructing a Lyapunov function, employing a fractional inequality and the comparison principle of linear fractional equation with delay. The corresponding numerical simulations demonstrate the feasibility of the theoretical result.
Similar content being viewed by others
1 Introduction
Neural networks have attracted great attention due to their wide applications, including the signal processing, parallel computation, optimization, and artificial intelligence. The dynamical behaviors of neural networks have been widely studied, particularly synchronization, which is one of the most important topics and therefore has been given much attention [1–6]. However, the majority of existing results considered modeling integer-order neural networks.
It is well known that fractional calculus is the generalization of integer-order calculus to arbitrary order. Compared to classical integer-order models, fractional-order calculus offers an excellent instrument for the description of memory and hereditary properties of dynamical processes. The existence of infinite memory can help fractional-order models better describe the system’s dynamical behaviors as illustrated in [7–23]. Taking these factors into consideration, fractional calculus was introduced to neural networks forming fractional-order neural networks, and some interesting results on synchronization were demonstrated [24–29]. Among all kinds of synchronization, projective synchronization, in which the master and slave systems are synchronized up to a scaling factor, is an important concept in both theoretical and practical manners. Recently, some results with respect to projective synchronization of fractional-order neural networks were considered [30–32]. In [30], projective synchronization for fractional neural networks was studied. Through the employment of a fractional-order differential inequality, the projective synchronization of fractional-order memristor-based neural networks was shown in [31]. By using an LMI-based approach, the global Mittag–Leffler projective synchronization for fractional-order neural networks was investigated in [32].
However, time delay, which is unavoidable in biological, engineering systems, and neural networks, was not taken into account in most of the previous works. To the best of our knowledge, projective synchronization of fractional-order neural networks was previously investigated at the presence of time delay through the use of Laplace transform [33], and no special Lyapunov functions were derived for synchronization analysis. In this paper, new methods are introduced to investigate the projective synchronization of fractional-order delayed neural networks. The study includes constructing a Lyapunov function, applying a fractional inequality and the comparison principle of linear fractional equation with delay, and obtaining new sufficient conditions.
The rest of this article is organized as follows. In Sect. 2, some definitions and lemmas are introduced, and the model description is given. In Sect. 3, the projective synchronization schemes are presented, and sufficient conditions for projective synchronization are obtained. Numerical simulations are presented in Sect. 4. Conclusions are drawn in Sect. 5.
2 Preliminaries and model description
It has to be noted that Riemann–Liouville fractional derivative and Caputo fractional derivative are the most commonly used among all the definitions of fractional-order integrals and derivatives. Due to the advantages of the Caputo fractional derivative, it is adopted in this work.
Definition 1
([7])
The fractional integral with non-integer order \(\alpha> 0\) of a function \(x(t)\) is defined by
where \(t\geq t_{0}\), \(\Gamma(\cdot)\) is the gamma function, \(\Gamma(s)=\int_{0}^{\infty} t^{s-1}e^{-t}\,dt\).
Definition 2
([7])
The Caputo derivative of fractional order α of a function \(x(t)\) is defined by
where \(t\geq t_{0}\), \(n-1<\alpha<n\in Z^{+}\).
In this paper, we consider a class of fractional-order neural networks with time delay as a master system, which is described by
or equivalently, by
where \(0<\alpha<1\), n is the number of units in a neural network, \(x(t)=(x_{1}(t),\ldots, x_{n}(t))^{T}\in R^{n}\) denotes the state variable of the neural network, \(C=\operatorname{diag}(c_{1}, c_{2}, \ldots, c_{n})\) is the self-regulating parameters of the neurons, where \(c_{i}\in R^{+}\). \(I=(I_{1}, I_{2}, \ldots, I_{n})^{T}\) represents the external input, \(A=(a_{ij})_{n\times n}\) and \(B=(b_{ij})_{n\times n}\) are the connective weight matrices without and with delay, respectively. Functions \(f(x(t))=(f_{1}(x_{1}(t)), \ldots, f_{n}(x_{n}(t)))^{T} \), \(g(x(t))=(g_{1}(x_{1}(t)), \ldots, g_{n}(x_{n}(t)))^{T}\) are the neuron activation functions.
The slave system is given by
or equivalently, by
where \(y(t)=(y_{1}(t),\ldots, y_{n}(t))^{T}\in R^{n}\) is the state vector of system’s response, \(U(t)=(u_{1}(t), \ldots, u_{n}(t))^{T}\) is a suitable controller.
For generalities, the following definition, assumption, and lemmas are presented.
Definition 3
If there exists a nonzero constant β such that, for any two solutions \(x(t)\) and \(y(t)\) of systems (1) and (3) with different initial values, one can get \(\lim_{t\rightarrow\infty} \Vert y(t)-\beta x(t) \Vert =0\), then the master system (1) and the slave system (3) can achieve globally asymptotically projective synchronization, where \(\Vert \cdot \Vert \) denotes the Euclidean norm of a vector.
Assumption 1
The neuron activation functions \(f_{j}(x)\), \(g_{j}(x)\) satisfy the following Lipschitz condition with Lipschitz constants \(l_{j}>0\), \(h_{j}>0\):
for all \(u, v\in R\), denote \(L=\operatorname{diag}(l_{1}, l_{2}, \ldots, l_{n}), H=\operatorname{diag}(h_{1}, h_{2}, \ldots, h_{n})\), \(l_{\max}=\max\{l_{1}, l_{2}, \ldots, l_{n}\}\), \(h_{\max}=\max\{h_{1}, h_{2}, \ldots, h_{n}\}\).
Lemma 1
([32])
Suppose that \(x(t)=(x_{1}(t), \ldots, x_{n}(t))^{T}\in R^{n}\) is a differentiable vector-valued function and \(P\in R^{n\times n}\) is a symmetric positive matrix. Then, for any time instant \(t\geq0\), we have
where \(0<\alpha<1\).
When \(P=E\) is an identity matrix, then \(\frac{1}{2}D^{\alpha }[x^{T}(t)x(t)]\leq x^{T}(t)D^{\alpha}x(t)\).
Lemma 2
([34])
Suppose that \(V(t)\in R^{1}\) is a continuous differentiable and nonnegative function, which satisfies
where \(t\in[0, +\infty)\). If \(a>b>0 \) for all \(\varphi(t)\geq0, \tau >0\), then \(\lim_{t\rightarrow+\infty}V(t)=0\).
Lemma 3
([34])
Suppose that \(x(t)=(x_{1}(t), x_{2}(t), \ldots, x_{n}(t))^{T}\in R^{n}\) and \(y(t)=(y_{1}(t), y_{2}(t), \ldots, y_{n}(t))^{T}\in R^{n}\) are vectors, for all \(Q=(q_{ij})_{n\times n}\), the following inequality holds:
where \(k_{\max}=\frac{1}{2} \Vert Q \Vert _{\infty}=\frac{1}{2}\max_{i=1}^{n}(\sum_{j=1}^{n}|q_{ij}|), \bar{k}_{\max}=\frac{1}{2}\| Q\|_{1}=\frac{1}{2}\max_{j=1}^{n}(\sum_{i=1}^{n}|q_{ij}|)\).
3 Projective synchronization
In this section, master–slave projective synchronization of delayed fractional-order neural networks is discussed. The aim is to design a suitable controller to achieve the projective synchronization between the slave system and the master system.
Let \(e_{i}(t)=y_{i}(t)-\beta x_{i}(t)\) (\(i=1, 2, \ldots, n\)) be the synchronization errors.
Select the control input function \(u_{i}(t)\) (\(i=1, 2, \ldots, n\)) as the following form:
where \(d_{i}\) are positive constants, β is the projective coefficient.
Remark 1
The control function \(u_{i}(t)\) is a hybrid control, \(v_{i}(t)\) is an open loop control, and \(w_{i}(t)\) is a linear control.
Then the error system is obtained:
or equivalently,
where \(e(t)=(e_{1}(t), \ldots, e_{n}(t))^{T}\), \(D=\operatorname{diag}(d_{1}, d_{2}, \ldots, d_{n})\).
Theorem 1
Under Assumption 1, if there exists a symmetric positive definite matrix \(P\in R^{n\times n}\) such that
then the fractional-order delayed neural networks systems (1) and (3) can achieve globally asymptotically projective synchronization based on the control schemes (8), (9), (10), where \(\hat{\lambda}_{\max}\) denotes the greatest eigenvalue of \(-PC-PD\), \({k_{1}}_{\max}=\frac{1}{2} \Vert PA \Vert _{\infty}\), \(\bar {k_{1}}_{\max}=\frac{1}{2} \Vert PA \Vert _{1}\), \({k_{2}}_{\max}=\frac{1}{2} \Vert PB \Vert _{\infty}\), \(\bar{k_{2}}_{\max}=\frac{1}{2} \Vert PB \Vert _{1}\), \(\lambda_{\min}\) and \(\lambda_{\max}\) denote the minimum and the maximum eigenvalue of P, respectively.
Proof
Construct a Lyapunov function:
Taking the time fractional-order derivative of \(V(t)\), according to Lemma 1, (13) can be rewritten as
From Lemma 3, we have
Submitting (15) and (16) into (14) yields
Then
From Lemma 2, we have that, if
then system (1) synchronizes system (3). □
Remark 2
If the projective coefficient \(\beta=1\), the projective synchronization is simplified to complete synchronization, and the control input function (8) becomes
Remark 3
If the projective coefficient \(\beta=-1\), the projective synchronization is simplified to anti-synchronization, and the control input function (8) becomes
In the following, we choose the control input function \(u_{i}(t)\) in system (3):
where \(d_{i}(t)+d_{i}^{*}\) are feedback gains, \(d_{i}(t)\geq0, d_{i}^{*}>0\) are positive constants, \(\gamma_{i}\) are any positive constants, and β is the projective coefficient.
Remark 4
The control function \(u_{i}(t)\) is a hybrid control, \(v_{i}(t)\) is an open loop control, and \(w_{i}(t)\) is an adaptive feedback control.
Remark 5
Let \(d_{i}(0)\geq0\), then \(d_{i}(t)=d_{i}(0)+I^{\alpha}(\gamma_{i} \Vert y_{i}(t)-\beta x_{i}(t) \Vert ^{2})\geq d_{i}(0)\). So it is easy to get \(d_{i}(t)\geq0\).
Then the system’s error is given as follows:
or equivalently,
where \(D(t)=\operatorname{diag}(d_{1}(t), \ldots, d_{n}(t))\), \(D^{*}=\operatorname{diag}(d_{1}^{*}, \ldots, d_{n}^{*})\).
Theorem 2
Under Assumption 1, if there exists a symmetric positive definite matrix \(P\in R^{n\times n}\) such that
then the fractional-order delayed neural networks systems (1) and (3) can achieve globally asymptotically projective synchronization based on the control schemes (21), (22), (23), (24), where \(\check{\lambda }_{\max}\) denotes the greatest eigenvalue of \(-PC-PD^{*}\), \(\lambda_{\min }\) and \(\lambda_{\max}\) denote the minimum and the maximum eigenvalues of P, respectively.
Proof
Construct the auxiliary function
Taking the time fractional-order derivative of \(V(t)\), according to Lemma 1, (27) can be given as follows:
The rest is the same as the proof of Theorem 1, hence omitted here. □
Remark 6
If the projective coefficient \(\beta=1\), the control input function (21) becomes
where
Remark 7
If the projective coefficient \(\beta=-1\), the control input function (21) becomes
where
Remark 8
By using an LMI-based approach, Wu et al. investigated global Mittag–Leffler projective synchronization for fractional-order neural networks [32], but without considering delay.
Remark 9
In [33], by using the Laplace transform, the hybrid projective synchronization of fractional-order memristor-based neural networks with time delays was discussed, but the theoretical synchronization results are poor and the sufficient conditions are complex. For comparison purposes, in this paper, the projective synchronization of fractional-order delayed neural networks is studied by constructing a Lyapunov function, with the employment of a fractional inequality and the comparison principle of linear fractional equation with delay. The results are simpler and more theoretical.
4 Numerical simulations
The following two-dimensional fractional-order delayed neural networks are considered in this section:
where \(x(t)=(x_{1}(t), x_{2}(t))^{T}\), \(\alpha=0.97\), \(I=(0, 0)^{T}\). The activation functions are given by \(f(x(t))=g(x(t))=\tanh(x(t))\), \(\tau=1\). Obviously, \(f(x)\) and \(g(x)\) satisfy Assumption 1 with \(L=H=\operatorname{diag}(1, 1)\) and \(C=\bigl( {\scriptsize\begin{matrix}{} 1& 0 \cr 0&1 \end{matrix}} \bigr) \), \(A=\bigl( {\scriptsize\begin{matrix}{} 2.0& -0.1 \cr -5.0&2.0 \end{matrix}} \bigr) \), \(B=\bigl( {\scriptsize\begin{matrix}{} -1.5& -0.1 \cr -0.2& -1.5 \end{matrix}} \bigr) \).
Under these parameters, system (33) has a chaotic attractor, which is shown in Fig. 1.
Chaotic behavior of system (17) with initial value \((2, 4)\)
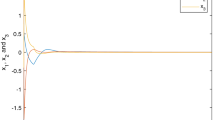
In the control scheme (8), (9), (10), we select the symmetric positive definite matrix \(P=\bigl( {\scriptsize\begin{matrix}{} 1& 0 \cr 0&2 \end{matrix}} \bigr) \). By simple computing, we can get \(d_{1}=18\), \(d_{2}=10\). Select the projective coefficients \(\beta=2\), initial values \(x_{1}(0)=4\), \(x_{2}(0)=2\), \(y_{1}(0)=3\), \(y_{2}(0)=1\), the projective synchronization error is shown in Fig. 2. The synchronization trajectories are shown in Fig. 3 and Fig. 4.
Similarly, projective synchronization with projective coefficient \(\beta =-3\) is given in Fig. 5–Fig. 7.
In the control scheme (21), (22), (23), (24), we select the symmetric positive definite matrix \(P=\bigl( {\scriptsize\begin{matrix}{} 1& 0 \cr 0&\frac{1}{2} \end{matrix}} \bigr) \). By simple computing, we can get \(d_{1}(0)=10\), \(d_{2}(0)=24\). Select the projective coefficients \(\beta=3\), \(d_{1}^{*}=1\), \(d_{2}^{*}=2\), initial values \(x_{1}(0)=4\), \(x_{2}(0)=1\), \(y_{1}(0)=3\), \(y_{2}(0)=2\), the projective synchronization error is shown in Fig. 8. The synchronization trajectories are shown in Fig. 9 and Fig. 10. In addition, the adaptive gains \(d_{i}(t)\) (\(i=1, 2\)) converge to some positive constants, see Fig. 11.
Similarly, projective synchronization with projective coefficient \(\beta =-2\) is shown in Fig. 12–Fig. 15.
Remark 10
In simulations, the projective coefficient β is a nonzero constant, which is selected arbitrarily.
5 Conclusions
In this paper, the projective synchronization of delayed fractional-order neural networks is investigated. In order to obtain general results, an effective controller is designed, a fractional inequality and the comparison principle of linear fractional equation with delay are implemented, and some sufficient conditions are given to ensure that the master–slave systems are able to obtain projective synchronization. Numerical simulations are used to show the effectiveness of the method proposed.
References
Cao, J., Chen, G., Li, P.: Global synchronization in an array of delayed neural networks with hybrid coupling. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 38, 488–498 (2008)
Cao, J., Wan, Y.: Matrix measure strategies for stability and synchronization of inertial BAM neural networks with time delays. Neural Netw. 53, 165–172 (2014)
Lu, J., Ho, D., Cao, J., Kurths, J.: Exponential synchronization of linearly coupled neural networks with impulsive disturbances. IEEE Trans. Neural Netw. 22, 329–336 (2011)
Park, M., Kwon, O., Lee, S., Park, J., Cha, E.: Synchronization criteria for coupled stochastic neural networks with time-varying delays and leakage delay. J. Franklin Inst. 349, 1699–1720 (2012)
Yang, X., Zhu, Q., Huang, C.: Lag stochastic synchronization of chaotic mixed time-delayed neural networks with uncertain parameters or perturbations. Neurocomputing 74, 1617–1625 (2011)
Song, Q.: Synchronization analysis of coupled connected neural networks with mixed time delays. Neurocomputing 72, 3907–3914 (2009)
Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1999)
Butzer, P.L., Westphal, U.: An Introduction to Fractional Calculus. World Scientific Press, Singapore (2000)
Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific Press, Singapore (2000)
Ozalp, N., Demirci, E.: A fractional order SEIR model with vertical transmission. Math. Comput. Model. 54, 1–6 (2011)
Zhang, H., Ye, R.Y., Cao, J.D., Alsaedie, A.: Lyapunov functional approach to stability analysis of Riemann–Liouville fractional neural networks with time-varying delays. Asian J. Control 20, 1–14 (2017)
Laskin, N.: Fractional quantum mechanics and Levy path integrals. Phys. Lett. A 268, 298–305 (2000)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Application of Fractional Differential Equations. Elsevier, New York (2006)
Ahmed, E., Elgazzar, A.: On fractional order differential equations model for nonlocal epidemics. Physica A 379, 607–614 (2007)
Zhang, W.W., Chen, D.Y.: Hybrid projective synchronization of different dimensional fractional order chaotic systems with time delay and different orders. Chinese Journal of Engineering Mathematics 34, 321–330 (2017)
Zhang, H., Ye, R.Y., Cao, J.D., Alsaedie, A.: Delay-independent stability of Riemann Liouville fractional neutral-type delayed neural networks. Neural Process. Lett. 21, 1–16 (2017)
Wu, G.C., Baleanu, D., Zeng, S.D.: Finite-time stability of discrete fractional delay systems: Gronwall inequality and stability criterion. Commun. Nonlinear Sci. Numer. Simul. 57, 299–308 (2018)
Wu, G.C., Baleanu, D., Luo, W.H.: Lyapunov functions for Riemann–Liouville-like fractional difference equations. Appl. Math. Comput. 314, 228–236 (2017)
Baleanu, D., Wu, G.C., Bai, Y.R., Chen, F.L.: Stability analysis of Caputo-like discrete fractional systems. Commun. Nonlinear Sci. Numer. Simul. 48, 520–530 (2017)
Wu, G.C., Baleanu, D., Xie, H.P., Chen, F.L.: Chaos synchronization of fractional chaotic maps based on stability condition. Physica A 460, 374–383 (2016)
Jajarmi, A., Hajipour, M., Baleanu, D.: New aspects of the adaptive synchronization and hyperchaos suppression of a financial model. Chaos Solitons Fractals 99, 285–296 (2017)
Baleanu, D., Jajarmi, A., Asad, J.H., Blaszczyk, T.: The motion of a bead sliding on a wire in fractional sense. Acta Phys. Pol. A 131, 1561–1564 (2017)
Jajarmi, A., Baleanu, D.: Suboptimal control of fractional-order dynamic systems with delay argument. J. Vib. Control (2017). https://doi.org/10.1177/1077546316687936
Zhang, W.W., Cao, J.D., Alsaedi, A., Alsaadi, F.: New methods of finite-time synchronization for a class of fractional-order delayed neural networks. Math. Probl. Eng. 2017, 1–9 (2017)
Stamova, I.: Global Mittag–Leffler stability and synchronization of impulsive fractional-order neural networks with time-varying delays. Nonlinear Dyn. 77, 1251–1260 (2014)
Yu, J., Hu, C., Jiang, H.: α-stability and α-synchronization for fractional-order neural networks. Neural Netw. 35, 82–87 (2012)
Chen, J., Zeng, G., Jiang, P.: Global Mittag–Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw. 51, 1–8 (2014)
Wang, F., Yang, Y., Hu, M., Xu, X.: Projective cluster synchronization of fractional-order coupled-delay complex network via adaptive pinning control. Phys. A, Stat. Mech. Appl. 434, 134–143 (2015)
Bao, H.B., Park, J.H., Cao, J.D.: Adaptive synchronization of fractional-order memristor-based neural networks with time delay. Nonlinear Dyn. 158, 1343–1354 (2015)
Yua, J., Hua, C., Jiang, H., Fan, X.: Projective synchronization for fractional neural networks. Neural Netw. 49, 87–95 (2014)
Bao, H.B., Cao, J.D.: Projective synchronization of fractional-order memristor-based neural networks. Neural Netw. 63, 1–9 (2015)
Wu, H., Wang, L., Wang, Y., Niu, P., Fang, B.: Global Mittag–Leffler projective synchronization for fractional-order neural networks: an LMI-based approach. Adv. Differ. Equ. 2016, 132 (2016)
Velmurugan, G., Rakkiyappan, R.: Hybrid projective synchronization of fractional-order memristor-based neural networks with time delays. Nonlinear Dyn. 83, 419–432 (2016)
Liang, S., Wu, R.C., Chen, L.P.: Adaptive pinning synchronization in fractional order uncertain complex dynamical networks with delay. Physica A 444, 49–62 (2016)
Acknowledgements
This study is supported by the National Natural Science Foundation of China (No. 11571016), the Natural Science Foundation of Anhui Province (No. 1608085MA14), and the Natural Science Foundation of the Higher Education Institutions of Anhui Province (No. KJ2015A152).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the manuscript. All the authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, W., Cao, J., Wu, R. et al. Projective synchronization of fractional-order delayed neural networks based on the comparison principle. Adv Differ Equ 2018, 73 (2018). https://doi.org/10.1186/s13662-018-1530-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1530-1