1 Introduction

Over the past few decades, the stability of real-valued neural networks (RVNNs) have been extensively investigated because of their widespread applications in various areas such as associative memory, pattern recognition, parallel computation, combinatorial optimization and quantum communication [1–8], and a lot of existing work considers the μ-stability, power-stability, Lagrange stability and exponent-stability of the neural networks [9–13]. However, when designing neural networks, firstly the problem of robust stability should be investigated due to the parameter uncertainty in the system and the perturbation of parameters or system characteristics is often unavoidable. The reasons lie in two aspects: one is that the actual values of the characteristics or parameters will deviate from their initial values due to the inaccurate measurement, the other is that the characteristics or parameters will drift slowly in the course of system’s operation which is influenced by the environmental factors. These phenomena can be seen anywhere, such as image and signal processing, combinatorial optimization problems and pattern recognition [14]. So in recent years, the robustness of neural networks has become the most important topics in the control domain and attracted great attention of the scholars [12, 15–19].

For many applications of neural networks, the states are often objected to instantaneous disturbance and experienced abrupt changes at fixed time, which may be caused by switching phenomenon, frequency changes or other sudden noise and often assumed to be in the form of impulses in the modeling process. Consequently, impulsive differential equation provides a more natural description of such systems, the basic theorem of impulsive differential equation can be seen in [20]. There are also numerical and fruitful results as regards its applications; see [21–25] and the references therein. On the other hand, due to the neural processing and signal transmissions, the time delay is often occurred, and the existence of time delay may cause the instability and poor performance of the system [26]. For a specific neural network, delay may be caused by the measuring element or the measuring process, it may also be caused by the control element and the execution element. Strictly speaking, the time delay of the control system is common, therefore, many effort have been made devoted to the delay dependent stability analysis of neural networks [10, 27–30].

Comparing with RVNNs, the advantage of complex-valued neural networks (CVNNs) is that they can directly deal with the two-dimensional data, which can also be processed by RVNNs but needs double neurons. And in the application of CVNNS, the complex signals are proved to be more relevant [31–37], which is more natural to deal with the complex-valued date, weights and neuron activation functions. Consequently, as a class of complex-valued systems, CVNNs have received a growing number of studies and explored the application of neural networks. These fruitful results promote the rapid development of control theory. However, few articles consider the robust stability of neural networks with time delay and impulse in the complex domain. In [15], the authors investigated the existence, uniqueness and global robust stability of equilibrium point for complex-valued recurrent neural networks with time delays, in which the activation functions are separated by the real and imaginary parts, the analysis methods are skillful but cannot be used to dealt with complex-valued neural networks directly. In [19], the author also considered the dynamics of the same system, regretfully, the activation functions there are required to be bounded. So, the obtained stability criteria in [15, 19] cannot be applied if the activation functions cannot be expressed by separating their real and imaginary parts or are unbounded. In [38], the robust stability with time delays and impulse in the complex domain is considered, and the given stability criteria for complex-valued neural networks are obtained using different methods. However, the main conditions for the global robust stability are restricted by two matrix inequalities, and there are only discrete delays in the model. Therefore, in this article, the robust stability of impulsive complex-valued neural networks with mixed time delays and parameter uncertainties is considered, the improved sufficient conditions are given for the existence, uniqueness and robust stability of the system in complex domain, moreover, numerical simulations manifest that the complex-valued neural networks work efficiently on storing and retrieving the image patterns.

The structure of this paper is arranged as follows. In Sect. 2, we introduce the CVNNs model and give some preliminaries, including some notations and important lemmas. The existence and uniqueness of the equilibrium will be proved using homeomorphic mapping principle in Sect. 3. The main part of Sect. 4 considers the global robust stability of the neural networks by building the proper Lyapunov functions and using the modulus inequality technique. In Sect. 5, two numerical examples are presented to show the effectiveness of our theoretical analysis. Section 6 concludes the paper.

2 Problems formulation and preliminaries

First, we give some notations of this paper. let i denote the imaginary unit, i.e. \(\mathrm{i}=\sqrt{-1}\). \(\mathbb{C}^{n}\), \(\mathbb{R}^{m\times n}\) and \(\mathbb{C}^{m\times n}\) denote, respectively, the set of n-dimensional complex vectors, \(m\times n\) real matrices and complex matrices. The subscripts T and ∗ denote matrix transposition and matrix conjugate transposition, respectively. For complex vector \(z\in\mathbb{C}^{n}\), let \(\vert z \vert =( \vert z_{1} \vert , \vert z_{2} \vert ,\ldots, \vert z_{n} \vert )^{T}\) be the module of the vector z, and \(\Vert z \Vert =\sqrt{ \sum_{i=1}^{n} \vert z_{i} \vert ^{2}}\) be the norm of the vector z. For complex matrix \(A=(a_{ij})_{n\times n}\in\mathbb{C}^{n\times n}\), let \(\vert A \vert =( \vert a_{ij} \vert )_{n\times n}\) denote the module of the matrix A, and \(\Vert A \Vert =\sqrt{\sum_{i=1}^{n}\sum_{j=1}^{n} \vert a_{ij} \vert ^{2}}\) denote the norm of the matrix A. I denotes the identity matrix with appropriate dimensions. The notation \(X\geq Y\) (respectively, \(X>Y\)) means that \(X-Y\) is positive semi-definite (respectively, positive definite). In addition, \(\lambda_{\max}(P)\) and \(\lambda_{\min}(P)\) are defined as the largest and the smallest eigenvalue of positive definite matrix P, respectively.

Motivated by [15], we will consider an impulsive complex-valued neural networks model with time delays whose dynamical behavior is governed by the following nonlinear differential equations:

$$ \textstyle\begin{cases} \dot{z}_{i}(t)=-d_{i} z_{i}(t)+\sum_{j=1}^{n} a_{ij}f_{j}(z_{j}(t))+ \sum_{j=1}^{n} b_{ij} f_{j}(z_{j}(t-\tau_{j})) \\ \hphantom{\dot{z}_{i}(t)=}{} +\sum_{j=1}^{n} c_{ij} \int_{-\infty}^{t} k_{j}(t-s)f_{j}(z_{j}(s)) \,\mathrm{d}s+J_{i},\quad t\geq0, t\neq t_{k}, \\ \Delta z_{i}(t_{k})= I_{ik}(z_{i}(t_{k}^{-})), \quad k=1,2,\ldots, i=1,2,\ldots,n, \end{cases} $$
(1)

where n is the number of the neurons, \(z_{i}(t)\in\mathbb{C}\) denotes the state of the neuron i at time t, \(f_{j}(t)\) is the complex-valued activation function, \(\tau_{j}\) (\(j=1,2,\ldots,n\)) represents the discrete transmission delay and satisfies \(0\leq\tau _{j}\leq\rho\), \(d_{i}\in\mathbb{R}\) with \(d_{i} > 0\) is the self-feedback connection weight, \(a_{ij}\in\mathbb{C}\) and \(b_{ij}\in\mathbb{C}\) are the connection weights, \(k_{j}\) (\(j=1,2,\ldots,n\)) is the distributed delay kernel function, \(J_{i}\in \mathbb{C}\) is the external input. Here \(I_{ik}\) is a linear map, \(\Delta z_{i}(t_{k})=z_{i}(t_{k}^{+})-z_{i}(t_{k}^{-})\) is the jump of \(z_{i}\) at moments \(t_{k}\) and \(0< t_{1}< t_{2}<\cdots\) is a strictly increasing sequence such that \(\lim_{k\to\infty}t_{k}=+\infty\).

Now we can rewrite (1) in an equivalent matrix-vector form as follows:

$$ \textstyle\begin{cases} \dot{z}(t)=-D z(t)+A f(z(t))+B f(z(t-\tau))+C\int _{-\infty}^{t} K(t-s)f(z(s)) \,\mathrm{d}s+J, \\ \Delta z(t_{k})=I(z(t_{k}^{-})),\quad k=1,2,\ldots, \end{cases} $$
(2)

where \(z(t)=(z_{1}(t),z_{2}(t),\ldots,z_{n}(t))^{T}\in\mathbb{C} ^{n}\), \(D=\mathrm{diag}\{d_{1},d_{2},\ldots,d_{n}\}\), \(A=(a_{ij})_{n \times n}\in\mathbb{C}^{n\times n}\), \(B=(b_{ij})_{n\times n}\in \mathbb{C}^{n\times n}\), \(f(z(t))=(f_{1}(z_{1}(t)),f_{2}(z_{2}(t)),\ldots, f_{n}(z_{n}(t)))^{T}\), \(f(z(t-\tau))=(f_{1}(z_{1}(t-\tau _{1})),f_{2}(z_{2}(t-\tau_{2})),\ldots,f_{n}(z_{n}(t-\tau_{n})))^{T}\), \(K(t-s)=\mathrm{diag}\{k_{1}(t-s),k_{2}(t-s),\ldots,k_{n}(t-s)\}\), \(J=(J_{1},J_{2},\ldots,J_{n})^{T}\in\mathbb{C}^{n}\), \(\Delta z(t _{k})=(\Delta z_{1}(t_{k}), \Delta z_{2}(t_{k}),\ldots,\Delta z_{n}(t _{k}))^{T}\), and \(I(z(t_{k}^{-}))=(I_{1k}(z(t_{k}^{-})), I_{2k}(z(t _{k}^{-})),\ldots, I_{nk}(z(t_{k}^{-})))^{T}\).

We assume that system (1) or (2) is supplemented with the initial values given by

$$ z_{i}(s)=\varphi_{i}(s),\quad s\in(-\infty,0], i=1,2,\ldots, $$
(3)

or in an equivalent vector form

$$ z(s)=\varphi(s), \quad s\in(-\infty,0], $$
(4)

where \(\varphi_{i}(\cdot)\) is complex-valued continuous function defined on \((-\infty,0]\), and \(\varphi(s)=(\varphi_{1}(s),\varphi _{2}(s),\ldots,\varphi_{n}(s))^{T}\in C((-\infty,0],\mathbb{C}^{n})\) with the norm \(\Vert \varphi(s) \Vert =\sup_{s\in(-\infty ,0]}\sqrt{\sum_{i=1}^{n} \vert \varphi_{i}(t) \vert ^{2}}\).

Let us define a partial order ⪯ over \(\mathbb{C}\): For \(z_{1},z_{2}\in\mathbb{C}\), \(z_{1}\preceq z_{2}\) if and only if \(x_{1}\leq x_{2}\) and \(y_{1}\leq y_{2}\), where \(x_{1}=\mathrm{Re}(z_{1})\), \(y_{1}=\mathrm{Im}(z_{1})\), \(x_{2}=\mathrm{Re}(z_{2})\) and \(y_{2}=\mathrm{Im}(z _{2})\). Then define a partial order ⪯ over \(\mathbb{C}^{n \times n}\): For \(A, B\in\mathbb{H}^{n\times n}\), \(A\preceq B\) if only if \(a_{ij}\preceq b_{ij}\), \(i,j=1,2,\ldots,n\), where \(A=(a_{ij})_{n \times n}\) and \(B=(b_{ij})_{n\times n}\).

The following assumptions will be needed throughout the paper:

(\(\mathbf{H}_{1}\)):

The parameters D, A, B, C, J in CVNNs (2) are assumed to be in the following sets, respectively:

$$\begin{aligned}& D_{I}= \bigl\{ D\in\mathbb{R}^{n\times n}_{d}: 0< \check{D}\preceq D \preceq\hat{D} \bigr\} , \\& A_{I}= \bigl\{ A\in\mathbb{C}^{n\times n}: \check{A}\preceq A \preceq \hat{A} \bigr\} , \\& B_{I}= \bigl\{ B\in\mathbb{C}^{n\times n}: \check{B}\preceq B \preceq \hat{B} \bigr\} , \\& C_{I}= \bigl\{ C\in\mathbb{C}^{n\times n}: \check{C}\preceq C \preceq \hat{C} \bigr\} , \\& J_{I}= \bigl\{ J\in\mathbb{C}^{n}: \check{J}\preceq J \preceq\hat{J} \bigr\} , \end{aligned}$$

where \(\check{D}, \hat{D}\in\mathbb{R}^{n\times n}_{d}\), \(\check{A}, \hat{A}, \check{B}, \hat{B}, \check{C}, \hat{C}\in\mathbb{C}^{n \times n}\), and \(\check{J}, \hat{J}\in\mathbb{C}^{n}\). Moreover, let \(\check{A}=(\check{a}_{ij})_{n\times n}\), \(\hat{A}=(\hat{a}_{ij})_{n \times n}\), \(\check{B}=(\check{b}_{ij})_{n\times n}\), \(\hat{B}=( \hat{b}_{ij})_{n\times n}\), \(\check{C}=(\check{c}_{ij})_{n\times n}\), and \(\hat{C}=(\hat{c}_{ij})_{n\times n}\). Then define \(\tilde{A}=( \tilde{a}_{ij})_{n\times n}\), \(\tilde{B}=(\tilde{b}_{ij})_{n\times n}\) and \(\tilde{C}=(\tilde{c}_{ij})_{n\times n}\), where \(\tilde{a}_{ij}= \max\{ \vert \check{a}_{ij} \vert , \vert \hat {a}_{ij} \vert \}\), \(\tilde{b}_{ij}=\max\{ \vert \check{b}_{ij} \vert , \vert \hat{b}_{ij} \vert \}\), \(\tilde{c}_{ij}=\max\{ \vert \check{c} _{ij} \vert , \vert \hat{c}_{ij} \vert \}\).

(\(\mathbf{H}_{2}\)):

For \(j=1,2,\ldots,n\), the neuron activation function \(f_{j}\) is continuous and satisfies

$$ \bigl\vert f_{j}(z_{1})-f_{j}(z_{2}) \bigr\vert \leq\gamma_{j} \vert z_{1}-z_{2} \vert , $$

for any \(z_{1},z_{2}\in\mathbb{C}\), where \(\gamma_{j}\) is a real constant. Furthermore, define \(\Gamma=\mathrm{diag}\{\gamma_{1},\gamma _{2}, \ldots,\gamma_{n}\}\).

(\(\mathbf{H}_{3}\)):

For \(j=1,2,\ldots,n\), the delay kernel \(k_{j}\) is a real value non-negative continuous function defined on \([0,+\infty)\) and satisfies,

$$ \int_{0}^{+\infty}k_{j}(s)\,\mathrm{d}s=1, \int_{0}^{+\infty }sk(s)\,\mathrm{d}s< + \infty. $$

Remark 1

For assumption (\(\mathbf{H}_{1}\)), the matrix intervals \(D_{I}\), \(A_{I}\), \(B_{I}\), \(C_{I}\) and \(J_{I}\) represent the allowed ranges of the parameters of the designed system due to parameter uncertainties caused by inaccurate measurements or environmental factors. For assumption (\(\mathbf{H}_{2}\)), the assumption of Lipschitz condition is very general since the common activations, such as piece-wise linear function, logistic sigmoid function and hyperbolic tangent function, all satisfy the Lipschitz condition. For assumption (\(\mathbf{H}_{3}\)), it is a standardization assumption for delay kernel functions. If the delay kernel function \(\tilde{k}_{j}\) satisfies \(\int_{0}^{\infty}\tilde{k}_{j}(s)\,\mathrm{d}s=K<+ \infty\), \(k_{j}\) will satisfy assumption (\(\mathbf{H}_{3}\)) by letting \(k_{j}=\tilde{k}_{j} / K\).

Definition 1

A function \(z(t)\in C((-\infty,+\infty),\mathbb{C}^{n})\) is a solution of system (2) satisfying the initial value condition (4), if the following conditions are satisfied:

  1. (i)

    \(z(t)\) is absolutely continuous on each interval \((t_{k}, t_{k+1})\subset(-\infty,+\infty)\), \(k=1,2,\ldots\) ,

  2. (ii)

    for any \(t_{k}\in[0,+\infty)\), \(k=1,2,\ldots\) , \(z(t_{k}^{+})\) and \(z(t_{k}^{-})\) exist and \(z(t_{k}^{+})=z(t_{k})\).

Definition 2

The neural network defined by (1) with the parameter ranges defined by (\(\mathbf{H}_{1}\)) is globally asymptotically robust stable if the unique equilibrium point \(\check{z}=(\check{z}_{1},\check{z} _{2},\ldots, \check{z}_{n})^{T}\) of the neural system (1) is globally asymptotically stable for all \(D\in D _{I}\), \(A\in A_{I}\), \(B\in B_{I}\), \(C\in C_{I}\) and \(J\in J_{I}\).

Lemma 1

([39])

For any \(a,b\in\mathbb{C}^{n}\), if \(P\in \mathbb{C}^{n\times n}\) is a positive definite Hermitian matrix, then \(a^{*}b+b^{*}a\leq a^{*}Pa+b^{*}P^{-1}b\).

The following modulus inequalities of complex numbers play a central role for the results of the paper.

Lemma 2

Suppose \(A\in\mathbb{C}^{n\times n}\), \(\check{A}=(\check{a}_{ij})_{n \times n}\in\mathbb{C}^{n\times n}\), \(\hat{A}=(\hat{a}_{ij})_{n \times n}\in\mathbb{C}^{n\times n}\), and \(\check{A}\preceq A\preceq \hat{A}\). Then, for any \(x,y\in\mathbb{C}^{n}\), the following inequalities hold:

$$\begin{aligned}& x^{*}A^{*}Ax\leq \vert x \vert ^{*} \vert A \vert ^{*} \vert A \vert \vert x \vert \leq \vert x \vert ^{*}\tilde{A}^{*} \tilde{A} \vert x \vert , \end{aligned}$$
(5)

where \(\tilde{A}=(\tilde{a}_{ij})_{n\times n}\), \(\tilde{a}_{ij}= \max\{ \vert \check{a}_{ij} \vert , \vert \hat {a}_{ij} \vert \}\).

Proof

By Cauchy–Schwarz inequality, the modulus inequalities (5) can be obtained. The proof is direct so we omit the details. □

Lemma 3

([39])

A given Hermitian matrix

$$ S= \begin{pmatrix} S_{11} & S_{12} \\ S_{21} & S_{22} \end{pmatrix} < 0, $$

where \(S_{11}^{*}=S_{11}\), \(S_{12}^{*}=S_{21}\) and \(S_{22}^{*}=S_{22}\), is equivalent to any one of the following conditions:

  1. (i)

    \(S_{22}<0\) and \(S_{11}-S_{12}S_{22}^{-1}S_{21}<0\),

  2. (ii)

    \(S_{11}<0\) and \(S_{22}-S_{21}S_{11}^{-1}S_{12}<0\).

Lemma 4

([39])

If \(H(z):\mathbb{C}^{n}\to\mathbb{C}^{n}\) is a continuous map and satisfies the following conditions:

  1. (i)

    \(H(z)\) is injective on \(\mathbb{C}^{n}\),

  2. (ii)

    \(\lim_{ \Vert z \Vert \to\infty} \Vert H(z) \Vert =\infty\),

then \(H(z)\) is a homeomorphism of \(\mathbb{C}^{n}\) onto itself.

3 Existence and uniqueness of equilibrium point

In this section, we will derive sufficient conditions for the existence and uniqueness of equilibrium point of system (2). An equilibrium solution of (2) is a constant complex vector \(\check{z}\in\mathbb{C}^{n}\) which satisfies

$$ -D\check{z}+Af(\check{z})+Bf(\check{z})+Cf(\check{z})+J=0, $$
(6)

when the impulsive jumps \(I_{k}(\cdot)\) as assumed to satisfy \(I_{k}(\check{z})=0\), \(k=1,2,\ldots\) .

Hence, to prove the existence and uniqueness of a solution of (6), it suffices to show that the following map \(\mathcal{H}:\mathbb{C}^{n}\to\mathbb{C}^{n}\) has a unique zero point,

$$ \mathcal{H}(z)=-Dz+Af(z)+Bf(z)+Cf(z)+J. $$
(7)

Obviously, the existence of a zero point for \(\mathcal{H}\) can be investigated via the homeomorphic mapping principle.

Theorem 1

For the CVNNs defined by (2), assume that the network parameters and the activation function satisfy conditions (\(\mathbf{H}_{1}\)), (\(\mathbf{H}_{2}\)) and (\(\mathbf{H}_{3}\)). Then the neural network (2) has a unique equilibrium point for every input vector \(J=(J_{1},J_{2},\ldots,J_{n})^{T}\in\mathbb{C}^{n}\), if there exist two real positive diagonal matrices U and V such that the linear matrix inequality (LMI) holds:

$$ \begin{pmatrix} -\check{D}U-U\check{D}+\Gamma V\Gamma& U(\tilde{A}+\tilde{B}+ \tilde{C}) \\ (\tilde{A}^{*}+\tilde{B}^{*}+\tilde{C}^{*})U & -V \end{pmatrix} < 0, $$
(8)

where \(\tilde{A}=(\tilde{a}_{ij})_{n\times n}\), \(\tilde{B}=(\tilde{b} _{ij})_{n\times n}\), \(\tilde{C}=(\tilde{c}_{ij})_{n\times n}\), \(\tilde{a}_{ij}=\max\{ \vert \check{a}_{ij} \vert , \vert \hat{a}_{ij} \vert \}\), \(\tilde{b} _{ij}=\max\{ \vert \check{b}_{ij} \vert , \vert \hat {b}_{ij} \vert \}\) and \(\tilde{c}_{ij}= \max\{ \vert \check{c}_{ij} \vert , \vert \hat {c}_{ij} \vert \}\).

Proof

To prove the existence and uniqueness of system (2), it suffices to show \(\mathcal{H}(z)\) is a homeomorphism of \(\mathbb{C} ^{n}\) onto itself by using the homeomorphic mapping theorem on complex domain.

First, we prove that \(\mathcal{H}(z)\) is an injective map on \(\mathbb{C}^{n}\). Suppose that there exist \(z,\tilde{z}\in\mathbb{C} ^{n}\) with \(z\neq\tilde{z}\), such that \(\mathcal{H}(z)=\mathcal{H}( \tilde{z})\). Then we can write

$$ \mathcal{H}(z)-\mathcal{H}(\tilde{z})=-D(z-\tilde{z})+(A+B+C) \bigl(f(z)-f( \tilde{z}) \bigr)=0. $$
(9)

Multiplying both sides of (9) by \((z-\tilde{z})^{*}U\), we can obtain

$$ 0= -(z-\tilde{z})^{*}U D(z-\tilde{z})+(z- \tilde{z})^{*}U(A+B+C) \bigl(f(z)-f( \tilde{z}) \bigr). $$
(10)

Then, taking the conjugate transpose of (10) leads to

$$ 0= -(z-\tilde{z})^{*} D U^{*} (z- \tilde{z})+ \bigl(f(z)-f(\tilde{z}) \bigr)^{*} \bigl(A ^{*}+B^{*}+C^{*} \bigr)U^{*}(z- \tilde{z}). $$
(11)

Summing (10) and (11), applying Lemmas 1 and 2, we have

$$\begin{aligned} 0 &= -(z-\tilde{z})^{*}(UD+DU) (z-\tilde{z}) \\ &\quad{}+(z-\tilde{z})^{*}U(A+B+C) \bigl(f(z)-f(\tilde{z}) \bigr) \\ &\quad{}+ \bigl(f(z)-f(\tilde{z}) \bigr)^{*} \bigl(A^{*}+B^{*}+C^{*} \bigr)U(z-\tilde{z}) \\ &\leq-(z-\tilde{z})^{*}(U D+D U) (z-\tilde{z}) \\ &\quad{}+(z-\tilde{z})^{*}U(A+B+C)V^{-1} \bigl(A^{*}+B^{*}+C^{*} \bigr)U(z- \tilde{z}) \\ &\quad{}+ \bigl(f(z)-f(\tilde{z}) \bigr)^{*}V \bigl(f(z)-f(\tilde{z}) \bigr) \\ &\leq \vert z-\tilde{z} \vert ^{*} \bigl[-\check{D}U-U\check {D}+U(\tilde{A}+ \tilde{B}+\tilde{C})V^{-1} \bigl(\tilde{A}^{*}+ \tilde{B}^{*}+\tilde{C}^{*} \bigr)U \bigr] \vert z- \tilde{z} \vert \\ &\quad{}+ \bigl(f(z)-f(\tilde{z}) \bigr)^{*}V \bigl(f(z)-f(\tilde{z}) \bigr). \end{aligned}$$
(12)

Since V is a positive diagonal matrix, from assumption (\(\mathbf{H}_{2}\)), we can get

$$\begin{aligned} \bigl(f(z)-f(\tilde{z}) \bigr)^{*}V \bigl(f(z)-f( \tilde{z}) \bigr) &\leq(z-\tilde{z})^{*} \Gamma V\Gamma(z-\tilde{z}) \\ &= \vert z-\tilde{z} \vert ^{*} \Gamma V\Gamma \vert z- \tilde{z} \vert . \end{aligned}$$
(13)

It follows from (12) and (13) that

$$ 0\leq \vert z-\tilde{z} \vert ^{*} \Upsilon \vert z-\tilde{z} \vert , $$
(14)

where \(\Upsilon=-\check{D}U-U\check{D}+\Gamma V\Gamma+U(\tilde{A}+ \tilde{B}+\tilde{C})V^{-1}(\tilde{A}^{*}+\tilde{B}^{*}+\tilde{C}^{*})U\). From Lemma 3 and the LMI (8), we can see that \(\Upsilon< 0\). Then \(z-\tilde{z}=0\) from (14). Therefore, \(\mathcal{H}(z)\) is an injective map on \(\mathbb{C}^{n}\).

Second, we prove \(\Vert \mathcal{H}(z) \Vert \to\infty\) as \(\Vert z \Vert \to\infty \). Let \(\widetilde{\mathcal{H}}(z)=\mathcal{H}(z)-\mathcal{H}(0)\). By Lemma 1 and 2, we have

$$\begin{aligned}& z^{*}U\widetilde{\mathcal{H}}(z)+ \widetilde{\mathcal{H}}(z)^{*}Uz \\& \quad = -z^{*}(UD+DU)z +z^{*}U(A+B+C) \bigl(f(z)-f(0) \bigr) \\& \quad \quad{}+ \bigl(f(z)-f(0) \bigr)^{*} \bigl(A^{*}+B^{*}+C^{*} \bigr)Uz \\& \quad \leq-z^{*}(UD+DU)z \\& \quad \quad{}+z^{*}U(A+B+C)V^{-1} \bigl(A^{*}+B^{*}+C^{*} \bigr)Uz \\& \quad \quad{}+ \bigl(f(z)-f(0) \bigr)^{*}V \bigl(f(z)-f(0) \bigr) \\& \quad \leq \vert z \vert ^{*} \bigl[-\check{D}U-U\check{D}+U(\tilde {A}+\tilde{B}+ \tilde{C})V^{-1} \bigl(\tilde{A}^{*}+ \tilde{B}^{*}+\tilde{C}^{*} \bigr)U \bigr] \vert z \vert + \vert z \vert ^{*} \Gamma V\Gamma \vert z \vert \\& \quad \leq \vert z \vert ^{*} \Upsilon \vert z \vert \leq- \lambda_{\min}(-\Upsilon) \Vert z \Vert ^{2}. \end{aligned}$$

An application of the Cauchy–Schwartz inequality yields

$$ \lambda_{\min}(-\Upsilon) \Vert z \Vert ^{2}\leq2 \bigl\Vert z^{*} \bigr\Vert \Vert U \Vert \bigl\Vert \widetilde{ \mathcal{H}}(z) \bigr\Vert . $$

When \(z\neq0\), we have

$$ \bigl\Vert \widetilde{\mathcal{H}}(z) \bigr\Vert \geq\frac{\lambda _{\min}(- \Upsilon) \Vert z \Vert }{2 \Vert U \Vert }. $$

Therefore, \(\Vert \widetilde{\mathcal{H}}(z) \Vert \to\infty \) as \(\Vert z \Vert \to\infty\), which implies \(\Vert \mathcal{H}(z) \Vert \to \infty\) as \(\Vert z \Vert \to\infty\). From Lemma 4, we know that \(\mathcal{H}(z)\) is a homeomorphism of \(\mathbb{C}^{n}\). Thus, the system (2) has a unique equilibrium point. The proof is completed. □

4 Global robust stability results

In the preceding section, we have shown the existence and uniqueness of the equilibrium point for system (2). In this section, to investigate the global robust stability of the unique equilibrium point, we should give the following assumption for the impulsive operators:

(\(\mathbf{H}_{4}\)):

For \(i=1,2,\ldots,n\) and \(k=1,2,\ldots\) , the impulse operator \(I_{ik}(\cdot)\) satisfies

$$ I_{ik} \bigl(z_{i} \bigl(t_{k}^{-} \bigr) \bigr) = -\delta_{ik} \bigl(z_{i} \bigl(t_{k}^{-} \bigr)-\check{z} _{i} \bigr), $$

where \(\delta_{ik}\in[0,2]\) is a real constant, and \(\check{z}_{i}\) is the ith component of the equilibrium point \(\check{z}=(\check{z} _{1},\check{z}_{2},\ldots,\check{z}_{n})^{T}\).

Remark 2

For (\(\mathbf{H}_{4}\)), the assumption can guarantee that the impulse is zero at the equilibrium point, i.e., \(I_{ik}(\check{z})=0\), which is one of the necessary conditions such that the equilibrium point is asymptotically robust stable.

Theorem 2

Suppose the conditions (\(\mathbf{H}_{1}\)), (\(\mathbf{H}_{2}\)) and (\(\mathbf{H}_{3}\)) are satisfied. There exist four real positive diagonal matrices P, Q, R and S such that the following LMI holds:

$$ \Omega= \begin{pmatrix} \Omega_{11} & P\tilde{A} & P\tilde{B} & P\tilde{C} \\ \star& -S & 0 & 0 \\ \star& \star& -Q & 0 \\ \star& \star& \star& -R \end{pmatrix} < 0, $$
(15)

where \(\Omega_{11}=-\check{D}P-P\check{D}+\Gamma(S+Q+R)\Gamma\), \(\tilde{A}=(\tilde{a}_{ij})_{n\times n}\), \(\tilde{B}=(\tilde{b}_{ij})_{n \times n}\), \(\tilde{C}=(\tilde{c}_{ij})_{n\times n}\), \(\tilde{a}_{ij}= \max\{ \vert \check{a}_{ij} \vert , \vert \hat {a}_{ij} \vert \}\), \(\tilde{b}_{ij}=\max\{ \vert \check{b}_{ij} \vert , \vert \hat{b}_{ij} \vert \}\) and \(\tilde{c}_{ij}=\max\{ \vert \check{c}_{ij} \vert , \vert \hat{c}_{ij} \vert \}\). Then (2) has a unique equilibrium point ž. Furthermore, if the condition (\(\mathbf{H}_{4}\)) is satisfied, the equilibrium point ž is globally asymptotically robust stable.

Proof

The theorem will be proved in two steps.

Step 1: We will show system (2) has a unique equilibrium point under LMI (15) by the matrix congruence method. Let

$$\begin{aligned}& \Omega_{1}= \begin{pmatrix} \Omega_{11} & P(\tilde{A}+\tilde{B}+\tilde{C}) & P\tilde{B} & P \tilde{C} \\ \star& -S-Q-R & -Q & -R \\ \star& \star& -Q & 0 \\ \star& \star& \star& -R \end{pmatrix} , \\& \Omega_{2}= \begin{pmatrix} \Omega_{11} & P(\tilde{A}+\tilde{B}+\tilde{C}) \\ \star& -S-Q-R \end{pmatrix} , \quad\quad T = \begin{pmatrix} I & 0 & 0 & 0 \\ 0 & I & 0 & 0 \\ 0 & I & I & 0 \\ 0 & I & 0 & I \end{pmatrix} , \end{aligned}$$

where I is an identity matrix of order n. It should be noted that T is invertible and

$$ \Omega_{1} = T^{*}\Omega T. $$

Thus \(\Omega_{1}\) and Ω are congruent, which means that \(\Omega_{1}\) is negative definite since Ω is negative definite. It should be also noted that \(\Omega_{2}\) is a principal submatrix of \(\Omega_{1}\). Therefore \(\Omega_{2}\) is negative definite, i.e.,

$$ \Omega_{2}< 0. $$
(16)

Based on (16), we can see that there exist \(U=P>0\) and \(V=S+Q+R>0\) such that LMI (8) holds. Consequently, system (2) has a unique equilibrium point ž by Theorem 1.

Step 2: We will show the equilibrium point ž is globally robust stable by Lyapunov’s direct method. For convenience, we shift the equilibrium to origin by letting \(\tilde{z}(t)=z(t)-\check{z}\), and then the system (2) can be transformed into

$$ \textstyle\begin{cases} \dot{\tilde{z}}(t)=-D\tilde{z}(t)+A g(\tilde{z}(t))+B g(\tilde{z}(t- \tau))+C\int_{-\infty}^{t} K(t-s)g(\tilde{z}(s))\,\mathrm{d}s, \\ \Delta\tilde{z}(t)= \tilde{I}(\tilde{z}(t_{k}^{-})), \quad k=1,2,\ldots, \end{cases} $$
(17)

where \(g(\tilde{z}(t))=f(z(t))-f(\check{z})\) and \(\tilde{I}(\tilde{z}(t _{k}^{-}))=-\delta_{ik}\tilde{z}_{i}(t_{k}^{-})\). Meanwhile the initial condition (4) can be transformed into

$$ \tilde{z}(s)=\tilde{\varphi}(s), \quad s\in(-\infty,0], $$
(18)

where \(\tilde{\varphi}(s)=\varphi(s)-\check{z}\in C((-\infty,0], \mathbb{C}^{n})\).

Let \(P=\mathrm{diag}\{p_{1},p_{2},\ldots,p_{n}\}\), \(Q=\mathrm{diag}\{q_{1},q _{2},\ldots,q_{n}\}\) and \(R=\mathrm{diag}\{r_{1},r_{2},\ldots,r_{n} \}\). Consider the following Lyapunov–Krasovskii functional candidate:

$$ V \bigl(\tilde{z}(t) \bigr)=V_{1} \bigl(\tilde{z}(t) \bigr)+V_{2} \bigl(\tilde{z}(t) \bigr)+V_{3} \bigl( \tilde{z}(t) \bigr), $$
(19)

where

$$\begin{aligned}& V_{1} \bigl(\tilde{z}(t) \bigr)= \sum_{j=1}^{n} p_{j} \tilde{z}^{*}_{j}(t) \tilde{z}_{j}(t), \end{aligned}$$
(20)
$$\begin{aligned}& V_{2} \bigl(\tilde{z}(t) \bigr)= \sum_{j=1}^{n} q_{j} \int_{t-\tau_{j}}^{t} g^{*} _{j} \bigl( \tilde{z}_{j}(t) \bigr)g_{j} \bigl(\tilde{z}_{j}(t) \bigr) \,\mathrm{d}t, \end{aligned}$$
(21)
$$\begin{aligned}& V_{3} \bigl(\tilde{z}(t) \bigr)= \sum_{j=1}^{n} r_{j} \int_{0}^{\infty}k_{j}(s) \int_{t-s}^{t} g^{*}_{j} \bigl( \tilde{z}_{j}(t) \bigr)g_{j} \bigl(\tilde{z}_{j}(t) \bigr) \,\mathrm{d}t\,\mathrm{d}s. \end{aligned}$$
(22)

When \(t\neq t_{k}\), \(k=1,2,\ldots\) , calculating the upper right derivative of V along the solution of (17), applying Lemmas 1 and 2, we get

$$\begin{aligned}& D^{+}V_{1} \bigl(\tilde{z}(t) \bigr) = \dot{ \tilde{z}}^{*}(t)P\tilde{z}(t)+ \tilde{z}^{*}(t)P\dot{ \tilde{z}}(t) \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}=-\tilde{z}^{*}(t)DP\tilde{z}(t)-\tilde{z}^{*}(t)PD \tilde{z}(t)+g ^{*} \bigl(\tilde{z}(t) \bigr)A^{*}P \tilde{z}(t) \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\quad{}+\tilde{z}^{*}(t)PAg \bigl(\tilde{z}(t) \bigr)+g^{*} \bigl(\tilde{z}(t-\tau) \bigr)B ^{*}P\tilde{z}(t) \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\quad{}+\tilde{z}^{*}(t)PBg \bigl(\tilde{z}(t-\tau) \bigr)+ \biggl[ \int_{-\infty }^{t} K(t-s)g \bigl(\tilde{z}(s) \bigr) \, \mathrm{d}s \biggr]^{*} C^{*}P\tilde{z}(t) \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\quad{}+\tilde{z}^{*}(t)PC \biggl[ \int_{-\infty}^{t} K(t-s)g \bigl( \tilde{z}(s) \bigr) \, \mathrm{d}s \biggr] \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\leq-\tilde{z}^{*}(t) (DP+PD)\tilde{z}(t)+g^{*} \bigl( \tilde{z}(t) \bigr) S g \bigl( \tilde{z}(t) \bigr)+\tilde{z}^{*}(t)PAS^{-1}A^{*}P \tilde{z}(t) \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\quad{}+g^{*} \bigl(\tilde{z}(t-\tau) \bigr)Q g \bigl(\tilde{z}(t- \tau) \bigr)+\tilde{z} ^{*}(t)PBQ^{-1}B^{*}P \tilde{z}(t) \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\quad{}+ \biggl[ \int_{-\infty}^{t} K(t-s)g \bigl(\tilde{z}(s) \bigr) \, \mathrm{d}s \biggr]^{*} R \biggl[ \int_{-\infty}^{t} K(t-s)g \bigl(\tilde{z}(s) \bigr) \, \mathrm{d}s \biggr] \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\quad{}+\tilde{z}^{*}(t) PCR^{-1}C^{*}P \tilde{z}(t) \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\leq \bigl\vert \tilde{z}(t) \bigr\vert ^{*} \bigl(-DP-PD+\Gamma S\Gamma +PAS^{-1}A^{*}P+PBQ ^{-1}B^{*}P \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\quad{}+PCR^{-1}C^{*}P \bigr) \bigl\vert \tilde{z}(t) \bigr\vert +g^{*} \bigl(\tilde{z}(t-\tau) \bigr)Q g \bigl( \tilde{z}(t- \tau) \bigr) \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\quad{}+ \biggl[ \int_{-\infty}^{t} K(t-s)g \bigl(\tilde{z}(s) \bigr) \, \mathrm{d}s \biggr]^{*} R \biggl[ \int_{-\infty}^{t} K(t-s)g \bigl(\tilde{z}(s) \bigr) \, \mathrm{d}s \biggr] \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\leq \bigl\vert \tilde{z}(t) \bigr\vert ^{*} \bigl(-\check{D}P-P \check {D}+\Gamma S\Gamma+P \tilde{A}S^{-1}\tilde{A}^{*}P+P \tilde{B}Q^{-1}\tilde{B}^{*}P \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\quad{}+P\tilde{C}R^{-1}\tilde{C}^{*}P \bigr) \bigl\vert \tilde{z}(t) \bigr\vert +g^{*} \bigl( \tilde{z}(t-\tau) \bigr)Q g \bigl( \tilde{z}(t-\tau) \bigr) \\& \hphantom{D^{+}V_{1} \bigl(\tilde{z}(t) \bigr)}\quad{}+ \biggl[ \int_{-\infty}^{t} K(t-s)g \bigl(\tilde{z}(s) \bigr) \, \mathrm{d}s \biggr]^{*} R \biggl[ \int_{-\infty}^{t} K(t-s)g \bigl(\tilde{z}(s) \bigr) \, \mathrm{d}s \biggr], \end{aligned}$$
(23)
$$\begin{aligned}& \begin{aligned}[b] D^{+}V_{2} \bigl(\tilde{z}(t) \bigr) &= g^{*} \bigl(\tilde{z}(t) \bigr)Qg \bigl(\tilde{z}(t) \bigr)-g^{*} \bigl( \tilde{z}(t-\tau) \bigr)Qg \bigl(\tilde{z}(t-\tau) \bigr) \\ &\leq \bigl\vert \tilde{z}(t) \bigr\vert ^{*}\Gamma Q\Gamma \bigl\vert \tilde{z}(t) \bigr\vert -g^{*} \bigl( \tilde{z}(t-\tau) \bigr)Qg \bigl(\tilde{z}(t-\tau) \bigr), \end{aligned} \end{aligned}$$
(24)
$$\begin{aligned}& \begin{aligned}[b] D^{+}V_{3} \bigl(\tilde{z}(t) \bigr) &= \sum _{j=1}^{n} r_{j} \int_{0}^{+\infty}k _{j}(s)g_{j}^{*} \bigl(\tilde{z}(t) \bigr)g_{j} \bigl(\tilde{z}(t) \bigr)\,\mathrm{d}s \\ &\quad{}-\sum_{j=1}^{n} r_{j} \int_{0}^{+\infty}k_{j}(s)g_{j}^{*} \bigl( \tilde{z}(t-s) \bigr)g_{j} \bigl(\tilde{z}(t-s) \bigr)\, \mathrm{d}s \\ &= g^{*} \bigl(\tilde{z}(t) \bigr)Rg \bigl(\tilde{z}(t) \bigr) \\ &\quad{}-\sum_{j=1}^{n} r_{j} \int_{0}^{+\infty}k_{j}(s)\,\mathrm{d}s \int _{0}^{+\infty}k_{j}(s)g_{j}^{*} \bigl(\tilde{z}(t-s) \bigr)g_{j} \bigl(\tilde{z}(t-s) \bigr) \, \mathrm{d}s \\ &\leq \bigl\vert \tilde{z}(t) \bigr\vert ^{*}\Gamma R\Gamma \bigl\vert \tilde{z}(t) \bigr\vert \\ &\quad{}-\sum_{j=1}^{n} r_{j} \int_{0}^{+\infty}k_{j}(s)g_{j}^{*} \bigl( \tilde{z}(t-s) \bigr)\,\mathrm{d}s \int_{0}^{+\infty}k_{j}(s)g_{j} \bigl(\tilde{z}(t-s) \bigr) \,\mathrm{d}s \\ &= \bigl\vert \tilde{z}(t) \bigr\vert ^{*}\Gamma R\Gamma \bigl\vert \tilde{z}(t) \bigr\vert \\ &\quad{}- \biggl[ \int_{0}^{+\infty}k(s)g \bigl(\tilde{z}(t-s) \bigr) \, \mathrm{d}s \biggr]^{*}R \biggl[ \int_{0}^{+\infty}k(s)g \bigl(\tilde{z}(t-s) \bigr) \, \mathrm{d}s \biggr]. \end{aligned} \end{aligned}$$
(25)

It follows from (23), (24) and (25) that

$$ D^{+}V \bigl(\tilde{z}(t) \bigr)\leq \bigl\vert \tilde{z}(t) \bigr\vert ^{*}\Sigma \bigl\vert \tilde{z}(t) \bigr\vert , $$

where

$$ \Sigma=-\check{D}P-P\check{D}+\Gamma S\Gamma+\Gamma Q\Gamma+\Gamma R\Gamma+P \tilde{A}S^{-1}\tilde{A}^{*}P+P\tilde{B}Q^{-1} \tilde{B}^{*}P+P \tilde{C}R^{-1}\tilde{C}^{*}P. $$

By LMI (15) and Lemma 3, we can deduce that \(\Sigma\leq0\). Then

$$ D^{+}V \bigl(\tilde{z}(t) \bigr)\leq0, \quad t\neq t_{k}. $$
(26)

When \(t=t_{k}\), \(k=1,2,\ldots\) , it should be noted that \(V_{2}(t_{k})=V _{2}(t_{k}^{-})\) and \(V_{3}(t_{k})=V_{3}(t_{k}^{-})\). Then we can compute

$$\begin{aligned} V \bigl(\tilde{z}(t_{k}) \bigr)-V \bigl(\tilde{z} \bigl(t_{k}^{-} \bigr) \bigr) & = \sum _{j=1}^{n} p_{j} \tilde{z}^{*}_{j}(t_{k}) \tilde{z}_{j}(t_{k})-\sum_{j=1}^{n} p_{j} \tilde{z}^{*}_{j} \bigl(t_{k}^{-} \bigr)\tilde{z}_{j} \bigl(t_{k}^{-} \bigr) \\ &= \sum_{j=1}^{n} (1-\delta_{jk})^{2} p_{j} \tilde{z}^{*}_{j} \bigl(t_{k} ^{-} \bigr)\tilde{z}_{j} \bigl(t_{k}^{-} \bigr)-\sum_{j=1}^{n} p_{j} \tilde{z}^{*}_{j} \bigl(t _{k}^{-} \bigr) \tilde{z}_{j} \bigl(t_{k}^{-} \bigr) \\ &\leq0. \end{aligned}$$
(27)

It follows from (26) and (27) that \(V(t)\) is non-increasing for \(t\geq0\). According to assumption (\(\mathbf{H}_{3}\)), we can let \(\int_{0}^{+\infty}sk(s)\,\mathrm{d}s=\beta\), where β is a non-negative real constant. Then, by definition of \(V(t)\), we can infer

$$\begin{aligned} V \bigl(\tilde{z}(t) \bigr) &\leq V \bigl(\tilde{z}(0) \bigr)= V_{1} \bigl(\tilde{z}(0) \bigr)+V_{2} \bigl( \tilde{z}(0) \bigr)+V_{3} \bigl(\tilde{z}(0) \bigr) \\ & = \sum_{j=1}^{n} p_{j} \tilde{z}^{*}_{j}(0)\tilde{z}_{j}(0)+\sum _{j=1}^{n} q_{j} \int_{-\tau_{j}}^{0} g^{*}_{j} \bigl( \tilde{z}_{j}(t) \bigr)g_{j} \bigl( \tilde{z}_{j}(t) \bigr) \,\mathrm{d}t \\ &\quad{}+ \sum_{j=1}^{n} r_{j} \int_{0}^{\infty}k_{j}(s) \int_{-s} ^{0} g^{*}_{j} \bigl( \tilde{z}_{j}(t) \bigr)g_{j} \bigl( \tilde{z}_{j}(t) \bigr) \,\mathrm{d}t\,\mathrm{d}s \\ &\leq\sum_{j=1}^{n} p_{j} \bigl\vert \tilde{\varphi}_{j}(0) \bigr\vert ^{2}+\sum _{j=1} ^{n} q_{j} \gamma_{j}^{2} \int_{-\tau_{j}}^{0} \bigl\vert \tilde{ \varphi}_{j}(t) \bigr\vert ^{2} \,\mathrm{d}t \\ &\quad{}+ \sum_{j=1}^{n} r_{j} \gamma_{j}^{2} \int_{0}^{\infty}k_{j}(s) \int_{-s}^{0} \bigl\vert \tilde{ \varphi}_{j}(t) \bigr\vert ^{2} \,\mathrm{d}t\,\mathrm{d}s \\ &\leq\sum_{j=1}^{n} \bigl(p_{j}+ \rho q_{j}\gamma_{j}^{2}+\beta r_{j} \gamma_{j}^{2} \bigr)\sup_{t\in(-\infty,0]}\sum _{j=1}^{n} \bigl\vert \tilde{ \varphi}_{j}(t) \bigr\vert ^{2} \\ &=\sum_{j=1}^{n} \bigl(p_{j}+ \rho q_{j}\gamma_{j}^{2}+\beta r_{j} \gamma _{j}^{2} \bigr) \bigl\Vert \tilde{\varphi}(t) \bigr\Vert ^{2}. \end{aligned}$$
(28)

On the other hand, by the definition of \(V(\tilde{z}(t))\), we have

$$ V \bigl(\tilde{z}(t) \bigr)\geq V_{1} \bigl( \tilde{z}(t) \bigr)\geq\sum_{j=1}^{n} p_{j} \bigl\Vert \tilde{z}(t) \bigr\Vert ^{2}, \quad t \geq0. $$
(29)

From (28) and (29), we obtain

$$ \bigl\Vert \tilde{z}(t) \bigr\Vert \leq\sqrt{\frac{\sum_{j=1}^{n} (p_{j}+\tau q_{j} \gamma_{j}^{2}+\beta r_{j}\gamma_{j}^{2})}{\sum_{j=1}^{n} p_{j}}} \bigl\Vert \tilde{\varphi}(t) \bigr\Vert , $$

from which it can be concluded that the origin of (17), or equivalently the equilibrium point of system (2), is globally asymptotically robust stable by standard Lyapunov theorem. □

If the impulsive operator \(I(\cdot)\equiv0\) in (2), we get the following complex-valued neural networks without impulses:

$$ \dot{z}(t)=-D z(t)+A f \bigl(z(t) \bigr)+B f \bigl(z(t-\tau) \bigr)+C \int_{-\infty}^{t} K(t-s)f \bigl(z(s) \bigr) \, \mathrm{d}s+J, $$
(30)

where D, A, B, C, J and \(f(\cdot)\) are defined as same as in (2). According to Theorem 2, we can obtain the following corollary on the global robust stability conditions of (30).

Corollary 1

Suppose the conditions (\(\mathbf{H}_{1}\)), (\(\mathbf{H}_{2}\)) and (\(\mathbf{H}_{3}\)) are satisfied. There exist four real positive diagonal matrices P, Q, R and S such that the LMI (15) holds. Then system (30) has a unique equilibrium point which is globally asymptotically robust stable.

If the impulsive operator \(I(\cdot)\equiv0\) and \(C\equiv0\) in (2), we get the following complex-valued neural networks with discrete time delays:

$$ \dot{z}(t)=-D z(t)+A f \bigl(z(t) \bigr)+B f \bigl(z(t-\tau) \bigr)+J, $$
(31)

where D, A, B, J and \(f(\cdot)\) are defined as same as in (2). According to Theorem 2, we can obtain the following corollary on the global robust stability conditions of (31).

Corollary 2

Suppose the conditions (\(\mathbf{H}_{1}\)) and (\(\mathbf{H}_{2}\)) are satisfied. There exist three real positive diagonal matrices P, Q and S such that the following LMI holds:

$$ \Omega= \begin{pmatrix} \Omega_{11} & P\tilde{A} & P\tilde{B} \\ \star& -S & 0 \\ \star& \star& -Q \end{pmatrix} < 0, $$
(32)

where \(\Omega_{11}=-\check{D}P-P\check{D}+\Gamma(S+Q)\Gamma\), \(\tilde{A}=(\tilde{a}_{ij})_{n\times n}\), \(\tilde{B}=(\tilde{b}_{ij})_{n \times n}\), \(\tilde{a}_{ij}=\max\{ \vert \check{a}_{ij} \vert , \vert \hat{a}_{ij} \vert \}\) and \(\tilde{b}_{ij}=\max\{ \vert \check{b}_{ij} \vert , \vert \hat{b}_{ij} \vert \}\). Then system (31) has a unique equilibrium point which is globally asymptotically robust stable.

If \(\check{D}=D=\hat{D}\), \(\check{A}=A=\hat{A}\), \(\check{B}=D=\hat{B}\), \(\check{C}=C=\hat{C}\) and \(\check{J}=J=\hat{J}\) in condition (\(\mathbf{H}_{1}\)), the asymptotical robust stability will reduced to the asymptotical stability by Definition 2. Therefore, according to Corollaries 1 and 2, we can obtain the following corollaries on the global asymptotical stability conditions of (30) and (31).

Corollary 3

Suppose the conditions (\(\mathbf{H}_{2}\)) and (\(\mathbf{H}_{3}\)) are satisfied. There exist four real positive diagonal matrices P, Q, R and S such that the following LMI holds:

$$ \Omega= \begin{pmatrix} \Omega_{11} & P \vert A \vert & P \vert B \vert & P \vert C \vert \\ \star& -S & 0 & 0 \\ \star& \star& -Q & 0 \\ \star& \star& \star& -R \end{pmatrix} < 0, $$
(33)

where \(\Omega_{11}=-DP-PD+\Gamma(S+Q+R)\Gamma\). Then system (30) has a unique equilibrium point, which is globally asymptotically stable.

Corollary 4

Suppose the condition (\(\mathbf{H}_{2}\)) is satisfied. There exist three real positive diagonal matrices P, Q and S such that the following LMI holds:

$$ \Omega= \begin{pmatrix} \Omega_{11} & P \vert A \vert & P \vert B \vert \\ \star& -S & 0 \\ \star& \star& -Q \end{pmatrix} < 0, $$
(34)

where \(\Omega_{11}=-DP-PD+\Gamma(S+Q)\Gamma\). Then system (31) has a unique equilibrium point which is globally asymptotically stable.

Remark 3

In [40, 41], the criteria for stability of CVNNs are expressed in terms of complex-valued LMIs. As pointed out in [40], the complex-valued LMIs cannot be solved by MATLAB LMI Toolbox straightforwardly. An feasible approach is to convert complex-valued LMIs to real-valued ones but this could double the dimension of the LMIs. In this paper, we express the stability criteria for CVNNs directly by terms of real-valued LMIs, which can be solved by MATLAB LMI Toolbox straightforwardly.

Remark 4

In [15], the authors investigate the problem of global robust stability of complex-valued recurrent neural networks with time delays and uncertainties. In Theorem 3.4 of [15], to check robust stability of complex-valued neural networks, the boundedness of activation function \(f_{i}\) is required. However, in this paper, the boundedness condition is removed. See in Example 1 of next section the activation function \(f_{i}\) is unbounded.

5 Numerical examples

In this section, we will give two numerical examples to demonstrate the effectiveness and superiority of our results.

Example 1

Assume that the network parameters of system (2) are given as follows:

$$\begin{aligned}& \check{D}= \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix} ,\quad\quad \check{A}= \begin{pmatrix} -3.2-2.4{\mathrm{i}}& -1.8-2.4{\mathrm{i}} \\ -2.4-1.8{\mathrm{i}}& -1.6-1.2{\mathrm{i}} \end{pmatrix} , \\& \hat{A}= \begin{pmatrix} 3.2+2.4{\mathrm{i}}& 1.8+2.4{\mathrm{i}} \\ 2.4+1.8{\mathrm{i}}& 1.2+1.6{\mathrm{i}} \end{pmatrix} ,\quad\quad \check{B}= \begin{pmatrix} -2.4 - 1.8{\mathrm{i}}& -1.6 - 1.2{\mathrm{i}} \\ -1.8 - 2.4{\mathrm{i}}& -2.4 - 1.8{\mathrm{i}} \end{pmatrix} , \\& \hat{B}= \begin{pmatrix} 2.4 + 1.8{\mathrm{i}}& 1.2 + 1.6{\mathrm{i}} \\ 1.8 + 2.4{\mathrm{i}}& 2.4 + 1.8{\mathrm{i}} \end{pmatrix} ,\quad\quad \check{C}= \begin{pmatrix} -1.08 - 1.44{\mathrm{i}}& -0.6 - 0.8{\mathrm{i}} \\ -1.6 - 1.2{\mathrm{i}}& -1.2 - 1.6{\mathrm{i}} \end{pmatrix} , \\& \hat{C}= \begin{pmatrix} 1.08 + 1.44{\mathrm{i}}& 0.8 + 0.6{\mathrm{i}} \\ 1.2 + 1.6{\mathrm{i}}& 1.6 + 1.2{\mathrm{i}} \end{pmatrix} ,\quad\quad \Gamma= \begin{pmatrix} 0.2 & 0 \\ 0 & 0.2 \end{pmatrix} . \end{aligned}$$

Moreover, the activation functions \(f_{1}(\cdot)\) and \(f_{2}(\cdot)\) satisfy assumption (\(\mathbf{H}_{2}\)) with \(\Gamma= \bigl({\scriptsize\begin{matrix}{} 0.2 & 0 \cr 0 & 0.2 \end{matrix}}\bigr) \), the delay kernel functions \(k_{1}(\cdot)\) and \(k_{2}(\cdot)\) satisfy assumption (\(\mathbf{H}_{3}\)), and the impulsive functions \(I_{1k}(\cdot)\) and \(I_{2k}(\cdot)\) satisfy assumption (\(\mathbf{H}_{4}\)) for \(k=1,2,\ldots\) .

Using the matrices Ǎ, Â, B̌ and B̂, we obtain the following matrices:

$$\begin{aligned}& \tilde{A}= \begin{pmatrix} 4 & 3 \\ 3 & 2 \end{pmatrix} ,\quad\quad \tilde{B}= \begin{pmatrix} 3 & 2 \\ 3 & 3 \end{pmatrix} ,\quad\quad \tilde{C}= \begin{pmatrix} 1.8 & 1 \\ 2 & 2 \end{pmatrix} . \end{aligned}$$

Then via YALMIP with solver of LMILAB in MATLAB, LMI (15) in Theorem 2 has the following feasible solutions:

$$\begin{aligned}& P= \begin{pmatrix} 1.0620 & 0 \\ 0 & 0.8229 \end{pmatrix} ,\quad\quad Q= \begin{pmatrix} 27.8474 & 0 \\ 0 & 22.5707 \end{pmatrix} , \\& R= \begin{pmatrix} 17.2166 & 0 \\ 0 & 13.9893 \end{pmatrix} ,\quad\quad S= \begin{pmatrix} 33.1135 & 0 \\ 0 & 23.6366 \end{pmatrix} . \end{aligned}$$

Thus, the specified network has a unique equilibrium point which is globally robust asymptotically stable. To perform numerical simulation, let us choose D, A, B and C from the indicated intervals above, respectively, and obtain

$$ \begin{gathered} D= \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix} ,\quad\quad A= \begin{pmatrix} 3-2{\mathrm{i}}& 1+\mathrm{i} \\ -2-\mathrm{i}& -1.5+\mathrm{i} \end{pmatrix} ,\quad\quad B= \begin{pmatrix} 2-1.5{\mathrm{i}}& 1+1.5{\mathrm{i}} \\ 1.5-2{\mathrm{i}}& 2+\mathrm{i} \end{pmatrix} , \\ C= \begin{pmatrix} 1+1.2{\mathrm{i}}& 0.6-0.8{\mathrm{i}} \\ 1-\mathrm{i}& 1.5-1.5{\mathrm{i}} \end{pmatrix} ,\quad\quad J= \begin{pmatrix} 3-2{\mathrm{i}} \\ 2+3{\mathrm{i}} \end{pmatrix} . \end{gathered} $$
(35)

Besides, we choose discrete delays, activation functions, delay kernel functions and impulse functions as follows:

$$\begin{aligned}& \tau_{1}=\tau_{2}=0.5, \end{aligned}$$
(36)
$$\begin{aligned}& f_{1}(u)=f_{2}(u)=0.2 \bigl(\max\{0,x\}+\max\{0,y\} \bigr),\quad u=x+y \mathrm{i}\in\mathbb{C}, \end{aligned}$$
(37)
$$\begin{aligned}& k_{1}(s)=k_{2}(s)=e^{-s}, \quad s\in[0,+\infty), \end{aligned}$$
(38)
$$\begin{aligned}& I_{ik} \bigl(z_{i} \bigl(t_{k}^{-} \bigr) \bigr) = -\delta_{ik} \bigl(z_{i} \bigl(t_{k}^{-} \bigr)-\check{z} _{i} \bigr),\quad i=1,2, \end{aligned}$$
(39)

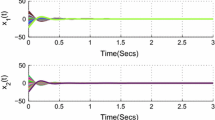
where \(\check{z}_{1}=1.7813 - 0.7372{\mathrm{i}}\), \(\check {z}_{2}=0.8132 + 0.6370{\mathrm{i}}\), \(\delta_{1k}=1+\frac{1}{2}\sin(1+k)\), \(\delta_{2k}=1+ \frac{2}{3}\cos(2k^{3})\), \(k=1,2,\ldots\) , and \(t_{1}=0.5\), \(t_{k}=t_{k-1}+0.2k\), \(k=2,3,\ldots\) . Figure 1 and 2 depict the real and imaginary parts of states of the considered system (2) with parameters (35)–(39), where the initial conditions are chosen by 10 random constant vectors.

Figure 1
figure 1

Real part of the state trajectories for system (2) with parameters (35)–(39)

Full size image
Figure 2
figure 2

Imaginary part of the state trajectories for system (2) with parameters (35)–(39)

Full size image

Remark 5

In [15], the problem of global robust stability of CVNNs with discrete time delays but without distributed time delays. So the stability criteria obtained in [15] cannot be applied to check the robust stability of the system in Example 1.

Next we give a second numerical example on application of associative memories based on CVNNs.

Example 2

Consider the image patterns “G” and “A” shown in Fig. 3 and design CVNNs in the form of (31) for associatively memorizing the images.

Figure 3
figure 3

Image patterns in Example 2

Full size image

It should be noted that, as shown in Fig. 3, “G” and “A” are composed of 52 and 50 black block, respectively. Therefore, we need to design CVNNs (31) composed of 52 neurons, which have a 52-dimensional equilibrium point storing the coordinates of the black blocks. Design the parameters of CVNNs (31) as follows:

$$\begin{aligned}& d_{i}=9, \quad\quad d_{i+1}=10, \quad\quad d_{i+2}=7,\quad i=1,4,7,\ldots, 49, \quad \text{and} \quad d_{52}=5, \end{aligned}$$
(40)
$$\begin{aligned}& a_{ij}= \textstyle\begin{cases} 0.5+0.4{\mathrm{i}},& i=j, \\ 0.4-0.5{\mathrm{i}},& i\neq j, \end{cases}\displaystyle \end{aligned}$$
(41)
$$\begin{aligned}& b_{ij}= \textstyle\begin{cases} 0.2+0.3{\mathrm{i}},& i< j, \\ 0.5+0.3{\mathrm{i}},& i=j, \\ -0.1+0.2{\mathrm{i}},& i>j, \end{cases}\displaystyle \end{aligned}$$
(42)
$$\begin{aligned}& f_{j}(u)=\frac{0.8}{1+e^{-u}},\quad u\in\mathbb{C}, j=1,2,\ldots,52. \end{aligned}$$
(43)

Then the activation functions satisfy the condition (\(\mathbf{H}_{2}\)) with \(\Gamma=\mathrm{diag}\{0.2,0.2, \ldots,0.2\}\in\mathbb{R} ^{52\times52}\). It is easy to check that LMI (34) in Corollary 4 has feasible solutions via YALMIP with the solver of SDPT3 in MATLAB. Therefore, the designed CVNNs with parameters (40)–(43) are globally asymptotically stable by Corollary 4.

In order to store the image pattern “G”, the equilibrium point of the designed CVNNs should be

$$ \check{z}=(3+\mathrm{i},3+2{\mathrm{i}},\ldots,8+10{\mathrm{i}})^{T} \in \mathbb{C}^{52}, $$

which correspond the coordinates \((3,1), (3,2),\ldots, (8,10)\) of the black block in image pattern “G”. According to the equilibrium point ž, we can calculate the external inputs J as follows:

$$ J=(-7.3442 +17.2369{\mathrm{i}},-5.2027 +29.3254{\mathrm{i}}, \ldots,21.8742 +33.4738 {\mathrm{i}})^{T}. $$
(44)

Here we just list some of the elements of ž and J due to space limitations. Two simulations with random initial values depicted in Fig. 4 show that the designed CVNNs with parameters (40)–(44) have the ability of recalling the above pattern “G” reliably.

Figure 4
figure 4

Two simulations of retrieving the pattern “G” with random initial values

Full size image

Next, we take use of the above neural network with the same parameters (40)–(43) to memorize another image pattern “A”. However, the parameter J should be recomputed since the positions of the black block in image pattern “A” are different from those in image pattern “G”. Noting that the pattern “A” composed of 50 black blocks, we should add 2 additional block such that there are 52 blocks. Then the equilibrium point ž is designed as

$$ \check{z}=(2+\mathrm{i},2+2{\mathrm{i}},\ldots,-10-10{\mathrm {i}},-10-10{ \mathrm{i}})^{T} \in\mathbb{C}^{52}, $$

where the first 50 elements of ž correspond the 50 coordinates of the black block in image pattern “A”, and the last two elements are additional. According to the equilibrium point ž, the external inputs J can be computed as follows:

$$ J=(-6.2332 + 8.3721{\mathrm{i}}, -4.0371 +19.3896{\mathrm{i}}, \ldots,-62.0099 -46.0415 {\mathrm{i}})^{T}. $$
(45)

Two simulations with random initial values depicted in Fig. 5 show that the designed CVNNs with parameters (40)–(43) and (45) have the ability of recalling the above pattern “A” reliably.

Figure 5
figure 5

Two simulations of retrieving the pattern “A” with random initial values

Full size image

Remark 6

In Example 2, since the neurons are complex-valued, each neuron contains the horizontal and vertical coordinates of the black blocks in the images. Thus the designed CVNNs require less neurons than RVNNs to store the image patterns.

6 Conclusion

In this paper, the problem of robust stability for impulsive complex-valued neural networks time delays has been investigated. Applying homeomorphic mapping theorem in complex domain, we presented some sufficient conditions to guarantee the existence of a unique equilibrium point for the complex-valued neural networks. In addition, by constructing appropriate Lyapunov–Krasovskii functionals, and employing the matrix inequality techniques, we obtained several conditions for checking the robust stability of the complex-valued neural networks which are established in LMIs. Finally, two numerical examples have been given to illustrate the effectiveness of the proposed theoretical results.