1 Introduction

Recently, neural networks have attracted much attention due to their great potential prospectives in various areas, such as signal processing, associative memory, pattern recognition, and so on [1–18]. As a general class of recurrent neural networks, Cohen-Grossberg neural networks, including Hopfield neural networks and cellular neural networks as two special cases, were proposed by Cohen and Grossberg in 1983. From then on, many researchers have investigated this type of neural networks extensively [19–24]. In [19], the robust stability about the integer-order Cohen-Grossberg neural networks is explored based on the comparison principle. Liu et al. [20] investigate the multistability of Cohen-Grossberg neural networks with nonlinear activation functions in any open interval. In addition, the dynamic properties of Cohen-Grossberg neural networks can describe the evolution of the competition between species in living nature, where the equilibrium points stand for the survival or extinction of the species.

From the viewpoint of mathematics, fractional calculus generalizes integer-order calculus. Meanwhile, fractional derivatives can depict real situations more elaborately than integer-order derivatives, especially when the situations posses hereditary properties or have memory. Due to these facts, fractional-order systems play an important role in scientific modeling and practical applications [25–35]. In [25], the Mittag-Leffler stability of fractional-order memristive neural networks is investigated by utilizing the Lyapunov method. In [29], global Mittag-Leffler stability and asymptotic ω-periodicity of fractional-order fuzzy neural networks with time-varying input are considered. The Mittag-Leffler stability for a general class of Hopfield neural networks is explored in [33] by using the generalized second Lyapunov method. Because of the difference between fractional-order systems and integer-order systems, the analysis method in integer-order systems cannot be applied directly to fractional-order systems. The investigation on fractional-order systems is still at an early stage. Furthermore, the study of fractional-order systems is complex due to the absence of general approaches. Hence, the investigation on the dynamics of fractional-order systems is a valuable and challenging problem.

Fuzzy logic has the property of fuzzy uncertainties and has the advantages of simulating the human way of thinking. Traditional neural networks with fuzzy logic are called fuzzy neural networks; they can be used for broadening the range of application of traditional neural networks. Studies have shown that fuzzy neural networks are useful models for exploring human cognitive activities. There are many profound reports about the fuzzy neural networks (see, for example, [36–40]).

Neural networks with deviating argument, which are proposed in the model of recurrent neural networks by Akhmet et al. [41], are suitable for modeling situations in physics, economy, and biology. In these situations, not only past but also future events are critical for the current properties. The deviating argument changes its type from advanced to retarded alternately and it can link past and future events [42–49]. Neural networks with deviating argument conjugate continuous neural networks and discrete neural networks. Hence, this type of neural networks has the properties of both continuous neural networks and discrete neural networks. From a mathematical perspective, these neural networks are of a mixed type. With the evolution of the process, the deviating state can be advanced and retarded, commutatively. The dynamic behavior of this type of neural networks is studied extensively [50–52] and deserves further investigation.

Inspired by the above discussions, this paper formulates the global Mittag-Leffler stability of fractional-order fuzzy Cohen-Grossberg neural networks with deviating argument. Roughly stated, there are three aspects of contribution in this paper:

  • The existence and uniqueness of solution for fractional-order fuzzy Cohen-Grossberg neural networks with deviating argument are addressed.

  • Sufficient conditions are derived to guarantee the global Mittag-Leffler stability of fractional-order fuzzy Cohen-Grossberg neural networks with deviating argument.

  • The existing approaches for the stability of neural networks cannot be applied straightforwardly to fractional-order fuzzy Cohen-Grossberg neural networks with deviating argument. In accordance with the theory of differential equations with deviating argument and in conjunction with the properties of fractional-order calculus, the global Mittag-Leffler stability of such type of neural networks is explored in detail.

The rest of the paper is arranged as follows. Some preliminaries and model descriptions are presented in Section 2. The main results are stated in Section 3. The validity of the obtained results is substantiated in Section 4. Concluding remarks are given in Section 5.

2 Preliminaries and model description

2.1 Preliminaries about fractional-order calculus

Let us give a brief introduction to fractional calculus with some concepts, definitions, and useful lemmas.

The Caputo derivative of the function \(\mathcal{F}(\cdot) \in C^{n+1}([t_{0}, +\infty],R)\) with order q is defined by

$$ {}_{t_{0}}^{C}D_{t}^{q}\mathcal{F}(t)= \frac{1}{\Gamma(n-q)} \int_{t_{0}}^{t}\frac{\mathcal{F}^{(n)}(s)}{(t-s)^{q-n+1}}\,\mathrm{d}s. $$

Correspondingly, the fractional integral of the function \(\mathcal{F}(\cdot)\) with order q is defined by

$$ I^{q}_{t_{0}}\mathcal{F}(t)=\frac{1}{\Gamma(q)} \int _{t_{0}}^{t}(t-s)^{q-1}\mathcal{F}(s)\, \mathrm{d}s, $$

where \(t\geq t_{0}\), n is a positive integer such that \(n-1< q< n\), and \(\Gamma(q){=\int_{0}^{+\infty}r^{q-1}\exp(-r)\,\mathrm {d}r}\) is the Gamma function.

The one-parameter Mittag-Leffler function is defined as

$$ E_{q}(s)=\sum_{k=0}^{+\infty} \frac{s^{k}}{\Gamma(kq+1)}, $$

while the two-parameter Mittag-Leffler function is defined as

$$ E_{q,p}(s)=\sum_{k=0}^{+\infty} \frac{s^{k}}{\Gamma(kq+p)}, $$

where \(q>0\), \(p>0\), and s is a complex number.

2.2 Model

Let \(\mathcal{N}\) denote the set of natural numbers and let \(\mathcal{R}^{+}\) and \(\mathcal{R}^{n}\) stand for the set of nonnegative real numbers and an n-dimensional Euclidean space. For a vector \(x \in\mathcal{R}^{n}\), its norm is defined as \(\|x\|=\sum_{i=1}^{n}|x_{i}|\). Take two real-valued sequences \(\{\eta_{k}\}\) and \(\{\xi_{k}\}\), \(k \in\mathcal{N}\) satisfying \(\eta_{k}<\eta_{k+1}\), \(\eta_{k}\leq\xi_{k}\leq\eta_{k+1}\) for any \(k \in\mathcal{N}\), and \(\lim_{k\rightarrow+\infty}\eta_{k}=+\infty\).

In this paper, we consider a general class of fractional-order fuzzy Cohen-Grossberg neural networks with deviating argument described by the following fractional-order differential equations:

$$ \begin{aligned}[b] {}_{t_{0}}^{C}D^{q}_{t}x_{i}(t)={}& \omega_{i}\bigl(x_{i}(t)\bigr) \Biggl[-\alpha_{i} \bigl(x_{i}(t)\bigr)+\sum_{j=1}^{n}b_{ij}f_{j} \bigl(x_{j}(t)\bigr) +\sum_{j=1}^{n}c_{ij}g_{j} \bigl(x_{j}\bigl(\gamma(t)\bigr)\bigr) \\ & +\sum_{j=1}^{n}d_{ij}u_{j}+I_{i}+ \bigwedge_{j=1}^{n}h_{ij}f_{j} \bigl(x_{j} \bigl(\gamma(t)\bigr)\bigr)+\bigvee _{j=1}^{n}l_{ij}f_{j} \bigl(x_{j}\bigl(\gamma(t)\bigr)\bigr) \\ &+\bigwedge_{j=1}^{n}p_{ij}u_{j} +\bigvee_{j=1}^{n}r_{ij}u_{j} \Biggr], \quad i=1,2,\ldots,n,\end{aligned} $$
(1)

where the fractional order q satisfies \(0< q<1\), \(x_{i}(t)\) is the state of the ith neuron, \(\omega_{i}(\cdot)\) and \(\alpha(\cdot)\) are continuous functions, \(b_{ij}\) and \(c_{ij}\) are synaptic weights from the ith neuron to the jth neuron at time t and \(\gamma(t)\), respectively, \(d_{ij}\) denotes the synaptic weight for the bias of the ith neuron, \(h_{ij}\), \(l_{ij}\), \(p_{ij}\), and \(r_{ij}\) signify the synaptic weights of fuzzy local operations, and ⋀ and ⋁ stand for the fuzzy AND and fuzzy OR operation, respectively. \(\gamma(t)=\xi_{k}\), for \(t \in[\eta_{k},\eta_{k+1})\), \(k \in\mathcal{N}\), \(t \in \mathcal{R}^{+}\), which is a piecewise constant function, is called a deviating argument. \(f_{j}(\cdot)\) and \(g_{j}(\cdot)\) are activation functions, while \(u_{j}\) and \(I_{i}\) represent the bias and the input, respectively.

It is clear that (1) is of the mixed type. When \(t \in[\eta_{k},\xi_{k})\) and \(\gamma(t)=\xi_{k}>t\), (1) is an advanced system. When \(t \in[\xi_{k},\eta_{k+1})\) and \(\gamma(t)=\xi_{k}< t\), (1) is a retarded system. Hence, (1) changes its deviation type during the process and is of the mixed type.

2.3 Definitions and lemmas

In this subsection, some useful definitions and lemmas are given as follows.

Definition 2.1

See [19]

An equilibrium point of (1) is a constant vector \(x^{*}= (x_{1}^{*},x_{2}^{*},\ldots,x_{n}^{*})^{T}\), such that

$$\begin{aligned} 0={}&{-}\alpha_{i}\bigl(x_{i}^{*}\bigr)+\sum _{j=1}^{n}b_{ij}f_{j} \bigl(x_{j}^{*}\bigr) +\sum_{j=1}^{n}c_{ij}g_{j} \bigl(x_{j}^{*}\bigr)+\sum_{j=1}^{n}d_{ij}u_{j} +I_{i} \\ &+\bigwedge_{j=1}^{n}h_{ij}f_{j} \bigl(x_{j}^{*}\bigr) +\bigvee_{j=1}^{n}l_{ij}f_{j} \bigl(x_{j}^{*}\bigr)+\bigwedge _{j=1}^{n}p_{ij}u_{j} +\bigvee _{j=1}^{n}r_{ij}u_{j}. \end{aligned}$$

Definition 2.2

See [25]

The equilibrium point \(x^{*}=(x_{1}^{*},x_{2}^{*}, \ldots,x_{n}^{*})^{T}\) of (1) is globally Mittag-Leffler stable if, for any solution \(x(t)\) of (1) with initial condition \(x_{0}\), there exist two positive constants κ and ε such that

$$ \big\| x(t)-x^{*}\big\| ^{2}\leq\kappa\big\| x_{0}-x^{*} \big\| ^{2} E_{q}\bigl(-\varepsilon(t-t_{0})^{q} \bigr), \quad t\geq t_{0}. $$

Remark 2.1

The same way the exponent function is broadly used in integer-order neural networks, the Mittag-Leffler function is widely used in fractional-order neural networks. From Definition 2.2, Mittag-Leffler stability possesses the power-law property \((t-t_{0})^{-q}\), which is entirely different from exponential stability.

Lemma 2.1

Let \(q>0\), let \(\mathcal{X}\) and \(\mathcal{G}\) be non-negative constants, and suppose \(\mathcal{Y}(t)\) is non-negative and locally integrable on \([t_{0},\bar{t} )\) with

$$ \mathcal{Y}(t)\leq\mathcal{X}+\mathcal{G} \int_{t_{0}}^{t}(t-s)^{q-1} \mathcal{Y}(s)\, \mathrm{d}s,\quad t \in[t_{0},\bar{t} ), $$

or

$$ \mathcal{Y}(t)\leq\mathcal{X}+\mathcal{G} \int_{t}^{T}(T-s)^{q-1} \mathcal{Y}(s)\, \mathrm{d}s,\quad t,T \in[t_{0},\bar{t} ) \textit{ and } t< T. $$

Then

$$ \mathcal{Y}(t)\leq\mathcal{X}E_{q} \bigl(\mathcal{G} \Gamma(q) (t-t_{0})^{q} \bigr),\quad t \in[t_{0},\bar{t} ), $$

or

$$ \mathcal{Y}(t)\leq\mathcal{X}E_{q} \bigl(\mathcal{G} \Gamma(q) (T-t)^{q} \bigr),\quad t,T \in[t_{0},\bar{t} ) \textit{ and } t< T. $$

The proof of Lemma 2.1 is almost identical to that of Theorem 1 and Corollary 2 in [30], and it is omitted here for the sake of convenience.

Lemma 2.2

See [34]

Let \(\mathcal{F}(t) \in R^{n}\) be a continuous and derivable function. Then

$$ {}_{t_{0}}^{C}D_{t}^{q} \mathcal{F}^{2}(t)\leq2 \mathcal {F}(t){}_{t_{0}}^{C}D_{t}^{q} \mathcal{F}(t), $$

for all \(t\geq t_{0}\) and \(0<\alpha<1\).

Lemma 2.3

See [40]

Suppose \(x=(x_{1},x_{2},\ldots ,x_{n})^{T}\) and \(y=(y_{1},y_{2}, \ldots,y_{n})^{T}\) are two states of (1). Then

$$\begin{gathered} \Bigg|\bigwedge_{j=1}^{n}\alpha_{ij}f_{j}(x_{j})- \bigwedge_{j=1}^{n}\alpha_{ij}f_{j}(y_{j}) \Bigg| \leq\sum_{j=1}^{n}|\alpha_{ij}|\big|f_{j}(x_{j}) -f_{j}(y_{j})\big|, \\ \Bigg|\bigvee_{j=1}^{n}\beta_{ij}f_{j}(x_{j}) -\bigvee_{j=1}^{n}\beta_{ij}f_{j}(y_{j}) \Bigg| \leq\sum_{j=1}^{n}|\beta_{ij}|\big|f_{j}(x_{j})-f_{j}(y_{j})\big|.\end{gathered} $$

Lemma 2.4

See [29]

Let \(0< q<1\). \(\mathcal{F}(t)\) is a continuous function on \([t_{0},+\infty)\), if there exist two constants \(\mu_{1}>0\) and \(\mu_{2}\geq0\) such that

$$ \left \{ \textstyle\begin{array}{l} {}_{t_{0}}^{C}D_{t}^{q}\mathcal{F}(t)\leq-\mu_{1}\mathcal{F}(t)+\mu _{2}, \\ \mathcal{F}(t_{0})=\mathcal{F}_{t_{0}}. \end{array}\displaystyle \right . $$

Then

$$ \mathcal{F}(t)\leq\mathcal{F}_{t_{0}}E_{q}\bigl(- \mu_{1}(t-t_{0})^{q}\bigr) +\mu_{2}t^{q}E_{q,q+1} \bigl(-\mu_{1}(t-t_{0})^{q}\bigr), \quad t\geq t_{0}. $$

Remark 2.2

There are distinct differences between fractional-order differential equations and integer-order differential equations. Properties in integer-order differential equations cannot be simply extended to fractional-order differential equations. Lemma 2.1, Lemma 2.2, and Lemma 2.4 provide powerful tools for exploring fractional-order differential equations.

2.4 Notations and assumptions

For the sake of convenience, some notations are introduced in this subsection. First, let us define some notations, which will be used later:

$$\begin{aligned}& \tilde{A}=\max_{1\leq i\leq n}\Biggl(\overline{\omega}_{i} \overline{\alpha}_{i} +\sum_{j=1}^{n} \overline{\omega}_{j}|b_{ji}|\tilde{c}_{i}\Biggr), \\& A_{1}=\max_{1\leq i\leq n}\Biggl(\widetilde{ \omega}_{i}\overline{\alpha}_{i} +\sum _{j=1}^{n}\overline{\omega}_{j}|b_{ji}| \tilde{c}_{i}\Biggr), \\& A_{2}=\max_{1\leq i\leq n}\Biggl(\sum _{j=1}^{n}\overline{\omega}_{j}\bigl(|c_{ji}| \hat{c}_{i} +|h_{ji}|\tilde{c}_{i}+|l_{ji}| \tilde{c}_{i}\bigr)\Biggr), \\& \begin{aligned}A_{3}={}&\frac{1}{n}\min_{1\leq i\leq n}\Biggl(2 \underline{\omega}_{i}\underline {\alpha}_{i}- \sum _{j=1}^{n}\bigl(\overline{\omega}_{i}|b_{ij}| \tilde{c}_{i} +\overline{\omega}_{j}|b_{ji}| \tilde{c}_{j}\bigr) \\ &-\sum_{j=1}^{n}\overline{ \omega}_{i}\bigl(|c_{ij}|\hat{c}_{j} +|h_{ij}|\tilde{c}_{j}+|l_{ij}| \tilde{c}_{j}\bigr)\Biggr),\end{aligned} \\& A_{4}=\max_{1\leq i\leq n}\Biggl(\sum _{j=1}^{n}\overline{\omega}_{j}\bigl(|c_{ji}| \hat{c}_{i} +|h_{ji}|\tilde{c}_{i}+|l_{ji}| \tilde{c}_{i}\bigr)\Biggr), \\& \theta_{1}=A_{1}+\widetilde{\omega}M, \qquad \theta_{2}=\frac{\eta ^{q}}{\Gamma(q+1)}, \quad M=\max_{1\leq i \leq n}(M_{i}), \\& \widetilde{\omega}=\max_{1\leq i\leq n}(\widetilde{ \omega}_{i}), \qquad\tau=(1+A_{2}\theta_{2})E_{q} \bigl(A_{1}\eta^{q}\bigr), \\ & \\ & C_{i}=\sum_{j=1}^{n}d_{ij}u_{j}+I_{i}+ \bigwedge_{j=1}^{n}p_{ij}u_{j} +\bigvee_{j=1}^{n}r_{ij}u_{j}, \\& B=\frac{\eta^{q}(\tilde{A}+A_{2})}{\Gamma(q+1)}, \\& \mathcal{B}=\frac{1}{1-B}\Biggl(\big\| x^{0}\big\| +\theta_{2} \sum_{i=1}^{n}\overline{ \omega}_{i}|C_{i}|\Biggr), \\& \begin{aligned}M_{i}={}&\max_{|x|< \mathcal{B}} \bigl(\big|\alpha_{i}(x)\big| \bigr) +\sum_{j=1}^{n}|b_{ij}|\max _{|x|< \mathcal{B}} \bigl(\big|f_{j}(x)\big| \bigr) +\sum _{j=1}^{n}|c_{ij}|\max_{|x|< \mathcal{B}} \bigl(\big|g_{j}(x)\big| \bigr) \\ &+\bigwedge_{j=1}^{n}|h_{ij}| \max_{|x|< \mathcal{B}} \bigl(\big|f_{j}(x)\big| \bigr) +\bigvee _{j=1}^{n}|h_{ij}|\max_{|x|< \mathcal{B}} \bigl(\big|f_{j}(x)\big| \bigr)+|C_{i}|,\end{aligned} \\& \varrho=\bigl[1-\theta_{2}(A_{1}\tau+A_{2}) \bigr]^{-1}, \\& \begin{aligned}F_{i}^{m}(s)={}&{-}\alpha_{i}\bigl(z_{i}^{m}(s) \bigr)+\sum_{j=1}^{n}b_{ij}f_{j} \bigl(z_{j}^{m}(s)\bigr) +\sum_{j=1}^{n}c_{ij}g_{j} \bigl(z_{j}^{m}\bigl(\gamma(s)\bigr)\bigr) \\ &+\bigwedge_{j=1}^{n}h_{ij}f_{j} \bigl(z_{j}^{m}\bigl(\gamma(s)\bigr)\bigr) +\bigvee _{j=1}^{n}l_{ij}f_{j} \bigl(z_{j}^{m}\bigl(\gamma(s)\bigr)\bigr).\end{aligned} \end{aligned}$$
(2)

Throughout this paper, the parameters and activation functions of (1) are supposed to satisfy the following assumptions:

  1. (A1)

    for functions \(\omega_{i}(\cdot)\) and \(\alpha_{i}(\cdot)\), there exist positive constants \(\underline{\omega}_{i}\), \(\overline{\omega}_{i}\), \(\underline{\alpha}_{i}\), and \(\overline{\alpha}_{i}\) and Lipschitz constants \(\widetilde{\omega}_{i}\) such that

    $$ \underline{\omega}_{i}\leq\omega_{i}(x_{i})\leq \overline{\omega}_{i}, \qquad\big|\omega_{i}(x_{i})- \omega_{i}(y_{i})\big|\leq\widetilde{\omega}_{i}|x_{i}-y_{i}|, \qquad \underline{\alpha}_{i}\leq\frac{\alpha_{i}(x_{i}) -\alpha_{i}(y_{i})}{x_{i}-y_{i}}\leq\overline{ \alpha}_{i}, $$

    and \(\alpha_{i}(0)=0\), for any \(x_{i},y_{i} \in \mathcal{R}\), \(x_{i}\neq y_{i}\), \(i=1,2,\ldots,n\);

  2. (A2)

    for activation functions \(f_{i}(\cdot)\) and \(g_{i}(\cdot)\), there exist Lipschitz constants \(\tilde{c}_{i}\) and \(\hat{c}_{i}\) such that

    $$ \big|f_{i}(x_{i})-f_{i}(y_{i})\big|\leq \tilde{c}_{i}|x_{i}-y_{i}|, \qquad \big|g_{i}(x_{i})-g_{i}(y_{i})\big|\leq \hat{c}_{i}|x_{i}-y_{i}|, $$

    while \(f_{i}(0)=g_{i}(0)=0\), for any \(x_{i},y_{i} \in\mathcal{R}\), \(i=1,2,\ldots,n\);

  3. (A3)

    there exists a positive constant \(\eta>0\) such that

    $$ \eta_{k+1}-\eta_{k}\leq\eta, \quad\mbox{for } k \in \mathcal{N}; $$
  4. (A4)

    \(\frac{\eta^{q}(\tilde{A}+A_{2})}{\Gamma(q+1)}<1\);

  5. (A5)

    \(\theta_{2}(\theta_{1}+A_{2})<1\), \(\frac{\theta_{2}(\theta_{1}+A_{2})E_{q}(\theta_{1} \eta^{q})}{1-A_{2}\theta_{2}E_{q}(\theta_{1}\eta^{q})}<1\);

  6. (A6)

    \(\theta_{2}(A_{1}\tau+A_{2})<1\).

Fix \(k \in\mathcal{N}\), for every \((t_{0},x^{0}) \in[\eta_{k},\eta_{k+1}]{\times\mathcal{R}^{n}}\) and assume \(\eta_{k}\leq t_{0} <\xi_{k}\leq\eta_{k+1}\) without loss of generality. Construct a sequence \(\{z_{i}^{m}(t)\}\), \(i=1,2,\ldots,n\), such that

$$ z_{i}^{m+1}(t)=x_{i}^{0}+ \frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1}\omega _{i}\bigl(z_{i}^{m}(s)\bigr) \bigl(F_{i}^{m}(s)+C_{i}\bigr)\,\mathrm{d}s, $$
(3)

for \(m \in\mathcal{N}\) and \(z_{i}^{0}(t)=x_{i}^{0}\), where \(F_{i}^{m}(s)\) and \(C_{i}\) are defined in (2). We obtain

$$ \big\| z^{m+1}(t)\big\| \leq\big\| x^{0}\big\| +\frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1}\Biggl(\tilde{A} \big\| z^{m}(s)\big\| +A_{2}\big\| z^{m}(\xi _{k})\big\| +\sum_{i=1}^{n}\overline{ \omega}_{i}|C_{i}|\Biggr)\,\mathrm{d}s. $$

Define a norm \(\|z(t)\|_{M}=\max_{t_{0}\leq t \leq\xi_{k}}\|z(t)\|\). Then

$$\begin{aligned} \big\| z^{m+1}(t)\big\| _{M}\leq{}&\big\| x^{0}\big\| + \frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1}\Biggl(\tilde{A} \big\| z^{m}(s)\big\| _{M} +A_{2}\big\| z^{m}(s)\big\| _{M} +\sum _{i=1}^{n}\overline{\omega}_{i}|C_{i}| \Biggr)\,\mathrm{d}s \\ \leq{}& \big\| x^{0}\big\| +B\big\| z^{m}(s)\big\| _{M}+ \theta_{2}\sum_{i=1}^{n} \overline{\omega}_{i}|C_{i}|, \end{aligned}$$

where B and \(\theta_{2}\) are defined in (2).

Hence

$$\begin{gathered} \big\| z^{1}(t)\big\| _{M}\leq(1+B)\big\| x^{0}\big\| + \theta_{2} \sum_{i=1}^{n} \overline{\omega}_{i}|C_{i}|, \\ \big\| z^{2}(t)\big\| _{M}\leq\bigl(1+B+B^{2}\bigr) \big\| x^{0}\big\| +(1+B)\theta_{2}\sum_{i=1}^{n} \overline{\omega}_{i}|C_{i}|, \\ \cdots \\ \begin{aligned}\big\| z^{m+1}(t)\big\| _{M}\leq{}&\bigl(1+B+B^{2}+ \cdots+B^{m+1}\bigr)\big\| x^{0}\big\| +\bigl(1+B+\cdots+B^{m}\bigr)\theta_{2}\sum _{i=1}^{n}\overline{\omega}_{i}|C_{i}|.\end{aligned} \end{gathered}$$

Under (A4),

$$ \big\| z^{m+1}(t)\big\| _{M}\leq\frac{1}{1-B}\Biggl( \big\| x^{0}\big\| +\theta_{2}\sum_{i=1}^{n} \overline{\omega}_{i}|C_{i}|\Biggr), $$

for \(m \in\mathcal{N}\).

In combination with the continuity of the functions \(\alpha(\cdot)\), \(f(\cdot)\), and \(g(\cdot)\), we conclude that

$$ \big|F^{m}_{i}(s)+C_{i}\big|\leq M_{i}, $$

for \(m\in\mathcal{N}\) with initial condition \(x^{0}\), where \(M_{i}\) is defined in (2), \(i=1,2,\ldots, n\).

3 Main results

3.1 Existence and uniqueness of solution

From the viewpoint of theory and application, the existence and uniqueness of solution for differential equations is a precondition, so we begin with the theorem for the existence and uniqueness of solution for (1).

Theorem 3.1

Let (A1)-(A5) hold. Then, for each pair \((t_{0},x^{0}) \in\mathcal{R}^{+} \times\mathcal{R}^{n}\), (1) has a unique solution \(x(t)=x(t,t_{0},x^{0})\), \(t\geq t_{0}\), with the initial condition \(x(t_{0})=x^{0}\).

Proof

First, we prove the existence of solutions.

Take \(k \in\mathcal{N}\). Without loss of generality, assume \(\eta_{k}\leq t_{0} <\xi_{k} \leq\eta_{k+1}\). We first prove (1) exists a unique solution \(x(t,t_{0},x^{0})\) for every \((t_{0},x^{0}) \in[\eta_{k},\eta_{k+1}]\).

Denote \(z_{i}(t)=x_{i}(t,t_{0},x_{0})\) for simplicity and construct the following equivalent integral equation:

$$\begin{aligned} z_{i}(t)={}&z_{i}(t_{0})+\frac{1}{\Gamma(q)} \int _{t_{0}}^{t}(t-s)^{q-1} \Biggl\{ \omega_{i}\bigl(z_{i}(s)\bigr) \Biggl[-\alpha_{i} \bigl(z_{i}(s)\bigr) \\ &+\sum_{j=1}^{n}b_{ij}f_{j} \bigl(z_{j}(s)\bigr)+\sum_{j=1}^{n}c_{ij}g_{j} \bigl(z_{j}\bigl(\gamma(s)\bigr)\bigr)+\sum _{j=1}^{n}d_{ij}u_{j} +I_{i} \\ &+\bigwedge_{j=1}^{n}h_{ij}f_{j} \bigl(z_{j}\bigl(\gamma(s)\bigr)\bigr)+\bigvee_{j=1}^{n}l_{ij}f_{j} \bigl(z_{j}\bigl(\gamma(s)\bigr)\bigr) +\bigwedge _{j=1}^{n}p_{ij}u_{j}+\bigvee _{j=1}^{n}r_{ij}u_{j} \Biggr] \Biggr\} \,\mathrm{d}s. \end{aligned}$$

From (3), we have

$$\begin{gathered} \big|z_{i}^{m+1}(t)-z_{i}^{m}(t)\big| \\ \quad=\frac{1}{\Gamma(q)} \bigg| \int_{t_{0}}^{t}(t-s)^{q-1} \bigl[ \omega_{i}\bigl(z_{i}^{m}(s)\bigr) \bigl(F_{i}^{m}(s)+C_{i}\bigr) \\ \qquad{}-\omega_{i}\bigl(z_{i}^{m-1}(s)\bigr) \bigl(F_{i}^{m-1}(s)+C_{i}\bigr)\bigr]\,\mathrm{d}s \bigg| \\ \quad=\frac{1}{\Gamma(q)} \bigg| \int_{t_{0}}^{t}(t-s)^{q-1} \bigl[ \omega_{i}\bigl(z_{i}^{m}(s)\bigr) \bigl(F_{i}^{m}(s)+C_{i}\bigr) - \omega_{i}\bigl(z_{i}^{m-1}(s)\bigr) \bigl(F_{i}^{m}(s)+C_{i}\bigr) \\ \quad\quad{}+\omega_{i}\bigl(z_{i}^{m-1}(s)\bigr) \bigl(F_{i}^{m}(s)+C_{i}\bigr) - \omega_{i}\bigl(z_{i}^{m-1}(s)\bigr) \bigl(F_{i}^{m-1}(s)+C_{i}\bigr)\bigr]\,\mathrm{d}s \bigg| \\ \quad=\frac{1}{\Gamma(q)} \bigg| \int_{t_{0}}^{t}(t-s)^{q-1} \bigl[\bigl( \omega_{i}\bigl(z_{i}^{m}(s)\bigr)-\omega _{i}\bigl(z_{i}^{m-1}(s)\bigr)\bigr) \bigl(F_{i}^{m}(s)+C_{i}\bigr) \\ \quad\quad{}+\omega_{i}\bigl(z_{i}^{m-1}(s)\bigr) \bigl(F_{i}^{m}(s)-F_{i}^{m-1}(s)\bigr) \bigr]\,\mathrm {d}s \bigg| \\ \quad\leq\frac{1}{\Gamma(q)} \bigg| \int_{t_{0}}^{t}(t-s)^{q-1} \bigl( \omega_{i}\bigl(z_{i}^{m}(s)\bigr)- \omega_{i}\bigl(z_{i}^{m-1}(s)\bigr)\bigr) \bigl(F_{i}^{m}(s)+C_{i}\bigr)\,\mathrm{d}s \bigg| \\ \quad\quad{}+\frac{1}{\Gamma(q)} \bigg| \int_{t_{0}}^{t}(t-s)^{q-1} \omega_{i}\bigl(z_{i}^{m-1}(s)\bigr) \bigl(F_{i}^{m}(s)-F_{i}^{m-1}(s)\bigr) \,\mathrm{d}s \bigg|. \end{gathered}$$

Combining this with

$$\begin{gathered} \sum_{i=1}^{n}\frac{1}{\Gamma(q)} \bigg| \int_{t_{0}}^{t}(t-s)^{q-1}\bigl( \omega_{i}\bigl(z_{i}^{m}(s)\bigr) - \omega_{i}\bigl(z_{i}^{m-1}(s)\bigr)\bigr) \bigl(F_{i}^{m}(s)+C_{i}\bigr)\,\mathrm{d}s \bigg| \\ \quad\leq\sum_{i=1}^{n}\widetilde{ \omega}_{i}M_{i} \frac{1}{\Gamma(q)} \bigg| \int_{t_{0}}^{t}(t-s)^{q-1}\bigl(z_{i}^{m}(s)-z_{i}^{m-1}(s) \bigr) \,\mathrm{d}s \bigg| \\ \quad\leq\widetilde{\omega}M\frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1} \big\| z^{m}(s)-z^{m-1}(s)\big\| \,\mathrm{d}s \end{gathered}$$

and

$$\begin{gathered} \sum_{i=1}^{n}\frac{1}{\Gamma(q)} \bigg| \int_{t_{0}}^{t}(t-s)^{q-1} \omega_{i}\bigl(z_{i}^{m-1}(s)\bigr) \bigl(F_{i}^{m}(s)-F_{i}^{m-1}(s)\bigr) \,\mathrm{d}s \bigg| \\ \quad\leq A_{1}\frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1} \big\| z^{m}(s)-z^{m-1}(s)\big\| \,\mathrm{d}s+A_{2} \theta_{2}\big\| z^{m}(\xi _{k})-z^{m-1}( \xi_{k})\big\| , \end{gathered}$$

we get

$$\begin{gathered} \big\| z^{m+1}(t)-z^{m}(t)\big\| \\ \quad\leq\theta_{1}\frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1} \big\| z^{m}(s)-z^{m-1}(s)\big\| \,\mathrm{d}s +A_{2} \theta_{2}\big\| z^{m}(\xi_{k})-z^{m-1}( \xi_{k})\big\| , \end{gathered}$$

where ω̃, \(M_{i}\), M, \(A_{1}\), \(A_{2}\), \(\theta_{1}\), and \(\theta_{2}\) are defined in (2).

From the definition of the norm of \(\|z(t)\|_{M}=\max_{t_{0}\leq t\leq\xi_{k}}(\|z(t)\|)\), we have

$$\begin{gathered} \big\| z^{m+1}(t)-z^{m}(t)\big\| _{M} \\ \quad\leq \max_{t_{0}\leq t\leq\xi_{k}} \biggl(\theta_{1} \frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1}\big\| z^{m}(s)-z^{m-1}(s) \big\| \,\mathrm{d}s \\ \quad\quad{}+A_{2}\theta_{2}\big\| z^{m}( \xi_{k})-z^{m-1} (\xi_{k})\big\| \biggr) \\ \quad\leq\max_{t_{0}\leq t\leq\xi_{k}} \biggl(\theta_{1} \frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1}\big\| z^{m}(s)-z^{m-1}(s) \big\| \,\mathrm{d}s \biggr) \\ \quad\quad{}+ \max_{t_{0}\leq t\leq\xi_{k}} \bigl(A_{2}\theta_{2} \big\| z^{m} (\xi_{k})-z^{m-1}(\xi_{k})\big\| \bigr) \\ \quad\leq \bigl[\theta_{2}(\theta_{1}+A_{2}) \bigr] \big\| z^{m}(t)-z^{m-1}(t)\big\| _{M} \\ \quad\leq \bigl[\theta_{2}(\theta_{1}+A_{2}) \bigr]^{m} \big\| z^{1}(t)-z^{0}(t)\big\| _{M} \\ \quad\leq \bigl[\theta_{2}(\theta_{1}+A_{2}) \bigr]^{m}\mathcal{H}, \end{gathered}$$

where \(\mathcal{H}=\theta_{2}(\lambda_{1}\|x^{0}\|+ \lambda_{2}\sum_{i=1}^{n}|u_{i}|+\sum_{i=1}^{n}|I_{i}|)\), \(\lambda_{1}=\max_{1\leq i\leq n} [\overline{\omega}_{i} (\overline{\alpha}_{i} +\sum_{j=1}^{n}(|b_{ji}|\tilde{c}_{i}+|c_{ji}|\hat{c}_{i} +|h_{ji}|\tilde{c}_{i}+|l_{ji}|\tilde{c}_{i}) ) ]\), and \(\lambda_{2}=\max_{1\leq i\leq n} (\sum_{j=1}^{n} \overline{\omega}_{i}(|d_{ji}|+|p_{ji}+|d_{ji}) )\). Hence, there exists a unique solution \(z(t)=x(t,t_{0},x^{0})\) for (1) on \([\xi_{k},t_{0}]\). Assumptions (A1) and (A2) imply that \(z(t)=x(t,t_{0},x^{0})\) can be continued to \(\eta_{k+1}\). In a similar way, \(z(t)=x(t,t_{0},x^{0})\) can continue from \(\eta_{k+1}\) to \(\xi_{k+1}\) and then to \(\eta_{k+2}\). Hence, we conclude that for (1) there exists a solution \(x(t)=x(t,t_{0},x^{0})\), \(t\geq t_{0}\), by mathematical induction.

Now, we prove the uniqueness of the solution.

Let

$$\begin{aligned} H_{i}^{l}(s)={}&{-}\alpha_{i}\bigl(x_{i}^{l}(s) \bigr)+\sum_{j=1}^{n}b_{ij}f_{j} \bigl(x_{j}^{l}(s)\bigr) +\sum_{j=1}^{n}c_{ij}g_{j} \bigl(x_{j}^{l}(\xi_{k})\bigr) \\ & +\bigwedge_{j=1}^{n}h_{ij}f_{j} \bigl(x_{j}^{l}(\xi_{k})\bigr) +\bigvee _{j=1}^{n}l_{ij}f_{j} \bigl(x_{j}^{l}(\xi_{k})\bigr), \end{aligned}$$

for \(l=1,2\) and \(i=1,2,\ldots,n\).

Denote by \(x^{1}(t)\) and \(x^{2}(t)\) two different solutions for (1) with initial conditions \((t_{0},x^{1})\) and \((t_{0},x^{2})\), respectively, where \(t_{0} \in[\eta_{k},\eta_{k+1}]\). To prove the uniqueness, it is sufficient to check that \(x^{1}\neq x^{2}\) implies \(x^{1}(t)\neq x^{2}(t)\) for every \(t \in[\eta_{k},\eta_{k+1}]\). Then we get

$$\begin{gathered} \big\| x^{1}(t)-x^{2}(t)\big\| \\ \quad\leq \big\| x^{1}-x^{2}\big\| +\frac{1}{\Gamma(q)}\sum _{i=1}^{n} \bigg| \int_{t_{0}}^{t}(t-s)^{q-1}\bigl[\omega _{i}\bigl(x_{i}^{1}(s)\bigr) \bigl(H_{i}^{1}(s)+C_{i}\bigr) \\ \quad \quad{}-\omega_{i}\bigl(x_{i}^{2}(s)\bigr) \bigl(H_{i}^{2}(s)+C_{i}\bigr)\bigr] \, \mathrm{d}s \bigg| \\ \quad\leq \big\| x^{1}-x^{2}\big\| +\frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1} \sum _{i=1}^{n}M_{i}\widetilde{ \omega}_{i}\big|x_{i}^{1}(s)-x_{i}^{2}(s)\big| \,\mathrm{d}s \\ \quad\quad{}+\frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1} \sum _{i=1}^{n}\overline{\omega}_{i}\big|H_{i}^{1}(s)-H_{i}^{2}(s)\big|\, \mathrm {d}s \\ \quad\leq \big\| x^{1}-x^{2}\big\| +\theta_{1} \frac{1}{\Gamma(q)} \int_{t_{0}}^{t}(t-s)^{q-1}\big\| x^{1}(s)-x^{2}(s) \big\| \,\mathrm{d}s \\ \quad \quad{}+A_{2}\theta_{2}\big\| x^{1}( \xi_{k})-x^{2}(\xi_{k})\big\| . \end{gathered}$$

Applying Lemma 2.1, we get

$$ \big\| x^{1}(t)-x^{2}(t)\big\| \leq\bigl(\big\| x^{1}-x^{2} \big\| +A_{2}\theta_{2} \big\| x^{1}(\xi_{k})-x^{2}( \xi_{k})\big\| \bigr)E_{q}\bigl(\theta_{1} \eta^{q}\bigr). $$
(4)

Particularly,

$$ \big\| x^{1}(\xi_{k})-x^{2}(\xi_{k})\big\| \leq\bigl(\big\| x^{1}-x^{2}\big\| +A_{2} \theta_{2}\big\| x^{1}(\xi_{k})-x^{2}( \xi_{k})\big\| \bigr)E_{q}\bigl(\theta_{1}\eta ^{q}\bigr) $$

and

$$ \big\| x^{1}(\xi_{k})-x^{2}(\xi_{k})\big\| \leq\frac{E_{q}(\theta_{1} \eta^{q})}{1-A_{2}\theta_{2}E_{q}(\theta_{1}\eta^{q})}\big\| x^{1}-x^{2}\big\| . $$
(5)

Substituting (5) into (4), we obtain

$$ \big\| x^{1}(t)-x^{2}(t)\big\| \leq\frac{E_{q}(\theta_{1}\eta^{q})}{1-A_{2}\theta _{2}E_{q}(\theta_{1}\eta^{q})} \big\| x^{1}-x^{2}\big\| . $$
(6)

Suppose that there exists some \(\bar{t} \in[\eta_{k}, \eta_{k+1}]\) such that \(x^{1}(\bar{t})=x^{2}(\bar{t})\). Then

$$ \big\| x^{1}-x^{2}\big\| \leq\theta_{1}\frac{1}{\Gamma(q)} \int_{t_{0}}^{\bar {t}}(t-s)^{q-1} \big\| x^{1}(s)-x^{2}(s)\big\| \,\mathrm{d}s+A_{2} \theta_{2}\big\| x^{1}(\xi _{k})-x^{2}( \xi_{k})\big\| . $$
(7)

Combining this with (5), (6), and (7), we get

$$ \big\| x^{1}-x^{2}\big\| \leq\frac{\theta_{2}(\theta_{1}+A_{2}) E_{q}(\theta_{1}\eta^{q})}{1-A_{2}\theta_{2}E_{q}(\theta_{1}\eta^{q})} \big\| x^{1}-x^{2}\big\| . $$

Applying (A5), it follows that

$$ \big\| x^{1}-x^{2}\big\| < \big\| x^{1}-x^{2}\big\| . $$

This poses a contradiction and it demonstrates the validity of the uniqueness of solution for (1). Hence, (1) has a unique solution \(x(t)\) for every initial condition \((t_{0},x_{0}) \in\mathcal{R}^{+} \times\mathcal{R}^{n}\). This completes the proof. □

3.2 Estimation of deviating argument

In this subsection, we give the estimation of the norm of the deviating state.

From Schauder’s fixed point theorem and assumptions (A1) and (A2), the existence of the equilibrium point of (1) can be guaranteed. Denote the equilibrium point of (1) by \(x^{*}=(x_{1}^{*}, x_{2}^{*},\ldots, x_{n}^{*})^{T}\). Substitution of \(v(t)=x(t)-x^{*}\) into (1) leads to

$$\begin{aligned} {}_{t_{0}}^{C}D_{t}^{q}v_{i}(t)={}& \omega_{i}\bigl(v_{i}(t) +x_{i}^{*} \bigr) \Biggl(-\widetilde{\alpha}_{i}\bigl(v_{i}(t)\bigr) + \sum_{j=1}^{n}b_{ij}F_{j} \bigl(v_{j}(t)\bigr) +\sum_{j=1}^{n}c_{ij}G_{j} \bigl(v_{j}\bigl(\gamma(t)\bigr)\bigr) \\ & +\bigwedge_{j=1}^{n}h_{ij}F_{j} \bigl(v_{j}\bigl(\gamma(t)\bigr)\bigr) +\bigvee _{j=1}^{n}F_{j}\bigl(v_{j} \bigl(\gamma(t)\bigr)\bigr) \Biggr),\end{aligned} $$
(8)

where \(\widetilde{\alpha}_{i}(v_{i}(t))=\alpha_{i}(v_{i}(t) +x_{i}^{*})-\alpha_{i}(x_{i}^{*})\), \(F_{j}(v_{j}(t)) =f_{j}(v_{j}(t)+x_{j}^{*})-f_{j}(x_{j}^{*})\) and \(G_{j}(v_{j}(t))= g_{j}(v_{j}(t)+x_{j}^{*})-g_{j}(x_{j}^{*})\) for \(i,j=1,2,\ldots,n\).

Theorem 3.2

Let (A1)-(A6) hold and let \(v(t)=(v_{1}(t),v_{2}(t))^{T},\ldots, v_{n}(t)\) be a solution of (8). Then

$$ v\bigl(\gamma(t)\bigr)\leq\varrho v(t), $$

for any \(t \in\mathcal{R}^{+}\), where ϱ is defined in (2).

Proof

For any \(t \in\mathcal{R}^{+}\), there exists a unique \(k \in\mathcal{N}\) such that \(t \in[\eta_{k}, \eta_{k+1})\). It follows that

$$ \begin{aligned}[b] v_{i}(t)={}&v_{i}(\xi_{k})+\frac{1}{\Gamma(q)} \int_{\xi_{k}}^{t}(t-s)^{q-1} \Biggl\{ \omega_{i}\bigl(v_{i}(s)+x_{i}^{*} \bigr) \Biggl(-\widetilde{\alpha}_{i}\bigl(v_{i}(s)\bigr) \\ &+\sum_{j=1}^{n}b_{ij}F_{j} \bigl(v_{j}(s)\bigr) +\sum_{j=1}^{n}c_{ij}G_{j} \bigl(v_{j}\bigl(\gamma(s)\bigr)\bigr) \\ &+\bigwedge _{j=1}^{n}h_{ij}F_{j} \bigl(v_{j}\bigl(\gamma(s)\bigr)\bigr)+\bigvee_{j=1}^{n}F_{j} \bigl(v_{j}\bigl(\gamma(s)\bigr)\bigr) \Biggr) \Biggr\} \,\mathrm{d}s,\end{aligned} $$
(9)

for \(t \in[\xi_{k},\eta_{k+1})\), and

$$\begin{aligned} v_{i}(\xi_{k})={}&v_{i}(t)+\frac{1}{\Gamma(q)} \int_{t}^{\xi_{k}} (\xi_{k}-s)^{q-1} \Biggl\{ \omega_{i}\bigl(v_{i}(s)+x_{i}^{*} \bigr) \Biggl(-\widetilde{\alpha}_{i}\bigl(v_{i}(s)\bigr) \\ &+\sum_{j=1}^{n}b_{ij}F_{j} \bigl(v_{j}(s)\bigr) +\sum_{j=1}^{n}c_{ij}G_{j} \bigl(v_{j}\bigl(\gamma(s)\bigr)\bigr) \\ &+\bigwedge _{j=1}^{n}h_{ij}F_{j} \bigl(v_{j}\bigl(\gamma(s)\bigr)\bigr) +\bigvee_{j=1}^{n}F_{j} \bigl(v_{j}\bigl(\gamma(s)\bigr)\bigr) \Biggr) \Biggr\} \,\mathrm {d}s, \end{aligned}$$

for \(t \in[\eta_{k}, \xi_{k})\).

Without loss of generality, we only consider the case of \(t \in[\xi_{k},\eta_{k+1})\). The other case can be considered in a similar manner.

We have

$$\begin{aligned} \big\| v(t)\big\| \leq{}& \big\| v(\xi_{k})\big\| +\frac{1}{\Gamma(q)} \sum _{i=1}^{n} \int_{\xi_{k}}^{t}(t-s)^{q-1} \Biggl\{ \omega_{i}\bigl(v_{i}(t)+x_{i}^{*} \bigr) \Biggl(-\widetilde{\alpha}_{i}\bigl(v_{i}(t)\bigr) \\ &+\sum_{j=1}^{n}b_{ij}F_{j} \bigl(v_{j}(t)\bigr) +\sum_{j=1}^{n}c_{ij}G_{j} \bigl(v_{j}\bigl(\gamma(t)\bigr)\bigr) \\ &+\bigwedge _{j=1}^{n}h_{ij}F_{j} \bigl(v_{j}\bigl(\gamma(t)\bigr)\bigr)+\bigvee_{j=1}^{n}F_{j} \bigl(v_{j}\bigl(\gamma(t)\bigr)\bigr) \Biggr) \Biggr\} \,\mathrm {d}s \\ \leq{}& \big\| v(\xi_{k})\big\| +\frac{1}{\Gamma(q)} \int_{\xi_{k}}^{t}(t-s)^{q-1} \Biggl(\sum _{i=1}^{n}\overline{\omega}_{i} \bar{c}_{i}\big|v_{i}(s)\big| +\sum_{i=1}^{n} \sum_{j=1}^{n}\overline{ \omega}_{j}|b_{ji}|\tilde {c}_{i}\big|v_{i}(s)\big| \\ & +\sum_{i=1}^{n}\sum _{j=1}^{n}\overline{\omega}_{j}|c_{ji}| \hat {c}_{i}\big|v_{i}(\xi_{k})\big| +\sum _{i=1}^{n}\sum_{j=1}^{n} \overline{\omega}_{j}|h_{ji}|\tilde {c}_{i}\big|v_{i}( \xi_{k})\big| \\ & +\sum_{i=1}^{n}\sum _{j=1}^{n}\overline{\omega}_{j}|l_{ji}| \tilde {c}_{i}\big|v_{i}(\xi_{k})\big| \Biggr)\, \mathrm{d}s \\ \leq{}& \big\| v(\xi_{k})\big\| +\frac{1}{\Gamma(q)} \int_{\xi _{k}}^{t}(t-s)^{q-1} \bigl(A_{1}\big\| v(s)\big\| +A_{2}\big\| v(\xi_{k})\big\| \bigr)\, \mathrm{d}s \\ \leq{}& (1+A_{2}\theta_{2})\big\| v(\xi_{k})\big\| + \frac{1}{\Gamma(q)} \int_{\xi_{k}}^{t}A_{1}(t-s)^{q-1} \big\| v(s)\big\| \,\mathrm{d}s, \end{aligned}$$

where \(A_{1}\), \(A_{2}\), and \(\theta_{2}\) are defined in (2).

Applying Lemma 2.1, we have

$$\begin{aligned} \big\| v(t)\big\| \leq{}&(1+A_{2}\theta_{2})\big\| v(\xi_{k}) \big\| E_{q}\bigl(A_{1}(t{-\xi _{k}})^{q} \bigr) \\ \leq{}& (1+A_{2}\theta_{2})\big\| v(\xi_{k}) \big\| E_{q}\bigl(A_{1}\eta^{q}\bigr).\end{aligned} $$

In a similar way, by exchanging the locations of \(v_{i}(t)\) and \(v_{i}(\xi_{k})\) in (9), we get

$$ \big\| v(\xi_{k})\big\| \leq\big\| v(t)\big\| +\theta_{2}(A_{1} \tau+A_{2})\big\| v(\xi_{k})\big\| . $$

Hence

$$ \big\| v(\xi_{k})\big\| \leq\varrho\big\| v(t)\big\| , $$

where τ and ϱ are defined in (2).

Therefore, Theorem 3.2 is valid for any \(t \in\mathcal{R}^{+}\). □

3.3 Global Mittag-Leffler stability

Theorem 3.3

Let (A1)-(A6) hold. Then (1) is globally Mittag-Leffler stable if the following inequality is satisfied:

$$ A_{3}-A_{4}\varrho^{2}>0, $$

where \(A_{3}\), \(A_{4}\), and ϱ are defined in (2).

Proof

Define a Lyapunov function by

$$ W\bigl(v(t)\bigr)=\sum_{i=1}^{n}v_{i}^{2}(t). $$

From Lemma 2.2 and Lemma 2.3, we derive

$$\begin{aligned} {}_{t_{0}}^{C}D_{t}^{q}W\bigl(v(t)\bigr) \leq{}& 2\sum_{i=1}^{n}v_{i}(t){}_{t_{0}}^{C}D_{t}^{q}v_{i}(t) \\ ={}&2\sum_{i=1}^{n}v_{i}(t) \omega_{i}\bigl(v_{i}(t)+x_{i}^{*} \bigr) \Biggl(-\widetilde{\alpha}_{i}\bigl(v_{i}(t)\bigr)+ \sum_{j=1}^{n}b_{ij}F_{j} \bigl(v_{j}(t)\bigr) \\ &+\sum_{j=1}^{n}c_{ij}G_{j} \bigl(v_{j}\bigl(\gamma(t)\bigr)\bigr) +\bigwedge _{j=1}^{n}h_{ij}F_{j} \bigl(v_{j}\bigl(\gamma(t)\bigr)\bigr) +\bigvee _{j=1}^{n}F_{j}\bigl(v_{j} \bigl(\gamma(t)\bigr)\bigr) \Biggr) \\ \leq{}&2\sum_{i=1}^{n}\omega_{i} \bigl(v_{i}(t)+x_{i}^{*}\bigr) \Biggl(-v_{i}^{2}(t)\frac{\widetilde{\alpha}_{i}(v_{i}(t))}{v_{i}(t)} +\sum _{j=1}^{n}|b_{ij}|\tilde{c}_{j}\big|v_{i}(t)\big|\big|v_{j}(t)\big| \\ &+\sum_{j=1}^{n}|c_{ij}| \hat{c}_{j}\big|v_{i}(t)\big|\big|v_{j}\bigl(\gamma(t)\bigr)\big| +\sum_{j=1}^{n}|h_{ij}| \tilde{c}_{j}\big|v_{i}(t)\big|\big|v_{j}\bigl(\gamma(t) \bigr)\big| \\ & +\sum_{j=1}^{n}|l_{ij}| \tilde{c}_{j}\big|v_{i}(t)\big|\big|v_{j}\bigl(\gamma(t) \bigr)\big| \Biggr) \\ \leq{}&\sum_{i=1}^{n}\omega_{i} \bigl(v_{i}(t)+x_{i}^{*}\bigr) \Biggl(-2 \underline{\alpha}_{i}v_{i}^{2}(t) +\sum _{j=1}^{n}|b_{ij}|\tilde{c}_{i} \bigl(v_{i}^{2}(t)+v_{j}^{2}(t)\bigr) \\ &+\sum_{j=1}^{n}\bigl(|c_{ij}| \hat{c}_{j}+|h_{ij}|\tilde{c}_{j} +|l_{ij}|\tilde{c}_{j}\bigr) \bigl(v_{i}^{2}(t)+v_{j}^{2} \bigl(\gamma(t)\bigr)\bigr) \Biggr) \\ \leq{}& -2\sum_{i=1}^{n} \underline{ \omega}_{i}\underline{\alpha}_{i}v_{i}^{2}(t) +\sum_{i=1}^{n}\sum _{j=1}^{n}\overline{\omega}_{i}|b_{ij}| \tilde{c}_{i}\bigl(v_{i}^{2}(t)+v_{j}^{2}(t) \bigr) \\ &+\sum_{i=1}^{n}\sum _{j=1}^{n}\overline{\omega}_{i}\bigl(|c_{ij}| \hat{c}_{j}+|h_{ij}|\tilde{c}_{j}+|l_{ij}| \tilde{c}_{j}\bigr) \bigl(v_{i}^{2}(t) +v_{j}^{2}\bigl(\gamma(t)\bigr)\bigr) \\ \leq{}&-\sum_{i=1}^{n} \Biggl[2\underline{ \omega}_{i}\underline{\alpha}_{i} -\sum _{j=1}^{n}\bigl(\overline{\omega}_{i}|b_{ij}| \tilde{c}_{i} +k_{j}\overline{\omega}_{j}|b_{ji}| \tilde{c}_{j}\bigr) \\ & -\sum_{j=1}^{n} \overline{\omega}_{i}\bigl(|c_{ij}|\hat{c}_{j}+|h_{ij}|\tilde{c}_{j}+|l_{ij}| \tilde{c}_{j}\bigr) \Biggr]v_{i}^{2}(t) \\ &+\sum _{i=1}^{n}\sum_{j=1}^{n} \overline{\omega}_{j}\bigl(|c_{ji}|\hat{c}_{i}+|h_{ji}|\tilde{c}_{i}+|l_{ji}|\tilde {c}_{i}\bigr)v_{i}^{2}\bigl(\gamma(t)\bigr) \\\leq{}& -A_{3}\big\| v(t)\big\| ^{2}+A_{4}\big\| v\bigl( \gamma(t)\bigr)\big\| ^{2}. \end{aligned}$$

Applying Theorem 3.2, it follows that

$$ {}_{t_{0}}^{C}D_{t}^{q}W\bigl(v(t)\bigr) \leq-\bigl(A_{3} -A_{4}\varrho^{2}\bigr)\big\| v(t) \big\| ^{2}. $$

From the definition of \(W(v(t))\), it is clear that

$$ W\bigl(v(t)\bigr)=\sum_{i=1}^{n}v_{i}^{2}(t) \leq \Biggl(\sum_{i=1}^{n}\big|v_{i}(t)\big| \Biggr)^{2}= \big\| v(t)\big\| ^{2} $$

and

$$ W\bigl(v(t)\bigr)=\sum_{i=1}^{n}v_{i}^{2}(t)= \frac{1}{n}\sum_{i=1}^{n}nv_{i}^{2}(t) \geq\frac{1}{n} \Biggl(\sum_{i=1}^{n}\big|v_{i}(t)\big| \Biggr)^{2} =\frac{1}{n}\big\| v(t)\big\| ^{2}. $$

Hence

$$ {}_{t_{0}}^{C}D_{t}^{q}W\bigl(v(t)\bigr) \leq-\Delta W\bigl(v(t)\bigr), $$

where \(\Delta=(A_{3}-A_{4}\varrho^{2})>0\).

Based on Lemma 2.4, it follows that

$$ \frac{1}{n}\big\| v(t)\big\| ^{2}\leq W\bigl(v(t)\bigr) \leq W \bigl(v(t_{0})\bigr)E_{q}\bigl(-\Delta(t-t_{0})^{q} \bigr). $$

Therefore,

$$ \big\| x(t)-x^{*}\big\| ^{2} \leq\mathbf{M}\big\| x(t_{0})-x^{*} \big\| ^{2} E_{q}\bigl(-\Delta(t-t_{0})^{q} \bigr), $$

where \(\mathbf{M}=n\).

Hence, (1) is globally Mittag-Leffler stable. This completes the proof. □

Remark 3.1

Fractional-order neural networks have plenty of favorable characteristics, such as infinity memory and hereditary features, in contrast with integer-order ones, whereas the approaches investigated in integer-order neural networks cannot be applied straightforward to fractional-order ones.

Remark 3.2

In recent years, fractional-order neural networks have been under intensive investigation. A lot of results are reported about Mittag-Leffler stability and asymptotical ω-periodicity on fractional-order neural networks with or without deviating argument. Very few of them are about the stability of fractional-order Cohen-Grossberg neural networks with deviating argument and the existing results cannot be applied straightforwardly to fractional-order Cohen-Grossberg neural networks with deviating argument. From this point of view, the result derived in this paper can be viewed as an extension to the existing literature.

4 Illustrative examples

In this section, one example is given to demonstrate the validity of the results.

Example 1

Consider the following fractional-order neural network in the presence of deviating argument:

$$ \left \{ \textstyle\begin{array}{l} {}_{t_{0}}^{C}D_{t}^{0.98}x_{1}(t)=(2+\frac{1}{3}\sin(x_{1}(t))) (-4x_{1}(t)+0.04\tanh(x_{1}(t))\\ \phantom{{}_{t_{0}}^{C}D_{t}^{0.98}x_{1}(t)=} +0.01\tanh(x_{2}(t))+0.01\tanh(\frac{x_{1}(\gamma(t))}{3})\\ \phantom{{}_{t_{0}}^{C}D_{t}^{0.98}x_{1}(t)=}+0.02\tanh (\frac{x_{2}(\gamma(t))}{3}) +0.01\tanh(x_{1}(\gamma(t)))\\ \phantom{{}_{t_{0}}^{C}D_{t}^{0.98}x_{1}(t)=}\wedge0.02\tanh(x_{2}(\gamma(t))) +0.02\tanh(x_{1}(\gamma(t)))\\ \phantom{{}_{t_{0}}^{C}D_{t}^{0.98}x_{1}(t)=}\vee0.02\tanh(x_{2}(\gamma (t)))+0.01 ),\\ {}_{t_{0}}^{C}D_{t}^{0.98}x_{2}(t)=(1+\frac{1}{3}\cos(x_{2}(t))) (-3x_{2}(t)+0.02\tanh(x_{1}(t))\\ \phantom{{}_{t_{0}}^{C}D_{t}^{0.98}x_{2}(t)=} +0.02\tanh(x_{2}(t))+0.03\tanh(\frac{x_{1}(\gamma(t))}{3})\\ \phantom{{}_{t_{0}}^{C}D_{t}^{0.98}x_{2}(t)=}+0.01\tanh (\frac{x_{2}(\gamma(t))}{3}) +0.03\tanh(x_{1}(\gamma(t)))\\ \phantom{{}_{t_{0}}^{C}D_{t}^{0.98}x_{2}(t)=}\wedge0.02\tanh(x_{2}(\gamma(t))) +0.02\tanh(x_{1}(\gamma(t)))\\ \phantom{{}_{t_{0}}^{C}D_{t}^{0.98}x_{2}(t)=}\vee0.01\tanh(x_{2}(\gamma (t)))+0.01 ), \end{array}\displaystyle \right . $$
(10)

where \(\{\eta_{k}\}=\frac{k}{20}\), \(\{\xi_{k}\}=\frac{2k+1}{40}\) and \(\gamma(t)=\xi_{k}\) for \(t \in[\eta_{k},\eta_{k+1})\), \(k \in\mathcal{N}\).

It can be seen that \(\underline{\omega}_{1}=\frac{5}{3}\), \(\overline{\omega}_{1}= \frac{7}{3}\),\(\underline{\omega}_{2} =\frac{2}{3}\), \(\overline{\omega}_{2}=\frac{4}{3}\), \(\widetilde{\omega}_{1}=\widetilde{\omega}_{2}=\frac{1}{3}\), \(\underline{\alpha}_{1}=\overline{\alpha}_{1}=4\), \(\underline{\alpha}_{2}=\overline{\alpha}_{2}=3\), \(\tilde{c}_{1}=\tilde{c}_{2}=1\), \(\hat{c}_{1}=\hat{c}_{2}= \frac{1}{3}\), \(\eta=\frac{1}{20}\), \(b_{11}=0.04\), \(b_{12}=0.01\), \(b_{21}=0.02\), \(b_{22}=0.02\), \(c_{11}=0.01\), \(c_{12}=0.02\), \(c_{21}=0.03\), \(c_{22}=0.01\), \(d_{11}=d_{12}=d_{21}=d_{22}=0\), \(p_{11}=p_{12}=p_{21}=p_{22}=0\), \(r_{11}=r_{12}=r_{21}=r_{22}=0\), \(h_{11}=0.01\), \(h_{12}=0.02\), \(h_{21}=0.03\), \(h_{22}=0.02\), and \(l_{11}=0.02\), \(l_{12}=0.02\), \(l_{21}=0.02\), \(l_{22}=0.01\), \(I_{1}=I_{2}=0.01\).

Choose the initial value \(x^{0}\) satisfying \(|x_{1}^{0}|\leq0.5,|x_{2}^{0}|\leq0.5\). By calculation, we have

$$\begin{aligned}& \tilde{A}=\max_{1\leq i\leq2}\Biggl(\overline{\omega}_{i} \overline{\alpha}_{i}+\sum_{j=1}^{n} \overline{\omega}_{j} |b_{ji}|\tilde{c}_{i} \Biggr)=9.4533, \\& A_{1}=\max_{1\leq i\leq2}\Biggl(\widetilde{ \omega}_{i}\overline{\alpha}_{i} +\sum _{j=1}^{2}\overline{\omega}_{j}|b_{ji}| \tilde {c}_{i}\Biggr)=1.4533, \\& A_{2}=\max_{1\leq i\leq2}\Biggl(\sum _{j=1}^{2}\overline{\omega}_{j}\bigl(|c_{ji}| \hat{c}_{i}+|h_{ji}|\tilde{c}_{i}+|l_{ji}| \tilde {c}_{i}\bigr)\Biggr)=0.1578, \\& \theta_{2}=\frac{\eta^{q}}{\Gamma(q+1)}=0.0535, \\& B=\frac{\eta^{q}(\tilde{A}+A_{2})}{\Gamma(q+1)}=0.5145< 1, \\& \mathcal{B}=\frac{1}{1-B}\Biggl(\big\| x^{0}\big\| +\theta_{2} \sum_{i=1}^{n} \overline{ \omega}_{i}|C_{i}|\Biggr)=2.0639, \\& M=\max_{1\leq i \leq2}(M_{i})=8.3669, \\& \theta_{1}=A_{1}+\widetilde{\omega}M=4.2423, \\& \begin{aligned}A_{3}&=\frac{1}{2}\min_{1\leq i\leq2}\Biggl(2\underline{ \omega}_{i} \underline{\alpha}_{i}-\sum _{j=1}^{2}\bigl(\overline{\omega}_{i} |b_{ij}|\tilde{c}_{i}+\overline{\omega}_{j}|b_{ji}| \tilde{c}_{j}\bigr)-\sum_{j=1}^{2}\overline{ \omega}_{i}\bigl(|c_{ij}| \hat{c}_{j}+|h_{ij}| \tilde{c}_{j}+|l_{ij}|\tilde {c}_{j}\bigr)\Biggr)\\&=1.8928,\end{aligned} \\& A_{4}=\max_{1\leq i\leq2}\Biggl(\sum _{j=1}^{2} \overline{\omega}_{j}\bigl(|c_{ji}| \hat{c}_{i}+|h_{ji}|\tilde{c}_{i} +|l_{ji}|\tilde{c}_{i}\bigr)\Biggr)=0.1577, \\& \tau=(1+A_{2}\theta_{2})E_{q} \bigl(A_{1}\eta^{q}\bigr)=1.0910, \\& \theta_{2}(\theta_{1}+A_{2})=0.2354< 1, \\& \theta_{2}(A_{1}\tau+A_{2})=0.0933< 1, \\& \frac{\theta_{2}(\theta_{1}+A_{2}) E_{q}(\theta_{1}\eta^{q})}{1-A_{2}\theta_{2} E_{q}(\theta_{1}(\eta^{q}))}=0.2987< 1, \\& \varrho=\bigl[1-\theta_{2}(A_{1}\tau+A_{2}) \bigr]^{-1}=1.1029, \\& A_{3}-A_{4}\varrho^{2}=1.7010>0. \end{aligned}$$

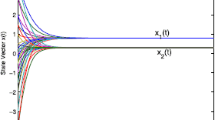
Based on Theorem 3.3, (10) is globally Mittag-Leffler stable. Simulation results from several initial values are depicted in Figures 1 and 2, which are well suited to show the theoretical predictions.

Figure 1
figure 1

Transient behavior of \(\pmb{x_{1}(t)}\) and \(\pmb{x_{2}(t)}\) in ( 10 ).

Full size image
Figure 2
figure 2

The phase plot of \(\pmb{x(t)}\) in ( 10 ).

Full size image

Remark 4.1

Example 1 shows that the derived criteria are applicable to the Mittag-Leffler stability of fractional-order fuzzy Cohen-Grossberg neural networks with deviating argument. As a special case of the obtained criteria, let \(\widetilde{\omega}=0\), that is, \(\omega_{i}(\cdot)\) degenerates into a constant, and \(d_{ij}=0\), \(h_{ij}=0\), \(l_{ij}=0\), \(p_{ij}=0\), and \(r_{ij}=0\), for \(i,j=1,2, \ldots,n\). It is obvious that the criteria are still valid, which is exactly the main theorem in [52]. Hence, the criteria proposed in this paper can be deemed a generalization of the existing literature.

5 Concluding remarks

In this paper, the global Mittag-Leffler stability of fractional-order fuzzy Cohen-Grossberg neural networks with deviating argument is considered. Sufficient conditions are obtained to ensure the existence and uniqueness of the solution. Furthermore, the global Mittag-Leffler stability of fractional-order fuzzy Cohen-Grossberg neural networks with deviating argument is investigated. A numerical example and the corresponding simulations show that global Mittag-Leffler stability can be guaranteed under the derived criteria. The results obtained in this paper supplement the existing literature. Future work may aim at exploring the multistability and multiperiodicity for fractional-order fuzzy Cohen-Grossberg neural networks with deviating argument.