1 Introduction

The Rossby waves on behalf of huge vortices which exist in the ocean and atmosphere play an increasingly significant role in transporting energy, which can determine the weather and climate change in the earth to a large extent [1–3]. In the last few decades , the research on constructing mathematical models to study the generation and evolution of Rossby waves has attracted a lot of attention, and a series of mathematical models, such as KdV [4, 5], mKdV [6, 7], ZK [8, 9], modified Kawahara equation [10], and so on [11, 12], have been obtained. Meanwhile, some natural phenomena related to Rossby waves were explained with the help of mathematical models [13]. We notice that the former research has the following two disadvantages:

(1) The motion equations describing ocean and atmosphere, including momentum equation, continuity equation, and so on, are very complicated. For the sake of simplicity, we can find that \((1+1)\) dimensional nonlinear partial differential equations are used to describe the evolution of nonlinear Rossby waves. However, real oceanic and atmospheric motions are not just in one direction. Providing higher dimensional theories for the nonlinear Rossby waves is necessary. So, in this paper, we discuss a new \((2+1)\) dimensional model [14].

(2) All the time, the complete Coriolis force has been an important research hot spot in dealing with the atmosphere and ocean. On the one hand, the horizontal component of the complete Coriolis force shows the imbalance of the motion, which is an important factor that causes the development of weather system. On the other hand, the theoretical research on the nonlinear Rossby waves in the atmosphere has been a very important subject in meteorology. So, it is necessary to analyze the effect of intact Coriolis force on atmospheric dynamics. However, in order to calculate and study it conveniently, many researchers ignore the complete Coriolis force. As we know, the TA is suitable for quantitative studies. In the past, Kasahara [15] pointed out that the errors made by ignoring the vertical acceleration may be much larger than those made by ignoring the horizontal component of complete Coriolis force. However, it is controversial from the dynamical perspective [16, 17]. White and Bromley [18] indicated the necessity to retain the horizontal component of Coriolis force by scale analysis of the zonal momentum equations. It is necessary to include the cosine Coriolis terms for fully understanding the atmospheric motion, which is named ‘non-traditional approximation’ (NTA). Based on the NTA, the near-inertial waves were considered by Gerkema and Shrira [19] from primitive equations. Using the variational method, a conserved potential vorticity equation with complete Coriolis force was obtained by Dellar and Salmon [20]. According to the Hamilton least-action principle [21], Dellar also derived a generalized beta plane equation. So, the NTA is more important for tropical atmosphere, such as the stability theory [22–24], the dispersion relation [25, 26], the Madden-Julian Oscillation(MJO) [27, 28], and so on [29–31].

Conservation laws [32, 33] are a power tool for studying the global stability of solutions and numerical integration for PDEs emerging in nonlinear science. Numerous powerful methods have been used to seek the conservation laws: Laplace direct technique [34], characteristic form given by Stuedel [35], q-homotopy analysis transform method (q-HATM) [36], multiplier approach [37, 38]. In this thesis, based on the modified Camassa-Holm equation [39] and ZK-BBM equations [40] for each multiplier, and the method of Ibragimov (nonlocal conservation method) [41–43], using the multiplier approach, conservation laws and the corresponding conserved quantities are discussed.

The investigation of the soliton solutions [44–46] for PDEs has become highly active in all areas of applied research. Many efficient techniques, such as homogeneous balance technique [47], symmetry theory [48], Jacobi elliptic function method [49], homotopy analysis transform method [50], homotopy perturbation transform method [51], Darboux transformation [52–54], Bilinear method [55, 56], and so on [57], have been proposed to seek solitary waves solutions. In addition, some numerical methods, i.e., modified binomial and Monte Carlo methods [58], high accurate NRK, and MWENO [59–61], have also been used to solve partial differential equations. In the paper, we use the semi-inverse variational principle [62, 63] to obtain the soliton solutions of PDEs.

In this article, by using multi-scale analysis and perturbation method, a \((2+1)\) dimensional combined ZK-mZK model for Rossby solitary waves is obtained. According to the new model, we have a discussion. The construction of this paper is as follows. In Section 2, applying the quasi-geostrophic potential vorticity equation, we obtain a new combined ZK-mZK equation. The property of conservation laws and the corresponding conserved quantities of the new equation are discussed in Section 3. Later, the soliton solutions of the combined ZK-mZK equation are established in Section 4. According to the soliton solution, we research the solitary wave profiles for various timescales and the collisions between two waves with different velocities and various timescales. Finally, some conclusions are drawn.

2 The derivation of combined ZK-mZK equation

Based on the basic equations of geophysical fluid dynamics, after reasonable assumption, we can easily obtain the following non-dimensional quasi-geostrophic potential vorticity equation:

$$ \begin{aligned}[b] &\biggl(\frac{\partial }{\partial t}+\frac{\partial \Psi }{\partial x}\frac{ \partial }{\partial y}-\frac{\partial \Psi }{\partial y} \frac{\partial }{\partial x}\biggr) \\ &\quad{}\cdot \biggl[\nabla^{2}\Psi +\frac{\partial }{\partial z} \biggl(\frac{f _{0}^{2}}{N(z)^{2}}\frac{\partial \Psi }{\partial z}\biggr)+\beta (y)y+ \frac{f _{0}}{H}G(x,y)-f_{H}\frac{\partial G(x,y)}{\partial y}\biggr]=0. \end{aligned} $$
(1)

The vertical velocity is

$$ W=\frac{f_{0}}{N(z)^{2}}\biggl(\frac{\partial }{\partial t}+\frac{\partial \Psi }{\partial x} \frac{\partial }{\partial y}-\frac{\partial \Psi }{ \partial y}\frac{\partial }{\partial x}\biggr)\frac{\partial \Psi }{\partial z}, $$
(2)

where Ψ is the stream function. Normal component of the complete Coriolis is \(f=f_{0}+\beta (y)y\), and horizontal component is \(f_{H}\), where \(f_{0}\), \(f_{H}\) are unknown constants. \(G(x,y)\) is the topographic effect. \(N(z)\) is the function of z. \(\nabla^{2}= \partial^{2}/\partial x^{2}+\partial^{2}/\partial y^{2}\) is the Laplace operator.

The lateral boundary condition is

$$ \Psi (0)=\Psi (+\infty )=0. $$
(3)

The vertical boundary condition is

$$ W(0)=W(+\infty )=0. $$
(4)

Take the dimensionless variables into Eq. (1) and Eq. (2), then Eq. (1) and Eq. (2) are transformed into the dimensionless equation:

$$\begin{aligned}& \begin{aligned}[b] &\biggl(\frac{\partial }{\partial t}+\frac{\partial \Psi }{\partial x}\frac{ \partial }{\partial y}-\frac{\partial \Psi }{\partial y} \frac{\partial }{\partial x}\biggr) \\ &\quad{}\cdot\biggl[\nabla^{2}\Psi +\frac{\partial }{\partial z} \biggl(K ^{2}\frac{ \partial \Psi }{\partial z}\biggr)+\beta (y)y+G(x,y)-\theta \frac{\partial G(x,y)}{\partial y}\biggr]=0, \end{aligned} \end{aligned}$$
(5)
$$\begin{aligned}& W=R_{0}K^{2}\biggl(\frac{\partial }{\partial t}+\frac{\partial \Psi }{ \partial x} \frac{\partial }{\partial y}-\frac{\partial \Psi }{\partial y}\frac{\partial }{\partial x}\biggr)\frac{\partial \Psi }{\partial z}, \end{aligned}$$
(6)

where \(K^{2}=L_{0}^{2}f_{0}^{2}/N^{2}H_{0}^{2}\), \(R_{0}=U_{0}/f_{0}L _{0}\), \(\theta =f_{H}*H/f_{0}*L_{0}\). \(L_{0}\) is the horizontal feature of space, \(U_{0}\) is the velocity characteristic quantity, and \(H_{0}\) is the characteristic quantity of fluid thickness.

Assume \(G(x,y)=\varepsilon^{\frac{3}{2}}O(y)\) and the stream function Ψ as the sum of zonal flow and perturbation stream function ψ

$$ \Psi =- \int^{y}\bigl(U(s)-c_{0}\bigr)\,ds+\varepsilon \psi , $$
(7)

where the constant \(c_{0}\) is the sign of the velocity of non-dispersive part of linear Rossby waves. \(\varepsilon \ll 1\) is a small parameter used to measure the magnitude of nonlinear feature.

Substituting the stream function Ψ into Eq. (5), we have

$$\begin{aligned}& \begin{aligned}[b] &\frac{\partial }{\partial t}\biggl[\nabla^{2}\psi + \frac{\partial }{\partial z}\biggl(K^{2}\frac{\partial \psi }{\partial z}\biggr) \biggr]+(U-c_{0})\frac{\partial }{ \partial x}\biggl[\nabla^{2}\psi + \frac{\partial }{\partial z}\biggl(K^{2}\frac{ \partial \psi }{\partial z}\biggr)\biggr]+\tilde{ \beta }\frac{\partial \psi }{ \partial x} \\ &\quad{} +\varepsilon^{\frac{3}{2}}J[\psi ,O]+ \varepsilon^{\frac{3}{2}}\theta J\biggl[ \psi ,\frac{\partial O}{\partial y}\biggr]+ \varepsilon J\biggl[\psi ,\nabla^{2} \psi +\frac{\partial }{\partial z}\biggl(K ^{2}\frac{\partial \psi }{\partial z}\biggr)\biggr]=0, \end{aligned} \end{aligned}$$
(8)
$$\begin{aligned}& W=\varepsilon R_{0}K^{2}\biggl[\frac{\partial }{\partial t}+(U-c_{0}) \frac{ \partial }{\partial x}\biggr]\frac{\partial \psi }{\partial z}+\varepsilon ^{2}J\biggl[\psi ,\frac{\partial \psi }{\partial z}\biggr], \end{aligned}$$
(9)

where \(\tilde{\beta }=(\beta (y)y)'-U''\). Further, \(J[A,B]=\frac{ \partial A}{\partial X}\frac{\partial B}{\partial Y}-\frac{\partial A}{ \partial Y}\frac{\partial B}{\partial X}\).

We introduce the following multiple time-space scale transform in the Rossby waves equation:

$$ T=\epsilon^{\frac{3}{2}}t, \qquad X=\epsilon^{\frac{1}{2}} x, \qquad Y= \epsilon^{\frac{3}{4}}y, \qquad z=z. $$
(10)

Substituting Eq. (10) into Eq. (8), we have

$$\begin{aligned} \begin{aligned}[b] &\varepsilon^{\frac{1}{2}}\biggl\{ \frac{\partial }{\partial X}\biggl[ \frac{ \partial^{2} \psi }{\partial y^{2}}+\frac{\partial }{\partial z}\biggl(K ^{2}\frac{\partial \psi }{\partial z} \biggr)\biggr]+\tilde{\beta }\frac{\partial \psi }{\partial X}\biggr\} +\varepsilon^{\frac{5}{4}} \biggl\{ 2(U-c_{0})\frac{ \partial^{3}\psi }{\partial X\partial y\partial Y}\biggr\} + \varepsilon^{\frac{6}{4}} \biggl\{ \frac{\partial^{3}\psi }{\partial T\partial y^{2}} \\ &\quad{} +\frac{\partial^{2}}{\partial T\partial z}\biggl(K^{2}\frac{ \partial \psi }{\partial z} \biggr)+(U-c_{0})\frac{\partial^{3}}{\partial X ^{3}}+\frac{\partial \psi }{\partial X} \frac{\partial^{3}\psi }{ \partial y^{3}}+\frac{\partial \psi }{\partial X}\frac{\partial^{2}}{ \partial y\partial z}\biggl(K^{2} \frac{\partial \psi }{\partial z}\biggr)-\frac{ \partial \psi }{\partial y}\frac{\partial^{3}\psi }{\partial X\partial y^{2}} \\ &\quad{} -\frac{\partial \psi }{\partial y}\frac{\partial^{2}}{ \partial X\partial z}\biggl(K^{2}\frac{\partial \psi }{\partial z} \biggr)\biggr\} + \varepsilon^{2}\biggl\{ (U-c_{0}) \frac{\partial^{3}\psi }{\partial X\partial Y^{2}}\biggr\} +\varepsilon^{2}\frac{\partial \psi }{\partial X} \frac{\partial O}{\partial y}+\varepsilon^{2}\theta \frac{\partial \psi }{\partial X} \frac{\partial^{2} O}{\partial y^{2}} \\ &\quad{} +\varepsilon^{\frac{9}{4}}\biggl\{ 2\frac{ \partial^{3}\psi }{\partial T\partial y\partial Y}+3\frac{\partial \psi }{\partial X} \frac{\partial^{3} \psi }{\partial y^{2}\partial Y}+\frac{ \partial \psi }{\partial X}\frac{\partial^{2}}{\partial z\partial Y}\biggl(K ^{2} \frac{\partial \psi }{\partial z}\biggr)-\frac{\partial \psi }{\partial y}\frac{\partial^{3} \psi }{\partial X\partial y\partial Y} \\ &\quad{} -\frac{ \partial \psi }{\partial Y}\frac{\partial^{3} \psi }{\partial X\partial y^{2}}-\frac{\partial \psi }{\partial Y}\frac{\partial^{2}}{\partial z\partial X} \biggl(K^{2}\frac{\partial \psi }{\partial z}\biggr)\biggr\} + \varepsilon^{\frac{5}{2}} \biggl\{ \frac{\partial^{3} \psi }{\partial T\partial X^{2}}+\frac{\partial \psi }{\partial X}\frac{\partial^{3} \psi }{ \partial y\partial X^{2}}-\frac{\partial \psi }{\partial y} \frac{ \partial^{3} \psi }{\partial X^{3}}\biggr\} \\ &\quad{} +\varepsilon^{3}\biggl\{ \frac{ \partial^{3} \psi }{\partial T\partial Y^{2}}+3\frac{\partial \psi }{ \partial X} \frac{\partial^{3} \psi }{\partial y\partial Y^{2}}-\frac{ \partial \psi }{\partial y}\frac{\partial^{3} \psi }{\partial X\partial Y^{2}}-2\frac{\partial \psi }{\partial Y} \frac{\partial^{3} \psi }{ \partial X\partial y\partial Y}\biggr\} +o\bigl(\varepsilon^{3}\bigr)=0. \end{aligned} \end{aligned}$$
(11)

The boundary conditions can be written in the following form:

$$ \psi (0)=\psi (+\infty )=0. $$
(12)

Therefore, in the vertical direction, the boundary satisfies

$$ \frac{\partial \psi }{\partial z}=0, \quad z\rightarrow +\infty . $$
(13)

Assume the perturbation stream function expanded with small parameter ε,

$$ \psi =\psi_{0}+\varepsilon^{\frac{1}{4}}\psi_{1}+ \varepsilon^{ \frac{2}{4}}\psi_{2}+\varepsilon^{\frac{3}{4}} \psi_{3}+ \varepsilon^{\frac{4}{4}}\psi_{4}+ \varepsilon^{\frac{5}{4}}\psi_{5}+ \varepsilon^{\frac{6}{4}} \psi_{6}+\cdots . $$
(14)

Substituting Eq. (14) into Eq. (11) leads to all-order perturbation equations about ϵ.

In the first place, introduce the operator L

$$ L=(U-c_{0})\frac{\partial }{\partial X}\biggl[\frac{\partial^{2}}{\partial y^{2}}+ \frac{\partial }{\partial z}\biggl(K^{2}\frac{\partial }{\partial z}\biggr)+ \frac{ \tilde{\beta }}{U-c_{0}}\biggr]. $$
(15)

First-order approximation

$$ o\bigl(\varepsilon^{\frac{1}{2}}\bigr): \quad L(\psi_{0})=0. $$
(16)

The boundary conditions can be written as follows:

$$ \psi_{0}(0)=\psi_{0}(+\infty )=0. $$
(17)

The vertical boundary condition is

$$ \frac{\partial \psi_{0}}{\partial z}=0, \quad z\rightarrow +\infty . $$
(18)

Owing to Eq. (16) being the linear equation, we assume the solution of \(\psi_{0}\) is as follows:

$$ \psi_{0}=A(X,Y,T)\phi_{0}(y)P_{0}(z). $$
(19)

Substituting the solution of \(\psi_{0}\) Eq. (19) into Eq. (16) and Eq. (17), we get the eigenvalue problem on level eigenfunction \(\phi_{0}\), \(P_{0}\):

$$ \textstyle\begin{cases} \phi_{0}^{\prime\prime}+k_{0}^{2}\phi_{0}+\frac{\tilde{\beta }}{U-c_{0}}\phi _{0}=0,\\ (K^{2}P_{0}')'+k_{0}^{2}P_{0}=0. \end{cases} $$
(20)

Similar to the first approximation, we continue to consider the higher order problem

$$ \varepsilon^{\frac{3}{4}}: \quad L(\psi_{1})=0. $$
(21)

Take the variables form of \(\psi_{1}\) in the following form:

$$ \psi_{1}=A^{2}(X,Y,T)\phi_{1}(y)P_{1}(z). $$
(22)

Further,

$$ \varepsilon^{1}: \quad L(\psi_{2})=0. $$
(23)

Similar to Eq. (19), assume the solution of \(\psi_{2}\)

$$ \psi_{2}=A(X,Y,T)\phi_{2}(y)P_{2}(z). $$
(24)

Substituting Eq. (22), Eq. (24) into Eq. (21) and Eq. (23), the eigenfunction equations about \(\psi_{1}\), \(\psi_{2}\), \(P_{1}\), \(P_{2}\) can be obtained as follows:

$$ \textstyle\begin{cases} \phi_{1}^{\prime\prime}+k_{1}^{2}\phi_{1}+\frac{\tilde{\beta }}{U-c_{0}}\phi _{1}=0,\\ (K^{2}P_{1}')'+k_{1}^{2}P_{1}=0,\\ \phi_{2}^{\prime\prime}+k_{2} ^{2}\phi_{2}+\frac{\tilde{\beta }}{U-c_{0}}\phi_{2}=0,\\ (K^{2}P_{2}')'+k _{2}^{2}P_{2}=0. \end{cases} $$
(25)

Analogously, the boundary conditions can be written as follows:

$$ \psi_{1}(0)=\psi_{1}(+\infty )=0, \qquad \psi_{2}(0)=\psi_{2}(+\infty )=0. $$
(26)

The vertical boundary condition is

$$ \frac{\partial \psi_{1}}{\partial z}=0, \qquad \frac{\partial \psi_{1}}{\partial z}=0, \quad z\rightarrow +\infty . $$
(27)

In order to obtain the singularity elimination condition, it is important to make further discussion.

$$ \varepsilon^{\frac{5}{4}}: \quad L(\psi_{3})=-2(U-c_{0}) \frac{\partial^{3}\psi_{0}}{\partial X\partial y\partial Y}. $$
(28)

Substituting Eq. (19) into Eq. (28), we get

$$ \textstyle\begin{cases} \phi_{3}^{\prime\prime}+k_{3}^{2}\phi_{3}+\frac{\tilde{\beta }}{U-c_{0}}\phi _{3}=-2\phi_{0}',\\ (K^{2}P_{3}')'+k_{3}^{2}P_{3}=-2P_{0}. \end{cases} $$
(29)

The boundary conditions are no less than the above conditions. Based on Eq. (28), we can have the separate variables form of \(\psi_{3}\)

$$\begin{aligned}& \psi_{3}=A_{Y}(X,Y,T)\phi_{3}(y)P_{3}(z), \end{aligned}$$
(30)
$$\begin{aligned}& \varepsilon^{\frac{3}{2}}: \\& L(\psi_{4}) =- \biggl\{ 2(U-c_{0})\frac{\partial^{3}\psi_{1}}{\partial X \partial y\partial Y}+\frac{\partial^{3}\psi_{0}}{\partial T\partial y^{2}}+ \frac{\partial^{2}}{\partial T\partial z}\biggl(K^{2}\frac{\partial \psi_{0}}{\partial z}\biggr)+(U-c_{0}) \frac{\partial^{3}\psi_{0}}{\partial X^{3}} \\& \hphantom{L(\psi_{4}) }\quad {}+\frac{\partial \psi_{0}}{\partial X}\frac{\partial^{3}\psi _{0}}{\partial y^{3}}+\frac{\partial \psi_{0}}{\partial X}\frac{ \partial^{2}}{\partial y\partial z} \biggl(K^{2}\frac{\partial \psi_{0}}{ \partial z}\biggr)-\frac{\partial \psi_{0}}{\partial y} \frac{\partial^{3} \psi_{0}}{\partial X\partial y^{2}}-\frac{\partial \psi_{0}}{\partial y}\frac{\partial^{2}}{\partial X\partial z}\biggl(K^{2} \frac{\partial \psi _{0}}{\partial z}\biggr)\biggr\} \\& \hphantom{L(\psi_{4}) }=-\bigl\{ A_{T}\bigl[\phi_{0}^{\prime\prime}P_{0}+k_{0}^{2} \phi _{0}\bigl(K^{2}P_{0}' \bigr)'\bigr]+(U-c_{0})A_{XXX} \phi_{0}P_{0}+AA_{X}\bigl(\phi_{0}\phi _{0}^{\prime\prime\prime}P_{0}^{2} \\& \hphantom{L(\psi_{4}) }\quad{} -\phi_{0}'\phi_{0}^{\prime\prime}P_{0}^{2} \bigr)+4(U-c_{0}) (A _{Y}A_{X}+AA_{XY}) \phi_{1}'P_{1}\bigr\} , \end{aligned}$$
(31)
$$\begin{aligned}& \varepsilon^{\frac{7}{4}}: \\& L(\psi_{5}) = - \biggl\{ 2(U-c_{0})\frac{\partial^{3}\psi_{2}}{\partial X \partial y\partial Y}+\frac{\partial^{3}\psi_{1}}{\partial T\partial y^{2}}+ \frac{\partial^{2}}{\partial T\partial z}\biggl(K^{2}\frac{\partial \psi_{1}}{\partial z}\biggr)+(U-c_{0}) \frac{\partial^{3}\psi_{1}}{\partial X^{3}} \\& \hphantom{L(\psi_{5}) =}{} +\frac{\partial \psi_{0}}{\partial X}\frac{\partial^{3}\psi _{1}}{\partial y^{3}}+\frac{\partial \psi_{0}}{\partial X}\frac{ \partial^{2}}{\partial y\partial z} \biggl(K^{2}\frac{\partial \psi_{1}}{ \partial z}\biggr)-\frac{\partial \psi_{0}}{\partial y} \frac{\partial^{3} \psi_{1}}{\partial X\partial y^{2}}-\frac{\partial \psi_{0}}{\partial y}\frac{\partial^{2}}{\partial X\partial z}\biggl(K^{2} \frac{\partial \psi _{1}}{\partial z}\biggr) \\& \hphantom{L(\psi_{5}) =} {} +\frac{\partial \psi_{1}}{\partial X}\frac{ \partial^{3}\psi_{0}}{\partial y^{3}}+\frac{\partial \psi_{1}}{\partial X}\frac{\partial^{2}}{\partial y\partial z} \biggl(K^{2}\frac{\partial \psi _{0}}{\partial z}\biggr)-\frac{\partial \psi_{1}}{\partial y} \frac{\partial ^{3}\psi_{0}}{\partial X\partial y^{2}} \\& \hphantom{L(\psi_{5}) =} {}-\frac{\partial \psi_{1}}{ \partial y}\frac{\partial^{2}}{\partial X\partial z}\biggl(K^{2} \frac{ \partial \psi_{0}}{\partial z}\biggr)\biggr\} , \end{aligned}$$
(32)
$$\begin{aligned}& \varepsilon^{2}: \\& L(\psi_{6}) =- \biggl\{ (U-c_{0})\frac{\partial^{3}\psi_{0}}{\partial X\partial Y^{2}}+2(U-c_{0}) \frac{\partial^{3}\psi_{3}}{\partial X\partial y \partial Y}+\frac{\partial^{3}\psi_{2}}{\partial T\partial y^{2}}+\frac{ \partial^{2}}{\partial T\partial z}\biggl(K^{2} \frac{\partial \psi_{2}}{ \partial z}\biggr) \\& \hphantom{L(\psi_{6}) }\quad{} +(U-c_{0})\frac{\partial^{3}\psi_{2}}{\partial X^{3}}+\frac{ \partial \psi_{0}}{\partial X} \frac{\partial^{3}\psi_{2}}{\partial y ^{3}}+\frac{\partial \psi_{0}}{\partial X}\frac{\partial^{2}}{\partial y\partial z}\biggl(K^{2} \frac{\partial \psi_{2}}{\partial z}\biggr)-\frac{\partial \psi_{0}}{\partial y}\frac{\partial^{3}\psi_{2}}{\partial X\partial y ^{2}} \\& \hphantom{L(\psi_{6}) }\quad{} -\frac{\partial \psi_{0}}{\partial y}\frac{\partial^{2}}{ \partial X\partial z}\biggl(K^{2}\frac{\partial \psi_{2}}{\partial z} \biggr)+\frac{ \partial \psi_{2}}{\partial X}\frac{\partial^{3}\psi_{0}}{\partial y ^{3}}+\frac{\partial \psi_{2}}{\partial X} \frac{\partial^{2}}{\partial y\partial z}\biggl(K^{2}\frac{\partial \psi_{0}}{\partial z}\biggr)- \frac{\partial \psi_{2}}{\partial y}\frac{\partial^{3}\psi_{0}}{\partial X\partial y ^{2}} \\& \hphantom{L(\psi_{6}) }\quad{} -\frac{\partial \psi_{2}}{\partial y}\frac{\partial^{2}}{ \partial X\partial z}\biggl(K^{2}\frac{\partial \psi_{0}}{\partial z} \biggr)+\frac{ \partial \psi_{1}}{\partial X}\frac{\partial^{3}\psi_{1}}{\partial y ^{3}}+\frac{\partial \psi_{1}}{\partial X} \frac{\partial^{2}}{\partial y\partial z}\biggl(K^{2}\frac{\partial \psi_{1}}{\partial z}\biggr)- \frac{\partial \psi_{1}}{\partial y}\frac{\partial^{3}\psi_{1}}{\partial X\partial y ^{2}} \\& \hphantom{L(\psi_{6}) }\quad{} -\frac{\partial \psi_{1}}{\partial y}\frac{\partial^{2}}{ \partial X\partial z}\biggl(K^{2}\frac{\partial \psi_{1}}{\partial z} \biggr)+\frac{ \partial \psi_{0}}{\partial X}\frac{\partial O}{\partial y}+\theta \frac{ \partial \psi_{0}}{\partial X} \frac{\partial^{2} O}{\partial y^{2}}\biggr\} \\& \hphantom{L(\psi_{6}) }=-\bigl\{ \bigl[\phi_{2}^{\prime\prime}P_{2}+k_{2}^{2} \phi_{2}\bigl(K^{2}P_{2}' \bigr)'\bigr]A_{T}+\bigl[ \phi_{0}^{\prime}O'(y)+ \theta \phi_{0}^{\prime\prime}O''(y) \bigr]P_{0}A_{X}+(U-c_{0}) A _{XXX} \\& \hphantom{L(\psi_{6}) }\quad{} \cdot \phi_{2}P_{2}+(U-c_{0}) A_{XYY} \bigl(2\phi '_{3}P_{3}+\phi _{0}P_{0} \bigr)+A\bigl\{ A_{X}\bigl[\phi_{0}\phi_{2}^{\prime\prime\prime}P_{0}P_{2}+k_{2}^{2} \phi _{0}\phi '_{2}\bigl(K^{2}P_{2}' \bigr)' \\& \hphantom{L(\psi_{6}) }\quad{} -\phi_{0}'\phi_{2}^{\prime\prime}P_{0}P_{2}-k _{2}^{2}\phi '_{0}\phi_{2} \bigl(K^{2}P_{2}'\bigr)'+ \phi_{2}\phi_{0}^{\prime\prime\prime}P_{0}P _{2}+k_{0}^{2}\phi_{2}\phi '_{0}\bigl(K^{2}P_{0}' \bigr)'-\phi_{2}'\phi_{0}^{\prime\prime}P _{0}P_{2} \\& \hphantom{L(\psi_{6}) }\quad{} -k_{0}^{2}\phi '_{2} \phi_{0}\bigl(K^{2}P_{0}' \bigr)'\bigr]+2A^{2}A_{X}\bigl[ \phi_{1}\phi_{1}^{\prime\prime\prime} P_{1}^{2}- \phi_{1}'\phi_{1}^{\prime\prime}P_{1}^{2} \bigr]\bigr\} \bigr\} . \end{aligned}$$
(33)

Multiplying Eq. (33) by \(\phi_{0}\), integrating Eq. (33) with respect to y, z from 0 to +∞, and using the following identical equation

$$ \phi_{0}\frac{\partial^{2}\psi_{6}}{\partial y^{2}}=\frac{\partial }{ \partial y}\biggl( \phi_{0}\frac{\partial \psi_{6}}{\partial y}\biggr)-\frac{ \partial }{\partial y}\biggl( \psi_{6}\frac{\partial \psi_{0}}{\partial y}\biggr)+ \psi_{6} \frac{\partial^{2}\psi_{0}}{\partial y^{2}}, $$
(34)

we can obtain

$$ A_{T}+a_{0}A_{X}+a_{1}AA_{X}+a_{2}A^{3}A_{X}+a_{3}A_{XXX}+a_{4}A_{XYY}=0, $$
(35)

where

$$\begin{aligned} \textstyle\begin{cases} a=\int _{0}^{+\infty }\int _{0}^{+\infty }\frac{1}{U-c _{0}}[\phi_{2}^{\prime\prime}P_{2}+k_{2}^{2}\phi_{2}(K^{2}P_{2}')']\,dy\,dz,\\ a _{0}=\int _{0}^{+\infty }\int _{0}^{+\infty }[\phi_{0} ^{\prime}O'(y)+\theta \phi_{0}^{\prime\prime}O''(y)]P_{0}\,dy\,dz/a,\\ a_{1}= \int _{0}^{+\infty }\int _{0}^{+\infty }\frac{1}{U-c_{0}}[\phi_{0} \phi_{2}^{\prime\prime\prime}P_{0}P_{2}+k_{2}^{2}\phi_{0}\phi '_{2}(K^{2}P_{2}')'- \phi_{0}'\phi_{2}^{\prime\prime}P_{0}P_{2}-k_{2}^{2}\phi '_{0}\phi_{2}(K^{2}P _{2}')'\\ \hphantom{a_{1}=}{} +\phi_{2}\phi_{0}^{\prime\prime\prime}P_{0}P_{2}+k_{0}^{2}\phi_{2}\phi '_{0}(K ^{2}P_{0}')'-\phi_{2}'\phi_{0}^{\prime\prime}P_{0}P_{2}-k_{0}^{2}\phi '_{2}\phi _{0}(K^{2}P_{0}')']\,dy\,dz/a,\\ a_{2}=\int _{0}^{+\infty }\int _{0}^{+\infty }\frac{2}{U-c_{0}}[\phi_{1}\phi_{1}^{\prime\prime\prime}P_{1} ^{2}-\phi_{1}'\phi_{1}^{\prime\prime}P_{1}^{2}]\,dy\,dz/a,\\ a_{3}=\int _{0} ^{+\infty }\int _{0}^{+\infty }\phi_{2}P_{2}\,dy\,dz/a,\\ a_{4}= \int _{0}^{+\infty }\int _{0}^{+\infty }(2\phi '_{3}P_{3}+ \phi_{0}P_{0})\,dy\,dz/a. \end{cases}\displaystyle \end{aligned}$$
(36)

Remark

Eq. (35) is a new \((2+1)\) dimensional model. The coefficient \(a_{0}\) is in connection with topographic effect G. The second term \(a_{0}A_{X}\) represents the effect of complete Coriolis force and topography on the evolution of Rossby solitary waves. Based on \(a_{1}AA_{X}\) and \(a_{2}A^{3}A_{X}\), we know that the new equation is the combination of ZK equation and mZK equation. So, the new model Eq. (35) is called combined ZK-mZK equation. Compared with other models, the combined ZK-mZK model can describe Rossby solitary waves more accurately.

In order to facilitate the calculation, we ignore the effect of complete Coriolis force. Introducing the transformation \(T'=T\), \(X'=X-a_{0}T\) and \(Y'=Y\), substituting the transformation into Eq. (35), and omitting the apostrophe, we can rewrite the combined ZK-mZK equation in the following form:

$$ A_{T}+a_{1}AA_{X}+a_{2}A^{3}A_{X}+a_{3}A_{XXX}+a_{4}A_{XYY}=0. $$
(37)

3 The derivation of conservation laws

To learn more about the new model, the conservation laws of the combined ZK-mZK equation are discussed. The research process of conservation laws is as follows. The Euler operator is defined as [64]

$$ \frac{\delta }{{\delta u}} = \frac{\partial }{{\partial u}} - {D_{t}} \frac{ \partial }{{\partial {u_{t}}}} - {D_{x}}\frac{\partial }{{\partial {u_{x}}}} - {D_{y}} \frac{\partial }{{\partial {u_{y}}}} + D_{t} ^{2}\frac{\partial }{{\partial {u_{tt}}}} + D_{x}^{2}\frac{\partial }{{\partial {u_{xx}}}} + D_{y}^{2} \frac{\partial }{{\partial {u_{yy}}}} \cdots , $$
(38)

where \({D_{t}}\), \({D_{x}}\),and \({D_{y}}\) are defined as follows:

$$\begin{aligned}& {D_{t}} = \frac{\partial }{{\partial t}} + {u_{t}}\frac{\partial }{ {\partial u}} + {u_{tt}}\frac{\partial }{{\partial {u_{t}}}} + {u_{xt}}\frac{ \partial }{{\partial {u_{x}}}} + {u_{yt}}\frac{\partial }{{\partial {u_{y}}}} + \cdots , \end{aligned}$$
(39)
$$\begin{aligned}& {D_{x}} = \frac{\partial }{{\partial x}} + {u_{x}}\frac{\partial }{ {\partial u}} + {u_{xx}}\frac{\partial }{{\partial {u_{x}}}} + {u_{tx}}\frac{ \partial }{{\partial {u_{t}}}} + {u_{yx}}\frac{\partial }{{\partial {u_{y}}}} + \cdots , \end{aligned}$$
(40)
$$\begin{aligned}& {D_{y}} = \frac{\partial }{{\partial y}} + {u_{y}}\frac{\partial }{ {\partial u}} + {u_{yx}}\frac{\partial }{{\partial {u_{x}}}} + {u_{ty}}\frac{ \partial }{{\partial {u_{t}}}} + {u_{yy}}\frac{\partial }{{\partial {u_{y}}}} + \cdots . \end{aligned}$$
(41)

Consider the nth-order partial differential equation of t, x, and y as follows:

$$ H(t,x,y,u,{u_{t}},{u_{x}},{u_{y}},{u_{tt}},{u_{tx}},{u_{ty}},\ldots )=0. $$
(42)

A vector \(Q = ({Q^{t}},{Q^{x}},{Q^{y}})\) such that

$$ {D_{t}}\bigl({Q^{t}}\bigr) + {D_{x}} \bigl({Q^{x}}\bigr) + {D_{y}}\bigl({Q^{y}}\bigr) = 0 $$
(43)

holds for all solutions of Eq. (42) and is defined as the conserved vector of Eq. (42).

The multiplier Δ for Eq. (42) has the property as follows:

$$ {D_{t}}\bigl({Q^{t}}\bigr) + {D_{x}} \bigl({Q^{x}}\bigr) + {D_{y}}\bigl({Q^{y}}\bigr) = \Delta H. $$
(44)

For an arbitrary function \(u(x,y,t)\), the determining equations for multiplier are acquired by taking the variational derivative of Eq. (44)

$$ \frac{\delta }{{\delta u}}(\Delta H) = 0. $$
(45)

For an arbitrary function \(u(x,y,t)\), Eq. (45) sets up forever. Using Eq. (44) and computing the multiplier from Eq. (45), we can derive the conserved vectors.

According to Section 2, the combined ZK-mZK equation is given by

$$ A_{T}+a_{1}AA_{X}+a_{2}A^{3}A_{X}+a_{3}A_{XXX}+a_{4}A_{XYY}=0. $$

According to the defining equation for multiplier \(\Delta (X,Y,T,A(X,Y,T))\) from Eq. (37), after simplification, we can have

$$ \begin{aligned}[b] &{\Delta_{A}}\bigl({A_{T}} + {a_{1}}A{A_{X}} + {a_{2}} {A^{3}} {A_{X}} + {a_{3}} {A_{XXX}} + {a_{4}} {A_{XYY}}\bigr)+\Delta \bigl({a_{1}} {A_{X}} + 2{a_{2}} {A^{2}} {A_{X}}\bigr) \\ & \quad{} - {D_{T}}(\Delta ) - {D_{X}}\bigl[\Delta \bigl({a_{1}}A + {a_{2}} {A^{3}}\bigr)\bigr] -D_{X}^{3}({a_{3}}\Delta ) - D_{Y}^{2} \bigl[{D_{X}}({a _{4}}\Delta )\bigr] = 0. \end{aligned} $$
(46)

The coefficients of different derivatives of A of Eq. (46) for multiplier Δ give

$$ \Delta (X,Y,T,A) = {c_{1}}A + F(Y). $$
(47)

By calculating, conserved quantities for Eq. (37) are obtained as follows:

$$\begin{aligned}& Q_{1}^{T} = \frac{1}{2}{A^{2}}, \end{aligned}$$
(48)
$$\begin{aligned}& {D_{T}}\bigl(Q_{1}^{T}\bigr) = A{A_{T}} + A{A_{T}} = 2A{A_{T}}, \end{aligned}$$
(49)
$$\begin{aligned}& Q_{1}^{X} = \frac{{{a_{1}}}}{3}{A^{3}} + \frac{{{a_{2}}}}{5}{A^{5}} - {a_{3}}\biggl(A{A_{XX}} - \frac{1}{2}A_{X}^{2}\biggr) - {a_{4}} \biggl(A{A_{YY}} + \frac{1}{2}A_{Y}^{2} \biggr), \end{aligned}$$
(50)
$$\begin{aligned}& {D_{X}}\bigl(Q_{1}^{X}\bigr) = {a_{1}} {A^{2}} {A_{X}} + {a_{2}} {A^{4}} {A_{X}} - {a_{3}}({A_{X}} {A_{XX}} + A{A_{XXX}} - {A_{X}} {A_{XX}})- {a_{4}}( {A_{X}} {A_{YY}} + A{A_{XYY}} \\& \hphantom{{D_{X}}\bigl(Q_{1}^{X}\bigr)}\quad{} + {A_{Y}} {A_{XY}})+ {A_{X}} \bigl({a_{1}} {A^{2}} + {a_{2}} {A^{4}} - {a_{3}} {A_{XX}} - {a_{4}} {A_{YY}} \bigr)-{a_{3}}(A {A_{XXX}} - {A_{x}} {A_{XX}}) \\& \hphantom{{D_{X}}\bigl(Q_{1}^{X}\bigr)}\quad{} - {a_{4}}(A{A_{XYY}} + {A_{Y}} {A_{XY}}), \end{aligned}$$
(51)
$$\begin{aligned}& Q_{1}^{Y} = {a_{4}} {A_{X}} {A_{Y}}, \end{aligned}$$
(52)
$$\begin{aligned}& {D_{Y}}\bigl(Q_{1}^{Y}\bigr) = 2{a_{4}}({A_{X}} {A_{YY}} + {A_{Y}} {A_{XY}}). \end{aligned}$$
(53)

So, we can have

$$ \begin{aligned}[b] &{D_{T}}\bigl(Q_{1}^{T}\bigr) + {D_{X}}\bigl(Q_{1}^{X}\bigr) + {D_{Y}}\bigl(Q_{1}^{Y}\bigr) \\ &\quad = 2A {A_{T}} + 2{a_{1}} {A^{2}} {A_{X}} + 2{a_{2}} {A^{4}} {A_{X}} - 2{a _{3}}A{A_{XXX}} - 2{a_{4}}A{A_{XYY}} \\ &\quad = 2A\bigl({A_{T}} + {a_{1}}A{A_{X}} + {a_{2}} {A^{3}} {A_{X}} - {a_{3}} {A_{XXX}} - {a_{4}} {A_{XYY}}\bigr). \end{aligned} $$
(54)

For the multiplier \(\Delta (X,Y,T,A) =F(Y)\), the physical conserved quantities are as follows:

$$\begin{aligned}& Q_{F}^{T} = F(Y)A, \end{aligned}$$
(55)
$$\begin{aligned}& \begin{aligned}[b] Q_{F}^{Y} &=\frac{1}{2}{a_{1}}F(Y){A^{2}} + \frac{1}{2}{a_{2}}F(Y) {A^{4}} - {a_{3}}F(Y){A_{XX}} + 2{a_{4}}F(Y){A_{YY}} \\ &\quad{} - \frac{1}{2} {a_{4}} {F_{Y}} {A_{Y}}- \frac{1}{2}{a_{4}} {F_{YY}}A, \end{aligned} \end{aligned}$$
(56)
$$\begin{aligned}& Q_{F}^{Y} = {a_{4}}\bigl({F_{Y}} {A_{X}} - F(Y){A_{XY}}\bigr). \end{aligned}$$
(57)

4 The soliton solutions

In order to seek the soliton solution [65, 66] of a partial differential equation, the semi-inverse variational principle is used. Its steps are as follows:

Step 1. For an arbitrary function \(u(x,y,t)\), assuming \(u(x,y,t)=u(x+y-ct)\) and \(\xi = x+y-ct\), we can convert the partial differential equation into an ordinary differential equation

$$ H(u,cu_{\xi },c_{0})=0, $$
(58)

where c is the wave speed and \(c_{0}\) is the integration constant.

Step 2. A steady integral is constructed in the following form:

$$ I= \int_{-\infty }^{+\infty }c_{0}\,d\xi . $$
(59)

Step 3. In order to find the one soliton to Eq. (42), we let

$$ u(\xi )=p \operatorname{sech}^{n}(q\xi ), $$
(60)

where p is the wave amplitude of Rossby solitary waves, q is the inverse width of Rossby solitary waves, n is the exponent, and it is obtained by equating the exponents of the highest derivatives and nonlinear terms.

Step 4. Substituting Eq. (37) into Eq. (59), letting \(\frac{\partial I}{\partial p}=0\) and \(\frac{\partial I}{\partial q}=0\), and solving them to determine the constants p and q, respectively, we determine the solitary wave solutions of Eq. (37).

In this section, by using the semi-inverse variational principle, we seek the soliton solutions of ZK-mZK equation. We convert Eq. (37) into ODE wave transformation:

$$ \xi = X+Y-cT, \quad \quad A(\xi )=A(X+Y-cT), $$
(61)

and Eq. (37) has the following form:

$$ - cA' + {a_{1}}\bigl({A^{2}} \bigr)' + \frac{1}{4}{a_{2}}\bigl({A^{4}} \bigr)' + ({a_{3}} + {a_{4}}){A^{(3)}} = 0 $$
(62)

and

$$ - cA + {a_{1}} {A^{2}} + \frac{1}{4}{a_{2}} {A^{4}} + ({a_{3}} + {a_{4}}) {A^{(2)}} = 0. $$
(63)

Assuming \(n = 2/3\), \(A = p\operatorname{sech}^{\frac{2}{3}}(q \xi )\) and integrating the above equation, we can get

$$ \begin{aligned}[b] I &= \int_{ - \infty }^{ + \infty } { - cA + {a_{1}} {A^{2}} + \frac{1}{4}{a_{2}} {A^{4}} + ({a_{3}} + {a_{4}}){A^{(2)}}} \,d\xi \\ &= \frac{1}{q} \int_{-\infty }^{+\infty }\biggl\{ -cp \operatorname{sech}^{ \frac{2}{3}}(q\xi )+a_{1}p^{2} \operatorname{sech}^{\frac{4}{3}}(q \xi )+\frac{1}{4}a_{2}p^{4} \operatorname{sech}^{\frac{8}{3}}(q \xi )+(a_{3}+a_{4})p \\ &\quad {}\cdot \bigl[\operatorname{sech}^{ \frac{2}{3}}(q\xi ) \bigr]'''\biggr\} \,d(q\xi ). \end{aligned} $$
(64)

Eq. (64) can be rewritten as follows:

$$ I= \frac{1}{q}\biggl[ - cp\frac{{\frac{{\sqrt{\pi }}}{3}\Gamma ( \frac{1}{6})}}{{\Gamma (\frac{2}{3})}} + {a_{1}} {p^{2}}\frac{{3\Gamma (\frac{2}{3})\Gamma (\frac{5}{6})}}{{\sqrt{\pi }}} + \frac{1}{4} {a_{2}} {p^{4}}\frac{{\sqrt{\pi }\Gamma (\frac{4}{3})}}{{\Gamma (\frac{ {11}}{6})}}\biggr], $$
(65)

where \(\Gamma (x) = \int_{0}^{ + \infty } {{t^{x - 1}}{e^{ - t}}\,dt}\), \({\tau_{1}} = \frac{{\frac{{\sqrt{\pi }}}{3}\Gamma (\frac{1}{6})}}{ {\Gamma (\frac{2}{3})}} = 4.21\), \({\tau_{2}} = \frac{{3\Gamma ( \frac{2}{3})\Gamma (\frac{5}{6})}}{{\sqrt{\pi }}} = 2.587\), \({\tau_{3}} = \frac{{\sqrt{\pi }\Gamma (\frac{4}{3})}}{{\Gamma (\frac{ {11}}{6})}} = 1.68\), \({\tau_{4}} = \frac{{3\sqrt{\pi }\Gamma ( \frac{4}{3})}}{{2\Gamma (\frac{{11}}{6})}} = 2.52\).

According to Eq. (65), taking a derivative with respect to q and p, we can have the following equations:

$$ \begin{aligned}[b] \frac{{\partial I}}{{\partial q}}&= 7 - \frac{1}{{{q^{2}}}}\biggl[ - cp \frac{ {\frac{{\sqrt{\pi }}}{3}\Gamma (\frac{1}{6})}}{{\Gamma (\frac{2}{3})}} + {a_{1}} {p^{2}}\frac{{3\Gamma (\frac{2}{3})\Gamma (\frac{5}{6})}}{ {\sqrt{\pi }}} + \frac{1}{4}{a_{2}} {p^{4}}\frac{{\sqrt{\pi } \Gamma (\frac{4}{3})}}{{\Gamma (\frac{{11}}{6})}}\biggr]+ ({a_{3}} + {a_{4}})p \\ &\quad{} \cdot \biggl[ - \frac{2}{3}\frac{{\frac{{\sqrt{\pi }}}{3}\Gamma ( \frac{1}{6})}}{{\Gamma (\frac{2}{3})}} + \frac{{10}}{9} \frac{{3\sqrt{ \pi }\Gamma (\frac{4}{3})}}{{2\Gamma (\frac{{11}}{6})}}\biggr]=0 \end{aligned} $$
(66)

and

$$ \begin{aligned}[b] \frac{{\partial I}}{{\partial p}} &= \frac{1}{q}\biggl[ - c \frac{{\frac{ {\sqrt{\pi }}}{3}\Gamma (\frac{1}{6})}}{{\Gamma (\frac{2}{3})}} + 2 {a_{1}}p\frac{{3\Gamma (\frac{2}{3})\Gamma (\frac{5}{6})}}{{\sqrt{ \pi }}} + {a_{2}} {p^{3}}\frac{{\sqrt{\pi }\Gamma (\frac{4}{3})}}{ {\Gamma (\frac{{11}}{6})}}\biggr] + ({a_{3}} + {a_{4}})q \\ &\quad{} \cdot \biggl[ - \frac{2}{3}\frac{{\frac{{\sqrt{\pi }}}{3}\Gamma (\frac{1}{6})}}{ {\Gamma (\frac{2}{3})}} + \frac{{10}}{9} \frac{{3\sqrt{\pi }\Gamma ( \frac{4}{3})}}{{2\Gamma (\frac{{11}}{6})}}\biggr] = 0. \end{aligned} $$
(67)

So, we can get the equation as follows:

$$ \textstyle\begin{cases} - [ - 4.21c + 2.587{a_{1}}p + \frac{1}{4}1.68{a_{2}}{p^{3}}] + ( {a_{3}} + {a_{4}}){q^{2}}[ - \frac{2}{3}4.21 + \frac{{10}}{9}2.52] = 0, \\ [- 4.21c + 2\times 2.587{a_{1}}p + 1.68{a_{2}}{p^{3}}] + ({a_{3}} + {a_{4}}){q^{2}}[ - \frac{2}{3}4.21 + \frac{{10}}{9}2.52] = 0. \end{cases} $$
(68)

After calculation, we can obtain the expression of p and q as follows:

$$\begin{aligned}& \begin{aligned}[b] p &= \frac{1}{5}\frac{{{{[(20\sqrt{5} \sqrt{\frac{{4a_{1}^{3}\tau _{2}^{3} + 5{a_{2}}{c^{2}}\tau_{1}^{2}{\tau_{3}}}}{{{\tau_{3}}{a_{2}}}}} + 100{\tau_{1}}c)\tau_{3}^{2}a_{2}^{2}]}^{\frac{1}{3}}}}}{{{\tau_{3}} {a_{2}}}} \\ &\quad{} -\frac{{4{\tau_{2}}{a_{1}}}}{{{{[(20\sqrt{5} \sqrt{\frac{ {4a_{1}^{3}\tau_{2}^{3} + 5{a_{2}}{c^{2}}\tau_{1}^{2}{\tau_{3}}}}{ {{\tau_{3}}{a_{2}}}}} + 100{\tau_{1}}c)\tau_{3}^{2}a_{2}^{2}]}^{ \frac{1}{3}}}}}, \end{aligned} \end{aligned}$$
(69)
$$\begin{aligned}& q = \sqrt{\frac{{ - {\tau_{2}}{a_{1}}p - \frac{3}{4}{\tau_{3}}{a _{2}}{p^{3}}}}{{2({a_{3}} + {a_{4}})[ - \frac{2}{3}{\tau_{1}} + \frac{ {10}}{9}{\tau_{4}}]}}}. \end{aligned}$$
(70)

At this time, we can get the soliton solution of the combined ZK-mZK equation in the following form:

$$ A = p\operatorname{sech}^{\frac{2}{3}}\biggl[{\biggl( \frac{{ - {\tau_{2}}{a _{1}}p - \frac{3}{4}{\tau_{3}}{a_{2}}{p^{3}}}}{{2({a_{3}} + {a_{4}})( - \frac{2}{3}{\tau_{1}} + \frac{{10}}{9}{\tau_{4}})}}\biggr)^{\frac{1}{2}}}(X + Y - cT)\biggr]. $$
(71)

Assuming \({a_{1}} =-0.5\), \({a_{2}} = 1\), \({a_{3}} = 5\), \({a_{2}} = 5\), \(c=0.5\) and substituting them into Eq. (69), Eq. (70), and Eq. (71), we can get \(p = 1.7\) and

$$ A= 1.7\operatorname{sech}^{\frac{2}{3}}\sqrt{30} (X + Y - 0.5T), \quad \text{as } c=0.5. $$
(72)

When \(c=5\), we also have the other equation about solution as follows:

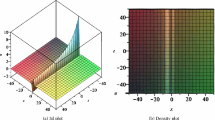
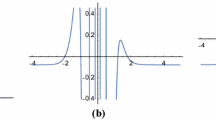
$$ A = 3\operatorname{sech}^{\frac{2}{3}}\sqrt{226} (X + Y - 5T), \quad \text{as } c=5. $$
(73)

Soliton is a solitary wave packet which is caused by the delicate balance between nonlinearity effect and dispersion effect. It is a single hump that has infinite tails or infinite wings and preserves their form and speed after an entire interaction with other solitons. In this section, we display the soliton solutions and the solitary wave profiles for various timescales in Figure 1. According to Figure 1, we can know that the soliton moves to the right with a fixed velocity and almost unaltered amplitude as time increases. In Figure 2, the collisions between two waves with different velocities and various timescales appear. We also know that the wave speed c plays a critical role in a physical structure of the solutions for the combined ZK-mZK equation. Then we can guess that the solitary wave profile moves in the positive axes when c is a positive value, and the solitary wave profile moves in the negative axes when c is a negative value.

Figure 1
figure 1

The soliton solution and the solitary wave profiles for various timescales for \(\pmb{T=0}\) , \(\pmb{T=3}\) , and \(\pmb{T=5}\) , respectively.

Full size image
Figure 2
figure 2

The collisions between two waves with different velocities for \(\pmb{c=0.5}\) and \(\pmb{c=5}\) , respectively, and various timescales for \(\pmb{t=0.08}\) , \(\pmb{t=0.1}\) , and \(\pmb{t=0.2}\) , respectively.

Full size image

5 Conclusions and discussions

In this paper, using the quasi-geostrophic potential vorticity equation, we get a new \((2+1)\) dimensional combined ZK-mZK model for Rossby solitary waves by applying the multi-scale analysis and perturbation method. Based on the new model, we study conservation laws and the soliton solutions of the new equation. By theory and image analysis, the following conclusions can be obtained:

(1) A combined ZK-mZK equation is a new \((2+1)\) dimensional model which includes the cosine Coriolis terms. Compared with \((1+1)\) dimensional models, it can describe the actual situation of ocean and atmosphere. Besides, in the actual ocean and atmosphere, the cosine Coriolis is not ignored. It is necessary to include the cosine Coriolis terms for fully understanding the atmospheric motion. So, the combined ZK-mZK equation is more suitable to describe Rossby solitary waves.

(2) According to the combined ZK-mZK equation, using the multiplier approach, we obtain conservation laws and the corresponding conserved quantities. In addition, the semi-inverse variational principle is a robust and efficient method which gives the variational principles for nonlinear problems. By using the semi-inverse variational principle, we obtain soliton solution for the new equation. According to the soliton solution, some propagation features of Rossby solitary waves are discussed.