Abstract
In this paper, we deal with a class of Gilpin-Ayala ecological models with discrete and distributed time delays. By employing a fixed point theorem of strict-set-contraction and inequality techniques, some sufficient conditions for the existence of periodic solutions are established. As an application, one example is given to illustrate the validity of our main results.
Similar content being viewed by others
1 Introduction
In this paper, we mainly study the following Gilpin-Ayala-like functional differential system with discrete and distributed time delays:
where \(x(t)=(x_{1}(t),x_{2}(t),\ldots,x_{n}(t))\), \(y(t)=(y_{1}(t),y_{2}(t),\ldots,y_{m}(t))\),
\(r_{i}, \hat{r}_{j}, a_{ik}, \hat{a}_{kj}, b_{il}, \hat{b}_{lj}, c_{ik}, \hat{c}_{kj}, d_{il}, \hat{d}_{lj}\in C(\mathbb{R},(0,\infty))\) (\(i,k=1,2,\ldots,n\); \(j,l=1,2,\ldots,m\)) and \(\tau_{ik}, \sigma_{il}, \hat{\tau}_{kj}, \hat{\sigma }_{lj}\in C(\mathbb{R},\mathbb{R})\) (\(i,k=1,2,\ldots,n\); \(j, l=1,2,\ldots,m\)) are ω-periodic functions. \(\theta_{i}>0\) (\(i=1,2,\ldots,n\)) and \(\vartheta_{j}>0\) (\(j=1,2,\ldots,m\)) are all constants. \(K_{ik}, \hat{K}_{kj}, L_{il}, \hat{L}_{lj}\in C((-\infty,0],(0,\infty))\) with \(\int_{-\infty}^{0}K_{ik}(s)\,ds=\int_{-\infty}^{0}\hat{K}_{kj}(s)\,ds =\int_{-\infty}^{0}L_{il}(s)\,ds=\int_{-\infty}^{0}\hat{L}_{lj}(s)\,ds=1\).
The importance of system (1.1) is due to the wide application of functional differential equations in the ecosystem. It is well known that functional differential equations are modeled by mathematical models to describe interactions and changes among species in many ecosystems or biological systems. One of the most famous and important population dynamics models is the Lotka-Volterra predator-prey model proposed by Lotka and Volterra in [1, 2]. This rudimentary and important model of mathematical ecology is expressed in the form of
where \(x(t)\) is the density of the prey species at time t, \(y(t)\) is the density of the predator species at time t. r is the intrinsic growth rate of the prey, a is the per-capita rate of predation of the predator, d is the death rate of the predator, b denotes the product of the per-capita rate of predation and the rate of converting the prey into the predator.
The Lotka-Volterra model and its various generalized forms have successfully described the interactions among species in a population dynamics. There have been many papers dealing with its various dynamical properties, and one has seen great progress [3–21]. However, regardless of this fact, the Lotka-Volterra system has a disadvantageous property, that is, the rate of change in the size of each species is a linear function of the sizes of the interacting species. It is worth noticing that Ayala and Gilpin et al. [22] conducted experiments on fruit fly dynamics to test the validity of competitions. The model accounting best for the experimental results is given by
where \(r_{i}\) is the intrinsic rate of growth of species, \(K_{i}\) is the environment carrying capacity of species i in the absence of competition, \(\theta_{i}\) provides a nonlinear measure of interspecific interference, and \(a_{ij}\) provides a measure of interspecific interference. Compared with the Lotka-Volterra system, this model called Gilpin-Ayala competition system is somewhat more complicated and accurate. As soon as it was put forward, the Gilpin-Ayala model received extensive attention. Many scholars have studied the dynamics of the Gilpin-Ayala system and its various generalized forms and obtained a lot of good results (see [23–31]).
To the best of our knowledge, there are few papers dealing with the existence of positive periodic solutions of system (1.1) by the theory of strict-set-contraction. Our main purpose of this paper is to establish some new existence conditions of positive periodic solutions for system (1.1) by using a fixed point theorem of strict-set-contraction.
2 Preliminaries
For convenience, we introduce the notation
where \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\) and \(f(t)\) is a continuous ω-periodic function on \(\mathbb{R}\).
Let \(x_{i}^{\theta_{i}}(t)=u_{i}(t)\), \(y_{j}^{\vartheta_{j}}(t)=v_{j}(t)\), \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\), then system (1.1) changes into the following system:
where \(u(t)=(u_{1}(t),u_{2}(t),\ldots,u_{n}(t))\), \(v(t)=(v_{1}(t),v_{2}(t),\ldots,v_{m}(t))\),
Obviously, if \((\bar{u}_{1}(t),\ldots,\bar{u}_{n}(t),\bar{v}_{1}(t),\ldots,\bar{v}_{m}(t))\) is a positive ω-periodic solution of system (2.1), then \((\bar{u}_{1}^{\frac{1}{\theta_{1}}}(t),\ldots,\bar{u}_{n}^{\frac {1}{\theta_{n}}}(t),\bar{v}_{1}^{\frac{1}{\vartheta_{1}}}(t),\ldots,\bar {v}_{m}^{\frac{1}{\vartheta_{m}}}(t))\) is a positive ω-periodic solution of system (1.1). Hence, we only need to argue the existence of a positive ω-periodic solutions of system (2.1). To do this, we introduce the following lemma.
Lemma 2.1
Let \(r\in C(\mathbb{R},\mathbb{R})\), \(a\in\mathbb{R}\) and \(y_{a}\in\mathbb{R}\), the unique solution of the initial value problem
is given by
The existence of periodic solutions of system (2.1) is equivalent to the existence of periodic solutions of the corresponding integral system. So the following lemma is important in our discussion.
Lemma 2.2
\(x(t)=(u(t),v(t))^{T}=(u_{1}(t),\ldots,u_{n}(t),v_{1}(t),\ldots,v_{m}(t))^{T}\) is an ω-periodic solution of (2.1) is equivalent to \(x(t)\) is an ω-periodic solution of the following integral system:
where
and
Proof
If \((u(t),v(t))\) is an ω-periodic solution of (2.1), by applying Lemma 2.1 and the first equation of (2.1), for \(\xi\geq t\), we have
Let \(\xi=t+\omega\) in the above equality and notice that \(u_{i}(t)=u_{i}(t+\omega)\), \(r_{i}(t+\omega)=r_{i}(t)\), we have
which implies that
Similarly, we get
Thus, we conclude that \((u(t),v(t))\) satisfies (2.2), and vice versa. The proof is complete. □
Lemma 2.3
If \(r_{i}(t),\hat{r}_{j}(t)>0\), \(\forall t\in\mathbb{R}\), and \(\theta_{i},\vartheta_{j}>0\), \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\), then \(G_{i}(t,s)\) (\(i=1,2,\ldots,n\)) and \(\hat{G}_{j}(t,s)\) (\(j=1,2,\ldots,m\)) defined by (2.2) and (2.3) satisfy the following:
-
(1)
\(\frac{\delta_{i}}{1-\delta_{i}}\leq G_{i}(t,s)\leq\frac {1}{1-\delta_{i}}\), \(\forall s\in[t,t+\omega]\), where \(\delta_{i}\triangleq e^{-\theta_{i}\int_{0}^{\omega}r_{i}(\tau)\,d\tau}\), \(i=1,2,\ldots,n\);
-
(2)
\(\frac{1}{\hat{\delta}_{j}-1}\leq\hat{G}_{j}(t,s)\leq \frac{\hat{\delta}_{j}}{\hat{\delta}_{j}-1}\), \(\forall s\in[t,t+\omega]\), where \(\hat{\delta}_{j}\triangleq e^{\vartheta_{j}\int_{0}^{\omega}\hat{r}_{j}(\tau)\,d\tau}\), \(j=1,2,\ldots,m\);
-
(3)
\(G_{i}(t+\omega,s+\omega)=G_{i}(t,s)\), \(i=1,2,\ldots,n\), \(\hat{G}_{j}(t+\omega,s+\omega)=\hat{G}_{j}(t,s)\), \(j=1,2,\ldots,m\).
Proof
Since \(e^{-\theta_{i}\int_{t}^{s} r_{i}(\tau)\,d\tau}\) is monotone decreasing and \(e^{\vartheta_{j}\int_{t}^{s} \hat{r}_{j}(\tau)\,d\tau}\) is monotone increasing on the variable s in \([t,t+\omega]\), respectively, we have
Thus, assertions (1) and (2) hold. Now we show that assertion (3) holds too. Indeed, by the integration by substitution, we have
It is similar to prove that \(\hat{G}_{j}(t+\omega,s+\omega)=\hat{G}_{j}(t,s)\). The proof of Lemma 2.3 is complete. □
For the sake of obtaining the existence of a periodic solution of system (2.2), we need the following preparations.
Let X be a real Banach space and K be a closed, nonempty subset of X. Then K is a cone provided
-
(i)
\(k\alpha+l\beta\in K\) for all \(\alpha,\beta \in K\) and all \(k,l\geq0\);
-
(ii)
\(\alpha,-\alpha\in K\) imply \(\alpha=\theta\), here θ is the zero element of X.
Let E be a Banach space and K be a cone in E. The semi-order induced by the cone K is denoted by ≤. That is, \(x\leq y\) if and only if \(y-x\in K\). In addition, for a bounded subset \(A\subset E\), let \(\alpha_{E}(A)\) denote the (Kuratowski) measure of non-compactness defined by
where \(\operatorname{diam}(A_{i})\) denotes the diameter of the set \(A_{i}\).
Let E, F be two Banach spaces and \(D\subset E \). A continuous and bounded map \(\Phi: \overline{\Omega}\rightarrow F\) is called k-set contractive if, for any bounded set \(S\subset D\), we have
Φ is called strict-set-contractive if it is k-set-contractive for some \(0\leq k<1\). Particularly, completely continuous operators are 0-set-contractive.
The following lemma is useful for the proof of our main results of this paper.
Lemma 2.4
Let K be a cone in the real Banach space X and \(K_{r,R}=\{x\in K: r\leq\|x\|\leq R\}\) with \(R>r>0\). Suppose that \(\Phi:K_{r,R}\rightarrow K\) is strict-set-contractive such that one of the following two conditions is satisfied:
-
(i)
\(\Phi x\nleq x\), \(\forall x\in K\), \(\|x\|=r\) and \(\Phi x\ngeq x\), \(\forall x\in K\), \(\|x\|=R\).
-
(ii)
\(\Phi x\ngeq x\), \(\forall x\in K\), \(\|x\|=r\) and \(\Phi x\nleq x\), \(\forall x\in K\), \(\|x\|=R\).
Then Φ has at least one fixed point in \(K_{r,R}\).
Let \(C(\mathbb{R},\mathbb{R}^{n+m})\) be a set of the continuous function \(x:\mathbb{R}\rightarrow\mathbb{R}^{n+m}\). Define \(X=\{x: x\in C(\mathbb{R},\mathbb{R}^{n+m}),x(t+\omega)=x(t)\}\) endowed with the norm defined by \(\|x\|= \max_{1\leq i\leq n+m}|x_{i}|_{0}\), where \(|x_{i}|_{0}=\sup_{t\in[0,\omega]_{\mathbb{T}}}\{ |x_{i}(t)|\}\), \(i=1,2,\ldots,n+m\). Then X is a Banach space. In view of Lemma 2.3, we define the cone K in X as
Let the map Φ be defined by
where \(x\in K\), \(t\in\mathbb{R}\),
and \(G_{i}(t,s)\) (\(i=1,2,\ldots,n\)), \(\hat{G}_{j}(t,s)\) (\(j=1,2,\ldots,m\)) defined by (2.2) and (2.3), respectively.
Lemma 2.5
\(\Phi: K\rightarrow K\) defined by (2.5) is well defined, that is, \(\Phi(K)\subset K\).
Proof
For any \(x\in K\), it is clear that \(\Phi x\in C(\mathbb{R},\mathbb{R}^{n+m})\). In view of Lemma 2.3 and (2.5), we obtain
that is, \((\Phi_{i} x)(t+\omega)=(\Phi_{i} x)(t)\), \(\forall t\in\mathbb{R}\), \(i=1,2,\ldots,n\). Similarly, we have \((\Psi_{j} x)(t+\omega)=(\Psi_{j} x)(t)\), \(\forall t\in\mathbb{R}\), \(j=1,2,\ldots,m\). So \(\Phi x\in X\). For any \(x\in K\), we have
and
So \(\Phi x\in K\). This completes the proof of Lemma 2.5. □
Lemma 2.6
\(\Phi: K\rightarrow K\) defined by (2.5) is completely continuous.
Proof
It is easy to see that Φ is continuous and bounded. Now we show that Φ maps bounded sets into relatively compact sets. Let \(\Omega\subset K\) be an arbitrary open bounded set in K, then there exists a number \(R>0\) such that \(\|x\|< R\) for any \(x=(u_{1},\ldots,u_{n}, v_{1},\ldots,v_{m})^{T}\in\Omega\). We prove that \(\overline{\Phi(\Omega)}\) is compact. In fact, for any \(x\in\Omega\) and \(t\in[0,\omega]\), we have
and
Similarly, for any \(x\in\Omega\) and \(t\in[0,\omega]\), we have
and
Hence,
It follows from Lemma 2.4 in [34] that \(\Phi(\bar{\Omega})\) is relatively compact in X. The proof of Lemma 2.6 is complete. □
3 Main results
In this section, we shall give our main results.
Theorem 3.1
If \(\Gamma<1\), then system (1.1) has at least one positive ω-periodic solution.
Proof
Take \(0< r<\Gamma\) and \(R>\Pi\). Noting that \(0<\delta_{i}<1\) and \(\hat{\delta}_{j}>1\), we have \(\Gamma_{i}>\Pi_{i}\) and \(\hat{\Gamma}_{j}>\hat{\Pi}_{j}\). Then we obtain \(0< r<\Gamma<\Pi<R\). It follows from Lemmas 2.5-2.6 and \(\Gamma<1\) that Φ is strict-set-contractive on \(K_{r,R}\). By Lemma 2.2, it is easy to see that if there exists \(x^{*}\in K\) such that \(\Phi x^{*}=x^{*}\), then \(x^{*}\) is one positive ω-periodic solution of system (2.1). Now, we shall prove that condition (ii) of Lemma 2.4 holds.
First, we prove that \(\Phi x\ngeq x\), \(\forall x\in K\), \(\|x\|=r\). Otherwise, there exists \(x\in K\), \(\|x\|=r\) such that \(\Phi x\neq x\). So, \(\|x\|>0\) and \(\Phi x-x\in K\), which implies that
and
Moreover, for \(t\in[0,\omega]\), we have
Similarly, for \(t\in[0,\omega]\), we have
From (3.1)-(3.4), we get \(\|x\|\leq\|\Phi x\|< r=\|x\|\), which is a contradiction. Next, we prove that \(\Phi x\nleq x\), \(\forall x\in K\), \(\|x\|=R\) also holds. Indeed, we only need to prove that \(\Phi x\nless x\), \(\forall x\in K\), \(\|x\|=R\). For the sake of contradiction, suppose that there exists \(x\in K\) and \(\|x\|=R\) such that \(\Phi x< x\). Thus \(x-\Phi x\in K\setminus\{\theta=(0,0,\ldots,0)^{T}\}\). Furthermore, for any \(t\in[0,\omega]\), we have
and
For any \(t\in[0,\omega]\), we have
Similarly, for \(t\in[0,\omega]\), we have
From (3.5)-(3.8), we obtain \(\|x\|>\|\Phi x\|\geq R\), which is a contradiction. Therefore, condition (ii) of Lemma 2.4 holds. By Lemma 2.4, we see that Φ has at least one positive nonzero fixed point in \(K_{r,R}\). Therefore, system (2.1) has at least one positive ω-periodic solution \((u_{1}^{*}(t),\ldots,u^{*}_{n}(t),v^{*}_{1}(t),\ldots,v_{m}^{*}(t))\). Thus, system (1.1) has at least one positive ω-periodic solution \(((u_{1}^{*}(t))^{\frac{1}{\theta_{1}}},\ldots,(u^{*}_{n}(t))^{\frac {1}{\theta_{n}}},(v^{*}_{1}(t))^{\frac{1}{\vartheta_{1}}},\ldots ,(v_{m}^{*}(t))^{\frac{1}{\vartheta_{m}}})\). The proof of Theorem 3.1 is complete. □
System (1.1) contains the following n-species Gilpin-Ayala competitive population dynamics model:
where \(i=1,2,\ldots,n\), \(r_{i}, a_{ik}, c_{ik}\in C(\mathbb{R},(0,\infty))\) (\(i,k=1,2,\ldots,n\)) and \(\tau_{ik}\in C(\mathbb{R},\mathbb{R})\) (\(i,k=1,2,\ldots,n\)) are ω-periodic functions. \(\theta_{k}>0\) (\(k=1,2,\ldots,n\)) is a constant. \(K_{ik}\in C((-\infty,0],(0,\infty))\) with \(\int_{-\infty}^{0}K_{ik}(s)\,ds=1\). There exists a positive integer p such that \(t_{i, k+p}=t_{k}+\omega\), \(k\in\mathbb{Z}\). Without loss of generality, we also assume that \([0,\omega)\cap\{t_{k}: k\in\mathbb{Z}\}=\{t_{1},t_{2},\ldots,t_{p}\}\).
Similar to the previous arguments, we conclude the existence of a positive ω-periodic solution for system (3.9) as follows.
Theorem 3.2
If \(\Lambda=\min \{\frac{1}{\Lambda_{1}},\frac{1}{\Lambda _{2}},\ldots,\frac{1}{\Lambda_{n}} \}<1\), where \(\Lambda_{i}=\frac{\theta_{i}}{1-\delta_{i}}\sum_{k=1}^{n}\int_{0}^{\omega}[a_{ik}(s)+c_{ik}(s) ]\,ds\), then system (3.9) has at least one positive ω-periodic solution.
4 Illustrative example
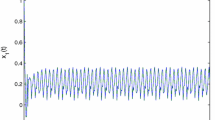
Consider the following two-species Gilpin-Ayala population model:
where \(\theta=\frac{1}{2}\), \(\vartheta=2\), \(r(t)=\frac{(2+\cos t)\ln2}{2\pi}\), \(\hat{r}(t)=\frac{(2+\sin t)\ln2}{8\pi}\), \(a(t)=\frac{3+\cos2t}{9\pi}\), \(b(t)=\frac{2-\sin3t}{9\pi}\), \(c(t)=\frac{1+\pi|\sin t|}{9\pi}\), \(d(t)=\frac{2+\cos5t}{24\pi}\), \(\hat{a}(t)=\frac{3-\cos2t}{9\pi}\), \(\hat{b}(t)=\frac{2+\sin4t}{24\pi}\), \(\hat{c}(t)=\frac{1+\pi |\sin t|}{24\pi}\), \(\hat{d}(t)=\frac{2+\cos3t}{24\pi}\), \(\tau(t)=\frac{|\sin t|}{2}\), \(\sigma(t)=\frac{1+\sin t}{3}\), \(\hat{\tau}(t)=\frac{|\cos2t|}{3}\), \(\hat{\sigma}(t)=\frac {2-|\cos t|}{4}\), \(K(s)=\hat{K}(s)=e^{s}\), \(L(s)=\hat{L}(s)=\sqrt{\frac{2}{\pi}}e^{-\frac{s^{2}}{2}}\).
Obviously, \(r(t)\), \(\hat{r}(t)\), \(a(t)\), \(b(t)\), \(c(t)\), \(d(t)\), \(\hat{a}(t)\), \(\hat{b}(t)\), \(\hat{c}(t)\), \(\hat{d}(t)\), \(\tau(t)\), \(\sigma(t)\), \(\hat{\tau}(t)\) and \(\hat{\sigma}(t)\) are all positive 2π-periodic functions. By a simple calculation, we have
Thus, all the assumptions of Theorem 3.1 are satisfied. Hence, system (4.1) has at least one positive 2π-periodic solution.
References
Volterra, V: Variazioni e fluttuazioni del numero d’individui in specie d’animali conviventi. Mem. R. Accad. Naz. Lincei 2, 31-113 (1926)
Lotka, A: Elements of Physical Biology. Williams & Wilkins, Baltimore (1924)
Kuang, Y: Delay Differential Equations with Applications in Population Dynamics. Academic Press, New York (1993)
Zhen, J, Ma, Z, Han, M: The existence of periodic solutions of the n-species Lotka-Volterra competition systems with impulsive. Chaos Solitons Fractals 22(1), 181-188 (2004)
Li, Y: Periodic solutions for delay Lotka-Volterra competition systems. J. Math. Anal. Appl. 246, 230-244 (2000)
Yang, P, Xu, R: Global attractivity of the periodic Lotka-Volterra system. J. Math. Anal. Appl. 233, 221-232 (1999)
Gopalsamy, K: Global asymptotic stability in a periodic Lotka-Volterra system. J. Aust. Math. Soc. Ser. B, Appl. Math 27, 66-72 (1985)
Li, Y, Kuang, Y: Periodic solutions of periodic delay Lotka-Volterra equations and systems. J. Math. Anal. Appl. 255, 260-280 (2001)
Yang, Z, Cao, J: Positive periodic solutions of neutral Lotka-Volterra system with periodic delays. Appl. Math. Comput. 149, 661-687 (2004)
Zhen, J, Han, M, Li, G: The persistence in a Lotka-Volterra competition systems with impulsive. Chaos Solitons Fractals 24, 1105-1117 (2005)
Zhao, K, Ye, Y: Four positive periodic solutions to a periodic Lotka-Volterra predatory-prey system with harvesting terms. Nonlinear Anal., Real World Appl. 11, 2448-2455 (2010)
Li, Y, Zhao, K, Ye, Y: Multiple positive periodic solutions of n species delay competition systems with harvesting terms. Nonlinear Anal., Real World Appl. 12, 1013-1022 (2011)
Zhao, K, Li, Y: Multiple positive periodic solutions to a non-autonomous Lotka-Volterra predator-prey system with harvesting terms. Electron. J. Differ. Equ. 2011, Article ID 49 (2011)
Zhao, K, Liu, J: Existence of positive almost periodic solutions for delay Lotka-Volterra cooperative systems. Electron. J. Differ. Equ. 2013, Article ID 157 (2013)
Yu, P, Han, M, Xiao, D: Four small limit cycles around a Hopf singular point in 3-dimensional competitive Lotka-Volterra systems. J. Math. Anal. Appl. 436(1), 521-555 (2016)
Li, J, Zhao, A: Stability analysis of a non-autonomous Lotka-Volterra competition model with seasonal succession. Appl. Math. Model. 40(2), 763-781 (2016)
Bao, X, Li, W, Shen, W: Traveling wave solutions of Lotka-Volterra competition systems with nonlocal dispersal in periodic habitats. J. Differ. Equ. 260(12), 8590-8637 (2016)
Li, S, Liu, S, Wu, J, Dong, Y: Positive solutions for Lotka-Volterra competition system with large cross-diffusion in a spatially heterogeneous environment. Nonlinear Anal., Real World Appl. 36, 1-19 (2017)
Ma, L, Guo, S: Stability and bifurcation in a diffusive Lotka-Volterra system with delay. Comput. Math. Appl. 72(1), 147-177 (2016)
Zhao, K, Ding, L, Yang, F: Existence of multiple periodic solutions to Lotka-Volterra networks-like food-chain system with delays and impulses on time scales. Int. J. Biomath. 7(1), 1-30 (2014)
Wang, Q, Liu, Z: Existence and stability of positive almost periodic solutions for a competitive system on time scales. Math. Comput. Simul. 138, 65-77 (2017)
Ayala, F, Gilpin, M, Eherenfeld, J: Competition between species: theoretical models and experimental tests. Theor. Popul. Biol. 4, 331-356 (1973)
Chen, F: Some new results on the permanence and extinction of nonautonomous Gilpin-Ayala type competition model with delays. Nonlinear Anal., Real World Appl. 7(5), 1205-1222 (2006)
Chen, F, Xie, X, Shi, J: Existence, uniqueness and stability of positive periodic solution for a nonlinear prey-competition model with delays. J. Comput. Appl. Math. 194, 368-387 (2006)
He, M, Li, Z, Chen, F: Permanence, extinction and global attractivity of the periodic Gilpin-Ayala competition system with impulses. Nonlinear Anal., Real World Appl. 11, 1537-1551 (2010)
Wang, D: Dynamic behaviors of an obligate Gilpin-Ayala system. Adv. Differ. Equ. 2016, Article ID 270 (2016)
Lu, H, Yu, G: Permanence of a Gilpin-Ayala predator-prey system with time-dependent delay. Adv. Differ. Equ. 2015, Article ID 109 (2015)
Lian, B, Hu, S: Asymptotic behaviour of the stochastic Gilpin-Ayala competition models. J. Math. Anal. Appl. 339, 419-428 (2008)
Ai, X, Sun, Y: An optimal stopping problem in the stochastic Gilpin-Ayala population model. Adv. Differ. Equ. 2012, Article ID 210 (2012)
Fang, H: Multiple positive periodic solutions for a food-limited two-species Gilpin-Ayala competition patch system with periodic harvesting terms. J. Inequal. Appl. 2012, Article ID 291 (2012)
Fang, H, Wang, Y: Four periodic solutions for a food-limited two-species Gilpin-Ayala type predator-prey system with harvesting terms on time scales. Adv. Differ. Equ. 2013, Article ID 278 (2013)
Các, N, Gatica, J: Fixed point theorems for mappings in ordered Banach spaces. J. Math. Anal. Appl. 71, 547-557 (1979)
Guo, D: Positive solutions of nonlinear operator equations and its applications to nonlinear integral equations. Adv. Math. 13, 294-310 (1984) (in Chinese)
Xing, Y, Han, M, Zheng, G: Initial value problem for first-order integro-differential equation of Volterra type on time scales. Nonlinear Anal., Theory Methods Appl. 60, 429-442 (2005)
Acknowledgements
The authors thank the referees for a number of suggestions which have improved many aspects of this article. This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant (No. 11161025, No. 11661047).
Author information
Authors and Affiliations
Contributions
The authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare to have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhao, K., Ren, Y. Existence of positive periodic solutions for a class of Gilpin-Ayala ecological models with discrete and distributed time delays. Adv Differ Equ 2017, 331 (2017). https://doi.org/10.1186/s13662-017-1386-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1386-9