Abstract
By using Mawhin’s coincidence degree theory, this paper establishes a new criterion on the existence of four periodic solutions for a food-limited two-species Gilpin-Ayala type predator-prey system with harvesting terms on time scales. An example is given to illustrate the effectiveness of the result.
Similar content being viewed by others
1 Introduction
The theory of calculus on time scales was initiated by Hilger [1] in order to unify continuous and discrete analysis, and it has become an effective approach to the study of mathematical models involving the hybrid discrete-continuous processes. Since the population dynamics in the real world usually involves the hybrid discrete-continuous processes, it may be more realistic to consider population models on time scales [2].
In recent years, some researchers studied the existence of periodic solutions for some population models on time scales under the assumption of periodicity of the parameters by using Mawhin’s coincidence degree theory (see [3–7]). To our best knowledge, few papers deal with the existence of multiple periodic solutions for population models with harvesting terms on time scales. The main difficulty is that the techniques used in continuous population models with harvesting terms are generally not available to population models with harvesting terms on time scales. Indeed, almost all papers involving continuous population models with harvesting terms used Fermat’s theorem on local extrema of differentiable functions in real analysis; for example, see [8–11]. However, Fermat’s theorem is not true in time scales calculus.
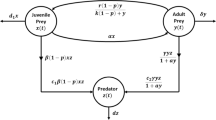
In this paper, we consider a food-limited two-species Gilpin-Ayala type predator-prey system with harvesting terms on time scales:
In system (1.1), let , . If the time scale (the set of all real numbers), then system (1.1) reduces to
where and denote the prey and the predator, respectively; (), (), () are all positive continuous functions denoting the intrinsic growth rate, the intra-specific competition rates and the harvesting rates, respectively; is the predation rate of the predator and represents the conversion rate; () are the population numbers of two species at saturation, respectively. () represent a nonlinear measure of interspecific interference. When (), () are the rate of replacement of mass in the population at saturation (including the replacement of metabolic loss and of dead organisms). In this case, system (1.2) is a food-limited population model. For other food-limited population models, we refer to [12–17] and the references cited therein. When (), system (1.2) is a Gilpin-Ayala type population model. Gilpin-Ayala type population models were firstly proposed by Gilpin and Ayala in [18]. For some recent work, we refer to [17, 19–22]. When , (), system (1.2) was consider by Zhao and Ye [9].
Motivated by the work of Bohner et al. [3] and Chen [8], we study the existence of multiple periodic solutions of (1.1) by using Mawhin’s coincidence degree.
2 Preliminaries from calculus on time scales
In this section, we briefly present some foundational definitions and results from the calculus on time scales so that the paper is self-contained. For more details, one can see [1, 23, 24].
Definition 2.1 [23]
A time scale  is an arbitrary nonempty closed subset of the real numbers ℝ.
is an arbitrary nonempty closed subset of the real numbers ℝ.
Let . Throughout this paper, the time scale  is assumed to be ω-periodic, i.e., implies . In particular, the time scale
is assumed to be ω-periodic, i.e., implies . In particular, the time scale  under consideration is unbounded above and below.
under consideration is unbounded above and below.
Definition 2.2 [23]
We define the forward jump operator , the backward jump operator , and the graininess by
respectively. If , then t is called right-dense (otherwise, right-scattered), and if , then t is called left-dense (otherwise, left-scattered).
Definition 2.3 [23]
Assume that is a function, and let . Then we define to be the number (provided it exists) with the property that given any , there is a neighborhood U of t (i.e., for some ) such that
In this case, is called the delta (or Hilger) derivative of f at t. Moreover, f is said to be delta or Hilger differentiable on  if exists for all .
if exists for all .
Definition 2.4 [23]
A function is called an antiderivative of provided for all . Then we define
Definition 2.5 [23]
A function is said to be rd-continuous if it is continuous at right-dense points in  and its left-sided limits exist (finite) at left-dense points in
and its left-sided limits exist (finite) at left-dense points in  . The set of rd-continuous functions will be denoted by .
. The set of rd-continuous functions will be denoted by .
The following notation will be used throughout this paper.
Let
where is a nonnegative ω-periodic real function, i.e., for all .
Lemma 2.1 [23]
Every rd-continuous function has an antiderivative.
Lemma 2.2 [23]
Assume that is a function, and let . Then we have:
-
(i)
If f is continuous at t and t is right-scattered, then f is differential at t with
-
(ii)
If f is right-dense, then f is differential at t iff the limit
exists as a finite number. In this case,
Lemma 2.3 [3]
Let and . If is ω-periodic, then
Lemma 2.4 [6]
Assume that is a function sequence on such that
-
(i)
is uniformly bounded on ;
-
(ii)
is uniformly bounded on .
Then there is a subsequence of converging uniformly on .
3 Existence of multiple periodic solutions
We first briefly state Mawhin’s coincidence degree theory (see [25]).
Let X, Z be normed vector spaces, be a linear mapping, be a continuous mapping. The mapping L will be called a Fredholm mapping of index zero if and ImL is closed in Z. If L is a Fredholm mapping of index zero, then there exist continuous projectors (i.e., linear and idempotent linear operators) and such that , . If we define as the restriction of L to , then is invertible. We denote the inverse of that map by . If Ω is an open bounded subset of X, the mapping N will be called L-compact on if is bounded and is compact, i.e., continuous and such that is relatively compact. Since ImQ is isomorphic to KerL, there exists an isomorphism .
For convenience, we introduce Mawhin’s continuation theorem [25] as follows.
Lemma 3.1 Let L be a Fredholm mapping of index zero, and let be L-compact on . Suppose
-
(a)
for every and every ;
-
(b)
for every ;
-
(c)
Brouwer degree .
Then has at least one solution in .
Set
Lemma 3.2 [17]
Assume that a, b, c, α are positive constants and
Then there exist such that
and
Set
From now on, we always assume that:
(H1) , , , (), () are positive continuous ω-periodic functions, () are positive constants.
(H2) .
(H3) .
Set
Lemma 3.3 Assume that (H1)-(H3) hold. Then the following assertions hold:
-
(1)
There exist such that
and
-
(2)
There exist such that
and
-
(3)
There exist such that
and
-
(4)
-
(5)
Proof It follows from (H1)-(H3) and Lemma 3.2 that assertions (1)-(3) hold. Noticing that
we have
By assertions (1)-(3), assertion (4) holds.
It follows from () that
Therefore, we have
which implies that assertion (5) also holds. □
Now, we are ready to state the main result of this paper.
Theorem 3.1 Assume that (H1)-(H3) hold. Then system (1.1) has at least four ω-periodic solutions.
Proof Take
and define
Equipped with the above norm , it is easy to verify that X and Z are both Banach spaces.
Set
Define the mappings , , and as follows:
We first show that L is a Fredholm mapping of index zero and N is L-compact on for any open bounded set . The argument is standard, one can see [3–5]. But for the sake of completeness, we give the details here.
It is easy to see that , is closed in Z, and . Therefore, L is a Fredholm mapping of index zero. Clearly, P and Q are continuous projectors such that
On the other hand, , the inverse to L, exists and is given by
Obviously, QN and are continuous. By Lemma 2.4, it is not difficult to show that is compact for any open bounded set . Moreover, is bounded. Hence, N is L-compact on for any open bounded set .
In order to apply Lemma 3.1, we need to find at least four appropriate open, bounded subsets , , , in X.
Corresponding to the operator equation , , we have
Suppose that is an ω-periodic solution of (3.1), (3.2) for some . Since , there exist , , such that
By Lemma 2.2, it is easy to see that
From this and (3.1), (3.2), we obtain that
and
Claim A
From (3.1), we obtain that
Therefore, we have
By (3.5), we have
which implies
Therefore, we have
From (3.7), (3.8) and Lemma 2.3, we have
From (3.2), we obtain that
Therefore, we have
From this and (3.9), we have
By (3.6), we have
which implies
Therefore, we have
From (3.10), (3.11) and Lemma 2.3, we have
Claim B
From (3.5) and noticing that
we have
Therefore, by (3.8), we have
From assertion (3) of Lemma 3.3 and the above inequality, we have
Similarly, from (3.6) and noticing that
we have
Therefore, by (3.11), we have
From assertion (3) of Lemma 3.3 and the above inequality, we have
Claim C
From (3.3), (H2) and noticing that
we have
Therefore, we have
From assertion (1) of Lemma 3.3 and (3.15), we have
By a similar argument, it follows from (3.4) that
From assertion (1) of Lemma 3.3 and (3.17), we have
It follows from (3.9), (3.13), (3.16) and assertions (4)-(5) of Lemma 3.3 that
It follows from (3.12), (3.14), (3.18) and assertions (4)-(5) of Lemma 3.3 that
Clearly, , () are independent of λ. Now, let us consider with . Note that
Therefore, it follows from assertion (2) of Lemma 3.3 that has four distinct solutions:
Let
Then , , , are bounded open subsets of X. It follows from assertion (4) of Lemma 3.3, (3.23) and (3.24) that (). From assertion (4) of Lemma 3.3, (3.19)-(3.22), it is easy to see that (, ) and satisfies (a) in Lemma 3.1 for . Moreover, for . By assertion (2) of Lemma 3.3, a direct computation gives
Here, J is taken as the identity mapping since . So far we have proved that satisfies all the assumptions in Lemma 3.1. Hence, (1.1) has at least four ω-periodic solutions () with . Obviously, () are different. □
Example 3.1 In system (1.1), take
where ℤ is the integer set. Clearly, the time scale  is ω-periodic, i.e., implies . In this case, we have
is ω-periodic, i.e., implies . In this case, we have
Take
Then
Therefore, we have
Hence, all the conditions in Theorem 3.1 are satisfied. By Theorem 3.1, system (1.1) has at least four 2-periodic solutions.
References
Hilger S: Analysis on measure chains - a unified approach to continuous and discrete calculus. Results Math. 1990, 18: 8–56.
Gamarra JGP, Solé RV: Complex discrete dynamics from simple continuous population models. Bull. Math. Biol. 2002, 64: 611–620. 10.1006/bulm.2002.0286
Bohner M, Fan M, Zhang J: Existence of periodic solutions in predator-prey and competition dynamic systems. Nonlinear Anal., Real World Appl. 2006, 7: 1193–1204. 10.1016/j.nonrwa.2005.11.002
Fazly M, Hesaaraki M: Periodic solutions for predator-prey systems with Beddington-DeAngelis functional response on time scales. Nonlinear Anal., Real World Appl. 2008, 9: 1224–1235. 10.1016/j.nonrwa.2007.02.012
Zhang WP, Bi P, Zhu DM: Periodicity in a ratio-dependent predator-prey system with stage-structured predator on time scales. Nonlinear Anal., Real World Appl. 2008, 9: 344–353. 10.1016/j.nonrwa.2006.11.011
Xing Y, Han M, Zheng G: Initial value problem for first-order integro-differential equation of Volterra type on time scale. Nonlinear Anal. 2005, 60: 429–442.
Yu SB, Wu HH, Chen JB: Multiple periodic solutions of delayed predator-prey systems with type IV functional responses on time scales. Discrete Dyn. Nat. Soc. 2012., 2012: Article ID 271672
Chen Y: Multiple periodic solutions of delayed predator-prey systems with type IV functional responses. Nonlinear Anal., Real World Appl. 2004, 59: 45–53.
Zhao K, Ye Y: Four positive periodic solutions to a periodic Lotka-Volterra predatory-prey system with harvesting terms. Nonlinear Anal., Real World Appl. 2010, 11: 2448–2455. 10.1016/j.nonrwa.2009.08.001
Zhang ZQ, Tian TS: Multiple positive periodic solutions for a generalized predator-prey system with exploited terms. Nonlinear Anal., Real World Appl. 2007, 9: 26–39.
Li YK, Zhao KH, Ye Y: Multiple positive periodic solutions of n species delay competition systems with harvesting terms. Nonlinear Anal., Real World Appl. 2011, 12: 1013–1022. 10.1016/j.nonrwa.2010.08.024
Gopalsamy K, Kulenovic MRS, Ladas G: Environmental periodicity and time delays in a food-limited population model. J. Math. Anal. Appl. 1990, 147: 545–555. 10.1016/0022-247X(90)90369-Q
Gourley SA, Chaplain MAJ: Travelling fronts in a food-limited population model with time delay. Proc. R. Soc. Edinb. A 2002, 132: 75–89.
Gourley SA, So JW-H: Dynamics of a food-limited population model incorporating non-local delays on a finite domain. J. Math. Biol. 2002, 44: 49–78. 10.1007/s002850100109
Chen FD, Sun DX, Shi JL: Periodicity in a food-limited population model with toxicants and state dependent delays. J. Math. Anal. Appl. 2003, 288: 136–146. 10.1016/S0022-247X(03)00586-9
Li YK: Periodic solutions of periodic generalized food limited model. Int. J. Math. Math. Sci. 2001, 25: 265–271. 10.1155/S0161171201004215
Fang H: Multiple positive periodic solutions for a food-limited two-species Gilpin-Ayala competition patch system with periodic harvesting terms. J. Inequal. Appl. 2012., 2012: Article ID 291
Gilpin ME, Ayala FJ: Global models of growth and competition. Proc. Natl. Acad. Sci. USA 1973, 70: 3590–3593. 10.1073/pnas.70.12.3590
Lian B, Hu S: Asymptotic behaviour of the stochastic Gilpin-Ayala competition models. J. Math. Anal. Appl. 2008, 339: 419–428. 10.1016/j.jmaa.2007.06.058
Lian B, Hu S: Stochastic delay Gilpin-Ayala competition models. Stoch. Dyn. 2006, 6: 561–576. 10.1142/S0219493706001888
He MX, Li Z, Chen FD: Permanence, extinction and global attractivity of the periodic Gilpin-Ayala competition system with impulses. Nonlinear Anal., Real World Appl. 2010, 11: 1537–1551. 10.1016/j.nonrwa.2009.03.007
Zhang SW, Tan DJ: The dynamic of two-species impulsive delay Gilpin-Ayala competition system with periodic coefficients. J. Appl. Math. Inform. 2011, 29: 1381–1393.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston; 2001.
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston; 2003.
Gaines RE, Mawhin JL: Coincidence Degree and Nonlinear Differential Equation. Springer, Berlin; 1997.
Acknowledgements
This research is supported by the National Natural Science Foundation of China (Grant No. 10971085).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the manuscript and read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fang, H., Wang, Y. Four periodic solutions for a food-limited two-species Gilpin-Ayala type predator-prey system with harvesting terms on time scales. Adv Differ Equ 2013, 278 (2013). https://doi.org/10.1186/1687-1847-2013-278
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-278