An optimal stopping problem in the stochastic Gilpin-Ayala population model

Abstract

We present an explicit solution to an optimal stopping problem of the stochastic Gilpin-Ayala population model by applying the smooth pasting technique (Dixit in The Art of Smooth Pasting, 1993 and Dixit and Pindyck in Investment under Uncertainty, 1994). The optimal stopping rule is to find an optimal stopping time and an optimal stopping boundary of maximizing the expected discounted reward, which are given in this paper explicitly.

1 Introduction

Optimal stopping problems of stochastic systems play an important role in the field of stochastic control theory. A special interest in such problems is attracted by many fields such as finance, biology models and so on.

The aim of the optimal stopping problems is to search for random times at which the stochastic processes should be stopped to make the expected values of the given reward functionals optimal. Lots of explicitly solvable stopping problems with exponentially discounted stopping problems are mainly those for one-dimensional diffusion processes. The optimal stopping times are the first time at which the underlying processes exit certain regions restricted by constant boundaries.

In this paper, the optimal stopping time for the stochastic Gilpin-Ayala model [1–4], whose solution is a diffusion process, is introduced, and the explicit expressions for the value functions and the boundaries in such optimal stopping problems are obtained. To our best knowledge, there have been few tries to research the optimal harvesting problems based on optimal stopping, and many scholars studied stochastic logistic models such as [5, 6]. There are only a few results about the corresponding stochastic Gilpin-Ayala model, which is our motivation.

The Gilpin-Ayala population model is one of the most important and classic mathematical bio-economic models due to its theoretical and practical significance. In 1973, Gilpin and Ayala [7] claimed the following model:

$$d{X}_t=(r{X}_t-b{X}_t^{\theta +1})dt,\theta >0,$$

(1.1)

where $X_t$ denotes the density of resource population at time t, $r>0$ is called the intrinsic growth rate and $b=r/K>0$, K is the environmental carrying capacity. It is obvious that (1.1) becomes the classic logistic population model when $\theta =1$.

Recently, Eq. (1.1) has been extensively studied and many important results have been obtained; see, e.g., [8–11].

However, the population systems are affected by random disturbances such as environment effects, financial events and so on in the real world. In order to fit the real world better, the white noise is introduced into the population systems by many researchers [2, 3, 12–14]. In this paper, we study the optimal stopping problem of the stochastic Gilpin-Ayala population model

$$d{X}_t=(r{X}_t-b{X}_t^{\theta +1})dt+\mu X_{t}d{B}_t,X_0=x\ge 0,t>0,\theta >0,$$

(1.2)

where the constants r, b are mentioned in (1.1) and $B_t$ is one-dimensional Brownian motion [15].

The outline for this paper is as follows. Section 2 of this paper is concerned with the general problem of choosing an optimal stopping time for the stochastic Gilpin-Ayala population model. In Section 3, a closed-form candidate function for the value function is given. We verify the candidate for the expected reward is optimal and the optimal stopping boundary is expressed by the smooth pasting technique.

2 Formulation of the problem

Let the probability space $(\mathrm{\Omega },\mathfrak{F},\mathbb{P})$ satisfy the usual conditions. Suppose the population with size $X_t$ at time t is given by the stochastic Gilpin-Ayala population model

$$d{X}_t=(r{X}_t-b{X}_t^{\theta +1})dt+\mu X_{t}d{B}_t,X_0=x\ge 0,t>0.$$

(2.1)

It can be proved that if $r>0$ and $b>0$, then the stochastic Gilpin-Ayala equation (2.1) has a global, continuous positive solution $X_t$ defined by

$$X_t^x={(\frac{1}{x^{\theta }}{e}^{-\theta ((r-\frac{1}{2}{\mu }^2)t+\mu B(t))}+{\int }_0^{t}b\theta e^{-\theta ((r-\frac{1}{2}{\mu }^2)(t-s)+\mu (B(t)-B(s)))}ds)}^{-1}$$

(2.2)

for all $t\ge 0$, $B(t)$ is one-dimensional Brownian motion (see [16]), and note that $0\le X_t<K$.

The optimal stopping rule here can be considered to find an optimal value function Φ and an optimal stopping time ${\tau }^{\ast }$ such that

$$\mathrm{\Phi }(s,x)=\underset{\tau }{sup}{E}^{(0,x)}[e^{-\rho \tau }(X_{\tau }-a)+w]=E^{(0,x)}[e^{-\rho {\tau }^{\ast }}(X_{{\tau }^{\ast }}-a)+w],a>0.$$

(2.3)

The sup is taken over all stopping times τ of the process $X_t$ and the reward function

$$g(s,x)=e^{-\rho s}(x-a)+w,$$

(2.4)

where the discounting exponent $\rho >0$, $e^{-\rho \tau }(X_{\tau }-a)$ is the profit at time τ and a represents a fixed fee and it is natural to assume that $a<K$. The positive constant w represents the permanent assets. $E^x$ denotes the expectation with respect to the probability law $Q^x$ of the process $X_t$, $t\ge 0$ starting at $X_0=x>0$.

Note that it is trivial that the initial value $x\le a$. So we further assume that $x>a$ and the stopping time τ is bounded since $0<X_{\tau }<K$.

3 Analysis

Let us start with the infinitesimal generator [15]$\mathcal{A}$ of the Itô diffusion $Y_t={(t,X_t)}^T$, which is defined by

$$f(y)=\underset{t\downarrow 0}{lim}\frac{{\mathbb{E}}^y[f(Y_t)]-f(y)}{t},y\in {\mathbb{R}}^2,f\in C^2\left({\mathbb{R}}^2\right).$$

(3.1)

By the application of Itô formula, we have

$$\mathcal{A}f(s,x)=\frac{\partial f}{\partial s}+(rx-b{x}^{\theta +1})\frac{\partial f}{\partial x}+\frac{1}{2}{\mu }^2{x}^2\frac{{\partial }^{2}f}{\partial x^2},f\in C^2\left({\mathbb{R}}^2\right),$$

(3.2)

which is based on

$$d{Y}_t=\left(\begin{array}{c}1\\ r{X}_t-b{X}_t^{\theta +1}\end{array}\right)dt+\left(\begin{array}{c}0\\ \mu X_t\end{array}\right)d{B}_t.$$

(3.3)

And

$$\begin{array}{rcl}\mathcal{A}g& =& \frac{\partial g}{\partial s}+(rx-b{x}^{\theta +1})\frac{\partial g}{\partial x}+\frac{1}{2}{\mu }^2{x}^2\frac{{\partial }^{2}g}{\partial x^2}\\ =& (r-\rho -b{x}^{\theta })e^{-\rho s}x+\rho a{e}^{-\rho s}\end{array}$$

(3.4)

for all $s>0$, $x>0$ [15]. In order to find the unknown value function Φ from (2.3) and the unknown boundary $x_0^{\ast }$, we consider

$$\mathcal{A}f(s,x)=0,(s,x)\in R_{+}^2.$$

(3.5)

If we try a solution of (3.5) of the form

$$f(s,x)=e^{-\rho s}\varphi (x),$$

(3.6)

and substitute (3.6) into (3.5), we obtain

$$-\rho \varphi (x)+(rx-b{x}^{\theta +1}){\varphi }^{\prime }(x)+\frac{1}{2}{\mu }^2{x}^2{\varphi }^{″}(x)=0,x>0.$$

(3.7)

The general solution ϕ of (3.7) is

$$\varphi (x)=C_1{x}^{\theta a_1}U(a_1,b_1,\frac{2b}{{\mu }^2\theta }{x}^{\theta })+C_2{x}^{\theta a_1}M(a_1,b_1,\frac{2b}{{\mu }^2\theta }{x}^{\theta })$$

(3.8)

by setting

$$a_1=\frac{1}{2}\frac{{\mu }^2-2r+\sqrt{{\mu }^4+(-4r+8\rho ){\mu }^2+4r^2}}{{\mu }^2\theta }$$

(3.9)

and

$$b_1=\frac{{\mu }^2\theta +\sqrt{{\mu }^4+(-4r+8\rho ){\mu }^2+4r^2}}{{\mu }^2\theta },$$

(3.10)

where $C_1$, $C_2$ are arbitrary constants. Here $U(a_2,b_2,x)$ is the confluent hypergeometric function, whose integral representation is

$$U(a_2,b_2,x)=\frac{1}{\mathrm{\Gamma }(a_2)}{\int }_0^{\mathrm{\infty }}{e}^{-xt}{t}^{a_2-1}{(1+t)}^{b_2-a_2-1}dt$$

(3.11)

for $a_2>0$ and $b_2>1$ (see [7, 17, 18]). $M(a,b,x)$ is the Kummer hypergeometric function and Γ denotes the gamma function.

If $\varphi (x)$ goes to ∞ as $x\to \mathrm{\infty }$, we must have $C_2=0$ since $\varphi (x)$ is bounded. Then we define the candidate $h(s,x):{\mathbb{R}}_{+}^2\to \mathbb{R}$ for the optimal value function Φ in (2.3) by

$$h(s,x)=f(s,x)+w=\{\begin{array}{cc}{e}^{-\rho s}\hat{f}(x)+w,\hfill & 0<x<x_0,\hfill \\ e^{-\rho s}\hat{g}(x)+w,\hfill & x\ge x_0,\hfill \end{array}$$

(3.12)

where

$$\hat{f}(x)=C_1{x}^{\theta a_1}U(a_1,b_1,\frac{2b}{{\mu }^2\theta }{x}^{\theta }),0<x<x_0$$

and

$$\hat{g}(x)=x-a,x\ge x_0.$$

We observe that the constant

$$C_1=(x_0-a){\left[{(x_0)}^{\theta a_1}U(a_1,b_1,\frac{2b}{{\mu }^2\theta }{(x_0)}^{\theta })\right]}^{-1}$$

(3.13)

is determined by

• (1) value matching condition [19, 20]

  $$\hat{f}(x_0)=\hat{g}(x_0)$$

  (3.14)

and

• (2) smooth pasting condition

  $${\hat{f}}^{\prime }(x_0)={\hat{g}}^{\prime }(x_0).$$

  (3.15)

In fact, $x_0^{\ast }=\frac{\theta a{a}_1}{\theta a_1-1}$ is showed to be the unique solution of (3.15) by the following assumptions and Lemma 3.1.

We assume the following.

Assumption 1

$$\rho >r.$$

(3.16)

Assumption 2

$$K>\frac{\theta a_{1}a}{\theta a_1-1}.$$

(3.17)

The following lemma provides an optimal stopping boundary.

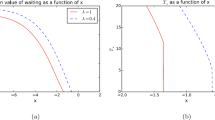
Lemma 3.1 $x_0^{\ast }=\frac{\theta a{a}_1}{\theta a_1-1}$ is the maximum value point of $h(s,x)$ given by (3.12) with respect to $x_0$, $0<x_0<K$ for fixed $s>0$, $0<x<K$.

Proof Let $\frac{\partial h}{\partial x_0}(s,x)=0$ for arbitrary $s>0$, $0<x<K$, then we derive

$$C(s,x)x_0^{-\theta a_1-1}{U}^{-1}(a_1,b_1,\frac{2b}{{\mu }^2\theta }{x}_0^{\theta })((1-\theta a_1)x_0+\theta a_{1}a)(1-\frac{L(y_0)}{R(x_0)+1})=0$$

(3.18)

by setting $C(s,x)=e^{-\rho s}{x}^{\theta a_1}U(a_1,b_1,\frac{2b}{{\mu }^2\theta }{x}^{\theta })$ and $y_0=\frac{2b}{{\mu }^2\theta }{x}_0^{\theta }$ together with

$$L(y_0)=\frac{y_{0}U(a_1+1,b_1+1,y_0)}{U(a_1,b_1,y_0)}$$

(3.19)

and

$$R(x_0)=\frac{x_0}{\theta a_1(a-x_0)}.$$

(3.20)

Since $R(x_0)$ increases on the interval $[0,a)$ with $R(0)=0$ and $R(a-)=+\mathrm{\infty }$, and $R(x_0)$ is an increasing function on the interval $(a,+\mathrm{\infty })$ with $R(a+)=-\mathrm{\infty }$ and $R(+\mathrm{\infty })=-{(\theta a_1)}^{-1}$, we can deduce that $L(y_0)$ is a decreasing function on $(0,\mathrm{\infty })$ with $L(0+)>0$. In fact, we only need to check that $L(x)$ decreases on ${\mathbb{R}}_{+}$ with $L(0+)>0$ and $L(+\mathrm{\infty })=0$. $L(+\mathrm{\infty })=0$ is trivial due to the fact that $U(a,b,x)\sim z^{-a}$ as $z\to \mathrm{\infty }$. To prove $L(0+)>0$, we take the change-of-variable formula to (3.11), then it follows

$$U(a_2,b_2,y_0)=\frac{y_0^{1-b_2}}{\mathrm{\Gamma }(a_2)}{\int }_0^{\mathrm{\infty }}{e}^{-t}{t}^{a_2-1}{(t+y_0)}^{b_2-a_2-1}dt,$$

(3.21)

which directly implies

$$\underset{y_0\downarrow 0}{lim}L(y_0)=\frac{\mathrm{\Gamma }(a_1)\mathrm{\Gamma }(b_1)}{\mathrm{\Gamma }(1+a_1)\mathrm{\Gamma }(1+b_1)}=\frac{b_1-1}{a_1}$$

(3.22)

for $b_1>1+a_1>1$. Next, with the help of the integral representation (3.21), we observe that

$$L(y_0)=\frac{{\int }_0^{\mathrm{\infty }}t(t+1)f_{y_0}(t)dt}{a_1{\int }_0^{\mathrm{\infty }}(t+1)f_{y_0}(t)dt},$$

(3.23)

where ${\int }_0^{\mathrm{\infty }}{f}_{y_0}(t)dt={\int }_0^{\mathrm{\infty }}A{e}^{-t}{t}^{a_1}{(t+y_0)}^{b_1-a_1-2}dt=1$, $t\ge 0$, with some normalizing constant A for $b_1>1+a_1>1$. Then by applying the Jensen inequality and considering the obvious fact that $b_1>1+a_1>1$, we deduce $\frac{d}{d{y}_0}L(y_0)\le 0$, which gives the monotonicity of $L(y_0)$ on $(0,K)$ (similar discussion can be found in [21]).

Then we conclude that

• (1) There exists a unique solution, which satisfies $L(y_0)=R(x_0)+1$, of (3.16) on $(0,a)$ and note that $P(x_0)\triangleq L(y_0)-R(x_0)-1>0$ on $(a,K)$ under Assumption 2.

• (2) The maximum value is given by

  $$x_0^{\ast }=\frac{\theta a{a}_1}{\theta a_1-1}>0$$

  (3.24)

under (3.9) and Assumption 1 on the interval $(a,K)$. The proof is completed.

 □

Now, let us give the following lemma for our main Theorem 3.3.

Lemma 3.2 Under Assumptions 1 and 2, the function $h(s,x):{\mathbb{R}}_{+}^2\to \mathbb{R}$ satisfies the following properties (1)-(3):

• (1) $h(s,x)\ge g(s,x)$ given by (2.4) for all $x>0$, $s>0$.

• (2) For $x\ge \frac{\theta a{a}_1}{\theta a_1-1}$, $s>0$,

  $$\mathcal{A}f(s,x)=\frac{\partial f}{\partial s}+(rx-b{x}^2)\frac{\partial f}{\partial x}+\frac{1}{2}{\mu }^2{x}^2\frac{{\partial }^{2}f}{\partial x^2}\le 0.$$

  (3.25)

• (3) $\mathcal{A}h=0$, $0<x<\frac{\theta a{a}_1}{\theta a_1-1}$, $s>0$.

Proof It is clear that $\mathcal{A}h=0$ by construction, for $0<x<\frac{\theta a{a}_1}{\theta a_1-1}$, $s>0$. We check that

• (1) $h(s,x)>g(s,x)$ for $0<x<\frac{\theta a{a}_1}{\theta a_1-1}$, i.e., $h(s,x)>e^{-\rho s}(x-a)+w$ for $0<x<\frac{\theta a{a}_1}{\theta a_1-1}$ and

• (2) $\mathcal{A}h(x)=\mathcal{A}g(x)<0$ for $x\ge \frac{\theta a{a}_1}{\theta a_1-1}$. This is easily done by routine calculation under Assumptions 1 and 2.

 □

Let us give our main theorem.

Theorem 3.3 Under Assumptions 1 and 2, setting $y=(s,x)$ and $Y_t={(t,X_t)}^T$, the function $h^{\ast }(y):{\mathbb{R}}_{+}^2\to \mathbb{R}$ defined by

$$h^{\ast }(y)=\{\begin{array}{cc}\frac{e^{-\rho s}(\frac{a}{\theta a_1-1})}{{(\theta a{a}_1)}^{\theta a_1}U(a_1,b_1,\frac{2b}{{\mu }^2\theta }{(\frac{\theta a{a}_1}{\theta a_1-1})}^{\theta })}{((\theta a_1-1)x)}^{\theta a_1}U(a_1,b_1,\frac{2b}{{\mu }^2\theta }{x}^{\theta })+w,\hfill & 0<x<\frac{\theta a{a}_1}{\theta a_1-1},\hfill \\ e^{-\rho s}(x-a)+w,\hfill & x\ge \frac{\theta a{a}_1}{\theta a_1-1}\hfill \end{array}$$

is the optimal value function. Moreover, the optimal stopping region F and the optimal stopping time ${\tau }^{\ast }$ are given by

$$F=\{y\in {\mathbb{R}}_{+}^2:h^{\ast }(y)=g(y)\}=\{(s,x):s>0,\frac{\theta a{a}_1}{\theta a_1-1}<x<\mathrm{\infty }\}$$

(3.26)

and

$${\tau }^{\ast }:={\tau }_F=inf\{t>0,Y_t^y\in F\}<+\mathrm{\infty }.$$

(3.27)

Proof Let τ be any stopping time with ${\mathbb{E}}^x[\tau ]<\mathrm{\infty }$ for the process $\{Y_t,t>0\}$ and any $t\in {\mathbb{R}}_{+}$, then by Dynkin’s formula [15]

$${\mathbb{E}}^y[h(Y_{\tau \wedge t})]=h(y)+{\mathbb{E}}^y[{\int }_0^{\tau \wedge t}\mathcal{A}h(Y_t)dt].$$

(3.28)

Therefore, by (1) and (2) in Lemma 3.2, we get

$$h(y)\ge {\mathbb{E}}^y[g(Y_{\tau \wedge t})].$$

(3.29)

Taking ${\underline{lim}}_{t\to \mathrm{\infty }}$ of both sides of (3.29), we have by the Fatou lemma [22]

$$h(y)\ge {\mathbb{E}}^y[g(Y_{\tau })1_{\{\tau <\mathrm{\infty }\}}].$$

(3.30)

Since τ is arbitrary with ${\mathbb{E}}^x[\tau ]<\mathrm{\infty }$, we conclude that

$$h(y)\ge h^{\ast }(y),y\in {\mathbb{R}}_{+}^2.$$

(3.31)

We proceed to prove $h(y)\le h^{\ast }(y)$.

• (a) If $y\in F$, then $h(y)=g(y)\le h^{\ast }(y)$. So, we have $h(y)=h^{\ast }(y)$ by (3.31) and ${\tau }^{\ast }=0$ is optimal for $y\in D$.

• (b) Next, suppose $y\notin F$. By Dynkin’s formula [15] and the fact that ${\tau }^{\ast }<\mathrm{\infty }$ a.s. $R^y$ for $y\in {\mathbb{R}}_{+}^2$, we have

  $$h(y)={\mathbb{E}}^y[{\int }_0^{{\tau }_F\wedge t}\mathcal{A}h(Y_s)ds+h(Y_{{\tau }_F\wedge t})].$$

  (3.32)

So, by (1), (3) in Lemma 3.2 and the fact that ${\tau }^{\ast }<\mathrm{\infty }$ a.s. $R^y$ for $y\in {\mathbb{R}}_{+}^2$ and $h\in C^2({\mathbb{R}}_{+}^2)$ [18], we get

$$\begin{array}{rcl}h(y)& =& \underset{t\to \mathrm{\infty }}{lim}{\mathbb{E}}^y[{\int }_0^{{\tau }_F\wedge t}\hat{\mathcal{A}}h(Y_s)ds+h(Y_{{\tau }_F\wedge t})]\\ =& {\mathbb{E}}^y[h(Y_{{\tau }_F})]={\mathbb{E}}^y[g(Y_{{\tau }_F})]\le h^{\ast }(y).\end{array}$$

(3.33)

Combining the two cases (a), (b) and (3.31), we obtain

$$h(y)\ge h^{\ast }(y)\ge h(y).$$

(3.34)

So, $h(y)=h^{\ast }(y)$ and ${\tau }^{\ast }={\tau }_F$ is optimal, $y\in F$.

We conclude that $h(y)=h^{\ast }(y)$ for all $y\in {\mathbb{R}}_{+}^2$ and the stopping time ${\tau }^{\ast }$ is defined by

$${\tau }^{\ast }=\{\begin{array}{cc}0,\hfill & y\notin F,\hfill \\ {\tau }_F,\hfill & y\in F.\hfill \end{array}$$

(3.35)

 □

4 Conclusion and further studies/research

This paper describes the optimal harvesting problems of the stochastic Gilpin-Ayala population model as an optimal stopping problem, which is our first try. Meanwhile, we obtain the explicit optimal value function and optimal stopping time by using the smooth pasting technique. Finally, we prove the result. Furthermore, our work can lead a new way for the optimal harvesting problem in the real world. In further direction, the optimal harvesting problems for the stochastic predator-prey model and related stochastic models will be considered.