1 Introduction

Ebola is a severe and often deadly illness killing between 50% and 90% of those infected with the virus [1–3] named after a river in the Democratic Republic of Congo (formerly Zaire) where it was first identified in 1976 with a high case fatality rate. The disease first came into the lime light in 1976 in Zaire and Sudan. It is a disease of humans and other primates caused by an Ebola virus. Symptoms start two days to three weeks after contacting the virus with a fever, sore throat, muscle pain and headaches [4–8]. Typically, vomiting, diarrhea and rash flow, along with decreased functioning of the liver and kidneys. Around this time, the affected people may begin to bleed within the body and externally. The virus may be acquired upon contact with blood or bodily fluids of an infected people or animal. Spreading through the air has not been documented in the natural environment. Fruit bats are believed to be a carrier and may spread the virus without being affected [9–15]. Once human infection occurs, the disease may spread among people, as well. Male survivors may be able to transmit the disease via semen for nearly two months. To make the diagnosis, typically other diseases with similar symptoms such as malaria, cholera and other viral hemorrhagic fevers are first excluded. To confirm the diagnosis, blood samples are tested for viral antibodies, viral RNA, or the virus itself. What makes the disease the worst of all is the absence of specific effective treatment. Efforts to help those who are infected are supportive and include giving either oral rehydration therapy (slightly sweet and salty water to drink) or intravenous. As the effective measures for controlling Ebola epidemic still lack, it needs more attention by medical staff, epidemiologists, mathematicians and other stakeholders.

Mathematical modeling is one of the most important tools in analyzing the epidemiological characteristics of an infectious disease and can provide some useful insights into the dynamics of the disease. Various models have been used to study different aspects of Ebola epidemic.

Chowell et al. constructed a mathematical model for Ebola virus disease transmission (Congo 1995 and Uganda 2000) and fitted it to historical data in estimation of \(R_{o}\) [16]. Althaus presented a SEIR mathematical model and fitted the model to the reported data of infected cases and deaths for Ebola virus disease in Guinea, Sierra Leone and Liberia [17]. The latest study by Rachah and Torres recommends inclusion of intervention factors like quarantine procedure in the mathematical model to treat the infected individuals and investigate the effect of vaccination on Ebola virus disease [18].

Besides, according to the World Health Organization (WHO) report 2016, an experimental Ebola vaccine and quarantine was highly protective against the deadly Ebola virus in a major trial [19].

In this work, our goal is to develop a new mathematical model to study the effect of both vaccination and quarantine on the spread of Ebola virus as per the recommendation from World Health Organization (WHO) using both classical and fractional-order SIRD Ebola epidemic models. Our model differs from other mathematical models that have been used to study the Ebola epidemics [9, 16–18, 20, 21] in that it incorporates both vaccination and quarantine interventions. In addition, our work differs in that it uses one of the top ten most influential algorithms known as Markov Chain Monte Carlo algorithm to simulate the process as the spread of Ebola virus is a random process. To the best of our knowledge, this is the first integrated simulation method used beside the Euler method for this kind of infectious disease of humans. In the Euler method, the parameters are regarded constant, which may not be true in the practical case. To eliminate such defects, we used the Monte Carlo method which enabled to observe the reality in a better way and see how the Ebola virus is transmitted in crowd more accurately. In other words, the states (susceptible, infected, recovered/removed, death) at time \(t+1\) depend only on the state at time t (that means our physical state is Markov process). Hence, the Monte Carlo method is more sensible way to reflect the reality.

The text is organized as follows. In this section we have provided background information about Ebola disease; in Section 2, we give the definition of the Caputo fractional derivative of order α; in Section 3, we develop a basic mathematical model to describe the dynamics of the Ebola virus and its extension using Caputo fractional order; in Section 4, we find parameters with statistical data based on WHO; Section 5 deals with the basic properties of the model; in Section 6 we show the existence of the disease-free equilibrium for the model, derive the basic reproduction number and prove stability conditions. The parameters in Section 4 are used to simulate the basic model in Section 7 using both the Euler method and the Monte Carlo method. Finally, a conclusion and future work are presented.

2 Fractional-order model

In this section we discuss the definition of Caputo derivative and present the fractional-order SIRD model with vaccination and quarantine interventions in the sense of the Caputo derivative of order \(\alpha \in (0,1]\) in the next section.

Definition 2.1

The fractional integral of order \(\alpha > 0\) of a function \(g: R^{+} \rightarrow R\) is defined by \(I^{\alpha}g(t)= \frac{1}{\Gamma(\alpha)}\int_{0}^{t} (t-x)^{\alpha-1} g(x) \,dx\), where \(\Gamma(\cdot)\) is a gamma function.

Definition 2.2

The Caputo fractional derivative of order α> 0, \(n-1<\alpha<n\), \(n\in\mathbb{N}\) is defined as \(D^{\alpha}g(t)= \frac{1}{\Gamma(n-\alpha)}\int_{0}^{t} \frac {g(x)^{(n)}}{(t-x)^{\alpha+n-1}} g(x) \,dx\), where the function \(g(t)\) has absolutely continuous derivatives up to order \((n-1)\).

3 Mathematical model formulation and description

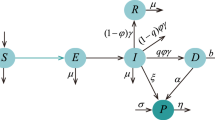
A compartmental model with a constant population was used to describe the natural history and epidemiology of Ebola. Briefly, the population is divided into four compartments: susceptible individuals (S) may become infected (I) after the contact with Ebola-infected individuals who are capable of infecting others including nurses, doctors etc. at hospitals and with a chance of infecting others before being recovered/removed from the disease (R) or die of Ebola and then join (D).

The susceptible population is increased by the susceptibility of individuals (rate of loss of infection acquired immunity) into the population at the rate γ. This population will be decreased if it acquires infection after the contact with an infected non-quarantined individual at the rate \(\beta=pc\), where p is the probability of successfully getting Ebola after the contact with an Ebola-infected individual and c is the per-capita contact rate. As there is a proved possibility of treatment of Ebola by vaccination [19, 22, 23], the susceptible individuals are further decreased at the rate v because of vaccination.

The population of infected individuals is generated by the infection of susceptible individuals at the rate β. This population is decreased by recovering from Ebola disease at the rate of \(\alpha_{1}\) and \(\alpha_{2}\), where \(\alpha_{1}\) is the recovery rate of an infected quarantined individual and \(\alpha_{2}\) is the recovery rate of an infected non-quarantined individual. This population is further decreased by death due to Ebola at a rate \(\delta _{1}\) and \(\delta_{2}\), where \(\delta_{1}\) is the death rate of an infected quarantined individual and \(\delta_{2}\) is the death rate of an infected non-quarantined individual due to Ebola. Here it is assumed that \(\alpha_{1}\) is greater than \(\alpha_{2}\) and \(\delta_{1}\) is less than \(\delta_{2}\), which is biologically reasonable.

The population of recovered infected individuals is generated by those recovered from Ebola and those individuals from susceptible because of vaccination at the rate of v and decreased by individuals that lost immunity and rejoined the susceptible group at the rate of γ.

Finally, the population of individuals who deceased is generated by individuals who are killed by Ebola. The compartmental flow of this model is given in Figure 1 below. Besides, the system of ordinary differential equations describing this model is given below and parameters are defined in Section 4.

$$\begin{aligned} &{\frac{dS}{dt}= \gamma R-\frac{\beta(1-q)SI}{N}-v S,} \end{aligned}$$
(3.1)
$$\begin{aligned} &{\frac{dI}{dt}=\frac{\beta(1-q)SI}{N}-\alpha_{1}q I- \alpha_{2}(1-q) I-\delta_{1} I- \delta_{2}I,} \end{aligned}$$
(3.2)
$$\begin{aligned} &{\frac{dR}{dt}=\alpha_{1}q I+ \alpha_{2}(1-q) I +v S-\gamma R,} \end{aligned}$$
(3.3)
$$\begin{aligned} &{\frac{dD}{dt}=\delta_{1} I+\delta_{2}I,} \end{aligned}$$
(3.4)
$$\begin{aligned} &{N=S + I + R+ D,} \end{aligned}$$
(3.5)
$$\begin{aligned} &{\beta=pc.} \end{aligned}$$
(3.6)

In this section we discuss the extension of the classical model above and study using Caputo fractional derivatives, which has an advantage over the classical integer order models due to its memory effect property and its accuracy in solutions of real world problems. Now, by replacing integer-order derivatives of the above system with fractional derivatives of order \(\alpha\in(0, 1]\) in the sense of Caputo fractional derivatives, we consider the fractional-order SIRD model with vaccination and quarantine as follows:

$$\begin{aligned} &{D_{t}^{\alpha}S(t)=\gamma R-\frac{\beta(1-q)SI}{N}-v S,} \end{aligned}$$
(3.7)
$$\begin{aligned} &{D_{t}^{\alpha}I(t) =\frac{\beta(1-q)SI}{N}-\alpha_{1} q I-\alpha_{2}(1-q) I-\delta_{1} I- \delta_{2}I,} \end{aligned}$$
(3.8)
$$\begin{aligned} &{D_{t}^{\alpha}R(t) =\alpha_{1}q I+ \alpha_{2}(1-q) I +v S-\gamma R,} \end{aligned}$$
(3.9)
$$\begin{aligned} &{D_{t}^{\alpha}D(t) =\delta_{1} I+ \delta_{2}I.} \end{aligned}$$
(3.10)

This type of mathematical formulation has been considered by many researchers [24–27]. Clearly, there is a mismatch of model dimensions in the fractional-order model above. However, this drawback of fractionalization has been addressed by Diethelm [28]. Following the method by Diethelm [28], our system can be written as follows:

$$\begin{aligned} &{D_{t}^{\alpha}S(t)=\gamma^{\alpha} R-\frac{\beta^{\alpha}(1-q^{\alpha})SI}{N}- v^{\alpha} S,} \end{aligned}$$
(3.11)
$$\begin{aligned} &{D_{t}^{\alpha}I(t)=\frac{\beta^{\alpha}(1-q^{\alpha })SI}{N}-\alpha_{1}^{\alpha} q^{\alpha} I-\alpha_{2}^{\alpha } \bigl(1-q^{\alpha} \bigr) I-\delta_{1}^{\alpha} I- \delta_{2}^{\alpha} I,} \end{aligned}$$
(3.12)
$$\begin{aligned} &{D_{t}^{\alpha}R(t) =\alpha_{1}^{\alpha} q^{\alpha} I+\alpha _{2}^{\alpha} \bigl(1- q^{\alpha} \bigr) I +v^{\alpha} S-\gamma ^{\alpha} R,} \end{aligned}$$
(3.13)
$$\begin{aligned} &{D_{t}^{\alpha}D(t) =\delta_{1}^{\alpha} I+ \delta_{2}^{\alpha}I.} \end{aligned}$$
(3.14)

As the population is closed, \(D(t)=N(t)-S(t)-I(t)-R(t)\). Hence, we can consider only the first three equations of our system above in our analysis.

Figure 1
figure 1

Compartmental flow of a mathematical model for Ebola epidemics.

Full size image

4 Model parameters

See Table 1.

Table 1 Model parameters for simulation
Full size table

5 Basic properties

Since the model monitors changes in the human population, all the variables and parameters are assumed to be positive for all t≥0.

The model is therefore analyzed in a suitable feasible region \(D = \{S(t), I(t), R(t), D(t) \in R_{+}^{4}\}\), which is positively invariant for system (3.11) to (3.14) above.

Proof

Assume the initial conditions \(S(0)\ge 0\), \(I(0)\ge 0\), \(R(0)\ge 0\) and \(D(0)\ge 0\).

The second equation of our model can be written as

$$\begin{aligned} &{D_{t}^{\alpha}I(t) =\frac{\beta^{\alpha}(1-q^{\alpha })SI}{N}-\alpha_{1}^{\alpha} q^{\alpha} I-\alpha_{2}^{\alpha } \bigl(1- q^{\alpha} \bigr) I-\delta_{1}^{\alpha} I- \delta_{2}^{\alpha} I,} \end{aligned}$$
(5.1)
$$\begin{aligned} &{D_{t}^{\alpha}I(t)= \biggl[\frac{\beta^{\alpha}(1-q^{\alpha })S}{N}-\alpha_{1}^{\alpha}q^{\alpha} -\alpha_{2}^{\alpha } \bigl(1-q^{\alpha} \bigr) -\delta_{1}^{\alpha} - \delta_{2}^{\alpha} \biggr] I.} \end{aligned}$$
(5.2)

Rearranging, we get

$$\begin{aligned} D_{t}^{\alpha}I(t)- \biggl[\frac{\beta^{\alpha}(1-q^{\alpha })S}{N}- \alpha_{1}^{\alpha}q^{\alpha} -\alpha_{2}^{\alpha } \bigl(1-q^{\alpha} \bigr) -\delta_{1}^{\alpha} - \delta_{2}^{\alpha} \biggr] I =&0. \end{aligned}$$
(5.3)

This is a linear first-order equation in I, and its solution is \(I(t)=I(0)\exp(\int_{0}^{t} -A(z) \,dz) \) where \(A(z)=\frac{\beta^{\alpha }(1-q^{\alpha})S(z)}{N}-\alpha_{1}^{\alpha}q^{\alpha} -\alpha_{2}^{\alpha}(1-q^{\alpha}) -\delta_{1}^{\alpha} -\delta_{2}^{\alpha}\), which implies \(I(t) \ge0\) for all \(t\ge0\).

To show the nonnegativity of the remaining variables, consider the subsystem

$$\begin{aligned} &{D_{t}^{\alpha}S(t) =\gamma^{\alpha} R-\frac{\beta^{\alpha}(1-q^{\alpha})SI}{N}- v^{\alpha} S,} \end{aligned}$$
(5.4)
$$\begin{aligned} &{D_{t}^{\alpha}R(t) =\alpha_{1}^{\alpha} q^{\alpha} I+\alpha _{2}^{\alpha} \bigl(1- q^{\alpha} \bigr) I +v^{\alpha} S-\gamma ^{\alpha} R,} \end{aligned}$$
(5.5)
$$\begin{aligned} &{D_{t}^{\alpha}D(t) =\delta_{1}^{\alpha} I+ \delta_{2}^{\alpha}I} \end{aligned}$$
(5.6)

which can be rewritten in a matrix form \(\frac {dY(t)}{d(t)}=MY(t)+H(t)\), where

$$\begin{aligned}& Y(t)= \begin{pmatrix} S(t) \\ R(t) \\ D(t) \end{pmatrix}, \end{aligned}$$
(5.7)
$$\begin{aligned}& M= \begin{pmatrix} \frac{\beta(1-q)I}{N}-v & \gamma& 0 \\ v & -\gamma& 0 \\ 0 & 0 & 0 \end{pmatrix} \end{aligned}$$
(5.8)

and

$$ H(t)= \begin{pmatrix} 0 \\ \alpha_{1}qI+\alpha_{2}(1-q)I \\ \delta_{1} I+\delta_{2} I \end{pmatrix}. $$
(5.9)

Clearly, M is a Metzler matrix in a view of already established nonnegativity of the parameter I. Thus, the equation \(\frac {dY(t)}{dt}=M Y(t)+B(t)\) is a monotone system [29]. Hence, \(D = \{S(t), I(t), R(t), D(t) \in R_{+}^{4}\}\) is positively invariant for system (3.11) to (3.14). □

6 Analysis of the model

6.1 Existence and stability of disease-free equilibrium point

At the disease-free equilibrium state, we have absence of infection. Thus, all the Ebola-infected classes will be zero, and the entire population will comprise of only Ebola-free, susceptible individuals. A disease-free equilibrium state of the model above is given by \(E_{0}=(S^{*}, I^{*}, R^{*}, D^{*})\). Equating the model to zero and solving, we get \(E_{0}=(S^{*}, I^{*}, R^{*}, D^{*})=(S_{0}, 0, \frac{v}{\gamma}S_{0}, N-S_{0}-\frac{v}{\gamma}S_{0})\).

Theorem 6.1

If

$$ R_{0} = \frac{\beta^{\alpha}(1-q^{\alpha})S_{0}}{N(\alpha _{1}^{\alpha}q^{\alpha} +\alpha_{2}^{\alpha}(1-q^{\alpha}) + \delta_{1}^{\alpha} +\delta_{2}^{\alpha})}< 1, $$
(6.1)

then the disease-free equilibrium of our system is locally asymptotically stable.

Proof

According to Theorem 6.1, to prove the stability of the disease-free equilibrium, it suffices to show that all the eigenvalues of the Jacobian matrix of our system evaluated at the disease-free equilibrium have negative real parts. This Jacobian matrix is derived as follows: As our population is closed, let \(X=(I^{\alpha}, R^{\alpha})^{T}\), then \(\frac{dX}{dt}^{\alpha}= f(x)-v(x)\), where

$$ f(x)^{\alpha}= \begin{pmatrix} \frac{\beta^{\alpha} (1-q^{\alpha})SI}{N}\\ 0 \end{pmatrix} $$
(6.2)

and

$$ v(x)^{\alpha}= \begin{pmatrix} \alpha_{1}^{\alpha}q^{\alpha} I +\alpha_{2}(1-q^{\alpha })I +\delta_{1}^{\alpha} I+\delta_{2}^{\alpha} I\\ \gamma^{\alpha} R-\alpha_{1}^{\alpha}q^{\alpha} I-\alpha _{2}^{\alpha}(1-q^{\alpha})I-v^{\alpha} S \end{pmatrix}. $$
(6.3)

The Jacobian matrices of \(f(x)\) and \(v(x)\) evaluated at the disease-free equilibrium \(E_{0}\) are

$$ Df(E_{0})=F^{\alpha}= \begin{pmatrix} \frac{\beta^{\alpha} (1-q^{\alpha})S_{0}}{N}&0 \\ 0&0 \end{pmatrix} $$
(6.4)

and

$$ Dv(E_{0})=V^{\alpha}= \begin{pmatrix} \alpha_{1}^{\alpha}q^{\alpha} +\alpha_{2}^{\alpha}(1-q^{\alpha}) +\delta_{1}^{\alpha} +\delta_{2}^{\alpha} & 0 \\ -\alpha_{1}^{\alpha}q^{\alpha} -\alpha_{2}^{\alpha}(1-q^{\alpha})& \gamma^{\alpha} \end{pmatrix}. $$
(6.5)

The Jacobian matrix is therefore given by

$$ (F-V)^{\alpha}= \begin{pmatrix} \frac{\beta^{\alpha} (1-q^{\alpha})S_{0}}{N}-\alpha _{1}^{\alpha}q^{\alpha} -\alpha_{2}^{\alpha}(1-q^{\alpha})-\delta_{1}^{\alpha}-\delta_{2}^{\alpha} & 0 \\ \alpha_{1}^{\alpha}q^{\alpha} + \alpha_{2}^{\alpha}(1-q^{\alpha}) &-\gamma^{\alpha} \end{pmatrix}. $$
(6.6)

The eigenvalues of this matrix are as follows:

$$\begin{aligned} &{\lambda_{1}=-\gamma_{1}^{\alpha},} \\ &{\lambda_{2}=-\biggl(\alpha_{1}^{\alpha}q^{\alpha} - \alpha _{2}\bigl(1-q^{\alpha}\bigr) -\delta_{1}^{\alpha}+\delta_{2}^{\alpha }-\beta^{\alpha}\bigl(q^{\alpha}-1\bigr)\frac{S_{0}}{N}\biggr) < 0\quad\mbox{for }R_{0} < 1.} \end{aligned}$$

Therefore, for \(R_{0}<1\), the disease-free equilibrium is locally asymptotically stable. □

Theorem 6.2

For system (3.11) to (3.14), the disease-free equilibrium is globally asymptotically stable if \(R_{0}<1\).

Proof

First, let us find Jacobian matrices (of order 3) evaluated at the disease-free equilibrium (\(F'\)) and (\(V'\)). They are given below:

$$ Df(E_{0})=F^{\prime \alpha}= \begin{pmatrix} \frac{\beta^{\alpha}(1-q^{\alpha})(S_{0})}{N} & 0 & 0 \\ \alpha_{1}^{\alpha}q^{\alpha}+\alpha_{2}(1-q^{\alpha}) & 0 & 0 \\ 0 &0 & 0 \end{pmatrix} $$
(6.7)

and

$$ Dv(E_{0})=V^{\prime \alpha}= \begin{pmatrix} \alpha_{1}^{\alpha}q^{\alpha} +\alpha_{2}^{\alpha}(1-q^{\alpha}) + \delta_{1}^{\alpha} +\delta_{2}^{\alpha} & 0 &0 \\ 0 & \gamma^{\alpha}&0\\ -\delta_{1}^{\alpha}-\delta_{2}^{\alpha} &0&0 \end{pmatrix}. $$
(6.8)

To prove, the comparison theorem was used. The rate of change of the variables (I, R, D) of the system above can be re-written as follows:

$$ \begin{pmatrix} \frac{dI}{dt}^{\alpha} \\ \frac{dR}{dt}^{\alpha} \\ \frac{dD}{dt}^{\alpha} \end{pmatrix} = \bigl(F'-V' \bigr)^{\alpha} \begin{pmatrix} I \\ R \\ D \end{pmatrix} - \biggl(1-\frac{ S}{S_{0}} \biggr) \begin{pmatrix} \frac{\beta^{\alpha}(1-q^{\alpha})S_{0}}{N} & 0 & 0 \\ 0 & -\frac{v^{\alpha}S_{0}S}{(S_{0}-S)R} & 0 \\ 0 &0 & 0 \end{pmatrix} \begin{pmatrix} I \\ R \\ D \end{pmatrix}, $$
(6.9)

where (\(F^{\prime \alpha}\)) and (\(V^{\prime \alpha}\)) are Jacobian matrices (of order 3) evaluated at the disease-free equilibrium. Clearly,

$$ \begin{pmatrix} \frac{dI}{dt}^{\alpha} \\ \frac{dR}{dt}^{\alpha} \\ \frac{dD}{dt}^{\alpha} \end{pmatrix} \leq \bigl(F'-V' \bigr)^{\alpha} \begin{pmatrix} I \\ R \\ D \end{pmatrix}. $$
(6.10)

Since the eigenvalues of the matrix \((F^{\prime \alpha}-V^{\prime \alpha})\) have negative real parts (this comes from the stability results in Lemma 1 in [30, 31], then system (3.11) to (3.14) is stable whenever \(R_{0}<1\). So \((I, R, D)\to(0,\frac{v}{\gamma}S_{0}, N-S_{0}-\frac{v}{\gamma }S_{0})\) and \(S\to S_{0}\) as \(t\to\infty\). By the comparison theorem [2, 32] \((S, I, R, D)\to E_{0}\) as \(t\to \infty\). Therefore, \(E_{0}\) is globally asymptotically stable. □

7 Numerical simulation

7.1 Numerical simulation using the Euler method

7.1.1 Experiment 1

To approximate the solutions of the model built above, we give some simulations using the parameter values of Table 1 in Section 4 above using the Euler method. The result is given in Figure 2.

Figure 2
figure 2

Simulation result using the Euler method ( \(\pmb{\alpha =1}\) ).

Full size image

From Figure 2 we see that the population of susceptible individuals immediately begins to drop because of the high degree of how infectious the Ebola virus is. Consequently, the population of the dead people starts rising.

7.1.2 Experiment 2

See Figure 3.

Figure 3
figure 3

Simulation result using the Euler method ( \(\pmb{\alpha =0.90}\) ).

Full size image

7.1.3 Experiment 3

See Figure 4.

Figure 4
figure 4

Simulation result using the Euler method ( \(\pmb{\alpha=0.85}\) ).

Full size image

7.2 Simulation using the Monte Carlo method

Monte Carlo simulations are used to model the probability of different outcomes in a process that cannot easily be predicted due the intervention of random variables. As the spread of Ebola virus is a random process, the Monte Carlo algorithm is used to simulate the Markov Chain process of which the transfer matrix changes over time. In a Markov Chain process the physical state at time \(t+1\) depends only on the state at time t. In other words, for random variables \(\{x_{t}\}\), \(t= 0, 1, 2, 3,\ldots\)

$$\begin{aligned} P(X_{t}=j/x_{0}=i_{0}, x_{1}=i_{1}, \ldots,x_{t-1}=i_{t-1})=P(x_{t}=j/x_{t-1}=i_{t-1}). \end{aligned}$$
(7.1)

Define the state matrix as \(X(t)=(S(t),I(t),R(t),D(t))\) to represent the compartments in a population. Then, the initial state matrix \(X(0)\) is obtained as \(X(0)=(1-I_{0}, I_{0},0,0)\). According to Markov Chain theory, the transition matrix can be given as \(p(t)=\{P(i,j)\}_{4\times 4}\), where \(P(i, j)\) is the transition probability from state i to state j for i, j an element of {1, 2, 3, 4}.

$$ P(t)= \begin{pmatrix} Variables & S & I& R& D\\ S & P(1,1) & P(1,2) & P(1,3) & P(1,4)\\ I & P(2,1) & P(2,2) & P(2,3) & P(2,4)\\ R & P(3,1) & P(3,2) & P(3,3) & P(3,4)\\ D & P(4,1) & P(4,2)& P(4,3)& P(4,4) \end{pmatrix}. $$
(7.2)

Besides, \(P(1,4)=P(2,1)=P(3,2)=P(3,4)=P(4,1)=P(4,2)=P(4,3)=0\) as there is no transition and \(P(1,1)+P(1,2)+P(1,3)=P(2,2)+P(2,3)+P(2,4)=P(3,1)+P(3,3)=P(4,4)=1\). Finally, the state matrix is given by

$$X(t)=X(0)\prod_{t=1} P(t). $$

In Experiment 1, we regard the constant parameters and ignored the influence of latent period. To eliminate this defect, the Monte Carlo method is used. Figure 5 shows the Monte Carlo simulation of the process under the conditions given above over time.

Figure 5
figure 5

Simulation result using the Monte Carlo method.

Full size image

7.2.1 Experiment 4

From Figure 5 we clearly see that the number of Ebola-infected individuals increases and then decreases. At the same time the population of those who die by Ebola rises swiftly and reaches the peak showing the biological reality that Ebola is fatal. The model is more realistic to show the situation. Therefore, the medical, health departments and other stakeholders should focus on this moment. Moreover, the population of the susceptible also decrease at this time as more people get infected showing that the spread of Ebola is high unless controlled.

7.2.2 Experiment 5

Here the experiment deals with the relation between quarantine and the population of Ebola-infected individuals.

From Figure 6 we see the effect of the rate of infected quarantine on the Ebola-infected population. It is clearly seen that when the rate of infected quarantine increases, the population of Ebola-infected individuals decreases.

Figure 6
figure 6

Effect of the rate of infected quarantine on infected population.

Full size image

7.2.3 Experiment 6

When vaccination rate \(\gamma=0\) (without vaccination), the result is given in Figure 7.

Figure 7
figure 7

Markov Chain Monte Carlo simulation when vaccination rate \(\pmb{v=0}\) (without vaccination).

Full size image

7.2.4 Experiment 7

(Figure 8 shows simulation result when vaccination rate is increased to \(v=0.25\).)

Figure 8
figure 8

Markov Chain Monte Carlo simulation when vaccination rate \(\pmb{v=0.25}\) .

Full size image

7.2.5 Experiment 8

In this experiment (Figure 9) the vaccination rate is more increased than in the previous two experiments conducted.

Figure 9
figure 9

Markov Chain Monte Carlo simulation when vaccination rate \(\pmb{v=0.45}\) .

Full size image

From Figures 7, 8 and 9, we see the effect of the rate of vaccination on the Ebola-infected population for \(v=0\), \(v=0.25\) and \(v=0.45\). When v changes from 0 to 0.45, the number of Ebola-infected individuals reduces from 1,150 to 779. It is clearly seen that when the rate of vaccination increases, the population of Ebola-infected individuals decreases.

7.2.6 Experiment 9

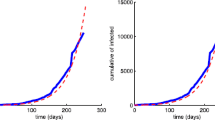
Real data from WHO is fitted to the Ebola infected \(I(t)\) of the model (see Figure 10).

Figure 10
figure 10

Ebola-infected \(\pmb{I(t)}\) versus the real data of confirmed Ebola cases in Liberia, 2014. (Real data source: WHO report of 2014 Ebola outbreak in Liberia from July 14 to October 12, 2014.)

Full size image

8 Conclusion

Overall, the dynamical behavior of the formulated Ebola epidemic model is investigated, which plays a vital role in controlling the spread of Ebola virus. The classical SIRD model with vaccination and quarantine interventions is extended to a system of fractional-order derivatives in the sense of the Caputo derivative of order \(\alpha \in(0,1]\) because of its accuracy in solutions of real world problems. Our new model has the details about all compartments, and we found it fits well the data of confirmed cases provided by WHO for the Ebola outbreak in West Africa. The parameter values used are all the latest values. To secure more realistic approach, we used two different simulation methods, i.e., the Euler and Monte Carlo methods. As the spread of Ebola virus is a random process, the Monte Carlo algorithm is used to simulate the Markov Chain process of which the transfer matrix changes over time. From the point of view of our result of Markov Chain Monte Carlo simulation, we claim that there is less possibility of an individual getting Ebola virus for the second time if they survived the first infection. None of the previous research discovered weather a person can re-catch Ebola or not if they survived the first case. Moreover, from our experimental results, we also see that Ebola is really fatal and spreads swiftly, which means a regulation that reflects the reality very well is obtained and the model works better and more efficiently for the Ebola outbreak in West Africa.

Once again, from our experimental results we see that though Ebola spreads swiftly, it can be controlled upon increasing vaccination. Vaccination is a very efficient method in reducing the number of Ebola-infected individuals in a short period of time and increases the number of recovered individuals. Increasing the rate of infected quarantine is also another efficient method to control the Ebola epidemic as seen from our study. Hence, vaccination and isolation of the Ebola patient and providing great treatment are crucial measures to control the Ebola epidemics. Besides, as the cost of vaccination might be high for Ebola-infected countries, we recommend an optimal control to reduce the cost and number of infected individuals. Moreover, in order to prevent Ebola epidemics, through the analysis of the model, the government must strictly manage the policy on Ebola and carry it out. This in turn helps health campaigning and raising health literacy, which plays a vital role in controlling a quick spread of the disease. We finally strongly believe that our study will play its own role in the current effort of controlling Ebola.