Abstract
Ebola is a world health problem and with a recent outbreak. There exist different models in the literature to predict its behavior, most of them based on data coming from previous outbreaks or using restricted number of persons in the population variable. This paper deals both with classical and fractional order SEIR (susceptible, exposed, infections, removed) Ebola epidemic model and its comparison with real data extracted from the reports periodically published by the World Health Organization (WHO), starting from March 27th, 2014. As it has been shown in the literature, one physical meaning of the fractional order in fractional derivatives is that of index of memory; and therefore, it seems to be useful for epidemic models, as in this paper. The number of confirmed cases by the WHO in its reports is used for our analysis and estimation of the parameters in our classical and fractional SEIR models. Our approach gives a good approximation to real data. Following our results, the current outbreak will continue for approximately two years, assuming that no new outbreak appears at a different community or country. Our estimates give a number of the order nine million confirmed cases.
Similar content being viewed by others
1 Introduction
Ebola is a highly lethal virus, which has caused at least 18 confirmed outbreaks in Africa between 1976 and 2014. In October 2014 cases also appeared in the USA and Spain after treating infected patients at Texas Health Presbyterian Hospital Dallas and Hospital Carlos III de Madrid, respectively.
The origin of Ebola is somewhat not clear. Peter Piot discovered the Ebola virus in 1976 and helped to contain the first-ever recorded Ebola epidemic that same year in the first recorded outbreak held at Nzara, Maridi and surrounding areas (Sudan) between June and November 1976.
Up to 2012, about 2,400 cases and 1,600 deaths have been registered due to Ebola virus(es). In the outbreak of 2014 (Guinea, Liberia, Nigeria, Senegal, and Sierra Leone) we have about 15,935 cases and 5,689 deaths at the time of writing this article (December 1st, 2014).
There exist five Ebola viruses according to the International Committee on Taxonomy of Viruses currently: Ebola virus (EBOV), Sudan virus (SUDV), Reston virus (RESTV), Taï Forest virus (TAFV), and Bundibugyo virus (BDBV). Four of these viruses (excepting RESTV) are known to cause Ebola virus disease in humans. Up to 2014, the SUDV was present at 784 cases, the BDBV virus at 226 cases, one person was infected by the TAFV virus, and the remaining cases (about 2,169) were due to the EBOV virus. The 2014 outbreak is related with the EBOV virus.
Despite extensive search, the reservoir of the Ebola virus has not yet been identified but may include fruit bats [1]. Ebola is transmitted by physical contact with body fluids, secretions, tissues, or semen from infected persons. The incubation period is 2-21 days, and the infectious period is 4-10 days. The diagnosis of Ebola is not easy since many times it is misdiagnosed as, for example, malaria and typhoid. The onset of Ebola is characterized by severe headaches, malaise, fever, vomiting, bloody diarrhea, and rash.
The mortality rate of Ebola varies from 50% to 90%. Very recently a new study has provided strong evidence that individual genetic differences play a major role in whether people die from the disease [2]. This might help to understand the big differences in the mortality rate of Ebola at different communities which are observed in the official data reported. As an example, the estimates of the basic reproduction number [3], \(R_{0}\), are 1.71 (95% CI, 1.44 to 2.01) for Guinea, 1.83 (95% CI, 1.72 to 1.94) for Liberia, 1.20 (95% CI, 0.67 to 1.96) for Nigeria, and 2.02 (95% CI, 1.79 to 2.26) for Sierra Leone [4].
In the 2014 outbreak the mean incubation period is 11.4 days, and it does not vary by country [4]. The mean time from the onset of symptoms to hospitalization, a measure of the period of infectiousness in the community, is \(5.0 \pm4.7~\mbox{days}\), and it is not shorter for health care workers than for other case patients. The mean time to death after admission to the hospital is \(4.2 \pm6.4~\mbox{days}\), and the mean time to discharge is \(11.8 \pm6.1~\mbox{days}\) [4]. The mean length of stay in hospital is 6.4 days in Guinea, Liberia, and Sierra Leone.
In this paper we have analyzed both classical and fractional SEIR (susceptible-exposed-infectious-removed) epidemic model for different values of the parameters, as compared with the official data obtained from the World Health Organization (WHO). These models have been used to compare the existing data of previous outbreaks [5–7] which have less information as compared with the 2014 outbreak.
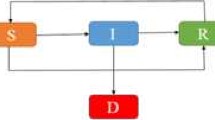
We shall denote by \(S(t)\), \(E(t)\), \(I(t)\), and \(R(t)\) the susceptible, exposed, infectious, and removed at time t. We shall also assume that
is the population (constant) studied in the model. Notice that N includes the recovered individuals \(R(t)\).
For our purposes we have followed the Ebola disease outbreak news published by the WHO. In their webpage it is possible to find a number of reports from the starting cases (March 23rd, 2014) up to the time of writing this article (December 1st, 2014). We have followed the number of confirmed cases in Guinea, Liberia, and Sierra Leone. In order to make the model as much accurate as possible, we have followed also the information published by Humanitarian Data Exchange (HDX) which provide more detailed information about the spread of the outbreak. More precisely, in Liberia there exist confirmed cases in all the 15 counties (Bomi, Bong, Gbarpolu, Grand Bassa, Grand Cape Mount, Grand Gedeh, Grand Kru, Lofa, Margibi, Maryland, Montserrado, Nimba, Rivercess, River Gee, and Sinoe). Moreover, in Sierra Leone there also exist confirmed cases in all the 12 districts (Bo, Bombali, Bonthe, Kailahun, Kambia, Kenema, Koinadugu, Kono, Moyamba, Port Loko, Pujehun, Tonkolili, Western Rural, and Western Urban). Nevertheless, in Guinea there do not exist confirmed cases in the following prefectures: Fria, Gaoual, Koubia, Koundara, Labé, Lélouma, Mali, Mandiana, and Tougué. Therefore, the total population in our model (according to updated data) is fixed to be 18,805,278 people. As will be noted later, we will consider as N in our model a portion of such total population.
There exist some other models for the 2014 Ebola outbreak [8–12] and previous outbreaks [5–7].
2 Materials and methods
2.1 Classical model
Using [13], we have the following system of differential equations as model:
In this model the parameter \(\beta=pc\), where p is the probability of successfully getting infected when coming into contact with an infected individual, and c is the per-capita contact rate. That is, β is an average of the number of infected people by contact with one symptomatic individual who has been infected with Ebola virus. However, Ebola virus can be also transmitted by latent individuals; that is, asymptomatic people who are infected (\(E(t)\) in our model). Of course, it is well known that an individual has a higher chance of getting infected for an infectious individual than for a latent individual. This justifies factor \(q\in[0,1]\) in the second equation of (1). Moreover, the parameter γ is the per-capita death rate, which also depends on the country; this parameter has been fixed to \(1/7~\mbox{days}^{-1}\) in our numerical computations. Furthermore, the parameter δ is the per-capita infectious rate, we have fixed to \(1/12\).
2.2 Fractional model
Fractional calculus has recently found wide applications in many areas of science and engineering, for example, viscoelastic systems, fluid dynamics, solid dynamics, to cite some of them [14]. Recently, it has been used to analyze a dengue epidemic model [15]. Despite the fact that the operator of fractional derivative is more complicated than the classical one, there exist numerical methods for solving systems of nonlinear differential equations [16]. One physical meaning of the fractional order in fractional derivatives is that of index of memory [17]. Moreover, fractional calculus plays an important role in superdiffusive and subdiffusive processes, which makes it a useful tool in epidemiology [18]. Some properties of fractional orthogonal polynomials have been recently presented in [19, 20].
The fractional Riemann-Liouville derivative of order α of f is defined as [21, 22]
This is well defined if, for example, \(f \in{{L}}^{1}_{\mathrm{loc}}({\mathbb{R}})\).
There are many more fractional derivatives. We are not giving a complete list, but recall the Caputo derivative [21, 22]
which is well defined, for example, for absolutely continuous functions. Note that the value of the Caputo fractional derivative of the function f at point t involves all the values of \(f'(s)\) for \(s \in[0,t]\).
As in the integer case we have
but \(I^{\alpha}(D^{\alpha}f)\) or \(I^{\alpha}({}^{c}D^{\alpha}f)\) are not, in general, equal to f. Indeed
and (see [22], (2.113), p.71)
where \(c_{1}\in{\mathbb{R}}\). Also [21], (2.4.4), p.91
Notice that \({}^{c}D^{\alpha}f(t)\) tends to \(f'(t)\) as \(\alpha\to1\).
We have written system (1) in terms of fractional differential equations as
where the parameters β, γ, δ, and q have the same meaning as in the classical model (1), N is the total population and \(\alpha\in(0,1)\) is the derivation order.
2.3 Initial conditions and values of the parameters
As already mentioned, we have the following values for the parameters in the classical (1) and fractional model (2)
where TP is the total population of the three countries considered (as indicated in Table 1). Moreover, the initial conditions are fixed as follows in the numerical experiments performed:
where m is a value to be fixed later, i.e., the susceptible population is a percentage of the total population. Notice that in this case \(N=TP\frac{m}{100}+15\). As it was indicated before, the mortality of Ebola depends on individual genetic differences [2], so that we shall analyze different values of m. If \(m=100\) then \(S(0)=TP\), \(R(0)=0\) and all the population is considered as susceptible. Up to now there has been no empirical evidence that a person can be immune. In such a case, \(m<100\) and \(R(0)>0\). The initial number of infected people is fixed to 15 following the WHO Ebola virus disease in Guinea - update dated March 27th, 2014: ‘To date, 15 cases have tested positive by PCR testing for the ebolavirus, confirmed by collaborating laboratories including the Institut Pasteur Lyon, France, Institut Pasteur (IP) Dakar, Senegal and Bernhard-Nocht Institute of Tropical Medicine Hamburg, Germany. Laboratories studies demonstrated that Zaire ebolavirus is the virus responsible for the outbreak.’
In Table 1 we have included the data we have considered for our numerical computations.
3 Results and discussion
3.1 Results
By using the predictor-corrector PECE method of Adams-Bashforth-Moulton [16], we have solved numerically the above systems of differential equations (1) and (2) and found the best value of the parameter q that minimizes the \({\ell}_{2}\) norm between the real data and the models, defined by
where \(r_{j}\) is the cumulative number of infected people according to the data at day j and \(m_{j}\) is the prediction proposed by the model. Notice that we will not use α, the order of derivation, as optimization parameter.
The system has been solved for times starting at \(t_{0}=0\) and ending at \(t_{d}=300~\mbox{days}\). In each plot, we show in blue line the real data and in red dashed line the results of our model for the fixed parameters. We have also included the norm ρ of the difference in each case.
In each picture we show both model and real data as accumulated values.
To evaluate the equilibrium points, we consider the system
which has as solution \(E(t)=I(t)=0\). Hence \(S(t)+R(t)=N\). If, for example, \(R(0)=0\), then \(S(0)=N\). In this case \(m=100\).
The Jacobian
at the equilibrium point \(E(t)=I(t)=0\) is given by
for the specific values of β, γ, δ, and N indicated before. Therefore, the eigenvalues
For \(q \in[0,1]\) and \(m \geq58\) (that is, \(S(0)\) is at least 58% of the total population, which is a reasonable assumption), we have that \(\lambda_{3}<0\) and \(\lambda_{4}>0\).
The qualitative analysis of a fractional model is a difficult problem. The stability of the disease-free equilibrium needs further study, and it will be considered in the future.
3.1.1 Classical derivatives model (1)
We would like to mention here that for \(m\ge90\) the value of q in (4) that best fits the real data is negative which has no probability meaning.
The results for classical derivative are shown in Figures 1, 2, and 3.
Comparison between our model and real data. In this figure we show a comparison between our model given by the system of nonlinear differential equations (1) and real data coming from the WHO included as Table 1. The values of the parameters are \(m=80\), \(q=0.030\) (left) and \(m=75\), \(q=0.067\) (right). The errors using \(\ell^{2}\) norm are 5,185.344 and 5,309.831, respectively.
Another comparison between our model and real data. In this case we consider \(m=70\), \(q=0.110\) (left) and \(m=65\), \(q=0.159\) (right). Using the \(\ell^{2}\) norm we obtain similar errors as in Figure 1, 5,462.073 and 5,610.436, respectively.
In Figure 1, the picture on the left has been obtained for \(m=80\) in (4) and \(q=0.030\); the picture on the right has been obtained for \(m=75\) in (4) and \(q=0.067\). The \(\ell_{2}\) norms are \(5{,}185.344\) and \(5{,}309.831\), respectively. Therefore, the daily difference between our prediction of cumulative cases and real data is less than 22 cases each day. Despite the difficulty of the real data analyzed (see Table 1, e.g., the difference in confirmed cases in Liberia from October 17th to October 22nd), we would like to notice that our model is quite accurate to the real data of confirmed cases extracted from the WHO.
In Figure 2, we show the prediction of our model during a shorter interval of time using the same values of the parameters as in Figure 1.
In Figure 3 we consider at first \(m=70\) in (4) and \(q=0.110\); the right-hand side of Figure 3 has been obtained for \(m=65\) in (4) and \(q=0.159\). The \(\ell_{2}\) norms are \(5{,}462.073\) and \(5{,}610.436\), respectively. The daily difference is in these cases less than 23 confirmed cases, which is about 0.01% of error as compared with the mean of the data.
3.1.2 Fractional derivatives model (2)
The results for the fractional derivatives model are shown in Figures 4, 5, and 6.
Comparison between our model and real data. In this figure we show a comparison between our model given by the system of nonlinear fractional differential equations (2) and real data coming from the WHO included as Table 1. The values of the parameters are \(m=90\), \(q=0.058\), \(\alpha=0.9\) (left) and \(m=85\), \(q=0.090\), \(\alpha=0.9\) (right). The errors using \(\ell^{2}\) norm are 5,848.597 and 5,959.564, respectively.
Another comparison between our model and real data when \(\pmb{\alpha =0.9}\) . In this case we consider \(m=80\), \(q=0.169\) (left) and \(m=75\), \(q=0.128\) (right). Using the \(\ell^{2}\) norm we obtain similar errors as in Figure 4, 6,078.286 and 6,208.718, respectively.
In Figure 4, the picture on the left has been obtained for \(m=90\) in (4), \(q=0.058\), and \(\alpha=0.9\); the picture on the right has been obtained for \(m=85\) in (4), \(q=0.090\), and \(\alpha=0.9\). The \(\ell_{2}\) norms are \(5{,}848.597\) and \(5{,}959.564\), respectively.
In Figure 5, we show the prediction of our model during a shorter interval of time using the same values of the parameters as in Figure 4.
In Figure 6 we consider at first \(m=80\) in (4), \(q=0.127\), and \(\alpha=0.9\). The right-hand side of Figure 6 has been obtained for \(m=75\) in (4), \(q=0.169\), and \(\alpha=0.9\). The \(\ell_{2}\) norms are 6,078.286 and 6,208.718, respectively.
It is also possible to relax the parameter of derivation α. As an example, for \(\alpha=0.75\), the best fitting is shown in Figure 7. Notice that when α is smaller, then it seems that q must be bigger.
Fractional model with small α . This graph has been obtained for \(m=80\) in (4), \(q=0.345\), and \(\alpha =0.75\).
In Figure 8 we show the prediction of our model with \(m=80\) in (4), \(q=0.127\), and \(\alpha=0.9\) for a period of time of two years (730 days).
Our prediction for a long period of time. In this graph we show the prediction of our model given by the system of nonlinear fractional differential equations (2) for a long period of time (two years). We have considered \(m=80\), \(q=0.127\), and \(\alpha =0.9\).
As we show in Figure 9 and Figure 10, state trajectories of \(E(t)\) and \(R(t)\) have a similar behavior to those of \(I(t)\) for classical and fractional order model.
This graph shows evolution of exposed (left) and removed (right) population. We have considered the same values of the parameters as on left side of Figure 1.
This graph shows evolution of exposed (left) and removed (right) population. We have considered the same values of the parameters as on left side of Figure 8.
3.2 Discussion
We have analyzed both classical and new fractional SEIR (susceptible, exposed, infectious, removed) epidemic model for different values of the parameters, as compared with the official data obtained from the WHO. These models have been used to compare the existing data of previous outbreaks, which is much less detailed than the 2014 outbreaks. Our model gives a good approximation to real data and may be useful for some predictions and help to implement some effective public health measures.
Up to now it has not been possible to decide which model (classical derivative or fractional derivative) is giving better approximation to the real data, but with classical derivative the value of m in (4) must be smaller than or equal to 85 in order that \(q>0\) gives the minimum value of ρ.
It seems that the number of confirmed cases will be increasing, but the implementation of effective public health measures would help to stop the rising number of cases. Numerical experiments show that with the current real data the number of confirmed cases becomes stable in approximately two years after the start of the outbreak as shown in Figure 8.
4 Conclusions
In this paper we have analyzed the data published by the World Health Organization in order to provide a prediction of the outbreak in Liberia, Guinea, and Sierra Leone. The number of confirmed cases since the beginning of the outbreak has increased to about 16,000 infected people at the time of writing this article. Our model fits accurately the real data considered. Following our results, the current outbreak will continue for approximately two years for a total estimate of the order of nine million infected people. If the high fatality of Ebola is considered, the urgency of public health measures is mandatory. We have used mathematical models which consider susceptible, exposed, infectious, and removed people. Our models are based on differential equations which are numerically solved to provide the graphs included in the paper. First, we consider classical differential equations and secondly fractional differential equations which generalize the classical approach. Our estimates give a number of the order \(9\times 10^{6}\) confirmed cases. Despite the fact that individual genetic differences play a major role in whether people die from the disease, by using the available data and our analysis the number of predicted dead people is extremely high. Finally, it is worth mentioning here that the integer order differential equation SEIR model (1) gives better results in terms of the \(\ell_{2}\) norm than the fractional SEIR model (2).
References
Chua, KB, Crameri, G, Hyatt, A, Yu, M, Tompang, MR, et al.: A previously unknown reovirus of bat origin is associated with an acute respiratory disease in humans. Proc. Natl. Acad. Sci. 104, 11424-11429 (2007)
Gire, SK, Goba, A, Andersen, KG, Sealfon, RSG, Park, DJ, et al.: Genomic surveillance elucidates Ebola virus origin and transmission during the 2014 outbreak. Science 345, 1369-1372 (2014)
Chowell, G, Hengartner, N, Castillo-Chavez, C, Fenimore, P, Hyman, J: The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda. J. Theor. Biol. 229, 119-126 (2004)
WHO Ebola Response Team: Ebola virus disease in West Africa - the first 9 months of the epidemic and forward projections. N. Engl. J. Med. 371, 1481-1495 (2014)
Astacio, J, Briere, DM, Guillén, M, Martínez, J, Rodríguez, F, et al.: Mathematical models to study the outbreaks of Ebola. Technical report, MTBI Technical Report (1996) https://mtbi.asu.edu/research/archive/paper/mathematical-models-study-outbreaks-ebola
Lekone, PE, Finkenstädt, BF: Statistical inference in a stochastic epidemic SEIR model with control intervention: Ebola as a case study. Biometrics 62, 1170-1177 (2006)
Ndanguza, D, Tchuenche, JM, Haario, H: Statistical data analysis of the 1995 Ebola outbreak in the Democratic Republic of Congo. Afr. Math. 24, 55-68 (2013)
Althaus, CL: Estimating the reproduction number of Ebola virus (EBOV) during the 2014 outbreak in West Africa. Technical report, PLOS Current Outbreaks (2014)
Atangana, A, Doungmo Goufo, EF: On the mathematical analysis of Ebola hemorrhagic fever: deathly infection disease in West African countries. BioMed Research International (2014)
Gomes, MFC, Pastore y Piontti, A, Rossi, L, Chao, D, Longini, I, et al.: Assessing the international spreading risk associated with the 2014 West African Ebola outbreak. Technical report, PLOS Currents Outbreaks (2014)
Rivers, CM, Lofgren, ET, Marathe, M, Eubank, S, Lewis, BL: Modeling the impact of interventions on an epidemic of Ebola in Sierra Leone and Liberia. Technical report, PLOS Currents Outbreaks (2014)
Rachah, A, Torres, DFM: Mathematical modelling, simulation, and optimal control of the 2014 Ebola outbreak in West Africa. Discrete Dyn. Nat. Soc. 2015, Article ID 842792 (2015)
Anderson, R, May, R: Infectious Diseases of Humans: Dynamics and Control. Oxford Science Publications, Oxford (1992)
Li, C, Zeng, F, Liu, F: Spectral approximations to the fractional integral and derivative. Fract. Calc. Appl. Anal. 15, 383-406 (2012)
Al-Sulami, H, El-Shahed, M, Nieto, JJ, Shammakh, W: On fractional order dengue epidemic model. Math. Probl. Eng. (2014). doi:10.1155/2014/456537
Diethelm, K, Freed, AD: The FracPECE subroutine for the numerical solution of differential equations of fractional order (2002) http://www.mpg.de/billing/hbp98/diethelm.pdf
Du, M, Wang, Z, Hu, H: Measuring memory with the order of fractional derivative. Sci. Rep. 3, 3431 (2013)
Skwara, U, Martins, J, Ghaffari, P, Aguiar, M, Boto, J, Stollenwerk, N: Fractional calculus and superdiffusion in epidemiology: shift of critical thresholds. In: Proceedings of the 12th International Conference on Computational and Mathematical Methods in Science and Engineering, La Manga (2012)
Area, I, Djida, JD, Losada, J, Nieto, JJ: On fractional orthonormal polynomials of a discrete variable. Discrete Dyn. Nat. Soc. 2015, Article ID 141325 (2015)
Area, I, Losada, J, Manintchap, A: Fract. Calc. Appl. Anal. 18(5) (2015, to appear). doi:10.1515/fca-2015-0067; http://www.degruyter.com/view/j/fca
Kilbas, AA, Srivastava, HM, Trujillo, JJ: Theory and Applications of Fractional Differential Equations, xvi+523 p. North-Holland Mathematics Studies, vol. 204. Elsevier, Amsterdam (2006)
Podlubny, I: Fractional Differential Equations. Mathematics in Science and Engineering, vol. 198. Academic Press, San Diego (1999)
Acknowledgements
The authors thank the anonymous reviewers for their detailed remarks and constructive criticism. The work of I Area has been partially supported by the Ministerio de Economía y Competitividad of Spain under grant MTM2012-38794-C02-01, co-financed by the European Community fund FEDER. JJ Nieto and J Losada also acknowledge partial financial support by the Ministerio de Economía y Competitividad of Spain under grant MTM2010-15314 and MTM2013-43014-P, XUNTA under grant R2014/002, and co-financed by the European Community fund FEDER. This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, under grant No. (88-130-35-HiCi). The authors, therefore, acknowledge technical and financial support of KAU.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Area, I., Batarfi, H., Losada, J. et al. On a fractional order Ebola epidemic model. Adv Differ Equ 2015, 278 (2015). https://doi.org/10.1186/s13662-015-0613-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-015-0613-5