1 Introduction

The study of epidemiology has attracted much interest during the recent years. In this direction, mathematical models have been developed to imply more realistic aspects of disease spreading [1, 2]. Most mathematical epidemic models descend from the classical SIR model of Kermack and McKendrick established in 1927 [3]. Recently, many researchers have discussed the SIR model allowing vaccination [4–6]. Epidemiologically, vaccines are extremely important and have been proved to be the most effective and cost-efficient method of preventing infectious diseases such as measles, polio, diphtheria, tetanus, pertussis, tuberculosis, etc. [7, 8]. Mathematically, the epidemic models containing vaccination lead to multiple equilibrium points and show bifurcation phenomena. For example, Kribs-Zaleta and Velasco-Hernández in [9] constructed a SIS model with vaccination and showed that it exhibits a backward bifurcation. Also, Allen et al. introduced a stochastic SIR model with vaccination and showed that their model may have multiple endemic equilibriums [10]. Most of the vaccination models have been established based on ordinary differential equations (ODEs) [11–14].

Recently, fractional calculus has been extensively applied in many fields [15–18]. Many mathematicians and applied researchers have tried to model real processes using the fractional calculus [19–22]. The fractional modeling is an advantageous approach which has been used to study the behavior of diseases because the fractional derivative is a generalization of the integer-order derivative. Also, the integer derivative is local in nature, while the fractional derivative is global. This behavior is very useful to model epidemics problems. In addition, the fractional derivative is used to increase the stability region of the system. Fractional calculus has previously been applied in epidemiological studies [23–26]. Previous works rarely discussed an epidemics model with vaccination strategies that lead to multiple equilibrium points. In this work, we extend the SIR model with vaccination to a fractional-order model and give a detailed analysis of the equilibrium points of the model by applying fractional calculus.

This paper is organized as follows. In the next section, we give the definition of the Caputo derivative and present the fractional-order SIR model with vaccination in the sense of the Caputo derivative of order \(\alpha\in(0,1]\). In Section 3, we analyze the existence and stability of disease-free and endemic equilibrium points. To verify our results, we provide some numerical simulations for real data related to pertussis disease in Section 4. Finally, conclusions are given in Section 5.

2 Fractional-order model

In this section, we introduce the definition of fractional-order integration and derivative. There are different definitions of the fractional derivative. Among them, Riemann-Liouville and Caputo’s fractional derivative have been used more than others [27]. Comparing these two fractional derivatives, one easily arrives at the fact that Caputo’s derivative of a constant is equal to zero, which is not the case for the Riemann-Liouville derivative. The main concern of the paper thus focuses on the Caputo derivative of order \(\alpha>0\), which is rather applicable in real application.

Definition 1

The fractional integral of order \(\alpha>0\) of a function \(g:\mathbb{R}^{+} \rightarrow R\) is defined by

$$\begin{aligned} {I^{\alpha}}g(t) = \frac{1}{{\Gamma( \alpha)}} \int_{0}^{t} {{{(t - x)}^{\alpha - 1}} {g}(x)\,dx}, \end{aligned}$$
(1)

where \(\Gamma(\cdot)\) is a gamma function.

Definition 2

The Caputo fractional derivative of order \(\alpha>0\) of a continuous function \(g:\mathbb{R}^{+} \rightarrow \mathbb{R}\) is defined by

$$\begin{aligned} {D^{\alpha}}g(t) = {I^{n - \alpha}} {D^{n}}g(t), \end{aligned}$$
(2)

where n is an integer number satisfying \(\alpha\in(n-1,n)\) and \(D = \frac{d}{{dt}}\).

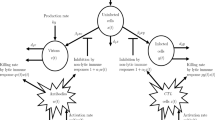
In our study, we present the fractional-order SIR model with vaccination using the first-order Caputo derivatives of order \(\alpha \in(0,1]\). First, we introduce the classical SIR allowing vaccination, which has been studied by many researchers [6, 10, 13]. In this model, the population \(N(t)\) is divided into four subpopulations: the susceptible, \(S(t)\), infected, \(I(t)\), recovered, \(R(t)\), and vaccinated, \(V(t)\), subpopulations. In addition, it is assumed that death and birth occur with the same constant rate \(b>0\), i.e. the population size is constant. Newborns are vaccinated with the rate \(\delta\in[0,1]\) at birth. Parameter β is the transmission rate between infected and susceptible individuals. Furthermore, the factor \(1-\sigma\) is the effect of vaccine, which means that if \(\sigma=0\), the vaccine is complete and if \(0< \sigma< 1\), the vaccine is incomplete. Moreover, ϕ is the vaccination rate. The vaccine does not provide lifelong protection and its protection is reduced with the rate θ. Infective individuals are recovered with the rate \(\mu>0\) and have temporary immunity. Recovered individuals leave this immunity with the rate ϑ. Using the model diagram depicted in Figure 1, the classical SIR model with vaccination is given by

$$ \left \{ \textstyle\begin{array}{ll} \frac{dS}{dt} = (1 - \delta)bN - bS ( t ) - \frac{{\beta I ( t )S ( t )}}{N} - \phi S ( t ) + \theta V(t) + \vartheta R ( t ), \\ \frac{dI}{dt}=\frac{{\beta I ( t )S ( t )}}{N} + \sigma\frac{{\beta I ( t )V(t)}}{N} - ( {b + \mu} )I ( t ), \\ \frac{dR}{dt}= \mu I ( t ) - ( {\vartheta + b} )R ( t ), \\ \frac{dV}{dt}= \delta bN + \phi S ( t ) - (b + \theta)V(t) - \sigma\frac{{\beta I ( t )V(t)}}{N}, \end{array}\displaystyle \right . $$
(3)

with the following non-negative initial conditions:

$$\begin{aligned} S(0)=S_{0},\qquad I(0)=I_{0},\qquad R(0)=R_{0},\qquad V(0)=V_{0}. \end{aligned}$$
(4)
Figure 1
figure 1

Flow diagram of the classical SIR mathematical model with vaccination.

Full size image

Now, by replacing integer-order derivatives of the above system with fractional derivatives of order \(\alpha\in(0, 1]\) in the sense of Caputo, we consider the fractional-order SIR model with vaccination as follows:

$$ \left \{ \textstyle\begin{array}{@{}l} D_{t}^{\alpha}S ( t ) = (1 - \delta)bN - bS ( t ) - \frac{{\beta I ( t )S ( t )}}{N} - \phi S ( t ) + \theta V(t) + \vartheta R ( t ), \\ D_{t}^{\alpha}I ( t ) = \frac{{\beta I ( t )S ( t )}}{N} + \sigma\frac{{\beta I ( t )V(t)}}{N} - ( {b + \mu} )I ( t ), \\ D_{t}^{\alpha}R ( t ) = \mu I ( t ) - ( {\vartheta + b} )R ( t ), \\ D_{t}^{\alpha}V ( t ) = \delta bN + \phi S ( t ) - (b + \theta)V(t) - \sigma\frac{{\beta I ( t )V(t)}}{N}. \end{array}\displaystyle \right . $$
(5)

Similar to [28], it is easy to show that system (5) with non-negative initial conditions (4) has a unique non-negative solution. As the population is constant, we have \(V ( t ) = N - S ( t ) - I ( t ) - R ( t )\) at any time t. Therefore, we write the following system instead of system (5):

$$ \left \{ \textstyle\begin{array}{@{}l} D_{t}^{\alpha}S ( t )= (1 - \delta)bN - bS ( t ) - \frac{{\beta I ( t )S ( t )}}{N} - \phi S(t)+ \theta(N - S(t) - I(t) - R(t)) + \vartheta R ( t ), \\ D_{t}^{\alpha}I ( t ) = \frac{{\beta I ( t )S ( t )}}{N} + \sigma\frac{{\beta I ( t )}}{N}(N - S(t) - I(t) - R(t)) - ( {b + \mu} )I ( t ), \\ D_{t}^{\alpha}R ( t ) = \mu I ( t ) - ( {\vartheta + b} )R ( t ). \end{array}\displaystyle \right . $$
(6)

In the next section, we investigate the existence and stability conditions of the equilibrium points of system (6).

3 Existence and stability of equilibrium points

According to the mentioned above, if \(E=( S_{e}, I_{e}, R_{e})\) is an equilibrium point of system (6) then \(E=( S_{e}, I_{e}, R_{e}, V_{e})\) is an equilibrium point of system (5) where \(V_{e}=1-S_{e}-I_{e}- R_{e}\). The equilibrium point of system (6) satisfies the following system:

$$ \textstyle\begin{cases} {D_{t}^{\alpha}} S ( t )=0, \\ {D_{t}^{\alpha}} I ( t )=0, \\ {D_{t}^{\alpha}} R ( t )=0. \end{cases} $$
(7)

To investigate the stability of the equilibrium points of system (6), we use the following theorem from [29, 30].

Theorem 1

Consider the following commensurate fractional-order system:

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} {D^{\alpha}}\boldsymbol {x}(t) = \boldsymbol {f} (t,\boldsymbol {x}(t)),\\ \boldsymbol {x}({t_{0}}) = {\boldsymbol {x}_{0}}, \end{array}\displaystyle \right . \end{aligned}$$
(8)

where \(D^{\alpha}\) is Caputo’s derivative of the order \(0 < \alpha \le 1\) and \(\boldsymbol {f} (t,\boldsymbol {x}(t)):\mathbb{R}^{+} \times\mathbb{R}^{n} \to\mathbb{R}^{n}\) is a vector field. The equilibrium points of this system are locally asymptotically stable if all eigenvalues \({\lambda_{i}}\) of the Jacobian matrix \(\frac{{\partial \boldsymbol {f}(t,\boldsymbol {x})}}{{\partial\boldsymbol {x}}}\) evaluated at the equilibrium points satisfy the following condition:

$$\begin{aligned} \vert {\arg {\lambda_{i}}} \vert > \alpha \frac{\pi}{2}. \end{aligned}$$
(9)

3.1 Existence and stability of disease-free equilibrium point

It is clear that system (6) always has the following unique disease-free equilibrium:

$$\bar{E} = (\bar{S},0,0 ) = \biggl(\frac{{b + \theta-\delta b }}{{b + \theta + \phi}}N,0,0 \biggr). $$

The following theorem is established for the stability of the disease-free equilibrium Ē.

Theorem 2

If

$$\begin{aligned} R_{0}=\frac{\beta}{{b + \mu}} \biggl( {\frac{{b + \theta + \sigma\phi -\delta b(1-\sigma)}}{{b + \theta + \phi}}} \biggr) < 1, \end{aligned}$$
(10)

then the disease-free equilibrium Ē of system (6) is locally asymptotically stable.

Proof

According to Theorem 1, to prove the stability of Ē, it is enough to show that all eigenvalues of Jacobian matrix of system (6) at Ē have negative real parts. This Jacobian matrix is

$$ \begin{bmatrix} - b - \phi - \theta& \frac{{ - \beta(1-\delta) b - \beta\theta }}{{b + \phi + \theta}} - \theta& - \theta + \vartheta\\ 0 & \beta ( {1 - \sigma} )\frac{{b(1-\delta) + \theta }}{{b + \phi + \theta}} + \sigma\beta - b - \mu& 0 \\ 0 & \mu& - b - \vartheta \end{bmatrix}. $$

The eigenvalues of this matrix are as follows:

$$- ( {b + \vartheta} ),\qquad - ( {b + \theta + \phi} ),\qquad \frac{{\beta ( {b + \theta + \sigma\phi+\delta b \sigma-\delta b } ) - ( {b + \mu} ) ( {b + \theta + \phi} )}}{{b + \theta + \phi}}. $$

Therefore, we see that if \(R_{0}< 1\), then

$$\frac{{\beta ( {b + \theta + \sigma\phi+\delta b \sigma-\delta b} ) - ( {b + \mu} ) ( {b + \theta + \phi} )}}{{b + \theta + \phi}}< 0. $$

 □

3.2 Existence conditions of endemic equilibrium points

According to system (7), the endemic equilibrium points are obtained by solving the quadratic equation \(P ( I ) = A{I^{2}} + BI + C = 0\), where

$$\begin{aligned} &A = - \frac{{\sigma{\beta^{2}}(b + \vartheta + \mu)}}{{N(b + \vartheta)}},\\ &B = \sigma{\beta^{2}} - \sigma\beta b - \sigma\beta\phi - \sigma \beta\mu - \beta b - \beta\theta - \frac{{\beta\mu}}{{b + \vartheta}} ( {b + \theta + \sigma\phi} ),\\ &C = N\beta ( {b + \sigma\phi + \theta+\sigma\delta b -\delta b } ) - N ( {b + \mu} ) ( {b + \phi + \theta} ). \end{aligned}$$

It can be shown that if \(I^{*}\) be a positive real root of the above quadratic equation, then \(E^{*}=(S^{*},I^{*},R^{*})\) is the endemic equilibrium point of system (6) where

$$ \begin{aligned} &{S^{*}} = \frac{{N ( {b + \vartheta} ) ( {b + \mu - \sigma\beta} ) + \sigma\beta{I^{*}} ( {b + \vartheta + \mu } )}}{{ ( {b + \vartheta} )\beta ( {1 - \sigma} )}},\\ &{R^{*}} = \frac{{\mu{I^{*}}}}{{b + \vartheta}}. \end{aligned} $$
(11)

Theorem 3

If \(\beta\le b + \mu\), then system (6) has no endemic equilibrium point.

Proof

According to system (7), if \(E^{*}=(S^{*},I^{*},R^{*})\) is an endemic equilibrium point then

$$\frac{\beta}{N}{I^{*}} {S^{*}} + \frac{{\sigma\beta}}{N}{I^{*}} {V^{*}} - ( {b + \mu} ){I^{*}} = 0, $$

therefore, we have

$$\beta\biggl(\frac{{{S^{*}} + \sigma{V^{*}}}}{N}\biggr) = b + \mu. $$

Since the population size is constant, we have \(\frac{{{S^{*}} + \sigma {V^{*}}}}{N} < 1\). Then we obtain \(\beta>b + \mu\). Thus if \(\beta\le b + \mu\), then system (6) has no endemic equilibrium point. □

It is easy to show that \(C = N ( {b + \mu} ) ( {b + \theta + \phi} ) ( {{R_{0}} - 1} )\). Therefore, the following equation can be considered instead of the equation \(P(I)=0\):

$$Q ( I ) := \frac{{ - A{I^{2}}}}{{N ( {b + \mu} ) ( {b + \theta + \phi} )}} + \frac{{ - BI}}{{N ( {b + \mu} ) ( {b + \theta + \phi} )}} + 1 = {R_{0}}. $$

Thus, the existence of endemic equilibrium points of system (6) is dependent on the existence of positive real roots of quadratic equation \(Q(I)=R_{0}\). In the following, we obtain a certain threshold value of \(R_{0}\) and summarize the existence conditions of the endemic equilibrium points of system (6).

Lemma 1

The curve \(Q(I)\) has the minimum point \((I_{\min},R_{\min})\) where

$$\begin{aligned}& {I_{\min}} = \frac{{ - N}}{2}\frac{{ ( {b + \vartheta} ) ( { - \sigma\beta + b + \theta + \sigma ( {b + \phi + \mu} )} ) + \mu ( {b + \theta + \sigma\phi} )}}{{\sigma\beta ( {b + \vartheta + \mu} )}},\\& {R_{\min}} = 1 - \frac{{{{ ( { ( {b + \vartheta} ) ( {\sigma ( {b + \phi + \mu} ) - \sigma{\beta} + b + \theta} ) + \mu ( {b + \theta + \sigma\phi} )} )}^{2}}}}{{4\sigma ( {b + \vartheta} ){{ ( {b + \mu } )}} ( {b + \vartheta + \mu} ) ( {b + \theta + \phi} )}}. \end{aligned}$$

Proof

Since \(A<0\), the curve \(Q(I)\) has a minimum value. By direct calculation, we see that this minimum value occurs at the point \((I_{\min},R_{\min})\). □

Theorem 4

If \(\beta> b + \mu\), then:

  1. (i)

    If \(R_{0}>1\) or \(R_{0}=1\), \(B>0\) then system (6) has the unique endemic equilibrium point  \(E_{u}^{*}\).

  2. (ii)

    If \(R_{\min}=R_{0}<1\) and \(B>0\) then system (6) has the unique endemic equilibrium point  \(E_{c}^{*}\).

  3. (iii)

    If \(R_{\min}< R_{0}<1\) and \(B>0\) then system (6) has two endemic equilibrium points \(E_{1}^{*}\), \(E_{2}^{*}\).

  4. (iv)

    If \(R_{0} < R_{\min}\) there is no endemic equilibrium point.

Proof

As mentioned above, the y-intercept of the curve \(y=Q(I)\) is 1. Therefore, we have the following cases:

  1. (i)

    If \(R_{0}>1\), the quadratic equation \(Q(I)=R_{0}\) has two real roots and one of them is non-negative and greater than \(I_{\min}\). If \(R_{0}=1\), the quadratic equation \(Q(I)=R_{0}\) has a non-zero real root such that it is non-negative and greater than \(I_{\min}\) when \(B>0\). So, system (6) has the unique endemic equilibrium point \(E_{u}^{*}\) such that \(I_{u}^{*}>I_{\min}\).

  2. (ii)

    If \(R_{\min}=R_{0}<1\), the equation \(Q(I)=R_{0}\) has a repeated real root which is non-negative when \(B>0\). Thus, system (6) has the unique endemic equilibrium point \(E_{c}^{*}\) such that \(I_{c}^{*}=I_{\min}\).

  3. (iii)

    If \(R_{\min}< R_{0}<1\), the equation \(Q(I)=R_{0}\) has two real roots \(I_{1}^{*}\) and \(I_{2}^{*}\). If \(B>0\), these roots are non-negative. Therefore, system (6) has two endemic equilibrium points \(E_{1}^{*}\) and \(E_{2}^{*}\) such that \(I_{1}^{*}< I_{\min}< I_{2}^{*}\).

 □

3.3 Stability and α-stability of endemic equilibrium points

The following theorem shows that the stability region of endemic equilibrium points of system (6) can be increased by choosing an appropriate value of fractional order α.

Theorem 5

Suppose \(E^{*}_{u}\), \(E^{*}_{c}\), \(E^{*}_{1}\), and \(E^{*}_{2}\) are endemic equilibrium points as introduced in Theorem  4, then:

  1. (i)

    The endemic equilibrium points \(E^{*}_{c}\) and \(E^{*}_{1}\) are unstable.

  2. (ii)

    If \(\alpha\leq\frac{2}{3}\), the endemic equilibrium points \(E^{*}_{u}\) and \(E^{*}_{2}\) are locally asymptotically α-stable.

  3. (iii)

    If \(\alpha> \frac{2}{3}\) and \(\vartheta\geq\theta\), \(E^{*}_{u}\) and \(E^{*}_{2}\) are locally asymptotically stable.

Proof

According to Theorem 1, to prove the stability of the endemic equilibrium point \(E^{*}\), it is enough to show that all eigenvalues of the following Jacobian matrix satisfy the condition (9):

$$ \begin{bmatrix} { - b - \phi - \theta - \frac{{\beta{I^{*}}}}{N}}&{\frac{{-\beta {S^{*}}}}{N} - \theta}&{ - \theta + \vartheta}\\ {\frac{{\beta{I^{*}}}}{N} ( {1 - \sigma} )}&{\frac{{ - \sigma \beta{I^{*}}}}{N}}&{\frac{{ - \sigma\beta{I^{*}}}}{N}}\\ 0&\mu&{ - b - \vartheta} \end{bmatrix}. $$

The characteristic equation of this matrix is \(P(\lambda)=\lambda^{3}+a_{2} \lambda^{2}+a_{1} \lambda+a_{0}=0\) where

$$\begin{aligned} {a_{2}} ={}& 2b + \vartheta + \theta + \phi + \frac{{\beta I^{*}}}{{{N}}} ( {1 + \sigma} ),\\ {a_{1}} ={}& (b+\vartheta) (b + \phi+\theta)+ \frac{{\beta {I}^{*}}}{{{N}}} ( {2b \sigma + \sigma\mu + \sigma\phi + \sigma\vartheta+b+\vartheta+\theta} )\\ &{}+ \frac{{\beta^{2} I^{*}}}{{N^{2}}} \bigl(\sigma I^{*}+(1-\sigma)S^{*} \bigr),\\ {a_{0}} ={}& \frac{{\beta{I^{*}}}}{N} \bigl[ {N\mu ( {\theta - \vartheta} ) + \sigma N\mu ( {b + \vartheta + \phi} ) + N ( {b + \vartheta} ) ( {\theta + \sigma b + \sigma \phi} )} \bigr]\\ &{}+ \frac{{{\beta^{2}}{I^{*}}}}{N} \bigl[ { ( {1 - \sigma} ) ( {b + \vartheta} ){S^{*}} + \sigma{I^{*}} ( {\mu + b + \vartheta} )} \bigr]\\ ={}&\frac{{2\sigma{\beta^{2}}(b + \vartheta + \mu)I^{*}}}{{{N^{2}}}} \bigl( {I^{*} - {I_{\min}}} \bigr). \end{aligned}$$

For every endemic equilibrium point \(E^{*}\), it is obvious that \(a_{1},a_{2} >0\). According to the proof of Theorem 4, for the endemic equilibrium point \(E^{*}_{c}\), we have \(I^{*}_{c}=I_{\min}\) and \(a_{0}=0\). So, the equation \(P(\lambda)=0\) has a zero root and the endemic equilibrium point \(E^{*}_{c}\) is unstable. Similarly, for the endemic equilibrium point \(E^{*}_{1}\), we have \(I^{*}_{1}< I_{\min}\), then \(a_{0}<0\). From Descartes’ rule of signs, it is clear that the equation \(P(\lambda)=0\) has at least one positive real root. Therefore, the endemic equilibrium point \(E^{*}_{1}\) is unstable. For the endemic equilibrium points \(E^{*}_{u}\) and \(E^{*}_{2}\), we have \(I^{*}_{u} >I_{\min}\) and \(I^{*}_{2} >I_{\min}\), respectively. So we obtain \(a_{0}>0\). From Descartes’ rule of signs, the equation \(P(\lambda)=0\) has three negative real roots or one negative real root and two complex roots. If the equation \(P(\lambda)=0\) has three negative real roots, then \(E^{*}_{u}\) and \(E^{*}_{2}\) are stable. We now assume the equation \(P(\lambda)=0\) has one negative real root \(\lambda_{1}=-z\) and two complex roots \(\lambda _{2,3}=x\pm iy\), then

$$P(\lambda)=\lambda^{3}+\lambda^{2}(-2x+z)+\lambda \bigl(x^{2}+y^{2}-2xz\bigr)+z\bigl(x^{2}+y^{2} \bigr). $$

Therefore, we have

$$a_{2}=-2x+z,\qquad a_{1}=x^{2}+y^{2}-2xz,\qquad a_{0}=z\bigl(x^{2}+y^{2}\bigr). $$

We know \(a_{2}, a_{1}\geq0\), so \(x^{2}+y^{2}\geq2xz\) and \(z \geq2x\). Thus we obtain

$$x^{2}\biggl(1+\frac{{{x^{2}}}}{{{y^{2}}}}\biggr)\geq2xz \geq4x^{2}. $$

The above equation show that \(\sec^{2}(\operatorname{Arg} \lambda_{2,3})\geq4\) and \(\frac{\pi}{3} \leq \operatorname{Arg}(\lambda_{2,3})\leq\frac{2\pi}{3}\). So, if \(\alpha\leq\frac{2}{3}\), then \(|\operatorname{Arg} \lambda_{2,3}| > \alpha\frac{\pi }{2}\) and \(E^{*}_{u}\), \(E^{*}_{2}\) are stable. Furthermore, if \(a_{2} a_{1} -a_{0} > 0\), then \(- 2x [ {{{ ( {x - z} )}^{2}} + {y^{2}}} ] > 0\). So, if \(a_{2} a_{1} -a_{0} > 0\), then \(\lambda_{2}\) and \(\lambda_{3}\) must have negative real parts. It can be shown that if \(\vartheta\geq\theta\), then \(a_{2}a_{1}-a_{0} > 0\) and the roots of the equation \(P(\lambda)=0\) have negative real parts. □

4 Numerical results

To illustrate the results of Theorem 4, we consider \(R_{0}\), \(R_{\min}\), and B as functions of σ and ϕ; meanwhile the other parameters are fixed and given by

$$\delta=0.9, \qquad\mu = \frac{1}{{21}},\qquad b = \frac{1}{{75 \times365}},\qquad \beta = 0.4, \qquad\theta = \frac{1}{{5 \times365}},\qquad \vartheta = \frac {1}{{31}}, $$

where these values are related to pertussis disease [31]. In Figure 2, the diagram with \(R_{0} = R_{\min}\), \(R_{0} = 1\), and \(B = 0\) is plotted. In this figure, we have the following sets:

$$\begin{aligned} &R_{EEP}^{1}=\bigl\{ (\phi, \sigma)| R_{0}>1\bigr\} ,\\ &R_{EEP}^{2}=\bigl\{ (\phi, \sigma)|R_{\min} < R_{0}< 1 , B>0\bigr\} ,\\ &R_{EEP}^{0}=\bigl\{ (\phi, \sigma)| R_{0}< R_{\min}< 1 \bigr\} . \end{aligned}$$

According to Theorem 4, system (6) has two endemic equilibrium points in the region \(R_{EEP}^{2}\) and has a unique endemic equilibrium point in the region \(R_{EEP}^{1}\). Moreover, it has a disease-free equilibrium point in the region \(R_{EEP}^{0}\). Hence, pertussis disease can be contained by choosing appropriate values for σ and ϕ.

Figure 2
figure 2

Plot diagrams \(\pmb{R_{0} = R_{\min}}\) , \(\pmb{R_{0} = 1}\) , and \(\pmb{B = 0}\) for different values of σ and ϕ . The regions of \(R_{EEP}^{0}\), \(R_{EEP}^{1}\) and \(R_{EEP}^{2}\) illustrate the regions that system (6) has zero, one, and two endemic equilibrium point, respectively.

Full size image

Now, we consider \(\sigma=0.08\), \(\phi=0.02\), and \(N=1{,}000\); these values of σ and ϕ belong to the set \(R_{EEP}^{2}\) in Figure 2. By directly calculating, it can be shown that the fractional-order model (6) have the following endemic equilibrium points:

$$\begin{aligned} &E_{1}^{*}=(45.49997509,13.74525715,20.26766619),\\ &E_{2}^{*}=(101.4923621,273.9622965,403.9630769), \end{aligned}$$

which obtained results are compatible with Theorem 4 and Figure 2.

In order to observe the effects that the parameter α has on the dynamics of the fractional-order model 6, we include several numerical simulations varying the value of the parameter. To simulate the fractional-order model (6), we apply an Adams-type predictor corrector method [32, 33]. This method is well known for numerical solutions of first-order problems [34, 35]. For the above parameter values and the following initial values:

$$ S(0) = 920,\qquad I(0) = 80,\qquad R(0) = 0, $$
(12)

the numerical simulations \(S(t)\), \(I(t)\), and \(R(t)\) are shown in Figures 3-5 for \(\alpha= 0.65\), \(\alpha= 0.85\), \(\alpha=0.95\), and \(\alpha=1\). These figures reveal that a change of the value α affects the dynamics of epidemic. For example, Figure 4 shows that for lower values of α, the epidemic peak is wider and lower. This feature is important from an epidemiological point of view since its interpretation shows a longer period in which infected individuals can affect the health system.

Figure 3
figure 3

Size of the susceptible class over time. The approximate solutions \(S(t)\) of system (6) with initial values (12) for \(\alpha= 0.65\), \(\alpha= 0.85\), \(\alpha=0.95\), and \(\alpha=1\).

Full size image
Figure 4
figure 4

Size of the infected class over time. The approximate solutions \(I(t)\) of system (6) with initial values (12) for \(\alpha= 0.65\), \(\alpha= 0.85\), \(\alpha=0.95\), and \(\alpha=1\).

Full size image
Figure 5
figure 5

Size of the recovered class over time. The approximate solutions \(R(t)\) of system (6) with initial values (12) for \(\alpha= 0.65\), \(\alpha= 0.85\), \(\alpha=0.95\), and \(\alpha=1\).

Full size image

According to Theorem 5, we expect the equilibrium point \(E_{1}^{*}\) to be unstable for different values of α. Since \(\vartheta\geq\theta\), we envisage that the equilibrium point \(E_{2}^{*}\) is asymptotically stable for \(\alpha> 2/3\) and α-stable for \(\alpha\leq2/3\). Figures 3-5 show that the model presented here gradually approaches the steady state for different values of α but the dynamics of the model is governed by the distinct paths.

5 Conclusion

In this paper, we extended the classical SIR model with vaccination to a system of fractional ordinary differential equations (FODEs). For our fractional-order model, we determined the basic reproduction \(R_{0}\) and proved that if \(R_{0}<1\), the disease-free equilibrium is locally asymptotically stable. In the classical SIR model with vaccination, it is shown that \(R_{0}\) must be further reduced to less than a threshold value in order to ensure that the disease exterminates, but this value has not been obtained exactly [10]. In this work, we analytically obtained the threshold value of \(R_{0}\), denoted by \(R_{\min}\). Using the values of \(R_{0}\) and \(R_{\min}\), we established the existence conditions of endemic equilibrium points in Theorem 4. We proved Theorem 5 about the stability and α-stability of the endemic equilibrium points which are introduced in Theorem 4. Theorem 5 shows that the stability of endemic equilibrium points can be controlled by modifying the value of α. In fact, the fractional-order model can be achieved in the steady state by controlling the parameters which affect the value of α. Finally, the analytical results are confirmed by some numerical simulations for real data related to pertussis disease. In Figure 2, it is shown that pertussis disease can be contained by choosing appropriate values for σ and ϕ. The numerical simulations presented in Figures 3-5 are compatible by Theorems 4 and 5.