1 Introduction

There has been much interest over the last two decades in fractional calculus and its applications. A comprehensive treatment of fractional calculus and applications can be found in Miller and Ross [1], Oldham and Spanier [2], Podlubny [3] and Samko et al. [4]. Many researchers have used numerical methods to solve biological and fluid dynamics type models and investigated the stability and convergence analysis, see [5–9]. Here, the modified anomalous sub-diffusion equation has been proposed to describe the processes that become less anomalous as time progresses by inclusion of a secondary fractional time derivative acting on diffusion operator [10–13].

Many researchers have solved this problem with different methods. Li and Wang [14] proposed an improved efficient difference method for modified anomalous sub-diffusion equation with a nonlinear source term. They used weighted and shifted Grünwald-Letnikov for Riemann-Liouville fractional derivative and compact difference for space derivative and used second-order interpolation formula for nonlinear source term. Dehghan et al. [15] used a finite difference scheme for Riemann-Liouville fractional derivative and the Legendre spectral element method for space component. For a semi-discrete scheme, they took integral on both sides and then for full discretization used the Legendre spectral element method for one- and two-dimensional modified anomalous sub-diffusion equation. Liu et al. [13] demonstrated a new implicit numerical method for modified anomalous sub-diffusion equation with nonlinear source term in a bounded domain and analyzed stability and convergence by a new energy method. Cao et al. [16] studied the implicit midpoint method and constructed a new numerical scheme for modified fractional sub-diffusion equation with nonlinear source term. Ding and Li [17] used second-order Riemann-Liouville fractional derivative and constructed two kinds of novel numerical schemes and discussed stability, convergence and solvability by the Fourier method. So many authors have used a high-order difference scheme with different methods for modified anomalous sub-diffusion equation and applied Grünwald-Letnikov definition for Riemann-Liouville fractional derivative and also discussed stability and convergence [11, 18, 19].

In this paper, we modify the implicit difference method completely numerically for modified anomalous fractional sub-diffusion equation by applying the discretized form of Riemann-Liouville integral operator and the backward difference formula to remove the partial derivative with respect to time. We also analyze the stability and convergence of the modified scheme by the Fourier series method.

In this paper, we consider the following modified anomalous fractional sub-diffusion equation [18]:

$$ \frac{\partial u(x,y,t)}{\partial t}= \biggl(A\frac{\partial^{1-\alpha} }{\partial t^{1-\alpha}}+B \frac{\partial^{1-\beta} }{\partial t^{1-\beta}} \biggr) \biggl[ \frac{\partial^{2} u(x,y,t)}{\partial x^{2}}+\frac {\partial^{2} u(x,y,t)}{\partial y^{2}} \biggr]+f(x,y,t) $$
(1)

subject to the initial and boundary conditions

$$\begin{aligned}& u(x,y,0)=\varphi(x,y), \end{aligned}$$
(2)
$$\begin{aligned}& u(0,y,t)=\varphi_{1}(y,t),\qquad u(L,y,t)=\varphi_{2}(y,t), \\& u(x,0,t)=\varphi_{3}(x,t), \qquad u(x,L,t)=\varphi_{4}(x,t), \\& \quad 0\leq x,y\leq L, 0\leq t\leq T, \end{aligned}$$
(3)

where φ, \(\varphi_{1}\), \(\varphi_{2}\), \(\varphi_{3}\) and \(\varphi_{4}\) are known functions, A, B are constants and \(\frac{\partial ^{1-\alpha}}{\partial t^{1-\alpha}}\) and \(\frac{\partial^{1-\beta }}{\partial t^{1-\beta}}\) are the Riemann-Liouville fractional derivatives of fractional order \(1-\alpha\) and \(1-\beta\), respectively, defined by [3, 20].

$$\begin{aligned}& \frac{\partial^{1-\alpha} }{\partial t^{1-\alpha}} u(x,y,t)=\frac {1}{\Gamma(\alpha)}\frac{\partial}{\partial t} \int_{0}^{t}\frac {u(x,y,\eta)}{(t-\eta)^{1-\alpha}}\,d\eta= \frac{\partial}{\partial t} I_{0}^{\alpha}u(x,y,t), \end{aligned}$$
(4)
$$\begin{aligned}& \frac{\partial^{1-\beta} }{\partial t^{1-\beta}} u(x,y,t)=\frac {1}{\Gamma(\beta)}\frac{\partial}{\partial t} \int_{0}^{t}\frac {u(x,y,\eta)}{(t-\eta)^{1-\beta}}\,d\eta= \frac{\partial}{\partial t} I_{0}^{\beta}u(x,y,t). \end{aligned}$$
(5)

Here

$$\begin{aligned}& I_{0}^{\alpha}u(x,y,t)=\frac{1}{\Gamma(\alpha)} \int_{0}^{t}\frac {u(x,y,\eta)}{(t-\eta)^{1-\alpha}}\,d\eta, \end{aligned}$$
(6)
$$\begin{aligned}& I_{0}^{\beta}u(x,y,t)=\frac{1}{\Gamma(\beta)} \int_{0}^{t}\frac {u(x,y,\eta)}{(t-\eta)^{1-\beta}}\,d\eta, \end{aligned}$$
(7)

is the Riemann-Liouville integral of fractional order \(0<\alpha, \beta <1\).

The following two lemmas will be used in this paper [20].

Lemma 1

If \(u(t) \in C^{1} [0,T]\), then

$$ I_{0}^{\gamma}u(t_{k})= \frac{\tau^{\gamma}}{\Gamma(\gamma+1)}\sum_{j=0}^{k-1}b_{j}^{(\gamma)}u(t_{k-j})+R_{k}^{\gamma}, $$
(8)

where \(|R_{k}^{\gamma}|\leq C b_{k}^{\gamma}\tau\).

Lemma 2

The coefficients \(b_{k}^{(\gamma)}\) (\(k=0,1,2,\ldots\)) satisfy the following properties:

  1. (i)

    \(b_{0}^{(\gamma)}=1\), \(b_{k}^{(\gamma)}>0\), \(k=0,1,2,\ldots\) .

  2. (ii)

    \(b_{k-1}^{(\gamma)}>b_{k}^{(\gamma)}\), \(k=1,2,\ldots\) .

  3. (iii)

    There exists a positive constant \(C>0\) such that \(\tau\leq C b_{k}^{(\gamma)} \tau^{\gamma}\), \(k=1, 2,\ldots\) .

  4. (iv)

    \(\sum_{j=0}^{k}b_{j}^{(\gamma)} \tau^{\gamma}=(k+1)^{\gamma}\leq T^{\gamma}\).

2 Modified implicit difference approximation

In this section, we develop a modified implicit difference scheme for the modified anomalous fractional sub-diffusion equation (1)-(3). For the discretization of the Riemann-Liouville fractional derivative, we use the definition in (4)-(5) and replace the second-order space derivatives by central difference approximation. We take the space steps as \(x_{i}=i\Delta x\), in the x-direction with \(i=1,2,\ldots,M-1\), \(\Delta x=\frac{L}{M}\), and the time step is \(t_{k}=k\tau\), \(k=1,2,\ldots,N\), where \(\tau=\frac {T}{N}\). Let \(u_{i}^{k}\) be the numerical approximation to \(u(x_{i},t_{k})\). By applying (4) and (5) to equation (1), we obtain

$$ \frac{\partial u(x,y,t)}{\partial t}= \biggl(A\frac{\partial}{\partial t} I_{0}^{\alpha}+B \frac{\partial}{\partial t} I_{0}^{\beta} \biggr) \biggl[ \frac{\partial^{2} u(x,y,t)}{\partial x^{2}}+\frac{\partial^{2} u(x,y,t)}{\partial y^{2}} \biggr]+f(x,y,t). $$
(9)

Firstly, for the discretization of equation (9), we are using Lemma 1 for the Riemann-Liouville integral operator, then central difference approximation for second-order space derivatives and applying backward difference approximation for the partial derivative with respect to time, we have

$$\begin{aligned} u_{i,j}^{k} - u_{i,j}^{k-1} =& r_{1} \sum_{s=0}^{k-1} b_{s}^{(\alpha )}\delta x^{2} \bigl( u_{i,j}^{k-s}- u_{i,j}^{k-s-1} \bigr)+ r_{2} \sum _{s=0}^{k-1} b_{s}^{(\alpha)} \delta y^{2} \bigl( u_{i,j}^{k-s}-u_{i,j}^{k-s-1} \bigr) \\ &{}+ r_{3} \sum_{s=0}^{k-1} b_{s}^{(\beta)}\delta x^{2} \bigl( u_{i,j}^{k-s}- u_{i,j}^{k-s-1} \bigr)+ r_{4} \sum _{s=0}^{k-1} b_{s}^{(\beta)} \delta y^{2} \bigl( u_{i,j}^{k-s}-u_{i,j}^{k-s-1} \bigr) \\ &{}+\tau f(x_{i},y_{j},t_{k}) +R_{i,j,k}^{\alpha}+R_{i,j,k}^{\beta}. \end{aligned}$$
(10)

Here,

$$ \begin{aligned} &r_{1}= \frac{A \tau^{\alpha}}{\Gamma({\alpha} +1) {\Delta x}^{2}},\qquad r_{2}= \frac{A \tau^{\alpha}}{\Gamma({\alpha} +1) {\Delta y}^{2}}, \qquad r_{3}= \frac{B \tau^{\beta}}{\Gamma({\beta} +1) {\Delta x}^{2}}, \\ &r_{4}= \frac{B \tau^{\beta}}{\Gamma({\beta} +1) {\Delta y}^{2}},\qquad \bigl\vert R_{i,k}^{\alpha} \bigr\vert \leq C b_{k}^{(\alpha)} \tau^{\alpha} \bigl( \tau+\tau \Delta x^{2}\bigr), \\ &\bigl\vert R_{i,k}^{\beta} \bigr\vert \leq C b_{k}^{(\beta)} \tau^{\beta} \bigl(\tau +\tau\Delta x^{2}\bigr), \end{aligned} $$
(11)

and

$$ \delta x^{2} u_{i,j}^{k}=u_{i+1,j}^{k}-2u_{i,j}^{k}+u_{i-1,j}^{k}, \qquad \delta y^{2} u_{i,j}^{k}=u_{i,j+1}^{k}-2u_{i,j}^{k}+u_{i,j-1}^{k}. $$
(12)

From the above, we present a modified implicit difference scheme for the modified anomalous fractional sub-diffusion equation (1)-(3) with the initial and boundary conditions as follows:

$$\begin{aligned} u_{i,j}^{k} - u_{i,j}^{k-1} =&r_{1} \delta x^{2} u_{i,j}^{k}-r_{1} b_{k-1}^{(\alpha)} \delta x^{2} u_{i,j}^{0}+r_{2} \delta y^{2} u_{i,j}^{k}-r_{2} b_{k-1}^{(\alpha)} \delta y^{2} u_{i,j}^{0} \\ &{}-\sum_{s=1}^{k-1}\bigl(b_{s-1}^{(\alpha)}-b_{s}^{(\alpha)} \bigr) \bigl( r_{1} \delta x^{2} u_{i,j}^{k-s}+r_{2} \delta y^{2} u_{i,j}^{k-s}\bigr) \\ &{}+r_{3} \delta x^{2} u_{i,j}^{k}-r_{3} b_{k-1}^{(\beta)} \delta x^{2} u_{i,j}^{0}+r_{4} \delta y^{2} u_{i,j}^{k}-r_{4} b_{k-1}^{(\beta)} \delta y^{2} u_{i,j}^{0} \\ &{}-\sum_{s=1}^{k-1}\bigl(b_{s-1}^{(\beta)}- b_{s}^{(\beta)}\bigr) \bigl( r_{3} \delta x^{2} u_{i,j}^{k-s}+r_{4} \delta y^{2} u_{i,j}^{k-s}\bigr) +\tau f_{i,j}^{k}, \end{aligned}$$
(13)

where \(i=1,2,\ldots M_{x}-1\), \(j=1,2,\ldots M_{y}-1 \) and \(k=1,2,\ldots N-1 \) with

$$\begin{aligned}& u_{i,j}^{0}=\varphi(x_{i},y_{j}), \end{aligned}$$
(14)
$$\begin{aligned}& u_{0,j}^{k}=\varphi_{1}(y_{j},t_{k}), \qquad u_{M,j}^{k}=\varphi_{2}(y_{j}, t_{k}), \\& u_{i,0}^{k}=\varphi_{3}(x_{i},t_{k}), \qquad u_{i,M}^{k}=\varphi_{4}(x_{i}, t_{k}), \\& \quad 0\leq x,y\leq L, 0\leq t\leq T. \end{aligned}$$
(15)

3 Stability of the modified implicit scheme

In this section, we investigate the stability of the modified implicit numerical scheme using the Fourier series method. Let \(U_{i}^{k} \) be the approximate solution for (13), and we have

$$\begin{aligned} U_{i,j}^{k} - U_{i,j}^{k-1} =&r_{1} \delta x^{2} U_{i,j}^{k}-r_{1} b_{k-1}^{(\alpha)} \delta x^{2} U_{i,j}^{0}+r_{2} \delta y^{2} U_{i,j}^{k}-r_{2} b_{k-1}^{(\alpha)} \delta y^{2} U_{i,j}^{0} \\ &{}-\sum_{s=1}^{k-1}\bigl(b_{s-1}^{(\alpha)}-b_{s}^{(\alpha)} \bigr) \bigl( r_{1} \delta x^{2} U_{i,j}^{k-s}+r_{2} \delta y^{2}U_{i,j}^{k-s}\bigr) \\ &{}+r_{3} \delta x^{2} U_{i,j}^{k}-r_{3} b_{k-1}^{(\beta)} \delta x^{2} U_{i,j}^{0}+r_{4} \delta y^{2} U_{i,j}^{k}-r_{4} b_{k-1}^{(\beta)} \delta y^{2} U_{i,j}^{0} \\ &{}-\sum_{s=1}^{k-1}\bigl(b_{s-1}^{(\beta)}- b_{s}^{(\beta)}\bigr) \bigl( r_{3} \delta x^{2} U_{i,j}^{k-s}+r_{4} \delta y^{2} U_{i,j}^{k-s}\bigr) +\tau f_{i,j}^{k}, \end{aligned}$$
(16)

where \(i=1,2,\ldots,M_{x}-1\), \(j=1,2,\ldots,M_{y}-1\) and \(k=1,2,\ldots ,N-1\).

Next, the error is defined as

$$ e_{i,j}^{k}=u_{i,j}^{k}-U_{i,j}^{k}, $$
(17)

where \(e_{i,j}^{k}\) satisfies (16) and

$$\begin{aligned} e_{i,j}^{k} - e_{i,j}^{k-1} =&r_{1} \bigl(e_{i+1,j}^{k}-2e_{i,j}^{k}+e_{i-1,j}^{k} \bigr)-r_{1} b_{k-1}^{(\alpha)} \bigl(e_{i+1,j}^{0}-2 e_{i,j}^{0}+e_{i-1,j}^{0}\bigr) \\ &{}+r_{2} \bigl(e_{i,j+1}^{k}-2e_{i,j}^{k}+e_{i,j-1}^{k} \bigr)-r_{2} b_{k-1}^{(\alpha)} \bigl(e_{i,j+1}^{0}-2 e_{i,j}^{0}+e_{i,j-1}^{0}\bigr) \\ &{}-\sum_{s=1}^{k-1}\bigl(b_{s-1}^{(\alpha)}-b_{s}^{(\alpha)} \bigr) \bigl(r_{1} \bigl(e_{i+1,j}^{k-s}- 2 e_{i,j}^{k-s}+e_{i-1,j}^{k-s} \bigr) \\ &{}+r_{2} \bigl(e_{i,j+1}^{k-s}-2 e_{i,j}^{k-s}+e_{i,j-1}^{k-s}\bigr) \bigr) \\ &{}+r_{3} \bigl(e_{i+1,j}^{k}-2e_{i,j}^{k}+e_{i-1,j}^{k} \bigr)- r_{3} b_{k-1}^{(\beta)} \bigl(e_{i+1,j}^{0}-2 e_{i,j}^{0}+e_{i-1,j}^{0}\bigr) \\ &{}+r_{4} \bigl(e_{i,j+1}^{k}-2e_{i,j}^{k}+e_{i,j-1}^{k} \bigr)- r_{4} b_{k-1}^{(\beta)} \bigl(e_{i,j+1}^{0}-2 e_{i,j}^{0}+e_{i,j-1}^{0}\bigr) \\ &{}-\sum_{s=1}^{k-1}\bigl(b_{s-1}^{(\beta )}-b_{s}^{(\beta)} \bigr) \bigl(r_{3} \bigl(e_{i+1,j}^{k-s}-2 e_{i,j}^{k-s}+e_{i-1,j}^{k-s} \bigr) \\ &{}+r_{4} \bigl(e_{i,j+1}^{k-s}- 2 e_{i,j}^{k-s}+e_{i,j-1}^{k-s}\bigr) \bigr). \end{aligned}$$
(18)

The error and initial conditions are given by

$$ e_{0}^{k}=e_{M}^{k}=e_{i,j}^{0}=0. $$
(19)

By defining the following grid functions for \(k=1,2,\ldots,N\)

$$ e^{k}(x,y)= \textstyle\begin{cases} e_{i,j}^{k},& \mbox{when }x_{i-\frac{\Delta x}{2}}< x\leq x_{i+\frac{\Delta x}{2}}, y_{j-\frac{\Delta y}{2}}< y\leq y_{j+\frac{\Delta y}{2}}, \\ 0,& \mbox{when }0\leq x\leq\frac{\Delta x}{2}\mbox{ or }L-\frac{\Delta x}{2}\leq x\leq L, \\ 0,& \mbox{when }0\leq y\leq\frac{\Delta y}{2}\mbox{ or }L-\frac{\Delta y}{2}\leq y\leq L, \end{cases} $$
(20)

\(e^{k} (x,y)\) can be expanded in Fourier series such as

$$ e^{k}(x,y)=\sum_{{l_{1}, l_{2}}=-\infty}^{\infty} \lambda^{k}(l_{1}, l_{2})e^{2\sqrt{-1}\pi(l_{1} x/L+l_{2} y/L)}, $$
(21)

where

$$ \lambda^{k}(l_{1}, l_{2})=\frac{1}{L} \int_{0}^{L} \int_{0}^{L} e^{k}(x,y)e^{-2\sqrt{-1}\pi(l_{1} x/L+l_{2} y/L)} \,dx\,dy. $$
(22)

From the definition of \(l^{2} \) norm and Parseval’s equality, we have

$$ \bigl\Vert e^{k} \bigr\Vert _{\infty}^{2}=\sum _{i=1}^{M_{x}-1} \sum _{j=1}^{M_{y}-1} \Delta x \Delta y \bigl\vert e_{i,j}^{k} \bigr\vert ^{2}=\sum _{l_{1},l_{2}=-\infty}^{\infty} \bigl\vert \lambda ^{k}(l_{1}, l_{2}) \bigr\vert ^{2}. $$
(23)

Supposing that

$$ e_{i,j}^{k}=\lambda^{k} e^{\sqrt{-1} (\sigma_{1} i \Delta x+\sigma_{2} j \Delta y)}, $$
(24)

where \(\sigma_{1}=2\pi l_{1}/L\), \(\sigma_{2}=2\pi l_{2}/L\) and substituting (24) in (18), we obtain

$$\begin{aligned} \lambda^{k} =&\frac{1}{(1+\mu_{1}+\mu_{2})} \Biggl(\lambda^{k-1}+\bigl( \mu_{1} b_{k-1}^{(\alpha)}+\mu_{2} b_{k-1}^{(\beta)}\bigr)\lambda^{0}+\mu_{1} \sum _{s=1}^{k-1}\bigl(b_{s-1}^{(\alpha)}-b_{s}^{(\alpha)} \bigr)\lambda^{k-s} \\ &{}+\mu_{2} \sum_{s=1}^{k-1} \bigl(b_{s-1}^{(\beta)}-b_{s}^{(\beta)}\bigr) \lambda^{k-s} \Biggr), \end{aligned}$$
(25)

where

$$\begin{aligned}& \mu_{1}=4 \biggl(r_{1} \sin^{2}\biggl( \frac{\sigma_{1} \Delta x}{2}\biggr)+r_{2} \sin^{2}\biggl( \frac {\sigma_{2} \Delta y}{2}\biggr) \biggr), \end{aligned}$$
(26)
$$\begin{aligned}& \mu_{2}=4 \biggl(r_{3} \sin^{2}\biggl( \frac{\sigma_{1} \Delta x}{2}\biggr)+r_{4} \sin^{2}\biggl( \frac {\sigma_{2} \Delta y}{2}\biggr) \biggr). \end{aligned}$$
(27)

Proposition 1

If \(\lambda^{k}\) (\(k=1,2,\ldots,N\)) satisfy (25), then \(|\lambda ^{k} |\leq|\lambda^{0}|\).

Proof

By using mathematical induction, we take \(k=1\) in (25)

$$ \lambda^{1}=\frac{ (1+ b_{0}^{(\alpha)}\mu_{1}+ b_{0}^{(\beta)}\mu_{2})\lambda ^{0}}{(1+\mu_{1}+\mu_{2})}, $$

and as \(\mu_{1}, \mu_{2}\geq0\) and \(b_{0}^{(\alpha)}=b_{0}^{(\beta)}=1\), then

$$ \bigl\vert \lambda^{1} \bigr\vert \leq \bigl\vert \lambda^{0} \bigr\vert . $$
(28)

Now, assuming that

$$ \bigl|\lambda^{m}\bigr|\leq\bigl|\lambda^{0}\bigr|; \quad m=1,2,\ldots,k-1 $$

and as \(0<\alpha, \beta<1\), from (25) and Lemma 2, we obtain

$$\begin{aligned} \bigl\vert \lambda^{k} \bigr\vert \leq&\frac{1}{(1+\mu_{1}+\mu_{2})} \Biggl[ \bigl\vert \lambda^{k-1} \bigr\vert + \bigl(\mu_{1} b_{k-1}^{(\alpha)}+\mu_{2} b_{k-1}^{(\beta)} \bigr) \bigl\vert \lambda^{0} \bigr\vert +\mu_{1} \sum _{s=1}^{k-1}\bigl(b_{s-1}^{(\alpha)}-b_{s}^{(\alpha)} \bigr) \bigl\vert \lambda^{k-s} \bigr\vert \\ &{}+\mu_{2} \sum_{s=1}^{k-1} \bigl(b_{s-1}^{(\beta)}-b_{s}^{(\beta)}\bigr) \bigl\vert \lambda ^{k-s} \bigr\vert \Biggr] \\ \leq& \biggl[\frac{1+ (\mu_{1} b_{k-1}^{(\alpha)}+\mu_{2} b_{k-1}^{(\beta )})+\mu_{1} \sum_{s=1}^{k-1}(b_{s-1}^{(\alpha)}-b_{s}^{(\alpha)})+\mu_{2} \sum_{s=1}^{k-1}(b_{s-1}^{(\beta)}-b_{s}^{(\beta)})}{(1+\mu_{1}+\mu_{2})} \biggr] \bigl\vert \lambda^{0} \bigr\vert \\ =& \biggl[\frac{1+ \mu_{1} b_{k-1}^{(\alpha)}+\mu_{2} b_{k-1}^{(\beta)}+\mu_{1} (1-b_{k-1}^{(\alpha)})+\mu_{2} (1-b_{k-1}^{(\beta)})}{(1+\mu_{1}+\mu_{2})} \biggr] \bigl\vert \lambda^{0} \bigr\vert \\ =& \biggl[\frac{1+\mu_{1} +\mu_{2}}{1+\mu_{1} +\mu_{2}} \biggr] \bigl\vert \lambda^{0} \bigr\vert , \quad \bigl\vert \lambda^{k} \bigr\vert \leq \bigl\vert \lambda^{0} \bigr\vert . \end{aligned}$$
(29)

The proof of Proposition 1 by induction is completed. □

Proposition 1 and equation (23) concluded that the solution of equation (13) satisfies

$$ \bigl\Vert \lambda^{k} \bigr\Vert _{2}\leq \bigl\Vert \lambda^{0} \bigr\Vert _{2}, $$
(30)

this proved that the modified implicit difference scheme in (13) is unconditionally stable.

4 Convergence of the modified implicit scheme

In this section, we analyze the convergence of the modified implicit scheme by following a similar approach as that in Section 3.

Let the exact solution \(u(x_{i}, y_{j}, t_{k})\) be represented by Taylor series, then the truncation error of the modified implicit scheme is obtained as

$$\begin{aligned} R_{i,j}^{k} =& u(x_{i},y_{j},t_{k})-u(x_{i},y_{j}, t_{k-1}) \\ &{}-r_{1} \sum_{s=0}^{k-1}b_{s}^{(\alpha)} \delta x^{2} \bigl(u(x_{i},y_{j},t_{k-s})-u(x_{i},y_{j},t_{k-s-1}) \bigr) \\ &{}-r_{2} \sum_{s=0}^{k-1}b_{s}^{(\alpha)} \delta y^{2} \bigl(u(x_{i},y_{j},t_{k-s})-u(x_{i},y_{j},t_{k-s-1}) \bigr) \\ &{}-r_{3} \sum_{s=0}^{k-1}b_{s}^{(\beta)} \delta x^{2} \bigl(u(x_{i},y_{j},t_{k-s})-u(x_{i},y_{j},t_{k-s-1}) \bigr) \\ &{}-r_{4}\sum_{s=0}^{k-1}b_{s}^{(\beta)} \delta y^{2} \bigl(u(x_{i},y_{j},t_{k-s})-u(x_{i},y_{j},t_{k-s-1}) \bigr)-\tau f(x_{i},y_{j},t_{k}), \end{aligned}$$
(31)

with \(i=1,2,\ldots,M_{x}-1\), \(j=1,2,\ldots,M_{y}-1\), \(k=1,2,\ldots,N\).

From (1), we have

$$\begin{aligned} R_{i,j}^{k} =& \frac{u_{i,j}^{k}-u_{i,j}^{k-1}}{\tau}-\frac{\partial u(x_{i},y_{j},t_{k})}{\partial t}+{}_{0}D_{t}^{1-\alpha} \biggl(\frac{\partial^{2} u(x_{i},y_{j},t_{k})}{\partial x^{2}} \biggr) \\ &{}-r_{1} \sum _{s=0}^{k-1}b_{s}^{(\alpha )}\delta x^{2}\bigl(u_{i,j}^{k-s}-u_{i,j}^{k-s-1} \bigr) +{}_{0}D_{t}^{1-\alpha} \biggl(\frac{\partial^{2} u(x_{i},y_{j},t_{k})}{\partial y^{2}} \biggr) \\ &{}-r_{2} \sum_{s=0}^{k-1}b_{s}^{(\alpha )} \delta y^{2}\bigl(u_{i,j}^{k-s}-u_{i,j}^{k-s-1} \bigr)+{}_{0}D_{t}^{1-\alpha} \biggl(\frac {\partial^{2} u(x_{i},y_{j},t_{k})}{\partial x^{2}} \biggr) \\ &{}-r_{3} \sum_{s=0}^{k-1}b_{s}^{(\beta)} \delta x^{2}\bigl(u_{i,j}^{k-s}-u_{i,j}^{k-s-1} \bigr)+{}_{0}D_{t}^{1-\beta} \biggl(\frac{\partial^{2} u(x_{i},y_{j},t_{k})}{\partial y^{2}} \biggr) \\ &{}-r_{4} \sum_{s=0}^{k-1}b_{s}^{(\beta )} \delta y^{2}\bigl(u_{i,j}^{k-s}-u_{i,j}^{k-s-1} \bigr) \\ =&O\bigl(\tau+\tau(\Delta x)^{2}+\tau(\Delta y)^{2}\bigr). \end{aligned}$$
(32)

Since i, j and k are finite, thus there is a positive constant \(C_{1}\) for all i, j and k, which then leads to

$$ \bigl\vert R_{i,j}^{k} \bigr\vert \leq C_{1} \bigl(\tau+\tau(\Delta x)^{2}+\tau(\Delta y)^{2} \bigr), $$
(33)

with \(i=1,2,\ldots,M_{x}-1\), \(j=1,2,\ldots,M_{y}-1\), \(k=1,2,\ldots,N\). The error is defined as

$$ E_{i,j}^{k}=u(x_{i},y_{j},t_{k})-u_{i,j}^{k}. $$
(34)

From (31), we have

$$\begin{aligned} u(x_{i},y_{j},t_{k}) =&u(x_{i},y_{j},t_{k-1})+r_{1} \bigl(u(x_{i+1},y_{j},t_{k})-2u(x_{i},y_{j},t_{k})+u(x_{i-1},y_{j},t_{k}) \bigr) \\ &{}-r_{1} b_{k-1}^{(\alpha )}\bigl(u(x_{i+1},y_{j},t_{0})-2u(x_{i},y_{j},t_{0})+u(x_{i-1},y_{j},t_{0}) \bigr)+r_{2} \bigl(u(x_{i},y_{j+1},t_{k}) \\ &{}-2u(x_{i},y_{j},t_{k})+u(x_{i},y_{j-1},t_{k}) \bigr)- r_{2} b_{k-1}^{(\alpha )}\bigl(u(x_{i},y_{j+1},t_{0})-2u(x_{i},y_{j},t_{0}) \\ &{}+u(x_{i},y_{j-1},t_{0})\bigr)-\sum _{s=1}^{k-1}\bigl(b_{s-1}^{(\alpha)}-b_{s}^{(\alpha)} \bigr) \bigl(r_{1}\bigl( u(x_{i+1},y_{j},t_{k-s})-2u(x_{i},y_{j},t_{k-s}) \\ &{}+u(x_{i-1},y_{j},t_{k-s})\bigr)+r_{2} \bigl( u(x_{i},y_{j+1},t_{k-s})-2u(x_{i},y_{j},t_{k-s})+u(x_{i},y_{j-1},t_{k-s}) \bigr) \bigr) \\ &{}+r_{3} \bigl(u(x_{i+1},y_{j},t_{k})-2u(x_{i},y_{j},t_{k})+u(x_{i-1},y_{j},t_{k}) \bigr) \\ &{}-r_{3} b_{k-1}^{(\beta )}\bigl(u(x_{i+1},y_{j},t_{0})-2u(x_{i},y_{j},t_{0})+u(x_{i-1},y_{j},t_{0}) \bigr) \\ &{}+r_{4} \bigl(u(x_{i},y_{j+1},t_{k})-2u(x_{i},y_{j},t_{k})+u(x_{i},y_{j-1},t_{k}) \bigr) \\ &{}-r_{4} b_{k-1}^{(\beta )}\bigl(u(x_{i},y_{j+1},t_{0})-2u(x_{i},y_{j},t_{0})+u(x_{i},y_{j-1},t_{0}) \bigr) \\ &{}-\sum_{s=1}^{k-1}\bigl(b_{s-1}^{(\beta)}-b_{s}^{(\beta)} \bigr) \bigl(r_{3} \bigl( u(x_{i+1},y_{j},t_{k-s})-2 u(x_{i},y_{j},t_{k-s})+u(x_{i-1},y_{j},t_{k-s}) \bigr) \\ &{}+r_{4} \bigl( u(x_{i},y_{j+1},t_{k-s})-2 u(x_{i},y_{j},t_{k-s})+u(x_{i},y_{j-1},t_{k-s}) \bigr)\bigr)+\tau f(x_{i},y_{j},t_{k}). \end{aligned}$$
(35)

To obtain the error equation, subtract (35) from (13) to obtain

$$\begin{aligned} E_{i,j}^{k} - E_{i,j}^{k-1} =&r_{1} \bigl(E_{i+1,j}^{k}-2 E_{i,j}^{k}+E_{i-1,j}^{k} \bigr)-r_{1} b_{k-1}^{(\alpha)} \bigl(E_{i+1,j}^{0}-2 E_{i,j}^{0}+E_{i-1,j}^{0}\bigr) \\ &{}+r_{2} \bigl(E_{i,j+1}^{k}-2E_{i,j}^{k}+E_{i,j-1}^{k} \bigr)-r_{2} b_{k-1}^{(\alpha)} \bigl(E_{i,j+1}^{0}-2 E_{i,j}^{0}+E_{i,j-1}^{0}\bigr) \\ &{} -\sum_{s=1}^{k-1}\bigl(b_{s-1}^{(\alpha)}-b_{s}^{(\alpha)} \bigr) \bigl(r_{1} \bigl(E_{i+1,j}^{k-s}-2 E_{i,j}^{k-s}+E_{i-1,j}^{k-s} \bigr)+r_{2} \bigl(E_{i,j+1}^{k-s}-2 E_{i,j}^{k-s}+E_{i,j-1}^{k-s}\bigr) \bigr) \\ &{}+r_{3} \bigl(E_{i+1,j}^{k}-2E_{i,j}^{k}+E_{i-1,j}^{k} \bigr)-r_{3} b_{k-1}^{(\beta)} \bigl(E_{i+1,j}^{0}-2 E_{i,j}^{0}+E_{i-1,j}^{0}\bigr) \\ &{}+r_{4} \bigl(E_{i,j+1}^{k}-2E_{i,j}^{k}+E_{i,j-1}^{k} \bigr)- r_{4} b_{k-1}^{(\beta)} \bigl(E_{i,j+1}^{0}-2 E_{i,j}^{0}+E_{i,j-1}^{0}\bigr) \\ &{}-\sum_{s=1}^{k-1}\bigl(b_{s-1}^{(\beta )}-b_{s}^{(\beta)} \bigr) \bigl(r_{3} \bigl(E_{i+1,j}^{k-s}-2 E_{i,j}^{k-s}+E_{i-1,j}^{k-s}\bigr) \\ &{}+r_{4} \bigl(E_{i,j+1}^{k-s}- 2 E_{i,j}^{k-s}+E_{i,j-1}^{k-s}\bigr) \bigr) + \tau R_{i,j}^{k}, \end{aligned}$$
(36)

with error boundary conditions

$$ E_{0}^{k}=E_{M}^{k}=0, \quad k=1,2, \ldots,N, $$
(37)

and the initial condition

$$ E_{i,j}^{0}=0,\quad i=1,2,\ldots M_{x}, j=1,2, \ldots,M_{y}. $$
(38)

Next, we define the following grid functions for \(k=1,2,\ldots,N\):

$$ E^{k}(x,y)= \textstyle\begin{cases} E_{i,j}^{k},& \mbox{when }x_{i-\frac{\Delta x}{2}}< x\leq x_{i+\frac{\Delta x}{2}}, y_{j-\frac{\Delta y}{2}}< y\leq y_{j+\frac{\Delta y}{2}}, \\ 0,& \mbox{when }0\leq x\leq\frac{\Delta x}{2}\mbox{ or }L-\frac{\Delta x}{2}\leq x\leq L, \\ 0,& \mbox{when }0\leq y\leq\frac{\Delta y}{2}\mbox{ or }L-\frac{\Delta y}{2}\leq y\leq L, \end{cases} $$
(39)

and

$$ R^{k}(x,y)= \textstyle\begin{cases} R_{i,j}^{k}, &\mbox{when }x_{i-\frac{\Delta x}{2}}< x\leq x_{i+\frac{\Delta x}{2}}, y_{j-\frac{\Delta y}{2}}< y\leq y_{j+\frac{\Delta y}{2}}, \\ 0,& \mbox{when }0\leq x\leq\frac{\Delta x}{2}\mbox{ or }L-\frac{\Delta x}{2}\leq x\leq L, \\ 0,& \mbox{when }0\leq y\leq\frac{\Delta y}{2}\mbox{ or }L-\frac{\Delta y}{2}\leq y\leq L, \end{cases} $$
(40)

\(i=1,2,\ldots,M_{x}-1\), \(j=1,2,\ldots,M_{y}-1\), \(k=1,2,\ldots,N\).

Here, \(E^{k}(x,y)\) and \(R^{k}(x,y)\) can be expanded in Fourier series such as

$$\begin{aligned}& E^{k}(x,y)=\sum_{{l_{1},l_{2}}=-\infty}^{\infty} \xi^{k}(l_{1},l_{2})e^{2\sqrt {-1}\pi(l_{1} x/L+l_{2} y/L)},\quad k=1,2, \ldots N, \end{aligned}$$
(41)
$$\begin{aligned}& R^{k}(x,y)=\sum_{{l_{1},l_{2}}=-\infty}^{\infty} \Psi^{k}(l_{1},l_{2})e^{2\sqrt {-1}\pi(l_{1} x/L+l_{2} y/L)},\quad k=1,2, \ldots N, \end{aligned}$$
(42)

where

$$\begin{aligned}& \xi^{k}(l_{1},l_{2})=\frac{1}{L} \int_{0}^{L} \int_{0}^{L} E^{k}(x,y) e^{-2\sqrt{-1}\pi(l_{1} x/L+l_{2} y/L)} \,dx\,dy, \end{aligned}$$
(43)
$$\begin{aligned}& \Psi^{k}(l_{1},l_{2})=\frac{1}{L} \int_{0}^{L} \int_{0}^{L} R^{k}(x,y) e^{-2\sqrt{-1}\pi(l_{1} x/L+l_{2} y/L)} \,dx\,dy. \end{aligned}$$
(44)

From the definition of \(l^{2}\) norm and Parseval’s equality, we have

$$ \bigl\Vert E^{k} \bigr\Vert _{l^{2}}^{2}=\sum _{i=1}^{M_{x}-1} \sum _{j=1}^{M_{y}-1}\Delta x \Delta y \bigl\vert e_{i,j}^{k} \bigr\vert ^{2}=\sum _{{l_{1},l_{2}}={-\infty}}^{\infty} \bigl\vert \rho ^{k}(l_{1},l_{2}) \bigr\vert ^{2}, $$
(45)

and

$$ \bigl\Vert R^{k} \bigr\Vert _{l^{2}}^{2}=\sum _{i=1}^{M_{x}-1} \sum _{j=1}^{M_{y}-1} \Delta x \Delta y \bigl\vert e_{i,j}^{k} \bigr\vert ^{2}=\sum _{{l_{1},l_{2}}={-\infty}}^{\infty} \bigl\vert \Psi ^{k}(l_{1},l_{2}) \bigr\vert . $$
(46)

Based on the above, suppose that

$$\begin{aligned}& E_{i,j}^{k}=\xi^{k}e^{\sqrt{-1}(\sigma_{1} i \Delta x+\sigma_{2} j \Delta y)}, \end{aligned}$$
(47)
$$\begin{aligned}& R_{i,j}^{k}=\Psi^{k}e^{\sqrt{-1}(\sigma_{1} i \Delta x+\sigma_{2} j \Delta y)}, \end{aligned}$$
(48)

respectively, substituting (47) and (48) into (36) gives

$$\begin{aligned} \xi^{k} =&\frac{1}{(1+\mu_{1}+\mu_{2})} \Biggl(\xi^{k-1}+ \bigl( \mu_{1} b_{k-1}^{(\alpha)}+\mu_{2} b_{k-1}^{(\beta)}\bigr)\xi^{0}+\mu_{1} \sum _{s=1}^{k-1}\bigl(b_{s-1}^{(\alpha)}-b_{s}^{(\alpha)} \bigr)\xi^{k-s} \\ &{}+ \mu_{2} \sum_{s=1}^{k-1} \bigl(b_{s-1}^{(\beta)}-b_{s}^{(\beta)}\bigr) \xi^{k-s}+\tau \Psi^{k} \Biggr), \end{aligned}$$
(49)

where \(\mu_{1}\) and \(\mu_{2}\) are mentioned in Section 3.

Proposition 2

Let \(\xi^{k}\) (\(k=1,2,\ldots,N\)) be the solution of (49), then there is a positive constant \(C_{2}\) so that

$$ \bigl\vert \xi^{k} \bigr\vert \leq C_{2}k \tau \bigl\vert \Psi^{1} \bigr\vert . $$

Proof

From \(E^{0}=0\) and (43), we have

$$ \xi^{0}=\xi^{0}(l_{1},l_{2})=0. $$
(50)

From (44) and (46), then there is a positive constant \(C_{2}\) such that

$$ \bigl\vert \Psi^{k} \bigr\vert \leq C_{2} \bigl\vert \Psi^{1} (l_{1}, l_{2}) \bigr\vert . $$
(51)

Using mathematical induction for \(k=1\), then from (49) and (50), we obtain

$$ \xi^{1}=\frac{1}{(1+\mu_{1}+\mu_{2})}\bigl(\tau\Psi^{1}\bigr). $$

Since \(\mu_{1}, \mu_{2}\geq0\), from (51), we get

$$ \bigl\vert \xi^{1} \bigr\vert \leq\tau \bigl\vert \Psi^{1} \bigr\vert \leq C_{2}\tau \bigl\vert \Psi^{1} \bigr\vert . $$
(52)

Now suppose that

$$ \bigl\vert \xi^{m} \bigr\vert \leq C_{2} m\tau \bigl\vert \Psi^{1} \bigr\vert ,\quad m=1,2,\ldots,k-1. $$
(53)

As \(0<\alpha, \beta<1\), from (48), (50) and Lemma 2, we have

$$\begin{aligned} \bigl\vert \xi^{k} \bigr\vert \leq&\frac{|\xi^{k-1}|+\mu_{1} \sum_{s=1}^{k-1}(b_{s-1}^{(\alpha )}-b_{s}^{(\alpha)})|\xi^{k-s}|+\mu_{2} \sum_{s=1}^{k-1}(b_{s-1}^{(\beta )}-b_{s}^{(\beta)})|\xi^{k-s}|+\tau|\Psi^{k}|}{(1+\mu_{1}+\mu_{2})} \\ \leq& \biggl[\frac{( k-1)+(k-1)\mu_{1} \sum_{s=1}^{k-1}(b_{s-1}^{(\alpha )}-b_{s}^{(\alpha)})+(k-1) \mu_{2} \sum_{s=1}^{k-1}(b_{s-1}^{(\beta )}-b_{s}^{(\beta)})+1}{(1+\mu_{1}+\mu_{2})} \biggr]C_{2} \tau\bigl|\Psi^{1}\bigr| \\ =& \biggl[\frac{ (k-1) (1+\mu_{1} (1-b_{k-1}^{(\alpha)})+ \mu_{2} (1-b_{k-1}^{(\beta)}) )+1}{(1+\mu_{1}+\mu_{2})} \biggr]C_{2} \tau \bigl\vert \Psi^{1} \bigr\vert . \end{aligned}$$

As \(\mu_{1}, \mu_{2}\geq0\) and \((1- b_{k-1})\geq0\), for all values, so

$$ \leq k C_{2} \tau \bigl\vert \Psi^{1} \bigr\vert . $$
(54)

The proof of Proposition 2 by induction is completed. □

Theorem 1

The modified implicit difference scheme is \(l^{2}\) convergent and the order of convergence is \(O(\tau+\tau(\Delta x)^{2}+\tau(\Delta y)^{2})\).

Proof

From (32) and (46), we obtain

$$ \bigl\Vert R^{k} \bigr\Vert \leq\sqrt{M \Delta x \Delta y} C_{1}\bigl(\tau+\tau(\Delta x)^{2}+\tau (\Delta y)^{2}\bigr)=L C_{1}\bigl(\tau+\tau(\Delta x)^{2}+ \tau(\Delta y)^{2}\bigr). $$
(55)

In view of Proposition 2, (45), (46) and (55)

$$ \bigl\Vert E^{k} \bigr\Vert _{l^{2}}\leq k C_{2} \tau \bigl\Vert R^{1} \bigr\Vert \leq C_{1} C_{2} k \tau L\bigl(\tau+\tau (\Delta x)^{2}+\tau(\Delta y)^{2}\bigr), $$
(56)

as \(k \tau\leq R\), thus

$$ \bigl\Vert E^{k} \bigr\Vert _{l^{2}}\leq C_{1} C_{2} R L\bigl(\tau+\tau(\Delta x)^{2}+\tau(\Delta y)^{2}\bigr), $$
(57)

where \(C=C_{1} C_{2} R L\).

This completes the proof of the theorem. □

5 Numerical experiments

In this section, we solve a numerical example to test the theoretical analysis. The maximum errors between the numerical solution and the exact solution are compared with the mentioned references, i.e., the maximum error is defined as follows:

$$ E_{\infty}=\max_{0\leq i\leq M_{x}-1,0\leq j\leq M_{y}-1,0\leq k\leq N } \bigl\vert u(x_{i},y_{j},t_{k})-u_{i,j}^{k} \bigr\vert . $$
(58)

Example 1

Consider the following two-dimensional modified anomalous fractional sub-diffusion equation [18]:

$$ \frac{\partial u(x,y,t)}{\partial t}= \biggl(\frac{\partial^{1-\alpha} }{\partial t^{1-\alpha}}+\frac{\partial^{1-\beta} }{\partial t^{1-\beta }} \biggr) \biggl[ \frac{\partial^{2} u(x,y,t)}{\partial x^{2}}+\frac{\partial^{2} u(x,y,t)}{\partial y^{2}} \biggr]+f(x,y,t), \quad 0\leq t\leq T, $$
(59)

where

$$\begin{aligned} f(x,y,t) =&\sin(x+y) \biggl((1+\alpha+\beta) t^{\alpha+\beta}+ \frac{2\Gamma (2+\alpha+\beta)}{\Gamma(1+2\alpha+\beta)}t^{2\alpha+\beta} \\ &{}+\frac{2\Gamma(2+\alpha+\beta)}{\Gamma(1+\alpha+2\beta)}t^{\alpha+2\beta } \biggr), \end{aligned}$$

subject to the initial and boundary conditions

$$\begin{aligned}& u(x,y,0)=0, \quad 0\leq x,y\leq1, \end{aligned}$$
(60)
$$\begin{aligned}& u(0,y,t)=t^{1+\alpha+\beta} \sin(y),\qquad u(L,y,t)=t^{1+\alpha+\beta} \sin(L+y), \\& u(x,0,t)=t^{1+\alpha+\beta} \sin(x), \qquad u(x,L,t)=t^{1+\alpha+\beta} \sin(L+x), \\& \quad 0\leq x,y\leq L, 0\leq t\leq T. \end{aligned}$$
(61)

The exact solution is given by

$$ u(x,t)=t^{1+\alpha+\beta} \sin(x+y). $$
(62)

The developed modified implicit scheme is applied to problem (59)-(61). Table 1 shows the errors \(E_{\infty}\) at \(T=1.0\) for the space step size \(\Delta x=\Delta y=\frac{1}{10}\) and for various values of τ. Note that the time step τ is defined by \(\tau =\frac{T}{N}\).

Table 1 Comparison of numerical methods at \(\pmb{T=1.0}\) , \(\pmb{\Delta x=\Delta y=\frac{1}{10}}\) , \(\pmb{\alpha=0.25}\) , \(\pmb{\beta=0.45}\)
Full size table

In Tables 1 and 2, the numerical results seem to confirm our theoretical analysis for various values of time step size τ, α and β.

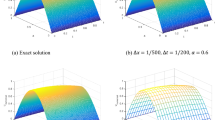
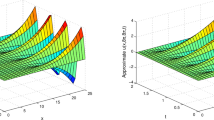
Table 2 Comparison of numerical methods at \(\pmb{T=1.0}\) , \(\pmb{\Delta x=\Delta y=\frac{1}{10}}\) , \(\pmb{\alpha=0.75}\) , \(\pmb{\beta=0.85}\)
Full size table

Figures 1 and 2 show the numerical solution of equation (59) and compare it with the exact solution at \(\alpha=0.25, 75\), \(\beta=0.45, 0.85\), \(y=0.1\) and \(T=1.0\), respectively. It can be seen that the numerical solution is in excellent agreement with the exact solution. These results proved our theoretical analysis.

Figure 1
figure 1

Comparison of the numerical scheme ( 59 ) and the exact solution ( 44 ) at \(\pmb{\alpha=0.75}\) , \(\pmb{\beta=0.75}\) , \(\pmb{T=1}\) , \(\pmb{y=0.1}\) and \(\pmb{N=80}\) .

Full size image
Figure 2
figure 2

Comparison of the numerical scheme ( 59 ) and the exact solution ( 44 ) at \(\pmb{\alpha=0.25}\) , \(\pmb{\beta=0.45}\) , \(\pmb{T=1}\) , \(\pmb{y=0.1}\) and \(\pmb{N=160}\) .

Full size image

6 Conclusion

A modified implicit difference scheme for two-dimensional modified anomalous fractional sub-diffusion equation has been described in this paper. The modified scheme has the advantage of low complexity, low computation and it is easy to implement. We have used the Fourier series method and found that the scheme with convergence order \((\tau +\tau(\Delta x)^{2}+\tau(\Delta y)^{2})\) is unconditionally stable and convergent. The result of an application to a particular example has been discussed graphically and numerically. A comparison of the numerical methods with the proposed scheme for the example has shown that the scheme is feasible and accurate. This technique can also be extended to explicit and Crank-Nicolson method and can be applied to other types of fractional differential equations.