1 Introduction

Fractional calculus deals with derivatives and integrals of arbitrary real or complex order [1]. This subject has attracted attention of many scientists in mathematics, physics and engineering. So, it has become a hot issue in recent years. However, fractional calculus extends the notion of derivative for those cases that the derivative order is not integer. Many phenomena in engineering and applied sciences can be described successfully by developing models using fractional calculus, such as material science and mechanics, anomalous diffusion, signal processing, finance, biological systems, hydrology [1,2,3,4,5,6,7,8]. The interested reader is referred to [9,10,11,12,13,14,15,16,17,18,19,20] for recent developments in fractional calculus and its applications.

Anomalous diffusion equations are an important class of fractional differential equations, which have been widely applied in modeling of anomalous diffusive systems, unification of diffusion, description of fractional random walk and wave propagation phenomenon, etc. [21].

The fractional sub-diffusion equation, which is obtained by replacing the time derivative in ordinary diffusion by a fractional derivative of order ϑ with \(0 < \vartheta < 1\), has been observed in numerous complex system, such as biopolymers, polymers, liquid crystals, organisms, proteins, ecosystems, and fractal and percolation clusters [22]. Some analytical and numerical solutions of sub-diffusion equations have been proposed in [23,24,25,26,27,28,29,30,31,32,33,34,35,36]. An implicit difference approximation is suggested by Zhuang and Liu for solving two-dimensional space-time and time fractional diffusion equations [37, 38]. In [39], Liu et al. have developed an implicit meshless approach based on the radial basis functions for solving two-dimensional time fractional diffusion equations. In [40], Chen et al. have constructed a two-dimensional anomalous sub-diffusion equation. In [41], Zhang and Sun have proposed two numerical techniques for solving the solution of a two-dimensional anomalous sub-diffusion equation with a time fractional derivative.

It is worth noting that the computational complexity and CPU time are the main problems of applying the numerical algorithms for solving high-dimensional equations, particularly for the systems defined on the large domain. It motivates our interest to propose an efficient and accurate method to avoid the mentioned issue in such problems. Based on the above discussions, the main objective of this paper is to propose an efficient and accurate method based on the VIM upgraded by an auxiliary parameter for solving the following three-dimensional modified anomalous sub-diffusion equation:

$$\begin{aligned} \frac{\partial u(x,y,z,t)}{\partial t} =& \biggl(\mathcal{A}\frac{ \partial ^{1-\alpha }}{\partial t^{1-\alpha }}+ \mathcal{B} \frac{ \partial ^{1-\beta }}{\partial t^{1-\beta }}+\mathcal{C}\frac{ \partial ^{1-\gamma }}{\partial t^{1-\gamma }} \biggr) \\ &{}\times \biggl[ \frac{ \partial ^{2}u(x,y,z,t)}{\partial x^{2}}+\frac{\partial ^{2}u(x,y,z,t)}{ \partial y^{2}}+ \frac{\partial ^{2}u(x,y,z,t)}{\partial z^{2}} \biggr] \\ &{}+g(x,y,z,t), \quad (x,y,z,t)\in \varOmega , \end{aligned}$$
(1.1)

where \(\varOmega =[0,a]\times [0,b]\times [0,c]\times [0,T]\), with the initial condition

$$ u(x,y,z,0)=\phi (x,y,z), $$
(1.2)

where \(0<\alpha \), \(\beta , \gamma <1\) and \(\mathcal{A}\), \(\mathcal{B}\), \(\mathcal{C}\) are the positive constants. The symbols \(\frac{ \partial ^{1-\alpha }}{\partial t^{1-\alpha }}\), \(\frac{\partial ^{1- \beta }}{\partial t^{1-\beta }}\) and \(\frac{\partial ^{1-\gamma }}{ \partial t^{1-\gamma }}\) are the Riemann–Liouville fractional derivative operators, defined as follows:

$$ \textstyle\begin{cases} \frac{\partial ^{1-\alpha }u(x,y,z,t)}{\partial t^{1-\alpha }}=\frac{1}{ \varGamma (\alpha )}\frac{\partial }{\partial t}\int _{0}^{t}\frac{u(x,y,z,s)}{(t-s)^{1- \alpha }}\,ds, \\ \frac{\partial ^{1-\beta }u(x,y,z,t)}{\partial t^{1-\beta }}=\frac{1}{ \varGamma (\beta )}\frac{\partial }{\partial t}\int _{0}^{t}\frac{u(x,y,z,s)}{(t-s)^{1- \beta }}\,ds, \\ \frac{\partial ^{1-\gamma }u(x,y,z,t)}{\partial t^{1-\gamma }}=\frac{1}{ \varGamma (\gamma )}\frac{\partial }{\partial t}\int _{0}^{t}\frac{u(x,y,z,s)}{(t-s)^{1- \gamma }}\,ds. \end{cases} $$
(1.3)

The VIM was proposed by Ji-Huan He [42] as a modification of general Lagrange multipliers method [43]. The main characteristic of the method is the flexibility and the ability to obtain solutions of nonlinear equations accurately and conveniently [44,45,46]. It is worth noting that the identification of Lagrange multipliers is very important in the VIM, but the main problem in the fractional calculus is that the integral by parts in integer order case cannot hold in fractional calculus. The interested reader can consult [47, 48] to identify the Lagrange multiplier by use of the Laplace transform. We recall that there are many modifications of the VIM, among which the Herisanu and Marincas modification is much more attractive, where the VIM is coupled with the least squares method, and it should be noted that one iteration leads to ideal results [49]. In [46], Yilmaz and Inc constructed a variational iteration algorithm, where an auxiliary parameter was introduced to adjust the convergence rate, but they did not give a general rule for the best choice of the auxiliary parameter. This modification was further developed by Hosseini et al., which gave some profitable rules for optimally determination of the auxiliary parameter [50,51,52,53].

In the present paper VIM with an auxiliary parameter is successfully used to obtain an approximate solution of three-dimensional modified anomalous fractional sub-diffusion equation on the large domains. The residual function and its norm two error are defined to choose the auxiliary parameter optimally. The obtained results confirm the reliability and efficiency of the proposed method for such problems on the large domains.

The paper is organized as follows: In Sect. 2, the VIM and VIM with an auxiliary parameter are described. In Sect. 3, the proposed method is described for solving three-dimensional modified anomalous fractional sub-diffusion equation. In Sect. 4, the convergence of the VIM with an auxiliary parameter is discussed. In Sect. 5, some numerical examples are chosen to investigate the applicability of the described approach. Finally, a conclusion is drawn in Sect. 6.

2 The VIM and VIM with an auxiliary parameter

In this section, we briefly review the standard VIM and then the VIM upgraded by an auxiliary parameter.

To illustrate the basic concepts of the VIM, we consider the following partial deferential equation (PDE):

$$ \mathcal{L}u(x,y,z,t)+\mathcal{N}u(x,y,z,t)=g(x,y,z,t), $$
(2.1)

where \(\mathcal{L}\) is a linear operator, \(\mathcal{N}\) is a nonlinear operator, and g is the source term.

In the VIM, a correction functional for Eq. (2.1) can be written as follows:

$$\begin{aligned}& u_{n+1}(x,y,z,t) \\& \quad =u_{n}(x,y,z,t)+ \int _{0}^{t}\lambda (s) \bigl\{ \mathcal{L}u _{n}(x,y,z,s)+\mathcal{N}\widetilde{u}_{n}(x,y,z,s)-g(x,y,z,s) \bigr\} \,ds, \end{aligned}$$
(2.2)

where λ is a general Lagrange multiplier, which can be identified optimally via the variational theory, \(u_{n}\) is the nth approximate solution, and \(\widetilde{u}_{n}\) denotes a restricted variation, which means \(\delta \widetilde{u}_{n}=0\). After identification of the multiplier, a variational iteration algorithm is constructed as

$$ u(x,y,z,t)=\lim_{n\rightarrow \infty } u_{n}(x,y,z,t). $$
(2.3)

Accordingly, the following variational iteration formula for (2.1) is highlighted as

$$ \textstyle\begin{cases} u_{0}(x,y,z,t) \text{ is an initial approximation}, \\ u_{n+1}(x,y,z,t) \\ \quad =u_{n}(x,y,z,t)+\int _{0}^{t}\lambda (s) \{\mathcal{L}u _{n}(x,y,z,s)+\mathcal{N}u_{n}(x,y,z,s)-g(x,y,z,s) \}\,ds,\quad n \geq 0. \end{cases} $$
(2.4)

Considering Eq. (2.4), an auxiliary parameter h can be inserted into the variational iteration algorithm, to obtain

$$ \textstyle\begin{cases} u_{0}(x,y,z,t) \text{ is an initial approximation}, \\ u_{1}(x,y,z,t,h) \\ \quad =u_{0}(x,y,z,t)+h\int _{0}^{t}\lambda (s) \{\mathcal{L}u _{0}(x,y,z,s)+\mathcal{N}u_{0}(x,y,z,s)-g(x,y,z,s) \}\,ds, \\ u_{n+1}(x,y,z,t,h) \\ \quad =u_{n}(x,y,z,t,h)+h\int _{0}^{t}\lambda (s) \{\mathcal{L}u _{n}(x,y,z,s,h)+\mathcal{N}u_{n}(x,y,z,s,h)-g(x,y,z,s) \}\,ds, \\ \qquad n\geq 1. \end{cases} $$
(2.5)

The approximate solutions \(u_{n+1}(x,y,z,t,h)\), \(n \geq 1\) contain the unknown auxiliary parameter h. The validity of the method is based on the assumption that the approximation \(u_{n+1} (x,y,z,t,h)\), \(n \geq 1\) converges to the exact solution. It is the auxiliary parameter which ensures that this assumption can be satisfied. In general, by means of the error of norm two of the residual function, it is straightforward to choose a proper value for h which approves that the approximate solutions are convergent. In fact, the described methodology approximates the solution more accurately on a large area.

3 Implementation of the proposed method

We construct an iteration formula by applying Eqs. (1.1) and (2.1) as follows:

$$\begin{aligned}& u_{n+1}(x,y,z,t) \\& \quad =u_{n}(x,y,z,t)+ \int _{0}^{t}\lambda (s)\biggl\{ \frac{ \partial u_{n}(x,y,z,s)}{\partial s}- \biggl(\mathcal{A}\frac{ \partial ^{1-\alpha }}{\partial s^{1-\alpha }}+\mathcal{B} \frac{ \partial ^{1-\beta }}{\partial s^{1-\beta }}+\mathcal{C}\frac{ \partial ^{1-\gamma }}{\partial s^{1-\gamma }} \biggr) \\& \qquad {}\times \biggl[\frac{\partial ^{2}u_{n}(x,y,z,s)}{\partial x^{2}}+\frac{ \partial ^{2}u_{n}(x,y,z,s)}{\partial y^{2}}+ \frac{\partial ^{2}u_{n}(x,y,z,s)}{ \partial z^{2}} \biggr]-g(x,y,z,s)\biggr\} \,ds. \end{aligned}$$
(3.1)

By taking the variation with respect to \(u_{n}\) and noticing that \(\delta u_{n}(x,y,z,0)=0\), we obtain the stationary conditions

$$ \textstyle\begin{cases} 1+\lambda (s)|_{s=t}=0, \\ \lambda ^{\prime }(s)=0. \end{cases} $$
(3.2)

The Lagrangian multiplier can consequently be identified as, \(\lambda (s)=-1\). Substituting \(\lambda (s)=-1\) into the correction functional equation system (3.1) results in the following iteration formula:

$$\begin{aligned} \textstyle\begin{cases} u_{0}(x,y,z,t) \text{ is an initial approximation}, \\ u_{n+1}(x,y,z,t) \\ \quad =u_{n}(x,y,z,t)-\int _{0}^{t}\{\frac{\partial u _{n}(x,y,z,s)}{\partial s}- (\mathcal{A}\frac{\partial ^{1-\alpha }}{\partial s^{1-\alpha }}+\mathcal{B}\frac{\partial ^{1-\beta }}{ \partial s^{1-\beta }}+\mathcal{C}\frac{\partial ^{1-\gamma }}{\partial s^{1-\gamma }} ) \\ \qquad {}\times[\frac{\partial ^{2}u_{n}(x,y,z,s)}{\partial x^{2}}+\frac{\partial ^{2}u_{n}(x,y,z,s)}{\partial y^{2}}+\frac{ \partial ^{2}u_{n}(x,y,z,s)}{\partial z^{2}} ]-g(x,y,z,s)\}\,ds, \quad n\geq 1. \end{cases}\displaystyle \end{aligned}$$

So the VIM with an auxiliary parameter is defined as

$$ \textstyle\begin{cases} u_{0}(x,y,z,t) \text{ is an initial approximation}, \\ u_{1}(x,y,z,t,h) \\ \quad =u_{0}(x,y,z,t)-h\int _{0}^{t}\{\frac{\partial u _{0}(x,y,z,s)}{\partial s}- (\mathcal{A}\frac{\partial ^{1-\alpha }}{\partial s^{1-\alpha }}+\mathcal{B}\frac{\partial ^{1-\beta }}{ \partial s^{1-\beta }}+\mathcal{C}\frac{\partial ^{1-\gamma }}{\partial s^{1-\gamma }} ) \\ \qquad {}\times[\frac{\partial ^{2}u_{0}(x,y,z,s)}{\partial x^{2}}+\frac{\partial ^{2}u_{0}(x,y,z,s)}{\partial y^{2}}+\frac{ \partial ^{2}u_{0}(x,y,z,s)}{\partial z^{2}} ]-g(x,y,z,s)\}\,ds, \\ u_{n+1}(x,y,z,t,h) \\ \quad =u_{n}(x,y,z,t,h)-h\int _{0}^{t}\{\frac{\partial u_{n}(x,y,z,s,h)}{\partial s}- (\mathcal{A}\frac{\partial ^{1- \alpha }}{\partial s^{1-\alpha }}+\mathcal{B}\frac{\partial ^{1-\beta }}{\partial s^{1-\beta }}+\mathcal{C}\frac{\partial ^{1-\gamma }}{ \partial s^{1-\gamma }} ) \\ \qquad {}\times[\frac{\partial ^{2}u_{n}(x,y,z,s,h)}{ \partial x^{2}}+\frac{\partial ^{2}u_{n}(x,y,z,s,h)}{\partial y^{2}}+\frac{ \partial ^{2}u_{n}(x,y,z,s,h)}{\partial z^{2}} ]-g(x,y,z,s)\}\,ds, \quad n\geq 1. \end{cases} $$
(3.3)

By starting from \(u_{0}(x,y,z,t)=u(x,y,z,0)\), and using the iterative formula (3.3) for the first few \(n=N\) iterations, we obtain an approximate solution \(u(x,y,z,t)\simeq u_{N}(x,y,z,t,h)\) with an unknown suitable h. In order to find a proper value for h to obtain an accurate approximate solution, we define the following residual function:

$$\begin{aligned}& r_{N}(x,y,z,t,h) \\& \quad = \frac{\partial u_{N}(x,y,z,t,h)}{\partial t}- \biggl(\mathcal{A} \frac{ \partial ^{1-\alpha }}{\partial t^{1-\alpha }}+ \mathcal{B}\frac{ \partial ^{1-\beta }}{\partial t^{1-\beta }}+\mathcal{C} \frac{ \partial ^{1-\gamma }}{\partial t^{1-\gamma }} \biggr) \\& \qquad {}\times\biggl[\frac{ \partial ^{2}u_{N}(x,y,z,t,h)}{\partial x^{2}}+ \frac{\partial ^{2}u_{N}(x,y,z,t,h)}{ \partial y^{2}} + \frac{\partial ^{2}u_{N}(x,y,z,t,h)}{\partial z^{2}}\biggr]-g(x,y,z,t), \end{aligned}$$

and the following error of norm two of the residual function:

$$ e_{N}(h)= \biggl( \int _{0}^{T} \int _{0}^{c} \int _{0}^{b} \int _{0}^{a}r_{N} ^{2}(x,y,z,t,h)\, dx\, dy\, dz\, dt \biggr)^{\frac{1}{2}}. $$

Now we apply a numerical integration scheme to calculate \(e_{N}(h)\), approximately. Note that the optimal value of h minimizes the norm two of the residual function.

4 Convergence of the proposed method

Now we investigate the convergence of the proposed method for three-dimensional equation. In the sequel, the linear operator is \(\mathcal{L}=\frac{\partial }{\partial t}\). Also, we define the operator \(\mathcal{F}\) as follows:

$$ \mathcal{F}u(x,y,z,t,h)=-h \int _{0}^{t}\mathcal{R}u(x,y,z,s,h)\,ds, $$
(4.1)

where

$$\begin{aligned}& \mathcal{R}u(x,y,z,t,h) \\& \quad =\frac{\partial u(x,y,z,t,h)}{\partial t}- \biggl(\mathcal{A} \frac{\partial ^{1-\alpha }}{\partial t^{1-\alpha }}+ \mathcal{B}\frac{\partial ^{1-\beta }}{\partial t^{1-\beta }}+ \mathcal{C} \frac{\partial ^{1-\gamma }}{\partial t^{1-\gamma }} \biggr) \\& \qquad {}\times\biggl[\frac{\partial ^{2}u(x,y,z,t,h)}{\partial x^{2}}+ \frac{\partial ^{2}u(x,y,z,t,h)}{\partial y^{2}} + \frac{\partial ^{2}u(x,y,z,t,h)}{\partial z^{2}}\biggr]-g(x,y,z,t). \end{aligned}$$

Moreover, the recurrence scheme can be defined as follows:

$$ \textstyle\begin{cases} v_{0}(x,y,z,t)=u_{0}(x,y,z,t), \\ s_{0}(x,y,z,t)= v_{0}(x,y,z,t), \end{cases}\displaystyle \quad \mbox{and} \quad \textstyle\begin{cases} v_{1}(x,y,z,t,h)=\mathcal{F}s_{0}(x,y,z,t), \\ s_{1}(x,y,z,t,h)= s_{0}(x,y,z,t)+v_{1}(x,y,z,t,h), \end{cases} $$

and in general for \(n\geq 1\),

$$ \textstyle\begin{cases} v_{n+1}(x,y,z,t,h)=\mathcal{F}s_{n}(x,y,z,t,h), \\ s_{n+1}(x,y,z,t,h)= s_{n}(x,y,z,t,h)+v_{n+1}(x,y,z,t,h). \end{cases} $$
(4.2)

Consequently we have

$$ u(x,y,z,t,h)=\lim_{n\rightarrow \infty } s_{n}(x,y,z,t,h)=v_{0}(x,y,z,t)+ \sum _{n=1}^{\infty }v_{n}(x,y,z,t,h). $$
(4.3)

The initial approximation \(u_{0}(x,y,z,t)\) can be freely chosen and the only restriction is satisfaction of the given initial conditions defined in (2) with \(\mathcal{L}u_{0}(x,y,z,t)= 0\). For the approximation purpose, the solution \(u(x,y,z,t,h)=v_{0}(x,y,z,t)+\sum_{n=1}^{\infty }v_{n}(x,y,z,t,h)\) is approximated by the Nth-order truncated series \(u_{N}(x,y,z,t,h)=v_{0}(x,y,z,t)+\sum_{n=1}^{N}v_{n}(x,y,z,t,h)\). The approximate solution \(u_{N}(x,y,z,t,h)\) contains the auxiliary parameter h. It is the auxiliary parameter which ensures that the assumption can be satisfied by means of the error of norm two of the residual function. The following theorems provide the sufficient conditions for convergence and validity of the proposed method.

Theorem 4.1

Let H be a real Hilbert space and \(\mathcal{F}\) be an operator on H. If there is \(h^{\ast }\neq 0\) and \(0<\xi <1\) such that

$$ \textstyle\begin{cases} \Vert \mathcal{F}s_{0}(x,y,z,t) \Vert \leq \xi \Vert s_{0}(x,y,z,t) \Vert , \\ \Vert \mathcal{F}s_{1}(x,y,z,t,h^{\ast }) \Vert \leq \xi \Vert \mathcal{F}s_{0}(x,y,z,t) \Vert , \\ \Vert \mathcal{F}s_{n}(x,y,z,t,h^{\ast }) \Vert \leq \xi \Vert \mathcal{F}s_{n-1}(x,y,z,t,h^{\ast }) \Vert ,\quad n=2,3,\ldots , \end{cases} $$
(4.4)

then the series solution defined in (4.3) with

$$ u(x,y,z,t,h)=\lim_{n\rightarrow \infty } s_{n} \bigl(x,y,z,t,h^{\ast } \bigr)=v _{0}(x,y,z,t)+\sum _{n=1}^{\infty }v_{n} \bigl(x,y,z,t,h^{\ast } \bigr) $$
(4.5)

converges.

Proof

The proof is straightforward by noting the proof of Theorem 4.1 in [53]. □

Theorem 4.2

Let \(\mathcal{L}=\frac{\partial }{\partial t}\). If we have \(u(x,y,z,t)=v _{0}(x,y,z,t)+\sum_{n=1}^{\infty }v_{n}(x,y,z,t,h^{\ast })\), then \(u(x,y,z,t)\), is the exact solution of the problem (1.1).

Proof

The proof is straightforward by noting the proof of Theorem 4.2 in [53]. □

Theorem 4.3

Suppose that the series solution \(u(x,y,z,t)=v_{0}(x,y,z,t)+\sum_{n=1} ^{\infty }v_{n}(x,y,z,t, h^{\ast })\) defined in (4.3), is convergent to the exact solution of the problem (1.1). If the truncated series \(u_{N}(x,y,z,t)=v_{0}(x,y,z,t)+\sum_{n=1}^{N}v_{n}(x,y,z,t,h ^{\ast })\), is used as an approximate solution, then the maximum error is estimated as

$$ \bigl\Vert u(x,y,z,t)-u_{N}(x,y,z,t) \bigr\Vert \leq \frac{1}{1-\xi }\xi ^{N+1} \Vert v_{0} \Vert . $$

Proof

The proof is straightforward by noting the proof of Theorem 4.3 in [53]. □

5 Numerical examples

In this section, some test problems are provided to investigate the practical computational efficiency and reliability of the proposed method.

Example 1

Consider the following three-dimensional modified anomalous fractional sub-diffusion equation:

$$\begin{aligned}& \frac{\partial u(x,y,z,t)}{\partial t} \\& \quad = \biggl(\frac{\partial ^{1- \alpha }}{\partial t^{1-\alpha }} + \frac{\partial ^{1-\beta }}{\partial t^{1-\beta }}+ \frac{\partial ^{1-\gamma }}{\partial t^{1-\gamma }} \biggr) \biggl[\frac{\partial ^{2}u(x,y,z,t)}{\partial x^{2}} + \frac{\partial ^{2}u(x,y,z,t)}{\partial y^{2}}+ \frac{\partial ^{2}u(x,y,z,t)}{\partial z^{2}} \biggr] \\& \qquad {}+g(x,y,z,t),\quad (x,y,z,t)\in \varOmega , \end{aligned}$$
(5.1)

where

$$\begin{aligned} g(x,y,z,t) =&\sin ( x+y+z ) \biggl( ( 1+\alpha + \beta +\gamma ) {t}^{ \alpha +\beta +\gamma }+3 {\frac{ \varGamma ( 2+\alpha +\beta +\gamma )}{\varGamma ( 1+2 \alpha +\beta +\gamma ) }} {t}^{2 \alpha +\beta +\gamma } \\ &{}+3 { \frac{\varGamma ( 2+\alpha +\beta +\gamma ) }{ \varGamma ( 1+\alpha +2 \beta +\gamma ) }} {t}^{\alpha +2 \beta +\gamma }+3 { \frac{\varGamma ( 2+\alpha +\beta +\vartheta )}{\varGamma ( 1+\alpha +\beta +2 \vartheta ) }} {t}^{\alpha +\beta +2 \vartheta } \biggr), \end{aligned}$$

with the initial condition \(u(x,y,z,0)=0\), which admits the exact solution \(u(x,y,z,t)={t}^{1+\alpha +\beta +\gamma }\sin (x+y+z )\).

Take \(\varOmega =[0,8\pi ]\times [0,8\pi ]\times [0,8\pi ]\times [0,2]\). According to the standard VIM, we have the following variational iteration formula:

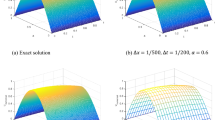
$$\begin{aligned}& u_{n+1}(x,y,z,t) \\& \quad =u_{n}(x,y,z,t)- \int _{0}^{t}\biggl\{ \frac{\partial u _{n}(x,y,z,s)}{\partial s}- \biggl(\frac{\partial ^{1-\alpha }}{\partial s^{1-\alpha }}+\frac{\partial ^{1-\beta }}{\partial s^{1-\beta }}+ \frac{ \partial ^{1-\gamma }}{\partial s^{1-\gamma }} \biggr) \\& \qquad {}\times \biggl[\frac{\partial ^{2}u_{n}(x,y,z,s)}{\partial x^{2}}+\frac{ \partial ^{2}u_{n}(x,y,z,s)}{\partial y^{2}}+ \frac{\partial ^{2}u_{n}(x,y,z,s)}{ \partial z^{2}} \biggr]-g(x,y,z,s)\biggr\} \,ds,\quad n\geq 0. \end{aligned}$$

By starting the solution procedure from \(u_{0}(x,y,z,t)=u(x,y,z,0)=0\), we may stop at \(u_{7}(x,y,z,t)\). The graphs of the approximate solution and the absolute error function of \(u_{7}(x,8\pi ,8\pi ,t)\) for \((x,t)\in [0,8\pi ]\times [0,2]\) and \((\alpha =\beta =\frac{1}{4}, \gamma =\frac{1}{2})\) are shown in Figs. 1 and 2 (left side), respectively. Also, the graphs of the absolute error function of \(u_{7}(x,8\pi ,8\pi ,0.5)\) and \(u_{7}(x,8\pi ,8\pi ,1.5)\) for \(x\in [0,8\pi ]\) are shown in Figs. 3 and 4 (left side), respectively. From these figures it can be seen that \(u_{7}(x,y,z,t)\) is not accurate for the large values of x, y, z and t. Now, by applying the recurrence scheme (3.3), we successively have

$$\begin{aligned}& u_{0}(x,y,z,t) =u(x,y,z,0)=0, \\& u_{1}(x,y,z,t,h) \\& \quad =h\sin ( x+y+z ) \biggl(3 \frac{\varGamma (2+\alpha +\beta +\gamma )}{\varGamma (2+2 \alpha +\beta +\gamma )} t ^{1+2 \alpha +\beta +\gamma } +3 \frac{\varGamma (2+\alpha +\beta + \gamma )}{\varGamma (2+\alpha +2 \beta +\gamma )} t^{1+\alpha +2 \beta +\gamma } \\& \qquad {}+3 \frac{\varGamma (2+\alpha +\beta +\gamma )}{\varGamma (2+ \alpha +\beta +2 \gamma )} t^{1+\alpha +\beta +\gamma }+t^{1+\alpha +\beta +2 \gamma }\biggr), \end{aligned}$$

and in general

$$\begin{aligned}& u_{n+1}(x,y,z,t,h) \\& \quad =u_{n}(x,y,z,t,h)-h \int _{0}^{t}\biggl\{ \frac{\partial u_{n}(x,y,z,s,h)}{\partial s}- \biggl(\frac{\partial ^{1-\alpha }}{ \partial s^{1-\alpha }}+\frac{\partial ^{1-\beta }}{\partial s^{1- \beta }}+ \frac{\partial ^{1-\gamma }}{\partial s^{1-\gamma }} \biggr) \\& \qquad {}\times \biggl[\frac{\partial ^{2}u_{n}(x,y,z,s,h)}{\partial x^{2}}+\frac{\partial ^{2}u_{n}(x,y,z,s,h)}{\partial y^{2}}+ \frac{ \partial ^{2}u_{n}(x,y,z,s,h)}{\partial z^{2}} \biggr]-g(x,y,z,s)\biggr\} \,ds, \\& \qquad n\geq 1. \end{aligned}$$

In order to find a proper value for h to obtain an accurate approximate solution of (5.1), we define the following residual function:

$$\begin{aligned}& r_{7}(x,y,z,t,h) \\& \quad =\frac{\partial u_{7}(x,y,z,t,h)}{\partial t}- \biggl( \frac{ \partial ^{1-\alpha }}{\partial t^{1-\alpha }}+ \frac{\partial ^{1- \beta }}{\partial t^{1-\beta }}+\frac{\partial ^{1-\gamma }}{\partial t^{1-\gamma }} \biggr) \\& \qquad {}\times\biggl[\frac{\partial ^{2}u_{7}(x,y,z,t,h)}{ \partial x^{2}}+\frac{\partial ^{2}u_{7}(x,y,z,t,h)}{\partial y^{2}} + \frac{\partial ^{2}u_{7}(x,y,z,t,h)}{\partial z ^{2}}\biggr]-g(x,y,z,t), \end{aligned}$$

and the following error defined based on the norm two of residual function:

$$ e_{7}(h)= \biggl( \int _{0}^{2} \int _{0}^{8\pi } \int _{0}^{8\pi } \int _{0} ^{8\pi }r_{7}^{2}(x,y,z,t,h) \, dx\, dy\, dz\, dt \biggr)^{\frac{1}{2}}. $$

The minimum point of \(e_{7}(h)\) when \((\alpha =\beta =\frac{1}{4}, \gamma =\frac{1}{2})\) is obtained at \(h\simeq 0.18\) by using Maple software. Substituting \(h =0.18\) in \(u_{7}(x,8\pi ,8\pi ,t,h)\), reduces the absolute error of the 7th-step remarkably. The graphs of the approximate solution and the absolute error functions of \(u_{7}(x,8 \pi ,8\pi ,t,0.18)\) for \((x,t)\in [0,8\pi ]\times [0,2]\) are shown in Figs. 1 (right side) and 2 (right side), respectively. Also, the graphs of the absolute error functions of \(u_{7}(x,8\pi ,8 \pi ,0.5,0.18)\) and \(u_{7}(x,8\pi ,8\pi ,1.5,0.18)\) for \(x\in [0,8 \pi ]\) are shown in Figs. 3 and 4 (right side), respectively. These figures imply that \(u_{7}(x,y,z,t,0.18)\) is a highly accurate approximate solution even for large values of x, y, z and t.

Figure 1
figure 1

The graphs of the approximate solution \(u(x,8\pi ,8\pi ,t)\) for Example 1 via the standard VIM (left side) and the upgraded VIM with \(h=0.18\) as an auxiliary parameter (right side) in the case \((\alpha =\beta =\frac{1}{4}, \gamma =\frac{1}{2})\)

Full size image
Figure 2
figure 2

The graphs of the absolute error function of \(u(x,8\pi ,8\pi ,t)\) for Example 1 via the standard VIM (left side) and the upgraded VIM with \(h=0.18\) as an auxiliary parameter (right side) in the case \((\alpha =\beta =\frac{1}{4}, \gamma =\frac{1}{2})\)

Full size image
Figure 3
figure 3

The graphs of the absolute error function of \(u(x,8\pi ,8\pi ,0.5)\) for Example 1 via the standard VIM (left side) and the upgraded VIM with \(h=0.18\) as an auxiliary parameter (right side) in the case \((\alpha =\beta =\frac{1}{4}, \gamma =\frac{1}{2})\)

Full size image
Figure 4
figure 4

The graphs of the absolute error function of \(u(x,8\pi ,8\pi ,1.5)\) for Example 1 via the standard VIM (left side) and the upgraded VIM with \(h=0.18\) as an auxiliary parameter (right side) in the case \((\alpha =\beta =\frac{1}{4}, \gamma =\frac{1}{2})\)

Full size image

Example 2

Consider the following three-dimensional modified anomalous fractional sub-diffusion equation:

$$\begin{aligned}& \frac{\partial u(x,y,z,t)}{\partial t} \\& \quad = \biggl(\frac{1}{\pi ^{2}} \frac{ \partial ^{1-\alpha }}{\partial t^{1-\alpha }}+\frac{1}{\pi ^{2}} \frac{ \partial ^{1-\beta }}{\partial t^{1-\beta }}+ \frac{1}{\pi ^{2}}\frac{ \partial ^{1-\gamma }}{\partial t^{1-\gamma }} \biggr) \\& \qquad {}\times \biggl[\frac{ \partial ^{2}u(x,y,z,t)}{\partial x^{2}}+ \frac{\partial ^{2}u(x,y,z,t)}{ \partial y^{2}}+ \frac{\partial ^{2}u(x,y,z,t)}{\partial z^{2}} \biggr] \\& \qquad {}+g(x,y,z,t), \quad (x,y,z,t)\in [0,40]\times [0,40]\times [0,40]\times [0,2], \end{aligned}$$
(5.2)

where

$$ g(x,y,z,t)=\cos \bigl( \pi ( x+y+z ) \bigr) \biggl( 2 t+6 { \frac{{t}^{1+\alpha }}{\varGamma ( 2+\alpha ) }}+6 {\frac{{ t}^{1+\beta }}{\varGamma ( 2+\beta ) }}+6 {\frac{ {t}^{1+ \gamma }}{\varGamma ( 2+\gamma ) }} \biggr), $$

with the initial condition \(u(x,y,z,0)=0\), and the exact solution \(u(x,y,z,t)=\cos (\pi (x+y+z) )t^{2}\).

According to the standard VIM, we have the following variational iteration formula:

$$\begin{aligned}& u_{n+1}(x,y,z,t) \\& \quad =u_{n}(x,y,z,t)- \int _{0}^{t}\biggl\{ \frac{\partial u _{n}(x,y,z,s)}{\partial s}- \biggl(\frac{1}{\pi ^{2}}\frac{ \partial ^{1-\alpha }}{\partial s^{1-\alpha }}+ \frac{1}{\pi ^{2}} \frac{ \partial ^{1-\beta }}{\partial s^{1-\beta }}+\frac{1}{\pi ^{2}} \frac{ \partial ^{1-\gamma }}{\partial s^{1-\gamma }} \biggr) \\& \qquad {}\times \biggl[\frac{\partial ^{2}u_{n}(x,y,z,s)}{\partial x^{2}}+\frac{ \partial ^{2}u_{n}(x,y,z,s)}{\partial y^{2}}+ \frac{\partial ^{2}u_{n}(x,y,z,s)}{ \partial z^{2}} \biggr]-g(x,y,z,s)\biggr\} \,ds, \quad n\geq 0. \end{aligned}$$

By starting the solution procedure from \(u_{0}(x,y,z,t)=u(x,y,z,0)=0\), we may repeat until to compute \(u_{7}(x,y,z,t)\). The graphs of the approximate solution and the absolute error functions of \(u_{7}(x,40,40,t)\) for \((x,t)\in [0,40]\times [0,2]\) and \((\alpha = \frac{1}{4}, \beta =\frac{1}{2}, \gamma =\frac{3}{4})\) are shown in Figs. 5 (left side) and 6 (left side), respectively. Also, the graphs of the absolute error functions of \(u_{7}(x,40,40,0.5)\) and \(u_{7}(x,40,40,1.5)\) for \(x\in [0,40]\) are, respectively, shown in Figs. 7 and 8 (left side). It can be seen that \(u_{7}(x,y,z,t)\) is not accurate for large values of x, y, z and t. Now, by using the recurrence formula defined in (3.3), we successively have

$$\begin{aligned}& u_{0}(x,y,z,t)=u(x,y,z,0)=0, \\& u_{1}(x,y,z,t,h)=h\cos \bigl( \pi ( x+y+z ) \bigr) \biggl(6 { \frac{{t}^{2+\alpha }}{\varGamma ( 3+\alpha ) }}+6 {\frac{{t}^{2+\beta }}{\varGamma ( 3+\beta ) }}+6 {\frac{ {t}^{2+\gamma }}{\varGamma ( 3+\gamma ) }}+t^{2} \biggr), \end{aligned}$$

and in general

$$\begin{aligned}& u_{n+1}(x,y,z,t,h) \\& \quad =u_{n}(x,y,z,t,h)-h \int _{0}^{t}\biggl\{ \frac{ \partial u_{n}(x,y,z,s,h)}{\partial s}- \biggl(\frac{1}{\pi ^{2}}\frac{ \partial ^{1-\alpha }}{\partial s^{1-\alpha }}+ \frac{1}{\pi ^{2}} \frac{ \partial ^{1-\beta }}{\partial s^{1-\beta }}+\frac{1}{\pi ^{2}} \frac{ \partial ^{1-\gamma }}{\partial s^{1-\gamma }} \biggr) \\& \qquad {}\times \biggl[\frac{\partial ^{2}u_{n}(x,y,z,s,h)}{\partial x^{2}}+\frac{ \partial ^{2}u_{n}(x,y,z,s,h)}{\partial y^{2}}+ \frac{\partial ^{2}u_{n}(x,y,z,s,h)}{ \partial z^{2}} \biggr] -g(x,y,z,s)\biggr\} \,ds, \\& \qquad n\geq 1. \end{aligned}$$

In order to find a proper value for h which leads to the accurate approximation, we define the following residual function:

$$\begin{aligned}& r_{7}(x,y,z,t,h) \\& \quad =\frac{\partial u_{7}(x,y,z,t,h)}{\partial t}- \biggl( \frac{1}{ \pi ^{2}}\frac{\partial ^{1-\alpha }}{\partial t^{1-\alpha }}+ \frac{1}{ \pi ^{2}} \frac{\partial ^{1-\beta }}{\partial t^{1-\beta }}+\frac{1}{\pi ^{2}} \frac{\partial ^{1-\gamma }}{\partial t^{1-\gamma }} \biggr) \\& \qquad {}\times\biggl[\frac{ \partial ^{2}u_{7}(x,y,z,t,h)}{\partial x^{2}}+\frac{\partial ^{2}u_{7}(x,y,z,t,h)}{ \partial y^{2}} + \frac{\partial ^{2}u_{7}(x,y,z,t,h)}{\partial z ^{2}}\biggr]-g(x,y,z,t), \end{aligned}$$

and the following error of norm two of residual function:

$$ e_{7}(h)= \biggl( \int _{0}^{2} \int _{0}^{40} \int _{0}^{40} \int _{0}^{40}r _{7}^{2}(x,y,z,t,h) \, dx\, dy\, dz\, dt \biggr)^{\frac{1}{2}}. $$

The minimum point of \(e_{7}(h)\) when \((\alpha =\frac{1}{4}, \beta = \frac{1}{2}, \gamma =\frac{3}{4})\) is obtained at \(h\simeq 0.18\) by using Maple software. Substituting \(h =0.18\) in \(u_{7}(x,40,40,t,h)\), remarkably reduces the absolute error of approximation method. The graphs of the approximate solution and the absolute error functions of \(u_{7}(x,40,40,t,0.18)\) for \((x,t)\in [0,40]\times [0,2]\) are shown in Figs. 5 (right side) and 6 (right side), respectively. The graphs of the absolute error functions of \(u_{7}(x,40,40,0.5,0.18)\) and \(u_{7}(x,40,40,1.5,0.18)\) for \(x\in [0,40]\) are respectively shown in Figs. 7 and 8 (right side). The demonstrated figures reveal that \(u_{7}(x,y,z,t,0.18)\) is the highly accurate approximate solution even for the large values of x, y, z and t.

Figure 5
figure 5

The graphs of the approximate solution \(u(x,40,40,t)\) for Example 2 via the standard VIM (left side) and the upgraded VIM with \(h=0.18\) as an auxiliary parameter (right side) in the case \((\alpha =\frac{1}{4}, \beta =\frac{1}{2}, \gamma =\frac{3}{4})\)

Full size image
Figure 6
figure 6

The graphs of the absolute error function of \(u(x,40,40,t)\) for Example 2 via the standard VIM (left side) and the upgraded VIM with \(h=0.18\) as an auxiliary parameter (right side) in the case \((\alpha =\frac{1}{4}, \beta =\frac{1}{2}, \gamma =\frac{3}{4})\)

Full size image
Figure 7
figure 7

The graphs of the absolute error function of \(u(x,40,40,0.5)\) for Example 2 via the standard VIM (left side) and the upgraded VIM with \(h=0.18\) as an auxiliary parameter (right side) in the case \((\alpha =\frac{1}{4}, \beta =\frac{1}{2}, \gamma =\frac{3}{4})\)

Full size image
Figure 8
figure 8

The graphs of the absolute error function of \(u(x,40,40,1.5)\) for Example 2 via the standard VIM (left side) and the upgraded VIM with \(h=0.18\) as an auxiliary parameter (right side) in the case \((\alpha =\frac{1}{4}, \beta =\frac{1}{2}, \gamma =\frac{3}{4})\)

Full size image

6 Conclusion

The well-known anomalous diffusion equations are an important class of fractional differential equations. Since they have been widely applied in modeling of many phenomena, finding the accurate solution of this system still is of interest for many researchers. In this paper, a three-dimensional modified anomalous fractional sub-diffusion equation defined on the large domain has been studied. The VIM with an auxiliary parameter which is famed for computational efficiency on the large domain, was proposed and scrutinized. This method provides a simple way to extend the convergence region for the approximate solutions. An optimal auxiliary parameter was determined by the error of norm two of the residual function. The experimental results and graphical representations confirm the reliability and the efficiency of the proposed method. In the future, the problem investigated in this paper might be solved by other numerical methodologies like those discussed in [54, 55].