Skip to main content
SpringerLink
Log in

High Order Numerical Scheme for Generalized Fractional Diffusion Equations

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

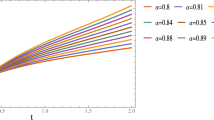
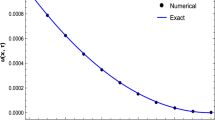
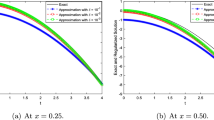
Abstract

In this paper, a higher order finite difference scheme is proposed for generalized fractional diffusion equations (GFDEs). The fractional diffusion equation is considered in terms of the generalized fractional derivatives (GFDs) which uses the scale and weight functions in the definition. The GFD reduces to the Riemann–Liouville, Caputo derivatives and other fractional derivatives in a particular case. Due to importance of the scale and the weight functions in describing behaviour of real-life physical systems, we present the solutions of the GFDEs by considering various scale and weight functions. The convergence and stability analysis are also discussed for the finite difference scheme (FDS) to validate the proposed method. We consider test examples for numerical simulation of FDS to justify the proposed numerical method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data Availability

Data sharing not applicable to this article as no data sets were generated or analysed during the current study.

References

  1. Meerschaert, M., Zhang, Y., Baeumer, B.: Particle tracking for fractional diffusion with two-time scales. Comput. Math. Appl. 59(3), 1078–1086 (2010)

    Article  MathSciNet  Google Scholar 

  2. Goychuk, I., Hanggi, P.: Fractional diffusion modeling of ion channel gating. Phys. Rev. E 70(5), 9 (2004)

    Article  MathSciNet  Google Scholar 

  3. Berestycki, H., Roquejoffre, J., Rossi, L.: The periodic patch model for population dynamics with fractional diffusion. Discrete Contin. Dyn. Syst. 4(1), 1–13 (2011)

    MathSciNet  Google Scholar 

  4. Cartea, A., Del-Castillo-Negrete, D.: Fractional diffusion models of option prices in markets with jumps. Physica A 374(2), 749–763 (2007)

    Article  Google Scholar 

  5. Tarasov, V.E.: Fractional integro-differential equations for electromagnetic waves in dielectric media. Theor. Math. Phys. 158(3), 355–359 (2009)

    Article  MathSciNet  Google Scholar 

  6. Bagley, R.L., Torvik, P.J.: A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 27, 201–210 (1983)

    Article  Google Scholar 

  7. Elsaid, A.: The variational iteration method for solving Riesz fractional partial differential equations. Comput. Math. Appl. 60(7), 1940–1947 (2010)

    Article  MathSciNet  Google Scholar 

  8. Kumar, S., Yildirim, A., Khan, Y., Wei, L.: A fractional model of the diffusion equation and its analytical solution using Laplace transform. Sci. Iran. 19(4), 1117–1123 (2012)

    Article  Google Scholar 

  9. Pang, H., Sun, H.: Multigrid method for fractional diffusion equations. J. Comput. Phys. 231(2), 693–703 (2012)

    Article  MathSciNet  Google Scholar 

  10. Gao, G., Sun, Z., Zhang, Y.: A finite difference scheme for fractional sub-diffusion equations on an unbounded domain using artificial boundary conditions. J. Comput. Phys. 231(7), 2865–2879 (2012)

    Article  MathSciNet  Google Scholar 

  11. Hu, X., Zhang, L.: On finite difference methods for fourth-order fractional diffusion-wave and subdiffusion systems. Appl. Math. Comput. 218(9), 5019–5034 (2012)

    MathSciNet  Google Scholar 

  12. Çelik, C., Duman, M.: Crank–Nicolson method for the fractional diffusion equation with the Riesz fractional derivative. J. Comput. Phys. 231(4), 1743–1750 (2012)

    Article  MathSciNet  Google Scholar 

  13. Wang, W., Shu, C., Yee, H., Sjögreen, B.: High order finite difference methods with subcell resolution for advection equations with stiff source terms. J. Comput. Phys. 231(1), 190–214 (2012)

    Article  MathSciNet  Google Scholar 

  14. Meerschaert, M., Tadjeran, C.: Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 172, 65–77 (2004)

    Article  MathSciNet  Google Scholar 

  15. Meerschaert, M., Tadjeran, C.: Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 56(1), 80–90 (2006)

    Article  MathSciNet  Google Scholar 

  16. Roop, J.: Numerical approximation of a one-dimensional space fractional advection–dispersion equation with boundary layer. Comput. Math. Appl. 56(7), 1808–1819 (2008)

    Article  MathSciNet  Google Scholar 

  17. Sharma, S., Pandey, R.K., Kumar, K.: Galerkin and collocation methods for weakly singular fractional integro-differential equations, Iran. J. Sci. Technol. Trans. A Sci. 43(4), 1649–1656 (2019)

    Article  MathSciNet  Google Scholar 

  18. Sharma, S., Pandey, R.K., Kumar, K.: Collocation method with convergence for generalized fractional integro-differential equations. J. Comput. Appl. Math. 342, 419–430 (2018)

    Article  MathSciNet  Google Scholar 

  19. Kumar, K., Pandey, R.K., Sharma, S.: Comparative study of three numerical schemes for fractional integro-differential equations. J. Comput. Appl. Math. 315, 287–302 (2017)

    Article  MathSciNet  Google Scholar 

  20. Pandey, R.K., Sharma, S., Kumar, K.: Collocation method for generalized Abel’s integral equations. J. Comput. Appl. Math. 302, 118–128 (2016)

    Article  MathSciNet  Google Scholar 

  21. Kumar, K., Pandey, R.K., Sharma, S.: Approximations of fractional integrals and Caputo derivatives with application in solving Abel’s integral equations. J. King Saud Univ. Sci. 31(4), 692–700 (2019)

    Article  Google Scholar 

  22. Kumar, K., Pandey, R.K., Sharma, S.: Numerical schemes for the generalized Abel’s integral equations. Int. J. Appl. Comput. Math. 4(2), 68 (2018)

    Article  MathSciNet  Google Scholar 

  23. Saadatmandi, A., Dehghan, M.: A Legendre collocation method for fractional integro-differential equations. J. Vib. Control 17(13), 2050–2058 (2011)

    Article  MathSciNet  Google Scholar 

  24. Saadatmandi, A., Dehghan, M.: A Tau approach for solution of the space fractional diffusion equation. Comput. Math. Appl. 62(3), 1135–1142 (2011)

    Article  MathSciNet  Google Scholar 

  25. Dehghan, M., Abbaszadeh, M., Mohebbi, A.: Error estimate for the numerical solution of fractional reaction–subdiffusion process based on a meshless method. J. Comput. Appl. Math. 280, 14–36 (2015)

    Article  MathSciNet  Google Scholar 

  26. Dehghan, M., Abbaszadeh, M., Mohebbi, A.: Legendre spectral element method for solving time fractional modified anomalous sub-diffusion equation. Appl. Math. Model. 40(5–6), 3635–3654 (2016)

    Article  MathSciNet  Google Scholar 

  27. Saadatmandi, A., Dehghan, M., Azizi, M.R.: The Sinc-Legendre collocation method for a class of fractional convection–diffusion equations with variable coefficients. Commun. Nonlinear Sci. Numer. Simul. 17(11), 4125–4136 (2012)

    Article  MathSciNet  Google Scholar 

  28. Gao, G., Sun, Z., Zhang, H.: A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 259, 33–50 (2014)

    Article  MathSciNet  Google Scholar 

  29. Agrawal, O.P.: Some generalized fractional calculus operators and their applications in integral equations. Fract. Calc. Anal. Appl. 15(4), 700–711 (2012)

    Article  MathSciNet  Google Scholar 

  30. Xu, Y., He, Z., Agrawal, O.P.: Numerical and analytical solutions of new generalized fractional diffusion equation. Comput. Math. Appl. 66, 2019–2029 (2013)

    Article  MathSciNet  Google Scholar 

  31. Xu, Y., Agrawal, O.P.: Numerical solutions and analysis of diffusion for new generalized fractional advection–diffusion equations. Open Phys. 11(10), 1178–1193 (2013)

    Article  Google Scholar 

  32. Xu, Y., Agrawal, O.P.: Numerical solutions and analysis of diffusion for new generalized fractional Burger’s equation. Fract. Calc. Appl. Anal. 16(3), 709–736 (2013)

    Article  MathSciNet  Google Scholar 

  33. Kumar, K., Pandey, R.K., Sharma, S., Xu, Y.: Numerical scheme with convergence for a generalized time-fractional Telegraph-type equation. Numer. Methods Partial Differ. Equ. 35(3), 1164–1183 (2019)

    Article  MathSciNet  Google Scholar 

  34. Kumar, K., Pandey, R.K., Yadav, S.: Finite difference scheme for a fractional telegraph equation with generalized fractional derivative terms. Physica A Stat. Mech. Appl. 535, 122271 (2019)

    Article  MathSciNet  Google Scholar 

  35. Yadav, S., Pandey, R.K., Shukla, A.K., Kumar, K.: High-order approximation for generalized fractional derivative and its application. Int. J. Numer. Methods Heat Fluid Flow 29, 3515–3534 (2019)

    Article  Google Scholar 

  36. Yavuz, M., Ozdemir, N.: Numerical inverse Laplace homotopy technique for fractional heat equations. Therm. Sci. 22(Suppl. 1), 185–194 (2018)

    Article  Google Scholar 

  37. Yavuz, M., Özdemir, N.: A different approach to the European option pricing model with new fractional operator. Math. Model. Nat. Phenom. 13(1), 12 (2018)

    Article  MathSciNet  Google Scholar 

  38. Tajadodi, H., Jafari, H., Ncube, M.N.: Genocchi polynomials as a tool for solving a class of fractional optimal control problems. Int. J. Optim. Control Theor. Appl. 12(2), 160–168 (2022)

    Article  MathSciNet  Google Scholar 

  39. Esmaeelzade Aghdam, Y., Farnam, B.: A numerical process of the mobile–immobile advection–dispersion model arising in solute transport. Math. Comput. Sci. 3(3), 1–10 (2022)

    Google Scholar 

  40. Aghdam, Y.E., Farnam, B., Jafari, H.: Numerical approach to simulate diffusion model of a fluid-flow in a porous media. Therm. Sci. 25(2), 255–261 (2021)

    Article  Google Scholar 

  41. Aghdam, Y.E., Mesgrani, H., Javidi, M., Nikan, O.: A computational approach for the space–time fractional advection–diffusion equation arising in contaminant transport through porous media. Eng. Comput. 37(4), 3615–3627 (2021)

    Article  Google Scholar 

  42. Aghdam, Y.E., Mesgarani, H., Moremedi, G.M., Khoshkhahtinat, M.: High-accuracy numerical scheme for solving the space–time fractional advection–diffusion equation with convergence analysis. Alex. Eng. J. 61(1), 217–225 (2022)

    Article  Google Scholar 

  43. Safdari, H., Mesgarani, H., Javidi, M., Aghdam, Y.E.: Convergence analysis of the space fractional-order diffusion equation based on the compact finite difference scheme. Comput. Appl. Math. 39, 1–15 (2020)

    Article  MathSciNet  Google Scholar 

  44. Tuan, N.H., Aghdam, Y.E., Jafari, H., Mesgarani, H.: A novel numerical manner for two-dimensional space fractional diffusion equation arising in transport phenomena. Numer. Methods Partial Differ. Equ. 37(2), 1397–1406 (2021)

    Article  MathSciNet  Google Scholar 

  45. Kumar, K., Pandey, R.K., Sultana, S.: Numerical schemes with convergence for generalized fractional integro-differential equations. J. Comput. Appl. Math. 388, 113318 (2021)

    Article  MathSciNet  Google Scholar 

  46. Ascher, U.: Numerical Methods for Evolutionary Differential Equations. SIAM, Philadelphia (2008)

    Book  Google Scholar 

  47. Varga, R.: On diagonal dominance arguments for bounding ∥A−1∥∞. Linear Algebra Appl. 14, 211–217 (1976)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Authors are thankful to the reviewers for their comments to improve the presentation of the paper.

Funding

No funding was provided for the completion of this study.

Author information

Authors and Affiliations

  1. Department of Sciences (Mathematics), Manav Rachna University, Faridabad, Haryana, India

    Kamlesh Kumar

  2. School of Business, University of Petrolium and Energy Studies, Dehradun, Uttarakhand, India

    A. K. Pandey

  3. Department of Mathematical Sciences, Indian Institute of Technology (BHU) Varanasi, Varanasi, Uttar Pradesh, India

    Rajesh K. Pandey

Authors
  1. Kamlesh Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. K. Pandey
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rajesh K. Pandey
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Kamlesh Kumar: Conceptualization, formal analysis ,Investigation, methodology. Awadhesh K Pandey: Validation, Originality Rajesh K. Pandey: Supervision ,Validation

Corresponding authors

Correspondence to Kamlesh Kumar or Rajesh K. Pandey.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, K., Pandey, A.K. & Pandey, R.K. High Order Numerical Scheme for Generalized Fractional Diffusion Equations. Int. J. Appl. Comput. Math 10, 105 (2024). https://doi.org/10.1007/s40819-024-01725-5

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40819-024-01725-5

Keywords

Search

Navigation