1 Introduction

Neural networks, including Hopfield neural networks and cellular neural networks, have been widely investigated in past decades [1–23]. Synchronization, as a typical collective dynamical behavior of neural networks, has attracted more and more attention in various fields. For achieving the synchronization of neural networks, especially of chaotic neural networks, many control methods and techniques have been adopted to design proper and effective controllers, such as feedback control, intermittent control, adaptive control, impulsive control, and so on.

In real world, because of switching phenomenon or sudden noise, many real systems have been found to be subject to instantaneous perturbations and abrupt changes at certain instants. That is, these systems cannot be controlled by continuous control and endure continuous disturbance. Therefore, impulsive control, as a typical discontinuous control scheme, has been widely adopted to design proper controllers for achieving synchronization or stability [1–9]. Based on the Lyapunov function method, the Razumikhin technique, or the comparison principle, many valuable results have been obtained, and synchronization criteria have been derived. For a given neural network, we can estimate the largest impulsive interval from the derived criteria by fixing impulsive gains and calculating some system constants, for example, Lipschitz or Lipschitz-like constants with respect to neuron activation functions, and vice versa. As we know, different neural networks usually have totally different system parameters and activation functions, which means that the impulsive controllers with fixed impulsive gains and intervals are not unified. In other words, the system parameters have more restrictions on the choice of impulsive gains and intervals. For relaxing the restrictions, adaptive strategy is introduced to design adaptive impulsive controllers. The Lipschitz (or Lipschitz-like) and other constants with respect to system parameters and activation functions need not be known beforehand and can be calculated according to the proposed adaptive strategy [24–26].

On the other hand, due to the transmission speed of signals or information between neurons is finite, neural networks with coupling delay should be considered. Motivated by the above discussions, in this paper, we investigate the impulsive synchronization of drive-response chaotic delayed neural networks. Firstly, we give some sufficient conditions for achieving synchronization, from which we can easily estimate the largest impulsive intervals for given neural networks and impulsive gains. Secondly, we adopt adaptive strategy to design adaptive impulsive controllers for relaxing the restrictions. Noticeably, the designed controllers are universal for different neural networks. Finally, we perform some numerical examples to verify the obtained results.

The rest of this paper is organized as follows. In Section 2, we introduce the model and some preliminaries. In Section 3, we study the impulsive synchronization of drive-response chaotic delayed neural networks. In Section 4, we provide several numerical simulations to verify the effectiveness of the theoretical results. Section 5 concludes this paper.

2 Model and preliminaries

Consider the following chaotic neural network with time-varying delays:

$$ \begin{aligned} &\dot{x}_{i}(t) = -c_{i}x_{i}(t)+ \sum_{j=1}^{n}a_{ij}f_{j} \bigl(x_{j}(t)\bigr)+\sum_{j=1}^{n}b_{ij}g_{j} \bigl(x_{j}\bigl(t-\tau(t)\bigr)\bigr)+J_{i},\quad t>0, \\ &x_{i}(t) = \phi_{i}(t),\quad t\in[-\tau_{0},0], \end{aligned} $$
(1)

or, in the compact form,

$$ \begin{aligned} &\dot{x}(t) = -Cx(t)+Af\bigl(x(t)\bigr)+Bg\bigl(x \bigl(t-\tau(t)\bigr)\bigr)+J,\quad t>0, \\ &x(t) = \phi(t),\quad t\in[-\tau_{0},0], \end{aligned} $$
(2)

where \(i=1,2,\ldots,n\), \(x(t)=(x_{1}(t),x_{2}(t),\ldots,x_{n}(t))^{T}\in R^{n}\) is the neuron state vector, n is the number of neurons, \(f(x(t))=(f_{1}(x_{1}(t)),f_{2}(x_{2}(t)),\ldots,f_{n}(x_{n}(t)))^{T}\) and \(g(x(t))=(g_{1}(x_{1}(t)), g_{2}(x_{2}(t)),\ldots,g_{n}(x_{n}(t)))^{T}\) denote the neuron activation functions, \(C=\operatorname{diag}\{c_{1},c_{2},\ldots,c_{n}\}\) is a positive diagonal matrix, \(A=(a_{ij})_{n\times n}\) and \(B=(b_{ij})_{n\times n}\) are the coupling weight matrices, \(\tau(t)\) is the time-varying delay satisfying \(0<\tau(t)\leq\tau_{0}\), \(\phi(t)\) is bounded and continuous on \([-\tau_{0},0]\) and denotes the initial condition, and \(J=(J_{1},J_{2},\ldots,J_{n})^{T}\in R^{n}\) is an external input vector.

We regard neural network (2) as the drive network and consider the following neural network as the response network:

$$ \begin{aligned} &\dot{y}(t) = -Cy(t)+Af\bigl(y(t)\bigr)+Bg\bigl(y \bigl(t-\tau(t)\bigr)\bigr)+J, \quad t>0, \\ &y(t) = \varphi(t),\quad t\in[-\tau_{0},0], \end{aligned} $$
(3)

where \(y(t)=(y_{1}(t),y_{2}(t),\ldots,y_{n}(t))^{T}\in R^{n}\) is the neuron state vector, and \(\varphi(t)\) is bounded and continuous on \([-\tau _{0},0]\) and denotes the initial condition.

The drive-response networks (2) and (3) are said to achieve synchronization if \(\lim_{t\to\infty}\|y(t)-x(t)\|=0\).

For achieving the synchronization, the controlled network with impulsive controllers are described by

$$\begin{aligned}& \dot{y}(t) = -Cy(t)+Af\bigl(y(t)\bigr)+Bg\bigl(y\bigl(t-\tau(t) \bigr)\bigr)+J,\quad t>0, t\neq t_{k}, \\& y\bigl(t_{k}^{+}\bigr) = y\bigl(t_{k}^{-}\bigr)+b(t_{k}) \bigl(y\bigl(t_{k}^{-}\bigr)-x\bigl(t_{k}^{-}\bigr)\bigr),\quad t=t_{k}, \\& y(t) = \varphi(t),\quad t\in[-\tau_{0},0], \end{aligned}$$
(4)

where \(k=1,2,3,\ldots \) , the impulsive time instants \(t_{k}\) satisfy \(0= t_{0}< t_{1}< t_{2}<\cdots<t_{k}<\cdots\), \(t_{k}\rightarrow\infty\) as \(k\rightarrow \infty\), \(y(t_{k}^{+})=\lim_{t\rightarrow t_{k}^{+}}y(t)\), \(y(t_{k}^{-})=\lim_{t\rightarrow t_{k}^{-}}y(t)\) and \(y(t_{k}^{-})=y(t_{k})\); \(b(t_{k})\in (-2,-1)\cup(-1,0)\) is the impulsive gain at \(t=t_{k}\), \(b(t_{k})=b(t_{k}^{+})=b(t_{k}^{-})\) and \(b(t)=0\) for \(t\neq t_{k}\).

Letting \(e(t)=y(t)-x(t)\) be the synchronization error, we can obtain the following error system:

$$ \begin{aligned} &\dot{e}(t) = -Ce(t)+A\bigl(f\bigl(y(t)\bigr)-f \bigl(x(t)\bigr)\bigr) \\ &\hphantom{\dot{e}(t) ={}}{}+B\bigl(g\bigl(y\bigl(t-\tau(t)\bigr)\bigr)-g\bigl(x\bigl(t- \tau(t)\bigr)\bigr)\bigr),\quad t>0, t\neq t_{k}, \\ &e\bigl(t_{k}^{+}\bigr) = e\bigl(t_{k}^{-} \bigr)+b(t_{k})e\bigl(t_{k}^{-}\bigr),\quad t=t_{k}, \\ &e(t) = \varphi(t)-\phi(t), \quad t\in[-\tau_{0},0], \end{aligned} $$
(5)

Assumption 1

The neuron activation functions \(f_{i}(\cdot)\) and \(g_{i}(\cdot)\) are nondecreasing, bounded, and globally Lipschitz, that is, there exist two positive constants \(L_{f}\) and \(L_{g}\) such that

$$ \bigl\vert f_{i}(y)-f_{i}(x)\bigr\vert \leq L_{f}\vert y-x\vert \quad \mbox{and}\quad \bigl\vert g_{i}(y)-g_{i}(x)\bigr\vert \leq L_{g}\vert y-x\vert $$

for any \(x,y\in R\), \(i=1,2,\ldots,n\).

Assumption 2

The time-varying delay \(\tau(t)\) is differentiable and satisfies \(\dot{\tau}(t)\leq\mu<1\).

Lemma 1

[27]

For any vectors \(x,y\in R^{n}\) and positive-definite matrix \(Q\in R^{n\times n}\), the following matrix inequality holds:

$$ 2x^{T}y\leq x^{T}Qx+y^{T}Q^{-1}y. $$

3 Main result

In what follows, let \(d_{k}=t_{k}-t_{k-1}\), λ be the largest eigenvalue of matrix \(-C+(1-\mu)^{-1}I_{n}+AA^{T}+L_{f}^{2}I_{n}+L_{g}^{2}BB^{T}\), \(\beta(t_{k})=(1+b(t_{k}))^{2}\), and \(\beta(t)=1\) for \(t\neq t_{k}\).

Theorem 1

Suppose that Assumptions 1 and 2 hold. If there exists a constant \(\alpha>0\) such that

$$ \ln\beta(t_{k})+\alpha+L d_{k}< 0,\quad k=1,2,\ldots, $$
(6)

where \(L=2\max\{\lambda,0\}\), then the drive-response delayed neural networks (2) and (4) can achieve synchronization.

Proof

Consider the following Lyapunov functional candidate:

$$ V\bigl(e(t)\bigr)=\frac{1}{2}e^{T}(t)e(t)+\frac{\beta(t)}{1-\mu} \int_{t-\tau (t)}^{t}e^{T}(\theta)e(\theta)\,d \theta. $$

When \(t\in(t_{k-1},t_{k})\), the function \(V(e(t))\) can be written as

$$ V\bigl(e(t)\bigr)=\frac{1}{2}e^{T}(t)e(t)+\frac{1}{1-\mu} \int_{t-\tau (t)}^{t}e^{T}(\theta)e(\theta)\,d \theta, $$

and the derivative of \(V(t)\) along the trajectory (5) is

$$\begin{aligned} \dot{V}\bigl(e(t)\bigr) =&e^{T}(t)\dot{e}(t)+\frac{1}{1-\mu}e^{T}(t)e(t)- \frac{1-\dot {\tau}(t)}{1-\mu}e^{T}\bigl(t-\tau(t)\bigr)e\bigl(t-\tau(t)\bigr) \\ =&-e^{T}(t)Ce(t)+e^{T}(t)A\bigl(f\bigl(y(t)\bigr)-f \bigl(x(t)\bigr)\bigr) \\ &{}+e^{T}(t)B\bigl(g\bigl(y\bigl(t-\tau(t)\bigr)\bigr)-g\bigl(x \bigl(t-\tau(t)\bigr)\bigr)\bigr) \\ &{}+\frac{1}{1-\mu}e^{T}(t)e(t)-\frac{1-\dot{\tau}(t)}{1-\mu}e^{T} \bigl(t-\tau (t)\bigr)e\bigl(t-\tau(t)\bigr). \end{aligned}$$

According to Assumptions 1 and 2 and Lemma 1, we have

$$\begin{aligned} \dot{V}\bigl(e(t)\bigr) \leq&e^{T}(t) \bigl(-C+(1- \mu)^{-1}I_{n}+AA^{T}+L_{g}^{2}BB^{T} \bigr)e(t) \\ &{}+\bigl(f\bigl(y(t)\bigr)-f\bigl(x(t)\bigr)\bigr)^{T}\bigl(f \bigl(y(t)\bigr)-f\bigl(x(t)\bigr)\bigr) \\ &{}+L_{g}^{-2}\bigl(g\bigl(y\bigl(t-\tau(t)\bigr)\bigr)-g \bigl(x\bigl(t-\tau(t)\bigr)\bigr)\bigr)^{T} \\ &{}\times\bigl(g\bigl(y\bigl(t-\tau(t)\bigr)\bigr)-g\bigl(x\bigl(t-\tau(t) \bigr)\bigr)\bigr) \\ &{}-\frac{1-\dot{\tau}(t)}{1-\mu}e^{T}\bigl(t-\tau(t)\bigr)e\bigl(t-\tau(t)\bigr) \\ \leq&e^{T}(t) \bigl(-C+(1-\mu)^{-1}I_{n}+AA^{T}+L_{f}^{2}I_{n}+L_{g}^{2}BB^{T} \bigr)e(t) \\ &{}+\frac{\dot{\tau}(t)-\mu}{1-\mu}e^{T}\bigl(t-\tau(t)\bigr)e\bigl(t-\tau(t)\bigr) \\ \leq& \frac{L}{2}e^{T}(t)e(t). \end{aligned}$$

Since \(L=2\max\{\lambda,0\}\geq0\) and \(\frac{1}{1-\mu}\int_{t-\tau(t)}^{t}e^{T}(\theta)e(\theta)\,d\theta\geq0\), we have

$$\frac{L}{2}e^{T}(t)e(t)\leq L \biggl(\frac{1}{2}e^{T}(t)e(t)+ \frac{1}{1-\mu } \int_{t-\tau(t)}^{t}e^{T}(\theta)e(\theta)\,d \theta \biggr)=LV\bigl(e(t)\bigr) $$

and

$$\dot{V}\bigl(e(t)\bigr)\leq LV\bigl(e(t)\bigr), $$

which gives

$$ V\bigl(e(t)\bigr)\leq V\bigl(e\bigl(t_{k-1}^{+}\bigr) \bigr)e^{L(t-t_{k-1})}. $$
(7)

When \(t=t_{k}\), we have

$$\begin{aligned} V\bigl(e\bigl(t_{k}^{+}\bigr)\bigr) =& \frac{1}{2}e^{T}\bigl(t_{k}^{+}\bigr)e \bigl(t_{k}^{+}\bigr)+\frac{\beta(t_{k}^{+})}{1-\mu } \int_{t_{k}^{+}-\tau(t)}^{t_{k}^{+}}e^{T}(\theta)e(\theta)\,d \theta \\ =&\frac{(1+b(t_{k}))^{2}}{2}e^{T}\bigl(t_{k}^{-}\bigr)e \bigl(t_{k}^{-}\bigr)+\frac{\beta (t_{k})}{1-\mu} \int_{t_{k}^{-}-\tau(t)}^{t_{k}^{-}}e^{T}(\theta)e(\theta)\,d \theta \\ =& \beta(t_{k})V\bigl(e\bigl(t_{k}^{-}\bigr)\bigr). \end{aligned}$$
(8)

By mathematical induction we have

$$ V\bigl(e\bigl(t_{k}^{+}\bigr)\bigr)\leq V\bigl(e\bigl(t_{0}^{+} \bigr)\bigr)\prod_{\sigma=1}^{k} \beta(t_{\sigma}) e^{Ld_{\sigma}},\quad k=1,2,\ldots. $$

From conditions (6) we have

$$ \beta(t_{\sigma})e^{Ld_{\sigma}}< e^{-\alpha}, \quad \sigma=1,2, \ldots, $$

and

$$ V\bigl(e\bigl(t_{k}^{+}\bigr)\bigr)\leq V\bigl(e\bigl(t_{0}^{+} \bigr)\bigr)e^{-k\alpha}, $$

which shows that \(\lim_{k\to\infty}V(t_{k}^{+})=0\). Then, for \(t\in (t_{k},t_{k+1})\), we have

$$ V\bigl(e(t)\bigr)\leq e^{L(t-t_{k})}V\bigl(e\bigl(t_{k}^{+}\bigr) \bigr)\to0 \quad \mbox{as } t\to\infty, $$

which shows that \(\lim_{t\to\infty}\|e_{i}(t)\|=0\), that is, the synchronization of drive-response delayed neural networks (2) and (4) is achieved, and the proof is completed. □

Remark 1

For any given neural network (2), the positive constants \(L_{f}\) and \(L_{g}\) in Assumption 1 and the largest eigenvalue λ can be estimated by simple calculations. Thus, if the constant α and the impulsive gain \(b(t_{k})\) are fixed, then from conditions (6) the impulsive intervals \(d_{k}\) can be estimated. However, the neuron activation functions and coefficient matrices are usually nonidentical for different neural networks, that is, the proposed impulsive controllers with fixed impulsive intervals are not universal. In the following, adaptive strategy is adopted to design universal impulsive controllers.

Theorem 2

Suppose that Assumptions 1 and 2 hold. If there exists a constant \(\alpha>0\) such that

$$ \ln\beta(t_{k})+\alpha+\hat{L}(t_{k})d_{k}< 0, \quad k=1,2,\ldots, $$
(9)

where \(\hat{L}(t)\) is the time-varying estimation of L satisfying \(\dot{\hat{L}}(t)=\delta e^{T}(t)e(t)\) with \(\hat{L}(0)>0\), and \(\delta >0\) is the adaptive gain, then the synchronization of drive-response delayed neural networks (2) and (4) is achieved.

Proof

Consider the following Lyapunov functional candidate:

$$ V\bigl(e(t)\bigr)=\frac{1}{2}e^{T}(t)e(t)+\frac{\beta(t)}{4\delta} \bigl(\hat {L}(t)-L\bigr)^{2}+\frac{\beta(t)}{1-\mu} \int_{t-\tau(t)}^{t}e^{T}(\theta)e(\theta )\,d \theta. $$

When \(t\in(t_{k-1},t_{k})\), the function \(V(e(t))\) can be written as

$$ V\bigl(e(t)\bigr)=\frac{1}{2}e^{T}(t)e(t)+\frac{1}{4\delta} \bigl(\hat{L}(t)-L\bigr)^{2}+\frac {1}{1-\mu} \int_{t-\tau(t)}^{t}e^{T}(\theta)e(\theta)\,d \theta, $$

and the derivative of \(V(t)\) along the trajectory (5) is

$$\begin{aligned} \dot{V}\bigl(e(t)\bigr) =&e^{T}(t)\dot{e}(t)+\frac{1}{2\delta}\bigl( \hat{L}(t)-L\bigr)\dot {\hat{L}}(t)+\frac{1}{1-\mu}e^{T}(t)e(t) \\ &{}-\frac{1-\dot{\tau}(t)}{1-\mu}e^{T}\bigl(t-\tau(t)\bigr)e\bigl(t-\tau(t)\bigr) \\ \leq& \frac{L}{2}e^{T}(t)e(t)+\frac{1}{2}\bigl( \hat{L}(t)-L\bigr)e^{T}(t)e(t) \\ \leq& \hat{L}(t)V\bigl(e(t)\bigr). \end{aligned}$$

Since \(\hat{L}(t)\) is an increasing function, we have \(0<\hat{L}(t)\leq\hat{L}(t_{k})\) for \(t\in(t_{k-1},t_{k})\) and

$$\dot{V}\bigl(e(t)\bigr)\leq\hat{L}(t_{k})V\bigl(e(t)\bigr), $$

which gives

$$ V\bigl(e(t)\bigr)\leq V\bigl(e\bigl(t_{k-1}^{+}\bigr) \bigr)e^{\hat{L}(t_{k})(t-t_{k-1})}. $$
(10)

When \(t=t_{k}\), we have

$$\begin{aligned} V\bigl(e\bigl(t_{k}^{+}\bigr)\bigr) =& \frac{1}{2}e^{T}\bigl(t_{k}^{+}\bigr)e \bigl(t_{k}^{+}\bigr)+\frac{\beta(t_{k}^{+})}{4\delta }\bigl(\hat{L} \bigl(t_{k}^{+}\bigr)-L\bigr)^{2} \\ &{}+\frac{\beta(t_{k}^{+})}{1-\mu} \int_{t_{k}^{+}-\tau(t)}^{t_{k}^{+}}e^{T}(\theta )e(\theta)\,d \theta \\ =&\frac{(1+b(t_{k}))^{2}}{2}e^{T}\bigl(t_{k}^{-}\bigr)e \bigl(t_{k}^{-}\bigr)+\frac{\beta (t_{k})}{4\delta}\bigl(\hat{L}(t_{k})-L \bigr)^{2} \\ &{}+\frac{\beta(t_{k})}{1-\mu} \int_{t_{k}^{-}-\tau(t)}^{t_{k}^{-}}e^{T}(\theta )e(\theta)\,d \theta \\ =& \beta(t_{k})V\bigl(e\bigl(t_{k}^{-}\bigr)\bigr). \end{aligned}$$
(11)

Then, similarly to the proof of Theorem 1, the proof can be completed. □

Remark 2

From conditions (9) in Theorem 2 it is clear that some constants with respect to the neuron activation functions and coefficient matrices need not be known beforehand. For any given neural network, the constants can be estimated by \(\hat{L}(t)\) with proper adaptive gain δ. When impulsive instants or intervals are fixed, we can give the updating law of impulsive gain with time from conditions (9). When impulsive gains are fixed, we can give a method for estimating the impulsive instants as well. Detailed methods are provided in the following remarks. That is, the proposed adaptive impulsive control scheme is universal for those neural networks, provided that their activation functions satisfy Assumption 1.

Remark 3

For any given impulsive intervals \(d_{k}\) and positive constant α, we can choose

$$ -e^{-\frac{\alpha+\hat{L}(t_{k})d_{k}}{2}}-1+\varepsilon\leq b(t_{k})\leq e^{-\frac{\alpha+\hat{L}(t_{k})d_{k}}{2}}-1- \varepsilon, $$

so that conditions (9) in Theorem 2 hold, where ε is a small positive constant.

Remark 4

By conditions (9), for any given \(b(t_{k})\) and α, we can estimate the control instants \(t_{k}\) through finding the maximum value of \(t_{k}\) subject to \(t_{k}< t_{k-1}-(\ln\beta(t_{k})+\alpha)\hat{L}^{-1}(t_{k})\) with \(t_{0}=0\), \(k=1,2,\ldots\) .

4 Numerical simulations

Example 1

Consider the chaotic delayed Hopfield neural network with time-varying delays as the drive system described by

$$ \dot{x}_{i}(t)=-c_{i}x_{i}(t)+\sum _{j=1}^{2}a_{ij}f_{j} \bigl(x_{j}(t)\bigr)+\sum_{j=1}^{2}b_{ij}g_{j} \bigl(x_{j}\bigl(t-\tau(t)\bigr)\bigr),\quad i=1,2, $$

where \(c_{i}=1\), \(f_{i}(x_{i})=g_{i}(x_{i})=\tanh(x_{i})\), \(\tau(t)=0.9-0.9\sin t\), and

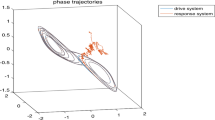
$$A=\left [\textstyle\begin{array}{@{}c@{\quad}c@{}} 2.1 & -0.12 \\ -5.1 & 3.2 \end{array}\displaystyle \right ],\qquad B= \left [\textstyle\begin{array}{@{}c@{\quad}c@{}} -1.6 & -0.1 \\ -0.2 & -2.4 \end{array}\displaystyle \right ]. $$

Clearly, we can choose \(L_{f}=L_{g}=1\) and \(\mu=0.9\) such that Assumptions 1 and 2 hold. In numerical simulations, choose \(b(t_{k})=-0.99\), \(d_{k}=0.08\), and \(\alpha =0.2\). By simple calculations we have \(\beta(t_{k})=0.0001\), \(\lambda =54.9719\), \(L=109.9438\), and \(\ln0.0001+0.2+109.9438\times 0.08=-0.2148<0\), that is, conditions (6) in Theorem 1 are satisfied. Therefore, the synchronization can be achieved when \(d_{k}=0.08\). Choose the initial values of \(x(t)\) and \(y(t)\) randomly. Figure 1 shows the orbits of state variables \(x_{i}(t)\) and \(y_{i}(t)\), \(i=1,2\).

Figure 1
figure 1

The orbits of state variables \(\pmb{x_{i}(t)}\) and \(\pmb{y_{i}(t)}\) , \(\pmb{i=1,2}\) .

Full size image

Example 2

Consider the synchronization of the same neural network via the adaptive impulsive control scheme proposed in Theorem 2. In numerical simulations, choose \(\delta=1\), the initial value of \(\hat{L}(t)\) as \(\hat{L}(0)=1\), and the other parameters as in the previous example.

Firstly, fix the impulsive interval \(d_{k}=0.08\) and choose \(b(t_{k})=e^{-\frac{\alpha+\hat{L}(t_{k})d_{k}}{2}}-1-\varepsilon\) with \(\varepsilon=0.001\) according to Remark 3. That is, the impulsive gain adjusts itself to proper value according to the adaptive law. Figure 2 shows the orbits of state variables \(x_{i}(t)\) and \(y_{i}(t)\) and impulsive gain.

Figure 2
figure 2

The orbits of state variables \(\pmb{x_{i}(t)}\) and \(\pmb{y_{i}(t)}\) and impulsive gain.

Full size image

Secondly, fix the impulsive gain \(b(t_{k})=-0.99\) and estimate the control instants \(t_{k}\) or impulsive interval \(d_{k}\) according to Remark 4. That is, the impulsive intervals adjust themselves to proper values according to the adaptive law. Figure 3 shows the orbits of state variables \(x_{i}(t)\) and \(y_{i}(t)\) and impulsive intervals. Clearly, the needed value of \(d_{k}\) is much larger than the estimated value from conditions (6). That is, the adaptive pinning impulsive control scheme can make the impulsive interval as large as possible and reduce the control cost.

Figure 3
figure 3

The orbits of state variables \(\pmb{x_{i}(t)}\) and \(\pmb{y_{i}(t)}\) and impulsive intervals.

Full size image

Example 3

Consider the synchronization of the following cellular neural network via the adaptive impulsive control, which is described by [28]:

$$ \dot{x}_{i}(t)=-c_{i}x_{i}(t)+\sum _{j=1}^{2}a_{ij}f_{j} \bigl(x_{j}(t)\bigr)+\sum_{j=1}^{2}b_{ij}g_{j} \bigl(x_{j}\bigl(t-\tau(t)\bigr)\bigr),\quad i=1,2, $$

where \(c_{i}=1\), \(f_{i}(x_{i})=g_{i}(x_{i})=(|x_{i}+1|-|x_{i}-1|)/2\), \(\tau(t)=1\), and

$$\begin{aligned}& A=\left [\textstyle\begin{array}{@{}c@{\quad}c@{}} 1+\pi/4 & 20 \\ 0.1 & 1+\pi/4 \end{array}\displaystyle \right ], \\& B=\left [\textstyle\begin{array}{@{}c@{\quad}c@{}} -13\sqrt{2}\pi/40 & 0.1 \\ 0.1 & -13\sqrt{2}\pi/40 \end{array}\displaystyle \right ]. \end{aligned}$$

Firstly, fix the impulsive interval \(d_{k}=0.5\) and choose \(b(t_{k})=e^{-\frac{\alpha+\hat{L}(t_{k})d_{k}}{2}}-1-\varepsilon\) with \(\alpha=0.5\) and \(\varepsilon=0.001\). In numerical simulations, choose \(\delta=0.2\), the initial value of \(\hat{L}(t)\) as \(\hat{L}(0)=1\), and the initial values of \(x(t)\) and \(y(t)\) randomly. Figure 4 shows the orbits of state variables \(x_{i}(t)\) and \(y_{i}(t)\) and impulsive gain.

Figure 4
figure 4

The orbits of state variables \(\pmb{x_{i}(t)}\) and \(\pmb{y_{i}(t)}\) and impulsive gain.

Full size image

Secondly, fix the impulsive gain \(b(t_{k})=-0.8\) and estimate the control instants \(t_{k}\) or impulsive interval according to Remark 4. In numerical simulations, choose \(\alpha=0.2\), \(\delta=0.2\), the initial value of \(\hat{L}(t)\) as \(\hat{L}(0)=0.2\), and the initial values of \(x(t)\) and \(y(t)\) randomly. Figure 5 shows the orbits of state variables \(x_{i}(t)\) and \(y_{i}(t)\) and impulsive intervals.

Figure 5
figure 5

The orbits of state variables \(\pmb{x_{i}(t)}\) and \(\pmb{y_{i}(t)}\) and impulsive intervals.

Full size image

5 Conclusions

In this paper, the synchronization problem of drive-response chaotic delayed neural networks has been investigated via impulsive control scheme. Firstly, some sufficient conditions for achieving synchronization were provided according to the Lyapunov function method and impulsive stability theory. For given neural networks, the largest impulsive interval can be estimated by fixing impulsive gains, and vice versa. Secondly, an adaptive strategy, combined with impulsive control scheme, was used to design universal controllers for different neural networks and relax the restrictions on impulsive intervals and gains. Finally, some numerical examples were performed to verify the correctness and effectiveness of the obtained results.