1 Introduction

In the last two decades, the chaotic systems have drawn considerable attention due to interesting features for secure communication. It can be applied to encode a message, which suggests that the secure message communication between sender and receiver can be guaranteed by chaos synchronization. But an isolated chaotic system is too sensible to tiny variations of initial data to synchronize with any other system. However, Pecora and Carroll [16] first introduced the idea that two chaotic systems can be synchronized even with different initial conditions. Since then, chaos synchronization has been flurry research activity over decades. Up to now, many researchers have studied the chaos synchronization and presented some interesting results [7, 11, 12, 27].

In recent years, stochastic systems have been a focal subject for research due to random disturbances that exist in real systems. Stochastic modeling plays an important role in many branches of science and industry. Therefore it is significant to consider stochastic effects for the stability property of systems [14]. It is well known that stability in probability, moment stability, and almost sure stability are three types of classical stochastic stability, which describe the asymptotic behavior of the solutions of stochastic systems as time goes to infinity. There are many research results on the stability of deterministic and stochastic systems [8–10, 13, 22]. However, in many practical control problems, it is often asked that the trajectories of the systems converge to an equilibrium state in finite time [4]. For deterministic systems, a Lyapunov-type theorem on finite-time stability was established by Bhat and Bernstein [1], but for the stochastic case, similar results were provided in [3, 23, 25]. Later, some improved results and applications were given in [17, 20, 21, 28]. Meanwhile, the synchronization of complex networks and neural networks under random environment were intensively investigated due to their potential applications in various fields; see [5, 18, 19, 24, 29, 30] and the references therein.

Motivated by the previous works on stability and synchronization for deterministic and stochastic systems, we will study the finite-time synchronization for chaotic neural networks disturbed by noise. At the same time, we also explore some basic characteristics with respect to the drive system, the response system, and the synchronization error system. The rest of the paper is organized as follows. In Sect. 2, we give some notations and preliminaries and provide a generalized definition of finite-time stability in probability. In Sect. 3, we design a novel control law such that the synchronization of the chaotic neural networks with stochastic disturbances can be reached in finite time. In Sect. 4, we provide simulation results to show the effectiveness and feasibility of the proposed method. Finally, we give a conclusion in Sect. 5.

2 Notations and preliminary results

Let \(\|x\|\) be the Euclidean norm of x on \(\mathbb{R}^{n}\), let \(\mathrm{1}_{x}:=x/\|x\|\mathrm{1}_{x\neq 0}\), \(x\in \mathbb{R}^{n}\), and let \(\mathbb{R}^{+}\) be the interval \([0,+\infty )\). Denote by \(\operatorname{diag}(a_{1},a_{2},\ldots,a_{n})\) the \(n\times n\) diagonal matrix with diagonal entries \(a_{1}, a_{2}, \ldots, a_{n}\). Denote \(\|z\|^{2}=\operatorname*{trace}(z^{T} z)\) for any \(z\in \mathbb{R}^{n\times d}\) and \(\|x\|_{T}:=\sup_{t_{0}\leq t\leq T} \|x(t)\|\) for a deterministic continuous function \((x(t))_{t\geq 0}\). By \(C^{1,2}([t_{0},+\infty )\times \mathbb{R}^{n}; \mathbb{R}^{+})\) we denote the set nonnegative functions that are continuously twice differentiable in \(x\in \mathbb{R}^{n}\) and once differentiable in \(t\geq t_{0}\). Let \((B(t))_{t\geq 0}\) be a standard d-dimensional Brownian motion defined on a completed probability space \((\Omega , \mathscr{F}, \mathbb{P})\) endowed with natural filtration \((\mathscr{F}_{t})_{t\geq 0}\) generated by this Brownian motion.

We first introduce the stochastic differential equation (SDE)

$$ \mathrm {d}x(t) = f\bigl(t,x(t)\bigr) \,\mathrm {d}t + g\bigl(t, x(t) \bigr) \,\mathrm {d}B(t),\qquad x(t_{0})=x_{0},\quad t\geq t_{0}, $$
(1)

where \(f(t,x):[t_{0},+\infty )\times \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) and \(g(t,x):[t_{0},+\infty )\times \mathbb{R}^{n} \rightarrow \mathbb{R}^{n \times d}\) are Borel-measurable functions satisfying \(f(t,0)=g(t,0)\equiv 0\) for \(t\geq t_{0}\). For any nonnegative function \(V(t,x) \in C^{1,2}([t_{0},+\infty )\times \mathbb{R}^{n}; \mathbb{R}^{+})\), we put

$$ \mathscr{L}V(t,x) = V_{t}(t,x)+ V_{x}(t,x)f(t,x)+ \frac{1}{2}\operatorname*{trace}\bigl\{ g^{T}(t,x)V_{xx}(t,x)g(t,x) \bigr\} . $$

Set

$$ f^{\#}_{\rho }(t):=\sup \bigl\{ \bigl\Vert f(t,x) \bigr\Vert \mid \Vert x \Vert \leq \rho \bigr\} ,\quad t\geq t_{0}, \rho \geq 0. $$

We introduce the following assumptions for the coefficients f and g.

  1. (H1)

    Continuity: for any \(t\geq t_{0}\), \(f(t,x)\) is continuous in x;

  2. (H2)

    Monotonicity: \(\langle x-y, f(t,x)-f(t,y)\rangle \leq \mu (t)\|x-y\|^{2}\), \(x,y \in \mathbb{R}^{n}\), for some functions \(\mu : [t_{0},+\infty ] \rightarrow \mathbb{R}^{+}\) with \(\int _{t_{0}}^{T}\mu (s) \,\mathrm {d}s<+\infty \) for \(T\geq t_{0}\);

  3. (H3)

    Boundedness: \(\int _{t_{0}}^{T_{1}} f_{\rho }^{\#}(s) \,\mathrm {d}s<+\infty \), \(\int _{t_{0}}^{T_{2}} \Vert g(t,0) \Vert ^{2} \,\mathrm {d}t<+ \infty \) for \(T_{1}, T_{2} \geq t_{0}\);

  4. (H4)

    Lipschitz condition: \(\Vert g(t,x)-g(t,y) \Vert \leq \ell (t)\|x-y\|\), \(x,y \in \mathbb{R}^{n}\), for some functions \(\ell : [t_{0},+\infty ] \rightarrow \mathbb{R}^{+}\) with \(\int _{t_{0}}^{T}\ell ^{2}(s) \,\mathrm {d}s<+\infty \) for \(T\geq t_{0}\);

To establish our main results, we present the following definition and lemmas.

Lemma 1

(Theorem 3.21 in [15])

Let assumptions (H1)–(H4) be satisfied. If \(x_{0}\in \mathbb{R}^{n}\), then the SDE (1) has a unique continuous \(\mathscr{F}_{t}\)-adapted solution, which is denoted by \(x(t; t_{0}, x_{0})\).

Definition 1

(See definitions in [13, 23, 25, 26])

We set \(\tau _{x_{0}}:=\inf \{t\geq t_{0} \mid x(t;t_{0},x_{0}) =0 \} \), which is called the stochastic settling time. The trivial solution of SDE (1) is said to be stochastically finite-time stable if the equation admits a solution for any initial data \(x_{0}\in \mathbb{R}^{n}\) and the following properties hold:

  1. (i)

    Finite-time attractiveness in probability: For every initial value \(x_{0}\in \mathbb{R}^{n}\) and any solution \(x(t;t_{0}, x_{0})\), the first hitting time of \(x(t;t_{0},x_{0})\) is finite almost surely, \(\mathbb{P}(\tau _{x_{0}}<+\infty )=1\). Furthermore,

    $$ x(t+\tau _{x_{0}},t_{0},x_{0})=0,\quad \forall t \geq 0, \mathbb {P}\hbox{-}\mathrm {a.s.}, $$
  2. (ii)

    Stability in probability: For any solution \(x(t;t_{0},x_{0})\), every pair of \(\varepsilon \in (0,1)\) and \(r>0\), there exists \(\delta (\varepsilon , r, t_{0})>0\) such that

    $$ \mathbb{P}\bigl( \bigl\Vert x(t;t_{0}, x_{0}) \bigr\Vert \leq r \text{ for all } t\geq t_{0}\bigr) \geq 1-\varepsilon $$

    whenever \(\|x_{0}\|\leq \delta (\varepsilon , r, t_{0})\).

According to Theorem 2 in [26], we present the following lemma.

Lemma 2

(Theorem 2 in [26])

For SDE (1), suppose that there exists a positive definite radically unbounded function \(V(t,x)\in C^{1,2}([t_{0},+\infty )\times \mathbb{R}^{n}; \mathbb{R}^{+})\) with \(V(t,0)=0\) for all \(t\geq t_{0}\) and \(V(t,x)>0\) for \(t\geq t_{0}\), \(x\neq 0\), such that

$$ \mathscr{L}V(t,x) \leq 0,\quad \forall t\geq t_{0}, \forall x \in \mathbb{R}^{n}, $$
(2)

and for any \(t\geq t_{0}\) and \(x\in \mathbb{R}^{n}\setminus \{0\}\),

$$ 2K\bigl(V(t,x)\bigr) \bigl[\lambda (t)K\bigl(V(t,x)\bigr)+ \mathscr{L}V(t,x) \bigr] \leq K'\bigl(V(t,x)\bigr) \bigl\Vert V_{x}(t,x)g(t,x) \bigr\Vert ^{2}, $$
(3)

where \(\lambda (\cdot ): [t_{0},+\infty ) \rightarrow \mathbb{R}^{+}\) is a Borel-measurable function, and \(K(\cdot ): \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}\) is a continuously differentiable function with \(K'(s)\geq 0\), \(K(s)>0\) for any \(s>0\), and, moreover,

$$ \int _{0}^{c} \frac{1}{K (s)} \,\mathrm {d}s < +\infty ,\qquad \int _{t_{0}}^{c'} \lambda (s) \,\mathrm {d}s < +\infty ,\quad \forall c>0,c'>t_{0},\qquad \int _{t_{0}}^{+\infty } \lambda (s) \,\mathrm {d}s=+\infty . $$

Then the trivial solution of SDE (1) is stochastically finite-time stable, and the stochastic settling time \(\tau _{x_{0}}\) satisfies

$$ \mathbb {E}\biggl[ \int _{t_{0}}^{\tau _{x_{0}}}\lambda (s) \,\mathrm {d}s \biggr] \leq \int _{0}^{V(t_{0},x_{0})} \frac{1}{K (s)} \,\mathrm {d}s . $$

Corollary 1

If \(\lambda (t)=\kappa (t-t_{0})^{\theta }\) for \(t> t_{0}\) with \(\lambda (t_{0})=0\), \(\theta \in (-1,0)\), and \(\kappa >0 \), then

$$ \mathbb {E}\bigl[(\tau _{x_{0}}-t_{0})^{1+\theta }\bigr] \leq \frac{1+\theta }{\kappa } \int _{0}^{V(t_{0},x_{0})} \frac{1}{K (x)} \,\mathrm {d}x. $$

Corollary 2

If \(\lambda (t)=\kappa (t-t_{0})^{\theta }\) for \(t\geq t_{0}\) with \(\theta \in (0,1)\) and \(\kappa >0 \), then

$$ \mathbb {E}[\tau _{x_{0}}]\leq \biggl(\frac{1+\theta }{\kappa } \int _{0}^{V(t_{0},x_{0})} \frac{1}{K (x)} \,\mathrm {d}x \biggr)^{1/(1+\theta )}+t_{0}. $$

Corollary 3

If

$$ \lambda (t)= \textstyle\begin{cases} 0,& t_{0}\leq t \leq 1+t_{0}, \\ \frac{1}{t-t_{0}}, & t>t_{0}+1, \end{cases} $$

then we have

$$ \mathbb {E}\bigl[ \log (\tau _{x_{0}}-t_{0})\bigr]\leq \int _{0}^{V(t_{0},x_{0})} \frac{1}{K (x)} \,\mathrm {d}x. $$

Corollary 4

If \(t_{1}>t_{0}\), \(c>0\), and

$$ \lambda (t)= \textstyle\begin{cases} 0,& t_{0}\leq t \leq t_{1}, \\ c, & t>t_{1}, \end{cases} $$

then we have

$$ \mathbb {E}[\tau _{x_{0}}]\leq \frac{1}{c} \biggl[ \int _{0}^{V(t_{0},x_{0})} \frac{1}{K (x)} \,\mathrm {d}x +c t_{1} \biggr]. $$

Corollary 5

Furthermore, if we let \(\theta =0\), that is, \(\lambda (t) \equiv \kappa >0 \) with \(t\geq t_{0}\), then

$$ \mathbb {E}[\tau _{x_{0}} ]\leq \frac{1}{\kappa } \int _{0}^{V(t_{0},x_{0})} \frac{1}{K (x)} \,\mathrm {d}x+t_{0}. $$

Corollary 6

In practical problem for finite-time control, we usually take \(t_{0}=0\) and choose \(\lambda (s)\equiv \kappa >0 \). If we let

$$ K(x)=\mu x^{\chi }, \quad \forall x> 0, \mu >0, \chi \in (0,1), $$

then the estimate of settling time is

$$ \mathbb {E}[\tau _{x_{0}}] \leq \frac{V^{1-\chi }(0,x_{0})}{\kappa \mu (1-\chi )}. $$

Corollary 7

If \(t_{0}=0\), \(\lambda (s)\equiv \kappa >0 \), and

$$ K (x)=k_{1} x^{\chi _{1}} + k_{2} x^{\chi _{2}},\quad x \geq 0, \textit{with } k_{1},k_{2}>0, 0< {\chi _{1}}< 1 < {\chi _{2}}, $$

then the settling time is estimated by

$$ \begin{aligned} \mathbb {E}[\tau _{x_{0}} ]&\leq \frac{1}{\kappa } \int _{0}^{x_{0}} \frac{1}{k_{1}x^{\chi _{1}} +k_{2}x^{\chi _{2}} } \,\mathrm {d}x \leq \frac{1}{\kappa } \int _{0}^{+\infty } \frac{1}{k_{1}x^{\chi _{1}} +k_{2}x^{\chi _{2}} } \,\mathrm {d}x \\ &= \frac{1}{\kappa } \int _{0}^{1} \frac{1}{k_{1}x^{\chi _{1}} } \,\mathrm {d}x + \frac{1}{\kappa } \int _{1}^{+\infty } \frac{1}{ k_{2}x^{\chi _{2}} } \,\mathrm {d}x= \frac{1}{ k_{1}\kappa (1-{\chi _{1}})} + \frac{1}{k_{2}\kappa ({\chi _{2}} -1)}, \end{aligned} $$

which implies that the trivial solution of SDE (1) can achieve fixed-time stability.

3 Finite-time synchronization of chaotic neural networks

Now we consider the following drive system, which is a deterministic neural network:

$$ \mathrm {d}x(t)= \bigl[-\bar{B}x(t)+A\psi \bigl(x(t)\bigr) \bigr] \,\mathrm {d}t,\qquad x(0)=x_{0}, $$
(4)

where

$$ \begin{aligned} &x(t)=\bigl[x_{1}(t),\ldots , x_{n}(t)\bigr]^{T},\qquad \bar{B}=\operatorname{diag}(b_{1}, \ldots , b_{n}), \\ &A=(a_{i,j})_{n\times n},\qquad \psi (x)=\bigl[\psi _{1}(x_{1}), \ldots , \psi _{n}(x_{n}) \bigr]^{T}. \end{aligned} $$

Based on the drive-response concept for synchronization control of chaotic systems, we suppose that the response system with stochastic perturbation depends on the synchronization error. Then it can be described by the following SDE:

$$ \mathrm {d}y(t) = \bigl[-\bar{B}y(t)+A\psi \bigl(y(t)\bigr) \bigr] \,\mathrm {d}t + \sigma \bigl(t,e(t)\bigr) \,\mathrm {d}B(t),\qquad y(0)=y_{0}, $$
(5)

where \(e(t)= y(t)-x(t) \).

Our aim is to make the response system synchronize with the drive system in finite time by the designed controller

$$ u(t)=-\varGamma e(t) - \lambda (t) \bigl(\eta _{1} \bigl\Vert e(t) \bigr\Vert ^{\alpha }+ \eta _{2} \bigl\Vert e(t) \bigr\Vert ^{\beta } \bigr) \mathrm{1}_{\{e(t)\}}, $$
(6)

where \(\eta _{1},\eta _{2}>0\), \(0<\alpha < 1< \beta \), and \(\lambda (t)\geq 0\), \(t\geq 0\), with

$$ \Lambda (t)= \int _{0}^{t}\lambda (s) \,\mathrm {d}s< +\infty , \quad t \geq 0,\quad \text{and}\quad \Lambda (t)\longrightarrow +\infty\quad \text{as } t \longrightarrow +\infty . $$

Then we consider the response system with controller \(u(t)\) in the drift term:

$$ \mathrm {d}y(t) = \bigl[-\bar{B}y(t)+A\psi \bigl(y(t)\bigr) + u(t) \bigr] \,\mathrm {d}t + \sigma \bigl(t,e(t)\bigr) \,\mathrm {d}B(t),\quad t \geq 0. $$
(7)

Subtracting system (4) from (7), we obtain the following error dynamical system:

$$ \mathrm {d}e(t) = \bigl[-\bar{B}e(t)+A\tilde{\psi }(t) + u(t) \bigr] \,\mathrm {d}t + \sigma \bigl(t,e(t)\bigr) \,\mathrm {d}B(t), \quad t\geq 0, $$
(8)

where \(\tilde{\psi }(t):=\psi (y(t))-\psi (x(t))\) and \(e(0)=y_{0}-x_{0} \).

We further introduce the following assumptions.

  1. (A1)

    ψ satisfies the Lipschitz condition: There exists a matrix M of proper dimension such that

    $$ \bigl\Vert \psi (x)-\psi (y) \bigr\Vert \leq \bigl\Vert M (x-y) \bigr\Vert , \quad \forall x, y \in \mathbb{R}^{n} ; $$
  2. (A2)

    σ satisfies the Lipschitz condition: There exists a matrix N of proper dimension such that

    $$ \bigl\Vert \sigma (t,x)-\sigma (t,y) \bigr\Vert \leq \bigl\Vert N(x-y) \bigr\Vert ,\quad \forall x, y \in \mathbb{R}^{n} ; $$
  3. (A3)

    There exists a constant \(C>0\) such that

    $$ \bigl\Vert \psi (x) \bigr\Vert \leq C\bigl(1+ \Vert x \Vert \bigr),\quad \forall x\in \mathbb{R}^{n}; $$
  4. (A4)

    \(\sigma (t,0)=0\), \(\forall t\geq 0\).

For the systems discussed, we have the following basic results.

Theorem 1

Assume that assumptions (H1)–(H4) and (A1)–(A4) hold. Then all the systems, that is, drive system (4), response system (7), and error system (8), have a unique continuous solution.

Proof

The existence and uniqueness of a solution for the drive system (4) was discussed in [6]. Due to this reason, here we omit the discussion.

Then choosing the control law \(u(t)\) of the form (6), we can write the response system (7) and the error dynamical system (8) as

$$ \mathrm {d}y(t) = \bigl[-\bar{B}y(t)+A\psi \bigl(y(t)\bigr) + \hat{u}\bigl(t,y(t)-x(t)\bigr) \bigr] \,\mathrm {d}t + \sigma \bigl(t,y(t)-x(t)\bigr) \,\mathrm {d}B(t) $$
(9)

and

$$ \mathrm {d}e(t) = \bigl[-\bar{B}e(t)+A\hat{\psi }\bigl(t,e(t) \bigr) + \hat{u}\bigl(t,e(t)\bigr) \bigr] \,\mathrm {d}t + \sigma \bigl(t,e(t)\bigr) \,\mathrm {d}B(t),\quad t\geq 0, $$
(10)

respectively, where \(\hat{u}(t,z) :=-\varGamma z - \lambda (t) (\eta _{1} \|z\|^{\alpha } +\eta _{2} \|z\|^{\beta } ) \mathrm{1}_{z} \), and \(\hat{\psi }(t,z):=\psi (z+x(t))-\psi (x(t))\) for \(t \geq 0\) and \(z\in \mathbb{R}^{n}\).

Now we will prove the existence and uniqueness of solutions to systems (9) and (10). We first consider the response systems (9), which is a stochastic system with drift term \(f^{r}\) and diffusion term \(g^{r}\). Here \(f^{r}\) and \(g^{r}\) are defined as follows: for any \(t\geq 0\) and \(z\in \mathbb{R}^{n}\),

$$ f^{r}(t,z):= -\bar{B}z+A\psi (t,z)+\hat{u}\bigl(t,z-x(t)\bigr) \quad \text{and}\quad g^{r}(t,z):= \sigma \bigl(t,z-x(t)\bigr), $$

where \(x(t)\) is the state of drive system at time t. Denote \(\tilde{f}(t,z)=-\bar{B}z+A\psi (z) \). Then the drift term can be rewritten as \(f ^{r}(t,z)=\tilde{f}(t,z)+\hat{u}(t,z-x(t))\).

On the one hand, for the drift term \(f^{r} \), we have, for any \(z, z' \in \mathbb{R}^{n}\),

$$ \begin{aligned} &\bigl\langle z-z', f^{r}(t,z)-f^{r}\bigl(t,z'\bigr) \bigr\rangle \\ &\quad = \bigl\langle z-z', \tilde{f}(t,z)-\tilde{f} \bigl(t,z'\bigr) \bigr\rangle + \bigl\langle z-z', \hat{u}\bigl(t,z-x(t)\bigr)-\hat{u}\bigl(t,z'-x(t)\bigr) \bigr\rangle \\ &\quad \leq \bigl\langle z-z', -\bar{B}\bigl(z-z' \bigr)+A \bigl({\psi }(z)- {\psi }\bigl(z'\bigr) \bigr)+\hat{u} \bigl(t,z-x(t)\bigr)-\hat{u}\bigl(t,z'-x(t)\bigr) \bigr\rangle . \end{aligned} $$
(11)

The Lipschitz condition about ψ implies that

$$ \bigl\langle z-z', A \bigl({\psi }(z)- {\psi }\bigl(z'\bigr) \bigr) \bigr\rangle \leq \Vert A \Vert \Vert M \Vert \bigl\Vert z-z' \bigr\Vert ^{2}. $$
(12)

Since for any \(z, z' \in \mathbb{R}^{n}\),

$$ \begin{aligned} & \bigl\langle z-z', \Vert z \Vert ^{\alpha }\mathrm{1}_{z} - \bigl\Vert z' \bigr\Vert ^{\alpha }\mathrm{1}_{z'} \bigr\rangle \\ &\quad = \bigl\langle z, \Vert z \Vert ^{\alpha }\mathrm{1}_{z} \bigr\rangle - \bigl\langle z, \bigl\Vert z' \bigr\Vert ^{\alpha }\mathrm{1}_{z'} \bigr\rangle - \bigl\langle z', \Vert z \Vert ^{\alpha }\mathrm{1}_{z} \bigr\rangle + \bigl\langle z', \bigl\Vert z' \bigr\Vert ^{\alpha }\mathrm{1}_{z'} \bigr\rangle \\ &\quad \geq \Vert z \Vert ^{\alpha +1} - \Vert z \Vert \bigl\Vert z' \bigr\Vert ^{\alpha } - \bigl\Vert z' \bigr\Vert \Vert z \Vert ^{ \alpha } + \bigl\Vert z' \bigr\Vert ^{\alpha +1} \\ &\quad = \bigl( \Vert z \Vert ^{\alpha }- \bigl\Vert z' \bigr\Vert ^{\alpha }\bigr) \bigl( \Vert z \Vert - \bigl\Vert z' \bigr\Vert \bigr) \geq 0, \end{aligned} $$

we can get

$$ \bigl\langle z-z', \hat{u}\bigl(t,z-x(t)\bigr)- \hat{u}\bigl(t,z'-x(t)\bigr) \bigr\rangle \leq - \bigl(z-z'\bigr)^{T}\varGamma \bigl(z-z' \bigr)\leq \Vert \varGamma \Vert \bigl\Vert z-z' \bigr\Vert ^{2}. $$
(13)

Combining (11), (12), and (13), we have

$$ \bigl\langle z-z', f^{r}(t,z)-f^{r}\bigl(t,z'\bigr) \bigr\rangle \leq \bigl( \Vert \bar{B} \Vert + \Vert A \Vert \Vert M \Vert + \Vert \varGamma \Vert \bigr) \bigl\Vert z-z' \bigr\Vert ^{2}. $$

Additionally, we observe that

$$ \bigl\Vert \tilde{f}(t,z) \bigr\Vert \leq \Vert \bar{B} \Vert \Vert z \Vert + C\bigl(1+ \Vert z \Vert \bigr) $$

and

$$ \begin{aligned} \bigl\Vert \hat{u}\bigl(t,z-x(t)\bigr) \bigr\Vert &= \bigl\Vert -\varGamma \bigl(z-x(t)\bigr) - \lambda (t) \bigl( \eta _{1} \bigl\Vert z-x(t) \bigr\Vert ^{\alpha }+\eta _{2} \bigl\Vert z-x(t) \bigr\Vert ^{\beta } \bigr) \mathrm{1}_{\{z-x(t)\}} \bigr\Vert \\ &\leq \Vert \varGamma \Vert \bigl( \Vert z \Vert + \bigl\Vert x(t) \bigr\Vert \bigr)+\eta _{1} \lambda (t) \bigl( \Vert z \Vert ^{ \alpha }+ \bigl\Vert x(t) \bigr\Vert ^{\alpha }\bigr) \\ &\quad {}+ \eta _{2} \lambda (t) \bigl( \Vert z \Vert + \bigl\Vert x(t) \bigr\Vert \bigr)^{ \beta }, \end{aligned} $$

which implies that for any \(t\in [0,T]\) with \(0< T<+\infty \),

$$ \begin{aligned} f^{r,\#}_{\rho }(t) \leq {}&\sup _{ \Vert z \Vert \leq \rho } \bigl\Vert \tilde{f}(t,z) \bigr\Vert + \sup _{ \Vert z \Vert \leq \rho } \bigl\Vert \hat{u}\bigl(t,z-x(t)\bigr) \bigr\Vert \\ \leq {}& \rho \Vert \bar{B} \Vert + C(1+\rho )+ \Vert \varGamma \Vert \bigl(\rho + \bigl\Vert x(t) \bigr\Vert \bigr) + \eta _{1}\lambda (t) \bigl(\rho ^{\alpha } + \bigl\Vert x(t) \bigr\Vert ^{\alpha } \bigr) \\ &{}+\eta _{2}\lambda (t) \bigl(\rho + \bigl\Vert x(t) \bigr\Vert \bigr)^{\beta } \\ \leq {}& \rho \Vert \bar{B} \Vert + C(1+\rho )+ \Vert \varGamma \Vert \bigl(\rho + \Vert x \Vert _{T}\bigr) +\eta _{1} \lambda (t) \bigl(\rho ^{\alpha } + \Vert x \Vert _{T}^{\alpha } \bigr) \\ &{}+\eta _{2}\lambda (t) \bigl(\rho + \Vert x \Vert _{T} \bigr)^{\beta } \\ \leq {}&C_{1}^{\rho ,T}+C_{2}^{\rho ,T} \lambda (t), \end{aligned} $$

where \(C_{1}^{\rho ,T}:=\rho \|\bar{B}\|+ C(1+\rho )\|\varGamma \| (\rho + \|x \|_{T}) \) and \(C_{2}^{\rho ,T}:= \eta _{1} (\rho ^{\alpha } + \|x \|_{T}^{\alpha } ) + \eta _{2} (\rho + \|x \|_{T} )^{\beta } \). Therefore we can deduce that

$$ \int _{0}^{T} f^{r,\#}_{\rho }(t) \,\mathrm {d}t \leq C_{1}^{\rho ,T} T+ C_{2}^{ \rho ,T} \int _{0}^{T} \lambda (t) \,\mathrm {d}t< +\infty ,\quad \forall \rho , T>0. $$

On the other hand, for the diffusion term \(g^{r}\), we have, for any \(z, z' \in \mathbb{R}^{n}\),

$$ \bigl\Vert g^{r}(t,z)-g^{r}\bigl(t,z' \bigr) \bigr\Vert = \bigl\Vert \sigma \bigl(t,z-x(t)\bigr)-\sigma \bigl(t,z'-x(t)\bigr) \bigr\Vert \leq \Vert N \Vert \bigl\Vert z-z' \bigr\Vert $$

and

$$ \bigl\Vert g^{r}(t,0) \bigr\Vert = \bigl\Vert \sigma \bigl(t,x(t)\bigr) \bigr\Vert \leq \Vert N \Vert \bigl\Vert x(t) \bigr\Vert , \quad \forall t \geq 0, $$

which leads to

$$ \int _{0}^{T} \bigl\Vert g^{r}(t,0) \bigr\Vert \,\mathrm {d}t \leq \Vert N \Vert \Vert x \Vert _{T}T, \quad \forall T>0. $$

Based on the above discussion and Lemma 1, we can conclude that response system (9) has a unique solution.

To show that error dynamical system (10) also has a unique solution, we need to check the conditions in Lemma 1 for the coefficients \(f^{e}\) and \(g^{e}\) of error dynamical system (10). The procedure is even much simpler than those of response systems (9) since \(f^{e}(t,0)=g^{e}(t,0)=0\). Thus we omit it. The proof is completed. □

Theorem 2

Suppose that assumptions (A1)–(A2) and the following condition hold:

$$ -2\bar{B} +\varepsilon AA^{T} + \frac{1}{\varepsilon }M^{T} M +N^{T} N -2 \varGamma \leq 0$$
(14)

for some \(\varepsilon >0\), then the error dynamical system (10) is finite-time stable under the designed control law (6). Moreover, the settling time is estimated by

$$ \mathbb {E}\biggl[ \int _{0}^{\tau _{x_{0}}}\lambda (t) \,\mathrm {d}t \biggr] \leq \frac{1}{ \eta _{1}(1-\alpha )}+ \frac{1}{ \eta _{2} (\beta -1)}. $$

Proof

Choose the Lyapunov function as \(V(t,x) = x^{T} x\), for \(t\geq 0\) and \(x\in \mathbb{R}^{n}\) and set \(\hat{f} (t,x):=-\bar{B}x+A\hat{\psi }(t,x)+\hat{u}(t,x)\), \(\hat{g} (t,x):=\sigma (t,x)\). From condition (14) we get

$$ \begin{aligned} \mathscr{L}V(t,x) = {}& V_{t}(t,x)+ V_{x}(t,x)\hat{f} (t,x)+\frac{1}{2} \operatorname*{trace}\bigl\{ \hat{g} ^{T}(t,x)V_{xx}(t,x)\hat{g} (t,x) \bigr\} \\ = {}&{-}2x^{T} \bar{B}x + 2x^{T} A\hat{\psi }(t,x) +2x^{T} \hat{u}(t,x) + \operatorname*{trace}\bigl\{ \sigma ^{T}(t,x) \sigma (t,x) \bigr\} \\ \leq{}& x^{T} \biggl[ -2\bar{B} +\varepsilon AA^{T} + \frac{1}{\varepsilon }M^{T} M +N^{T} N -2 \varGamma \biggr] x \\ &{} - 2\lambda (t) \bigl[\eta _{1} \bigl(x^{T} x \bigr)^{\frac{\alpha +1}{2}}+ \eta _{2} \bigl(x^{T} x \bigr)^{\frac{\beta +1}{2}} \bigr] \\ \leq{}& {-}2\eta _{1} \lambda (t) \bigl(x^{T} x \bigr)^{\frac{\alpha +1}{2}}-2\eta _{2} \lambda (t) \bigl(x^{T} x\bigr)^{\frac{\beta +1}{2}} \\ ={}& {-}2\eta _{1} \lambda (t) \bigl(V(t,x)\bigr)^{\frac{\alpha +1}{2}}-2 \eta _{2} \lambda (t) (V(t,x)^{\frac{\beta +1}{2}} . \end{aligned} $$

Noting that \(\eta _{1}, \eta _{2}\geq 0\), \(V(t,x) \geq 0 \), and \(\lambda (t)\geq 0\) for any \(t\geq 0\) and \(x\in \mathbb{R}^{n}\), we can conclude that \(\mathscr{L}V(t,x)\leq 0\) and \(\lambda (t)K(V(t,x))+ \mathscr{L}V(t,x)\leq 0 \) with \(K(s)=2\eta _{1} s ^{\frac{\alpha +1}{2}}+2\eta _{2} s ^{ \frac{\beta +1}{2}}\) for \(s\geq 0\), which implies that conditions (2) and (3) are satisfied. Then by Lemma 2 we get that the error dynamical system (10) is finite-time stable, and the settling time satisfies

$$ \mathbb {E}\biggl[ \int _{0}^{\tau _{x_{0}}}\lambda (t) \,\mathrm {d}t \biggr] \leq \frac{1}{\eta _{1}(1-\alpha )}+ \frac{1}{\eta _{2} (\beta -1)}. $$

The proof is completed. □

Corollary 8

Furthermore, if \(\eta _{1}\neq 0\) and \(\eta _{2}=0\) in the controller u, then the settling time can be estimated by

$$ \mathbb {E}\biggl[ \int _{0}^{\tau _{x_{0}}}\lambda (t) \,\mathrm {d}t \biggr] \leq \frac{ \Vert x_{0}-y_{0} \Vert ^{ (1-\alpha )}}{ \eta _{1}(1-\alpha )}. $$

Corollary 9

If \(\lambda (t)\equiv \kappa \), then the estimate of the settling time is reduced to

$$ \mathbb {E}[\tau _{x_{0}} ]\leq \frac{1}{ \kappa \eta _{1}(1-\alpha )}+ \frac{1}{ \kappa \eta _{2} (\beta -1)}. $$

Furthermore, if \(\eta _{2}=0\), then we have

$$ \mathbb {E}[\tau _{x_{0}} ]\leq \frac{ \Vert x_{0}-y_{0} \Vert ^{ (1-\alpha )}}{ \kappa \eta _{1}(1-\alpha )}. $$

4 Simulations

To show the effectiveness of the methods provided, we consider the following 3-D chaotic cellular neural network as the drive system:

$$ \mathrm {d}x(t)= \bigl[-\bar{B}x(t)+A\psi \bigl(x(t)\bigr) \bigr] \,\mathrm {d}t, \quad t \geq 0,\qquad x(0)=x_{0}=[0.1, 0.1, 0.1 ]^{T}. $$
(15)

Moreover, the response system with stochastic perturbation is

$$ \mathrm {d}y(t) = \bigl[-\bar{B}y(t)+A\psi \bigl(y(t)\bigr) + u(t) \bigr] \,\mathrm {d}t + \sigma \bigl(t,e(t)\bigr) \,\mathrm {d}B(t),\qquad y(0)=y_{0}, $$
(16)

where \(e(t)= y(t)-x(t) \), \(\psi _{i}(x)=0.5 (|x_{i}+1|-|x_{i}-1| )\), \(i=1,2,3\), and

$$\begin{aligned}& \bar{B}= \begin{bmatrix} 1& 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} , \qquad A= \begin{bmatrix} 1.25& -3.2 & -3.2 \\ -3.2 & 1.1 & -4.4 \\ -3.2 & 4.4 & 1.0 \end{bmatrix} ,\qquad y_{0}=[0.8, -1.1, 1.2 ]^{T}, \\& \sigma (t,z)= \begin{bmatrix} x_{3}(t)-z_{3} & 2\sin (x_{1}(t)-z) \\ 2\sin (x_{3}(t)- z_{3}) & \vert x_{2}(t)-z_{2} \vert \\ \sin ( x_{1}(t)-z_{1}) & \sqrt{2}\sin (x_{2}(t)-z_{2}) \end{bmatrix} , \quad \forall t \geq 0, \text{and } z\in \mathbb{R}^{3}. \end{aligned}$$

From the results in [2] we know that (15) has a double scroll chaotic attractor. We also easily check that for any \(t\geq 0\) and \(z,z'\in \mathbb{R}^{3}\),

$$ \bigl\Vert \psi (z)-\psi \bigl(z'\bigr) \bigr\Vert \leq \bigl\Vert z-z' \bigr\Vert $$

and

$$ \bigl\Vert \sigma (t,z)-\sigma \bigl(t,z'\bigr) \bigr\Vert \leq \bigl\Vert \operatorname{diag}(\sqrt{5},\sqrt{3},\sqrt{5}) \bigl(z-z'\bigr) \bigr\Vert , $$

which implies that ψ and σ satisfy conditions (A1) and (A2) with \(M=I_{n}\) and \(N=\operatorname{diag}(\sqrt{5},\sqrt{3},\sqrt{5})\).

Therefore, using the Matlab toolbox to solve LMI in (14), we obtain

$$ \varGamma = \begin{bmatrix} 25.4913 & 6.5595 & -21.2785 \\ 6.5595 & 33.2578 & 10.6793 \\ -21.2785 & 10.6793 & 34.0476 \end{bmatrix} . $$

A. Finite-time synchronization

On the one hand, if the controller \(u_{1}\) is designed of the form

$$ u_{1}(t)=-\varGamma e(t) - \lambda (t) \bigl(\eta _{1} \bigl\Vert e(t) \bigr\Vert ^{\alpha }+\eta _{2} \bigl\Vert e(t) \bigr\Vert ^{\beta } \bigr) \mathrm{1}_{\{e(t)\}}, $$
(17)

with parameters \(\eta _{1}=1\), \(\eta _{2}=0\), \(\alpha =1/2\), \(\beta =2\), and

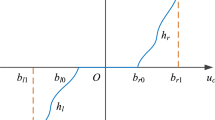
$$ \lambda (t)= \textstyle\begin{cases} 0,& 0\leq t \leq 1, \\ \frac{1}{t}, & t>1, \end{cases} $$

then the response system (16) can synchronize with the drive system (15) in finite time. The phase trajectories of the drive system and response system are depicted in Fig. 1. Figure 2 shows the designed control law. Additionally, we can also see from Fig. 3 that the response system (16) and the drive system (15) are synchronized in finite time

Figure 1
figure 1

The phase trajectories of the drive and response systems

Full size image
Figure 2
figure 2

The control law of the response system

Full size image
Figure 3
figure 3

The synchronization errors under the control law of \(u_{1}\)

Full size image

B. Fixed-time synchronization

On the other hand, if we design the controller \(u_{2}\) with parameters \(\lambda (t)\equiv 1\), \(t \geq 0\), and \(\eta _{1}=1 \), \(\eta _{2}=3 \), \(\alpha =1/2\), \(\beta =2\), then the response system (16) can synchronize with the drive system (15) in fixed time. Also, we make numerical studies, and the results are displayed in Fig. 4.

Figure 4
figure 4

Simulations for fixed-time case

Full size image

Compared with the previous simulations, the controllers \(u_{1}\) and \(u_{2}\) can greatly shorten the settling time of the synchronization error system and make the response system disturbed by noise converge quickly to the deterministic drive system. Then these types of control laws may have a better applicability.

5 Conclusions

In this paper, we studied the problem of finite/fixed-time stability for chaotic neural networks with noise perturbations by a continuous controller. By using Lyapunov stability theory and the LMI technique, we derived sufficient conditions guaranteeing the synchronization of stochastically chaotic neural networks to be realized in finite or fixed time. Finally, we provided a numerical example demonstrating the usefulness of the main results.