Stability analysis for HIV infection of CD4⁺ T-cells by a fractional differential time-delay model with cure rate

Abstract

In this paper, a fractional differential model of HIV infection of CD4⁺ T-cells is investigated. We shall consider this model, which includes full logistic growth terms of both healthy and infected CD4⁺ T-cells, time delay items, and cure rate items. A more appropriate method is given to ensure that both equilibria are asymptotically stable for $\tau \ge 0$ under some conditions. Furthermore, the dynamic behaviors of the fractional HIV models are described by applying an Amads-type predictor-corrector method algorithm.

1 Introduction

Mathematical models have played an important role in understanding the dynamics of HIV infection; there are several papers introducing the Human Immunodeficiency Virus (HIV) [1, 2]. When HIV infects the body, its target is the CD4⁺ T-cell. In these years, mathematical models have been proven valuable in the dynamics of HIV infection. Meanwhile, there are only some works for the dynamics of HIV infections of CD4⁺ T-cells [3, 4].

The consideration of the cure (or recovery) rate of infected cells is significant in the modeling for viral dynamics. The covalently closed circular (ccc) DNA of Hepatitis B viral has been shown to be eliminated from the nucleus of infected cells in the absence of hepatocyte injury during transient infections [5]. In 2010, Wang et al. [6] built and studied an improved HBV model with a standard incidence function and ‘cure’ rate. Inspired by the HBV dynamic model with cure rate, Zhou et al. [7] firstly introduced the cure rate into the HIV infection model. In recent years, the HIV model with cure rate has received a great deal of attention (see e.g. [8–11]).

In 2011, Liu et al. [12] considered a new model frame that included full logistic growth terms of both healthy and infected CD4⁺ T-cells:

$$\{\begin{array}{l}{T}^{\prime }(t)=s-\alpha T(t)+rT(t)(1-\frac{T(t)+I(t)}{T_{max}})-kT(t)V(t)+\rho I(t),\\ I^{\prime }(t)=kT(t)V(t)+rI(t)(1-\frac{T(t)+I(t)}{T_{max}})-(\beta +\rho )I(t),\\ V^{\prime }(t)=N\beta I(t)-dV(t).\end{array}$$

(1.1)

Fractional differential equations have been widely used in various fields, such as physics, chemical technology, biotechnology, and economics in recent years (see e.g. [13–16]). As is well known, the boundary value problem is an important topic, there is a great deal of attention for this (see [17–26]).

We introduce the fractional calculus into the HIV model for the memory property of fractional calculus. Both in mathematics and biology, fractional calculus will be more in line with the actual situation. It is particularly of significance for us to study the fractional HIV model.

Recently, Yan and Kou [2] have introduced fractional-order derivatives into a model of HIV infection of CD4⁺ T-cells with time delay:

$$\{\begin{array}{l}{D}^{\alpha }T(t)=s-{\mu }_{T}T(t)+rT(t)(1-\frac{T(t)+I(t)}{T_{max}})-k_{1}T(t)V(t),\\ D^{\alpha }I(t)=k_1^{\prime }T(t-\tau )V(t-\tau )-{\mu }_{I}I(t),\\ D^{\alpha }V(t)=N{\mu }_{b}I(t)-k_{1}T(t)V(t)-{\mu }_{v}V(t),\end{array}$$

(1.2)

with the initial conditions:

$$T(\theta )=T_0,I(0)=0,V(\theta )=V_0,\theta \in [-\tau ,0].$$

(1.3)

Motivated by the works mentioned above, we shall consider this model, which includes full logistic growth terms of both healthy and infected CD4⁺ T-cells, time delay items, and cure rate items; a more appropriate method is given to ensure that both equilibria are asymptotically stable for $\tau \ge 0$. In this paper, we establish the mathematical model as follows:

$$\{\begin{array}{l}{D}^{\alpha }T(t)=s-{\mu }_{T}T(t)+rT(t)(1-\frac{T(t)+I(t)}{T_{max}})-kT(t)V(t)+\rho I(t),\\ D^{\alpha }I(t)=k^{\prime }T(t-\tau )V(t-\tau )+rI(t)(1-\frac{T(t)+I(t)}{T_{max}})-({\mu }_I+\rho )I(t),\\ D^{\alpha }V(t)=N{\mu }_{b}I(t)-{\mu }_{v}V(t),\end{array}$$

(1.4)

with the initial conditions:

$$T(\theta )=T_0,I(0)=0,V(\theta )=V_0,\theta \in [-\tau ,0],$$

(1.5)

where $D^{\alpha }$ denotes the Caputo fractional derivative of order α with the lower limit zero. $T(t)$, $I(t)$, $V(t)$ represent the concentration of healthy CD4⁺ T-cell at time t, infected CD4⁺ T-cells at time t, and free HIV virus particles in the blood at time t, respectively. The positive constant τ represents the length of the delay in days. A complete list of the parameter values for the model is given in Table 1 (see [3]).

Table 1 Parameters and values of model ( 1.4 )

Furthermore, we assume that $T(t)>0$, $I(t)\ge 0$ and $V(t)\ge 0$ for all $t\ge -\tau$.

This article is organized in the following way. In the next section, some necessary definitions and lemmas are presented. In Section 3, the stability of the equilibria is given. In Section 4, we will give the numerical simulation for the fractional HIV model. Finally, the conclusions are given.

2 Preliminaries

In this section, we introduce some definitions and lemmas, which will be used later.

Definition 2.1 ([13, 14])

The fractional (arbitrary) order integral of the function $f:[0,\mathrm{\infty })\to R$ of order $p>0$ is defined by

$$I^{p}f(x)=\frac{1}{\mathrm{\Gamma }(p)}{\int }_0^x{(x-s)}^{p-1}f(s)ds.$$

Definition 2.2 ([13])

Let $\alpha \ge 0$, $n=[\alpha ]+1$, $n-1<\alpha \le n$, where $[\alpha ]$ denotes the integer part of number α. If $f\in A{C}^n[a,b]$, the Caputo fractional derivative of order α of f is defined by

$${}^{c}D^{\alpha }f(t)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_a^t\frac{f^{(n)}(s)}{{(t-s)}^{\alpha +1-n}}ds,t>0,n-1<\alpha <n.$$

Lemma 2.1 ([27, 28])

The equilibrium point $(x_{\mathrm{eq}},y_{\mathrm{eq}})$ of the fractional differential system

$$\{\begin{array}{l}{D}^{\alpha }x(t)=f_1(x,y),D^{\alpha }y(t)=f_2(x,y),\alpha \in (0,1],\\ x(0)=x_0,y(0)=y_0\end{array}$$

is locally asymptotically stable if all the eigenvalues of the Jacobian matrix

$$A=\left(\begin{array}{cc}\frac{\partial f_1}{\partial x}& \frac{\partial f_1}{\partial y}\\ \frac{\partial f_2}{\partial x}& \frac{\partial f_2}{\partial y}\end{array}\right)$$

evaluated at the equilibrium point satisfy the following condition:

$$|arg(eig(A))|>\frac{\alpha \pi }{2}.$$

Thestable and unstable regions for $0<\alpha \le 1$ are shown in Figure 1 [27, 29, 30].

Figure 1

Stability region of system ( 1.4 ) with order $\mathbf{0}\mathbf{<}\mathit{\alpha }\mathbf{\le }\mathbf{1}$ .

3 The stability of the equilibria

In this section, we investigate the existence of equilibria of system (1.4).

In order to find the equilibria of system (1.4), we put

$$\{\begin{array}{l}s-{\mu }_{T}T(t)+rT(t)(1-\frac{T(t)+I(t)}{T_{max}})-kT(t)V(t)+\rho I(t)=0,\\ k^{\prime }T(t-\tau )V(t-\tau )+rI(t)(1-\frac{T(t)+I(t)}{T_{max}})-({\mu }_I+\rho )I(t)=0,\\ N{\mu }_{b}I(t)-{\mu }_{v}V(t)=0.\end{array}$$

(3.1)

Following the analysis in [12], we find that system (3.1) has always the uninfected equilibrium $E_0=(T_0,0,0)$, where

$$T_0=\frac{T_{max}}{2r}(r-{\mu }_T+\sqrt{{(r-{\mu }_T)}^2+\frac{4rs}{T_{max}}}).$$

We define the parameter $N_{\mathrm{crit}}$ as

$$N_{\mathrm{crit}}=\frac{{\mu }_V}{k^{\prime }{\mu }_I{T}_0}(\frac{s}{T_0}+{\mu }_I-{\mu }_T+\rho )$$

and we also find that, if $N>N_{\mathrm{crit}}$, system (3.1) has a unique positive equilibrium, $E^{\ast }(T^{\ast },I^{\ast },V^{\ast })$. If $N=\frac{r{\mu }_V}{k^{\prime }{\mu }_I{T}_{max}}$, system (3.1) has a unique positive equilibrium $E^{\ast }(T^{\ast },I^{\ast },V^{\ast })$, where

$$\begin{array}{c}{T}^{\ast }=\frac{T_{max}}{2r}[2({\mu }_I+\rho )-r-{\mu }_T+\sqrt{{[r+{\mu }_T-2({\mu }_I+\rho )]}^2+4\rho (r-{\mu }_I-\rho )+\frac{4rs}{T_{max}}}],\hfill \\ I^{\ast }=\frac{{\mu }_V{V}^{\ast }}{N{\mu }_I},V^{\ast }=\frac{r-{\mu }_I-\rho }{k}.\hfill \end{array}$$

Next, we shall discuss the stability for the local asymptotic stability of the viral free equilibrium $E_0$ and the infected equilibrium $E^{\ast }$.

To discuss the stability of system (1.4), let us consider the following coordinate transformation:

$$x(t)=T(t)-\overline{T},y(t)=I(t)-\overline{I},z(t)=V(t)-\overline{V},$$

where $(\overline{T},\overline{I},\overline{V})$ denotes any equilibrium of (1.4). So we see that the corresponding linearized system of (1.4) is of the form

$$\{\begin{array}{l}{D}^{\alpha }x(t)=x(t)(-{\mu }_T+r-\frac{2r\overline{T}+r\overline{I}}{T_{max}}-k\overline{V})+y(t)(\rho -\frac{r\overline{T}}{T_{max}})-k\overline{T}z(t),\\ D^{\alpha }y(t)=k^{\prime }\overline{V}x(t-\tau )+k^{\prime }\overline{T}z(t-\tau )\\ \phantom{D^{\alpha }y(t)=}+y(t)(r-\frac{r\overline{T}+2r\overline{I}}{T_{max}}-({\mu }_I+\rho ))-\frac{r\overline{I}}{T_{max}}x(t),\\ D^{\alpha }z(t)=N{\mu }_{b}y(t)-{\mu }_{V}z(t).\end{array}$$

(3.2)

The characteristic equation of system (3.2) at $(\overline{T},\overline{I},\overline{V})$ is given by

$$\left|\begin{array}{ccc}\lambda -(-{\mu }_T+r-\frac{2r\overline{T}+r\overline{I}}{T_{max}}-k\overline{V})& -\rho +\frac{r\overline{T}}{T_{max}}& k\overline{T}\\ -k^{\prime }\overline{V}{e}^{-\lambda \tau }+\frac{r\overline{I}}{T_{max}}& \lambda -(r-({\mu }_I+\rho )-\frac{r\overline{T}+2r\overline{I}}{T_{max}})& -k^{\prime }\overline{T}{e}^{-\lambda \tau }\\ 0& -N{\mu }_b& \lambda +{\mu }_V\end{array}\right|=0.$$

For the local asymptotic stability of the viral free equilibrium $E_0$, we have the following result.

Theorem 3.1 If $N<N_{\mathrm{crit}}$, the uninfected state $E_0=(T_0,0,0)$ is locally asymptotically stable for $\tau \ge 0$.

Proof The associated transcendental characteristic equation at $E_0=(T_0,0,0)=(\overline{T},\overline{I},\overline{V})$ is given by

$$(\lambda +{\mu }_T-r+\frac{2r{T}_0}{T_{max}})((\lambda +{\mu }_V)(\lambda -r+{\mu }_I+\rho +\frac{r{T}_0}{T_{max}})-N{\mu }_b{k}^{\prime }{T}_0{e}^{-\lambda \tau })=0.$$

Obviously, the above equation has the characteristic root

$${\lambda }_1=r-{\mu }_T-\frac{2r{T}_0}{T_{max}}<0,$$

where $T_0=\frac{T_{max}}{2r}(r-{\mu }_T+\sqrt{{(r-{\mu }_T)}^2+\frac{4rs}{T_{max}}})$.

Next, we consider the transcendental polynomial

$${\lambda }^2+\lambda ({\mu }_V-r+{\mu }_I+\rho +\frac{r{T}_0}{T_{max}})+{\mu }_I{\mu }_V-r{\mu }_V+{\mu }_V\rho +\frac{r{T}_0{\mu }_V}{T_{max}}-N{\mu }_b{k}^{\prime }{T}_0{e}^{-\lambda \tau }=0.$$

For $\tau =0$, we get

$${\lambda }^2+\lambda ({\mu }_V-r+{\mu }_I+\rho +\frac{r{T}_0}{T_{max}})+{\mu }_I{\mu }_V-r{\mu }_V+{\mu }_V\rho +\frac{r{T}_0{\mu }_V}{T_{max}}-N{\mu }_b{k}^{\prime }{T}_0=0.$$

Then we note that

$${\mu }_I-r+\rho +\frac{r{T}_0}{T_{max}}=\frac{{\mu }_b}{{\mu }_I}(\frac{s}{T_0}+({\mu }_I-{\mu }_T)+\rho )>0,$$

we easily see that

$${\mu }_V({\mu }_I-r+\rho +\frac{r{T}_0}{T_{max}})=N_{\mathrm{crit}}{\mu }_b{k}^{\prime }{T}_0.$$

We have

$${\lambda }_{1,2}=\frac{-({\mu }_V-r+{\mu }_I+\rho +\frac{r{T}_0}{T_{max}})\pm \sqrt{{({\mu }_V-r+{\mu }_I+\rho +\frac{r{T}_0}{T_{max}})}^2-4(N_{\mathrm{crit}}-N){\mu }_b{k}^{\prime }{T}_0}}{2},$$

if $N<N_{\mathrm{crit}}$, the characteristic roots have negative real parts for $\tau =0$.

For $\tau \ne 0$, we get

$${\lambda }^2+\lambda ({\mu }_V-r+{\mu }_I+\rho +\frac{r{T}_0}{T_{max}})+{\mu }_I{\mu }_V-r{\mu }_V+{\mu }_V\rho +\frac{r{T}_0{\mu }_V}{T_{max}}-N{\mu }_b{k}^{\prime }{T}_0{e}^{-\lambda \tau }=0.$$

Assume that the above equation has roots $\lambda =\omega (cos\frac{\beta \pi }{2}\pm isin\frac{\beta \pi }{2})$, for $\omega >0$ and $\tau >0$; we get

$$\begin{array}{r}{\omega }^2{(cos\frac{\beta \pi }{2}\pm isin\frac{\beta \pi }{2})}^2+\omega (cos\frac{\beta \pi }{2}\pm isin\frac{\beta \pi }{2})({\mu }_V-r+{\mu }_I+\rho +\frac{r{T}_0}{T_{max}})\\ +{\mu }_I{\mu }_V-r{\mu }_V+{\mu }_V\rho +\frac{r{T}_0{\mu }_V}{T_{max}}-N{\mu }_b{k}^{\prime }{T}_0{e}^{-\tau \omega (cos\frac{\beta \pi }{2}\pm isin\frac{\beta \pi }{2})}=0.\end{array}$$

Separating the real and imaginary parts gives

$$\{\begin{array}{l}{\omega }^2({cos}^2\frac{\beta \pi }{2}-{sin}^2\frac{\beta \pi }{2})+\omega cos\frac{\beta \pi }{2}({\mu }_V-r+{\mu }_I+\rho +\frac{r{T}_0}{T_{max}})\\ +{\mu }_I{\mu }_V-r{\mu }_V+{\mu }_V\rho +\frac{r{T}_0{\mu }_V}{T_{max}}-N{\mu }_b{k}^{\prime }{T}_0{e}^{-\tau \omega cos\frac{\beta \pi }{2}}cos(\mp \tau \omega sin\frac{\beta \pi }{2})=0,\\ \pm 2{\omega }^{2}sin\frac{\beta \pi }{2}cos\frac{\beta \pi }{2}\pm \omega sin\frac{\beta \pi }{2}({\mu }_V-r+{\mu }_I+\rho +\frac{r{T}_0}{T_{max}})\\ -sin(\mp \tau \omega sin\frac{\beta \pi }{2})N{\mu }_b{k}^{\prime }{T}_0{e}^{-\tau \omega cos\frac{\beta \pi }{2}}=0.\end{array}$$

(3.3)

From the second equation of (3.3), we have

$$sin\frac{\beta \pi }{2}=0,$$

that is $\frac{\beta \pi }{2}=k\pi$, $k=0,1,2,\dots$ .

For $\frac{\beta \pi }{2}=k\pi$, $k=0,2,4,\dots$ , substituting into the first equation of (3.3), we have

$$\begin{array}{r}{\omega }^2+\omega ({\mu }_V-r+{\mu }_I+\rho +\frac{r{T}_0}{T_{max}})+{\mu }_I{\mu }_V-r{\mu }_V+{\mu }_V\rho +\frac{r{T}_0{\mu }_V}{T_{max}}\\ =N{\mu }_b{k}^{\prime }{T}_0{e}^{-\tau \omega }.\end{array}$$

(3.4)

For the parameter values given in Table 1, we take any $N<N_{\mathrm{crit}}$, the infected equilibrium $E_0=(1,000,0,0)$, and we find that the above equation is unequal for $\omega >0$. Therefore, $\beta \ge 2>\alpha$.

According to Lemma 2.1, the uninfected equilibrium $E^{\ast }$ is locally asymptotically stable. The proof is completed. □

Remark 3.1 ([2])

The stability region of a system with fractional order $\alpha \in (0,1)$ is always larger than that of a corresponding ordinary differential system. This means that a unstable equilibrium of an ordinary differential system may be stable in a fractional differential system.

Next, for the sake of convenience, at $E^{\ast }=(T^{\ast },I^{\ast },V^{\ast })$, we define the following symbols:

$$\begin{array}{c}{M}_1={\mu }_T-r+\frac{2r{T}^{\ast }+r{I}^{\ast }}{T_{max}}+k{V}^{\ast },M_2=-r+{\mu }_I+\rho +\frac{r{T}^{\ast }+2r{I}^{\ast }}{T_{max}},\hfill \\ A={\mu }_V+M_1+M_2,B=M_1{\mu }_V+M_2{\mu }_V+M_1{M}_2-\frac{r^2{I}^{\ast }{T}^{\ast }}{T_{max}^2}+\frac{\rho r{I}^{\ast }}{T_{max}},\hfill \\ C=-N{\mu }_b{k}^{\prime }{T}^{\ast }+\frac{r{T}^{\ast }{k}^{\prime }{V}^{\ast }}{T_{max}}-\rho k^{\prime }{V}^{\ast },\hfill \\ D=M_1{M}_2{\mu }_V-\frac{N{\mu }_{b}k{T}^{\ast }r{I}^{\ast }}{T_{max}}-\frac{{\mu }_{V}r{T}^{\ast }r{I}^{\ast }}{T_{max}^2}+\frac{{\mu }_V\rho r{I}^{\ast }}{T_{max}},\hfill \\ E=k^{\prime }{V}^{\ast }N{\mu }_{b}k{T}^{\ast }-N{M}_1{\mu }_b{k}^{\prime }{T}^{\ast }-{\mu }_V\rho k^{\prime }{V}^{\ast }+\frac{k^{\prime }{V}^{\ast }{\mu }_{V}r{T}^{\ast }}{T_{max}}.\hfill \end{array}$$

Then the characteristic equation of the linear system is

$${\lambda }^3+A{\lambda }^2+(B+C{e}^{-\lambda \tau })\lambda +D+E{e}^{-\lambda \tau }=0.$$

(3.5)

Using the results in [31], we get

$$D(\lambda )={\lambda }^3+A{\lambda }^2+(B+C)\lambda +D+E$$

and

$$D^{\prime }(\lambda )=3{\lambda }^2+2A\lambda +(B+C).$$

Denote

$$\begin{array}{rl}D(\lambda )& =-\left|\begin{array}{ccccc}1& A& B+C& D+E& 0\\ 0& 1& A& B+C& D+E\\ 3& 2A& B+C& 0& 0\\ 0& 3& 2A& B+C& 0\\ 0& 0& 3& 2A& B+C\end{array}\right|\\ =18A(B+C)(D+E)-4A^3(D+E)-27{(D+E)}^2-4{(B+C)}^3+A^2{(B+C)}^2.\end{array}$$

Theorem 3.2 Let $1\pm \frac{C{\tau }^2}{2}>0$, $(1\pm \frac{C{\tau }^2}{2})(B\pm C-E\tau )>0$, $D+E\ge 0$ and $N>N_{\mathrm{crit}}$, then the infected equilibrium $E^{\ast }$ is asymptotically stable for any time delay $\tau \ge 0$ if either

$$(\mathrm{i})D(\lambda )>0,A>0,D+E>0,A(B+C)>D+E,$$

or

$$(\mathrm{ii})D(\lambda )<0,A\ge 0,B+C\ge 0,0.5<\alpha <2/3.$$

Proof According to (3.5).

For $\tau =0$, we have

$${\lambda }^3+A{\lambda }^2+(B+C)\lambda +D+E=0.$$

Using the result in [31], the infected steady state $E^{\ast }$ is asymptotically stable if the Routh-Hurwitz condition is satisfied, i.e.

$$(\mathrm{i})D(\lambda )>0,A>0,D+E>0,A(B+C)>D+E,$$

or

$$(\mathrm{ii})D(\lambda )<0,A\ge 0,B+C\ge 0,0.5<\alpha <2/3.$$

For $\tau \ne 0$, we get

$${\lambda }^3+A{\lambda }^2+(B+C{e}^{-\lambda \tau })\lambda +D+E{e}^{-\lambda \tau }=0.$$

Assume that the above equation has roots $\lambda =\omega (cos\frac{\beta \pi }{2}\pm isin\frac{\beta \pi }{2})$, for $\omega >0$ and $\tau >0$; we get

$$\begin{array}{r}{\omega }^3{(cos\frac{\beta \pi }{2}\pm isin\frac{\beta \pi }{2})}^3+A{\omega }^2{(cos\frac{\beta \pi }{2}\pm isin\frac{\beta \pi }{2})}^2\\ +\omega (B+C{e}^{-\tau \omega (cos\frac{\beta \pi }{2}\pm isin\frac{\beta \pi }{2})})(cos\frac{\beta \pi }{2}\pm isin\frac{\beta \pi }{2})\\ +D+E{e}^{-\tau \omega (cos\frac{\beta \pi }{2}\pm isin\frac{\beta \pi }{2})}=0.\end{array}$$

Separating the real and imaginary parts yields

$$\{\begin{array}{l}{\omega }^3{cos}^3\frac{\beta \pi }{2}-3{\omega }^3{sin}^2\frac{\beta \pi }{2}cos\frac{\beta \pi }{2}+A{\omega }^2{cos}^2\frac{\beta \pi }{2}-A{\omega }^2{sin}^2\frac{\beta \pi }{2}\\ +\omega Bcos\frac{\beta \pi }{2}\pm \omega Ccos\frac{\beta \pi }{2}{e}^{-\tau \omega cos\frac{\beta \pi }{2}}cos(\mp \tau \omega sin\frac{\beta \pi }{2})\\ \mp sin\frac{\beta \pi }{2}C{e}^{-\tau \omega cos\frac{\beta \pi }{2}}sin(\mp \tau \omega sin\frac{\beta \pi }{2})+D\\ +E{e}^{-\tau \omega cos\frac{\beta \pi }{2}}cos(\mp \tau \omega sin\frac{\beta \pi }{2})=0,\\ \pm 3{\omega }^3{cos}^2\frac{\beta \pi }{2}sin\frac{\beta \pi }{2}\mp {\omega }^3{sin}^3\frac{\beta \pi }{2}\pm 2A{\omega }^{2}sin\frac{\beta \pi }{2}cos\frac{\beta \pi }{2}\\ \pm \omega Bsin\frac{\beta \pi }{2}\pm \omega sin\frac{\beta \pi }{2}C{e}^{-\tau \omega cos\frac{\beta \pi }{2}}cos(\mp \tau \omega sin\frac{\beta \pi }{2})\\ +\omega C{e}^{-\tau \omega cos\frac{\beta \pi }{2}}sin(\mp \tau \omega sin\frac{\beta \pi }{2})cos\frac{\beta \pi }{2}\\ +E{e}^{-\tau \omega cos\frac{\beta \pi }{2}}sin(\mp \tau \omega sin\frac{\beta \pi }{2})=0.\end{array}$$

(3.6)

From the second equation of (3.6), we have

$$sin\frac{\beta \pi }{2}=0,$$

that is, $\frac{\beta \pi }{2}=k\pi$, $k=0,1,2,\dots$ .

For $\frac{\beta \pi }{2}=k\pi$, $k=0,2,4,\dots$ , substituting into the first equation of (3.6), we have

$${\omega }^3+A{\omega }^2+\omega (B\pm C{e}^{-\tau \omega })+D+E{e}^{-\tau \omega }=0.$$

For the parameter values given in Table 1, we take any $N>N_{\mathrm{crit}}$; then we get the specific value on the infected equilibrium $E^{\ast }=(T^{\ast },I^{\ast },V^{\ast })$ and we can see that the above equation is unequal for $\omega >0$.

For $\frac{\beta \pi }{2}=k\pi$, $k=1,3,5,\dots$ , substituting into the first equation of (3.6), we have

$$-{\omega }^3+A{\omega }^2-\omega (B\pm C{e}^{\tau \omega })+D+E{e}^{\tau \omega }=0.$$

(3.7)

According to the development of Taylor type, we have

$$e^{\tau \omega }\approx 1+\tau \omega +\frac{{(\tau \omega )}^2}{2!}.$$

We take $\omega =-\theta$, and (3.7) becomes

$${\theta }^3(1\pm \frac{C{\tau }^2}{2})+{\theta }^2(A\mp \tau C+\frac{E{\tau }^2}{2})+\theta (B\pm C-E\tau )+D+E=0.$$

(3.8)

Let

$$\alpha =1\pm \frac{C{\tau }^2}{2},\beta =A\mp \tau C+\frac{E{\tau }^2}{2},\gamma =B\pm C-E\tau ,\rho =D+E,$$

then (3.8) becomes

$$h(\theta )=\alpha {\theta }^3+\beta {\theta }^2+\gamma \theta +\rho .$$

(3.9)

Notice that

$$h^{\prime }(\theta )=3\alpha {\theta }^2+2\beta \theta +\gamma .$$

Set

$$3\alpha {\theta }^2+2\beta \theta +\gamma =0.$$

(3.10)

Then the roots of (3.10) can be expressed as

$${\theta }_{1,2}=\frac{-\beta \pm \sqrt{{\beta }^2-3\alpha \gamma }}{3\alpha }.$$

Due to $\alpha \gamma >0$, we have $\sqrt{{\beta }^2-3\alpha \gamma }<\beta$. Hence, neither ${\theta }_1$ nor ${\theta }_2$ is positive. Thus, (3.10) does not have positive roots. Since $\alpha >0$, $h(0)=\rho \ge 0$, it follows that (3.9) has no positive roots.

Because of $\omega =-\theta$, the roots of (3.7) are positive, that is, ${\omega }_{1,2,3}>0$.

The proof is completed. □

4 Numerical simulations

In this section, we use the Adams-type predictor-corrector method for the numerical solution of the nonlinear system (1.4) and (1.5) with time delay.

Firstly, we shall replace system (1.4) and (1.5) by the following equivalent fractional integral equations:

$$\{\begin{array}{l}T(t)=T(0)+I^{\alpha }[s-{\mu }_{T}T(t)+rT(t)(1-\frac{T(t)+I(t)}{T_{max}})-kT(t)V(t)+\rho I(t)],\\ I(t)=I(0)+I^{\alpha }[k^{\prime }T(t-\tau )V(t-\tau )+rI(t)(1-\frac{T(t)+I(t)}{T_{max}})-({\mu }_I+\rho )I(t)],\\ V(t)=V(0)+I^{\alpha }[N{\mu }_{b}I(t)-{\mu }_{v}V(t)].\end{array}$$

(4.1)

Next, we apply the PECE (Predict, Evaluate, Correct, Evaluate) method.

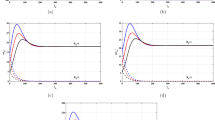
The approximate solution is displayed in Figure 2(A1)-(A3), Figure 3(B1)-(B3), Figure 4(C1)-(C3), Figure 5(D1)-(D3), Figure 6(E1)-(E3), Figure 7(F1)-(F3), Figure 8(G1)-(G4), and Figure 9(H1)-(H3). When $\alpha =1$, system (1.4) is the classical integer-order ODE.

Figure 2

In (A1)-(A3), $\mathit{\alpha }\mathbf{=}\mathbf{\{}\mathbf{0.7}\mathbf{,}\mathbf{0.8}\mathbf{,}\mathbf{0.9}\mathbf{,}\mathbf{1}\mathbf{\}}$ , $\mathit{N}\mathbf{=}\mathbf{800}$ , $\mathit{\tau }\mathbf{=}\mathbf{0}$ , $\mathit{\rho }\mathbf{=}\mathbf{0.1}$ .

Figure 3

In (B1)-(B3), $\mathit{\alpha }\mathbf{=}\mathbf{\{}\mathbf{0.7}\mathbf{,}\mathbf{0.8}\mathbf{,}\mathbf{0.9}\mathbf{,}\mathbf{1}\mathbf{\}}$ , $\mathit{N}\mathbf{=}\mathbf{1}\mathbf{,}\mathbf{400}$ , $\mathit{\tau }\mathbf{=}\mathbf{0}$ , $\mathit{\rho }\mathbf{=}\mathbf{0.1}$ .

Figure 4

In (C1)-(C3), $\mathit{\alpha }\mathbf{=}\mathbf{0.7}$ , $\mathit{N}\mathbf{=}\mathbf{800}$ , $\mathit{\tau }\mathbf{=}\mathbf{\{}\mathbf{0}\mathbf{,}\mathbf{1}\mathbf{,}\mathbf{2}\mathbf{,}\mathbf{3}\mathbf{,}\mathbf{4}\mathbf{,}\mathbf{5}\mathbf{\}}$ , $\mathit{\rho }\mathbf{=}\mathbf{0.1}$ .

Figure 5

In (D1)-(D3), $\mathit{\alpha }\mathbf{=}\mathbf{\{}\mathbf{0.7}\mathbf{,}\mathbf{0.8}\mathbf{,}\mathbf{0.9}\mathbf{,}\mathbf{1}\mathbf{\}}$ , $\mathit{N}\mathbf{=}\mathbf{100}$ , $\mathit{\tau }\mathbf{=}\mathbf{3}$ , $\mathit{\rho }\mathbf{=}\mathbf{0.1}$ .

Figure 6

In (E1)-(E3), $\mathit{\alpha }\mathbf{=}\mathbf{0.7}$ , $\mathit{N}\mathbf{=}\mathbf{800}$ , $\mathit{\tau }\mathbf{=}\mathbf{2}$ , $\mathit{\rho }\mathbf{=}\mathbf{\{}\mathbf{0}\mathbf{,}\mathbf{0.2}\mathbf{,}\mathbf{0.4}\mathbf{,}\mathbf{0.6}\mathbf{\}}$ .

Figure 7

In (F1)-(F3), $\mathit{\alpha }\mathbf{=}\mathbf{0.7}$ , $\mathit{N}\mathbf{=}\mathbf{800}$ , $\mathit{\tau }\mathbf{=}\mathbf{2}$ , $\mathit{\rho }\mathbf{=}\mathbf{1}$ .

Figure 8

In (G1)-(G4), $\mathit{\alpha }\mathbf{=}\mathbf{0.7}$ , $\mathit{N}\mathbf{=}\mathbf{800}$ , $\mathit{\tau }\mathbf{=}\mathbf{2}$ , $\mathit{\rho }\mathbf{=}\mathbf{1.1}$ .

Figure 9

In (H1)-(H3), $\mathit{\alpha }\mathbf{=}\mathbf{0.7}$ , $\mathit{N}\mathbf{=}\mathbf{\{}\mathbf{200}\mathbf{,}\mathbf{250}\mathbf{,}\mathbf{300}\mathbf{,}\mathbf{500}\mathbf{,}\mathbf{800}\mathbf{,}\mathbf{1}\mathbf{,}\mathbf{000}\mathbf{,}\mathbf{1}\mathbf{,}\mathbf{400}\mathbf{\}}$ , $\mathit{\tau }\mathbf{=}\mathbf{2}$ , $\mathit{\rho }\mathbf{=}\mathbf{0.1}$ .

For the parameter values given in Table 1, we take $\rho =0.1$, then $N_{\mathrm{crit}}=161.5385$.

We take $N=800$, $\tau =0$, then $E^{\ast }=(235.1366566,31.66823433,2,527.515631)$ and

$$A=2.7967,B=0.9725,C=-0.9077,D=0.0484,E=-0.0116,$$

and

$$\begin{array}{c}D(\lambda )=-3.1053<0,B+C=0.0647,\hfill \\ A(B+C)=0.1810,D+E=0.0368>0,\hfill \\ (1-\frac{C{\tau }^2}{2})(B-C-E\tau )=2.7504>0,(1+\frac{C{\tau }^2}{2})(B+C-E\tau )=0.0417>0.\hfill \end{array}$$

Hence, all the conditions in Theorem 3.2 are satisfied and the infection case $E^{\ast }$ is asymptotically stable. In addition, when we take $N=1,400$, $\tau =0$, all the conditions in Theorem 3.2 are also satisfied and the infection case $E^{\ast }$ is asymptotically stable.

Remark 4.1 Figures 2 and 3 show that, as α increases, the trajectory of the system closes in to the integer-order ODE.

Remark 4.2 Figure 4 shows that, as τ increases, the fluctuation of the trajectory of the system is smaller during the previous period of the time.

Remark 4.3 If $N<N_{\mathrm{crit}}$, Figure 5 shows that, as α closes in to 1, the number of steady states of T approaches the initial value, the numbers of steady states of I and V approach zero.

Remark 4.4 Figures 6, 7, and 8 show that, as p increases, the number of infected T-cells is decreased, the level of the steady state of T is higher, the fluctuations of the trajectories of I and V are smaller. For $\rho =0.6$, the trajectory of the system is fluctuating during the previous period of the time. As ρ (>0.6) is increasing, the fluctuation of the trajectory of the system is stronger. It is noticeable that, for ρ in a certain range, drugs can resist the virus. For $0.6<\rho \le 1$, the trajectory of the system is fluctuating during the previous period of the time, and it will tend to the steady state later. For $\rho \ge 1.1$, the trajectory of the system is unstable.

Remark 4.5 Figure 9 shows that, as N decreases, the number of steady states of T increases, the numbers of steady states of I and V are decreased and the trajectories of the system of I and V are also close to stable.

5 Conclusions

In this paper, we modified the ODE model proposed by Liu et al. [12] and the fractional model proposed by Yan and Kou [2] into a system of fractional order. We study a fractional differential model of HIV infection of the CD4⁺ T-cells. We shall consider this model, which includes full logistic growth terms of both healthy and infected CD4⁺ T-cells, time delay items, and cure rate items. Moreover, we study α, τ, N, and ρ, and we obtain some significant conclusions. For example, if the cure rate gets large in a certain range, it will control the HIV infection efficiently. In our analysis, the more appropriate method is given to ensure that both equilibria are asymptotically stable for $\tau \ge 0$. Both in mathematics and biology, it is particularly important to show stability of the infected and uninfected equilibrium point. In addition, we describe the dynamic behaviors of the fractional HIV model by using the Amads-type predictor-corrector method algorithm.