Global stability for a nonautonomous reaction-diffusion predator-prey model with modified Leslie–Gower Holling-II schemes and a prey refuge

Abstract

In this paper, a nonautonomous reaction-diffusion predator-prey model with modified Leslie–Gower Holling-II schemes and a prey refuge is proposed. Applying the comparison theory of differential equation, sufficient average criteria on the permanence of solutions and the existence of the positive periodic solutions are established. Moreover, the existence region of the positive periodic solutions is an invariant region dependent on t. Then, constructing a suitable Lyapunov function, we obtain sufficient conditions to guarantee the global asymptotic stability of the positive periodic solutions. Finally, we do some numerical simulations to verify our main results and investigate the effect of prey refuge on the dynamics of the system.

1 Introduction

In the past two decades, population biology has been greatly developed [3, 6, 10, 11, 20, 26]. One important aspect of population biology is the predator’s functional response [23], which is the key to describing the average feeding rate of a predator. A very popular predator’s functional response is the Holling-II type, which has the following form [15]:

$$ p(x)=\frac{ cx}{1+ax}, $$

(1)

where x represents the population density of prey, and c and a are all positive constants that represent the capture rate and handling time, respectively. Up to now, predator-prey models with Holling-II functional response have been investigated extensively [3, 6, 8, 13, 18, 20, 22, 24, 26, 28]. In 1948, Leslie [7] proposed the following famous Leslie predator-prey system:

$$ \textstyle\begin{cases} \frac{dx}{dt}=x(a-bx)-p(x)y, \\ \frac{dy}{dt}=y(c-d\frac{y}{x}), \end{cases} $$

(2)

where $d\frac{y}{x}$ is known as the Leslie–Gower term, which is based on the assumption that the carrying capacity of the predator’s environment is proportional to the number of prey. Moreover, the Leslie–Gower term measures the loss in the predator population due to rarity (per capita $\frac{y}{x}$) of its favorite food. In the case of severe scarcity, y can switch over to other populations but its growth will be limited by the fact that its most favorite food is not available in abundance. That is to say, $x=0$ will cause some singularity. In order to avoid this case, Aziz-Alaoui [1] proposed adding a positive constant k to the denominator. Hence, the second equation of (2) becomes $\frac{dy}{dt}=x(c-\frac{d y}{x+k})$. When $p(x)$ is taken as (1), system (2) becomes the famous and popular predator-prey model with modified Leslie–Gower Holling-II schemes:

$$ \textstyle\begin{cases} \frac{dx}{dt}=x(r_{1}-bx)-\frac{cxy}{x+k_{1}}, \\ \frac{dy}{dt}=y(r_{2}-\frac{dy}{x+k_{2}}). \end{cases} $$

(3)

Aziz-Alaqui and Daher [2] investigated model (3) and obtained the boundedness of solutions and the existence of an attracting set. Moreover, they obtained the global stability of the coexisting interior equilibrium. Nindjina et al. [14] incorporated the time delay into model (3) and obtained the permanence of the system, asymptotical stability of the positive equilibrium. Moreover, generalization and in-depth study of model (3) can be found in many references, such as [3, 6, 20, 26].

However, in fact, since most prey have refuges, it is difficult for predators to catch them. Hence, it is necessary to incorporate the prey refuge into the predator-prey system. As one of the hot topics in biological mathematics, the predator-prey model with prey refuges has attracted the attention of many scholars at home and abroad [3, 6, 20, 22, 26]. Zhang et al. [26] investigated a prey-predator model incorporating a prey refuge and the fear effect and found that prey refuge has great impact on the persistence of the predator. Moreover, Wang et al. [20] also proposed a prey-predator model incorporating a prey refuge and the fear effect and concluded that the prey refuge is beneficial to the coexistence of the prey and the predator, and with the increase of the level of the prey refuge, the positive equilibrium may change from stable spiral sink to unstable spiral source to stable spiral sink.

The rhythm of life on earth is shaped by seasonal changes in the environment. Plants and animals show profound annual cycles in physiology, health, morphology, behavior, and demography in response to environmental cues [17]. We note that any biological or environmental parameters are naturally subject to fluctuation in time. For example, when winter comes the wild goose will fly to the south to seek a better habitat, whereas they do not migrate in other seasons. For another example, in the Pacific Northwest, Larimichthys polyactis cross over deep water during the winter and migrate to the coast during the spring; then, 3–6 months after spawning, they scatter offshore and return to the depths of the sea during late autumn [12]. Considering the important roles that seasonal environmental factors play in the dynamics of plant and animal species dynamics, it is necessary and essential to take models with periodic parameters into consideration such as in Cushing [5].

Based on the above consideration, many nonautonomous predator-prey models with modified Leslie–Gower Holling-II schemes have been proposed to investigate the effect of the periodic environment on the dynamics of population [13, 22, 28]. Zhu and Wang [28] proposed the periodic predator-prey model with modified Leslie–Gower Holling-II schemes and obtained the existence and global attractivity of the positive periodic solutions. Xie et al. [22] extended the periodic system with a prey refuge and obtained a set of sufficient conditions which ensure the permanence of the system. By constructing a suitable Lyapunov function, they also investigated the stability property of the system. Nie et al. [13] proposed a nonautonomous modified Leslie–Gower Holling-II schemes with state dependent impulsive. By using the Poincareé map, some conditions for the existence and stability of semi-trivial solution and positive periodic solutions were obtained.

As we know, ODE(ordinary differential equation) models are relatively simple and easy to deal with, but they ignore the effect of the spatial heterogeneity and movements of individuals, and of course cannot exhibit spatial patterns of the population. To study the impact of spatial distribution and movements of individuals on the population dynamics, many reaction-diffusion models with modified Leslie–Gower and Holling-type II schemes have been proposed [3, 4, 6, 19, 25, 27]. In aforementioned PDE (partial differential equation) models, they all are autonomous PDE models, i.e., the parameters of the PDE models are positive constants independent of t. However, as discussed above, seasonality or any other periodic change of environmental conditions is very important for population dynamics. Moreover, the existing PDE models are mainly focused on the autonomous cases. In consideration of these factors, we incorporated the periodicity into the reaction-diffusion model, especially the diffusion parameters, and proposed the following model:

$$ \textstyle\begin{cases} \frac{\partial P(t,x)}{\partial t}=d_{1}(t)\triangle P(t,x)+P(t,x) [a_{1}(t)-b_{1}(t)P(t,x)- \frac{c_{1}(t)(1-m(t))Q(t,x)}{P(t,x)+k_{1}(t)} ],\\ \quad x\in \varOmega, t>0, \\ \frac{\partial Q(t,x)}{\partial t}=d_{2}(t)\triangle Q(t,x)+Q(t,x) [a_{2}(t)-\frac{c_{2}(t)Q(t,x)}{(1-m(t))P(t,x)+k_{2}(t)} ],\quad x \in \varOmega, t>0, \\ P(0,x)=P_{0}(x)>0, \qquad Q(0,x)=Q_{0}(x)>0, \quad x\in \bar{\varOmega }, \\ \frac{\partial P(t,x)}{\partial \mathbf{n}}= \frac{\partial Q(t,x)}{\partial \mathbf{n}}=0, \quad x\in \partial { \varOmega }, t>0, \end{cases} $$

(4)

where $P(t,x)$ and $Q(t,x)$ represent the prey and the predator densities at location x and time t, respectively; $d_{i}(t)(i=1,2)$ denotes diffusion coefficients at time t of the prey and predator, respectively; Ω is a bounded domain of $R^{n}$; n is the outward unit normal vector of the boundary ∂Ω; $P_{0}(x)$ and $Q_{0}(x)$ are the initial values of the prey and predator at location x and they are continuous functions of x; $a_{i}(t)(i=1,2)$ denotes the growth rates of the prey and predator at time t, respectively. $b_{1}(t)$ measures the strength of competition among individuals of prey. $c_{1}(t)$ is the maximum value which per capita reduction rate of prey P can attain; $c_{2}(t)$ has a similar meaning to $c_{1}(t)$; $k_{1}(t)$ (respectively, $k_{2}(t)$) measures the extent to which environment provides protection to prey P (respectively, to predator Q); $0< m(t)<1$ represents the protection rates of the prey P.

Our purpose in this paper is to investigate the dynamic behaviors of model (4). Applying the comparison theory of differential equation, sufficient average criteria on the permanence of solutions and the existence of the positive periodic solutions are established. Moreover, the existence region of the positive periodic solutions is an invariant region dependent on t. Finally, constructing a suitable Lyapunov function, we obtain the sufficient conditions to guarantee the global asymptotic stability of the positive periodic solutions.

The outline of the work is as follows. In Sect. 2, we study the permanence of solutions and the existence of the positive periodic solutions of the corresponding ODE system. In Sect. 3, we mainly discuss the global asymptotic stability of the positive periodic solutions for system (4). In Sect. 4, we give some number simulations to verify our theoretical analysis results. Finally, we give a brief conclusion in Sect. 5.

2 Analysis of the corresponding ODE system

In this section, we mainly investigate the corresponding ODE system of system (4). Sufficient average criteria on the permanence of solutions and the existence of the positive periodic solutions are established. Moreover, the existence region of the positive periodic solutions is an invariant region dependent on t, which is different from the previous results in Xie et al. [22].

2.1 Permanence of the ODE system

For a continuous T-periodic function $g(t)$, we denote its integral average by

$$ \bigl[g(t)\bigr]=\frac{1}{T} \int _{0}^{T}g(t)\,dt. $$

From system (4), we obtain that the corresponding ODE system is as follows:

$$ \textstyle\begin{cases} \frac{dP(t)}{dt}=P(t) [a_{1}(t)-b_{1}(t)P(t)- \frac{c_{1}(t)(1-m(t))Q(t)}{P(t)+k_{1}(t)} ], \\ \frac{d Q(t)}{dt}=Q(t) [a_{2}(t)- \frac{c_{2}(t)Q(t)}{(1-m(t))P(t)+k_{2}(t)} ]. \end{cases} $$

(5)

To obtain the permanence of system (5), we need the following lemma.

Lemma 1

Assume that$r_{1}(t)$and$r_{2}(t)$are continuous andT-periodic functions, $r_{2}(t)>0$and$[r_{1}(t)]>0$, then the logistic equation

$$ \frac{dx}{dt}=x(t) \bigl(r_{1}(t)-r_{2}(t)x(t) \bigr) $$

(6)

admits a unique positiveT-periodic solution$x^{*}(t)$. Moreover, $x^{*}(t)$is globally attractive. That is to say, if$x(t)$is any other positive solution of system (6), which yields that

$$ \lim_{t\rightarrow \infty } \bigl\vert x(t)-x^{*}(t) \bigr\vert =0. $$

Based on Lemma 1, we investigate the permanence of system (5). In system (5), we assume that $[a_{1}(t)]>0$ and $[a_{2}(t)]>0$. Let $\hat{P}(t)$ be a positive T-periodic solution of the following logistic equation:

$$ \frac{du}{dt}=u(t) \bigl(a_{1}(t)-b_{1}(t)u(t) \bigr) $$

(7)

and $\hat{Q}(t)$ be a positive T-periodic solution of the following logistic equation:

$$ \frac{dv}{dt}=v(t) \biggl(a_{2}(t)- \frac{c_{2}(t)v(t)}{(1-m(t))\hat{P}(t)+k_{2}(t)}\biggr). $$

(8)

Theorem 1

If

$$ \bigl[a_{1}(t)\bigr]> \biggl[\frac{c_{1}(t)(1-m(t)\hat{Q}(t))}{k_{1}(t)} \biggr] $$

(9)

holds, then for any positive solution$(P(t),Q(t))$of system (5), there exists$\tilde{t}>0$such that

$$ \check{P}(t)\leq P(t)\leq \hat{P}(t), \qquad \check{Q}(t)\leq Q(t) \leq \hat{Q}(t)\quad \textit{for } t>\tilde{t}, $$

where$\check{P}(t)$is a positiveT-periodic solution of the following logistic equation:

$$ \frac{du}{dt}=u(t) \biggl[ \biggl(a_{1}(t)- \frac{c_{1}(t)(1-m(t))\hat{Q}(t)}{k_{1}(t)} \biggr)-b_{1}(t)u(t) \biggr] $$

(10)

and$\check{Q}(t)$is a positiveT-periodic solution of the following logistic equation:

$$ \frac{dv}{dt}=v(t) \biggl(a_{2}(t)- \frac{c_{2}(t)v(t)}{(1-m(t))\check{P}(t)+k_{2}(t)} \biggr). $$

(11)

Proof

Let $(P(t), Q(t))$ be a positive solution of (5). From the first equation of system (5), we have

$$ \frac{dP(t)}{dt}\leq P(t) \bigl(a_{1}(t)-b_{1}(t)u(t) \bigr). $$

(12)

From $[a_{1}(t)]>0$ and Lemma 1, for all positive solutions of equation (7), we have

$$ \lim_{t\rightarrow \infty } \bigl\vert u(t)-\hat{P}(t) \bigr\vert =0. $$

From the comparison theorem of ordinary differential equations, we can obtain that there exists $t_{0}>0$ such that

$$ P(t)\leq \hat{P}(t)\quad \text{for all } t>t_{0}. $$

(13)

As a consequence, from the second equation of system (5), we can obtain that

$$ \frac{dQ(t)}{dt}\leq Q(t) \biggl(a_{2}(t)- \frac{c_{2}(t)Q(t)}{(1-m(t))\hat{P}(t)+k_{2}(t)} \biggr) $$

(14)

for $t>t_{0}$. From $[a_{2}(t)]>0$ and Lemma 1, for all positive solutions of equation (8), we have

$$ \lim_{t\rightarrow \infty } \bigl\vert v(t)-\hat{Q}(t) \bigr\vert =0. $$

From the comparison theorem of ordinary differential equations, we can obtain that there exists $t_{1}>0$ such that

$$ Q(t)\leq \hat{Q}(t) \quad\text{for all } t>t_{1}. $$

(15)

From system (15) and the first equation of system (5), we can obtain that

$$ \frac{dP(t)}{dt}\geq P(t) \biggl[ \biggl(a_{1}(t)- \frac{c_{1}(t)(1-m(t))\hat{Q}(t)}{k_{1}(t)} \biggr)-b_{1}(t)P(t) \biggr]\quad \text{for all } t>t_{1}. $$

(16)

From equation (9) and the comparison theorem, we can obtain that there exists $t_{2}>t_{1}$ such that

$$ P(t)\geq \check{P}(t) \quad\text{for all } t>t_{2}. $$

(17)

From equation (17) and the comparison theorem, we can obtain that

$$ \frac{dQ(t)}{dt}\geq Q(t) \biggl(a_{2}(t)- \frac{c_{2}(t)Q(t)}{(1-m(t))\check{P}(t)+k_{2}(t)} \biggr) \quad\text{for all } t>t_{2}. $$

(18)

With the same argument as above, there exists $\tilde{t}>t_{2}$ such that

$$ Q(t)\geq \check{Q}(t) \quad\text{for all } t>\tilde{t}. $$

(19)

Hence, the proof of Theorem 1 is completed. □

2.2 The existence of the periodic solutions for ODE system

In this subsection, we mainly discuss the existence of the periodic solutions for ODE system. By the Brouwer fixed-point theorem, we obtain that the ODE system has at least a positive T-periodic solution. Different from previous results, the existence region of the positive periodic solutions is an invariant region dependent on t.

Theorem 2

Suppose that (9) holds, then system (5) has at least a positive T-periodic solution$(P^{*}(t), Q^{*}(t))$such that

$$ \check{P}(t) \leq P^{*}(t) \leq \hat{P}(t),\qquad \check{Q}(t) \leq Q^{*}(t) \leq \hat{Q}(t),\quad t \in [0, T], $$

where the periodic functions$\check{P}(t), \hat{P}(t), \check{Q}(t), \hat{Q}(t)$are defined in the previous theorem.

Proof

Define

$$ M= \bigl[\check{P}(0),\hat{P}(0)\bigr] \times \bigl[\check{Q}(0),\hat{Q}(0) \bigr], $$

and suppose that $(P(t), Q(t))$ is a solution to system (5) with the initial condition $(P(0), Q(0))\in M$. Since $P(0) \leq \hat{P}(0)$ and

$$ \frac{dP(t)}{dt}\leq P(t) \bigl(a_{1}(t)-b_{1}(t)P(t) \bigr), $$

(20)

we deduce that $P(t) \leq \hat{P}(t)$ for all $t > 0$. Repeating these arguments as in Theorem 1, we can state

$$ \check{P}(0) = \check{P}(T) \leq P(T) \leq \hat{P}(T) = \hat{P}(0),\qquad \check{Q}(0) =\check{Q}(T) \leq Q(T) \leq \hat{Q}(T) =\hat{Q}(0), $$

(21)

thus

$$ \bigl(P(T),Q(T) \bigr) \in M. $$

Consider the map

$$ G: M \rightarrow M, G(x, y) = \bigl(P(T), Q(T) \bigr), $$

where $(P(t), Q(t) )$ is the solution of system (5) with the initial condition $P(0) = x, Q(0) = y$. By the previous argument, we get

$$ G(x, y) \in M, $$

so G is well defined. Since G is continuous, the Brouwer fixed-point theorem ensures the existence of a point $(\tilde{P},\tilde{Q}) \in M$ such that

$$ G(\tilde{P},\tilde{Q}) = (\tilde{P},\tilde{Q}). $$

By construction, the solution $(P^{*}(t), Q^{*}(t))$ with initial condition $(\tilde{P},\tilde{Q})$ verifies

$$ \bigl(P^{*}(0), Q^{*}(0) \bigr) = \bigl(P^{*}(T), Q^{*}(T) \bigr). $$

The properties of periodic differential equations guarantee that $(P^{*}(t), Q^{*}(t) )$ is the searched periodic solution to system (5). The proof of Theorem 2 is completed. □

3 Analysis of the diffusion system

In this section, we mainly discuss the reaction-diffusion predator-prey model (4). According to Theorems 1 and 2, we can obtain an invariant and attractive region for the solutions of system (4). Moreover, we obtain the global stability of the solution of system (4). Before giving our main results, we first give the following lemma.

Lemma 2

Suppose that$a(t), b(t), k(t)$are continuous, T-periodic functions with$[a(t)] > 0, b(t)>0$and$k(t) > 0$, then the unique positive solution to

$$ \textstyle\begin{cases} \frac{\partial w(t,x)}{\partial t}=k(t)\triangle w(t,x)+w(t,x) (a(t)-b(t)w(t,x) ),\quad x\in \varOmega, t>0, \\ w(t+T,x)=w(t,x)>0, \quad x\in \bar{\varOmega }, t\in R^{+}, \\ \frac{\partial w(t,x)}{\partial \mathbf{n}}=0, \quad x\in \partial { \varOmega }, t>0, \end{cases} $$

(22)

is the positive T-periodic solution$w^{*}(t)$to the logistic equation

$$ \frac{du}{dt} = u \bigl(a(t)-b(t)u \bigr). $$

Moreover, for any positive solution$w(t,x )$to (22) with homogeneous Neumann conditions and$w( 0, x) =w_{0}(x) \in C^{2}(\varOmega ) \cap C(\varOmega )$, one has

$$ \lim_{t\rightarrow \infty } \bigl\vert w(t, x)-w^{*}(t) \bigr\vert = 0 \quad\textit{uniformly w.r.t. } x \in \varOmega. $$

Consider the reaction-diffusion predator-prey model (4) and assume that $d_{1}(t)$, $d_{2}(t)$, $b_{1}(t)$, $c_{1}(t)$, $c_{2}(t)$, $k_{1}(t)$, $k_{2}(t)$ are all positive functions, $[a_{1}(t)]>0$, $[a_{2}(t)] > 0$ and $P_{0}(x), Q_{0}(x) \in C^{2}(\varOmega ) \cap C(\varOmega )$. The presence of an invariant region is shown below.

Theorem 3

Under the assumptions and notations of Theorem 2, the region

$$ D(t):= \bigl[\check{P}(t), \hat{P}(t)\bigr] \times \bigl[\check{Q}(t), \hat{Q}(t)\bigr] (t \geq 0) $$

is invariant and attractive for system (4).

• (a) If$(P(x, t), Q(x, t) )$is a positive solution of system (4) with$(P_{0}(x), Q_{0}(x) ) \in D(0)$for every$x \in \varOmega$, then$(P(x, t), Q(x, t) ) \in D(t)$for every$t > 0$and$x \in \varOmega$.

• (b) If$(P(x, t), Q(x, t))$is a positive solution of system (4), there exists$\bar{t} > 0$such that$(P(x, t), Q(x, t)) \in D(t)$for every$t >\bar{t}$and$x \in \varOmega$.

Proof

Assume that $P_{0}(x) = P(0,x) \leq \hat{P}(0)$ for every $x \in \varOmega$. Since $\hat{P}(t)$ is a positive periodic solution to

$$ \frac{dP(t)}{dt}= P(t) \bigl(a_{1}(t)-b_{1}(t)P(t) \bigr), $$

(23)

and it satisfies the equation

$$ \textstyle\begin{cases}\frac{\partial P(t,x)}{\partial t}=d_{1}(t)\triangle P(t,x)+P(t,x) (a_{1}(t)-b_{1}(t)P(t,x) ),\quad x\in \varOmega, t>0, \\ \frac{\partial P(t,x)}{\partial \mathbf{n}}=0, \quad x\in \partial { \varOmega }, t>0. \end{cases} $$

(24)

Hence, according to the comparison theorem for PDE [9], we get $P(x, t) \leq \hat{P}(t)$ for all $t > 0$ and $x \in \varOmega$. Assume that $\max_{x\in \varOmega }P(0,x) < \hat{P}(0)$ and denote by $P(t)$ the solution to the logistic equation

$$ \textstyle\begin{cases} \frac{dP(t)}{dt}\leq P(t)(a_{1}(t)-b_{1}(t)P(t)), \\ P(0)=\max_{x\in \bar{\varOmega }}P(0,x). \end{cases} $$

(25)

By applying the comparison theorem for PDE [9], we have that $P(t,x) \leq P(t)$ for all $t > 0$ and $x \in \varOmega$. On the other hand, taking Theorem 2 into account, there exists $t_{0} > 0$ such that $P(t) \leq \hat{P}(t)$ for all $t > t_{0}$. Consequently, for $t \geq t_{0}$ and $x \in \varOmega$,

$$ P(t,x ) \leq P(t) \leq \hat{P}(t). $$

Similarly, we can prove all the remaining parts of the statement. The proof of Theorem 3 is completed. □

For the global stability of the positive solutions of system (4), we transform system (4) into a differential system in which the periodic solution becomes the origin.

Lemma 3

Let$(P^{*}(t),Q^{*}(t))$be a positive periodic solution to system (5). If$(P( t,x), Q(t,x))$is a solution to (4), by applying the substitution

$$ P(t, x) =\frac{P(t, x)}{P^{*}(t)} -1,\qquad Q(t, x ) = \frac{Q(t, x)}{Q^{*}(t)} - 1, $$

(26)

system (4) turns into

$$ \textstyle\begin{cases} \frac{\partial S(t,x)}{\partial t}\\ \quad =d_{1}(t)\triangle S+(1+S) [ (-b_{1}(t)P^{*}(t)- \frac{c_{1}(t)(1-m(t))^{2}Q^{*}(t)}{P^{*}(t)(\theta (t)-m(t)) [(1-m(t))S+\theta (t)-m(t)]} )S \\ \qquad{}- \frac{c_{1}(t)(1-m(t))Q^{*}(t)I}{P^{*}(t)[(1-m(t))S+\theta (t)-m(t)]} ],\quad x\in \varOmega, t>0, \\ \frac{\partial I(t,x)}{\partial t} =d_{2}(t)\triangle I+ \frac{(1+I)c_{2}(t)Q^{*}(t)}{P^{*}(t)} [ \frac{(1-m(t))S}{[(1-m(t))S+\varphi (t)-m(t)](\varphi (t)-m(t))} \\ \phantom{\frac{\partial I(t,x)}{\partial t} =}{}-\frac{I}{(1-m(t))S+ \varphi (t)-m(t)} ], \quad x\in \varOmega, t>0, \\ S(0,x)=S_{0}(x)>-1, \qquad I(0,x)=I_{0}(x)>-1, \quad x\in \bar{\varOmega }, \\ \frac{\partial S(t,x)}{\partial \mathbf{n}} = \frac{\partial I(t,x)}{\partial \mathbf{n}}=0, \quad x\in \partial { \varOmega }, t>0, \end{cases} $$

(27)

where

$$ \begin{aligned}&\theta (t) =\frac{k_{1}(t)}{P^{*}(t)} + 1,\qquad \varphi (t) = \frac{k_{2}(t)}{P^{*}(t)}+ 1,\\ & S_{0}(x) =\frac{P(0,x)}{P^{*}(0)} -1,\qquad I_{0}(x) = \frac{Q(0,x)}{Q^{*}(0)} - 1. \end{aligned} $$

(28)

Proof

From (26) and the initial and boundary conditions in system (4), we can easily obtain the initial and boundary conditions (28). Moreover, we notice that

$$\begin{aligned} \frac{\partial S}{\partial t}={}&\frac{1}{P^{*}(t)} \biggl[ d_{1}(t) \triangle P(t,x)+P(t,x)\biggl[a_{1}(t)-b_{1}(t)- \frac{c_{1}(t)(1-m(t))Q(t,x)}{P(t,x)+k_{1}(t)}\biggr] \biggr] \\ &{}-\frac{P(t,x)}{P^{*}(t)} \biggl[a_{1}(t)-b_{1}(t)P^{*}(t)- \frac{c_{1}(t)(1-m(t))Q^{*}(t)}{(1-m(t))P^{*}(t)+k_{1}(t)} \biggr]. \end{aligned}$$

(29)

In the same way, we can obtain the second equation of system (27). The proof of Lemma 3 is completed. □

According to Theorem 3 and Lemma 3, we can obtain the following result.

Lemma 4

Assume that (9) holds and denote by$(P(x, t), Q(x, t))$and$(P^{*}(t), Q^{*}(t))$a solution of (4) and a positive periodic solution of (5), respectively. Then$(S(x, t),I(x, t)) \in \hat{D}(t) = [\check{S}(t), \hat{S}(t)] \times [\check{I}(t), \hat{I}(t)]$for all$t > \tilde{t}$and$x \in \varOmega$, where

$$ \check{S}(t) =\frac{\check{P}(t)}{P^{*}(t)}-1,\qquad \hat{S}(t) = \frac{\hat{P}(t)}{P^{*}(t)}-1,\qquad \check{I}(t) = \frac{\check{Q}(t)}{Q^{*}(t)}-1,\qquad \hat{I}(t) = \frac{\hat{Q}(t)}{Q^{*}(t)}-1. $$

Next, we begin to discuss the global stability of system (4). According to Lemma 3, once the global stability of the solutions of system (27) is obtained, as a consequence, the global stability of system (4) can be obtained. For convenience, we define

$$\begin{aligned} \gamma (t,S)={}& \frac{c_{2}(t)Q^{*}(t)}{P^{*}(t) [(1-m(t))S+\varphi (t)-m(t)]} \biggl(b_{1}(t)P^{*}(t) \\ &{}- \frac{c_{1}(t)(1-m(t))^{2}Q^{*}(t)}{P^{*}(t)(\theta (t)-m(t))[(1-m(t))S+ \theta (t)-m(t)]} \biggr) \\ &{}-\frac{(Q^{*}(t))^{2}(1-m(t))^{2}}{4(P^{*}(t))^{2}} \biggl[ \frac{c_{1}(t)}{(1-m(t))S+\theta (t)-m(t)} \\ &{}- \frac{c_{2}(t)}{[(1-m(t))S+\varphi (t)-m(t)](\varphi (t)-m(t))} \biggr], \end{aligned}$$

(30)

where $t>0, S \in [\check{S}(t), \hat{S}(t)]$.

Theorem 4

Let$(P^{*}(t),Q^{*}(t))$be the positive periodic solutions of system (5). And assume that (9) and$\gamma (t,S)>0$hold. Then the positive period solution$(P(t,x),Q(t,x))$of system (4) is globally asymptotically stable; in other words, $(P(t,x),Q(t,x))$attracts every positive solution of system (4).

Proof

Let $(P(t,x),Q(t,x))$ be a positive solution of system (4). Choose a Lyapunov function as follows:

$$ V(t)= \int _{\varOmega }L\bigl(S(t,x),I(t,x)\bigr)\,dx, $$

where

$$ L\bigl(S(t,x),I(t,x)\bigr)= \int _{1}^{S+1}\biggl(1-\frac{1}{\xi }\biggr)\,d \xi + \int _{1}^{I+1}\biggl(1- \frac{1}{\eta }\biggr)\,d \eta. $$

Straightforward computations yield that

$$\begin{aligned} \frac{dV(t)}{dt}={}& \int _{\varOmega }{L_{S}\bigl(S(t,x),I(t,x) \bigr)S_{t}+L_{I}\bigl(S(t,x),I(t,x)\bigr)I_{t}} \,dx \\ ={}& \int _{\varOmega } \biggl(\frac{S}{S+1}\,d_{1}(t) \triangle S+\frac{I}{I+1}d_{2}(t) \triangle I \biggr)\,dx \\ &{}+ \int _{\varOmega } \biggl\{ \frac{S}{S+1}(1+S) \biggl[ \biggl(-b_{1}(t)P^{*}(t) \\ &{}- \frac{c_{1}(t)(1-m(t))^{2}Q^{*}(t)}{P^{*}(t)(\theta (t)-m(t)) [(1-m(t))S+\theta (t)-m(t)]} \biggr)S \\ &{}- \frac{c_{1}(t)(1-m(t))Q^{*}(t)I}{P^{*}(t)[(1-m(t))S+\theta (t)-m(t)]} \biggr]+\frac{I}{I+1}\frac{(1+I)c_{2}(t)Q^{*}(t)}{P^{*}(t)} \\ &{}\times \biggl[ \frac{(1-m(t))S}{[(1-m(t))S+\varphi (t)-m(t)] (\varphi (t)-m(t))}- \frac{I}{(1-m(t))S+\varphi (t)-m(t)} \biggr] \biggr\} \,dx \\ ={}&V_{1}(t)+V_{2}(t), \end{aligned}$$

(31)

where

$$\begin{aligned} V_{1}(t)&= \int _{\varOmega } \biggl(\frac{S}{S+1}d_{1}(t) \triangle S+ \frac{I}{I+1}d_{2}(t)\triangle I \biggr)\,dx \\ &=- \int _{\varOmega } \biggl(d_{1}(t)\frac{ \vert \nabla S \vert ^{2}}{(S+1)^{2}}+d_{2}(t) \frac{ \vert \nabla I \vert ^{2}}{(I+1)^{2}} \biggr)\,dx\leq 0 \end{aligned}$$

(32)

and

$$\begin{aligned} V_{2}(t)={}& \int _{\varOmega } \biggl\{ \frac{S}{S+1}(1+S) \biggl[ \biggl(-b_{1}(t)P^{*}(t) \\ &{}- \frac{c_{1}(t)(1-m(t))^{2}Q^{*}(t)}{P^{*}(t) (\theta (t)-m(t))[(1-m(t))S+\theta (t)-m(t)} \biggr)S \\ &{}- \frac{c_{1}(t)(1-m(t))Q^{*}(t)I}{P^{*}(t)[(1-m(t))S+\theta (t)-m(t)]} \biggr]+\frac{I}{I+1}\frac{(1+I)c_{2}(t)Q^{*}(t)}{P^{*}(t)} \\ &{}\times \biggl[ \frac{(1-m(t))S}{[(1-m(t))S+(\varphi (t)-m(t))] (\varphi (t)-m(t))} \\ &{}- \frac{I}{(1-m(t))S+(\varphi (t)-m(t))} \biggr] \biggr\} \,dx \\ ={}& \int _{\varOmega }- \biggl[(b_{1}(t)P^{*}(t)- \frac{c_{1}(t)(1-m(t))^{2}Q^{*}(t)}{P^{*}(t)(\theta (t)-m(t)) [(1-m(t))S+\theta (t)-m(t)]} \biggr]S^{2} \\ &{}+\frac{Q^{*}(t)(1-m(t))}{P^{*}(t)} \\ & {}\times\biggl[\frac{c_{1}(t)}{(1-m(t))S+\varphi (t)-m(t)}- \frac{c_{2}(t)}{[(1-m(t))S+\varphi (t)-m(t)](\varphi (t)-m(t))} \biggr]SI \\ &{}-\frac{c_{2}(t)Q^{*}(t)}{P^{*}(t)[(1-m(t))S+\varphi (t)-m(t)]}I^{2} \}\,dx \\ ={}& \int _{\varOmega } \begin{pmatrix} S&I \end{pmatrix} \begin{pmatrix} A_{11}&A_{12} \\ A_{21}&A_{22} \end{pmatrix} \begin{pmatrix} S \\ I \end{pmatrix}\,dx, \end{aligned}$$

(33)

where

$$\begin{aligned} \begin{aligned} &A_{11}=- \biggl(b_{1}(t)P^{*}(t) - \frac{c_{1}(t)(1-m(t))^{2}Q^{*}(t)}{P^{*}(t)(\theta (t)-m(t))[(1-m(t))S+\theta (t)-m(t)]} \biggr), \\ &A_{12}=A_{21}=\frac{Q^{*}(t)(1-m(t))}{2P^{*}(t)} \biggl[ \frac{c_{1}(t)}{(1-m(t))S+\theta (t)-m(t)} \\ &\phantom{A_{12}=A_{21}=}{}- \frac{c_{2}(t)}{[(1-m(t))S+\varphi (t)-m(t)](\varphi (t)-m(t))} \biggr], \\ &A_{22}=\frac{c_{2}(t)Q^{*}(t)}{P^{*}(t)[(1-m(t))S+\varphi (t)-m(t)]}. \end{aligned} \end{aligned}$$

(34)

It can be seen that if $\gamma (t,S)>0$, the matrix

$$ \begin{pmatrix} A_{11}&A_{12} \\ A_{21}&A_{22} \end{pmatrix} $$

is negative definite. In addition, taking into account that $(S,I)$ belongs to the compact region $\hat{D}(t)$, there exists $\rho > 0$ such that

$$ \gamma (S,I)\leq -\rho \bigl(S^{2}+I^{2} \bigr). $$

(35)

Hence, from (35) we can obtain that

$$ \frac{dV}{dt}\leq -\rho \int _{\varOmega }\bigl(S^{2}+I^{2}\bigr)\,dx. $$

(36)

Integrating (36) from t̄ to t, we can obtain that

$$ \rho \int _{\bar{t}}^{t} \,d\xi \biggl( \int _{\varOmega }\bigl(S^{2}+I^{2}\bigr)\,dx \biggr)\leq V( \bar{t})-V(t)< V(\bar{t})< +\infty. $$

Thus

$$ \int _{\bar{t}}^{\infty }\,d\xi \biggl( \int _{\varOmega }\bigl(S^{2}+I^{2}\bigr)\,dx \biggr)< +\infty. $$

By Lemma 2.1 [21], we obtain that

$$ \lim_{t\rightarrow \infty } \bigl\Vert S(t,\cdot ) \bigr\Vert _{L^{2}( \varOmega )}=0=\lim_{t\rightarrow \infty } \bigl\Vert I(t,\cdot ) \bigr\Vert _{L^{2}(\varOmega )}=0. $$

(37)

Using standard arguments [16], we get our statement. Indeed, let $p > \max \{n, 2\}$, then the Sobolev inequality yields that

$$\begin{aligned} \bigl\vert S(t,x) \bigr\vert ^{P}&\leq \int _{\varOmega } \bigl\vert S(t,\cdot ) \bigr\vert ^{P}\,dx+ \int _{\varOmega } \bigl\vert \nabla S(t,\cdot ) \bigr\vert ^{P}\,dx \\ &\leq e_{1} \int _{\varOmega } \bigl\vert S(t,\cdot ) \bigr\vert ^{2} \,dx+e_{2} \int _{\varOmega } \bigl\vert \nabla S(t,\cdot ) \bigr\vert ^{2}\,dx \quad\text{for } (x, t) \in \bar{\varOmega } \times R^{+}. \end{aligned}$$

(38)

Moreover,

$$ \lim_{t\rightarrow \infty } \int _{\varOmega } \bigl\vert \nabla S(t,\cdot ) \bigr\vert ^{2}\,dx=0, $$

in fact, multiplying the first equation in (28) by S and integrating over Ω, there exists $e_{3}>0$ such that

$$\begin{aligned} d_{1}(t) \int _{\varOmega } \bigl\vert \nabla S(t,\cdot ) \bigr\vert ^{2}\,dx\leq -\frac{1}{2} \frac{d}{dt} \int _{\varOmega }S^{2}\,dx+ e_{3} \int _{\varOmega }\bigl(S^{2}+I^{2}\bigr)\,dx. \end{aligned}$$

(39)

From (37), (38), and (39), it follows that $\lim_{t\rightarrow \infty }|S(t,x)|= 0 \text{ uniformly w.r.t.} x \in \varOmega$. Arguing in the same way, $\lim_{t\rightarrow \infty }|I(t,x)|= 0 \text{ uniformly w.r.t.} x \in \varOmega$. Going back to $P(x, t), Q(x, t)$ through (26), we conclude

$$ \lim_{t\rightarrow \infty } \bigl\vert P(t,x)-P^{*}(t) \bigr\vert = 0 =\lim_{t \rightarrow \infty } \bigl\vert Q(t,x)-Q^{*}(t) \bigr\vert \quad \text{uniformly w.r.t.} x\in \varOmega. $$

 □

4 Numerical simulations

In this section, we do some numerical simulations to verify our analysis results. Moreover, we do some simulations to investigate the effect of the prey refuge. Firstly, we give Example 1 to illustrate the existence of the periodic solutions for an ODE system, and the existence region of the positive periodic solutions is an invariant region dependent on t. Then, we give Example 2 to illustrate the existence of the positive periodic solutions for PDE system (4) and their global asymptotic stability.

Example 1

For system (4), we take the parameters as shown in Table 1.

Table 1 Values of the parameters

Then system (5) becomes

$$ \textstyle\begin{cases} \frac{dP(t)}{dt}=P(t) [5+\sin (t)-(2-\sin (t))P(t)- \frac{(0.6+0.1\sin (t))0.9\times Q(t)}{P(t)+6} ], \\ \frac{d Q(t)}{dt}=Q(t) [0.4+0.1\sin (t)- \frac{(0.4+0.1\sin (t))Q(t)}{0.9\times P(t)+3} ]. \end{cases} $$

(40)

From Lemma 1 and Theorem 1, we can obtain that

$$\begin{aligned} &\hat{P}(t)= \frac{P(0)\times \exp (5t-\cos (t)+1)}{1+P(0)\times \int _{0}^{t}[(2-\sin (s))\times \exp (5s-\cos (s)+1)]\,ds}, \\ &\hat{Q}(t)= \frac{Q(0)\times \exp (0.4t-0.1\cos (t)+0.1)}{1+Q(0)\times \int _{0}^{t}[\frac{0.4+0.1\times \sin (s)}{0.8\times \hat{P}(s)+3}\times \exp (0.4s-0.1\cos (s)+0.1)]\,ds}, \\ &\check{P}(t)= \frac{P(0)\times \exp (\int _{0}^{t}(5+\sin (s)-\frac{(0.6+0.1\sin (s))0.9\times \hat{Q}(s)}{6})\,ds)}{1+P(0)\times \int _{0}^{t}[(2-\sin (s))\times \exp (\int _{0}^{s}(5+\sin (\tau )-\frac{(0.6+0.1\sin (\tau ))0.9\times \hat{Q}(\tau )}{6})\,d\tau )]\,ds}, \\ &\check{Q}(t)= \frac{Q(0)\times \exp (0.4t-0.1\cos (t)+0.1)}{1+P(0)\times \int _{0}^{t}[\frac{0.4+0.1\times \sin (s)}{0.8\times \check{P}(s)+3}\times \exp (0.4s-0.1\cos (s)+0.1)]\,ds}. \end{aligned}$$

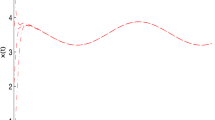
Moreover, we obtain that $[a_{1}(t)]=31.4159>6.7458=[ \frac{c_{1}(t)((1-m(t))\hat{Q}(t)}{k_{1}(t)}]$ when $P(0)=7,Q(0)=3$. Hence, system (40) has a positive 2π-periodic solution $(P^{*}(t),Q^{*}(t))$ (see Fig. 1). However, our major goal is to investigate the existence of the periodic solutions of system (4) and their global asymptotic stability. Hence, we give Example 2.

Figure 1

The periodic solution $(P^{*}(t),Q^{*}(t))$ with initial values $P(0)=7$, $Q(0)=3$. (a)–(b): the densities of prey $P^{*}(t)$ and predator $Q^{*}(t)$

Example 2

For system (4), we take the parameters $d_{1}(t)=0.9+0.5\sin (t), d_{2}(t)=0.7+0.5\sin (t)$, and $P_{0}(x)=7+0.2\sin (x), Q_{0}(x)=3+0.2\sin (x)$. And the other parameters are taken as in Table 1. Then system (4) becomes the following system:

$$ \textstyle\begin{cases} \frac{\partial P(t,x)}{\partial t}=(0.9+0.5\sin (t))\times \triangle P(t,x)+P(t,x) [5+\sin (t)-(2-\sin (t))P(t,x) \\ \phantom{\frac{\partial P(t,x)}{\partial t}=}{}-\frac{(0.6+0.1\sin (t))0.9\times Q(t,x)}{P(t,x)+6} ], \quad x\in \varOmega, t>0, \\ \frac{\partial Q(t,x)}{\partial t} =(0.7+0.5\sin (t))\times \triangle Q(t,x)+Q(t,x) [0.4+0.1\sin (t) \\ \phantom{\frac{\partial Q(t,x)}{\partial t} =}{}-\frac{(0.4+0.1\sin (t))Q(t,x)}{0.9\times P(t,x)+3} ], x\in \varOmega, \quad t>0, \\ P(0,x)=7+0.2\sin (x)>0, \qquad Q(0,x)=3+0.2\sin (x)>0, \quad x\in \bar{\varOmega }, \\ \frac{\partial P(t,x)}{\partial \mathbf{n}}= \frac{\partial Q(t,x)}{\partial \mathbf{n}}=0, \quad x\in \partial { \varOmega }, t>0. \end{cases} $$

(41)

At the same time, we can easily verify that conditions (9) and (30) hold. In order to verify the global stability of the positive periodic solutions, we keep other parameters unchanged and take the initial value functions $P(0,x)=7+0.2\sin (x)$, $Q(0,x)=3+0.2\sin (x)$ and $P(0,x)=10+0.2\sin (x)$, $Q(0,x)=6+0.2\sin (x)$, respectively. And we obtain Figs. 2 and 3 accordingly, which proves the global stability of the positive periodic solutions.

Figure 2

The periodic solution $(P(t,x),Q(t,x))$ with initial values $P(0,x)=7+0.2\sin (x)$, $Q(0)=3+0.2\sin (x)$. (a)–(b): the densities of prey $P(t,x)$ and predator $Q(t,x)$

Figure 3

The periodic solution $(P(t,x),Q(t,x))$ with initial values $P(0,x)=10+0.2\sin (x)$, $Q(0)=6+0.2\sin (x)$. (a)–(b): the densities of prey $P(t,x)$ and predator $Q(t,x)$

However, as we can see, conditions (9) and (30) both have the prey refuge $m(t)$. And changing the prey refuge $m(t)$ will change conditions (9) and (30). Hence, it is necessary to investigate the effect of the prey refuge $m(t)$ on the dynamic of the system. In Example 2, we keep other parameters unchanged and increase $m(t)=0.5$, we obtain Fig. 4. Contrasting Fig. 3 and Fig. 4, we can find that the number of the prey $P(t,x)$ will increase when we increase the prey refuge $m(t)$, and the number of the predator $Q(t,x)$ will decrease when we increase the prey refuge $m(t)$.

Figure 4

The periodic solution $(P(t,x),Q(t,x))$ with initial values $P(0,x)=10+0.2\sin (x)$, $Q(0)=6+0.2\sin (x)$. (a)–(b): the densities of prey $P(t,x)$ and predator $Q(t,x)$

5 Conclusions

In this paper, we propose and study a nonautonomous reaction-diffusion predator-prey model with modified Leslie–Gower Holling-II schemes and a prey refuge. We first study the corresponding ODE model and obtain the sufficient average criteria on the permanence of solutions and the existence of the positive periodic solutions by the comparison theory of differential equation. Moreover, the existence region of the positive periodic solutions is an invariant region dependent on t, which is different from the previous results. Finally, constructing a suitable Lyapunov function, we obtain the sufficient conditions to guarantee the global asymptotic stability of the positive periodic solutions.

In order to verify our analysis results, we do some numerical simulations. As the theory analysis indicates, when conditions (9) and (30) hold, the positive periodic solutions will be globally asymptotically stable. At the same time, we verify these results by Figs. 2 and 3. From the biological background, condition (9) implies that the prey refuge has a positive effect on the persistence of the system; that is to say, the predators have difficulty in catching the prey species with the increase in prey refuge, and this directly increases the survival possibility of the prey species. In order to investigate the effect of the prey refuge, we do the number simulations and obtain Fig. 4. Contrasting Fig. 3 and Fig. 4, we can easily verify the biological meaning of prey refuge.

However, in this paper, we just investigated the positive periodic solutions dependent on t under the homogeneous Neumann conditions. Whether the positive periodic solutions dependent on location x exist or not and whether they are globally asymptotically stable are all open problems that need to be investigated in the future.