Abstract
A Holling type III functional response predator-prey system with constant gestation time delay and impulsive perturbation on the prey is investigated. The sufficient conditions for the global attractivity of a predator-extinction periodic solution are obtained by the theory of impulsive differential equations, i.e. the impulsive period is less than the critical value \(T_{1}^{*}\). The conditions for the permanence of the system are investigated, i.e. the impulsive period is larger than the critical value \(T_{2}^{*}\). Numerical examples show that the system has very complex dynamic behaviors, including (1) high-order periodic and quasi-periodic oscillations, (2) period-doubling and -halving bifurcations, and (3) chaos and attractor crises. Further, the importance of the impulsive period, the gestation time delay, and the impulsive perturbation proportionality constant are discussed. Finally, the impulsive control strategy and the biological implications of the results are discussed.
Similar content being viewed by others
1 Introduction
The time delay population dynamics system describes the current state of the population not only related to the current state but also related to the state of the population in the past. That is to say, the time delay effect is very important in population dynamics, which tends to destabilize the positive equilibria and cause a loss of stability, bifurcate into various periodic solutions, even make chaotic oscillations. Recently, there has been much work dealing with time delayed population systems (see [1–12]). For example, a stage-structured prey-predator system with time delay and Holling type-III functional response is considered by Wang et al. [4], the existence and properties of the Hopf bifurcations are established. A delayed eco-epidemiology model with Holling-III functional response was instigated by Zou et al. [5], and one found that time delay may lead to Hopf bifurcation under certain conditions. The Hopf bifurcation of a delayed predator-prey system with Holling type-III functional response also has been considered in [6–8]. The existence of positive periodic solutions of a delayed nonautonomous prey-predator system with Holling type-III functional response was considered in [9–11], by using the continuation theorem of coincidence degree theory. Therefore, time delays would make the prey-predator system subject to periodic oscillations via a local Hopf bifurcation, and destroy the stability of the system.
Recently, more and more authors have discussed the impulsive perturbation on prey-predator systems, since the system would be stabilized by impulsive effects, and would make the system subject to complex dynamical behaviors [13–21]. For example, a predator-prey model with impulsive effect and generalized Holling type III functional response was studied by Su et al. [15], and the sufficient conditions for the existence of a pest-eradication periodic solution and permanence of the system are obtained. The existence of positive periodic solutions of the nonautonomous prey-predator system with Holling type III functional response and impulsive perturbation is considered in [17, 18]. By using a continuation theorem of coincidence degree theory, the sufficient conditions for the existence of a positive periodic solution are obtained for the system.
Note that harmful delays would destroy the stability of the system via bifurcations and even lead the system to extinction. At this point, the impulsive control strategies can be considered, which can both improve the stability of the system and control the amplitude of the bifurcated periodic solution effectively. For example, a time delayed Holling type II functional response prey-predator system with impulsive perturbations is investigated by Jia et al. [22], and the problems of the predator-extinction periodic solution and the permanence of the system are investigated. So, how does the dynamical behavior go when the delayed system with impulsive effect? Especially, what would happen for the delayed predator-prey system with Holling type III functional response under impulsive perturbation?
Motivated by the aforementioned observations, we assume the predator needs a certain time to gestate the prey, and we consider the following delayed Holling type III functional response prey-predator system with impulsive perturbation on the prey:
where \(x(t)\) and \(y(t)\) are the prey and predator populations at time t, respectively; r, K, α, β, k, d are positive. r is the intrinsic rate of increase of the prey, K is the carrying capacity of the prey. α is the predation coefficient of the predator, which reflects the size of the predator’s ability, and β is predation regulation factor (saturation factor) of the predator. d is the death rate of the predator, k (\(0 < k < 1\)) is the rate of conversing prey into predator. \(\Delta x(t) = x(t^{+} ) - x(t)\), \(\Delta y(t) = y(t^{+} ) - y(t)\), T is the impulsive periodic. \(n \in\mathbb{N}_{+}\), \(\mathbb{N}_{+} = \{ 1,2, \ldots\}\), \(p> 0\) is the proportionality constant which represents the rate of mortality due to the applied pesticide. The initial conditions for system (1) are
The paper is arranged as follows. Some notations and lemmas are given in the next section, and we consider the existence and global attraction of the predator-extinction periodic solutions of the system. The sufficient conditions for the permanence of the system are given by using the theory on impulsive and delay differential equation. Numerical examples are given to support the theoretical research, and some complex dynamic behaviors are shown. For example, we see period-halving and period-doubling bifurcations, periodic and high-order quasi-periodic oscillations, even chaotic oscillation. The importance of the impulsive period T, the gestation time delay τ, and the impulsive perturbation proportionality constant p are discussed. Finally, the impulsive control strategy and biological implications of the results are discussed.
2 Preliminaries
Let \(\mathbb{R}_{+}=[0,\infty)\), \(\mathbb{R}_{+} ^{2} = \{ x \in \mathbb{R}^{2} |x \ge0\} \). Denote by \(f=(f_{1},f_{2})\) the map defined by the right hand of the first two equations of system (1), and let \(\mathbb{N}\) be the set of all non-negative integers. Let \(V:\mathbb{R}_{+} \times\mathbb{R}_{+} ^{2} \to\mathbb{R}_{+} \), then V is said to belong to class \(V_{0}\) if:
-
(1)
V is continuous in \((t,x) \in(nT,(n + 1)T] \times\mathbb{R}_{+} ^{2} \) and for each \(x\in\mathbb{R}_{+}^{2}\), \(n\in\mathbb{N}\), \(\lim_{(t,y) \to(nT^{+} ,x)}V(t,y) = V(nT^{+} ,x)\) exists.
-
(2)
V is locally Lipschitzian in x.
Definition 2.1
Let \(V \in V_{0}\), then for \((t,x) \in (nT,(n + 1)T] \times\mathbb{R}_{+} ^{2} \), the upper right derivative of \(V(t,x)\) with respect to the impulsive differential system (1) is defined as
Definition 2.2
System (1) is said to be permanent if there exist two positive constants m, M, and \(T_{0}\) such that each positive solution \(X(t)=(x(t),y(t))\) of the system (1) satisfies \(m \le x(t) \le M\), \(m \le y(t) \le M\) for all \(t>T_{0}\).
The solution of system (1) is a piecewise continuous function \(x:\mathbb{R}_{+} \mapsto\mathbb{R}_{+} ^{2} \), \(x(t)\) is continuous on \((nT,(n + 1)T]\), \(n\in\mathbb{N}\), and \(x(nT^{+} ) = \lim_{t \to nT^{+} } x(t)\) exists, the smoothness properties of f guarantee the global existence and uniqueness of solutions of system (1), for details see [23, 24].
Lemma 2.1
Let \(X(t)\) be a solution of system (1) with \(X(0^{+})\geq0\), then \(X(t)\geq0\) for all \(t\geq0\) and further \(X(t)>0\) for all \(t\geq0\) if \(X(0^{+})>0\).
Lemma 2.2
[23]
Suppose \(V \in V_{0} \). Assume that
where \(g:\mathbb{R}_{+} \times\mathbb{R}_{+} \mapsto\mathbb{R}\) is continuous in \((nT,(n + 1)T] \times\mathbb{R}_{+} \) and for \(u \in\mathbb{R}_{+}\), \(n \in\mathbb{N}\), \(\lim_{(t,y) \to(nT^{+} ,u)} = g(nT^{+} ,u)\) exists, \(\psi_{n} :\mathbb{R}_{+} \to\mathbb{R}_{+} \) is non-decreasing. Let \(r(t)\) be the maximal solution of the scalar impulsive differential equation
existing on \([0,\infty)\). Then \(V(0^{+} ,x_{0} ) \le u_{0} \) implies that \(V(t,x(t)) \le r(t)\), \(t \ge0\) where \(X(t)\) is any solution of system (1).
We consider the following subsystem of system (1):
Clearly, if \((1 - p){e^{rT}} > 1\),
is a globally asymptotically stable positive periodic solution of system (5) [22].
Lemma 2.3
If \((1 - p){e^{rT}} > 1\), system (1) has a predator-extinction periodic solution \(X(t)=({x^{*}}(t),0)\) for \(t \in (nT,(n + 1)T]\), and for any solution \(X(t)=(x(t),y(t))\) of system (1), we have \(x(t) \to{x^{*}}(t)\) as \(t \to + \infty\).
Lemma 2.4
Consider the following delay differential equation [25]:
where a, b, τ are all positive constants and \(x(t)>0\) for \(t\in [-\tau,0]\).
-
(i)
If \(a< b\), then \(\lim_{t\to+\infty} x(t)=0\).
-
(ii)
If \(a>b\), then \(\lim_{t\to+\infty} x(t)=+\infty\).
3 Extinction and permanence
Denote
Theorem 3.1
If \({\Re_{1}} < 1\) and \((1 - p){e^{rT}} > 1\), then the predator-extinction periodic solution \(X(t) = ({x^{*}}(t),0)\) of system (1) is globally attractive.
Proof
Let \(X(t)=(x(t),y(t))\) be any solution of system (1) with initial conditions (2). By the second equation of system (1), we get
Consider the following delayed comparison equation:
If \(k\alpha< d\beta\), then \({{\Re}_{1}}<1\). According to Lemma 2.4, we have \(\lim_{t\to+\infty} z(t)=0\). Note that \(y(t)=z(t)={{\phi}_{2}}(t)>0\) for all \(t\in[-\tau,0]\), then we have \(y(t)\to0\) as \(t\to+\infty\). We assume that \(k\alpha >d\beta\) in the rest of this paper. \({{\Re}_{1}}<1\) and we note that \(\frac{k\alpha{{z}^{2}}}{1+\beta{{z}^{2}}}\) is a monotonically increasing function about variable z. Therefore, there exists a sufficiently small positive constant ε such that
By the first and third equations of system (1), we have
then we consider the following comparison system:
with \(z({{0}^{+}})=z(0)=x(0)\). Recalling system (5), we obtain a unique globally asymptotically stable positive T-periodic solution of system (6), where
Then, there exists an arbitrarily small positive constant ε and \({{n}_{1}} \in\mathbb{N}\) such that
for all \(t\ge{{n}_{1}}T\). From (7) and the second equation of system (1), we have
for \(t\ge{{n}_{1}}T+\tau\). Consider the following delayed comparison equation:
According to Lemma 2.4, we get \(\lim_{t\to+\infty} z(t)=0\). Note that \(y(t)=z(t)={{\phi}_{2}}(t)>0\) for all \(t\in [-\tau,0]\), then we have \(y(t)\to0\) as \(t\to+\infty\).
Without loss of generality, we may suppose that \(0< y(t)<\varepsilon\) and \({r_{1}} = r - \alpha K\varepsilon > 0\), \({K_{1}} = {r_{1}}K/r\) for ε small enough and \(t\ge0\). By the first equation of system (1), we obtain
Then we have \(z_{1}^{*}(t)\to{{x}^{*}}(t)\) as \(\varepsilon\to0\) (\(t\to +\infty\)), where \(z_{1}^{*}(t)\) is the unique periodic solution of the following comparison system:
with initial condition \({{z}_{1}}({{0}^{+}})=x({{0}^{+}})\). From (8), we get
where
Therefore, for any \({{\varepsilon}_{1}}>0\) there exists a \({{T}_{0}}>0\) such that
for \(t>{{T}_{0}}\).
By the first equation of system (1), we get
Consider the following comparison system:
with initial condition \({{z}_{2}}({{0}^{+}})=x({{0}^{+}})\). Then, we have
as \(t\to+\infty\) and \(z_{2}^{*}(t)={{x}^{*}}(t)\), where \(z_{2}^{*}(t)\) is the unique positive periodic solution of (10). Let \(\varepsilon\to0\), and by (9) and (11), we have
for sufficiently large t. This implies \(x(t)\to{{x}^{*}}(t)\) as \(t\to+\infty\). □
Theorem 3.2
There exists a constant \(Y_{0}=M_{1}/d-kK>0\), such that \(x(t) \le K\) and \(y(t) \le Y_{0}\) for any solution \(X(t) = (x(t),y(t))\) of system (1) with all t large enough.
Proof
Let \(V(t) = kx(t) + y(t+\tau)\). Note that \(V \in V_{0}\). We get \(V'(t)\) by calculating the upper right derivative of \(V(t)\) along a solution of system (1):
Let \({{M}_{1}}=\max \{ Kkd,\frac{K{{(r+d)}^{2}}}{4} \}\), then we have
Consider the following differential inequalities:
according to Lemma 2.2, we have
Therefore \(\lim_{t\to+\infty} V(t)\le {{M}_{1}}/d\triangleq M\), then \(V(t)\) is ultimately bounded. Therefore, any positive solution of system (1) is uniformly ultimately bounded. □
Denote
Theorem 3.3
If \({{\Re}_{2}}>1\) and \(r>\alpha KY_{0}\), then system (1) is uniformly persistent.
Proof
Suppose that \(X(t) = (x(t), y(t))\) is each positive solution of system (1) with initial conditions (2). Rewrite the second equation of system (1) as follows:
Define
Calculating \(V' (t)\) along the solution of system (1), we have
Since \({{\Re}_{2}}>1\), there exist two positive constants \(m_{2}^{*}\) and \({{\varepsilon}_{1}}\) small enough such that
where
We claim that: for any positive constant \({{t}_{0}}\), the inequality \(y(t)< m_{2}^{*}\) cannot hold for all \(t\ge{{t}_{0}}\). Otherwise, we can choose a positive constant \(t_{0}\) such that \(y(t)< m_{2}^{*}\) for all \(t\ge {{t}_{0}}\). By the first and third equations of system (1), we obtain
Then, we have \(z_{2}^{*}(t)\le x(t)\), where \(z_{2}^{*}(t)\) is an unique positive solution of the following comparison system:
with initial condition \({{z}_{2}}({{0}^{+}})=x({{0}^{+}})\). From (15), we obtain
for \(t\in(nT,(n+1)T]\), where
Then, for any \({{\varepsilon}_{1}}>0\) there exists a \({{T}_{1}}>0\) such that
for \(t>{{T}_{1}}\).
When \(t\ge{{T}_{1}}\), from (12) and (16) we get
Let \({{y}_{1}}=\min\{y(t)|{{T}_{1}}\le t\le{{T}_{1}}+\tau\}\). We show that \(y(t)\ge{{y}_{1}}\) for all \(t\ge{{T}_{1}}\). Otherwise, there exists a nonnegative constant \({{T}_{2}}\) such that
Thus, by the second equation of system (1), (13), and (17), we obtain
which is a contradiction. Hence, we get \(y(t)>{{y}_{1}}>0\) for all \(t\ge{{T}_{1}}\). From (17), we have
which implies \(V(t)\to+\infty\) as \(t\to+\infty\). This is a contradiction to \(V(t)\leq M\). Then, for any given positive constant \({{t}_{0}}\), the inequality \(y(t)< m_{2}^{*}\) cannot hold for all \(t\ge {{t}_{0}}\).
On the one hand, if \(y(t)\ge m_{2}^{*}\) holds true for all sufficiently large t, then our aim is reached. On the other hand, suppose \(y(t)\) is oscillatory about \(m_{2}^{*}\). Let \({{m}_{2}}=\min\{m_{2}^{*}/2, m_{2}^{*}\exp(-d\tau)\}\) and we will prove that \(y(t)\ge{{m}_{2}}\). There exist two positive constants t̄ and ω such that \(y(\bar{t})=y(\bar{t}+\omega )=m_{2}^{*}\) and \(y(t)< m_{2}^{*}\) for \(t\in(\bar{t},\bar{t}+\omega)\). The inequality \(x(t)>\rho\) holds true for \(t\in(\bar{t},\bar {t}+\omega)\) when t̄ is large enough.
Since there is no impulsive effect on \(y(t)\), \(y(t)\) is uniformly continuous. Then, there exists a constant \(T_{3}\) (with \(0<{{T}_{3}}<\tau \) and \({{T}_{3}}\) is dependent of the choice of t̄) such that \(y(t)>m_{2}^{*}/2\) for all \(t\in[\bar{t},\bar{t}+{{T}_{3}}]\).
If \(\omega\le{{T}_{3}}\), our aim is reached. If \({{T}_{3}}<\omega\le \tau\), by the second equation of system (1) we get \({y}'(t)\ge -dy(t)\) for \(t\in(\bar{t},\bar{t}+\omega]\). Then we get \(y(t)\ge m_{2}^{*}\exp(-d\tau)\) for \(\bar{t}< t\le\bar{t}+\omega\le\bar{t}+\tau\) since \(y(t)=m_{2}^{*}\). Therefore, \(y(t)\ge{{m}_{2}}\) for \(t\in(\bar{t},\bar {t}+\omega]\).
If \(\omega\ge\tau\), from the second equation of system (1), then we get \(y(t)\ge{{m}_{2}}\) for \(t\in(\bar{t},\bar{t}+\tau]\). Thus, we have \(y(t)\ge{{m}_{2}}\) for \(t\in[\bar{t}+\tau,\bar{t}+\omega]\). According to the above proof. Since the interval \([\bar{t},\bar {t}+\omega]\) is arbitrarily chosen, we have \(y(t)\ge{{m}_{2}}\) for sufficiently large t. From our arguments above, the choice of \({{m}_{2}}\) is independent of the positive solution of system (1) which shows that \(y(t)\ge{{m}_{2}}\) holds for sufficiently large t.
By Theorem 3.2, we obtain \(y(t)\le Y_{0}\) for sufficiently large t. Therefore, by the first equation of system (1), we get
for sufficiently large t, where \({{r}_{3}}=r-\alpha KY_{0}\) and \({{K}_{3}}=K{{r}_{3}}/r\). Therefore, we have \(x(t)\ge z_{3}^{*}(t)\), where \(z_{3}^{*}(t)\) is a unique globally asymptotically stable positive periodic solution of the following comparison system:
with initial condition \({{z}_{3}}({{0}^{+}})=x({{0}^{+}})\). Similarly, we can choose a \(\varepsilon>0\) small enough such that
holds for sufficiently large t. □
Remark 1
Let \((1-p){{e}^{rT}}>1\) and
Note that \({{F}_{1}}({{f}_{1}}(p,T))\) is a monotonically increasing function with respect to \({{f}_{1}}(p,T)\), and \({{f}_{1}}(p,T)\) is a monotonically increasing function with respect to T (\(T>-\ln(1-p)/r\)) and a monotonically decreasing function with respect to p (\(0< p<1-\exp (-rT)\)), since
So, there exists a unique \(T_{1}^{*}\) such that \({{F}_{1}}({{f}_{1}}(p,T_{1}^{*}))=0\) if we fix p, similarly, there exists a unique \(p_{1}^{*}\) such that \({{F}_{1}}({{f}_{1}}(p_{1}^{*},T))=0\) if we fix T. Therefore, the condition \({{\Re}_{1}}<1\) is equivalent to \(T< T_{1}^{*}\) (or \(p>p_{1}^{*}\)), where \(T_{1}^{*}(p_{1}^{*})\) is the unique solution of \({{F}_{1}}({{f}_{1}}(p,T))=0\).
Similarly, let
Note that \({{F}_{2}}({{f}_{2}}(p,T))\) is a monotonically increasing function with respect to \({{f}_{2}}(p,T)\), and \({{f}_{2}}(p,T)\) is a monotonically increasing function with respect to T (\(T>-\ln(1-p)/r\)) and a monotonically decreasing function with respect to p (\(0< p<1-\exp (-rT)\)), since
So, there exists a unique \(T_{2}^{*}\) such that \({{F}_{2}}({{f}_{2}}(p,T_{2}^{*}))=0\) if we fix p, similarly, there exists a unique \(p_{2}^{*}\) such that \({{F}_{2}}({{f}_{2}}(p_{2}^{*},T))=0\) if we fix T. Therefore, the condition \({{\Re}_{2}}>1\) is equivalent to \(T>T_{2}^{*}\) (or \(p< p_{2}^{*}\)), where \(T_{2}^{*}(p_{2}^{*})\) is the unique solution of \({{F}_{2}}({{f}_{2}}(p,T))=0\).
Remark 2
Note that \({{f}_{1}}(p,T)>{{f}_{2}}(p,T)\), so \(T_{1}^{*}< T_{2}^{*}\) for \({{F}_{1}}({{f}_{1}}(p,T_{1}^{*}))=0\) and \({{F}_{2}}({{f}_{2}}(p,T_{2}^{*}))=0\) with respect to the same value of the parameter p. Therefore, if \(T< T_{1}^{*}\) the predator-extinction periodic solution is globally attractive and if \(T>T_{2}^{*}\) the system has permanence. If system (1) is without time delay, according to [14], we know that there would be a threshold \(T_{\max} \). If \(T < T_{\max}\), then the prey- (or predator)-eradication periodic solution is locally asymptotically stable; if \(T > T_{\max} \) the system is permanent. But we get two thresholds \(T_{1}^{*}\) and \(T_{2}^{*}\), and there is no information as regards the system when \(T_{1}^{*}< T< T_{2}^{*}\). This is essentially different when system (1) is with or without time delay.
4 Numerical analysis
Numerical experiments are carried out to integrate the system by using the DDE23 algorithm method in MATLAB.
4.1 Example 1
We consider the following delayed Holling type-III response prey-predator system with impulsive perturbation:
where \(r=1.5\), \(K=5\), \(\alpha=0.75\), \(\beta=1\), \(k=0.5\), \(d=0.24\), with initial conditions \(({{\phi}_{1}}(t),{{\phi}_{2}}(t))=(1,1)\), \(t\in[-\tau,0]\). From Remark 1, we can get thresholds \(T_{1}^{*}\) and \(T_{2}^{*}\) when varying the values of parameter p from 0.01 to 0.9. From Figure 1, we see that \(T_{1}^{*}\) gets more and more close to \(T_{2}^{*}\) when p gets more and more close to zero.
The two thresholds \(\pmb{T_{1}^{*}}\) and \(\pmb{T_{2}^{*}}\) for system ( 18 ).
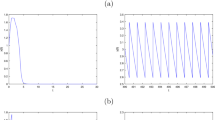
According to [4, 6], there would be a time delay critical value \(\tau_{0}\), and there is a Hopf bifurcation when the time delay τ crosses the critical value \(\tau_{0}\) when system (18) is without impulsive perturbation (i.e. \(p=0\)). From the time-series of the prey population (Figure 2 (left)) and the predator population (Figure 3 (left)) with time delay \(\tau=0.5,0.7,3,6\), respectively, we know that the time delay critical value \(\tau_{0}\) is between 0.5 and 0.7. The prey and predator populations are locally stable when the time delay \(\tau\leq0.5\) and coexist with sable cycles when \(\tau\geq0.7\).
Time-series of prey population \(\pmb{x(t)}\) of system ( 18 ) without (left) and with (right) impulsive period \(\pmb{T=0.5< T_{1}^{*}}\) when the time delay \(\pmb{\tau =0.5,0.7,3,6}\) , respectively.
Time-series of predator population \(\pmb{y(t)}\) of system ( 18 ) without (left) and with (right) impulsive period \(\pmb{T=0.5< T_{1}^{*}}\) when time delay \(\pmb{\tau=0.5,0.7,3,6}\) , respectively.
From Theorem 3.1, Theorem 3.3, and Remark 1, one knows that if \(T< T_{1}^{*}\) the predator-extinction periodic solution is globally attractive and if \(T>T_{2}^{*}\) the system has permanence. From Figure 1, we see \(T_{1}^{*}\approx0.5734\) and \(T_{2}^{*}\approx0.7634\) when \(p=0.5\). Then, the predator-extinction periodic solution is globally attractive when \(T=0.5< T_{1}^{*}\) (see Figure 2 (right) and Figure 3 (right)) where the time delay \(\tau=0.5,0.7,3,6\), respectively. The system is permanent when \(T=0.8>T_{2}^{*}\) where the time delay \(\tau=0.5,0.7,3,6\), respectively (see Figure 4). Furthermore, when the time delay \(\tau=0.5<\tau_{0}\) the predator and prey populations coexist with sable cycles, where the impulsive period \(T=1.8,2.8,3.8,4.8\), respectively (see Figure 5). That is to say, an impulsive effect would destabilize the system under some conditions. If we increasing the time delay from 2 to 4.8, that large time delay could stabilize the system (see Figure 6 and Figure 7).
Time-series of prey (left) and predator (right) population \(\pmb{y(t)}\) of system ( 18 ) with impulsive period \(\pmb{T=0.8>T_{2}^{*}}\) when the time delay \(\pmb{\tau=0.5,0.7,3,6}\) , respectively.
Time-series of prey (left) and predator (right) population \(\pmb{y(t)}\) of system ( 18 ) with time delay \(\pmb{\tau=0.5}\) when the impulsive period \(\pmb{T=1.8,2.8,3.8,4.8}\) , respectively.
Time-series of prey-predator population \(\pmb{y(t)}\) of system ( 18 ) with time delay \(\pmb{\tau=2}\) (left) and \(\pmb{\tau=2.5}\) (right) when the impulsive period \(\pmb{T=1.8,2.8,3.8,4.8}\) , respectively.
Time-series of prey predator population \(\pmb{y(t)}\) of system ( 18 ) with time delay \(\pmb{\tau=4}\) (left) and \(\pmb{\tau=4.8}\) (right) when the impulsive period \(\pmb{T=1.8,2.8,3.8,4.8}\) , respectively.
4.2 Example 2
We consider the following delayed Holling type-III response predator-prey system with impulsive perturbation:
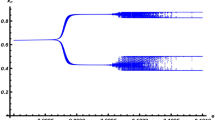
where \(r=2.2\), \(K=7\), \(\alpha=0.75\), \(\beta=0.9\), \(k=0.7\), \(d=0.34\), with initial condition \(({{\phi}_{1}}(s), {{\phi}_{2}}(s))=(1,1)\), \(s\in[-\tau,0]\). First of all, we let \(p=0.3\), \(\tau=3\), and we consider the effect of the impulsive period T on system (19). The bifurcation diagrams of the impulsive period T over \([0.5,8.5]\) and \([6.8,8.5]\), show that system (19) has complex dynamics (see Figure 8 and Figure 9), including high-order periodic and quasi-periodic oscillating, period-doubling and period-halving bifurcations, and chaos and attractor crises. For example, there exist 5T, 4T, 3T periodic solutions when \(T=3.5, 4.5, 6.5\), respectively (see Figure 10). When T increases from 6.8 to 7.1, there is an attractor crisis leading to a chaotic solution (see Figure 11). These results imply that an impulsive effect could destroy the stability of the system and lead to multiple attractors, bifurcations, even chaos oscillations, which makes the dynamical behaviors very complex.
Bifurcation diagrams of system ( 19 ): prey population \(\pmb{x(t)}\) (top) and predator population \(\pmb{y(t)}\) (bottom) when \(\pmb{p=0.3}\) , \(\pmb{\tau=3}\) with impulsive period T over \(\pmb{[0.5,8.5]}\) .
Bifurcation diagrams of system ( 19 ): prey population \(\pmb{x(t)}\) (top) and predator population \(\pmb{y(t)}\) (bottom) when \(\pmb{p=0.3}\) , \(\pmb{\tau=3}\) with impulsive period T over \(\pmb{[6.9,7.5]}\) .
Phase portrait of the system ( 19 ). 5T, 4T, 3T periodic solution when \(T=3.5, 4.5, 6.5\), respectively.
Second, we let \(p=0.3\), \(T=7\) and consider the effect of the time delay τ on system (19). The bifurcation diagrams of time delay τ over \([0.2,7.0]\) and \([2.5,3.1]\), show that system (19) has very complex dynamic behaviors (see Figure 12 and Figure 13). These results imply that the time delay would make the dynamical behaviors more complex. For example, there is a cascade of period-doubling bifurcations leading to chaos (see Figure 14).
Bifurcation diagrams of system ( 19 ): prey population \(\pmb{x(t)}\) (top) and predator population \(\pmb{y(t)}\) (bottom) when \(\pmb{p=0.3}\) , \(\pmb{T=7}\) with time delay τ over \(\pmb{[0.2,7.0]}\) .
Bifurcation diagrams of system ( 19 ): prey population \(\pmb{x(t)}\) (top) and predator population \(\pmb{y(t)}\) (bottom) when \(\pmb{p=0.3}\) , \(\pmb{T=7}\) with time delay τ over \(\pmb{[2.5,3.1]}\) .
Finally, we let \(\tau=7\), \(T=7\), and we investigate the impulsive perturbation proportionality constant p on system (19). The bifurcation diagrams of impulsive perturbation proportionality constant p over \([0.2,0.74]\) show that system (19) has complex dynamics (see Figure 15). These results imply that the impulsive perturbation proportionality constant p would make the dynamical behaviors more complex, too. From the bifurcation diagrams (Figures 8, 9, 12, 13 and 15), we know that the parameters impulsive period T, time delay τ, and impulsive perturbation proportionality constant p would be important factors to affect the dynamic behaviors of the system, and make the system subject to complex dynamical behaviors.
Bifurcation diagrams of system ( 19 ): prey population \(\pmb{x(t)}\) (top) and predator population \(\pmb{y(t)}\) (bottom) when \(\pmb{\tau=7}\) , \(\pmb{T=7}\) with parameter p over \(\pmb{[0.2,0.74]}\) .
5 Conclusion
In this paper, we have investigated a prey-predator system with constant gestation time delay and impulsive perturbation on the prey in detail. We have shown that there exists a globally attractive predator-extinction periodic solution when the impulsive period T is less than the critical value \(T_{1}^{*}\). The system is permanent when the impulsive period T is larger than the critical value \(T_{2}^{*}\). Therefore, we get two thresholds \(T_{1}^{*}\) and \(T_{2}^{*}\), and there is no information as regards the system (1) when \(T_{1}^{*}< T< T_{2}^{*}\). If the system (1) is without time delay, then \(T_{1}^{*}=T_{\max}=T_{2}^{*}\) would be the unique threshold. This is essentially different when system (1) is with or without time delay.
Numerical examples show that system (1) have various kinds of periodic oscillations, including high-order periodic and quasi-periodic oscillations, chaotic oscillations. These results imply that the parameters of impulsive period T, time delay τ, and impulsive perturbation proportionality constant p would be important factors to affect the dynamic behaviors of the system (1), and make the system (1) subject to complex dynamical behaviors. That large time delay could stabilize the system, an impulsive effect could destabilize the system. Therefore, the dynamical behaviors would be more complex when the system is subject to both time delay and an impulsive effect.
References
Li, S, Xue, Y, Liu, W: Hopf bifurcation and global periodic solutions for a three-stage-structured prey-predator system with delays. Int. J. Inf. Syst. Sci. 8(1), 142-156 (2012)
Li, S, Liu, W, Xue, X: Bifurcation analysis of a stage-structured prey-predator system with discrete and continuous delays. Appl. Math. 4(7), 1059-1064 (2013)
Li, S, Xiong, Z: Bifurcation analysis of a predator-prey system with sex-structure and sexual favoritism. Adv. Differ. Equ. 2013, Article ID 219 (2013)
Wang, L, Xu, R, Feng, G: A stage-structured predator-prey system with time delay and Holling type-III functional response. Int. J. Pure Appl. Math. 48(2), 53-66 (2008)
Zou, W, Xie, J, Xiong, Z: Stability and Hopf bifurcation for an eco-epidemiology model with Holling-III functional response and delays. Int. J. Biomath. 1(3), 377-389 (2008)
Zhang, X, Xu, R, Gan, Q: Periodic solution in a delayed predator prey model with Holling type III functional response and harvesting term. World J. Model. Simul. 7(1), 70-80 (2011)
Das, U, Kar, TK: Bifurcation analysis of a delayed predator-prey model with Holling type III functional response and predator harvesting. J. Nonlinear Dyn. 2014, Article ID 543041 (2014)
Zhang, Z, Yang, H, Fu, M: Hopf bifurcation in a predator-prey system with Holling type III functional response and time delays. J. Appl. Math. Comput. 44(1-2), 337-356 (2014)
Fan, Y, Wang, L: Multiplicity of periodic solutions for a delayed ratio-dependent predator-prey model with Holling type III functional response and harvesting terms. J. Math. Anal. Appl. 365(2), 525-540 (2010)
Cai, Z, Huang, L, Chen, H: Positive periodic solution for a multi species competition-predator system with Holling III functional response and time delays. Appl. Math. Comput. 217(10), 4866-4878 (2011)
Li, G, Yan, J: Positive periodic solutions for neutral delay ratio-dependent predator-prey model with Holling type III functional response. Appl. Math. Comput. 218(8), 4341-4348 (2011)
Xu, C, Wu, Y, Lu, L: Permanence and global attractivity in a discrete Lotka-Volterra predator-prey model with delays. Adv. Differ. Equ. 2014, Article ID 208 (2014)
Li, S: Complex dynamical behaviors in a predator-prey system with generalized group defense and impulsive control strategy. Discrete Dyn. Nat. Soc. 2013, Article ID 358930 (2013)
Li, S, Xiong, Z, Wang, X: The study of a predator-prey system with group defense and impulsive control strategy. Appl. Math. Model. 34(9), 2546-2561 (2010)
Su, H, Dai, B, Chen, Y, et al.: Dynamic complexities of a predator-prey model with generalized Holling type III functional response and impulsive effects. Comput. Math. Appl. 56(7), 1715-1725 (2008)
Fan, X, Jiang, F, Zhang, H: Dynamics of multi-species competition-predator system with impulsive perturbations and Holling type III functional responses. Nonlinear Anal., Theory Methods Appl. 74(10), 3363-3378 (2011)
Liu, Z, Zhong, S: An impulsive periodic predator-prey system with Holling type III functional response and diffusion. Appl. Math. Model. 36(12), 5976-5990 (2012)
Yan, C, Dong, L, Liu, M: The dynamical behaviors of a nonautonomous Holling III predator-prey system with impulses. J. Appl. Math. Comput. 47(1), 193-209 (2015)
Tan, R, Liu, W, Wang, Q: Uniformly asymptotic stability of almost periodic solutions for a competitive system with impulsive perturbations. Adv. Differ. Equ. 2014, Article ID 2 (2014)
Xu, L, Wu, W: Dynamics of a nonautonomous Lotka-Volterra predator-prey dispersal system with impulsive effects. Adv. Differ. Equ. 2014, Article ID 264 (2014)
Ju, Z, Shao, Y, Kong, W: An impulsive prey-predator system with stagestructure and Holling II functional response. Adv. Differ. Equ. 2014, Article ID 280 (2014)
Jia, J, Cao, H: Dynamic complexities of Holling type II functional response predator-prey system with digest delay and impulsive. Int. J. Biomath. 2(2), 229-242 (2009)
Bainov, DD, Simeonov, DD: Impulsive Differential Equations: Periodic Solutions and Applications. Longman, Harlow (1993)
Lakshmikantham, V, Bainov, DD, Simeonov, PS: Theory of Impulsive Differential Equations. World Scientific, Singapore (1989)
Kuang, Y: Delay Differential Equations with Applications in Population Dynamics. Academic Press, New York (1993)
Acknowledgements
This work was supported by the Joint Natural Science Foundation of Guizhou Province (Nos. LKQS[2013]12 and LH[2014]7437); Foundation of Qiannan Normal College for Nationalities (Nos. 2014ZCSX03 and 2014ZCSX11).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
SL carried out the main part of this manuscript. WL participated in the discussion and gave the examples. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, S., Liu, W. A delayed Holling type III functional response predator-prey system with impulsive perturbation on the prey. Adv Differ Equ 2016, 42 (2016). https://doi.org/10.1186/s13662-016-0768-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-016-0768-8