An impulsive prey-predator system with stage-structure and Holling II functional response

Abstract

Taking into account that individual organisms usually go through immature and mature stages, in this paper, we investigate the dynamics of an impulsive prey-predator system with a Holling II functional response and stage-structure. Applying the comparison theorem and some analysis techniques, the sufficient conditions of the global attractivity of a mature predator periodic solution and the permanence are investigated. Examples and numerical simulations are shown to verify the validity of our results.

1 Introduction

The Food and Agriculture Organization of the United Nations reported that, with the development of modern science and technology, many methods have been used for pest control, such as chemical pesticides and biological control (i.e., suppress the pests by natural enemies). Although great progress has been made in the Integrated Pest Management (IPM), people still cannot completely exterminate them all. For the IPM strategy on an ecosystem, the predators are released periodically every time T and periodic catching or spraying pesticides is also applied. Hence the predator and prey abruptly experience a change of state. In fact, many evolution processes are characterized by the fact that at certain moments their stage changes abruptly. Consequently, it is natural to assume that these processes act in the form of impulses. Impulsive methods have been applied in almost every field of the applied sciences. On the other hand, the purpose of IPM is to gain the biggest benefit with the minimum expense; see references [1–7]. For example, some authors [7] proposed an IPM predator-prey model concerning periodic biological and chemical management. It implied that the chemical pesticide is the most effective method which can eliminate a great quantity of pests in a short time. In recent work, biologists realized that appropriate human harvesting and stocking has vital significance on the permanent of biological resource. Jiang et al. [8] considered an impulsive prey-predator system with Holling type II functional response and state feedback control as follows:

$$\{\begin{array}{l}\begin{array}{l}\dot{x}(t)=rx(t)(1-x(t))-\frac{ax(t)y(t)}{1+x(t)},\\ \dot{y}(t)=\frac{ax(t)y(t)}{1+x(t)}-by(t),\end{array}\}x\ne h,\\ \begin{array}{l}\mathrm{\Delta }x(t)=-px(t),\\ \mathrm{\Delta }y(t)=qy(t)+\tau ,\end{array}\}x=h,\end{array}$$

where $x(t)$, $y(t)$ represent the densities of the prey and the predator, respectively. For the parameters $r,a,b>0$, r is the intrinsic growth rate of the prey, $\frac{axy}{1+x}$ is the Holling II function response, b denotes the death rate of the predator, $p\in (0,1)$, $h>0$, $q>0$, $\tau \ge 0$. One obtained the complex dynamics of the system.

However, in the real world, the development of an individual organism usually goes through two stages on the time: immaturity and maturity. Some stage-structured models for the prey-predator system consisting of immature and mature individuals were analyzed in [9–12]. For example, a stage-structured prey-predator model with impulsive stocking on prey and continuous harvesting on predator was considered in [10]. Song and Chen [11] studied optimal harvesting and stability for a two species competitive system with stage structure. Shao and Dai [12] considered a predator-prey model with time delay and impulsive harvesting on prey and stocking on the immature predator. Actually, as the literature [13, 14] pointed out, stage-structured differential equations exhibit much more complicated behaviors than ordinary ones since time delays could cause a stable equilibrium to become unstable and cause the population to fluctuate. Therefore, it is important to consider the dynamics of a prey-predator system with stage-structure; see [15] and references cited therein.

On the other hand, with food safety gaining importance, green food is being paid more and more attention to. In order to plant green food, one can use a periodic harvesting or stocking prey or predator, instead of using high toxic or high residues pesticide.

Based on the above discussion, in this paper, we consider a stage-structured prey-predator model with Holling II functional response and impulsive catching or poisoning the immature prey and stocking of the mature predator as follows:

$$\{\begin{array}{l}\begin{array}{l}{\dot{x}}_1(t)=r{x}_2(t)-r{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1)-d_1{x}_1(t),\\ {\dot{x}}_2(t)=r{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1)-\frac{k{x}_2(t)}{c+x_2(t)}{y}_2(t)-d_2{x}_2(t)-d_3{x}_2^2(t),\\ {\dot{y}}_1(t)=\frac{\lambda k{x}_2(t)}{c+x_2(t)}{y}_2(t)-\lambda k{e}^{-d_4{\tau }_2}\frac{x_2(t-{\tau }_2)}{c+x_2(t-{\tau }_2)}{y}_2(t-{\tau }_2)-d_4{y}_1(t),\\ {\dot{y}}_2(t)=\lambda k{e}^{-d_4{\tau }_2}\frac{x_2(t-{\tau }_2)}{c+x_2(t-{\tau }_2)}{y}_2(t-{\tau }_2)-d_5{y}_2(t),\end{array}\}t\ne nT,\\ \begin{array}{l}{x}_1(t^{+})=(1-p)x_1(t),\\ x_2(t^{+})=x_2(t),\\ y_1(t^{+})=y_1(t),\\ y_2(t^{+})=y_2(t)+\mu ,\end{array}\}t=nT,\end{array}$$

(1.1)

with initial conditions

$$\begin{array}{c}({\phi }_1(\xi ),{\phi }_2(\xi ),{\phi }_3(\xi ),{\phi }_4(\xi ))\in C_{+}=C([-\tau ,0],R_{+}^4),{\phi }_i(0)>0,i=1,2,3,4,\hfill \\ R_{+}^4=\{x\in R^4:x\ge 0\},\tau =max({\tau }_1,{\tau }_2),\hfill \end{array}$$

where $x_1(t)$ ($x_2(t)$), $y_1(t)$ ($y_2(t)$) denote the densities of immature (mature) prey and immature (mature) predator, respectively. The parameters r, k, λ, $d_1$, $d_2$, $d_3$, $d_4$, $d_5$ are all positive constants, r denotes the birth rate of the immature prey, k is the maximum number of the mature prey that can be eaten by a mature predator per unit of time, λ represents the rate of conversing prey into predator (i.e., the converse rate from mature prey to immature predator), $d_1$ ($d_1>d_2$), $d_2$ are the mortality rates of the immature and mature prey, respectively, and $d_4$ ($d_4>d_5$), $d_5$ are the mortality rates of the immature and mature predator, respectively, $d_3$ is the intra-specific competition rate of the mature prey, ${\tau }_1$, ${\tau }_2$ represent a constant time to reach maturity of prey and predator, respectively, μ (≥0) denotes the stocking amount of the mature predator, p ($0\le p<1$) is the catching rate of the immature prey at $t=nT$, $n\in Z_{+}$, and $Z_{+}=\{1,2,\dots \}$, T is the period of the impulsive effect.

In this paper, we aim to investigate the global attractivity of a mature predator periodic solution and the permanence of system (1.1). In agreement with the biological point of view, we only consider (1.1) in the biological sense, region $D=\{(x(t),y_1(t),y_2(t)):x(t)\ge 0,y_1(t)\ge 0,y_2(t)\ge 0\}$.

The organization of the paper is as follows. In Section 2, some preliminaries and lemmas are given. In Section 3, sufficient conditions for the global attractivity of a mature predator survival periodic solution are obtained. In Section 4, the permanence of system (1.1) is investigated. Some examples and numerical simulations are given to illustrate the main results in Section 5. Finally, in Section 6, a brief conclusion is presented.

2 Preliminaries and lemmas

In this section, some definitions and lemmas are introduced.

Let $R_{+}=[0,\mathrm{\infty })$, $R_{+}^4=\{x\in R^4,x\ge 0\}$. Denote by $f={(f_1,f_2,f_3,f_4)}^T$ the map defined by the right-hand side of system (1.1). Let $V:R_{+}\times R_{+}^4\to R_{+}$, if:

• (i) V is continuous in $(nT,(n+1)T]\times R_{+}^4$, for each $x\in R_{+}^4$, $n\in Z_{+}$,

  $$\begin{array}{c}\underset{(t,y)\to ((n-1)T,x)}{lim}V(t,y)=V((n-1)T,x)\text{and}\hfill \\ \underset{(t,y)\to (n{T}^{+},x)}{lim}V(t,y)=V(n{T}^{+},x)\text{exist};\hfill \end{array}$$

• (ii) V is locally Lipschitzian in x, then V is said to belong to class $V_0$.

Definition 2.1 Let $V\in V_0$, $(t,x)\in (nT,(n+1)T]\times R_{+}^4$, $n\in Z_{+}$, the upper right derivative of $V(t,x)$ with respect to impulsive differential system (1.1) is defined as

$$D^{+}V(t,x)=\underset{h\to 0^{+}}{lim}sup\frac{1}{h}[V(t+h,x+hf(t,x))-V(t,x)].$$

Next, we give some important lemmas which will be useful for our main results.

Lemma 2.1 [5]

Consider the impulsive differential system

$$\{\begin{array}{l}\dot{m}(t)\le p(t)m(t)+q(t),t\ne t_k,\\ m(t^{+})\le d_{k}m(t)+b_k,t=t_k,\end{array}$$

where $p,q\in C(R_{+},R)$, $k\in Z_{+}$, $d_k\ge 0$, and $b_k$ are constants.

Assume that:

• (i) the sequence $\{t_k\}$ satisfies $0\le t_0<t_1<t_2<\cdots$ , with ${lim}_{t_k\to +\mathrm{\infty }}{t}_k=\mathrm{\infty }$;

• (ii) $m\in p{c}^1(R_{+},R)$ and $m(t)$ is left-continuous at $t_k$, $k\in Z_{+}$.

Then we have

$$\begin{array}{rcl}m(t)& \le & m(t_0)\prod _{t_0<t_k<t}{d}_{k}exp({\int }_{t_0}^{t}p(x)ds)+\sum _{t_0<t_k<t}(\prod _{t_k<t_j<t}{d}_{j}exp({\int }_{t_k}^{t}p(s)ds))b_k\\ +{\int }_{t_0}^t\prod _{s<t_k<t}{d}_{k}exp({\int }_s^{t}p(\theta )d\theta )q(s)ds,t\ge t_0.\end{array}$$

Lemma 2.2 [6, 7]

Consider the following equation:

$$\dot{u}(t)=au(t-\tau )-bu(t)-c{u}^2(t),$$

where a, b, c, and τ are positive constants, $u(t)>0$ for $t\in [-\tau ,0]$. We have

• (i) if $a<b$, then ${lim}_{t\to +\mathrm{\infty }}u(t)=0$;

• (ii) if $a>b$, then ${lim}_{t\to +\mathrm{\infty }}u(t)=\frac{a-b}{c}$.

Lemma 2.3 [7]

Consider the following system:

$$\{\begin{array}{l}\dot{x}(t)=c-dx(t),t\ne nT,\\ x(t^{+})=x(t)+p,t=nT.\end{array}$$

(2.1)

System (2.1) has a positive periodic solution $x^{\ast }(t)$ with period T. For any solution $x(t)$ of system (2.1), we have

$$|x(t)-x^{\ast }(t)|\to 0\mathit{\text{as }}t\to \mathrm{\infty },$$

where

$$x^{\ast }(t)=\frac{c}{d}+\frac{p{e}^{-d(t-nT)}}{1-e^{-dT}},x^{\ast }\left(0^{+}\right)=\frac{c}{d}+\frac{p}{1-e^{-dT}},nT<t\le (n+1)T.$$

Lemma 2.4 Consider the following system:

$$\{\begin{array}{l}\dot{u}(t)=c-du(t),t\ne nT,\\ u(t^{+})=(1-p)u(t),t=nT.\end{array}$$

(2.2)

Then system (2.2) has a positive periodic solution $u^{\ast }(t)$ with period T. For any solution $u(t)$ of system (2.2), we have

$$|u(t)-u^{\ast }(t)|\to 0\mathit{\text{as }}t\to \mathrm{\infty },$$

where

$$\begin{array}{c}{u}^{\ast }(t)=\frac{c}{d}(1-\frac{p{e}^{-d(t-nT)}}{1-(1-p)e^{-dT}}),nT<t\le (n+1)T\mathit{\text{and}}\hfill \\ u^{\ast }\left(0^{+}\right)=\frac{c}{d}(1-\frac{p}{1-(1-p)e^{-dT}}).\hfill \end{array}$$

Proof Integrating the first equation of (2.2) on $nT<t\le (n+1)T$, we have

$$u(t)=\frac{c}{d}+(u\left(n{T}^{+}\right)-\frac{c}{d})e^{-d(t-nT)},nT<t<(n+1)T.$$

After the successive pulses, the stroboscopic map of system (2.2) is obtained as follows:

$$u((n+1)T^{+})=(1-p)u((n+1)T)=(1-p)(\frac{c}{d}+(u\left(n{T}^{+}\right)-\frac{c}{d})e^{-dT}).$$

(2.3)

There is a unique positive fixed point for (2.3), which is as follows:

$$\tilde{u}(t)=\frac{c}{d}(1-\frac{p}{1-(1-p)e^{-dT}}).$$

This means that there is a positive periodic solution

$$u^{\ast }(t)=\frac{c}{d}(1-\frac{p{e}^{-d(t-nT)}}{1-(1-p)e^{-dT}}),$$

with initial value $u^{\ast }(0^{+})=\frac{c}{d}(1-\frac{p}{1-(1-p)e^{-dT}})$, $nT<t\le (n+1)T$.

Suppose $u(t)$ is an arbitrary solution of (2.2), then applying the iterative technique, we have

$$\begin{array}{rcl}u(t)& =& \frac{c}{d}+(\frac{c}{d}(1-p)(1-e^{-dT})+\frac{c}{d}{(1-p)}^2(1-e^{-dT})e^{-dT}+\cdots \\ +\frac{c}{d}{(1-p)}^n(1-e^{-dT})e^{-(n-1)dT}+\frac{c}{d}u\left(0^{+}\right){(1-p)}^n(1-e^{-dT})e^{-ndT})e^{-(t-nT)}\\ =& u^{\ast }(t)+{(1-p)}^n{e}^{-ndT}(u\left(0^{+}\right)-u^{\ast }\left(0^{+}\right))e^{-(t-nT)},nT<t\le (n+1)T.\end{array}$$

Hence, ${lim}_{t\to \mathrm{\infty }}|u(t)-u^{\ast }(t)|=0$. The proof is completed. □

Lemma 2.5 There is a positive constant M such that $x_i(t)\le \frac{M}{\lambda }$, $y_i(t)\le M$, $i=1,2$, for every solution $(x_1(t),x_2(t),y_1(t),y_2(t))$ of system (1.1) with t sufficiently large, and λ is a positive constant defined in system (1.1).

Proof Define $V(t)=V_1(t)+V_2(t)$, $V_1(t)=\lambda (x_1(t)+x_2(t))$, $V_2(t)=y_1(t)+y_2(t)$.

If $t\ne nT$, by $d_1>d_2$, $d_4>d_5$, we let $d=min(d_2,d_5)$, then

$$\begin{array}{rcl}{D}^{+}V(t)+dV(t)& \le & D^{+}V(t)+d_2{V}_1(t)+d_5{V}_2(t)\\ =& -\lambda (d_1-d_2)x_1(t)-(d_4-d_5)y_1(t)+\lambda r{x}_2(t)-\lambda d_3{x}_2^2(t)\\ \le & \lambda r{x}_2(t)-\lambda d_3{x}_2^2(t)\le M_0=\frac{\lambda r^2}{4d_3}.\end{array}$$

If $t=nT$, then

$$V\left(n{T}^{+}\right)=\lambda x_1(nT)+\lambda \mu +\lambda x_2(nT)+y_1(nT)+(1-p)y_2(nT)\le V(nT)+\lambda \mu .$$

Hence, for $t\in (nT,(n+1)T]$, by using Lemma 2.1, we have

$$\begin{array}{rcl}V(t)& \le & V(0)e^{-dt}+{\int }_0^t{M}_0{e}^{-d(t-s)}ds+\sum _{0<nT<t}\lambda \mu e^{-(t-nT)}\\ <& V(0)e^{-dt}+\frac{M_0}{d}(1-e^{-dt})+\lambda \mu \frac{e^{-d(t-T)}}{1-e^{dT}}+\lambda \mu \frac{e^{dT}}{e^{dT}-1}\\ \to & \frac{M_0}{d}+\frac{\lambda \mu e^{dT}}{e^{dT}-1},t\to \mathrm{\infty }.\end{array}$$

It means that $V(t)$ is uniformly ultimately bounded. Therefore, according to the definition of $V(t)$, there is a constant

$$M=\frac{M_0}{d}+\frac{\lambda \mu e^{dT}}{e^{dT}-1}>0,$$

(2.4)

such that $x_i(t)\le \frac{M}{\lambda }$, $y_i(t)\le M$, $i=1,2$, with t large enough. This completes the proof. □

3 Global attractivity of mature predator periodic solution

In this section, we shall demonstrate the existence and global attractivity of the mature predator survival periodic solution of system (1.1).

Firstly, by Lemmas 2.2, 2.3, and 2.4, we can easily obtain the existence of a predator-extinction periodic solution for system (1.1).

Theorem 3.1 System (1.1) has a mature predator survival periodic solution $(0,0,0,y_2^{\ast }(t))$. For $t\in (nT,(n+1)T]$, and each solution $(0,0,0,y_2(t))$ of system (1.1), we have $y_2(t)\to y_2^{\ast }(t)$ as $t\to \mathrm{\infty }$, where $y_2^{\ast }(t)=\mu \frac{e^{-d_5(t-nT)}}{1-e^{-d_{5}T}}$ for $nT<t\le (n+1)T$, and $y_2^{\ast }(0^{+})=\frac{\mu }{1-e^{-d_{5}T}}$.

Next, we give the conditions on the global attractivity of the predator-extinction periodic solution $(x^{\ast }(t),0,0)$ of the system (1.1).

Theorem 3.2 The mature predator survival periodic solution $(0,0,0,y_2^{\ast }(t))$ of system (1.1) is globally attractive, if

$$({\mathrm{A}}_1)(r{e}^{-d_1{\tau }_1}-d_2)(c+\frac{M}{\lambda })<k\mu \frac{e^{-d_{5}T}}{1-e^{-d_{5}T}}.$$

Proof Let $(x_1(t),x_2(t),y_1(t),y_2(t))$ be any solution of system (1.1). From the fourth and the eighth of system (1.1), we have

$$\{\begin{array}{l}{\dot{y}}_2(t)\ge -d_5{y}_2(t),t\ne nT,\\ y_2(t^{+})=y_2(t)+\mu ,t=nT.\end{array}$$

(3.1)

Considering the auxiliary system of (3.1) as follows:

$$\{\begin{array}{l}{\dot{z}}_1(t)=-d_5{z}_1(t),t\ne nT,\\ z_1(t^{+})=z_1(t)+\mu ,t=nT.\end{array}$$

(3.2)

Applying Lemma 2.3, we have

$$z_1^{\ast }(t)=\mu \frac{e^{-d_5(t-nT)}}{1-e^{-d_{5}T}}\text{for }nT<t\le (n+1)T.$$

Then system (3.2) has a unique and globally attractive positive periodic solution. Applying the comparison theorem of the impulsive differential equation [16], there is a $n_0\in Z_{+}$ and a sufficiently small positive constant ε such that

$$y_2(t)\ge z_1(t)\ge z_1^{\ast }(t)-\epsilon =\mu \frac{e^{-d_5(t-nT)}}{1-e^{-d_{5}T}}-\epsilon \ge \mu \frac{e^{-d_{5}T}}{1-e^{-d_{5}T}}-\epsilon \triangleq \rho$$

(3.3)

for $t\ge n_{0}T$. By Lemma 2.5 and (3.3), we have

$${\dot{x}}_2(t)\le r{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1)-(\frac{k\rho }{c+\frac{M}{\lambda }}+d_2)x_2(t)-d_3{x}_2^2(t),$$

when $t\ge n_{0}T+{\tau }_1$. We consider the auxiliary impulsive differential equation

$${\dot{z}}_2(t)=r{e}^{-d_1{\tau }_1}{z}_2(t-{\tau }_1)-(\frac{k\rho }{c+\frac{M}{\lambda }}+d_2)z_2(t)-d_3{z}_2^2(t).$$

According to hypothesis (A₁), for the sufficiently small constant $\epsilon >0$, we can obtain

$$r{e}^{-d_1{\tau }_1}<\frac{k\rho }{c+\frac{M}{\lambda }}+d_2.$$

Applying Lemma 2.2, we have ${lim}_{t\to \mathrm{\infty }}{z}_2(t)=0$. Since $x_2(s)=z_2(s)={\phi }_2(s)>0$ for all $s\in [-{\tau }_1,0]$, applying the comparison theorem, we have $x_2(t)\to 0$ as $t\to \mathrm{\infty }$. Without loss of generality, suppose that there is a constant ${\epsilon }_1>0$ such that

$$x_2(t)<{\epsilon }_1,t\ge 0.$$

(3.4)

From the first and the fifth equations of (1.1) and (3.4), we have

$$\{\begin{array}{l}{\dot{x}}_1(t)\le r{\epsilon }_1-d_1{x}_1(t),t\ne nT,\\ x_1(t^{+})=(1-p)x_1(t),t=nT.\end{array}$$

(3.5)

Consider the following auxiliary impulsive differential system of (3.5):

$$\{\begin{array}{l}{\dot{z}}_3(t)=r{\epsilon }_1-d_1{z}_3(t),t\ne nT,\\ z_3(t^{+})=(1-p)z_3(t),t=nT.\end{array}$$

(3.6)

Applying Lemma 2.4, we have

$$z_3(t)=\frac{r{\epsilon }_1}{d_1}(1-\frac{p{e}^{-d_1(t-nT)}}{1-(1-p)e^{-d_{1}T}})\text{for }nT<t\le (n+1)T.$$

Taking into account the comparison theorem, for any small ${\epsilon }_2>0$, there exists $t_1>0$ such that $x_1(t)\le z_3(t)+{\epsilon }_2$, $t>t_1$. Let ${\epsilon }_1\to 0$, then $z_3(t)\to 0$ and

$$x_1(t)\le {\epsilon }_2.$$

(3.7)

From the fourth and the eighth equations of system (1.1), we have

$$\{\begin{array}{l}{\dot{y}}_2(t)\le \lambda k{e}^{-d_4\tau }\frac{{\epsilon }_{1}M}{c+{\epsilon }_1}-d_5{y}_2(t),t\ne nT,\\ y_2(t^{+})=y_2(t)+\mu ,t=nT.\end{array}$$

(3.8)

Consider the auxiliary system of (3.8),

$$\{\begin{array}{l}{\dot{z}}_4(t)=\lambda k{e}^{-d_4\tau }\frac{{\epsilon }_{1}M}{c+{\epsilon }_1}-d_5{z}_4(t),t\ne nT,\\ z_4(t^{+})=z_4(t)+\mu ,t=nT.\end{array}$$

(3.9)

By using Lemma 2.3, the unique positive periodic solution of system (3.9) is

$$z_4^{\ast }(t)=\lambda k{e}^{-d_4\tau }\frac{{\epsilon }_{1}M}{d_5(c+{\epsilon }_1)}+\frac{\mu e^{-d_5(t-nT)}}{1-e^{-d_{5}T}}\text{for }nT<t\le (n+1)T.$$

By the comparison theorem, for sufficiently small constants $\epsilon >0$, there exists $t_2>0$ such that $y_2(t)\le z_4^{\ast }(t)+\epsilon \triangleq {\rho }_1$, for all $t>t_2$. Let ${\epsilon }_1\to 0$, then $z_4^{\ast }(t)\to y_2^{\ast }(t)$ and we have $y_2(t)\le y_2^{\ast }(t)+\epsilon$. On the other hand, we can conclude from (3.1), (3.2), and (3.3) that $y_2(t)\ge y_2^{\ast }(t)-\epsilon$ for t large enough, which implies $y_2(t)\to y_2^{\ast }(t)$ as $t\to \mathrm{\infty }$.

From the third and the seventh equations of system (1.1) and (3.3), (3.4), we have

$${\dot{y}}_1(t)\le \lambda k\frac{{\epsilon }_1{\rho }_1}{c+{\epsilon }_1}-d_4{y}_1(t),t\ge 0.$$

(3.10)

Consider the auxiliary system of (3.10),

$${\dot{z}}_5(t)=\lambda k\frac{{\epsilon }_1{\rho }_1}{c+{\epsilon }_1}-d_4{z}_5(t),t\ge 0.$$

(3.11)

By simple calculation, we have

$$z_5(t)=\frac{\lambda k{\epsilon }_1{\rho }_1}{d_4(c+{\epsilon }_1)}+(z_5\left(0^{+}\right)-\frac{\lambda k{\epsilon }_1{\rho }_1}{d_4(c+{\epsilon }_1)})e^{-d_{4}t}.$$

It follows from the comparison theorem that, for sufficiently small constants ${\epsilon }_3>0$, there exists $t_3>0$, such that $y_1(t)\le z_5(t)+{\epsilon }_3$ for all $t>t_3$. Let ${\epsilon }_1\to 0$, then $z_5(t)\to 0$, and we have

$$y_1(t)\le {\epsilon }_3.$$

(3.12)

Since ε, ${\epsilon }_1$, ${\epsilon }_2$, ${\epsilon }_3$ are arbitrary small, we obtain $x_1(t)\to 0$, $x_2(t)\to 0$, $y_1(t)\to 0$, as t is large enough. The proof is completed. □

4 Permanence of system (1.1)

In the real world, from the principle of ecosystem balance and saving resources, we only need to control the prey under the economic threshold level, and not to eradicate the prey totally. Thus we focus on the permanence of system (1.1).

First, we give the definition of permanence.

Definition 4.1 System (1.1) is said to be permanent if there exist positive constants m and M such that each positive solution $(x_1(t),x_2(t),y_1(t),y_2(t))$ of system (1.1) satisfies $m\le x_i(t)$, $y_i(t)\le M$, $i=1,2$, for t large enough.

Theorem 4.1 Assume that:

$$\begin{array}{rl}({\mathrm{A}}_2)& r{e}^{-d_1{\tau }_1}-\frac{kq}{c}-d_2-d_3\frac{M}{\lambda }>0,\\ ({\mathrm{A}}_3)& d_5-\frac{\lambda k{m}_2^{\ast }}{c+m_2^{\ast }}>0,\\ ({\mathrm{A}}_4)& m_2-\frac{M}{\lambda }{e}^{-d_1{\tau }_1}>0,\\ ({\mathrm{A}}_5)& \frac{m_2}{c+m_2}{m}_4-\frac{M^2}{\lambda c+M}{e}^{-d_4{\tau }_2}>0,\end{array}$$

where M, $m_2$, $m_4$, q are defined in (2.4), (4.7), (4.10), (4.13), respectively, then system (1.1) is permanent.

Proof Firstly, we will prove that there exists a constant $m_2>0$ such that $x_2(t)>m_2$ for t sufficiently large. The second equation of (1.1) is equivalent to the following equality:

$$\begin{array}{rcl}{\dot{x}}^2(t)& =& (r{e}^{-d_1{\tau }_1}-\frac{k{y}_2(t)}{c+x_2(t)}-d_2-d_3{x}_2(t))x_2(t)\\ -r{e}^{-d_1{\tau }_1}\frac{d}{dt}{\int }_{t-{\tau }_1}^t{x}_2(s)ds.\end{array}$$

(4.1)

According to (4.1), we define

$$V(t)=x_2(t)+r{e}^{-d_1{\tau }_1}{\int }_{t-{\tau }_1}^t{x}_2(s)ds.$$

Calculating the derivative of $V(t)$, we obtain

$$\dot{V}(t)=(r{e}^{-d_1{\tau }_1}-\frac{k{y}_2(t)}{c+x_2(t)}-d_2-d_3{x}_2(t))x_2(t).$$

(4.2)

Applying Lemma 2.5, (4.2) can be re-written as follows:

$$\dot{V}(t)>(r{e}^{-d_1{\tau }_1}-\frac{k}{c}{y}_2(t)-d_2-d_3\frac{M}{\lambda })x_2(t).$$

(4.3)

By hypothesis (A₂), there is an arbitrary small positive ${\epsilon }_4$ such that

$$r{e}^{-d_1{\tau }_1}>\frac{k}{c}(q+{\epsilon }_4)+d_2+d_3\frac{M}{\lambda },$$

(4.4)

where $q=\frac{\mu }{1-e^{-(d_5-\frac{\lambda k{m}_2^{\ast }}{c+m_2^{\ast }})}}$.

Let $m_2^{\ast }$ be determined as follows:

$$\frac{c}{k}(r{e}^{-d_1{\tau }_1}-d_2-d_3\frac{M}{\lambda })=\frac{\mu }{1-e^{-(d_5-\frac{\lambda k{m}_2^{\ast }}{c+m_2^{\ast }})}}.$$

Then, for any $t_4>0$, it is impossible that $x_2(t)<m_2^{\ast }$ for all $t>t_4$. Suppose that the claim is invalid, then there is $t_4>0$ such that $x_2(t)<m_2^{\ast }$ for all $t_4>0$. It follows from the fourth and the eight equations of system (1.1) that

$$\{\begin{array}{l}{\dot{y}}_2(t)<-(d_5-\frac{\lambda k{m}_2^{\ast }}{c+m_2^{\ast }})y_2(t),t\ne nT,\\ y_2(t^{+})=y_2(t)+\mu ,t=nT\end{array}$$

(4.5)

for all $t>t_4+{\tau }_2$. Consider the following auxiliary impulsive system of (4.5):

$$\{\begin{array}{l}{\dot{z}}_6(t)=-z_6(t)(d_5-\frac{\lambda k{m}_2^{\ast }}{c+m_2^{\ast }}),t\ne nT,\\ z_6(t^{+})=z_6(t)+\mu ,t=nT.\end{array}$$

(4.6)

By using Lemma 2.3, the unique positive periodic solution of (4.6) is

$$z_6(t)=\frac{\mu e^{-(d_5-\frac{\lambda k{m}_2^{\ast }}{c+m_2^{\ast }})(t-nT)}}{1-e^{-(d_5-\frac{\lambda k{m}_2^{\ast }}{c+m_2^{\ast }})}},nT<t\le (n+1)T.$$

This is globally asymptotically stable by hypothesis (A₃). Taking into account the comparison theorem of an impulsive differential equation, there exists $t_5$ ($>t_4+{\tau }_2$) such that

$$y_2(t)\le z_6(t)+{\epsilon }_4.$$

For $t>t_5$, we have

$$z_6(t)\le \frac{\mu }{1-e^{-(d_5-\frac{\lambda k{m}_2^{\ast }}{c+m_2^{\ast }})}}\triangleq q.$$

(4.7)

Then

$$y_2(t)\le q+{\epsilon }_4\triangleq \sigma ,t\ge t_5.$$

(4.8)

According to (4.4), we have

$$r{e}^{-d_1{\tau }_1}>\frac{k\sigma }{c}+d_2+d_3\frac{M}{\lambda }.$$

By (4.3) and (4.8), we get

$$\dot{V}(t)>(r{e}^{-d_1{\tau }_1}-\frac{k\sigma }{c}-d_2-d_3\frac{M}{\lambda })x_2(t),t\ge t_5.$$

(4.9)

Let $x_2^m={min}_{t\in [t_1,t_1+\tau ]}{x}_2(t)$.

We will show that $x_2(t)\ge x_2^m$ for all $t\ge t_5$. Otherwise, there exists a $T_0>0$ such that $x_2(t)\ge x_2^m$ for $t_5\le t\le t_5+\tau +T_0$, $x_2(t_5+\tau +T_0)\ge x_2^m$ and ${\dot{x}}_2(t_5+\tau +T_0)<0$. From the second equation of system (1.1) and (4.8), we have

$${\dot{x}}_2(t_5+\tau +T_0)>(r{e}^{-d_1{\tau }_1}-\frac{k\sigma }{c}-d_2-d_3\frac{M}{\lambda })x_2^m>0.$$

This is a contradiction. Thus, we have $x_2(t)\ge x_2^m$, $t\ge t_5$.

By (4.4) and (4.9), we have

$$\dot{V}(t)>(r{e}^{-d_1{\tau }_1}-\frac{k\sigma }{c}-d_2-d_3\frac{M}{\lambda })x_2^m,t\ge t_5.$$

This means that $V(t)\to \mathrm{\infty }$ as $t\to \mathrm{\infty }$. It is a contradiction with $V(t)\le \frac{M}{\lambda }(1+r{\tau }_1{e}^{-d_1{\tau }_1})$.

Therefore, for any $t_4>0$, the inequality $x_2(t)<m_2^{\ast }$ cannot hold for all $t>t_4$. So there exist the following two possibilities.

• (i) If $x_2(t)\ge m_2^{\ast }$ holds for all t large enough, then our goal is obtained.

• (ii) If $x_2(t)$ is oscillatory about $m_2^{\ast }$. Setting

  $$m_2=min\{\frac{m_2^{\ast }}{2},m_2^{\ast }{e}^{-(kM+d_2+d_3{m}_2^{\ast }){\tau }_1}\},$$

  (4.10)

we prove that $x_2(t)\ge m_2$ for all t large enough. Suppose that there exist two positive constants γ, η such that $x_2(\gamma )=x_2(\gamma +\eta )$ and $x_2(t)<m_2^{\ast }$ for all $\gamma <t<\gamma +\eta$, where γ is large enough, and the inequality (4.8) holds true for $\gamma <t<\gamma +\eta$. Since $x_2(t)$ is continuous, bounded, and is not affected by impulses, we conclude that $x_2(t)$ is uniformly continuous. Hence, there exists a constant $T_1$ ($0<T_1<{\tau }_1$ and $T_1$ is independent of the choice of γ) such that $x_2(\gamma )>\frac{m_2^{\ast }}{2}$ for $\gamma \le t\le \gamma +T_1$. If $\eta \le T_1$, our aim is obtained. If $T_1<\eta \le {\tau }_1$, from the second equation of (1.1), we obtain, for $\gamma <t<\gamma +\eta$, ${\dot{x}}_2(t)\ge -\frac{k}{c}{x}_2(t)y_2(t)-d_2{x}_2(t)-d_3{x}_2^2(t)$. According to the assumption $x_2(\gamma )=m_2^{\ast }$ and $x_2(t)<m_2^{\ast }$ for $\gamma <t<\gamma +\eta$, we have ${\dot{x}}_2(t)\ge -(\frac{k}{c}M+d_2+d_3{m}_2^{\ast })x_2(t)$ for $\gamma <t\le \gamma +\eta \le \gamma +{\tau }_1$. Then we derive that $x_2(t)\ge m_2^{\ast }{e}^{-(\frac{k}{c}M+d_2+d_3{m}_2^{\ast }){\tau }_1}$. It is clear that $x_2(t)\ge m_2$ for $\gamma <t<\gamma +\eta$. If $\eta \ge {\tau }_1$, then we have $x_2(t)\ge m_2$ for $\gamma <t<\gamma +{\tau }_1$. The same arguments can be continued. We obtain $x_2(t)\ge m_2$ for $\gamma +{\tau }_1<t<\gamma +\eta$. Since the interval $[\gamma ,\gamma +\eta ]$ is arbitrarily chosen, we get $x_2(t)\ge m_2$ for t large enough. In view of our arguments above, the choice of $m_2$ is independent of the positive solution of (1.1), which satisfies $x_2(t)\ge m_2$ for t large enough.

Next, by the first and the fifth equations of system (1.1), we have

$$\{\begin{array}{l}{\dot{x}}_1(t)\ge r(m_2-\frac{M}{\lambda }{e}^{-d_1{\tau }_1})-d_1{x}_1(t),t\ne nT,\\ x_1(t^{+})=(1-p)x_1(t),t=nT.\end{array}$$

(4.11)

Consider the auxiliary system of (4.11) as follows:

$$\{\begin{array}{l}{\dot{z}}_7(t)=r(m_2-\frac{M}{\lambda }{e}^{-d_1{\tau }_1})-d_1{z}_7(t),t\ne nT,\\ z_7(t^{+})=(1-p)z_7(t),t=nT.\end{array}$$

(4.12)

By hypothesis (A₄), and applying Lemma 2.4, we have

$$z_7(t)=\frac{r(m_2-\frac{M}{\lambda }{e}^{-d_1{\tau }_1})}{d_1}(1-\frac{p{e}^{-d_1(t-nT)}}{(1-p)e^{-d_{1}T}}).$$

By the comparison theorem, there exists a positive constant ${\epsilon }_5$ sufficiently small such that ${\dot{x}}_1(t)\ge z_7(t)-{\epsilon }_5$ as t is large enough. Taking into account the comparison theorem of an impulsive differential equation, we obtain

$$x_1(t)\ge \frac{r(m_2-\frac{M}{\lambda }{e}^{-d_1{\tau }_1})}{d_1}(1-\frac{p}{(1-p)e^{-d_{1}T}})-{\epsilon }_5\triangleq m_1.$$

From (3.3), let $\rho \triangleq m_4$, then $y_2(t)\ge m_4$.

Finally, by the third equation of system (1.1), we have

$${\dot{y}}_1(t)\ge \lambda k(\frac{m_2}{c+m_2}{m}_4-\frac{M^2}{\lambda c+M}{e}^{-d_4{\tau }_2})-d_4{y}_1(t).$$

(4.13)

Consider the auxiliary system of (4.13),

$${\dot{z}}_8(t)=\lambda k(\frac{m_2}{c+m_2}{m}_4-\frac{M^2}{\lambda c+M}{e}^{-d_4{\tau }_2})-d_4{z}_8(t).$$

(4.14)

It is easy to calculate that

$$\begin{array}{rcl}{z}_8(t)& =& \frac{\lambda k(\frac{m_2}{c+m_2}{m}_4-\frac{M^2}{\lambda c+M}{e}^{-d_4{\tau }_2})}{d_4}\\ -(\lambda k(\frac{m_2}{c+m_2}{m}_4-\frac{M^2}{\lambda c+M}{e}^{-d_4{\tau }_2})-z_8\left(0^{+}\right))e^{-d_{4}t}.\end{array}$$

Applying the comparison theorem, by hypothesis (A₅), there exists a positive constant ${\epsilon }_6$ small enough when t is large enough, such that

$$y_1(t)\ge z_8(t)-{\epsilon }_6\ge \frac{\lambda k(\frac{m_2}{c+m_2}{m}_4-\frac{M^2}{\lambda c+M}{e}^{-d_4{\tau }_2})}{d_4}-{\epsilon }_6\triangleq m_3.$$

Then taking $m=min\{m_1,m_2,m_3,m_4\}$, we have $x_i(t),y_i(t)\ge m$, $i=1,2$. Considering Lemma 2.5 and the above discussion, we can find that system (1.1) is permanent. This completes the proof. □

5 Numerical simulations

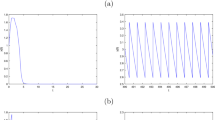
In this section, we give some examples and numerical simulations to show the effectiveness of the main results. In system (1.1), we let $r=1$, $d_1=0.5$, $k=1$, $c=1$, $d_2=0.3$, $d_3=0.2$, $\lambda =0.5$, $d_4=0.4$, $d_5=0.2$, $p=0.3$, $\mu =0.5$, ${\tau }_1=1$, ${\tau }_2=1$, $T=1$. It is quite clear that the parameters satisfy the conditions of Theorem 3.2, so we can obtain the global attractivity of the mature predator survival periodic solution, which is shown by Figure 1.

Figure 1

Dynamical behaviors of system ( 1.1 ) with $\mathit{r}\mathbf{=}\mathbf{1}$, ${\mathit{d}}_{\mathbf{1}}\mathbf{=}\mathbf{0.5}$, $\mathit{k}\mathbf{=}\mathbf{1}$, $\mathit{c}\mathbf{=}\mathbf{1}$, ${\mathit{d}}_{\mathbf{2}}\mathbf{=}\mathbf{0.3}$, ${\mathit{d}}_{\mathbf{3}}\mathbf{=}\mathbf{0.2}$, $\mathit{\lambda }\mathbf{=}\mathbf{0.5}$, ${\mathit{d}}_{\mathbf{4}}\mathbf{=}\mathbf{0.4}$, ${\mathit{d}}_{\mathbf{5}}\mathbf{=}\mathbf{0.2}$, $\mathit{p}\mathbf{=}\mathbf{0.3}$, $\mathit{\mu }\mathbf{=}\mathbf{0.5}$, ${\mathit{\tau }}_{\mathbf{1}}\mathbf{=}\mathbf{1}$, ${\mathit{\tau }}_{\mathbf{2}}\mathbf{=}\mathbf{1}$, $\mathit{T}\mathbf{=}\mathbf{1}$. (a) Time series of the immature prey population. (b) Time series of the mature prey population. (c) Time series of the immature predator population. (d) Time series of the mature predator population.

We let $r=1$, $d_1=0.5$, $k=2$, $c=1$, $d_2=0.3$, $d_3=0.2$, $\lambda =1$, $d_4=0.2$, $d_5=0.1$, $p=0.3$, $\mu =0.1$, ${\tau }_1=1$, ${\tau }_2=1$, $T=10$. By computation, the conditions of Theorem 4.1 are also satisfied, hence, by Theorem 4.1, system (1.1) is permanent; see Figure 2.

Figure 2

Dynamical behaviors of system ( 1.1 ) for $\mathit{r}\mathbf{=}\mathbf{1}$, ${\mathit{d}}_{\mathbf{1}}\mathbf{=}\mathbf{0.5}$, $\mathit{k}\mathbf{=}\mathbf{2}$, $\mathit{c}\mathbf{=}\mathbf{1}$, ${\mathit{d}}_{\mathbf{2}}\mathbf{=}\mathbf{0.3}$, ${\mathit{d}}_{\mathbf{3}}\mathbf{=}\mathbf{0.2}$, $\mathit{\lambda }\mathbf{=}\mathbf{1}$, ${\mathit{d}}_{\mathbf{4}}\mathbf{=}\mathbf{0.2}$, ${\mathit{d}}_{\mathbf{5}}\mathbf{=}\mathbf{0.1}$, $\mathit{p}\mathbf{=}\mathbf{0.3}$, $\mathit{\mu }\mathbf{=}\mathbf{0.1}$, ${\mathit{\tau }}_{\mathbf{1}}\mathbf{=}\mathbf{1}$, ${\mathit{\tau }}_{\mathbf{2}}\mathbf{=}\mathbf{1}$, $\mathit{T}\mathbf{=}\mathbf{10}$. (a) Time series of the immature prey population. (b) Time series of the mature prey population. (c) Time series of the immature predator population. (d) Time series of the mature predator population.

6 Conclusion

In this paper, by using the comparison theorem of an impulsive differential equation and some analysis techniques, we obtain the sufficient conditions of the mature predator survival periodic solution and permanence of system (1.1). Theorem 3.2 implies that increasing T and μ is propitious to the global attractivity of the mature predator survival periodic solution $(0,0,0,y_2^{\ast }(t))$. By Theorem 4.1, we may see that reducing T and μ plays an important role in the permanence of system (1.1). Combining the biological resource management, we believe that there exists a threshold value of economic benefits. Thus, it is unadvisable to make too much effort to destroy all the pest, and there must exist an optimal harvesting policy for system (1.1), that is, what we should do is to gain more, rather than wipe out all pest,so it is interesting for us to continue to study the optimal harvesting policy of system (1.1) in the near future.