Permanence and global attractivity in a discrete Lotka-Volterra predator-prey model with delays

Abstract

In this paper, we deal with a discrete Lotka-Volterra predator-prey model with time-varying delays. For the general non-autonomous case, sufficient conditions which ensure the permanence and global stability of the system are obtained by using differential inequality theory. For the periodic case, sufficient conditions which guarantee the existence of a unique globally stable positive periodic solution are established. The paper ends with some interesting numerical simulations that illustrate our analytical predictions.

MSC:34K20, 34C25, 92D25.

1 Introduction

After the pioneering work of Berryman [1] in 1992, the dynamic relationship between predators and their preys has become one of the dominant themes in both ecology and mathematical ecology due to its universal existence and importance. Dynamic nature (including the local and global stability of the equilibrium, the persistence, permanence and extinction of species, the existence of periodic solutions and positive almost periodic solutions, bifurcation and chaos and so on) of predator-prey models has been investigated in a number of notable studies [2–26]. In many applications, the nature of permanence is of great interest. For example, Fan and Li [27] made a theoretical discussion on the permanence of a delayed ratio-dependent predator-prey model with Holling-type functional response. Chen [28] addressed the permanence of a discrete n-species delayed food-chain system. Zhao and Jiang [29] focused on the permanence and extinction for a non-autonomous Lotka-Volterra system. Chen [30] analyzed the permanence and global attractivity of a Lotka-Volterra competition system with feedback control. Zhao and Teng et al. [31] established the permanence criteria for delayed discrete non-autonomous-species Kolmogorov systems. For more research on the permanence behavior of predator-prey models, one can see [32–44].

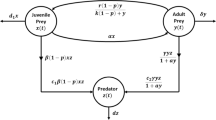
In 2010, Lv et al. [45] investigated the existence and global attractivity of a periodic solution to the following Lotka-Volterra predator-prey system:

$$\{\begin{array}{l}\frac{d{x}_1(t)}{dt}=x_1(t)[r_1(t)-a_{11}(t)x_1(t-{\tau }_{11}(t))-a_{12}(t)x_2(t-{\tau }_{12}(t))\\ \phantom{\frac{d{x}_1(t)}{dt}=}-a_{13}(t)x_3(t-{\tau }_{13}(t))],\\ \frac{d{x}_2(t)}{dt}=x_2(t)[-r_2(t)+a_{21}(t)x_1(t-{\tau }_{21}(t))-a_{22}(t)x_2(t-{\tau }_{22}(t))\\ \phantom{\frac{d{x}_2(t)}{dt}=}-a_{23}(t)x_3(t-{\tau }_{23}(t))],\\ \frac{d{x}_3(t)}{dt}=x_3(t)[-r_3(t)+a_{31}(t)x_1(t-{\tau }_{31}(t))-a_{32}(t)x_2(t-{\tau }_{32}(t))\\ \phantom{\frac{d{x}_3(t)}{dt}=}-a_{33}(t)x_3(t-{\tau }_{33}(t))],\end{array}$$

(1.1)

where $x_1(t)$ denotes the density of prey species at time t, $x_2(t)$ and $x_3(t)$ stand for the density of predator species at time t, $r_i,a_{ij}\in C(R,[0,\mathrm{\infty }))$ and ${\tau }_{ij}(t)>0$ ($i,j=1,2,3$). Using Krasnoselskii’s fixed point theorem and constructing the Lyapunov function, Lv et al. obtained a set of easily verifiable sufficient conditions which guarantee the permanence and global attractivity of system (1.1).

Many authors have argued that discrete time models governed by difference equations are more appropriate to describe the dynamics relationship among populations than continuous ones when the populations have non-overlapping generations. Moreover, discrete time models can also provide efficient models of continuous ones for numerical simulations [4, 16, 46]. Thus it is reasonable and interesting to investigate discrete time systems governed by difference equations. The principal object of this article is to propose a discrete analogue system (1.1) and explore its dynamics.

Following the ideas of [4, 11], we will discretize system (1.1). Assume that the average growth rates in system (1.1) change at regular intervals of time, then we can obtain the following modified system:

$$\{\begin{array}{l}\frac{{\dot{x}}_1(t)}{x_1(t)}=r_1([t])-a_{11}([t])x_1([t]-{\tau }_{11}([t]))-a_{12}([t])x_2([t]-{\tau }_{12}([t]))\\ \phantom{\frac{{\dot{x}}_1(t)}{x_1(t)}=}-a_{13}([t])x_3([t]-{\tau }_{13}([t])),\\ \frac{{\dot{x}}_2(t)}{x_2(t)}=-r_2([t])+a_{21}([t])x_1([t]-{\tau }_{21}([t]))-a_{22}([t])x_2([t]-{\tau }_{22}([t]))\\ \phantom{\frac{{\dot{x}}_2(t)}{x_2(t)}=}-a_{23}([t])x_3([t]-{\tau }_{23}([t])),\\ \frac{{\dot{x}}_3(t)}{x_3(t)}=-r_3([t])+a_{31}([t])x_1([t]-{\tau }_{31}([t]))-a_{32}([t])x_2([t]-{\tau }_{32}([t]))\\ \phantom{\frac{{\dot{x}}_3(t)}{x_3(t)}=}-a_{33}([t])x_3([t]-{\tau }_{33}([t])),\end{array}$$

(1.2)

where $[t]$ denotes the integer part of t, $t\in (0,+\mathrm{\infty })$ and $t\ne 0,1,2,\dots$ . We integrate (1.2) on any interval of the form $[k,k+1)$, $k=0,1,2,\dots$ , and obtain

$$\{\begin{array}{l}{x}_1(t)=x_1(k)exp\{[r_1(k)-a_{11}(k)x_1(k-{\tau }_{11}(k))-a_{12}(k)x_2(k-{\tau }_{12}(k))\\ \phantom{x_1(t)=}-a_{13}(k)x_3(k-{\tau }_{13}(k))](t-k)\},\\ x_2(t)=x_2(k)exp\{[-r_2(k)+a_{21}(k)x_1(k-{\tau }_{21}(k))-a_{22}(k)x_2(k-{\tau }_{22}(k))\\ \phantom{x_2(t)=}-a_{23}(k)x_3(k-{\tau }_{23}(k))](t-k)\},\\ x_3(t)=x_3(k)exp\{[-r_3(k)+a_{31}(k)x_1(k-{\tau }_{31}(k))-a_{32}(k)x_2(k-{\tau }_{32}(k))\\ \phantom{x_3(t)=}-a_{33}(k)x_3(k-{\tau }_{33}(k))](t-k)\},\end{array}$$

(1.3)

where for $k\le t<k+1$, $k=0,1,2,\dots$ .

Let $t\to k+1$, then (1.3) takes the following form:

$$\{\begin{array}{l}{x}_1(k+1)=x_1(k)exp\{r_1(k)-a_{11}(k)x_1(k-{\tau }_{11}(k))-a_{12}(k)x_2(k-{\tau }_{12}(k))\\ \phantom{x_1(k+1)=}-a_{13}(k)x_3(k-{\tau }_{13}(k))\},\\ x_2(k+1)=x_2(k)exp\{-r_2(k)+a_{21}(k)x_1(k-{\tau }_{21}(k))-a_{22}(k)x_2(k-{\tau }_{22}(k))\\ \phantom{x_2(k+1)=}-a_{23}(k)x_3(k-{\tau }_{23}(k))\},\\ x_3(k+1)=x_3(k)exp\{-r_3(k)+a_{31}(k)x_1(k-{\tau }_{31}(k))-a_{32}(k)x_2(k-{\tau }_{32}(k))\\ \phantom{x_3(k+1)=}-a_{33}(k)x_3(k-{\tau }_{33}(k))\},\end{array}$$

(1.4)

which is a discrete time analogue of system (1.1), where $k=0,1,2,\dots$ .

For the point of view of biology, we shall consider (1.4) together with the initial conditions $x_i(0)\ge 0$ ($i=1,2,3$). The principal object of this article is to explore the dynamics of system (1.4) applying the differential inequality theory to study the permanence of system (1.4). Using the method of Lyapunov function, we investigate the global asymptotic stability of system (1.4).

We assume that the coefficients of system (1.4) satisfy the following:

(H1) $r_i$, $a_{ij}$, ${\tau }_{ij}$ with $i,j=1,2,3$ are non-negative sequences bounded above and below by positive constants.

Let $\tau ={sup}_{1\le i,j\le 3,k\in Z}\{{\tau }_{ij}(k)\}$. We consider (1.4) together with the following initial conditions:

$$x_i(\theta )={\phi }_i(\theta )\ge 0,\theta \in N[-\tau ,0]=\{-\tau ,-\tau +1,\dots ,0\},{\phi }_i(0)>0.$$

(1.5)

It is not difficult to see that the solutions of (1.4) and (1.5) are well defined for all $k\ge 0$ and satisfy

$$x_i(k)>0\text{for }k\in Z,i=1,2,3.$$

The remainder of the paper is organized as follows. In Section 2, basic definitions and lemmas are given, some sufficient conditions for the permanence of system (1.4) are established. In Section 3, a series of sufficient conditions for the global stability of system (1.4) are included. The existence and stability of system (1.4) are analyzed in Section 4. In Section 5, we give an example which shows the feasibility of the main results. Conclusions are presented in Section 6.

2 Permanence

For convenience, in the following discussion, we always use the notations:

$$f^l=\underset{k\in Z}{inf}f(k),f^u=\underset{k\in Z}{sup}f(k),$$

where $f(k)$ is a non-negative sequence bounded above and below by positive constants. In order to obtain the main result of this paper, we shall first state the definition of permanence and several lemmas which will be useful in the proof of the main result.

Definition 2.1 [47]

We say that system (1.4) is permanent if there are positive constants M and m such that each positive solution $(x_1(k),x_2(k),x_3(k))$ of system (1.4) satisfies

$$m\le \underset{k\to +\mathrm{\infty }}{lim}inf{x}_i(k)\le \underset{k\to +\mathrm{\infty }}{lim}sup{x}_i(k)\le M(i=1,2,3).$$

Lemma 2.1 [47]

Assume that $\{x(k)\}$ satisfies $x(k)>0$ and

$$x(k+1)\le x(k)exp\{a(k)-b(k)x(k)\}$$

for $k\in N$, where $a(k)$ and $b(k)$ are non-negative sequences bounded above and below by positive constants. Then

$$\underset{k\to +\mathrm{\infty }}{lim}supx(k)\le \frac{1}{b^l}exp(a^u-1).$$

Lemma 2.2 [47]

Assume that $\{x(k)\}$ satisfies

$$x(k+1)\ge x(k)exp\{a(k)-b(k)x(k)\},k\ge N_0,$$

${lim}_{k\to +\mathrm{\infty }}supx(k)\le x^{\ast }$ and $x(N_0)>0$, where $a(k)$ and $b(k)$ are non-negative sequences bounded above and below by positive constants and $N_0\in N$. Then

$$\underset{k\to +\mathrm{\infty }}{lim}infx(k)\ge min\{\frac{a^l}{b^u}exp\{a^l-b^u{x}^{\ast }\},\frac{a^l}{b^u}\}.$$

Now we state our permanence result for system (1.4).

Theorem 2.1 Let $M_1$, $M_2$, $M_3$ and $m_1$ be defined by (2.4), (2.10), (2.15) and (2.20), respectively. In addition to condition (H1), assume that the following conditions:

$$(\mathrm{H}2)a_{21}^u{M}_1>r_2^l,a_{22}^u{M}_1>r_2^l,a_{31}^u{M}_1>r_3^l$$

and

$$(\mathrm{H}3)r_1^l>a_{12}^u{M}_1+a_{13}^u{M}_3,r_2^u>a_{23}^u{M}_3,a_{31}^l{m}_1>r_3^u+a_{32}^u{M}_2$$

hold, then system (1.4) is permanent, that is, there exist positive constants $m_i$, $M_i$ ($i=1,2,3$) which are independent of the solution of system (1.4), such that for any positive solution $(x_1(k),x_2(k),x_3(k))$ of system (1.4) with the initial condition $x_i(0)\ge 0$ ($i=1,2,3$), one has

$$m_i\le \underset{k\to +\mathrm{\infty }}{lim}inf{x}_i(k)\le \underset{k\to +\mathrm{\infty }}{lim}sup{x}_i(k)\le M_i.$$

Proof Let $(x_1(k),x_2(k),x_3(k))$ be any positive solution of system (1.4) with the initial condition $(x_1(0),x_2(0),x_3(0))$. It follows from the first equation of system (1.4) that

$$\begin{array}{rcl}x(k+1)& =& x_1(k)exp\left\{\right[r_1(k)-a_{11}(k)x_1(k-{\tau }_{11}(k))\\ -a_{12}(k)x_2(k-{\tau }_{12}(k))-a_{13}(k)x_3(k-{\tau }_{13}(k))\left]\right\}\\ \le & x_1(k)exp\{r_1(k)\}\le x_1(k)exp\left\{r_1^u\right\}.\end{array}$$

(2.1)

It follows from (2.1) that

$$x_1(k-{\tau }_{11}(k))\ge x_1(k)exp\{-r_1^u{\tau }^u\}.$$

(2.2)

Substituting (2.2) into the first equation of system (1.4), we get

$$x_1(k+1)\le x_1(k)[r_1^u-a_{11}^{l}exp\{-r_1^u{\tau }^u\}{x}_1(k)].$$

(2.3)

It follows from (2.3) and Lemma 2.1 that

$$\underset{k\to +\mathrm{\infty }}{lim}sup{x}_1(k)\le \frac{1}{a_{11}^l}exp\{r_1^u{\tau }^u+r_1^u-1\}:=M_1.$$

(2.4)

For any positive constant $\epsilon >0$, it follows from (2.4) that there exists $N_1>0$ such that for all $k>N_1$,

$$x_1(k)\le M_1+\epsilon .$$

(2.5)

For $k\ge N_1+{\tau }^u$, from (2.5) and the second equation of system (1.4), we have

$$\begin{array}{rcl}{x}_2(k+1)& =& x_2(k)exp\left\{\right[-r_2(k)+a_{21}(k)x_1(k-{\tau }_{21}(k))\\ -a_{22}(k)x_2(k-{\tau }_{22}(k))-a_{23}(k)x_3(k-{\tau }_{23}(k))\left]\right\}\\ \le & x_2(k)exp\left\{[-r_2(k)+a_{21}(k)x_1(k-{\tau }_{21}(k))]\right\}\\ \le & x_1(k)exp\left\{[-r_2^l+a_{21}^u(M_1+\epsilon )]\right\},\end{array}$$

(2.6)

which leads to

$$x_2(k-{\tau }_{22}(k))\ge x_2(k)exp\left\{[r_2^l-a_{21}^u(M_1+\epsilon )]{\tau }^u\right\}.$$

(2.7)

Substituting (2.7) into the second equation of system (1.4), we have

$$\begin{array}{rcl}{x}_2(k+1)& =& x_2(k)exp\left\{\right[-r_2(k)+a_{21}(k)x_1(k-{\tau }_{21}(k))\\ -a_{22}(k)x_2(k-{\tau }_{22}(k))-a_{23}(k)x_3(k-{\tau }_{23}(k))\left]\right\}\\ \le & x_2(k)exp\left\{\right[-r_2(k)+a_{21}(k)x_1(k-{\tau }_{21}(k))\\ -a_{22}(k)x_2(k-{\tau }_{22}(k))\left]\right\}\\ \le & x_2(k)[-r_2^l+a_{21}^u(M_1+\epsilon )-a_{22}^{l}exp\left\{[r_2^l-a_{21}^u(M_1+\epsilon )]{\tau }^u\right\}{x}_2(k)].\end{array}$$

(2.8)

Thus it follows from Lemma 2.1 and (2.8) that

$$\underset{k\to +\mathrm{\infty }}{lim}sup{x}_2(k)\le \frac{exp\{-r_2^l+a_{22}^u(M_1+\epsilon )-1\}}{a_{22}^{l}exp\{[r_2^l-a_{21}^u(M_1+\epsilon )]{\tau }^u\}}.$$

(2.9)

Setting $\epsilon \to 0$, we obtain

$$\underset{k\to +\mathrm{\infty }}{lim}sup{x}_2(k)\le \frac{exp\{-r_2^l+a_{22}^u{M}_1\}}{a_{22}^{l}exp\{(r_2^l-a_{21}^u{M}_1){\tau }^u\}}:=M_2.$$

(2.10)

For $k\ge N_1+{\tau }^u$, from (2.5) and the third equation of system (1.4), we have

$$\begin{array}{rl}{x}_3(k+1)=& x_3(k)[-r_3(k)+a_{31}(k)x_1(k-{\tau }_{31}(k))\\ -a_{32}(k)x_2(k-{\tau }_{32}(k))-a_{33}(k)x_3(k-{\tau }_{33}(k))]\\ \le & x_3(k)[-r_3(k)+a_{31}(k)x_1(k-{\tau }_{31}(k))]\le x_3(k)[-r_3^l+a_{31}^u(M_1+\epsilon )],\end{array}$$

(2.11)

which leads to

$$x_3(k-{\tau }_{33}(k))\ge x_3(k)exp\left\{[r_3^l-a_{31}^u(M_1+\epsilon )]{\tau }^u\right\}.$$

(2.12)

Substituting (2.12) into the third equation of system (1.4) leads to

$$x_3(k+1)\le x_3(k)\{-r_3^l+a_{31}^u(M_1+\epsilon )-a_{33}^{l}exp\left\{[r_3^l-a_{31}^u(M_1+\epsilon )]{\tau }^u\right\}{x}_3(k)\}.$$

(2.13)

In view of Lemma 2.1 and (2.13), one has

$$\underset{k\to +\mathrm{\infty }}{lim}sup{x}_3(k)\le \frac{exp\{-r_3^l+a_{31}^u(M_1+\epsilon )-1\}}{a_{33}^{l}exp\{[r_3^l-a_{31}^u(M_1+\epsilon )]{\tau }^u\}}.$$

(2.14)

Setting $\epsilon \to 0$, we get

$$\underset{k\to +\mathrm{\infty }}{lim}sup{x}_3(k)\le \frac{-r_3^l+a_{31}^u{M}_1}{a_{33}^{l}exp\{(r_3^l-a_{31}^u{M}_1){\tau }^u\}}:=M_3.$$

(2.15)

For $k\ge N_1+{\tau }^u$, it follows from the first equation of system (1.4) that

$$\begin{array}{rcl}{x}_1(k+1)& =& x_1(k)[r_1(k)-a_{11}(k)x_1(k-{\tau }_{11}(k))\\ -a_{12}(k)x_2(k-{\tau }_{12}(k))-a_{13}(k)x_3(k-{\tau }_{13}(k))]\\ \ge & x_1(k)[r_1^l-a_{11}^u(M_1+\epsilon )-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )],\end{array}$$

(2.16)

which leads to

$$x_1(k-{\tau }_{11}(k))\le x_1(k)exp\{-[r_1^l-a_{11}^u(M_1+\epsilon )-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )]{\tau }^u\}.$$

(2.17)

Substituting (2.17) into the first equation of system (1.4), we obtain

$$\begin{array}{rcl}{x}_1(k+1)& \ge & x_1(k)\{r_1^l-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )\\ -a_{11}^{u}exp\{-[r_1^l-a_{11}^u(M_1+\epsilon )-a_{12}^u(M_2+\epsilon )\\ -a_{13}^u(M_3+\epsilon )\left]{\tau }^u\right\}{x}_1(k)\}.\end{array}$$

(2.18)

According to Lemma 2.2, it follows from (2.18) that

$$\underset{k\to +\mathrm{\infty }}{lim}inf{x}_1(k)\ge min\{A_{1\epsilon },A_{2\epsilon }\},$$

(2.19)

where

$$\begin{array}{c}\begin{array}{rl}{A}_{1\epsilon }=& \frac{r_1^l-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )}{a_{11}^{u}exp\{-[r_1^l-a_{11}^u(M_1+\epsilon )-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )]{\tau }^u\}}\\ \times exp\{r_1^l-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )-a_{11}^{u}exp\{-[r_1^l-a_{11}^u(M_1+\epsilon )\\ -a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )\left]{\tau }^u\right\}\}{M}_1,\end{array}\hfill \\ A_{2\epsilon }=\frac{r_1^l-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )}{a_{11}^{u}exp\{-[r_1^l-a_{11}^u(M_1+\epsilon )-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )]{\tau }^u\}}.\hfill \end{array}$$

Setting $\epsilon \to 0$ in (2.19), we can get

$$\underset{k\to +\mathrm{\infty }}{lim}inf{x}_1(k)\ge \frac{1}{2}min\{A_1,A_2\}:=m_1,$$

(2.20)

where

$$\begin{array}{c}\begin{array}{rl}{A}_1=& \frac{r_1^l-a_{12}^u{M}_2-a_{13}^u{M}_3}{a_{11}^{u}exp\{-[r_1^l-a_{11}^u{M}_1-a_{12}^u{M}_2-a_{13}^u{M}_3]{\tau }^u\}}\\ \times exp\{r_1^l-a_{12}^u{M}_2-a_{13}^u{M}_3-a_{11}^{u}exp\{-[r_1^l-a_{11}^u{M}_1\\ -a_{12}^u{M}_2-a_{13}^u{M}_3\left]{\tau }^u\right\}\}{M}_1,\end{array}\hfill \\ A_2=\frac{r_1^l-a_{12}^u{M}_2-a_{13}^u{M}_3}{a_{11}^{u}exp\{-[r_1^l-a_{11}^u{M}_1-a_{12}^u{M}_2-a_{13}^u{M}_3]{\tau }^u\}}.\hfill \end{array}$$

For $k\ge N_1+{\tau }^u$, from the second equation of system (1.4), we have

$$\begin{array}{rcl}{x}_2(k+1)& =& x_2(k)[-r_2(k)+a_{21}(k)x_1(k-{\tau }_{21}(k))\\ -a_{22}(k)x_2(k-{\tau }_{22}(k))-a_{23}(k)x_3(k-{\tau }_{23}(k))]\\ \ge & x_2(t)[-r_2^u+a_{21}^l(m_1-\epsilon )-a_{22}^u(M_2+\epsilon )-a_{23}^u(M_3+\epsilon )],\end{array}$$

(2.21)

which leads to

$$x_2(k-{\tau }_{22}(k))\le x_2(k)exp\left\{[r_2^u-a_{21}^l(m_1-\epsilon )+a_{22}^u(M_2+\epsilon )+a_{23}^u(M_3+\epsilon )]{\tau }^u\right\}.$$

(2.22)

Substituting (2.22) into the second equation of system (1.4) leads to

$$\begin{array}{rcl}{x}_2(k+1)& \ge & x_2(k)\{r_2^u-a_{22}^{u}exp\left\{[r_2^u-a_{21}^l(m_1-\epsilon )+a_{22}^u(M_2+\epsilon )+a_{23}^u(M_3+\epsilon )]{\tau }^u\right\}{x}_2(k)\\ -a_{23}^u(M_3+\epsilon )\}.\end{array}$$

(2.23)

By Lemma 2.2 and (2.23), we can get

$$\underset{k\to +\mathrm{\infty }}{lim}inf{x}_2(k)\ge min\{B_{1\epsilon },B_{2\epsilon }\},$$

(2.24)

where

$$\begin{array}{c}\begin{array}{rl}{B}_{1\epsilon }=& \frac{r_1^l-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )}{a_{11}^{u}exp\{-[r_1^l-a_{11}^u(M_1+\epsilon )-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )]{\tau }^u\}}\\ \times exp\{r_1^l-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )\\ -a_{11}^{u}exp\{-[r_1^l-a_{11}^u(M_1+\epsilon )-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )]{\tau }^u\}\}{M}_1,\end{array}\hfill \\ B_{2\epsilon }=\frac{r_2^u-a_{23}^u(M_3+\epsilon )}{a_{22}^{u}exp\{[r_2^u-a_{21}^l(m_1-\epsilon )+a_{22}^u(M_2+\epsilon )+a_{23}^u(M_3+\epsilon )]{\tau }^u\}}.\hfill \end{array}$$

Setting $\epsilon \to 0$ in the above inequality, we have that

$$\underset{k\to +\mathrm{\infty }}{lim}inf{x}_2(k)\ge \frac{1}{2}min\{B_1,B_2\}:=m_2,$$

(2.25)

where

$$\begin{array}{c}\begin{array}{rl}{B}_1=& \frac{r_1^l-a_{12}^u{M}_2-a_{13}^u{M}_3}{a_{11}^{u}exp\{-[r_1^l-a_{11}^u{M}_1-a_{12}^u{M}_2-a_{13}^u{M}_3]{\tau }^u\}}\\ \times exp\{r_1^l-a_{12}^u{M}_2-a_{13}^u{M}_3\\ -a_{11}^{u}exp\{-[r_1^l-a_{11}^u{M}_1-a_{12}^u{M}_2-a_{13}^u{M}_3]{\tau }^u\}\}{M}_1,\end{array}\hfill \\ B_2=\frac{r_2^u-a_{23}^u{M}_3}{a_{22}^{u}exp\{[r_2^u-a_{21}^l{m}_1+a_{22}^u{M}_2+a_{23}^u{M}_3]{\tau }^u\}}.\hfill \end{array}$$

For $k\ge N_1+{\tau }^u$, it follows from the third equation of system (1.4) that

$$\begin{array}{rcl}{x}_3(k+1)& =& x_3(k)[-r_3(k)+a_{31}(k)x_1(k-{\tau }_{31}(k))\\ -a_{32}(k)x_2(k-{\tau }_{32}(k))-a_{33}(k)x_3(k-{\tau }_{33}(k))]\\ \ge & x_3(t)[-r_3^u+a_{31}^l(m_1-\epsilon )-a_{32}^u(M_2+\epsilon )-a_{33}^u(M_3+\epsilon )].\end{array}$$

(2.26)

Hence

$$x_3(k-{\tau }_{33}(k))\le x_3(k)exp\left\{[r_3^u-a_{31}^l(m_1-\epsilon )+a_{32}^u(M_2+\epsilon )+a_{33}^u(M_3+\epsilon )]{\tau }^u\right\}.$$

(2.27)

Substituting (2.27) into the third equation of system (1.4), we derive

$$\begin{array}{rcl}{x}_3(k+1)& \ge & x_3(k)\{-r_3^u+a_{31}^l(m_1-\epsilon )-a_{32}(M_2+\epsilon )\\ -a_{33}exp\left\{[r_3^u-a_{31}^l(m_1-\epsilon )+a_{32}^u(M_2+\epsilon )+a_{33}^u(M_3+\epsilon )]{\tau }^u\right\}{x}_3(k)\}.\end{array}$$

(2.28)

In view of Lemma 2.2 and (2.28), one has

$$\underset{K\to +\mathrm{\infty }}{lim}inf{x}_3(k)\ge min\{C_{1\epsilon },C_{2\epsilon }\},$$

(2.29)

where

$$\begin{array}{c}\begin{array}{rl}{C}_{1\epsilon }=& \frac{r_1^l-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )}{a_{11}^{u}exp\{-[r_1^l-a_{11}^u(M_1+\epsilon )-a_{12}^u(M_2+\epsilon )-a_{13}^u(M_3+\epsilon )]{\tau }^u\}}\\ \times exp\{-r_3^u+a_{31}^l(m_1-\epsilon )-a_{32}^u(M_2+\epsilon )\\ -a_{33}exp\left\{[r_3^u-a_{31}^l(m_1-\epsilon )+a_{32}^u(M_2+\epsilon )+a_{33}^u(M_3+\epsilon )]{\tau }^u\right\}\}{M}_1,\end{array}\hfill \\ C_{2\epsilon }=\frac{-r_3^u+a_{31}^l(m_1-\epsilon )-a_{32}^u(M_2+\epsilon )}{a_{33}exp\{[r_3^u-a_{31}^l(m_1-\epsilon )+a_{32}^u(M_2+\epsilon )+a_{33}^u(M_3+\epsilon )]{\tau }^u\}}.\hfill \end{array}$$

Setting $\epsilon \to 0$ in (2.29) leads to

$$\underset{k\to +\mathrm{\infty }}{lim}inf{x}_3(k)\ge \frac{1}{2}min\{C_1,C_2\}:=m_3,$$

(2.30)

where

$$\begin{array}{c}\begin{array}{rl}{C}_1=& \frac{r_1^l-a_{12}^u{M}_2-a_{13}^u{M}_3}{a_{11}^{u}exp\{-[r_1^l-a_{11}^u{M}_1-a_{12}^u{M}_2-a_{13}^u{M}_3]{\tau }^u\}}\\ \times exp\{-r_3^u+a_{31}^l{m}_1-a_{32}^u{M}_2\\ -a_{33}exp\left\{[r_3^u-a_{31}^l{m}_1+a_{32}^u{M}_2+a_{33}^u{M}_3]{\tau }^u\right\}\}{M}_1,\end{array}\hfill \\ C_2=\frac{-r_3^u+a_{31}^l{m}_1-a_{32}^u{M}_2}{a_{33}exp\{[r_3^u-a_{31}^l{m}_1+a_{32}^u{M}_2+a_{33}^u{M}_3]{\tau }^u\}}.\hfill \end{array}$$

In view of (2.4), (2.10), (2.15), (2.20), (2.25) and (2.30), we can conclude that system (1.4) is permanent. The proof of Theorem 2.1 is complete. □

Remark 2.1 Under the assumption of Theorem 2.1, the set $[m_1,M_1]\times [m_2,M_2]\times [m_3,M_3]$ is an invariant set of system (1.4).

3 Global stability

In this section, we formulate the stability property of positive solutions of system (1.4) when all the time delays are zero.

Theorem 3.1 Let ${\tau }_{ij}=0$ ($i,j=1,2,3$). In addition to (H1)-(H3), assume further that (H4)

$$\begin{array}{c}{\delta }_1=max\{|1-a_{11}^u{M}_1|,|1-a_{11}^l{m}_1|\}+a_{12}^u{M}_2+a_{13}^u{M}_3<1,\hfill \\ {\delta }_2=max\{|1-a_{22}^u{M}_2|,|1-a_{22}^l{m}_3|\}+a_{21}^u{M}_1+a_{23}^u{M}_3<1,\hfill \\ {\delta }_3=max\{|1-a_{33}^u{M}_3|,|1-a_{33}^l{m}_3|\}+a_{31}^u{M}_1+a_{32}^u{M}_2<1.\hfill \end{array}$$

Then, for any positive solution $(x_1(k),x_2(k),x_3(k))$ and $(x_1^{\ast }(k),x_2^{\ast }(k),x_3^{\ast }(k))$ of system (1.4), we have

$$\underset{k\to \mathrm{\infty }}{lim}[x_i^{\ast }(k)-x_i(k)]=0(i=1,2,3).$$

Proof Let

$$x_i(k)=x_i^{\ast }(k)exp(u_i(k)),i=1,2,3.$$

(3.1)

Then system (1.4) is equivalent to

$$\{\begin{array}{l}{u}_1(k+1)=u_1(k)-a_{11}(k)x_1^{\ast }(k)(exp(u_1(k))-1)\\ \phantom{u_1(k+1)=}-a_{12}(k)x_2^{\ast }(k)(exp(u_2(k))-1)\\ \phantom{u_1(k+1)=}-a_{13}(k)x_3^{\ast }(k)(exp(u_3(k))-1),\\ u_2(k+1)=u_2(k)+a_{21}(k)x_1^{\ast }(k)(exp(u_1(k))-1)\\ \phantom{u_2(k+1)=}-a_{22}(k)x_2^{\ast }(k)(exp(u_2(k))-1)\\ \phantom{u_2(k+1)=}-a_{23}(k)x_3^{\ast }(k)(exp(u_3(k))-1),\\ u_3(k+1)=u_3(k)-a_{31}(k)x_1^{\ast }(k)(exp(u_1(k))-1)\\ \phantom{u_3(k+1)=}-a_{32}(k)x_2^{\ast }(k)(exp(u_2(k))-1)\\ \phantom{u_3(k+1)=}-a_{33}(k)x_3^{\ast }(k)(exp(u_3(k))-1).\end{array}$$

(3.2)

Then

$$\{\begin{array}{l}{u}_1(k+1)=u_1(k)-a_{11}(k)x_1^{\ast }(k)(exp({\theta }_{11}(k)u_1(k))u_1(k)\\ \phantom{u_1(k+1)=}-a_{12}(k)x_2^{\ast }(k)(exp({\theta }_{12}(k)u_2(k))u_2(k)\\ \phantom{u_1(k+1)=}-a_{13}(k)x_3^{\ast }(k)(exp({\theta }_{13}(k)u_3(k))u_3(k),\\ u_2(k+1)=u_2(k)+a_{21}(k)x_1^{\ast }(k)(exp({\theta }_{21}(k)u_1(k))u_1(k)\\ \phantom{u_2(k+1)=}-a_{22}(k)x_2^{\ast }(k)(exp({\theta }_{22}(k)u_2(k))u_2(k)\\ \phantom{u_2(k+1)=}-a_{23}(k)x_3^{\ast }(k)(exp({\theta }_{23}(k)u_3(k))u_3(k),\\ u_3(k+1)=u_3(k)+a_{31}(k)x_1^{\ast }(k)(exp({\theta }_{31}(k)u_1(k))u_1(k)\\ \phantom{u_3(k+1)=}-a_{32}(k)x_2^{\ast }(k)(exp({\theta }_{32}(k)u_2(k))u_2(k)\\ \phantom{u_3(k+1)=}-a_{33}(k)x_3^{\ast }(k)(exp({\theta }_{33}(k)u_3(k))u_3(k),\end{array}$$

(3.3)

where ${\theta }_{ij}(k)\in [0,1]$ ($i,j=1,2,3$). To complete the proof, it suffices to show that

$$\underset{k\to +\mathrm{\infty }}{lim}{u}_i(k)=0(i=1,2,3).$$

(3.4)

In view of (H4), we can choose $\epsilon >0$ small enough such that

$${\delta }_1^{\epsilon }=max\{|1-a_{11}^u(M_1+\epsilon )|,|1-a_{11}^l(m_1-\epsilon )|\}+a_{12}^u(M_2+\epsilon )+a_{13}^u(M_3+\epsilon )<1,$$

(3.5)

$${\delta }_2^{\epsilon }=max\{|1-a_{22}^u(M_2+\epsilon )|,|1-a_{22}^l(m_3-\epsilon )|\}+a_{21}^u(M_1+\epsilon )+a_{23}^u(M_3+\epsilon )<1,$$

(3.6)

$${\delta }_3^{\epsilon }=max\{|1-a_{33}^u(M_3+\epsilon )|,|1-a_{33}^l(m_3-\epsilon )|\}+a_{31}^u(M_1+\epsilon )+a_{32}^u(M_2+\epsilon )<1.$$

(3.7)

For above $\epsilon >0$, in view of Theorem 2.1 in Section 2, there exists $k^{\ast }\in N$ such that

$$m_i-\epsilon \le x_i^{\ast }(k),x_i(k)\le M_i+\epsilon (i=1,2,3)$$

for all $k\ge k^{\ast }$.

Noticing that ${\theta }_{ij}(k)\in [0,1]$ ($i,j=1,2,3$) implies that $x_i^{\ast }(k)exp({\theta }_{ji}(k)u_i(k))$ lies between $x_i^{\ast }(k)$ and $x_i(k)$. From (3.3), we have

$$\begin{array}{rl}{u}_1(k+1)\le & max\{|1-a_{11}^u(M_1+\epsilon )|,|1-a_{11}^l(m_1-\epsilon )|\}|u_1(k)|\\ +a_{12}^u(M_2+\epsilon )|u_2(k)|+a_{13}^u(M_3+\epsilon )|u_3(k)|,\end{array}$$

(3.8)

$$\begin{array}{rl}{u}_2(k+1)\le & max\{|1-a_{22}^u(M_2+\epsilon )|,|1-a_{22}^l(m_3-\epsilon )|\}|u_2(k)|\\ +a_{21}^u(M_1+\epsilon )|u_1(k)|+a_{23}^u(M_3+\epsilon )|u_3(k)|,\end{array}$$

(3.9)

$$\begin{array}{rl}{u}_3(k+1)\le & max\{|1-a_{33}^u(M_3+\epsilon )|,|1-a_{33}^l(m_3-\epsilon )|\}|u_3(k)|\\ +a_{31}^u(M_1+\epsilon )|u_1(k)|+a_{32}^u(M_2+\epsilon )|u_2(k)|.\end{array}$$

(3.10)

Let $\rho =max\{{\delta }_1^{\epsilon },{\delta }_2^{\epsilon },{\delta }_3^{\epsilon }\}$, then $\rho <1$. By (3.8)-(3.10), for $k\ge k^{\ast }$, we have

$$max\{|u_1(k+1)|,|u_2(k+1)|,|u_3(k+1)|\}\le \rho max\{|u_1(k)|,|u_2(k)|,|u_3(k)|\},$$

which implies

$$max\{|u_1(k)|,|u_2(k)|,|u_3(k)|\}\le {\rho }^{k-k^{\ast }}max\{\left|u_1\left(k^{\ast }\right)\right|,\left|u_2\left(k^{\ast }\right)\right|,\left|u_3\left(k^{\ast }\right)\right|\}.$$

Thus (3.4) holds true and the proof is complete. □

4 Existence and stability of a periodic solution

In this section, we further assume that ${\tau }_{ij}=0$ ($i,j=1,2,3$) and the coefficients of system (1.4) satisfy the following condition:

(H5) There exists a positive integer ω such that for $k\in N$, $0<r_i(k+\omega )=r_i(k)$, $0<a_{ij}(k+\omega )=a_{ij}(k)$ ($i,j=1,2,3$).

Theorem 4.1 Assume that (H1)-(H5) are satisfied, then system (1.4) with all the delays ${\tau }_{ij}=0$ ($i,j=1,2,3$) admits at least one positive ω-periodic solution which we denote by $(x_1^{\ast }(k),x_2^{\ast }(k),x_3^{\ast }(k))$.

Proof As pointed out in Remark 2.1 of Section 2,

$$D^3\stackrel{\mathrm{def}}{=}[m_1,M_1]\times [m_2,M_2]\times [m_3,M_3]$$

is an invariant set of system (1.4). Then we define a mapping F on $D^3$ by

$$F(x_1(0),x_2(0),x_3(0))=(x_1(\omega ),x_2(\omega ),x_3(\omega )),\text{for }(x_1(0),x_2(0),x_3(0))\in D^3.$$

Clearly, F depends continuously on $(x_1(0),x_2(0),x_3(0))$. Thus F is continuous and maps the compact set $D^3$ into itself. Therefore, F has a fixed point. It is not difficult to see that the solution $(x_1^{\ast }(k),x_2^{\ast }(k),x_3^{\ast }(k))$ passing through this fixed point is an ω-periodic solution of system (1.4). The proof of Theorem 4.1 is complete. □

Theorem 4.2 Assume that (H1)-(H5) are satisfied, then system (1.4) with all the delays ${\tau }_{ij}=0$ ($i,j=1,2,3$) has a globally stable positive ω-periodic solution.

Proof Under assumptions (H1)-(H5), it follows from Theorem 4.1 that system (1.4) with all the delays ${\tau }_{ij}=0$ ($i,j=1,2,3$) admits at least one positive ω-periodic solution. In addition, Theorem 3.1 ensures that the positive solution is globally stable. Hence the proof. □

5 Numerical example

In this section, we will give an example which shows the feasibility of the main results (Theorem 2.1) of this paper. Let us consider the following discrete system:

$$\{\begin{array}{l}{x}_1(k+1)=x_1(k)exp\{(0.5+0.03sin\frac{k\pi }{2})-(0.4+0.02sin\frac{k\pi }{2})x_1(k-1)\\ \phantom{x_1(k+1)=}-(0.04+0.02cos\frac{k\pi }{2})x_2(k-1)-(0.03+0.02cos\frac{k\pi }{2})x_3(k-1)\},\\ x_2(k+1)=x_2(k)exp\{-(0.085+0.05cos\frac{k\pi }{2})+(0.5+0.3sin\frac{k\pi }{2})x_1(k-1)\\ \phantom{x_2(k+1)=}-(0.26+0.02sin\frac{k\pi }{2})x_2(k-1)-(0.5+0.04cos\frac{k\pi }{2})x_3(k-1)\},\\ x_3(k+1)=x_3(k)exp\{-(0.075+0.03sin\frac{k\pi }{2})+(0.5+0.02cos\frac{k\pi }{2})x_1(k-1)\\ \phantom{x_3(k+1)=}-(0.24+0.04sin\frac{k\pi }{2})x_2(k-1)-(0.4+0.06cos\frac{k\pi }{2})x_3(k-1)\}.\end{array}$$

(5.1)

Here

$$\begin{array}{c}{r}_1(k)=0.5+0.03sin\frac{k\pi }{2},r_2(t)=0.085+0.05cos\frac{k\pi }{2},\hfill \\ r_3(t)=0.075+0.03sin\frac{k\pi }{2},\hfill \\ a_{11}(k)=0.4+0.02sin\frac{k\pi }{2},a_{12}(k)=0.03+0.02cos\frac{k\pi }{2},\hfill \\ a_{13}(k)=0.03+0.02cos\frac{k\pi }{2},\hfill \\ a_{21}(k)=0.5+0.3sin\frac{k\pi }{2},a_{22}(k)=0.26+0.02sin\frac{k\pi }{2},\hfill \\ a_{23}(k)=0.5+0.04cos\frac{k\pi }{2},\hfill \\ a_{31}(k)=0.5+0.02cos\frac{k\pi }{2},a_{32}(k)=0.24+0.04sin\frac{k\pi }{2},\hfill \\ a_{33}(k)=0.4+0.06cos\frac{k\pi }{2},\hfill \\ {\tau }_{ij}(k)=1(i,j=1,2,3).\hfill \end{array}$$

All the coefficients $r_i(k)$ ($i=1,2,3$), $a_{ij}(k)$ ($i,j=1,2,3$), ${\tau }_{ij}(k)$ ($i,j=1,2,3$) are functions with respect to k, and it is not difficult to obtain that

$$\{\begin{array}{l}{r}_1^u=0.53,r_1^l=0.47,r_2^u=0.135,r_2^l=0.035,\\ r_3^u=0.105,r_3^l=0.045,\\ a_{11}^u=0.402,a_{11}^l=0.038,a_{12}^u=0.05,a_{12}^l=0.01,\\ a_{13}^u=0.05,a_{13}^l=0.01,\\ a_{21}^u=0.8,a_{21}^l=0.3,a_{22}^u=0.28,a_{22}^l=0.24,\\ a_{23}^u=0.54,a_{23}^l=0.46,\\ a_{31}^u=0.52,a_{31}^l=0.48,a_{32}^u=0.28,a_{32}^l=0.20,\\ a_{33}^u=0.46,a_{34}^l=0.34,\\ {\tau }_{ij}^u={\tau }_{ij}^l=1(i,j=1,2,3).\end{array}$$

It is easy to examine that the coefficients of system (5.1) satisfy all the conditions of Theorem 2.1. Thus system (5.1) is permanent which is shown in Figures 1-3.

Figure 1

The dynamic behavior of the first component of the solution $\mathbf{(}{\mathit{x}}_{\mathbf{1}}\mathbf{(}\mathit{k}\mathbf{)}\mathbf{,}{\mathit{x}}_{\mathbf{2}}\mathbf{(}\mathit{k}\mathbf{)}\mathbf{,}{\mathit{x}}_{\mathbf{3}}\mathbf{(}\mathit{k}\mathbf{)}\mathbf{)}$ of system ( 5.1 ).

Figure 2

The dynamic behavior of the second component of the solution $\mathbf{(}{\mathit{x}}_{\mathbf{1}}\mathbf{(}\mathit{k}\mathbf{)}\mathbf{,}{\mathit{x}}_{\mathbf{2}}\mathbf{(}\mathit{k}\mathbf{)}\mathbf{,}{\mathit{x}}_{\mathbf{3}}\mathbf{(}\mathit{k}\mathbf{)}\mathbf{)}$ of system ( 5.1 ).

Figure 3

The dynamic behavior of the third component of the solution $\mathbf{(}{\mathit{x}}_{\mathbf{1}}\mathbf{(}\mathit{k}\mathbf{)}\mathbf{,}{\mathit{x}}_{\mathbf{2}}\mathbf{(}\mathit{k}\mathbf{)}\mathbf{,}{\mathit{x}}_{\mathbf{3}}\mathbf{(}\mathit{k}\mathbf{)}\mathbf{)}$ of system ( 5.1 ).

6 Conclusions

In this paper, we have investigated the dynamic behavior of a discrete Lotka-Volterra predator-prey model with time-varying delays. Sufficient conditions which ensure the permanence of the system are established. Moreover, we also analyze the global stability of the system with all the delays ${\tau }_{ij}(k)=0$ ($i,j=1,2,3$) and deal with the existence and stability of the system. We have shown that delay has important influence on the permanence of the system. Therefore, delay is an important factor to decide the permanence of the system. When all the delays are zero, we obtain some sufficient conditions which guarantee the global stability of the system. Computer simulations are carried out to explain our main theoretical results.