1 Introduction

In population dynamics, the linkages between predator and prey are usually expressed by different functional response functions, which reflect different dynamical behaviors. Holling [1] carried out a large number of experiments on predator and prey and got some different functional response functions. For example, the mathematical expression of Holling \(x_{i}\) (\(i = 1,2 \)) model is as follows [2]:

$$ \Phi(X)=\frac{\alpha X^{2}}{\beta^{2}+X^{2}}. $$

Besides, in ecosystems, mutual interference between species is always present. The authors [3] proposed a mutual interference factor that tended to leave when the host or parasite met. A lot of articles studied the ecosystem with interference factors. Their obtained results showed that the effect of this factor should not be ignored [4–7]. For example, Wang et al. [6] concluded that mutual interference had great effect on the relative properties of predator-prey models.

In real life, time delay always exists. Food digestion time, resource regeneration time, mature time, pregnancy period and so on, these all can be expressed by time delay. Usually time delay plays a key role in many systems. For example, time delay can destroy the stability of the positive equilibrium. The obtained results showed that delayed differential equations exhibited more complex dynamical properties than ordinary differential equations [8–14]. Du et al. [10] gave the following model:

$$ \textstyle\begin{cases} \dot{x} = x ( t ) ( r_{1} ( t ) - b_{1} ( t ) x ( t - \tau ( t ) ) ) - \frac{c _{1} ( t ) x^{2} ( t ) }{x^{2} ( t ) + k ^{2}}y^{m} ( t ) , \\ \dot{y} = y ( t ) ( - r_{2} ( t ) - b_{2} ( t ) y ( t ) ) + \frac{c_{2} ( t ) x ^{2} ( t ) }{x^{2} ( t ) + k^{2}}y^{m} ( t ) , \end{cases} $$
(1.1)

where all parameter meanings can be seen in [10]. The time delay of system (1.1) made the system very unstable and led to more complex dynamical behaviors. At the same time, the research methods were also very different from other systems.

From the point of view of the interaction between biology and environment, Darwin thought that biological variation, heredity and natural selection could lead to the adaptive change of organisms. We know that natural environment is not a constant, and organisms can change their habits to adapt to the new environment, which is called adaptive control. In recent years, adaptive control has been widely used in biological control systems, aerospace systems, satellite tracking systems, and so on [15, 16].

On the other hand, in Ref. [10], the authors assume that the coefficients \(r_{1} ( t ) \), \(b_{1} ( t ) \), \(\tau ( t ) \), \(c _{1} ( t ) \), \(r_{2} ( t ) \), \(b_{2} ( t ) \), \(c _{2} ( t ) \) of system (1.1) are continuous positive almost periodic functions. It is well known that the assumption of almost periodicity of the coefficients in (1.1) is a way of incorporating the time-dependent variability of the environment, especially when the factors of the environment exhibit periodical changes with not necessarily commensurate periods, such as weather, food, mating habits, harvest, etc. In view of these factors, it is necessary to study the relevant properties of ecosystems by using almost periodic coefficients. Recently, many scholars have studied the almost periodic solution and got some nice results, which showed that the almost periodic solution of a population dynamical system with mutual interference and time delay had wider application value [10, 17–19].

However, in the actual ecosystem, predator and prey always coexist, which is a common and widespread phenomenon. The dynamical property of a multispecies predator-prey system is much more complex than the system with only two or three species, and the analytical methods are very different [11, 20–22].

Based on the above discussion, we establish a multispecies predator-prey model with almost periodic coefficients, mutual interference and time delays. The corresponding mathematical model is as follows:

$$ \textstyle\begin{cases} x_{i}^{\prime } ( t ) = x_{i} ( t ) [ r_{i} ( t ) - \sum_{k = 1}^{n} b_{ik} ( t ) x_{k} ( t - \tau_{k} ( t ) ) - \sum_{k = 1}^{m} \frac{c_{ik} ( t ) x_{i} ( t ) }{x_{i}^{2} ( t ) + f _{ik} ( t ) }y_{k}^{\alpha } ( t ) ] , \\ \quad i = 1,2,\ldots,n, \\ y_{j}^{\prime } ( t ) = y_{j} ( t ) [ - r _{j} ( t ) - \sum_{k = 1}^{m} p_{jk} ( t ) y_{k} ( t ) + \sum_{k = 1}^{n} \frac{q_{kj} ( t ) x_{k} ^{2} ( t ) }{x_{k}^{2} ( t ) + f_{kj} ( t ) }y _{j}^{\alpha - 1} ( t ) ] , \\ \quad j = 1,2,\ldots,m, \end{cases} $$
(1.2)

with the initial conditions

$$ x_{i} ( \chi ) = \phi_{i} ( \chi ) ,\quad\quad y_{j} ( \chi ) = \psi_{j} ( \chi ) ;\quad \phi_{i} ( \chi ) , \psi_{j} ( \chi ) \in C \bigl( [ - \tau ,0 ] ,R _{ +} \bigr),\chi \in [ - \tau ,0 ] , $$
(1.3)

where \(\tau = \max_{t \in R} \{ \tau_{k} ( t ) ,k = 1,2,\ldots,m \} \), \(\tau_{k} ( t ) \) is a nonnegative and continuously differentiable almost periodic function on R and \(\min_{t \in R} \{ 1 - \tau '_{k} ( t ) \} > 0\). \(r _{i} ( t ) \), \(b_{ik} ( t ) \), \(c_{ik} ( t ) \), \(f _{ik} ( t ) \), \(r_{j} ( t ) \), \(p_{jk} ( t ) \), \(q _{kj} ( t ) \), \(f_{kj} ( t ) \) are all continuous positive almost periodic functions on R and the brief description about other parameters used in system (1.2) is presented in Table 1.

Table 1 Notations used to denote parameters
Full size table

In this article, we aim to investigate the dynamical properties of almost periodic system (1.2), which can greatly enrich the biological background.

The structure of the article as follows. In Section 2, we introduce several important definitions and lemmas. We discuss the permanence of the system in Section 3. Next, we prove the global attractivity of system (1.2) in Section 4. In Section 5, we give conditions of the existence and uniqueness of almost periodic solutions for the system. We put numerical simulations in Section 6. In Section 7, we give a brief conclusion to this paper.

2 Main descriptions

In this part, we give some definitions and lemmas.

For continuous and bounded f on R, we denote \(f^{u} = \sup_{t \in R}f ( t ) \), \(f^{l} = \inf_{t \in R}f ( t ) \).

Definition 2.1

The positive solution \(( x ( t ) ,y ( t ) ) ^{T} = ( x_{1} ( t ) ,x_{2} ( t ) ,\ldots,x_{n} ( t ) ,y_{1} ( t ) ,y _{2} ( t ) ,\ldots, y_{m} ( t ) ) ^{T}\) of system (1.2) is said to be globally attractive if, for any other positive solution \(( \bar{x} ( t ) ,\bar{y} ( t ) ) ^{T} = ( \bar{x}_{1} ( t ) ,\bar{x}_{2} ( t ) ,\ldots, \bar{x}_{n} ( t ) ,\bar{y}_{1} ( t ) ,\bar{y}_{2} ( t ) ,\ldots,\bar{y}_{m} ( t ) ) ^{T}\) of (1.2), the following condition holds:

$$ \lim_{t \to + \infty } \Biggl( \sum_{i = 1}^{n} \bigl\vert x_{i} ( t ) - \bar{x}_{i} ( t ) \bigr\vert + \sum_{j = 1}^{n} \bigl\vert y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr\vert \Biggr) = 0. $$

Definition 2.2

([23])

A function \(f ( t,x ) \) is said to be almost periodic in t uniformly with respect to \(x \in X\) if \(f ( t,x ) \) is continuous and, for \(\forall \varepsilon > 0\), it is possible to find a constant \(I ( \varepsilon ) > 0\) such that, for any interval of length \(I ( \varepsilon ) \), there exists τ such that

$$ \bigl\vert f ( t + \tau ,x ) - f ( t,x ) \bigr\vert < \varepsilon , $$

where the number τ is called an ε-translation number of \(f ( t,x ) \).

By the continuity of almost periodic functions, we obtain that the almost periodic coefficients satisfy \(\min_{ i = 1,2,\ldots,n ; j = 1,2,\ldots,m} \{ r_{i}^{l},r_{j}^{l},b_{ik}^{l},p_{jk}^{l},c_{ik}^{l},q_{kj} ^{l} \} > 0\) and \(\max_{i = 1,2,\ldots,n ;j = 1,2,\ldots,m}\{ r_{i}^{u},r_{j}^{u},b_{ik}^{u}, p_{jk}^{u},c_{ik} ^{u},q_{kj}^{u} \} < + \infty \). For, the characteristics and relevant definitions of almost periodic functions, the reader may refer to [10, 17, 24].

Definition 2.3

([25])

An almost periodic function \(f:R \to R\) is said to be asymptotic if there exist an almost periodic function \(q ( t ) \) and a continuous function \(r ( t ) \) such that

$$ f ( t ) = q ( t ) + r ( t ) ,\quad \quad r ( t ) \to 0 \quad \mbox{as } t \to \infty . $$

Lemma 2.1

([26])

If the function \(f ( t ) \) is nonnegative, integral and uniformly continuous on \([ 0, + \infty )\), then \(\lim_{t \to \infty } f ( t ) = 0\).

Lemma 2.2

The set \(\{ ( x ( t ) ,y ( t ) ) ^{T} = ( x_{1} ( t ) ,x_{2} ( t ) ,\ldots,x_{n} ( t ) ,y _{1} ( t ) ,y_{2} ( t ) ,\ldots,y_{m} ( t ) ) ^{T} \in R^{n + m}| x_{i} ( t_{0} ) > 0,i = 1,2,\ldots,n;y_{j} ( t_{0} ) > 0,j = 1,2,\ldots, m,\exists t_{0} \in R \}\) is positive invariant with respect to system (1.2).

Proof

For \(x_{i} ( t_{0} ) > 0\), \(y_{j} ( t_{0} ) > 0\), we have

$$\begin{aligned}& x_{i} ( t ) = x_{i} ( t_{0} ) \exp \Biggl\{ \int _{t_{0}}^{t} \Biggl[ r_{i} ( s ) - \sum _{k = 1}^{n} b_{ik} ( s ) x_{k} \bigl( s - \tau_{k} ( s ) \bigr) - \sum _{k = 1}^{m} \frac{c_{ik} ( s ) x_{i} ( s ) }{x _{i}^{2} ( s ) + f_{ik} ( s ) }y_{k}^{\alpha } ( s ) \Biggr] \,ds \Biggr\} > 0, \\& y_{j} ( t ) = y_{j} ( t_{0} ) \exp \Biggl\{ \int _{t_{0}}^{t} \Biggl[ - r_{j} ( s ) - \sum_{k = 1}^{m} p_{jk} ( s ) y_{k} ( s ) + \sum_{k = 1}^{n} \frac{q_{kj} ( s ) x_{k}^{2} ( s ) }{x_{k}^{2} ( s ) + f_{kj} ( s ) }y_{j}^{\alpha - 1} ( s ) \Biggr] \,ds \Biggr\} > 0. \end{aligned}$$

Then Lemma 2.2 is obtained. □

Lemma 2.3

([27])

Suppose that the continuous operator A maps the closed and bounded convex set \(Q \subset R^{n}\) onto itself, then the operator A has at least one fixed point in the set Q.

Lemma 2.4

([28])

If \(x' \mathbin{{\ge} {( {\le} )}} x ( b - ax^{\alpha } ) \), where \(a > 0\), \(b > 0\) and α is a positive constant, then

$$ \lim_{t \to \infty } \sup x ( t ) \le \biggl( \frac{b}{a} \biggr) ^{\frac{1}{\alpha }}\quad\quad \biggl( \lim_{t \to \infty } \inf x ( t ) \ge \biggl( \frac{b}{a} \biggr) ^{\frac{1}{\alpha }} \biggr) . $$

Lemma 2.5

([29])

If \(x' \mathbin{{\ge} ( {\le} )} x^{m} ( t ) ( b - ax^{1 - m} ( t ) ) \), \(x ( 0 ) > 0\), \(a > 0\), \(b > 0\), then \(\forall t \ge 0\), we have

$$ x ( t ) \mathbin{{\ge} ( {\le} )} \biggl( \frac{b}{a} + \biggl( x ^{1 - m} ( 0 ) - \frac{b}{a} \biggr) e^{ - a ( 1 - m ) t} \biggr) ^{\frac{1}{1 - m}}. $$

3 Permanence of system (1.2)

Theorem 3.1

If the following condition holds:

$$[H _{1}]\quad \hat{g}_{i} = r_{i}^{l} - \sum_{k = 1,k \ne i}^{n} b_{ik} ^{u} ( t ) M_{k} - \sum_{k = 1}^{m} \frac{c_{ik}^{u}M_{i}N _{k}}{f_{ik}^{l}} > 0, $$

then system (1.2) is permanent, that is, there exists \(T>0\), for \(t > T > 0\), the solution \(( x ( t ) ,y ( t ) ) ^{T}\) of (1.2) satisfies \(m_{i} \le x_{i} ( t ) \le M_{i}\), \(n _{j} \le y_{j} ( t ) \le N_{j}\), where

$$\begin{aligned}& m_{i} = \frac{ \hat{g}_{i}}{b_{ii}^{u}}\exp \bigl( \bigl( \hat{g}_{i} - b_{ii}^{u}M _{i} \bigr) \tau \bigr) , \quad\quad M_{i} = \frac{r_{i}^{u}}{b_{ii}^{l}e^{ - r_{i}^{u}\tau }}, \\& n_{j} = \biggl( \frac{\sum_{k = 1}^{n} q_{kj}^{l}m_{k}^{2}}{2 ( \sum_{k = 1} ^{n} ( M_{k}^{2} + f_{kj}^{u} ) ) ( r_{j}^{u} + \sum_{k = 1}^{m} p_{jk}^{u}N_{k} ) } \biggr) ^{\frac{1}{1 - \alpha }}, \quad \quad N_{j} = \biggl( \frac{3\sum_{k = 1}^{n} q_{kj}^{u} ( t ) }{2r _{j}^{l}} \biggr) ^{\frac{1}{1 - \alpha }} \end{aligned}$$

for \(i = 1,2,\ldots,n\); \(j = 1,2,\ldots,m\). In this article, the values of i, j are no longer repeated.

Proof

By the first equation of (1.2), we get

$$ x'_{i} ( t ) \le x_{i} ( t ) r_{i} ( t ) . $$
(3.1)

Integrating (3.1), we have \(x_{i} ( t ) \le x_{i} ( t - \tau ) \exp ( r_{i}^{u}\tau ) \), \(t > \tau \), that is,

$$ x_{i} ( t - \tau ) \ge x_{i} ( t ) \exp \bigl( - r _{i}^{u}\tau \bigr) ,\quad t > \tau . $$
(3.2)

Combining (3.2) and the first equation of (1.2), we have

$$ x'_{i} ( t ) \le x_{i} ( t ) \bigl[ r_{i}^{u} - b _{ii}^{l}x_{i} ( t ) \exp \bigl( - r_{i}^{u}\tau \bigr) \bigr] ,\quad t > \tau . $$
(3.3)

By applying Lemma 2.4 to (3.3), we obtain

$$ \lim_{t \to + \infty } \sup x_{i} ( t ) \le \frac{r_{i}^{u}}{b _{ii}^{l}e^{ - r_{i}^{u}\tau }} \equiv M_{i}. $$
(3.4)

By (3.4), there exists \(T_{1} > \tau \), when \(t \ge T_{1}\) and \(T_{1} \to \infty \), then

$$ x_{i} ( t ) \le M_{i}. $$
(3.5)

By (3.5), there also exists \(T_{2} = T_{1} + \tau \), when \(t \ge T _{2}\), then

$$ x_{i} ( t - \tau ) \le M_{i}. $$
(3.6)

Combining (3.6) and the second equation of (1.2), we have

$$ \begin{aligned}[b] y'_{j} ( t ) & \le y_{j} ( t ) \Biggl[ \sum_{k = 1} ^{n} q_{kj}^{u} ( t ) y_{j}^{\alpha - 1} ( t ) - r _{j}^{l} ( t ) \Biggr] \\ &\le y_{j}^{\alpha } ( t ) \Biggl[ \sum _{k = 1}^{n} q_{kj} ^{u} ( t ) - r_{j}^{l} ( t ) y^{1 - \alpha } ( t ) \Biggr] ,\quad t \ge T_{2}. \end{aligned} $$
(3.7)

Using Lemma 2.5 to (3.7), then

$$ y_{j} ( t ) \le \biggl[ \frac{\sum_{k = 1}^{n} q_{kj}^{u} ( t ) }{r_{j}^{l} ( t ) } + \biggl( y^{1 - \alpha } ( 0 ) - \frac{\sum_{k = 1}^{n} q_{kj}^{u} ( t ) }{r _{j}^{l} ( t ) } \biggr) e^{ - r_{j}^{l} ( t ) ( 1 - \alpha ) t} \biggr] ^{\frac{1}{1 - \alpha }},\quad \forall t \ge 0. $$
(3.8)

Therefore, there exists \(T_{3} > 0\) such that

$$ y_{j} ( t ) \le \biggl( \frac{3\sum_{k = 1}^{n} q_{kj}^{u} ( t ) }{2r_{j}^{l}} \biggr) ^{\frac{1}{1 - \alpha }} \equiv N_{j},\quad t > T_{3}. $$
(3.9)

Combining (3.5), (3.6), (3.9) and the first equation of (1.2), we get

$$ x_{i}^{\prime } ( t ) \ge x_{i} ( t ) \Biggl[ r _{i}^{l} - \sum_{k = 1,k \ne i}^{n} b_{ik}^{u} ( t ) M_{k} - b_{ii}^{u}x_{i} \bigl( t - \tau_{i} ( t ) \bigr) - \sum_{k = 1}^{m} \frac{c_{ik}^{u}M_{i}N_{k}^{\alpha }}{f_{ik}^{l}} \Biggr] . $$
(3.10)

Suppose \(x_{i} ( \tilde{t} ) \) is any local minimal value of \(x_{i} ( t ) \), then we have

$$ 0 = x_{i}^{\prime } ( \tilde{t} ) \ge x_{i} ( \tilde{t} ) \Biggl[ r_{i}^{l} - \sum _{k = 1,k \ne i}^{n} b_{ik} ^{u} ( t ) M_{k} - b_{ii}^{u}x_{i} \bigl( \tilde{t} - \tau _{i} ( \tilde{t} ) \bigr) - \sum _{k = 1}^{m} \frac{c_{ik} ^{u}M_{i}N_{k}^{\alpha }}{f_{ik}^{l}} \Biggr] . $$
(3.11)

Let

$$ \hat{g}_{i} = r_{i}^{l} - \sum _{k = 1,k \ne i}^{n} b_{ik}^{u} ( t ) M_{k} - \sum_{k = 1}^{m} \frac{c_{ik}^{u}M_{i}N_{k}^{\alpha }}{f _{ik}^{l}}. $$
(3.12)

From (3.11) and (3.12), we have

$$ x_{i} \bigl( \tilde{t} - \tau_{i} ( \tilde{t} ) \bigr) \ge \frac{\hat{g}_{i}}{b_{ii}^{u}}. $$
(3.13)

Integrating (3.10) on \([ \tilde{t} - \tau_{i} ( \tilde{t} ) , \tilde{t} ] \) and noticing that \(\hat{g}_{i} - b_{ii}^{u}x_{i} ( \tilde{t} - \tau_{i} ( \tilde{t} ) ) \le 0\), we obtain

$$ \ln \biggl( \frac{x_{i} ( \tilde{t} ) }{x_{i} ( \tilde{t} - \tau_{i} ( \tilde{t} ) ) } \biggr) \ge \int_{\tilde{t} - \tau_{i} ( \tilde{t} ) }^{\tilde{t}} \bigl( \hat{g}_{i} - b_{ii}^{u}x_{i} \bigl( \tilde{t} - \tau_{i} ( \tilde{t} ) \bigr) \bigr) \,dt \ge \bigl( \hat{g}_{i} - b_{ii} ^{u}M_{i} \bigr) \tau . $$
(3.14)

From (3.13) and (3.14), then

$$ x_{i} ( \tilde{t} ) \ge \frac{\hat{g}_{i}}{b_{ii}^{u}}\exp \bigl( \bigl( \hat{g}_{i} - b_{ii}^{u}M_{i} \bigr) \tau \bigr) . $$
(3.15)

Hence, for \(T_{4} > 0\) and \(t > T_{4}\), we have

$$ x_{i} ( t ) \ge x_{i} ( \tilde{t} ) \ge \frac{ \hat{g}_{i}}{b_{ii}^{u}} \exp \bigl( \bigl( \hat{g}_{i} - b_{ii}^{u}M _{i} \bigr) \tau \bigr) \equiv m_{i}. $$
(3.16)

Combining (3.9), (3.16) and the second equation of (1.2), when \(T_{5} \ge \max \{ T_{3},T_{4} \} > 0\), for \(t > T_{5}\), we get

$$ \begin{aligned} y'_{j} ( t ) &\ge y_{j} ( t ) \Biggl[ - r_{j}^{u} - \sum_{k = 1}^{m} p_{jk}^{u}N_{k} + \sum _{k = 1}^{n} \frac{q_{kj}^{l}m _{k}^{2}}{M_{k}^{2} + f_{kj}^{u}}y_{j}^{\alpha - 1} ( t ) \Biggr] \\ &= y_{j}^{\alpha } ( t ) \Biggl[ \sum _{k = 1}^{n} \frac{q_{kj} ^{l}m_{k}^{2}}{M_{k}^{2} + f_{kj}^{u}} - \Biggl( r_{j}^{u} + \sum_{k = 1}^{m} p_{jk}^{u}N_{k} \Biggr) y_{j}^{1 - \alpha } ( t ) \Biggr] . \end{aligned} $$

It follows from Lemma 2.5 that there exists \(T_{6} > 0\) such that

$$ \begin{aligned} y_{j} ( t ) &\ge \biggl( \frac{\sum_{k = 1}^{n} \frac{q_{kj} ^{l}m_{k}^{2}}{M_{k}^{2} + f_{kj}^{u}}}{r_{j}^{u} + \sum_{k = 1}^{m} p _{jk}^{u}N_{k}} + \biggl( y_{j}^{1 - \alpha } ( 0 ) - \frac{ \sum_{k = 1}^{n} \frac{q_{kj}^{l}m_{k}^{2}}{M_{k}^{2} + f_{kj}^{u}}}{r _{j}^{u} + \sum_{k = 1}^{m} p_{jk}^{u}N_{k}} \biggr) e^{ - ( r _{j}^{u} + \sum_{k = 1}^{m} p_{jk}^{u}N_{k} ) ( 1 - \alpha ) t} \biggr) ^{\frac{1}{1 - \alpha }} \\ &\ge \biggl( \frac{\sum_{k = 1}^{n} q_{kj}^{l}m_{k}^{2}}{2 ( \sum_{k = 1}^{n} ( M_{k}^{2} + f_{kj}^{u} ) ) ( r _{j}^{u} + \sum_{k = 1}^{m} p_{jk}^{u}N_{k} ) } \biggr) ^{\frac{1}{1 - \alpha }} \equiv n_{j}. \end{aligned} $$

Make \(T \ge \max \{ T_{2},T_{5},T_{6} \} > 0\), for \(t > T\), we get \(m_{i} \le x_{i} ( t ) \le M_{i}\), \(n_{j} \le y_{j} ( t ) \le N_{j}\).

Therefore system (1.2) is permanent.

Next, we prove that system (1.2) has at least one bounded positive solution for \(t \ge 0\). Define \(\Omega = \{ ( x ( t ) ,y ( t ) ) ^{T} = ( x_{1} ( t ) ,x_{2} ( t ) ,\ldots,x_{n} ( t ) ,y _{1} ( t ) ,y_{2} ( t ) ,\ldots,y_{m} ( t ) ) ^{T}\in R^{n + m}| ( x ( t ) ,y ( t ) ) ^{T}\text{ is the solution of system (1.2), satisfying }m_{i} \le x_{i} ( t ) \le M_{i},n_{j} \le y_{j} ( t ) \le N_{j},t \in R \}\). □

Theorem 3.2

For system (1.2), the set \(\Omega \ne \emptyset\).

Proof

According to the characteristics of an almost periodic function, for a sequence of \(\{ t_{\gamma } \} \), \(t_{\gamma } \to \infty \) as \(\gamma \to \infty \), then \(r_{i} ( t + t_{\gamma } ) \to r_{i} ( t ) \), \(r_{j} ( t + t_{\gamma } ) \to r_{j} ( t ) \), \(b_{il} ( t + t_{\gamma } ) \to b_{il} ( t ) \), \(p_{jk} ( t + t_{\gamma } ) \to p_{jk} ( t ) \), \(c_{ik} ( t + t_{\gamma } ) \to c_{ik} ( t ) \), \(q_{lj} ( t + t_{\gamma } ) \to q_{lj} ( t ) \), \(\tau_{i} ( t + t_{\gamma } ) \to \tau_{i} ( t ) \), \(f_{ij} ( t + t_{\gamma } ) \to f_{ij} ( t ) \) (\(i,l = 1,2,\ldots,n\); \(j,k = 1,2,\ldots,m\)) uniformly on R as \(\gamma \to \infty \). By Lemma 2.3, system (1.2) has at least one solution \(z ( t ) = ( x ( t ) ,y ( t ) ) ^{T}\) satisfying \(m_{i} \le x_{i} ( t ) \le M_{i}\), \(n_{j} \le y_{j} ( t ) \le N_{j}\) when \(t > T\).

Obviously, the sequence \(z ( t + t_{\gamma } ) \) is uniformly bounded and equi-continuous on any bounded subset of R. By the Ascoli theorem, we know there exists a subsequence \(z ( t + t_{\lambda } ) \) which converges to a continuous function

$$ g ( t ) = \bigl( g_{1} ( t ) ,g_{2} ( t ) \bigr) ^{T} = \bigl( g_{11} ( t ) ,g_{21} ( t ) ,\ldots,g _{n1} ( t ) ,g_{12} ( t ) ,g_{22} ( t ) ,\ldots,g _{m2} ( t ) \bigr) ^{T} $$

as \(\lambda \to \infty \) uniformly on any bounded subset of R.

Make \(T_{7} \in R\), suppose \(T_{7} + t_{\lambda } \ge T\) for all λ. When \(t \ge 0\), we obtain

$$\begin{aligned}& \begin{aligned}[b] &x_{i} ( t + t_{\lambda } + T_{7} ) - x_{i} ( t_{\lambda } + T_{7} ) \\ &\quad = \int_{T_{7}}^{t + T_{7}} x_{i} ( s + t_{ \lambda } ) \Biggl( r_{i} ( s + t_{\lambda } ) - \sum _{k = 1}^{n} b_{ik} ( s + t_{\lambda } ) x_{k} \bigl( ( s + t_{\lambda } ) - \tau_{k} ( s + t_{\lambda } ) \bigr) \\ &\quad\quad{} - \sum_{k = 1}^{m} \frac{c_{ik} ( s + t_{\lambda } ) x_{i} ( s + t_{\lambda } ) }{x_{i}^{2} ( s + t_{\lambda } ) + f_{ik} ( s + t_{\lambda } ) }y_{k}^{\alpha } ( s + t_{\lambda } ) \Biggr) \,ds, \end{aligned} \end{aligned}$$
(3.17)
$$\begin{aligned}& \begin{aligned}[b] & y_{j} ( t + t_{\lambda } + T_{7} ) - y_{j} ( t_{\lambda } + T_{7} ) \\ &\quad = \int_{T_{7}}^{t + T_{7}} y_{j} ( t_{\lambda } + s ) \Biggl( - r_{j} ( s + t_{\lambda } ) - \sum _{k = 1}^{m} p_{jk} ( s + t_{\lambda } ) y_{k} ( s + t_{\lambda } ) \\ &\quad\quad{} + \sum_{k = 1}^{n} \frac{q_{kj} ( s + t_{\lambda } ) x_{k} ^{2} ( s + t_{\lambda } ) }{x_{k}^{2} ( s + t_{\lambda } ) + f_{kj} ( s + t_{\lambda } ) }y_{j}^{\alpha - 1} ( s + t_{\lambda } ) \Biggr) \,ds. \end{aligned} \end{aligned}$$
(3.18)

Letting \(\lambda \to \infty \) in (3.17) and (3.18), for \(\forall t \ge 0\), by the Lebesgue dominated convergence theorem, we get

$$\begin{aligned}& g_{i1} ( t + T_{7} ) - g_{i1} ( T_{7} ) \\& \quad = \int _{T_{7}}^{t + T_{7}} g_{i1} ( s ) \Biggl( r_{i} ( s ) - \sum_{k = 1}^{n} b_{ik} ( s ) g_{k1} \bigl( s - \tau_{k} ( s ) \bigr) - \sum_{k = 1}^{m} \frac{c_{ik} ( s ) g _{i1} ( s ) }{g_{i1}^{2} ( s ) + f_{ik} ( s ) }g _{k2}^{\alpha } ( s ) \Biggr) \,ds, \\& g_{j2} ( t + T_{7} ) - g_{j2} ( T_{7} ) \\& \quad = \int _{T_{7}}^{t + T_{7}} g_{j2} ( s ) \Biggl( - r_{j} ( s ) - \sum_{k = 1}^{m} p_{jk} ( s ) g_{k2} ( s ) + \sum _{k = 1}^{n} \frac{q_{kj} ( s ) g_{k1}^{2} ( s ) }{g _{k1}^{2} ( s ) + f_{kj} ( s ) }g_{j2}^{\alpha - 1} ( s ) \Biggr) \,ds. \end{aligned}$$

Since \(T_{7} \in R\) is arbitrarily given, \(g ( t ) \) is a solution of system (1.2) on R.

It is easy to know \(m_{i} \le g_{i1} ( t ) \le M_{i}\), \(n_{j} \le g_{j2} ( t ) \le N_{j}\) for any \(t \in R\). Thus, the set \(\Omega \ne \emptyset \), that is, system (1.2) has at least one bounded positive solution. □

4 Global attractivity of system (1.2)

Theorem 4.1

If the parameters of system (1.2) satisfy condition \([H_{1}]\) and the following conditions:

$$\begin{aligned}& [H _{2} ]\quad \lim_{t \to + \infty } \inf A_{i} ( t ) > 0, \\& [H _{3}] \quad \lim_{t \to + \infty } \inf B_{j} ( t ) > 0, \end{aligned}$$

where

$$\begin{aligned}& \begin{aligned} A_{i} ( t ) &= - \sum_{k = 1}^{m} c_{ik} ( t ) E _{ik} + \sum_{k = 1}^{n} b_{ik} ( t ) \\ &\quad{} - \sum_{k = 1}^{n} \Biggl[ r_{k} ( s ) + \sum_{j = 1}^{n} b_{kj} ( s ) M _{j} + \sum_{j = 1}^{m} \frac{q_{kj} ( s ) M_{k}N_{j}^{ \alpha }}{f_{kj}^{l} + m_{k}^{2}} \Biggr] \int_{t}^{\varphi_{k}^{ - 1} ( t ) } b_{ik} ( u ) \,du \\ &\quad{} - \sum_{k = 1}^{n} \sum _{j = 1}^{m} c_{ik} ( t ) M_{k}E_{kj} \int_{t}^{\varphi_{k}^{ - 1} ( t ) } b_{ik} ( u ) \,du \\ &\quad{} - \sum _{k = 1}^{n} \sum_{j = 1}^{n} \frac{M_{k}b_{kj} ( \varphi _{j}^{ - 1} ( t ) ) }{1 - \tau_{j}^{\prime } ( \varphi_{j}^{ - 1} ( l ) ) } \int_{\varphi_{j}^{ - 1} ( t ) }^{\varphi_{k}^{ - 1} ( \varphi_{j}^{ - 1} ( t ) ) } b_{ik} ( u ) \,du - \sum_{k = 1}^{m} q_{kj} ( t ) \frac{2M_{i}N_{j}^{\alpha - 1}}{f_{ik} ( t ) + m_{i}^{2}}, \end{aligned} \\& B_{j} ( t ) = - \sum_{k = 1}^{m} c_{ik} ( t ) F _{ik} - \sum_{k = 1}^{n} \sum_{j = 1}^{m} q_{kj} ( t ) M_{k}E _{kj} \int_{t}^{\varphi_{k}^{ - 1} ( t ) } b_{ik} ( u ) \,du + \sum _{k = 1}^{m} p_{jk} ( t ) , \\& E_{ik} = \frac{f_{ik}^{u}N_{k}^{\alpha } + 3M_{i}^{2}N_{k}^{\alpha }}{ ( f_{ik} + m_{i}^{2} ) ^{2}},\quad\quad F_{ik} = \frac{f_{ik}^{u}M_{i} + M_{i}^{3}}{ ( f_{ik} + m_{i}^{2} ) ^{2}} \end{aligned}$$

and \(\varphi_{i} ^{ - 1}\) is the inverse function of \(\varphi_{i} ( t ) = t - \tau_{i} ( t ) \), then the solution of system (1.2) is globally attractive.

Proof

Let \(( x ( t ) ,y ( t ) ) ^{T}\), \(( \bar{x} ( t ) ,\bar{y} ( t ) ) ^{T}\) be any two solutions of system (1.2). From Theorem 3.1, for \(\forall t > T\), we get

$$ m_{i} \le x_{i} ( t ) ,\bar{x}_{i} ( t ) \le M_{i};\quad\quad n _{j} \le y_{j} ( t ) , \bar{y}_{j} ( t ) \le N_{j}. $$
(4.1)

Next, we set up several Lyapunov functions. Let

$$ V_{i1} ( t ) = \bigl\vert \ln \bar{x}_{i} ( t ) - \ln x_{i} ( t ) \bigr\vert . $$
(4.2)

By calculating the upper right derivative of \(V_{i1} ( t ) \) along system (1.2), we have

$$\begin{aligned} D^{ +} V_{i1} ( t ) &= \operatorname {sign}\bigl( \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr) \biggl( \frac{\bar{x}_{i}^{\prime } ( t ) }{\bar{x}_{i} ( t ) } - \frac{x_{i}^{\prime } ( t ) }{x_{i} ( t ) } \biggr) \\ &= \operatorname {sign}\bigl( \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr) \Biggl\{ - \sum_{k = 1}^{n} b_{ik} ( t ) \bigl[ \bar{x}_{k} \bigl( t - \tau_{k} ( t ) \bigr) - x_{k} \bigl( t - \tau_{k} ( t ) \bigr) \bigr] \\ &\quad{} - \sum_{k = 1}^{m} \biggl[ \frac{c_{ik} ( t ) \bar{x}_{i} ( t ) \bar{y}_{k}^{\alpha } ( t ) }{\bar{x}_{i} ^{2} ( t ) + f_{ik} ( t ) } - \frac{c_{ik} ( t ) x_{i} ( t ) y_{k}^{\alpha } ( t ) }{x_{i} ^{2} ( t ) + f_{ik} ( t ) } \biggr] \Biggr\} \\ &= \operatorname {sign}\bigl( \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr) \Biggl\{ - \sum_{k = 1}^{n} b_{ik} ( t ) \bigl[ \bar{x}_{k} \bigl( t - \tau_{k} ( t ) \bigr) - x_{k} \bigl( t - \tau_{k} ( t ) \bigr) \bigr] \\ &\quad{} - \sum _{k = 1}^{m} c_{ik} ( t ) \biggl[ \frac{f_{ik} ( t ) \bar{y}_{k}^{\alpha } ( t ) + \bar{y}_{k}^{\alpha } ( t ) x_{i}^{2} ( t ) - x _{i} ( t ) y_{k}^{\alpha } ( t ) ( x_{i} ( t ) + \bar{x}_{i} ( t ) ) }{ ( \bar{x}_{i} ^{2} ( t ) + f_{ik} ( t ) ) ( x_{i}^{2} ( t ) + f_{ik} ( t ) ) } \bigl( \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr) \\ &\quad{} + \frac{f_{ik} ( t ) x_{i} ( t ) + x_{i}^{3} ( t ) }{ ( \bar{x}_{i}^{2} ( t ) + f_{ik} ( t ) ) ( x_{i}^{2} ( t ) + f_{ik} ( t ) ) } \bigl( \bar{y}_{k}^{\alpha } ( t ) - y_{k}^{\alpha } ( t ) \bigr) \biggr] \Biggr\} \\ &\le \sum_{k = 1}^{m} c_{ik} ( t ) E_{ik} \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert + \sum_{k = 1}^{m} c _{ik} ( t ) F_{ik} \bigl\vert \bar{y}_{k}^{\alpha } ( t ) - y_{k}^{\alpha } ( t ) \bigr\vert \\ &\quad{} - \sum _{k = 1}^{n} b_{ik} \bigl\vert \bar{x}_{k} ( t ) - x_{k} ( t ) \bigr\vert + \sum _{k = 1}^{n} b_{ik} \biggl\vert \int_{t - \tau_{k} ( t ) }^{t} \bar{x}_{k}^{\prime } ( s ) - x_{k}^{\prime } ( s ) \,ds \biggr\vert , \end{aligned}$$
(4.3)

where

$$ E_{ik} = \frac{f_{ik}^{u}N_{k}^{\alpha } + 3M_{i}^{2}N_{k}^{\alpha }}{ ( f_{ik} + m_{i}^{2} ) ^{2}}, \quad\quad F_{ik} = \frac{f_{ik}^{u}M_{i} + M_{i}^{3}}{ ( f_{ik} + m_{i}^{2} ) ^{2}}. $$

Substituting (1.2) into (4.3), we get

$$\begin{aligned} & D^{ +} V_{i1} ( t ) \\ &\quad \le \sum_{k = 1}^{m} c_{ik} ( t ) E _{ik} \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert + \sum_{k = 1}^{m} c_{ik} ( t ) F_{ik} \bigl\vert \bar{y}_{k}^{ \alpha } ( t ) - y_{k}^{\alpha } ( t ) \bigr\vert - \sum _{k = 1}^{n} b_{ik} ( t ) \bigl\vert \bar{x}_{k} ( t ) - x_{k} ( t ) \bigr\vert \\ &\quad \quad{} + \sum_{k = 1}^{n} b_{ik} ( t ) \Biggl\vert \int_{t - \tau_{k} ( t ) }^{t} \Biggl\{ \bar{x}_{k} ( s ) \Biggl[ r_{k} ( s ) - \sum_{j = 1} ^{n} b_{kj} ( s ) \bar{x}_{j} \bigl( s - \tau_{j} ( s ) \bigr) - \sum_{j = 1}^{m} \frac{c_{kj} ( s ) \bar{x}_{k} ( s ) \bar{y}_{j}^{\alpha } ( s ) }{f _{kj} ( s ) + \bar{x}_{k}^{2} ( s ) } \Biggr] \\ &\quad\quad{} - x_{k} ( s ) \Biggl[ r_{k} ( s ) - \sum_{j = 1} ^{n} b_{kj} ( s ) x_{j} \bigl( s - \tau_{j} ( s ) \bigr) - \sum _{j = 1}^{m} \frac{c_{kj} ( s ) x_{k} ( s ) y _{j}^{\alpha } ( s ) }{f_{kj} ( s ) + x_{k}^{2} ( s ) } \Biggr] \Biggr\} \,ds \Biggr\vert \\ &\quad = \sum_{k = 1}^{m} c_{ik} ( t ) E_{ik} \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert + \sum_{k = 1}^{m} c _{ik} ( t ) F_{ik} \bigl\vert \bar{y}_{k}^{\alpha } ( t ) - y_{k}^{\alpha } ( t ) \bigr\vert - \sum _{k = 1}^{n} b_{ik} ( t ) E_{ik} \bigl\vert \bar{x}_{k} ( t ) - x_{k} ( t ) \bigr\vert \\ &\quad \quad{} + \sum_{k = 1}^{n} b_{ik} ( t ) \Biggl\vert \int_{t - \tau_{k} ( t ) }^{t} \Biggl\{ \Biggl[ r_{k} ( s ) - \sum_{j = 1}^{n} b_{kj} ( s ) \bar{x}_{j} \bigl( s - \tau_{j} ( s ) \bigr) - \sum _{j = 1} ^{m} \frac{c_{kj} ( s ) \bar{x}_{k} ( s ) \bar{y} _{j}^{\alpha } ( s ) }{f_{kj} ( s ) + \bar{x}_{k} ^{2} ( s ) } \Biggr] \\ &\quad\quad{}\times \bigl( \bar{x}_{k} ( s ) - x _{k} ( s ) \bigr) - x_{k} ( s ) \sum_{j = 1}^{n} b_{kj} ( s ) \bigl( \bar{x}_{j} \bigl( s - \tau_{j} ( s ) \bigr) - x_{j} \bigl( s - \tau_{j} ( s ) \bigr) \bigr) \\ &\quad\quad{} - x_{k} ( s ) \sum _{j = 1}^{m} c_{kj} ( s ) \frac{f _{kj} ( s ) \bar{y}_{j}^{\alpha } ( s ) + \bar{y} _{j}^{\alpha } ( s ) x_{k}^{2} ( s ) - y_{j}^{ \alpha } ( s ) x_{k} ( s ) ( x_{k} ( s ) + \bar{x}_{k} ( s ) ) }{ ( f_{kj} ( s ) + x_{k}^{2} ( s ) ) ( f_{kj} ( s ) + \bar{x}_{k}^{2} ( s ) ) } \bigl( \bar{x}_{k} ( s ) - x_{k} ( s ) \bigr) \\ &\quad\quad{} - x_{k} ( s ) \sum_{j = 1}^{m} c_{kj} ( s ) \frac{f _{kj} ( s ) x_{k} ( s ) + x_{k}^{3} ( s ) }{ ( f_{kj} ( s ) + x_{k}^{2} ( s ) ) ( f_{kj} ( s ) + \bar{x}_{k}^{2} ( s ) ) } \bigl( \bar{y}_{j}^{\alpha } ( s ) - y_{j}^{\alpha } ( s ) \bigr) \Biggr\} \,ds \Biggr\vert \\ & \quad \le \sum_{k = 1}^{m} c_{ik} ( t ) E_{ik} \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert + \sum_{k = 1}^{m} c _{ik} ( t ) F_{ik} \bigl\vert \bar{y}_{k}^{\alpha } ( t ) - y_{k}^{\alpha } ( t ) \bigr\vert - \sum _{k = 1}^{n} b_{ik} ( t ) \bigl\vert \bar{x}_{k} ( t ) - x_{k} ( t ) \bigr\vert \\ &\quad \quad{} + \sum_{k = 1}^{n} b_{ik} ( t ) \int_{t - \tau_{k} ( t ) }^{t} \Biggl\{ \Biggl[ r_{k} ( s ) + \sum_{j = 1}^{n} b_{kj} ( s ) \bar{x}_{j} \bigl( s - \tau_{j} ( s ) \bigr) + \sum _{j = 1} ^{m} \frac{c_{kj} ( s ) \bar{x}_{k} ( s ) \bar{y} _{j}^{\alpha } ( s ) }{f_{kj} ( s ) + \bar{x}_{k} ^{2} ( s ) } \Biggr] \\ &\quad\quad{}\times \bigl\vert \bar{x}_{k} ( s ) - x _{k} ( s ) \bigr\vert + x_{k} ( s ) \sum_{j = 1}^{n} b_{kj} ( s ) \bigl\vert \bigl( \bar{x}_{j} \bigl( s - \tau_{j} ( s ) \bigr) - x_{j} \bigl( s - \tau_{j} ( s ) \bigr) \bigr) \bigr\vert \\ &\quad\quad{} + x_{k} ( s ) \sum _{j = 1}^{m} c_{kj} ( s ) E_{kj} \bigl\vert \bar{x}_{k} ( s ) - x_{k} ( s ) \bigr\vert + x _{k} ( s ) \sum_{j = 1}^{m} c_{kj} ( s ) F_{kj} \bigl\vert \bar{y}_{j}^{\alpha } ( s ) - y_{j}^{\alpha } ( s ) \bigr\vert \Biggr\} \,ds. \end{aligned}$$
(4.4)

Considering (4.1) and (4.4), for \(t \ge T + \tau \), we get

$$\begin{aligned} &D^{ +} V_{i1} ( t ) \\ &\quad \le \sum_{k = 1}^{m} c_{ik} ( t ) E _{ik} \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert + \sum_{k = 1}^{m} c_{ik} ( t ) F_{ik} \bigl\vert \bar{y}_{k}^{ \alpha } ( t ) - y_{k}^{\alpha } ( t ) \bigr\vert - \sum _{k = 1}^{n} b_{ik} ( t ) \bigl\vert \bar{x}_{k} ( t ) - x_{k} ( t ) \bigr\vert \\ &\quad \quad{} + \sum_{k = 1}^{n} b_{ik} ( t ) \int_{t - \tau_{k} ( t ) }^{t} \Biggl\{ \Biggl[ r_{k} ( s ) + \sum_{j = 1}^{n} b_{kj} ( s ) M _{j} + \sum_{j = 1}^{m} \frac{c_{kj} ( s ) M_{k}N_{j}^{ \alpha }}{f_{kj}^{l} + m_{k}^{2}} \Biggr] \bigl\vert \bar{x}_{k} ( s ) - x_{k} ( s ) \bigr\vert \\ &\quad\quad{} + M_{k}\sum _{j = 1}^{n} b_{kj} ( s ) \bigl\vert \bigl( \bar{x} _{j} \bigl( s - \tau_{j} ( s ) \bigr) - x_{j} \bigl( s - \tau _{j} ( s ) \bigr) \bigr) \bigr\vert \\ &\quad \quad{} + M_{k}\sum_{j = 1}^{n} c_{kj} ( s ) E_{kj} \bigl\vert \bar{x} _{k} ( s ) - x_{k} ( s ) \bigr\vert + M_{k}\sum _{j = 1}^{m} c_{kj} ( s ) F_{kj} \bigl\vert \bar{y} _{j}^{\alpha } ( s ) - y_{j}^{\alpha } ( s ) \bigr\vert \Biggr\} \,ds \\ &\quad \equiv \sum_{k = 1}^{m} c_{ik} ( t ) E_{ik} \bigl\vert \bar{x} _{i} ( t ) - x_{i} ( t ) \bigr\vert + \sum_{k = 1} ^{m} c_{ik} ( t ) F_{ik} \bigl\vert \bar{y}_{k}^{\alpha } ( t ) - y_{k}^{\alpha } ( t ) \bigr\vert - \sum _{k = 1}^{n} b_{ik} ( t ) \bigl\vert \bar{x}_{k} ( t ) - x_{k} ( t ) \bigr\vert \\ &\quad \quad{} + \sum_{k = 1}^{n} b_{ik} ( t ) \int_{t - \tau_{k} ( t ) }^{t} G_{k} ( s ) \,ds. \end{aligned}$$
(4.5)

Define

$$ V_{i2} ( t ) = \sum_{k = 1}^{n} \int_{t}^{\varphi_{k}^{ - 1} ( t ) } \int_{\tau_{k} ( u ) }^{t} b_{ik} ( u ) G _{k} ( s ) \,ds\,du. $$
(4.6)

Combining (4.5) and (4.6), for \(t \ge T + \tau \), we get

$$ \begin{aligned}[b] D^{ +} V_{i1} ( t ) + V_{i2}^{\prime } ( t ) &\le \sum_{k = 1}^{m} c_{ik} ( t ) E_{ik} \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert \\ &\quad{} + \sum_{k = 1}^{m} c _{ik} ( t ) F_{ik} \bigl\vert \bar{y}_{k}^{\alpha } ( t ) - y_{k}^{\alpha } ( t ) \bigr\vert - \sum _{k = 1}^{n} b_{ik} ( t ) \bigl\vert \bar{x}_{k} ( t ) - x_{k} ( t ) \bigr\vert \\ &\quad{} + \sum_{k = 1}^{n} \int_{t}^{\varphi_{k}^{ - 1} ( t ) } b _{ik} ( u ) \,du G_{k} ( t ) . \end{aligned} $$
(4.7)

Next, we define

$$ V_{i} ( t ) = V_{i1} ( t ) + V_{i2} ( t ) + V_{i3} ( t ) , $$
(4.8)

where

$$ V_{i3} ( t ) = \sum_{k = 1}^{n} \sum_{j = 1}^{n} M_{k} \int_{t - \tau_{j} ( t ) }^{t} \int_{\varphi_{j}^{ - 1} ( l ) }^{\varphi_{k}^{ - 1} ( \varphi_{j}^{ - 1} ( l ) ) } \frac{b_{ik} ( u ) b _{kj} ( \varphi_{j}^{ - 1} ( l ) ) }{1 - \tau_{j} ^{\prime } ( \varphi_{j}^{ - 1} ( l ) ) } \bigl\vert \bar{x}_{j} ( l ) - x_{j} ( l ) \bigr\vert \,du\,dl. $$
(4.9)

Considering (4.7)-(4.9), for \(t \ge T + \tau \), we get

$$\begin{aligned} & D^{ +} V_{i} ( t ) \\ &\quad \le \sum_{k = 1}^{m} c_{ik} ( t ) E _{ik} \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert + \sum_{k = 1}^{m} c_{ik} ( t ) F_{ik} \bigl\vert \bar{y}_{k} ^{\alpha } ( t ) - y_{k}^{\alpha } ( t ) \bigr\vert - \sum _{k = 1}^{n} b_{ik} ( t ) \bigl\vert \bar{x}_{k} ( t ) - x_{k} ( t ) \bigr\vert \\ & \quad \quad {} + \sum_{k = 1}^{n} \Biggl[ r_{k} ( s ) + \sum_{j = 1}^{n} b _{kj} ( s ) M_{j} + \sum_{j = 1}^{m} \frac{c_{kj} ( s ) M _{k}N_{j}^{\alpha }}{f_{kj}^{l} + m_{k}^{2}} \Biggr] \int_{t}^{\varphi _{k}^{ - 1} ( t ) } b_{ik} ( u ) \,du \bigl\vert \bar{x} _{k} ( t ) - x_{k} ( t ) \bigr\vert \\ & \quad \quad {} + \sum_{k = 1}^{n} \sum _{j = 1}^{m} c_{ik} ( t ) M_{k}E_{kj} \int_{t}^{\varphi_{k}^{ - 1} ( t ) } b_{ik} ( u ) \,du \bigl\vert \bar{x}_{k} ( t ) - x_{k} ( t ) \bigr\vert \\ & \quad \quad {} + \sum_{k = 1}^{n} \sum _{j = 1}^{m} c_{kj} ( t ) M_{k}F_{kj} \int_{t}^{\varphi_{k}^{ - 1} ( t ) } b_{ik} ( u ) \,du \bigl\vert \bar{y}_{j}^{\alpha } ( t ) - y_{j}^{\alpha } ( t ) \bigr\vert \\ & \quad \quad {} + \sum_{k = 1}^{n} \sum _{j = 1}^{n} \frac{M_{k}b_{kj} ( \varphi _{j}^{ - 1} ( t ) ) }{1 - \tau_{j}^{\prime } ( \varphi_{j}^{ - 1} ( l ) ) } \int_{\varphi_{j}^{ - 1} ( t ) }^{\varphi_{k}^{ - 1} ( \varphi_{j}^{ - 1} ( t ) ) } b_{ik} ( u ) \,du \bigl\vert \bar{x}_{j} ( t ) - x_{j} ( t ) \bigr\vert . \end{aligned}$$
(4.10)

Define

$$ V_{j} ( t ) = \bigl\vert \ln y_{j} ( t ) - \ln \bar{y}_{j} ( t ) \bigr\vert . $$
(4.11)

Calculating its Dini derivative along system (1.2), we get

$$\begin{aligned} D^{ +} V_{j} ( t ) &= \operatorname {sign}\bigl( y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr) \biggl( \frac{y_{j}^{\prime } ( t ) }{y_{j} ( t ) } - \frac{\bar{y}_{j}^{\prime } ( t ) }{\bar{y}_{j} ( t ) } \biggr) \\ &= \operatorname {sign}\bigl( y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr) \Biggl[ - \sum_{k = 1}^{m} p_{jk} ( t ) \bigl( y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr) \\ &\quad{}+ \sum _{k = 1}^{m} q _{kj} ( t ) \biggl( \frac{x_{k}^{2} ( t ) y_{j}^{ \alpha - 1} ( t ) }{f_{ik} ( t ) + x_{k}^{2} ( t ) } - \frac{\bar{x}_{k}^{2} ( t ) \bar{y}_{j}^{\alpha - 1} ( t ) }{f_{ik} ( t ) + \bar{x}_{k}^{2} ( t ) } \biggr) \Biggr] \\ &= - \sum_{k = 1}^{m} p_{jk} ( t ) \bigl\vert y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr\vert \\ &\quad{}+ \sum_{k = 1}^{m} q_{kj} ( t ) \operatorname {sign}\bigl( y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr) \biggl( \frac{x_{k}^{2} ( t ) y_{j}^{\alpha - 1} ( t ) }{f_{ik} ( t ) + x_{k}^{2} ( t ) } - \frac{ \bar{x}_{k}^{2} ( t ) \bar{y}_{j}^{\alpha - 1} ( t ) }{f _{ik} ( t ) + \bar{x}_{k}^{2} ( t ) } \biggr) \\ &= - \sum_{k = 1}^{m} p_{jk} ( t ) \bigl\vert y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr\vert + \sum_{k = 1}^{m} q_{kj} ( t ) \operatorname {sign}\bigl( y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr) \\ &\quad{}\times \biggl( \frac{x_{k}^{2} ( t ) y_{j}^{\alpha - 1} ( t ) }{f _{ik} ( t ) + x_{k}^{2} ( t ) } - \frac{x_{k}^{2} ( t ) \bar{y}_{j}^{\alpha - 1} ( t ) }{f_{ik} ( t ) + x_{k}^{2} ( t ) } + \frac{x_{k}^{2} ( t ) \bar{y}_{j}^{\alpha - 1} ( t ) }{f _{ik} ( t ) + x_{k}^{2} ( t ) } - \frac{\bar{x} _{k}^{2} ( t ) \bar{y}_{j}^{\alpha - 1} ( t ) }{f _{ik} ( t ) + \bar{x}_{k}^{2} ( t ) } \biggr) \\ &= - \sum_{k = 1}^{m} p_{jk} ( t ) \bigl\vert y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr\vert + \sum_{k = 1}^{m} q_{kj} ( t ) \operatorname {sign}\bigl( y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr) \\ &\quad{}\times \biggl( \frac{x_{k}^{2} ( t ) }{f_{ik} ( t ) + x_{k}^{2} ( t ) } \bigl( y_{j}^{\alpha - 1} ( t ) - \bar{y} _{j}^{\alpha - 1} ( t ) \bigr) \\ &\quad{} + \frac{f_{ik} ( t ) ( x_{k} ( t ) + \bar{x} _{k} ( t ) ) \bar{y}_{j}^{\alpha - 1} ( t ) }{ ( f_{ik} ( t ) + x_{k}^{2} ( t ) ) ( f_{ik} ( t ) + \bar{x}_{k}^{2} ( t ) ) } \bigl( x_{k} ( t ) - \bar{x}_{k} ( t ) \bigr) \biggr) \\ &\le - \sum_{k = 1}^{m} p_{jk} ( t ) \bigl\vert y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr\vert + \sum_{k = 1}^{m} q _{kj} ( t ) \frac{ ( x_{k} ( t ) + \bar{x} _{k} ( t ) ) \bar{y}_{j}^{\alpha - 1} ( t ) }{f _{ik} ( t ) + x_{k}^{2} ( t ) } \bigl\vert x_{k} ( t ) - \bar{x}_{k} ( t ) \bigr\vert \\ &\le - \sum_{k = 1}^{m} p_{jk} ( t ) \bigl\vert y_{j} ( t ) - \bar{y}_{j} ( t ) \bigr\vert + \sum_{k = 1}^{m} q _{kj} ( t ) \frac{2M_{i}N_{j}^{\alpha - 1}}{f_{ik} ( t ) + m_{i}^{2}} \bigl\vert x_{k} ( t ) - \bar{x}_{k} ( t ) \bigr\vert . \end{aligned}$$
(4.12)

Define the Lyapunov functional \(V ( t ) \) as follows:

$$ V ( t ) = \sum_{i = 1}^{n} V_{i} ( t ) + \sum_{j = 1}^{m} V_{j} ( t ) . $$
(4.13)

Considering (4.10), (4.11) and (4.12), for \(t \ge T + \tau \), we have

$$ D^{ +} V ( t ) \le - \sum_{i = 1}^{n} A_{i} ( t ) \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert - \sum_{j = 1}^{m} B_{j} ( t ) \bigl\vert \bar{y}_{j} ( t ) - y_{j} ( t ) \bigr\vert , $$
(4.14)

where \(A_{i} ( t ) \), \(B_{j} ( t ) \) are given in Theorem 4.1.

From conditions \([H _{2} ]\) and \([H _{3} ]\), there exist \(\alpha_{i}, \beta_{j} > 0\) and \(T_{0} \ge T + \tau \) such that

$$ 0 < \alpha_{i} \le A_{i} ( t ) ,\quad\quad 0 < \beta_{j} \le B_{j} ( t ) \quad \mbox{for } t \ge T_{0}. $$
(4.15)

Let \(\alpha_{0} = \min \{ \alpha_{1},\alpha_{2},\ldots,\alpha_{n}; \beta_{1},\beta_{2},\ldots,\beta_{m} \} \), combining (4.14) and (4.15), then

$$ D^{ +} V ( t ) \le - \alpha_{0} \Biggl( \sum _{i = 1}^{n} \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert + \sum_{j = 1}^{m} \bigl\vert \bar{y}_{j} ( t ) - y_{j} ( t ) \bigr\vert \Biggr) . $$
(4.16)

Integrating (4.16) on \([ T_{0},t ] \), we get

$$ V ( t ) + \alpha_{0} \int_{T_{0}}^{t} \Biggl( \sum _{i = 1} ^{n} \bigl\vert \bar{x}_{i} ( u ) - x_{i} ( u ) \bigr\vert + \sum_{j = 1}^{m} \bigl\vert \bar{y}_{j} ( u ) - y_{j} ( u ) \bigr\vert \Biggr) \,du \le V ( T_{0} ) ,\quad t \ge T_{0}. $$
(4.17)

So, \(\int_{T_{0}}^{ + \infty } ( \sum_{i = 1}^{n} \vert \bar{x}_{i} ( u ) - x_{i} ( u ) \vert + \sum_{j = 1}^{m} \vert \bar{y}_{j} ( u ) - y_{j} ( u ) \vert ) \,du < + \infty \) and \(V ( t ) \) is bounded on the interval \([ T_{0}, + \infty ) \). Combining Theorem 3.1 and (1.2), we get \(\bar{x}_{i} ( t ) - x_{i} ( t ) \), \(\bar{y}_{j} ( t ) - y_{j} ( t ) \) and \(( \bar{x}_{i} ( t ) - x_{i} ( t ) ) ^{\prime }\), \(( \bar{y}_{j} ( t ) - y_{j} ( t ) ) ^{\prime }\) are bounded on the interval \([ T_{0}, + \infty ) \). Then \(\sum_{i = 1}^{n} \vert \bar{x}_{i} ( u ) - x_{i} ( u ) \vert + \sum_{j = 1}^{m} \vert \bar{y}_{j} ( u ) - y_{j} ( u ) \vert \) is uniformly continuous.

Using Lemma 2.1, we get

$$ \begin{gathered} \lim_{t \to + \infty } \Biggl( \sum _{i = 1}^{n} \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert + \sum_{j = 1}^{m} \bigl\vert \bar{y}_{j} ( t ) - y_{j} ( t ) \bigr\vert \Biggr) = 0 \quad \mbox{and} \\ \lim_{t \to + \infty } \bigl\vert \bar{x}_{i} ( t ) - x_{i} ( t ) \bigr\vert = 0,\quad\quad \lim_{t \to + \infty } \bigl\vert \bar{y} _{j} ( t ) - y_{j} ( t ) \bigr\vert = 0. \end{gathered} $$
(4.18)

Therefore, system (1.2) is globally attractive. □

5 Existence of almost periodic solution

Theorem 5.1

Suppose \([H_{1}]\), \([H_{2}]\) and \([H_{3}]\) hold, then system (1.2) has a unique almost periodic solution.

Proof

From Theorem 3.2, we know \(( x ( t ) ,y ( t ) ) ^{T} \), \(t \in R\) is a bounded positive solution. Then there exists a sequence \(\{ t'_{\lambda } \} \), \(t'_{ \lambda } \to \infty \) as \(\lambda \to + \infty \) such that \(( x ( t + t'_{\lambda } ) ,y ( t + t'_{\lambda } ) ) ^{T}\) is a solution of the following system (5.1):

$$\begin{aligned} \textstyle\begin{cases} x'_{i} ( t ) = x_{i} ( t ) [ r_{i} ( t + t'_{ \lambda } ) - \sum_{k = 1}^{n} b_{ik} ( t + t'_{\lambda } ) x _{k} ( t - \tau_{k} ( t ) ) - \sum_{k = 1}^{m} \frac{c _{ik} ( t + t'_{\lambda } ) x_{i} ( t ) }{x_{i}^{2} ( t ) + f_{ik} ( t + t'_{\lambda } ) }y_{k}^{ \alpha } ( t ) ] , \\ y'_{j} ( t ) = y_{j} ( t ) [ - r_{j} ( t + t'_{\lambda } ) - \sum_{k = 1}^{m} p_{jk} ( t + t'_{\lambda } ) y_{k} ( t ) + \sum_{k = 1}^{n} \frac{q_{kj} ( t + t'_{\lambda } ) x_{k}^{2} ( t ) }{x_{k}^{2} ( t ) + f_{kj} ( t + t'_{\lambda } ) }y_{j}^{\alpha - 1} ( t ) ] . \end{cases}\displaystyle \end{aligned}$$
(5.1)

From the above and Theorem 3.1, we know \(( x ( t + t'_{ \lambda } ) ,y ( t + t'_{\lambda } ) ) ^{T}\) and \(( x' ( t + t'_{\lambda } ) ,y' ( t + t'_{\lambda } ) ) ^{T}\) are uniformly bounded. Clearly, the sequence \(( x ( t + t'_{\lambda } ) ,y ( t + t'_{\lambda } ) ) ^{T}\) is equi-continuous. By the Ascoli theorem, there exists a uniformly convergent subsequence \(\{ ( x ( t + t_{\lambda } ) ,y ( t + t_{\lambda } ) ) ^{T} \} \subseteq \{ ( x ( t + t'_{\lambda } ) ,y ( t + t'_{\lambda } ) ) ^{T} \} \) such that, for any \(\forall \varepsilon > 0\), there exists \(\lambda_{0} ( \varepsilon ) > 0\) with the property that if λ, \(\varpi > \lambda_{0} ( \varepsilon ) \), then

$$ \bigl\vert x_{i} ( t + t_{\varpi } ) - x_{i} ( t + t_{ \lambda } ) \bigr\vert < \varepsilon , \quad\quad \bigl\vert y_{j} ( t + t_{ \varpi } ) - y_{j} ( t + t_{\lambda } ) \bigr\vert < \varepsilon , $$

which indicates that \(( x ( t + t_{\lambda } ) ,y ( t + t_{\lambda } ) ) ^{T}\) is an almost periodic and asymptotic function. Then there exist functions \(g_{i1} ( t ) \), \(g_{j2} ( t ) \), \(h_{i1} ( t ) \), \(h_{j2} ( t ) \) such that

$$ x_{i} ( t ) = g_{i1} ( t ) + h_{i1} ( t ) , \quad\quad y _{j} ( t ) = g_{j2} ( t ) + h_{j2} ( t ) , $$

where

$$\begin{aligned}& \lim_{\lambda \to + \infty } g_{i1} ( t + t_{\lambda } ) = g _{i1} ( t ) ,\quad\quad \lim_{\lambda \to + \infty } g_{j2} ( t + t _{\lambda } ) = g_{j2} ( t ) , \\& \lim_{\lambda \to + \infty } h_{i1} ( t + t_{\lambda } ) = 0,\quad\quad \lim_{\lambda \to + \infty } h_{j2} ( t + t_{\lambda } ) = 0, \end{aligned}$$

\(g_{i1} ( t ) \), \(g_{j2} ( t ) \) are almost periodic functions. It shows that

$$ \lim_{\lambda \to + \infty } x_{i} ( t + t_{\lambda } ) = g _{i1} ( t ) ,\quad\quad \lim_{\lambda \to + \infty } y_{j} ( t + t _{\lambda } ) = g_{j2} ( t ) . $$

Besides, we still have

$$ \lim_{\lambda \to + \infty } x_{i}^{\prime } ( t + t_{\lambda } ) = \lim_{\lambda \to + \infty } \lim_{\bar{h} \to 0} \frac{x _{i} ( t + t_{\lambda } + \bar{h} ) - x_{i} ( t + t_{ \lambda } ) }{\bar{h}} = \lim_{\bar{h} \to 0}\frac{g_{i1} ( t + \bar{h} ) - g_{i1} ( t ) }{\bar{h}}, $$
(5.2)
$$ \lim_{\lambda \to + \infty } y_{j}^{\prime } ( t + t_{\lambda } ) = \lim_{\lambda \to + \infty } \lim_{\bar{h} \to 0} \frac{y _{j} ( t + t_{\lambda } + \bar{h} ) - y_{j} ( t + t_{ \lambda } ) }{\bar{h}} = \lim_{\bar{h} \to 0}\frac{g_{j2} ( t + \bar{h} ) - g_{j2} ( t ) }{\bar{h}}. $$
(5.3)

Therefore, the derivatives \(g_{i1}^{\prime } ( t ) \), \(g_{j2} ^{\prime } ( t ) \) exist.

Next, we prove \(g ( t ) = ( g_{1} ( t ) ,g _{2} ( t ) ) ^{T}\) is an almost periodic solution of system (1.2).

By the characteristics of almost periodic solution, there exists a sequence \(\{ t_{\gamma } \} \), \(t_{\gamma } \to \infty \) as \(\gamma \to + \infty \) such that \(r_{i} ( t + t_{\gamma } ) \to r_{i} ( t ) \), \(r_{j} ( t + t_{\gamma } ) \to r_{j} ( t ) \), \(b_{il} ( t + t_{\gamma } ) \to b_{il} ( t ) \), \(p_{jk} ( t + t_{\gamma } ) \to p_{jk} ( t ) \), \(c_{ik} ( t + t_{\gamma } ) \to c_{ik} ( t ) \), \(q_{lj} ( t + t_{\gamma } ) \to q_{lj} ( t ) \), \(\tau_{i} ( t + t_{\gamma } ) \to \tau_{i} ( t ) \), \(f_{ij} ( t + t_{\gamma } ) \to f_{ij} ( t ) \) (\(i,l = 1,2,\ldots,n\); \(j,k = 1,2,\ldots,m\)) as \(\gamma \to \infty \) uniformly on R. Obviously, \(\lim_{\gamma \to + \infty } x_{i} ( t + t_{\gamma } ) = g _{i1} ( t ) \), \(\lim_{\gamma \to + \infty } y_{j} ( t + t _{\gamma } ) = g_{j2} ( t ) \). So we have

$$\begin{aligned}& \begin{aligned} g_{i1}^{\prime } ( t ) &= \lim _{\gamma \to + \infty } x_{i} ^{\prime } ( t + t_{\gamma } ) \\ &= \lim_{\gamma \to + \infty } x_{i} ( t + t_{\gamma } ) \Biggl[ r_{i} ( t + t_{\gamma } ) - \sum _{k = 1}^{n} b_{ik} ( t + t_{\gamma } ) x_{k} \bigl( ( t + t_{\gamma } ) - \tau_{k} ( t + t_{\gamma } ) \bigr) \\ &\quad{} - \sum_{k = 1}^{m} \frac{c _{ik} ( t + t_{\gamma } ) x_{i} ( t + t_{\gamma } ) y _{k}^{\alpha } ( t + t_{\gamma } ) }{x_{i}^{2} ( t + t _{\gamma } ) + f_{ik} ( t + t_{\gamma } ) } \Biggr] \\ &= g_{i1} ( t ) \Biggl[ r_{i} ( t ) - \sum _{k = 1} ^{n} b_{ik} ( t ) g_{k1} \bigl( t - \tau_{k} ( t ) \bigr) - \sum_{k = 1}^{m} \frac{c_{ik} ( t ) g_{i1} ( t ) g_{k2}^{\alpha } ( t ) }{g_{i1}^{2} ( t ) + f_{ik} ( t ) } \Biggr] , \end{aligned} \\& \begin{aligned} g_{j2}^{\prime } ( t ) &= \lim _{\gamma \to + \infty } y_{j} ^{\prime } ( t + t_{\gamma } ) \\ &= \lim_{\gamma \to + \infty } y_{j} ( t + t_{\gamma } ) \Biggl[ - r_{j} ( t + t_{\gamma } ) - \sum _{k = 1}^{m} p_{jk} ( t + t_{\gamma } ) x_{k} \bigl( ( t + t_{\gamma } ) - \tau_{k} ( t + t_{\gamma } ) \bigr) \\ &\quad{}+ \sum_{k = 1}^{n} \frac{q _{ik} ( t + t_{\gamma } ) x_{k}^{2} ( t + t_{\gamma } ) y _{k}^{\alpha - 1} ( t + t_{\gamma } ) }{x_{k}^{2} ( t + t _{\gamma } ) + f_{kj} ( t + t_{\gamma } ) } \Biggr] \\ &= g_{j2} ( t ) \Biggl[ - r_{j} ( t ) - \sum _{k = 1} ^{m} b_{ik} ( t ) g_{k2} ( t ) + \sum_{k = 1}^{n} \frac{q_{kj} ( t ) g_{k1}^{2} ( t ) g_{k2}^{\alpha - 1} ( t ) }{g_{k1}^{2} ( t ) + f_{kj} ( t ) } \Biggr] . \end{aligned} \end{aligned}$$

From the above, we know \(g ( t ) \) satisfies (1.2), that is, it is a positive almost periodic solution.

Next, we prove that the positive almost periodic solution of system (1.2) is unique.

Let \(g ( t ) > 0\) and \(\bar{g} ( t ) > 0\) be any two almost periodic solutions of system (1.2), then we claim that \(g_{1} ( t ) \equiv \bar{g}_{1} ( t ) \) and \(g_{2} ( t ) \equiv \bar{g}_{2} ( t ) \) for \(\forall t \in R\). Otherwise, there is at least one \(\xi \in R\) such that \(g _{i1} ( \xi ) \ne \bar{g}_{i1} ( \xi ) \), that is, \(\vert g_{i1} ( \xi ) - \bar{g}_{i1} ( \xi ) \vert : = \delta > 0\). Then

$$ \delta = \bigl\vert g_{i1} ( \xi ) - \bar{g}_{i1} ( \xi ) \bigr\vert = \lim_{\gamma \to + \infty } \bigl\vert x_{i} ( \xi + t_{\gamma } ) - \bar{x}_{i} ( \xi + t_{\gamma } ) \bigr\vert = \lim_{t \to + \infty } \bigl\vert x_{i} ( t ) - \bar{x}_{i} ( t ) \bigr\vert > 0, $$

which is a contradiction to (4.18). Thus \(\forall t \in R\), \(g_{1} ( t ) \equiv \bar{g}_{1} ( t ) \) holds. By the same method, we can prove that \(\forall t \in R\), \(g_{2} ( t ) \equiv \bar{g}_{2} ( t ) \). □

Remark 5.1

If \(\tau_{i} ( t ) \equiv \tau_{i}\), where \(\tau_{i}\) (\(i = 1,2,\ldots,n \)) is a nonnegative constant, then assumptions \([H _{2} ] \) and \([H _{3} ] \) can be redefined. So, we give the following Corollary 5.1.

Corollary 5.1

Make \(\tau_{i} ( t ) \equiv \tau _{i}\), where \(\tau_{i} \ge 0\). If system (1.2) satisfies both \([H _{1} ]\) and the following two conditions:

$$\begin{aligned}& \lim_{t \to + \infty } \inf \Biggl\{ - \sum_{k = 1}^{m} c_{ik} ( t ) E_{ik} + \sum_{k = 1}^{n} b _{ik} ( t ) \\& \quad{} - \sum_{k = 1}^{n} \Biggl[ r_{k} ( s ) + \sum_{j = 1}^{n} b_{kj} ( s ) M_{j} + \sum_{j = 1}^{m} \frac{q _{kj} ( s ) M_{k}N_{j}}{f_{kj}^{l} + m_{k}^{2}} \Biggr] \int _{t}^{t + \tau_{i}} b_{ik} ( u ) \,du \\& \quad{} - \sum_{k = 1}^{n} \sum _{j = 1}^{m} c_{ik} ( t ) M_{k}E_{kj} \int_{t}^{t + \tau_{i}} b_{ik} ( u ) \,du - \sum _{k = 1}^{n} \sum_{j = 1}^{n} M_{k}p_{kj} ( t + \tau_{i} ) \int_{t + \tau_{i}}^{t + \tau_{k} + \tau_{i}} b_{ik} ( u ) \,du \\& \quad{} - \sum_{k = 1}^{m} q_{kj} ( t ) \frac{2M_{i}N_{j}^{\alpha - 1}}{f_{ik} ( t ) + m_{i}^{2}} \Biggr\} > 0, \\& \lim_{t \to + \infty } \inf \Biggl\{ - \sum_{k = 1}^{m} c _{ik} ( t ) F_{ik} - \sum_{k = 1}^{n} \sum_{j = 1}^{m} q_{kj} ( t ) M_{k}E_{kj} \int_{t}^{t + \tau_{i}} b_{ik} ( u ) \,du + \sum _{k = 1}^{m} q_{jk} ( t ) \Biggr\} > 0, \end{aligned}$$

then system (1.2) has a unique positive almost periodic solution which is globally attractive.

6 Model simulation

We give examples to verify the correctness of our theoretical results in this part.

Example 6.1

Consider the following system:

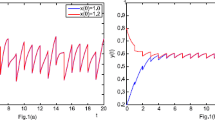
$$ \textstyle\begin{cases} x' ( t ) = x ( t ) [ ( 3 + 0.1\sin \sqrt{7} t ) - ( 2 - 0.1\sin t ) x ( t - 0.01 ) \\ \hphantom{x' ( t ) = }{}- \frac{ ( 0.05 - 0.01\sin t ) x ( t ) }{x ^{2} ( t ) + 1}y^{0.2} ( t ) ] , \\ y' ( t ) = y ( t ) [ - ( 0.02 + 0.01 \sin \sqrt{3} t ) - ( 0.05 - 0.01\sin t ) y ( t ) \\ \hphantom{y' ( t ) =}{}+ \frac{ ( 0.2 + 0.01\sin t ) x^{2} ( t ) }{x ^{2} ( t ) + 1}y^{ - 0.8} ( t ) ] , \end{cases} $$
(6.1)

with the initial conditions \(( \phi ( 0 ) ,\psi ( 0 ) ) = ( 1,1 ) \) and \(( \phi ( 0 ) , \psi ( 0 ) ) = ( 2.5,2 ) \).

By calculation, the parameters of (6.1) meet the conditions of Theorem 3.1 and Corollary 5.1. Using MATLAB, by simulation, time series diagrams of (6.1) are shown in Figure 1. Figure 1 indicates that (6.1) is persistent and has a unique positive almost periodic solution which is globally attractive.

Figure 1
figure 1

(a), (b) The time series diagrams with two initial values of prey and predator, respectively. (c) Two-dimensional periodic diagram of predator-prey. (d) Three-dimensional periodic diagram of predator-prey-time.

Full size image

In order to demonstrate the dynamical behaviors of a multispecies predator-prey system, we give the time series diagrams with only three species in system (1.2).

Example 6.2

Consider the following system:

$$\begin{aligned} \textstyle\begin{cases} x_{1}^{\prime } ( t ) = x_{1} ( t ) [ ( 1 + 0.1\sin \sqrt{7} t ) - ( 1.3 - 1.1\sin t ) x _{1} ( t - 0.01 ) \\ \hphantom{x_{1}^{\prime } ( t ) = }{}- ( 1.4 - 1.2\sin t ) x_{2} ( t - 0.01 ) - \frac{ ( 0.05 - 0.01\sin t ) x_{1} ( t ) }{x_{1}^{2} ( t ) + 30}y^{0.5} ( t ) ] , \\ x_{2}^{\prime } ( t ) = x_{2} ( t ) [ ( 1 + 0.1\sin \sqrt{7} t ) - ( 1.3 - 1.1\sin t ) x _{1} ( t - 0.01 ) \\ \hphantom{x_{2}^{\prime } ( t ) =}{}- ( 1.4 - 1.2\sin t ) x_{2} ( t - 0.01 ) - \frac{ ( 0.05 - 0.01\sin t ) x_{2} ( t ) }{x_{2}^{2} ( t ) + 30}y^{0.5} ( t ) ] , \\ y' ( t ) = y ( t ) [ - ( 0.02 + 0.01 \sin \sqrt{3} t ) - ( 0.05 - 0.01\sin t ) y ( t ) \\ \hphantom{y' ( t ) =}{} + \frac{ ( 0.5 + 0.01\sin t ) x_{1} ( t ) y ^{ - 0.5} ( t ) }{x_{1}^{2} ( t ) + 30} + \frac{ ( 0.5 + 0.01\sin t ) x_{2} ( t ) y^{ - 0.5} ( t ) }{x_{2}^{2} ( t ) + 30} ] , \end{cases}\displaystyle \end{aligned}$$
(6.2)

with the initial conditions \(( \phi_{1} ( 0 ) ,\phi_{2} ( 0 ) ,\psi ( 0 ) ) = ( 2,2,2 ) \) and \(( \phi_{1} ( 0 ) ,\phi_{2} ( 0 ) ,\psi ( 0 ) ) = ( 0.1, 0.1,0.1 ) \).

By calculation, these parameters of (6.2) meet the conditions of Theorem 3.1 and Corollary 5.1. Using MATLAB, by simulation, time series diagrams of (6.2) are shown in Figure 2. Figure 2 shows that (6.2) is persistent and has a unique positive almost periodic solution which is globally attractive.

Figure 2
figure 2

(a), (b) Time series diagrams with two initial values of prey \(x_{i}\) (\(i = 1,2 \)), respectively. (c) The time series diagram with two initial values of predator y. (d) Three-dimensional periodic diagram.

Full size image

7 Conclusion

We construct a multispecies predator-prey model with mutual interference and time delays in this article. We obtain the conditions of permanence, global attractivity and uniqueness of positive almost periodic solutions of the system by using the Ascoli theorem, Lebesgue dominated convergence theorem, Lyapunov functions and comparison theorem. Finally, simulation results indicate the correctness of the theoretical results and demonstrate the complex dynamical behaviors of the system.

Compared with Ref. [10], Du only considered the basic dynamics of two species, which can not be effectively promoted and applied in actual production and life. However, we comprehensively integrate the universal phenomenon of multispecies coexistence in the real ecosystem. By studying the dynamics of multispecies predator-prey system, we can better protect the ecosystem and practice the concept of green development.