1 Introduction and the model

The chemostat is an important laboratory apparatus to study the growth of microorganism in a continuous environment. It has begun to occupy an increasing central role in ecological studies. As a tool in biotechnology, the chemostat plays an important role in bio-processing and the chemostat has many applications in waste water treatment, production by genetically altered organisms, etc. Chemostats with periodic inputs are studied in [1–7], those with periodic washout rate in [8, 9], and those with periodic input and washout in [10]. The structure assigned to the organisms in the model accounts for the dependence of the growth on the past history of the cells, and hence it is capable of predicting the lag phases and transient oscillations observed in experiments. Many authors have directly incorporated time delays in the modeling equations and, as a result, the models take the form of delay differential equations [11–22].

Many scholars pointed out that it was necessary and important to consider models with periodic perturbations, since these models might be quite naturally exposed in many real world phenomena (for instance, food supply, mating habits, harvesting). In fact, almost perturbations occur in a more-or-less periodic fashion. However, there are some other perturbations such as fires, floods, and drainage of sewage which are not suitable to be considered continuous. These perturbations bring sudden changes to the system. A chemostat model with time delays was first studied by Caperon [23] based on some experimental data. Unfortunately, the model proposed by Caperon created the possibility of a negative concentration of the substrate (nutrient). To correct this, Bush and Cook [24] investigated a model of the growth of one microorganism in the chemostat with a delay in the intrinsic growth rate of the organism but with no delay in the nutrient equation. They have also established that oscillations are possible in their model. Systems with sudden perturbations are involved in the impulsive differential equation, which have been studied intensively and systematically in [25, 26].

In this paper, we want to introduce and study a delayed Monod model system in a chemostat with periodically pulsed substrate and nutrient recycling on two substrates. The model takes the form

$$ \left \{ \textstyle\begin{array}{l} \dot{S_{1}}(t)=-DS_{1}(t)- \frac{\mu_{1}S_{1}(t)x(t)}{\delta _{1}(k_{1}+S_{1}(t))},\quad t\neq nT,n\in Z_{+}, \\ \dot{S_{2}}(t)=-DS_{2}(t)- \frac{\mu_{2}S_{2}(t)x(t)}{\delta _{2}(k_{2}+S_{2}(t))},\quad t\neq nT,n\in Z_{+}, \\ \dot{x}(t)=-Dx(t)+e^{-D\tau_{1}} \frac{\mu_{1}S_{1}(t-\tau _{1})x(t-\tau_{1})}{k_{1}+S_{1}(t-\tau_{1})} \\ \hphantom{\dot{x}(t)={}}{}+e^{-D\tau_{2}} \frac{\mu_{2}S_{2}(t-\tau_{2})x(t-\tau _{2})}{k_{2}+S_{2}(t-\tau_{2})},\quad t\neq nT,n\in Z_{+}, \\ S_{1}(t^{+})=S_{1}(t)+p_{1},\quad t=nT, n\in Z_{+}, \\ S_{2}(t^{+})=S_{2}(t)+p_{2},\quad t=nT, n\in Z_{+}, \\ x(t^{+})=x(t),\quad t=nT, n\in Z_{+}, \end{array}\displaystyle \right . $$
(1.1)

where \(S_{1}(t)\), \(S_{2}(t)\) represent the concentrations of limiting substrates at time t, \(x(t)\) denotes the plankton concentration at time t, D is the washout rate; \(p_{i}\) (\(i=1,2\)) denotes the input concentration of the limiting of pulsing; \(\mu_{1}\) and \(\mu_{2}\) are the uptake constants of the plankton; \(\delta_{1}\) is the yield of the plankton per unit mass of the first substrate; \(\delta_{2}\) is the yield of the plankton per unit mass of the second substrate. The constant \(\tau_{i}\geq0\) (\(i=1,2\)) denotes the time delay involved in the biomass depending on the conversion of nutrient to viable biomass. The positive constant, \(e^{-D\tau_{i}}\) (\(i=1,2\)), is required, because it is assumed that the current change in biomass depends on the amount of nutrient consumed in \(\tau_{i}\) (\(i=1,2\)) units of time in the past by the microorganisms that were in the growth vessel at that time and managed to remain in the growth vessel for the \(\tau_{1}\) (\(i=1,2\)) units of time required to process the nutrient.

2 Preliminaries

In this section, we will give some notations and lemmas which will be used for our main results.

Let \(R_{+}=[0,\infty)\), \(R_{+}^{3}=\{(x_{1}, x_{2}, x_{3})\in R^{3}:x_{1}>0, x_{2}>0, x_{3}>0\}\). \(S_{1}(nT^{+})=\lim_{t\rightarrow nT^{+}}S_{1}(t)\), \(S_{2}(nT^{+})=\lim_{t\rightarrow nT^{+}}S_{2}(t)\), \(x(nT^{+})=\lim_{t\rightarrow nT^{+}}x(t)\), \(S_{1}(t)\), \(S_{2}(t)\) are left-continuous at \(t=nT\), \(x(t)\) is continuous at \(t=nT\).

Lemma 2.1

([25, 26])

Consider the following impulse differential inequalities:

$$\begin{aligned}& \omega'(t) \leq(\geq)\, p(t)\omega(t)+q(t),\quad t\neq t_{k}, \\& \omega\bigl(t_{k}^{+}\bigr) \leq(\geq)\, d_{k} \omega(t_{k})+b_{k},\quad t=t_{k},k\in N, \end{aligned}$$

where \(p(t),q(t)\in C(R_{+},R)\), \(d_{k}\geq0\), and \(b_{k}\) are constants.

Assume:

(A0):

the sequence \({t_{k}}\) satisfies \(0\leq t_{0}< t_{1}< t_{2}<\cdots\), with \(\lim_{t\to\infty}t_{k}=\infty\);

(A1):

\(\omega\in PC'(R_{+},R)\) and \(\omega(t)\) is left-continuous at \(t_{k}\), \(k\in N\).

Then

$$\begin{aligned} \omega \leq(\geq)\,& \omega(t_{0})\Pi_{t_{0}< t_{k}< t} d_{k} \exp \biggl(\int_{t_{0}}^{t}p(s)\,ds \biggr) \\ &{}+\sum_{t_{0}< t_{k}< t} \biggl(\Pi_{t_{k}< t_{j}< t}d_{j} \exp \biggl(\int_{t_{k}}^{t}p(s)\,ds \biggr) \biggr)b_{k} \\ &{}+\int_{t_{0}}^{t}\Pi_{s< t_{k}< t}d_{k} \exp \biggl(\int_{s}^{t}p(\theta)d\theta \biggr)q(s)\,ds,\quad t\geq t_{0}. \end{aligned}$$
(2.1)

Consider the following system:

$$ \left \{ \textstyle\begin{array}{l} \dot{S}(t)=-DS(t),\quad t\neq nT\ (i=1,2), n\in Z_{+}, \\ S(t^{+})=S(t)+p_{i},\quad t=nT\ (i=1,2), n\in Z_{+}. \end{array}\displaystyle \right . $$
(2.2)

Lemma 2.2

System (2.2) has a positive periodic solution \(u_{i}^{*}(t)=\frac{p_{i}\exp(-D(t-nT))}{1-\exp(-DT)}\) for all \(t\in(nT,(n+1)T]\), \(n\in Z_{+}\), which is globally uniformly attractive.

The proofs of Lemmas 2.1 and 2.2 are simple, we omit them here.

Lemma 2.3

([27])

Consider the following delay differential equation:

$$\frac{x(t)}{dt}=r_{1}x(t-\tau_{1})+r_{2}x(t- \tau_{2})-r_{3}x(t), $$

where \(r_{1}\), \(r_{2}\), \(r_{3}\), \(\tau_{1}\), \(\tau_{2}\) are all positive constants and \(x(t)>0\) for \(t\in[-\tau,0]\).

  1. (i)

    If \(r_{1}+r_{2}< r_{3}\), then \(\lim_{t\to\infty}x(t)=0\).

  2. (ii)

    If \(r_{1}+r_{2}>r_{3}\), then \(\lim_{t\to \infty}x(t)=+\infty\).

Consider the following system:

$$ \left \{ \textstyle\begin{array}{l} \dot{S}(t)=-S(t),\quad t\neq nT+\tau_{i}\ (i=1,2,\ldots,k), n\in Z_{+}, \\ S(t^{+})=S(t)+p_{i},\quad t=nT+\tau_{i}\ (i=1,2,\ldots,k), n\in Z_{+}, \end{array}\displaystyle \right . $$
(2.3)

where T is the period of the impulsive effect and \(\tau_{0}=0<\tau_{1}<\tau_{2}<\cdots<k=T\) are for the k times of impulsive effects per period T.

Lemma 2.4

The subsystem (2.3) has a positive periodic solution \(\tilde{S}(t)\) and for every solution \(S(t)\) of (2.3) we have \(|S(t)-\tilde{S}(t)|\to0\) as \(t\to\infty\), where

$$\left \{ \textstyle\begin{array}{l} \tilde{S}(t)=S_{i}^{+}\exp(-(t-nT-\tau_{i-1})),\quad t\in(nT+\tau_{i-1},nT+\tau _{i}], \\ \tilde{S}(0)=S_{0}^{+}= \frac{\sum_{j=1}^{k}p_{j}\exp((-T+\tau _{j}))}{1-\exp(-T)},\qquad S_{i}=S_{i-1}^{+}\exp(-p_{i}),\quad i=1,2,\ldots,k. \end{array}\displaystyle \right . $$

Lemma 2.5

Let \((S_{1}(t), S_{2}(t), x(t))\) be any solution of system (1.1) with initial values \((S_{1}(0^{+}), S_{2}(0^{+}), x(0))\in R_{+}^{3}\). There exists a constant \(L>0\) such that \(S_{1}(t)< L\), \(S_{2}(t)< L\), \(x(t)< L\).

Proof

Let \((S_{1}(t), S_{2}(t), x(t))\) be any solution of system (1.1) with initial value \((S_{1}(0^{+}), S_{2}(0^{+}), x(0))\in R_{+}^{3}\). Define a function

$$V(t)=\delta_{1}e^{-D\tau_{1}}S_{1}(t- \tau_{1})+\delta_{2}e^{-D\tau_{2}}S_{2}(t- \tau_{2})+x(t). $$

The upper right derivative of \(V(t)\) along the trajectories of (1.1) is

$$\left \{ \textstyle\begin{array}{l} \dot{V}(t)=-DV(t),\quad t\neq nT+\tau_{i}\ (i=1,2), n\in Z_{+}, \\ V(t^{+})=V(t)+\delta_{i}e^{-D\tau_{i}}p_{i},\quad t=nT+\tau_{i}\ (i=1,2), n\in Z_{+}. \end{array}\displaystyle \right . $$

Without loss of generality, we assume that \(\tau_{1}>\tau_{2}\). From the system (1.1), it is easy to see there exists a \(M_{1}\) such that

$$S_{1}(t)< M_{1},\qquad S_{2}(t)< M_{1}, \qquad x(t)< M_{1}, $$

as \(t\in[0,\tau_{1}]\). \(V(t)\) is for 2 times of the impulsive effects per period T as \(t\in(\tau_{1},\infty)\). Because \(\tau_{1}>\tau_{2}\), there exists a \(n_{0}\) such that

$$\tau_{2}^{*}\doteq n_{0}T+\tau_{2}\in( \tau_{1},\tau_{1}+T]. $$

Let

$$\begin{aligned}& \bar{\tau}_{1}=\tau_{2}^{*}-\tau_{1},\qquad \bar{ \tau}_{2}=T-\bar{\tau}_{1}, \\& \bar{p}_{1}=\frac{\delta_{2}e^{-D\tau_{2}}e^{-D\bar{\tau}_{2}}p_{2}+\delta _{1}e^{-D\tau_{1}}p_{1}}{1-e^{-DT}},\qquad \bar{p}_{2}= \frac{\delta_{1}e^{-D\tau_{1}}e^{-D\bar{\tau}_{1}}p_{1}+\delta _{2}e^{-D\tau_{2}}p_{2}}{1-e^{-DT}}. \end{aligned}$$

By Lemma 2.4, we obtain

$$\left \{ \textstyle\begin{array}{l} V(t)=\bar{p}_{1}e^{-D(t-nT-\tau_{1})},\quad (nT+\tau_{1},\tau_{1}+nT+\tau_{1}^{*}], \\ V(t)=\bar{p}_{2}e^{-D(t-\tau_{1}+nT+\tau_{1}^{*})},\quad (\tau_{1}+nT+\tau_{1}^{*},(n+1)T+\tau_{1}]. \end{array}\displaystyle \right . $$

So, we obtain \(V(t)\leq p\) as \(t\to\infty\). Here \(p=\max\{\bar{p}_{1}, \bar{p}_{2}\}\). According to the definition of \(V(t)\), it can be seen that \(S_{1}(t)<\frac{pe^{D\tau_{1}}}{\delta_{1}}\), \(S_{2}(t)<\frac{pe^{D\tau _{2}}}{\delta_{2}}\), \(x(t)< p\) as \(t\to\infty\). Let \(L=\max\{\frac{pe^{D\tau_{1}}}{\delta_{1}}, \frac{pe^{D\tau_{2}}}{\delta _{2}}, p\}\). This completes the proof. □

3 Main results

In this section, we investigate the extinction of the microorganism species, that is, microorganisms are entirely absent from the chemostat permanently, i.e.,

$$ x(t)=0, \quad t\geq0. $$
(3.1)

This is motivated by the fact that \(x^{*}=0\) is an equilibrium solution for the variable \(x(t)\), as it leaves us with \(x'(t)=0\). Under these conditions, we show below that the nutrient concentration oscillates with period T in synchronization with the periodic impulsive input of the nutrient concentration.

From the third equation of system (1.1), we have

$$ x'(t)\leq e^{-D\tau_{1}}\mu_{1}x(t- \tau_{1})+e^{-D\tau_{2}}\mu_{2}x(t-\tau _{2})-Dx(t). $$
(3.2)

By Lemma 2.2, if \(e^{-D\tau_{1}}\mu_{1}+e^{-D\tau_{2}}\mu_{2}< D\), then \(\lim_{t\to\infty}x(t)=0\), that is, the microorganism species becomes ultimately extinct. This shows that the specific growth of the microorganism species cannot supply the loss of the microorganism species to flow out no matter how much the nutrient input is. Therefore, we assume \(e^{-D\tau_{1}}\mu_{1}+e^{-D\tau_{2}}\mu_{2}>D\) in the rest of this paper.

For system (1.1), if we choose \(x(t)\equiv0\) then system (1.1) becomes the following subsystem:

$$\left \{ \textstyle\begin{array}{l} \dot{S}_{1}(t)=-DS_{1}(t),\quad t\neq nT, n\in Z_{+}, \\ \dot{S}_{2}(t)=-DS_{2}(t),\quad t\neq nT, n\in Z_{+}, \\ S_{1}(t^{+})=S_{1}(t)+p_{1},\quad t=nT, n\in Z_{+}, \\ S_{2}(t^{+})=S_{2}(t)+p_{2},\quad t=nT, n\in Z_{+}. \end{array}\displaystyle \right . $$

The subsystem has a unique globally uniform attractive positive T-periodic solution \((u_{1}^{*}(t), u_{2}^{*}(t))\), which is given in (2.1). Hence, system (1.1) has a T-periodic solution \((u_{1}^{*}(t), u_{2}^{*}(t), 0)\) at which the microorganism culture fails. On the global attractivity of \((u_{1}^{*}(t), u_{2}^{*}(t), 0)\) for system (1.1), we have the following result.

Theorem 3.1

A periodic solution \((u_{1}^{*}(t), u_{2}^{*}(t), 0)\) of system (1.1) is globally attractive if

$$ \frac{\mu_{1}e^{-D\tau_{1}}\frac{p_{1}}{1-e^{-DT}}}{k_{1}+\frac {p_{1}}{1-e^{-DT}}}+ \frac{\mu_{2}e^{-D\tau_{2}}\frac {p_{2}}{1-e^{-DT}}}{k_{2}+\frac{p_{2}}{1-e^{-DT}}}-D< 0. $$
(3.3)

Proof

Let \((S_{1}(t), S_{2}(t), x(t))\) be any solution of system (1.1) with initial values \((S_{1}(0^{+}),S_{2}(0^{+}), x(0))\in R_{+}^{3}\), we may choose a sufficiently small positive constant ε such that

$$ \frac{\mu_{1}e^{-D\tau_{1}}\eta_{1}}{k_{1}+\eta_{1}}+\frac{\mu_{2}e^{-D\tau_{2}}\eta _{2}}{k_{2}+\eta_{2}}< D, $$
(3.4)

where

$$\eta_{1}=\frac{p_{1}}{1-e^{-DT}}+\varepsilon,\qquad \eta_{2}= \frac{p_{2}}{1-e^{-DT}}+\varepsilon. $$

It follows from that the first and second equation of system (1.1) that \(S_{1}'(t)\leq S_{1}(t)\), \(S_{2}'(t)\leq S_{2}(t)\). So we consider the following impulse differential inequalities:

$$\left \{ \textstyle\begin{array}{l} \dot{S_{1}}(t)\leq-DS_{1}(t),\quad t\neq nT, n\in Z_{+}, \\ \dot{S_{2}}(t)\leq-DS_{2}(t),\quad t\neq nT, n\in Z_{+}, \\ S_{1}(t^{+})=S_{1}(t)+p_{1},\quad t=nT, n\in Z_{+}, \\ S_{2}(t^{+})=S_{2}(t)+p_{2},\quad t=nT, n\in Z_{+}. \end{array}\displaystyle \right . $$

By using Lemma 2.1, we have

$$\begin{aligned}& \limsup_{t\to\infty}S_{1}(t)\leq\frac{p_{1}}{1-e^{-DT}}, \\& \limsup_{t\to\infty}S_{2}(t)\leq\frac{p_{2}}{1-e^{-DT}}. \end{aligned}$$

Hence, there exist a positive integer \(n_{1}\) and an arbitrarily small positive constant ε such that, for all \(t\geq n_{1}T\),

$$ \begin{aligned} &S_{1}(t)\leq \frac{p_{1}}{1-e^{-DT}}+\varepsilon \doteq\eta_{1}, \\ &S_{2}(t)\leq \frac{p_{2}}{1-e^{-DT}}+\varepsilon\doteq \eta_{2}. \end{aligned} $$
(3.5)

From (3.5) and the third equation of (1.1) we get, for \(t\geq n_{T}+\tau\) where \(\tau=\max \{\tau_{1},\tau_{2} \}\),

$$ x'(t)\leq \frac{\mu_{1}\eta_{1}e^{-D\tau_{1}}}{k_{1}+\eta_{1}}x(t-\tau_{1})+ \frac{\mu_{2}\eta _{2}e^{-D\tau_{2}}}{k_{2}+\eta_{2}}x(t-\tau_{2})-Dx(t). $$
(3.6)

Consider the following comparison equation:

$$ z'(t)= \frac{\mu_{1}\eta_{1}e^{-D\tau_{1}}}{k_{1}+\eta_{1}}z(t-\tau_{1})+ \frac{\mu_{2}\eta _{2}e^{-D\tau_{2}}}{k_{2}+\eta_{2}}z(t-\tau_{2})-Dz(t). $$
(3.7)

By Lemma 2.3 and (3.3) we obtain

$$\lim_{t\to\infty}z(t)=0. $$

Since \(x(s)=z(s)>0\) for all \(s\in[-\tau, 0]\), by the comparison theorem in differential equations and the nonnegativity of the solution (\(x(t)\geq0\)), we have \(x(t)\to0\) as \(t\to\infty\).

Without loss of generality, we may assume that \(0< x(t)<\varepsilon\), for all \(t\geq0\), by the first equation of system (1.1), we have

$$S_{1}'(t)\geq- \biggl(D+\frac{\mu_{1}\varepsilon}{\delta_{1}k_{1}} \biggr)S_{1}(t). $$

Then we have \(\tilde{z}_{1}\leq S_{1}(t)\) and \(\tilde{z}_{1}\to u^{*}_{1}(t)\), as \(\varepsilon\to0\), where \(\tilde{z}_{1}(t)\) is a unique globally asymptotically stable positive periodic solution of

$$ \left \{ \textstyle\begin{array}{l} z'_{1}(t)=- (D+\frac{\mu_{1}\varepsilon}{\delta_{1}k_{1}} )z_{1}(t),\quad t\neq nT,n\in N, \\ z_{1}(t^{+})=z_{1}(t)+p_{1},\quad t=nT, n\in N, \\ z_{1}(0^{+})=S_{1}(0^{+}). \end{array}\displaystyle \right . $$
(3.8)

From (3.8), we have, for \(nT< t<(n+1)T\),

$$\tilde{z}_{1}(t)= \frac{p_{1}e^{-(D+\frac{\mu_{1}\varepsilon}{\delta _{1}k_{1}})(t-nT)}}{1-e^{-(D+\frac{\mu_{1}\varepsilon}{\delta_{1}k_{1}})T}}. $$

By using the comparison theorem of impulsive equations, for any \(\varepsilon_{1}>0\) there exists such a \(T_{1}>0\) that, for \(t>T_{1}\),

$$ S_{1}'(t)>\tilde{z}_{1}(t)- \varepsilon_{1}. $$
(3.9)

On the other hand, from the first equation of (1.1), it follows that

$$S_{1}'(t)\leq-DS_{1}(t). $$

Consider the following comparison system:

$$ \left \{ \textstyle\begin{array}{l} z'_{2}(t)=-Dz_{2}(t),\quad t\neq nT,n\in N, \\ z_{2}(t^{+})=z_{2}(t)+p_{1},\quad t=nT, n\in N, \\ z_{2}(0^{+})=S_{1}(0^{+}). \end{array}\displaystyle \right . $$
(3.10)

Then we have

$$ S_{1}(t)< \tilde{z}_{2}+\varepsilon_{1}, $$
(3.11)

as \(t\to\infty\) and \(\tilde{z}_{2}(t)=u^{*}(t)\), where \(\tilde{z}_{2}(t)\) is a unique positive solution of (3.10).

Let \(\varepsilon\to\infty\), then it follows from (3.9) and (3.11) that

$$ u_{1}^{*}(t)-\varepsilon_{1}< S_{1}(t)< u_{1}^{*}(t)+ \varepsilon_{1} $$
(3.12)

for t large enough, which implies \(S_{1}(t)\to u_{1}^{*}(t)\) as \(t\to\infty\).

By a similar argument to the above, we know \(S_{2}(t)\to u_{2}^{*}(t)\) as \(t\to\infty\). This completes the proof. □

Theorem 3.2

The system (1.1) is permanent, if

$$p_{1}>\frac{Dk_{1}(e^{DT}-1)}{\mu_{1}e^{-D\tau_{1}}-D} $$

or

$$p_{2}>\frac{Dk_{2}(e^{DT}-1)}{\mu_{2}e^{-D\tau_{2}}-D}. $$

Proof

Let \((S_{1}(t), S_{2}(t), x(t))\) be any positive solution of system (1.1). Without loss of generality, we may assume that

$$ p_{1}>\frac{Dk_{1}(e^{DT}-1)}{\mu_{1}e^{-D\tau_{1}}-D}. $$
(3.13)

So there is \(m_{1}\) such that

$$ 0< m_{1}< \frac{\delta_{1}k_{1}}{\mu_{1}} \biggl(\frac{1}{T}\ln \frac{p(\mu_{1}e^{-D\tau _{1}}-D)+Dk_{1}}{Dk_{1}}-D \biggr). $$
(3.14)

From the third equation of system (1.1), we have

$$ x'(t)\geq \biggl(\mu_{1}e^{-D\tau_{1}} \frac{S_{1}(t)}{k_{1}+S_{1}(t)}-D \biggr)x(t)-\mu _{1}e^{-D\tau_{1}} \frac{d}{dt}\int_{t-\tau_{1}}^{t}\frac{S_{1}(\theta)x(\theta )}{k_{1}+S_{1}(\theta)}\, d\theta. $$
(3.15)

Let

$$V(t)=x(t)+\mu_{1}e^{-D\tau_{1}}\int_{t-\tau_{1}}^{t} \frac{S_{1}(\theta)x(\theta )}{k_{1}+S_{1}(\theta)}\, d\theta. $$

Calculating the derivative of \(V(t)\) along the solution of (1.1), it follows from (3.15) that

$$ V'(t)\geq D \biggl(\mu_{1}e^{-D\tau_{1}} \frac{S_{1}(t)}{D(k_{1}+S_{1}(t))}-1 \biggr)x(t). $$
(3.16)

For the above \(m_{1}\) we can choose a positive constant \(\varepsilon_{1}\) small enough such that

$$ \frac{\mu_{1}e^{-D\tau_{1}}\psi_{1}}{D(k_{1}+\psi_{1})}>1, $$
(3.17)

where

$$\psi_{1}=\frac{p_{1}e^{-(D+\frac{\mu_{1}m_{1}}{\delta_{1}k_{1}})T}}{1-e^{-(D+\frac {\mu_{1}m_{1}}{\delta_{1}k_{1}})T}}-\varepsilon_{1}>0. $$

For any positive constant \(t_{0}\), we claim that the inequality \(x(t)< m_{1}\) cannot hold for all \(t\geq0\). Otherwise, there is a positive constant \(t_{0}\), such that \(t\geq t_{0}\). From the first and fourth equations of system (1.1), we have

$$\left \{ \textstyle\begin{array}{l} \dot{S}_{1}(t)\geq-DS_{1}(t)-\frac{\mu_{1}S_{1}(t)m_{1}}{\delta_{1}k_{1}},\quad t\neq nT, n\in Z_{+}, \\ S_{1}(t^{+})=S_{1}(t)+p_{1},\quad t=nT, n\in Z_{+}. \end{array}\displaystyle \right . $$

By Lemma 2.1 there exists such a \(T_{1}\geq t_{0}+\tau_{1}\), for \(t\geq T_{1}\), that

$$ S_{1}(t)>\frac{p_{1}e^{-(D+\frac{\mu_{1}m_{1}}{\delta_{1}k_{1}})T}}{1-e^{-(D+\frac {\mu_{1}m_{1}}{\delta_{1}k_{1}})T}}-\varepsilon_{1}\doteq \psi_{1}. $$
(3.18)

From (3.18) and (3.16), we have

$$ V'(t)> D \biggl(\mu_{1}e^{-D\tau_{1}} \frac{\psi_{1}}{D(k_{1}+\psi_{1})}-1 \biggr)x(t). $$
(3.19)

For all \(t\geq T_{1}\), let

$$x^{l}=\min_{t\in[T_{1},T_{1}+\tau_{1}]}x(t). $$

We show that \(x(t)\geq x^{l}\) for all \(t\geq T_{1}\). Otherwise, there exists a nonnegative constant \(T_{2}\) such that \(x(t)\geq x^{l}\) for \(t\in[T_{1},T_{1}+\tau_{1}+T_{2}]\), \(x(T_{1}+\tau_{1}+T_{2})=x^{l}\), and \(x'(T_{1}+\tau_{1}+T_{2})\leq0\). Thus from the third equation of (1.1) and (3.17), we easily see that

$$\begin{aligned} x'(T_{1}+\tau_{1}+T_{2})& > \biggl[\mu_{1}e^{-D\tau_{1}}\frac{\psi_{1}}{k_{1}+\psi_{1}}-D \biggr]x^{l} \\ & = D \biggl[\mu_{1}e^{-D\tau_{1}}\frac{\psi_{1}}{D(k_{1}+\psi_{1})}-1 \biggr]x^{l} \\ & > 0, \end{aligned}$$

which is a contradiction. Hence we get \(x(t)\geq x^{l}>0\) for all \(t\geq T_{1}\). From (3.19), we have

$$V'(t)> D \biggl(\mu_{1}e^{-D\tau_{1}} \frac{\psi_{1}}{D(k_{1}+\psi_{1})}-1 \biggr)x^{l}>0, $$

which implies \(V(t)\to+\infty\) as \(t \rightarrow\infty\). This is a contradiction to \(V(t)\leq L(1+\mu_{1}\tau_{1}e^{-D\tau_{1}})\). Therefore, for any positive constant \(t_{0}\), the inequality \(x(t)< m_{1}\) cannot hold for all \(t>t_{0}\). On the one hand, if \(x(t)\geq m_{1}\) holds true for all t large enough, then our aim is obtained. On the other hand, \(x(t)\) is oscillatory about \(m_{1}\). Let

$$m_{2}=\min \biggl\{ \frac{m_{1}}{2}, m_{1}e^{-D\tau_{1}} \biggr\} . $$

In the following, we shall show that \(x(t)\geq m_{2}\). There exist two positive constants t̄, ω such that

$$x(\bar{t})=x(\bar{t}+\omega)=m_{1} $$

and

$$x(t)< m_{1} \quad \mbox{for } \bar{t}< t< \bar{t}+\omega. $$

When t̄ is large enough, the inequality \(S_{1}(t)>\psi_{1}\) holds true for \(\bar{t}< t<\bar{t}+\omega\). Since \(x(t)\) is continuous and bounded and is not affect by the impulse, we conclude that \(x(t)\) is uniformly continuous. Hence there exists a constant \(T_{3}\) (with \(0< T_{3}<\tau_{1}\) and \(T_{3}\) independent of the choice t̄) such that \(x(t)>\frac{m_{1}}{2}\) for all \(\bar{t}< t<\bar{t}+T_{3}\). If \(\omega\leq T_{3}\), our aim is obtained. If \(T_{3}<\omega<\tau_{1}\), from the third equation of (1.1) we have \(x(t)\geq-Dx(t)\) for \(\bar{t}< t\leq\bar{t}+\omega\). Then we have \(x(t)\geq m_{1}e^{-D\tau_{1}}\) for \(\bar{t}< t<\bar{t}+\omega\leq\bar{t}+\tau_{1}\) since \(x(t)=m_{1}\). It is clear that \(x(t)\geq m_{2}\) for \(\bar{t}< t\leq\bar{t}+\omega\). If \(\omega>\tau_{1}\), then we have \(x(t)>m_{2}\) for \(\bar{t}< t\leq\bar{t}+\tau_{1}\). We show that \(x(t)\geq m_{2}\) for all \(\bar{t}+\tau_{1}\leq t\leq\bar{t}+\omega\). Otherwise, there exists a nonnegative constant \(\bar{t}_{2}\) such that \(x(t)\geq m_{2}\) for \(t\in[\bar{t}+\tau_{1},\bar{t}+\omega]\), \(x(\bar{t}+\tau_{1}+\bar{t}_{2})=m_{2}\) and \(x'(\bar{t}+\tau_{1}+\bar{t}_{2})\leq0\). Thus from the third equation of (1.1) and (3.17), we easily see that

$$\begin{aligned} x'(\bar{t}+\tau_{1}+\bar{t}_{2})& > \biggl[ \mu_{1}e^{-D\tau_{1}}\frac{\psi_{1}}{k_{1}+\psi_{1}}-D \biggr]m_{2} \\ & = D \biggl[\mu_{1}e^{-D\tau_{1}}\frac{\psi_{1}}{D(k_{1}+\psi_{1})}-1 \biggr]m_{2} \\ & > 0, \end{aligned}$$

which is a contradiction. Hence we get \(x(t)\geq m_{2}>0\) for all \(t\in[\bar{t}+\tau_{1},\bar{t}+\omega]\).

Since the interval \([\bar{t},\bar{t}+\omega]\) is arbitrarily chosen (we only need t̄ to be large), we get \(x(t)\geq m_{2}\) for t large enough. In view of our arguments above, the choice of \(m_{2}\) is independent of the positive solution of (1.1) which satisfies \(x(t)\geq m_{2}\) for sufficiently large t.

By Lemma 2.3, we have \(x(t)\leq L\) for \(t\geq0\). Hence, from the first equation of (1.1), we have

$$S'(t)\geq- \biggl( D+\frac{\mu_{1}L}{\delta_{1}k_{1}} \biggr)S_{1}(t). $$

Then we have \(S_{1}(t)\geq\tilde{z}_{3}(t)\), where \(\tilde{z}_{3}\) is a unique globally asymptotically stable positive periodic solution of

$$ \left \{ \textstyle\begin{array}{l} z'_{3}(t)=- (D+\frac{\mu_{1}L}{\delta_{1}k_{1}} )z_{3}(t),\quad t\neq nT, n\in N, \\ z_{3}(t^{+})=z_{3}(t)+p_{1},\quad t=nT, n\in N, \\ z_{3}(0^{+})=S_{1}(0^{+}). \end{array}\displaystyle \right . $$
(3.20)

There exists a \(\varepsilon>0\) small enough such that, for sufficiently large t,

$$S_{1}(t)\geq\tilde{z}_{3}(t)-\varepsilon\geq \frac{p_{1}e^{-(D+\frac{\mu_{1}L}{\delta _{1}k_{1}})T}}{1-e^{-(D+\frac{\mu_{1}L}{\delta_{1}k_{1}})T}}-\varepsilon\doteq m_{3}. $$

By a similar argument, there exists a positive constant \(m_{4}\) such that

$$S_{2}(t)\geq m_{4}. $$

The proof is complete. □

4 Numerical analysis and discussion

In this paper, we introduce a growth time delay and pulse input nutrient into the Monod type chemostat model, and theoretically analyze the influence of them on the extinction of the population of the microorganism and the permanence of the system. In Section 3, we give the conditions for extinction and permanence of the microorganisms. Our main results show that if the impulsive periodic nutrient concentration inputs \(p_{1}\) and \(p_{2}\) are under a certain value, then the population of microorganisms will be eventually extinct. Contrarily, if the impulsive periodic nutrient concentration input \(p_{1}\) or \(p_{2}\) is over a certain value, it will be permanent. In this case, the microorganism is kept.

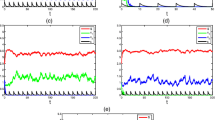
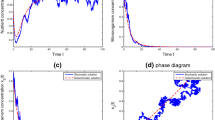
In the following, we substantiate the above results by numerical analysis. Then we arbitrarily consider a hypothetical set of parameter values as \(\mu_{1}=8\), \(\mu_{2}=10\), \(\delta_{1}=1\), \(\delta_{2}=1\), \(D=0.75\), \(\tau_{1}=0.1\), \(\tau_{2}=0.1\), \(T=1\), \(k_{1}=9\), \(k_{2}=4 \). If \(p_{1}=0.1\), \(p_{2}=0.1\), then Theorem 3.1 holds true, which implies that the microorganism species is extinct (see Figure 1(i)-(iv)). If \(p_{1}=2\), \(p_{2}=2\), then Theorem 3.2 holds true, which implies that the microorganism species is permanent (see Figure 2(i)-(iv)).

Figure 1
figure 1

Behavior and phase portrait of system ( 1.1 ). Dynamical behavior of the system (1.1) with \(\mu_{1}=8\), \(\mu_{2}=10\), \(\delta_{1}=1\), \(\delta_{2}=1\), \(D=0.75\), \(\tau_{1}=0.1\), \(\tau_{2}=0.1\), \(T=1\), \(p_{1}=0.1\), \(p_{2}=0.1\), \(k_{1}=9\), \(k_{2}=4 \). (i) Time-series of the nutrient \(S_{1}(t)\) for periodic oscillation. (ii) Time-series of nutrient \(S_{2}(t)\) for periodic oscillation. (iii) Time-series of the microorganism population \(x(t)\) for extinction. (iv) Phase portrait of \(S_{1}(t)\), \(S_{2}(t)\), \(x(t)\).

Full size image
Figure 2
figure 2

Behavior and phase portrait of system ( 1.1 ). Dynamical behavior of the system (1.1) with \(\mu_{1}=8\), \(\mu_{2}=10\), \(\delta_{1}=1\), \(\delta_{2}=1\), \(D=0.75\), \(\tau_{1}=0.1\), \(\tau_{2}=0.1\), \(T=2\), \(p_{1}=2\), \(p_{2}=2\), \(k_{1}=9\), \(k_{2}=4 \). (i) Time-series of the nutrient \(S_{1}(t)\) for periodic oscillation. (ii) Time-series of nutrient \(S_{2}(t)\) for periodic oscillation. (iii) Time-series of the microorganism population \(x(t)\) for extinction. (iv) Phase portrait of \(S_{1}(t)\), \(S_{2}(t)\), \(x(t)\).

Full size image