Permanence for a modified Leslie-Gower predator-prey model with Beddington-DeAngelis functional response and feedback controls

Abstract

A modified Leslie-Gower predator-prey system with Beddington-DeAngelis functional response and feedback controls is studied. By applying the differential inequality theory, sufficient conditions which guarantee the permanence of the system are obtained. Our results improve the main results of Zhang et al. (Abstr. Appl. Anal. 2014:252579, 2014). One example is presented to verify our main results.

1 Introduction

Let $f(t)$ be a continuous bounded function on ℝ, and we set

$$f^{l}=\inf_{t\in \mathbb{R}}f(t) , \qquad f^{u}=\sup _{t\in \mathbb{R}}f(t). $$

Leslie [1, 2] introduced the following two species Leslie-Gower predator-prey model:

$$ \left \{ \begin{array}{l} \dot{x}(t) = (r_{1}-b_{1}x(t) )x(t)-p(x(t))y(t), \\ \dot{y}(t) = (r_{2}-a_{2} \frac{y(t)}{x(t)} )y(t), \end{array} \right . $$

(1.1)

where $x(t)$, $y(t)$ stand for the population (the density) of the prey and the predator at time t, respectively. The parameters $r_{1}$ and $r_{2}$ are the intrinsic growth rates of the prey and the predator, respectively. $b_{1}$ measures the strength of competition among individuals of species x. The value $\frac{r_{1}}{b_{1}}$ is the carrying capacity of the prey in the absence of predation. The predator consumes the prey according to the functional response $p(x)$ and grows logistically with growth rate $r_{2}$ and carrying capacity $\frac{r_{2}x}{a_{2}}$ proportional to the population size of the prey (or prey abundance). The parameter $a_{2}$ is a measure of the food quantity that the prey provides and converted to predator birth. The term $y/x$ is the Leslie-Gower term which measures the loss in the predator population due to rarity (per capita $y/x$) of its favorite food. Leslie model is a predator-prey model where the carrying capacity of the predator is proportional to the number of prey, stressing the fact that there are upper limits to the rates of increase in both prey x and predator y, which are not recognized in the Lotka-Volterra model.

The main shortcoming of (1.1) is that in the case of severe scarcity, y can switch over to other populations but its growth will be limited by the fact that its most favorite food x is not available in abundance. In order to overcome this shortcoming, recently, Aziz-Alaoui and Daher Okiye [3] suggested to add a positive constant d to the denominator and proposed the following predator-prey model with modified Leslie-Gower and Holling-type II schemes:

$$ \left \{ \begin{array}{l} \dot{x}(t) = (r_{1}-b_{1}x(t)- \frac{a_{1}y(t)}{x(t)+k_{1}} )x(t), \\ \dot{y}(t) = (r_{2}- \frac{a_{2}y(t)}{x(t)+k_{2}} )y(t), \end{array} \right . $$

(1.2)

where $r_{1}$, $b_{1}$, $r_{2}$, $a_{2}$ have the same meaning as in models (1.1). $a_{1}$ is the maximum value of the per capita reduction rate of x due to y, $k_{1}$ (respectively, $k_{2}$) measures the extent to which the environment provides protection to prey x (respectively, to the predator y). They obtained the boundedness and global stability of positive equilibrium of system (1.2). Yu [4] studied the structure, linearized stability and the global asymptotic stability of equilibria of (1.2). Zhu and Wang [5] obtained sufficient conditions for the existence and global attractivity of positive periodic solutions of system (1.2) with periodic coefficients. Yu and Chen [6] further considered the permanence and existence of a unique globally attractive positive almost periodic solution of system (1.2) with almost periodic coefficients and mutual interference. Considering that Beddington-DeAngelis functional response preformed better than Holling-type II functional response, Yu [7] incorporated the Beddington-DeAngelis functional response into system (1.2) and considered the following model which is the generalization of model (1.2):

$$ \left \{ \begin{array}{l} \dot{x}(t) = (r_{1}-b_{1}x(t)- \frac{a_{1} y(t)}{\alpha+\beta x(t)+\gamma y(t)} )x(t), \\ \dot{y}(t) = (r_{2}- \frac{a_{2} y(t)}{x(t)+k_{2}} )y(t). \end{array} \right . $$

(1.3)

Sufficient conditions on the global asymptotic stability of a positive equilibrium were obtained by Yu [7]. Pal and Mandal [8] considered the Hopf bifurcation of system (1.3) with strong Allee effect. Zhang [9] studied the permanence and existence of an almost periodic solution of system (1.3) with almost periodic coefficients.

Based on Zhang [9], Zhang et al. [10] incorporated the feedback control into model (1.3) with almost periodic coefficients and considered the following model:

$$ \left \{ \begin{array}{l} \dot{x}(t) = x(t) (a_{1}(t)-b(t)x(t)- \frac{c(t)y(t)}{\alpha(t)+\beta(t)x(t)+\gamma(t)y(t)}-e_{1}(t)u(t) ), \\ \dot{y}(t) = y(t) (a_{2}(t)- \frac{r(t) y(t)}{x(t)+k(t)}-e_{2}(t)v(t) ), \\ \dot{u}(t) = -d_{1}(t)u(t)+p_{1}(t)x(t-\tau), \\ \dot{v}(t) = -d_{2}(t)v(t)+p_{2}(t)y(t-\tau), \end{array} \right . $$

(1.4)

where $b(t)$, $c(t)$, $r(t)$, $k(t)$, $\alpha(t)$, $\beta(t)$, $\gamma(t)$, $a_{i}(t)$, $d_{i}(t)$, $p_{i}(t)$ and $e_{i}(t)$ ($i=1,2$) are all continuous, almost periodic functions and satisfy

$$\begin{aligned} \begin{aligned} &\min_{i=1,2}\bigl\{ b^{l},c^{l},r^{l},k^{l}, \alpha^{l},\beta^{l},\gamma^{l},a_{i}^{l},d_{i}^{l},p_{i}^{l},e_{i}^{l} \bigr\} >0, \\ &\max_{i=1,2}\bigl\{ b^{u},c^{u},r^{u},k^{u}, \alpha^{u},\beta^{u},\gamma^{u},a_{i}^{u},d_{i}^{u},p_{i}^{u},e_{i}^{u} \bigr\} < +\infty. \end{aligned} \end{aligned}$$

Set

$$ M_{1}= \frac{a_{1}^{u}}{b^{l}}, \qquad M_{2}= \frac{a_{2}^{u}(M_{1}+k^{u})}{r^{l}}, \qquad L_{1}= \frac{p_{1}^{u}M_{1}}{d_{1}^{l}}, \qquad L_{2}= \frac{p_{2}^{u}M_{2}}{d_{2}^{l}}. $$

(1.5)

Suppose that system (1.4) holds together with the following initial conditions:

$$\begin{aligned}& x(s)=\phi(s)\ge0, \quad s\in[-\tau,0], \qquad \phi(0)>0, \\& y(s)=\varphi(s)\ge0, \quad s\in[-\tau,0], \qquad \varphi(0)>0, \\& u(0)>0, \qquad v(0)>0. \end{aligned}$$

(1.6)

By using the comparison theorem of differential equation, Zhang et al. [10] obtained the following result.

Theorem A

([10])

Assume that

$$(\mathrm{H}_{1})\quad a_{1}^{l}- \frac{c^{u}}{\gamma^{l}}-e_{1}^{u}L_{1}>0 \quad \textit{and}\quad a_{2}^{l}-e_{2}^{u}L_{2}>0 $$

hold, then system (1.4) with initial conditions (1.6) is permanent, i.e., any positive solution $(x(t),y(t),u(t),v(t))^{T}$ of system (1.4) with initial conditions (1.6) satisfies

$$\begin{aligned}& m_{1}\le\liminf_{t\rightarrow +\infty}x(t)\le \limsup _{t\rightarrow +\infty}x(t)\le M_{1},\qquad m_{2}\le\liminf _{t\rightarrow +\infty}y(t)\le \limsup_{t\rightarrow +\infty}y(t)\le M_{2}, \\& l_{1}\le\liminf_{t\rightarrow +\infty}u(t)\le \limsup _{t\rightarrow +\infty}y(t)\le L_{1}, \qquad l_{2}\le\liminf _{t\rightarrow +\infty}v(t)\le \limsup_{t\rightarrow +\infty}y(t)\le L_{2}, \end{aligned}$$

where $m_{i}$, $l_{i}$, $M_{i}$ and $L_{i}$ ($i=1,2$) are positive constants.

Theorem A shows that feedback control variables play important roles in the persistent property of system (1.4). But the question is whether or not the feedback control variables have influence on the permanence of the system. Many papers (see [11–13] and the references cited therein) have showed that feedback control variables have no influence on the permanent property of continuous system with feedback control. Thus, in this paper, we will apply the analysis technique of Chen et al. [11] to establish sufficient conditions, which is independent of feedback control variables, to ensure the permanence of the system. In fact, we obtain the following main result.

Theorem B

Assume that

$$(\mathrm{H}_{2})\quad a_{1}^{l}- \frac{c^{u}}{\gamma^{l}}>0 $$

holds, then system (1.4) with initial conditions (1.6) is permanent.

Comparing with Theorem A, it is easy to see that (H₂) in Theorem B is weaker than (H₁) in Theorem A, and feedback control variables have no influence on the permanent property of system (1.4), so our results improve the main results in Zhang et al. [10].

The organization of this paper is as follows. In Section 2, we introduce several lemmas, and the permanence of system (1.4) is then studied in this section. In Section 3, a suitable example together with its numerical simulations is given to illustrate the feasibility of the main results.

2 Permanence

Now let us state several lemmas which will be useful in proving the main results of this section.

Lemma 2.1

([14])

If $a>0$, $b>0$ and $\dot{x}\geq x(b-ax)$, when $t\geq 0$ and $x(0)>0$, we have

$$\liminf_{t\rightarrow +\infty}x(t)\geq \frac{b}{a}. $$

If $a>0$, $b>0$ and $\dot{x}\leq x(b-ax)$, when $t\geq 0$ and $x(0)>0$, we have

$$\limsup_{t\rightarrow +\infty}x(t)\leq \frac{b}{a}. $$

Lemma 2.2

([11])

Assume that $a > 0$, $b(t) > 0$ is a bounded continuous function and $x(0) > 0$. Further suppose that:

• (i)
  $$\dot{x}(t)\leq -ax(t)+b(t), $$

  then for all $t\geq s$,

  $$x(t)\leq x(t-s)\exp\{-as\}+ \int_{t-s}^{t}b(\tau) \exp\bigl\{ a(\tau-t)\bigr\} \, d\tau. $$

  Especially, if $b(t)$ is bounded above with respect to M, then

  $$\limsup_{t\rightarrow +\infty}x(t)\leq \frac{M}{a}. $$
• (ii)
  $$\dot{x}(t)\geq -ax(t)+b(t), $$

  then for all $t\geq s$,

  $$x(t)\geq x(t-s)\exp\{-as\}+ \int_{t-s}^{t}b(\tau) \exp\bigl\{ a(\tau-t)\bigr\} \, d\tau. $$

  Especially, if $b(t)$ is bounded above with respect to m, then

  $$\liminf_{t\rightarrow +\infty}x(t)\geq \frac{m}{a}. $$

The following lemma is a direct conclusion of [10].

Lemma 2.3

For any positive solution $(x(t),y(t),u(t),v(t))^{T}$ of system (1.4) with initial conditions (1.6), there exist four positive constants $M_{i}$ and $L_{i}$ ($i=1,2$) such that

$$ \begin{aligned} &\limsup_{t\rightarrow +\infty}x(t)\le M_{1},\qquad \limsup_{t\rightarrow +\infty}y(t)\le M_{2}, \\ &\limsup_{t\rightarrow +\infty}u(t)\le L_{1}, \qquad \limsup _{t\rightarrow +\infty}v(t)\le L_{2}, \end{aligned} $$

(2.1)

where $M_{i}$ and $L_{i}$ ($i=1,2$) are defined in (1.5).

Lemma 2.4

Suppose that (H₂) holds, then there exist two positive constants $m_{1}$ and $l_{1}$ such that any positive solution $(x(t),y(t),u(t),v(t))^{T}$ of system (1.4) with initial conditions (1.6) satisfies

$$\liminf_{t\rightarrow +\infty}x(t)\ge m_{1},\qquad \liminf _{t\rightarrow +\infty}u(t)\ge l_{1}, $$

where $m_{1}$ and $l_{1}$ are defined in the proof.

Proof

According to Lemma 2.3, there exists enough large $T_{1}>0$ such that for $t\ge T_{1}$,

$$ x(t)\le 2M_{1},\qquad u(t)\le 2L_{1}. $$

(2.2)

Thus, it follows from (2.2) and the first equation of system (1.4) that

$$\begin{aligned} \dot{x}(t) =&x(t) \biggl(a_{1}(t)-b(t)x(t)- \frac{c(t)y(t)}{\alpha(t)+\beta(t)x(t)+\gamma(t)y(t)}-e_{1}(t)u(t) \biggr) \\ \ge&x(t) \biggl(a_{1}^{l}-2b^{u}M_{1}- \frac{c^{u}}{\gamma^{l}}-2e_{1}^{u}L_{1} \biggr) \\ \triangleq&Qx(t), \end{aligned}$$

(2.3)

where $Q=a_{1}^{l}-2b^{u}M_{1}- \frac{c^{u}}{\gamma^{l}}-2e_{1}^{u}L_{1}< a_{1}^{l}-2b^{u}M_{1}<a_{1}^{u}-2b^{l} \frac{a_{1}^{u}}{b^{l}}=-a_{1}^{u}<0$.

Integrating both sides of (2.3) from η ($\eta\leq t$) to t leads to

$$\frac{x(t)}{x(\eta)}\geq \exp\bigl\{ Q(t-\eta)\bigr\} $$

or

$$ x(\eta)\leq x(t)\exp\bigl\{ -Q(t-\eta)\bigr\} . $$

(2.4)

Particularly, take $\eta=t-\tau$, one can get

$$ x(t-\tau)\leq x(t)\exp\{-Q\tau\}. $$

(2.5)

Substituting (2.5) into the third equation of system (1.4) leads to

$$ \dot{u}(t)\leq -d_{1}^{l}u(t)+p_{1}^{u}x(t) \exp\{-Q\tau\}. $$

(2.6)

Applying Lemma 2.2(i) to the above differential inequality, for $0\leq s\leq t$, one has

$$\begin{aligned} u(t) \leq&u(t-s)\exp\bigl\{ -d_{1}^{l}s\bigr\} + \int _{t-s}^{t} p_{1}^{u}x(\eta)\exp \{-Q\tau\}\exp\bigl\{ d_{1}^{l}(\eta-t)\bigr\} \, d\eta \\ \stackrel{\text{from (2.4)}}{\leq}& u(t-s)\exp\bigl\{ -d_{1}^{l}s\bigr\} \\ &{} +\int_{t-s}^{t} p_{1}^{u}x(t) \exp\bigl\{ -Q(t-\eta)\bigr\} \exp\{-Q\tau\}\exp\bigl\{ d_{1}^{l}( \eta-t)\bigr\} \, d\eta \\ \leq&u(t-s)\exp\bigl\{ -d_{1}^{l}s\bigr\} +p_{1}^{u}x(t) \frac{1}{Q} \bigl(1-\exp\{-Qs\} \bigr)\exp\{-Q\tau\}, \end{aligned}$$

(2.7)

where we have used the fact that $\max_{\eta\in[t-s,t]}\exp\{d_{1}^{l}(\eta-t)\}=\exp\{0\}=1$.

Note that there exists K such that $2e_{1}^{u}L_{1}\exp\{-d_{1}^{l}K\}< \frac{\beta}{2}$, as $s\ge K$, where $\beta=a_{1}^{l}- \frac{c^{u}}{\gamma^{l}}>0$ according to (H₂). In fact, we can choose $K> \frac{1}{d_{1}^{l}}\ln \frac{4e_{1}^{u}L_{1}}{\beta}$. And so, fix K, combined with (2.7), we can obtain

$$\begin{aligned} u(t) \leq&u(t-K)\exp\bigl\{ -d_{1}^{l}K\bigr\} +p_{1}^{u}x(t) \frac{1}{Q} \bigl(1-\exp\{-QK\} \bigr) \exp\{-Q\tau\} \\ \leq&2L_{1}\exp\bigl\{ -d_{1}^{l}K\bigr\} +p_{1}^{u}x(t) \frac{1}{Q} \bigl(1-\exp\{-QK\} \bigr) \exp\{-Q\tau\} \\ \leq&2L_{1}\exp\bigl\{ -d_{1}^{l}K\bigr\} +Dx(t) \end{aligned}$$

(2.8)

for all $t>T_{1}+K$, where $D=p_{1}^{u} \frac{1}{Q} (1-\exp\{-QK\} )\exp\{-Q\tau\}>0$.

Substituting (2.8) into the first equation of system (1.4), for all $t>T_{1}+K$, one has

$$\begin{aligned} \dot{x}(t) \ge&x(t) \biggl(a_{1}^{l}-b^{u}x(t)- \frac{c^{u}}{\gamma^{l}}-2e_{1}^{u}L_{1}\exp\bigl\{ -d_{1}^{l}K\bigr\} -e_{1}^{u}Dx(t) \biggr) \\ \ge&x(t) \biggl( \frac{\beta}{2}-\bigl(b^{u}+e_{1}^{u}D \bigr)x(t) \biggr). \end{aligned}$$

(2.9)

By Lemma 2.1, we have

$$ \liminf_{t\rightarrow +\infty}x(t)\geq \frac{\beta}{2(b^{u}+e_{1}^{u}D)}\triangleq m_{1}. $$

(2.10)

Thus, there exists $T_{2}>T_{1}+K$ such that for all $t>T_{2}$,

$$ x(t)\geq \frac{m_{1}}{2}. $$

(2.11)

Inequality (2.11) together with the third equation of (1.4) leads to

$$\dot{u}(t)\geq-d_{1}^{u}u(t)+p_{1}^{l} \frac{m_{1}}{2}\quad \mbox{for all } t>T_{2}+\tau. $$

By applying Lemma 2.2(ii) to the above differential inequality, we have

$$ \liminf_{t\rightarrow +\infty}u(t)\geq \frac{p_{1}^{l}m_{1}}{2d_{1}^{u}}\triangleq l_{1}. $$

(2.12)

Obviously, $m_{1}$ and $l_{1}$ are independent of the solution of system (1.4). Inequalities (2.10) and (2.12) show that the conclusion of Lemma 2.4 holds. The proof is completed. □

Lemma 2.5

For any positive solution $(x(t),y(t),u(t),v(t))^{T}$ of system (1.4) with initial conditions (1.6), there exist two positive constants $m_{2}$ and $l_{2}$ satisfying

$$\liminf_{t\rightarrow +\infty}y(t)\ge m_{2},\qquad \liminf _{t\rightarrow +\infty}v(t)\ge l_{2}, $$

where $m_{2}$ and $l_{2}$ are defined in the proof.

Proof

The proof of Lemma 2.5 is similar to the proof of Lemma 2.4. However, for the sake of completeness, we give the complete proof here.

According to Lemma 2.3, there exists enough large $T_{3}>0$ such that for $t\ge T_{3}$,

$$ y(t)\le 2M_{2},\qquad v(t)\le 2L_{2}. $$

(2.13)

Thus, it follows from (2.13) and the second equation of system (1.4) that

$$\begin{aligned} \dot{y}(t) =&y(t) \biggl(a_{2}(t)- \frac{r(t) y(t)}{x(t)+k(t)}-e_{2}(t)v(t) \biggr) \\ \ge&y(t) \biggl(a_{2}^{l}- \frac{2r^{u}M_{2}}{k^{l}}-2e_{2}^{u}L_{2} \biggr) \\ \triangleq &Py(t), \end{aligned}$$

(2.14)

where $P=a_{2}^{l}- \frac{2r^{u}M_{2}}{k^{l}}-2e_{2}^{u}L_{2}<0$.

Integrating both sides of (2.14) from η ($\eta\leq t$) to t, leads to

$$\frac{y(t)}{y(\eta)}\geq \exp\bigl\{ P(t-\eta)\bigr\} $$

or

$$ y(\eta)\leq y(t)\exp\bigl\{ -P(t-\eta)\bigr\} . $$

(2.15)

Particularly, take $\eta=t-\tau$, one can get

$$ y(t-\tau)\leq y(t)\exp\{-P\tau\}. $$

(2.16)

Substituting (2.16) into the fourth equation of system (1.4) leads to

$$ \dot{v}(t)\leq -d_{2}^{l}v(t)+p_{2}^{u}y(t) \exp\{-P\tau\}. $$

(2.17)

Applying Lemma 2.2(i) to the above differential inequality, for $0\leq s\leq t$, one has

$$\begin{aligned} v(t) \leq&v(t-s)\exp\bigl\{ -d_{2}^{l}s\bigr\} + \int _{t-s}^{t} p_{2}^{u}y(\eta)\exp \{-P\tau\}\exp\bigl\{ d_{2}^{l}(\eta-t)\bigr\} \, d\eta \\ \stackrel{\text{from (2.15)}}{\leq}&v(t-s)\exp\bigl\{ -d_{2}^{l}s\bigr\} \\ &{} +\int_{t-s}^{t} p_{2}^{u}y(t) \exp\bigl\{ -P(t-\eta)\bigr\} \exp\{-P\tau\}\exp\bigl\{ d_{1}^{l}( \eta-t)\bigr\} \, d\eta \\ \leq&v(t-s)\exp\bigl\{ -d_{2}^{l}s\bigr\} +p_{2}^{u}y(t) \frac{1}{P} \bigl(1-\exp\{-Ps\} \bigr)\exp\{-P\tau\}, \end{aligned}$$

(2.18)

where we have used the fact that $\max_{\eta\in[t-s,t]}\exp\{d_{2}^{l}(\eta-t)\}=\exp\{0\}=1$.

Note that there exists $K_{1}$ such that $2e_{2}^{u}L_{2}\exp\{-d_{2}^{l}K_{1}\}< \frac{a_{2}^{l}}{2}$ as $s\ge K_{1}$. In fact, we can choose $K_{1}> \frac{1}{d_{2}^{l}}\ln \frac{4e_{2}^{u}L_{2}}{a_{2}^{l}}$. And so, fix $K_{1}$, combined with (2.18), we can obtain

$$\begin{aligned} v(t) \leq&v(t-K_{1})\exp\bigl\{ -d_{2}^{l}K_{1} \bigr\} +p_{2}^{u}y(t) \frac{1}{P} \bigl(1-\exp \{-PK_{1}\} \bigr)\exp\{-P\tau\} \\ \leq&2L_{2}\exp\bigl\{ -d_{2}^{l}K_{1} \bigr\} +p_{2}^{u}y(t) \frac{1}{P} \bigl(1-\exp \{-PK_{1}\} \bigr)\exp\{-P\tau\} \\ \leq&2L_{2}\exp\bigl\{ -d_{2}^{l}K_{1} \bigr\} +By(t) \end{aligned}$$

(2.19)

for all $t>T_{1}+K_{1}$, where $B=p_{2}^{u} \frac{1}{P} (1-\exp\{-PK_{1}\} )\exp\{-P\tau\}$.

Substituting (2.19) into the second equation of system (1.4), for all $t>T_{3}+K_{1}$, one has

$$\begin{aligned} \dot{y}(t) \ge&y(t) \biggl(a_{2}^{l}- \frac{r^{u}y(t)}{k^{l}}-e_{2}^{u} \bigl(2L_{2}\exp\bigl\{ -d_{2}^{l}K_{1} \bigr\} +By(t) \bigr) \biggr) \\ =&y(t) \biggl(a_{2}^{l}-2e_{2}^{u}L_{2} \exp\bigl\{ -d_{2}^{l}K_{1}\bigr\} - \biggl( \frac{r^{u}}{k^{l}}+e_{2}^{u}B \biggr)y(t) \biggr) \\ \ge&x(t) \biggl( \frac{a_{2}^{l}}{2}- \biggl( \frac{r^{u}}{k^{l}}+e_{2}^{u}B \biggr)y(t) \biggr). \end{aligned}$$

(2.20)

By Lemma 2.1, we have

$$ \liminf_{t\rightarrow +\infty}x(t)\geq \frac{a_{2}^{l}k^{l}}{2(r^{u}+e_{2}^{u}k^{l}B)}\triangleq m_{2}. $$

(2.21)

Thus, there exists $T_{4}>T_{3}+K_{1}$ such that for all $t>T_{4}$,

$$ y(t)\geq \frac{m_{2}}{2}. $$

(2.22)

Inequality (2.22) together with the fourth equation of (1.4) leads to

$$\dot{v}(t)\geq-d_{2}^{u}v(t)+p_{2}^{l} \frac{m_{2}}{2} \quad \mbox{for all } t>T_{4}+\tau. $$

By applying Lemma 2.2(ii) to the above differential inequality, we have

$$ \liminf_{t\rightarrow +\infty}v(t)\geq \frac{p_{2}^{l}m_{2}}{2d_{2}^{u}}\triangleq l_{2}. $$

(2.23)

Obviously, $m_{2}$ and $l_{2}$ are independent of the solution of system (1.4). Inequalities (2.21) and (2.23) show that the conclusion of Lemma 2.5 holds. The proof is completed. □

Lemmas 2.3-2.5 show that the conclusion of Theorem B holds.

3 Examples and numeric simulations

Consider the following example:

$$ \left \{ \begin{array}{l} \dot{x}(t) = x(t) (11+\cos\sqrt{3}t-6x(t)- \frac {(0.8+0.7\sin\sqrt{5}t)y(t)}{20+(12+\sin\sqrt{7}t)x(t)+5 y(t)}-0.5u(t) ), \\ \dot{y}(t) = y(t) (5+0.3\sin\sqrt{7}t- \frac{(5+0.2\cos\sqrt{11}t)y(t)}{x(t)+2}-0.3v(t) ), \\ \dot{u}(t)=-0.2u(t)+(2+\sin\sqrt{2}t)x(t-0.5), \\ \dot{v}(t)=-(0.4+0.2\cos\sqrt{2}t)v(t)+3y(t-0.5), \end{array} \right . $$

(3.1)

in this case, we have

$$ a_{1}^{l}- \frac{c^{u}}{\gamma^{l}}=9.7>0. $$

(3.2)

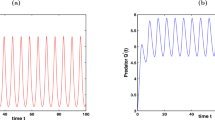
Equation (3.2) shows that (H₂) holds, so system (3.1) is permanent according to Theorem B. Our numerical simulation supports our result (see Figure 1). However,

$$ a_{1}^{l}- \frac{c^{u}}{\gamma^{l}}-e_{1}^{u}L_{1}=-5.3< 0 \quad \mbox{and}\quad a_{2}^{l}-e_{2}^{u}L_{2}=-15.175<0, $$

(3.3)

that is to say, (H₁) does not hold and we cannot obtain the result of the permanence from Theorem A. Thus our results improve the main results in Zhang et al. [10].

Figure 1

Dynamic behavior of system ( 3.1 ) with the initial conditions $\pmb{(x(0), y(0),u(0),v(0))=(1.2,4,1.5,3)^{T}}$ , $\pmb{(0.2,3,3.5,1.3)^{T}}$ , and $\pmb{(2.5,3,5,6)^{T}}$ , respectively.