1 Introduction

In recent past, there has been a remarkable development in the areas of fractional and functional differential equations and their applications. Many physical and engineering phenomena are modeled by fractional differential equations. Much progress has been made by implementing several numerical methods to approximate the solutions of such problems since most fractional and functional differential equations have no exact solutions, see [1–4].

In recent decades, many scientists in different fields of mathematics, physics and engineering have been interested in studying the fractional calculus (theories of derivatives and integrals with any non-integer arbitrary order) for its several applications in various areas of real life such as thermodynamics [5], modeling of viscoelastic dampers [6], bioengineering [7], psychology [8], finance [9] and others [10–16].

The operational matrix of fractional derivatives has been derived for some types of orthogonal polynomials, such as Chebyshev polynomials [17], Jacobi polynomials [18] and Bernstein polynomials [19], and it has been used to solve distinct types of fractional differential equations, see [20–23]. On the other hand, the operational matrix of fractional integrals has been derived for many types of orthogonal polynomials such as Legendre polynomials [24, 25], Jacobi polynomials [26] and Laguerre polynomials [27].

The optimal control problem refers to the minimization of a performance index subject to dynamic constraints on the state variable and the control variable. If the fractional differential equations are used as the dynamic constraints, this leads to the fractional optimal control problem. In recent years, many researchers have studied the fractional optimal control problems and have found numerical solutions for them, for instance, [28–38].

In this paper, we investigate and develop a direct numerical technique to solve the fractional optimal control problem given by

$$ \mathrm{Min.}\quad J= \int_{t_{0}}^{t_{1}}f \bigl(t,x(t),u(t) \bigr)\,dt, $$
(1)

subjected to the dynamic constraints

$$ \begin{aligned} & D^{\nu}x(t)=g \bigl(t,x(t) \bigr)+b(t)u(t), \\ & D^{(i)}x(t_{0})=x_{i},\quad i=0,1,\ldots, n-1, \end{aligned} $$
(2)

where \(n-1 <\nu\leq n\) and \(b(t)\neq0\).

The introduced scheme here consists of expanding the fractional derivative of the state variable \(D^{\nu} x (t) \) with the Jacobi orthonormal polynomials with unknown coefficients using the operational matrix of fractional integrals. Then the equation derived from the dynamic constraint (2) is coupled to the performance index (1) to construct an equivalent variational problem. The integration in the result variational problem may be more difficult to be computed exactly. In this case, the Legendre-Gauss quadrature’s formula is used for this purpose. Using the Rayleigh-Ritz method, the given fractional optimal control problem (1)-(2) is reduced to a problem of solving a system of algebraic equations that can be approximated by any iterative method.

This article is organized as follows. In Section 2, we introduce some definitions and notations of fractional calculus and some properties of the shifted orthonormal polynomials. In Section 3, we derive the operational matrix of fractional integrals based on the shifted Jacobi orthonormal polynomials. In Section 4, the operational matrix of fractional integrals and the properties of the shifted Jacobi orthonormal polynomials are used together with the help of the Legendre-Gauss quadrature formula and the Rayleigh-Ritz method to introduce an approximate solution for the fractional optimal control problem (1)-(2). In Section 5, several numerical examples and comparisons between the results achieved using the presented scheme with those achieved using other methods are introduced.

2 Preliminaries and notations

2.1 Fractional calculus definitions

Riemann-Liouville and Caputo fractional definitions are the two most used from other definitions of fractional derivatives which have been introduced recently.

Definition 2.1

The integral of order \(\gamma\geq0\) (fractional) according to Riemann-Liouville is given by

$$ \begin{aligned} &I^{\gamma}f(t)=\frac{1}{\Gamma(\gamma)} \int_{0}^{x}{(t-y)}^{\gamma-1} f(y)\, dy, \quad \gamma>0, t>0, \\ &I^{0} f(t)=f(t), \end{aligned} $$
(3)

where

$$\Gamma(\gamma)=\int_{0}^{\infty}t^{\gamma-1} e^{-t} \,dt $$

is a gamma function.

The operator \(I^{\nu}\) satisfies the following properties:

$$\begin{aligned}& I^{\gamma}I^{\delta}f(t)=I^{\gamma+\delta} f(t), \\& I^{\gamma}I^{\delta}f(t)=I^{\delta}I^{\gamma}f(t), \\& I^{\gamma}t^{\beta}= \frac{\Gamma{(\beta+1)}}{\Gamma{(\beta+1+\gamma )}} t^{\beta+\gamma}. \end{aligned}$$
(4)

Definition 2.2

The Caputo fractional derivative of order γ is defined by

$$ D^{\gamma}f(t)=\frac{1}{\Gamma(m-\gamma)} \int_{0}^{t}{(t-y)}^{m-\gamma -1} \frac{d^{m}}{dy^{m}}f(y)\, dy,\quad m-1< \gamma\leq m, t>0, $$
(5)

where m is the upper limit of γ.

The operator \(D^{\gamma}\) satisfies the following properties:

$$ \begin{aligned} &D^{\gamma}C=0\quad (C \mbox{ is constant}), \\ &I^{\gamma}D^{\gamma}f(t)=f(t)-\sum_{i=0}^{m-1}f^{(i)} \bigl(0^{+}\bigr)\frac {t^{i}}{i!}, \\ &D^{\gamma}t^{\beta}=\frac{\Gamma{(\beta+1)}}{\Gamma{(\beta+1-\gamma)}} t^{\beta-\gamma}, \\ &D^{\gamma}{\bigl(\lambda f{(t)}+\mu g{(t)}\bigr)}=\lambda D^{\gamma}f{(t)}+\mu D^{\gamma}g{(t)}. \end{aligned} $$
(6)

2.2 Shifted Jacobi orthonormal polynomials

The Jacobi polynomial of degree j, denoted by \(P^{(\alpha,\beta )}_{j}(z)\); \(\alpha\geq-1\), \(\beta\geq-1\) and defined on the interval \([-1,1]\), constitutes an orthogonal system with respect to the weight function \(w^{(\alpha,\beta)}(z)=(1-z)^{\alpha}(1+z)^{\beta}\), i.e.,

$$ \int_{-1}^{1}P^{(\alpha,\beta)}_{j}(z)P^{(\alpha,\beta)}_{k}(z)w^{(\alpha ,\beta)}(z) \, dz= \delta_{jk} \gamma^{(\alpha,\beta)}_{k}, $$
(7)

where \(\delta_{jk}\) is the Kronecker function and

$$\gamma^{(\alpha,\beta)}_{k}=\frac{2^{\alpha+\beta+1}\Gamma(k+\alpha +1)\Gamma(k+\beta+1)}{(2k+\alpha+\beta+1) k!\Gamma(k+\alpha+\beta+1)}. $$

The shifted Jacobi polynomial of degree j, denoted by \(P^{(\alpha ,\beta)}_{T,j}(t)\); \(\alpha\geq-1\), \(\beta\geq-1\) and defined on the interval \([0,T]\), is generated by introducing the change of variable \(z=\frac {2t}{T}-1\), i.e., \(P^{(\alpha,\beta)}_{j}(\frac{2t}{T}-1)\equiv P^{(\alpha,\beta)}_{T,j}(t)\). Then the shifted Jacobi polynomials constitute an orthogonal system with respect to the weight function \(w^{(\alpha,\beta)}_{T}(t)=t^{\beta}(T-t)^{\alpha}\) with the orthogonality property

$$ \int_{0}^{T} P^{(\alpha,\beta)}_{T,j}(t)P^{(\alpha,\beta)}_{T,k}(t) w^{(\alpha,\beta)}_{T}(t)\,dt = h^{(\alpha,\beta)}_{T,k} \delta_{jk}, $$
(8)

where

$$h^{(\alpha,\beta)}_{T,k}=\biggl(\frac{T}{2}\biggr)^{\alpha+\beta+1} \gamma^{(\alpha ,\beta)}_{j}= \frac{T^{\alpha+\beta+1}\Gamma(k+\alpha+1)\Gamma(k+\beta +1)}{(2k+\alpha+\beta+1) k!\Gamma(k+\alpha+\beta+1)}. $$

Introducing the shifted Jacobi orthonormal polynomials \(\grave {P}^{(\alpha,\beta)}_{T,k}(t)\), where

$$ \grave{P}^{(\alpha,\beta)}_{T,k}(t)\equiv \frac{1}{\sqrt{h^{(\alpha ,\beta)}_{T,k}}}P^{(\alpha,\beta)}_{T,k}(t), $$
(9)

we have

$$ \int_{0}^{T} \grave{P}^{(\alpha,\beta)}_{T,j}(t) \grave{P}^{(\alpha ,\beta)}_{T,k}(t) w^{(\alpha,\beta)}_{T}(t)\,dt = \delta_{jk}. $$
(10)

The shifted Jacobi orthonormal polynomials are generated from the three-term recurrence relations

$$ \grave{P}^{(\alpha,\beta)}_{T,j+1}(t)=(\mu_{j}t- \xi_{j})\grave{P}^{(\alpha ,\beta)}_{T,j}(t)-\zeta_{j} \grave{P}^{(\alpha,\beta)}_{T,j-1}(t),\quad j\geq1, $$
(11)

with

$$ \begin{aligned} &\grave{P}^{(\alpha,\beta)}_{T,0}(t)= \frac{\sqrt{ \Gamma(\alpha+\beta +2)}}{\sqrt{T^{\alpha+\beta+1}\Gamma(\alpha+1)\Gamma(\beta+1)}}, \\ &\grave{P}^{(\alpha,\beta)}_{T,1}(t)=\frac{\sqrt{(\alpha+\beta+3) \Gamma(\alpha+\beta+2)}}{\sqrt{T^{\alpha+\beta+3}\Gamma(\alpha+2)\Gamma (\beta+2)}} \bigl((\alpha+ \beta+2)t-T(\beta+1) \bigr), \end{aligned} $$
(12)

where

$$\begin{aligned}& \mu_{j}=\frac{(2j+\alpha+\beta+2)\sqrt{(2j+\alpha+\beta+3) (2j+\alpha +\beta+1)}}{T\sqrt{ (j+\alpha+1) (j+\beta+1)(j+1)(j+\alpha+\beta+1)} }, \\ & \xi_{j}=\frac{(2j^{2}+(1+\beta)(\alpha+\beta)+2j(\alpha+\beta+1))\sqrt {(2j+\alpha+\beta+3) (2j+\alpha+\beta+1)}}{(2j+\alpha+\beta)\sqrt{ (j+\alpha+1) (j+\beta+1)(j+1)(j+\alpha+\beta+1)}}, \\ & \zeta_{j}=\frac{(2j+\alpha+\beta+2) \sqrt{ (2j+\alpha+\beta+3) j (j+\alpha +\beta)(j+\alpha)(j+\beta) }}{(2j+\alpha+\beta)\sqrt{(2j+\alpha+\beta-1) (j+\alpha+1) (j+\beta+1)(j+1)(j+\alpha+\beta+1)}}. \end{aligned}$$

The explicit analytic form of the shifted orthonormal Jacobi polynomials \(\grave{P}^{(\alpha,\beta)}_{T,j}{(t)}\) of degree j is given by

$$ \grave{P}^{(\alpha,\beta)}_{T,j}{(t)}=\sum _{k=0}^{j} \frac{{(-1)}^{j-k}\sqrt{(2j+\alpha+\beta+1) j! \Gamma(j+\beta +1)}\Gamma{(j+k+\alpha+\beta+1)}}{ \sqrt{T^{2k+\alpha+\beta+1}\Gamma(j+\alpha+1)\Gamma(j+\alpha+\beta +1)}\Gamma(k+\beta+1)(j-k)!k!}t^{k}, $$
(13)

and this in turn implies

$$ \begin{aligned} &\grave{P}^{(\alpha,\beta)}_{T,j}(0)= \frac{{(-1)}^{j}\sqrt{(2j+\alpha +\beta+1) \Gamma(j+\beta+1)\Gamma{(j+\alpha+\beta+1)}}}{ \sqrt{T^{\alpha+\beta+1}\Gamma(j+\alpha+1)j!} \Gamma(\beta+1)}, \\ &D^{q} \grave{P}^{(\alpha,\beta)}_{T,j}(0)= \frac{{(-1)}^{j-q}\sqrt{(2j+\alpha+\beta+1) j! \Gamma(j+\beta +1)}\Gamma{(j+q+\alpha+\beta+1)}}{ \sqrt{T^{2q+\alpha+\beta+1}\Gamma(j+\alpha+1)\Gamma(j+\alpha+\beta +1)}\Gamma(q+\beta+1)(j-q)!}, \end{aligned} $$
(14)

which will be of important use later.

Assume that \(y(t)\) is a square integrable function with respect to the Jacobi weight function \(w^{(\alpha,\beta)}_{T}(t)\) in \((0,T)\), then it can be expressed in terms of shifted Jacobi orthonormal polynomials as

$$y{(t)}=\sum_{j=0}^{\infty}y_{j} \grave{P}^{(\alpha,\beta)}_{T,j}{(t)}, $$

from which the coefficients \(y_{j}\) are given by

$$ y_{j}= \int_{0}^{T}w^{(\alpha,\beta)}_{T}(t) y(t) \grave{P}^{(\alpha,\beta )}_{T,j}(t)\,dt,\quad j=0,1,\ldots. $$
(15)

If we approximate \(y(t)\) by the first \((N+1)\)-terms, then we can write

$$ y_{N}{(t)}\simeq\sum_{j=0}^{N}y_{j} \grave{P}^{(\alpha,\beta)}_{T,j}{(t)}, $$
(16)

which alternatively may be written in a matrix form

$$ y_{N}{(t)}\simeq\mathbf{Y}^{T} \Psi_{T,N}(t), $$
(17)

with

$$ \mathbf{Y}=\left ( \begin{array}{@{}c@{}} y_{0} \\ y_{1} \\ \vdots\\ y_{N} \end{array} \right ), \qquad \Psi_{T,N}(t)=\left ( \begin{array}{@{}c@{}} \grave{P}^{(\alpha,\beta)}_{T,0}(t) \\ \grave{P}^{(\alpha,\beta)}_{T,1}(t) \\ \vdots\\ \grave{P}^{(\alpha,\beta)}_{T,N}(t) \end{array} \right ). $$
(18)

3 Operational matrix for fractional integrals

The main objective of this section is to derive the operational matrix of fractional integrals based on the shifted Jacobi orthonormal polynomials.

Theorem 3.1

The fractional integral of order ν (in the sense of Riemann-Liouville) of the shifted Jacobi orthonormal polynomial vector \(\Psi_{T,N}(t)\) is given by

$$ I^{\nu}\Psi_{T,N}(t)=\mathbf{I}^{(\nu)} \Psi_{T,N}(t) , $$
(19)

where \(\mathbf{I}^{(\nu)}\) is the \((N+1)\times(N+1)\) operational matrix of fractional integral of order ν and is defined by

$$ \mathbf{I}^{(\nu)}=\left ( \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \vartheta_{\nu}(0,0,\alpha,\beta)& \vartheta_{\nu}(0,1,\alpha,\beta) & \cdots& \vartheta_{\nu}(0,j,\alpha,\beta) & \cdots&\vartheta_{\nu }(0,N,\alpha,\beta) \\ \vartheta_{\nu}(1,0,\alpha,\beta)& \vartheta_{\nu}(1,1,\alpha,\beta) & \cdots& \vartheta_{\nu}(1,j,\alpha,\beta) & \cdots&\vartheta_{\nu }(1,N,\alpha,\beta) \\ \vdots& \vdots & \ddots& \vdots & \ddots& \vdots \\ \vartheta_{\nu}(i,0,\alpha,\beta)& \vartheta_{\nu}(i,1,\alpha,\beta) & \cdots& \vartheta_{\nu}(i,j,\alpha,\beta) & \cdots&\vartheta_{\nu }(i,N,\alpha,\beta) \\ \vdots& \vdots & \ddots& \vdots & \ddots& \vdots \\ \vartheta_{\nu}(N,0,\alpha,\beta)& \vartheta_{\nu}(N,1,\alpha,\beta) & \cdots& \vartheta_{\nu}(N,j,\alpha,\beta) & \cdots&\vartheta_{\nu }(N,N,\alpha,\beta) \end{array} \right ) , $$
(20)

where

$$ \vartheta_{\nu}(i,j,\alpha,\beta)= \sum _{k=0}^{i} \varrho_{\nu }(i,j,k,\alpha,\beta) $$
(21)

and

$$\begin{aligned}& \varrho_{\nu}(i,j,k,\alpha,\beta) \\ & \quad = \frac{{(-1)}^{i-k}T^{ \nu-\alpha -\beta}\sqrt{(2i+\alpha+\beta+1) i! \Gamma(i+\beta+1)}\Gamma(i+k+\alpha +\beta+1)}{ \sqrt{ \Gamma(i+\alpha+1)\Gamma(i+\alpha+\beta+1)}\Gamma(k+\beta +1)(i-k)!\Gamma(k+\nu+1)} \\ & \qquad {} \times \sum_{l=0}^{j} \frac{{(-1)}^{j-l}\sqrt{(2j+\alpha+\beta+1) j! \Gamma(j+\beta +1)}\Gamma{(j+l+\alpha+\beta+1)}}{ \sqrt{ \Gamma(j+\alpha+1)\Gamma(j+\alpha+\beta+1)}\Gamma(l+\beta +1)(j-l)!l! (l+k+\nu+1)}. \end{aligned}$$
(22)

Proof

Using (6) and (13), the fractional integral of order ν for the shifted Jacobi polynomials \(\grave{P}^{(\alpha,\beta)}_{T,i}{(t)}\) is given by

$$\begin{aligned}& I^{\nu}\grave{P}^{(\alpha,\beta)}_{T,i}{(t)} \\ & \quad = \sum_{k=0}^{i} \frac{{(-1)}^{i-k}\sqrt{(2i+\alpha+\beta+1) i! \Gamma(i+\beta +1)}\Gamma{(i+k+\alpha+\beta+1)}}{ \sqrt{T^{2k+\alpha+\beta+1}\Gamma(i+\alpha+1)\Gamma(i+\alpha+\beta +1)}\Gamma(k+\beta+1)(i-k)!k!} I^{\nu} t^{k} \\ & \quad = \sum_{k=0}^{i} \frac{{(-1)}^{i-k}\sqrt{(2i+\alpha+\beta+1) i! \Gamma(i+\beta+1)}\Gamma{(i+k+\alpha+\beta+1)}t^{k+\nu}}{ \sqrt{T^{2k+\alpha+\beta+1}\Gamma(i+\alpha+1)\Gamma(i+\alpha+\beta +1)}\Gamma(k+\beta+1)(i-k)!\Gamma(k+\nu+1)} . \end{aligned}$$
(23)

Now we approximate \(t^{k+\nu}\) by \(N+1\) terms of shifted Jacobi orthonormal polynomials \(\grave{P}^{(\alpha,\beta)}_{T,j}(t)\) as

$$ t^{k+\nu}=\sum_{j=0}^{N} \theta_{kj}\grave{P}^{(\alpha,\beta)}_{T,j}(t), $$
(24)

where \(\theta_{kj}\) is given as in Eq. (15) with \(y(t)=t^{k+\nu }\), then

$$\begin{aligned} \theta_{kj}&=\int_{0}^{T} t^{k+\nu} \grave{P}^{(\alpha,\beta)}_{T,j}(t) \,dt \\ &=\sum_{l=0}^{j} \frac{{(-1)}^{j-l}\sqrt{(2j+\alpha+\beta+1) j! \Gamma(j+\beta +1)}\Gamma{(j+l+\alpha+\beta+1)}}{ \sqrt{T^{2l+\alpha+\beta+1}\Gamma(j+\alpha+1)\Gamma(j+\alpha+\beta +1)}\Gamma(l+\beta+1)(j-l)!l!}\int _{0}^{T} t^{l+k+\nu}\,dt \\ &=\sum_{l=0}^{j} \frac{{(-1)}^{j-l}\sqrt{T^{2k+2\nu-\alpha-\beta+1}(2j+\alpha+\beta+1) j! \Gamma(j+\beta+1)}\Gamma{(j+l+\alpha+\beta+1)}}{ \sqrt{ \Gamma(j+\alpha+1)\Gamma(j+\alpha+\beta+1)}\Gamma(l+\beta +1)(j-l)!l! (l+k+\nu+1)}. \end{aligned}$$
(25)

Employing Eqs. (23)-(25), we have

$$\begin{aligned} \begin{aligned}[b] I^{\nu}\grave{P}^{(\alpha,\beta)}_{T,i}(t)={}&\sum _{k=0}^{i} \sum _{j=0}^{N}\frac{{(-1)}^{i-k}\sqrt{(2i+\alpha+\beta+1) i! \Gamma(i+\beta+1)}}{ \sqrt{T^{2k+\alpha+\beta+1}\Gamma(i+\alpha+1)\Gamma(i+\alpha+\beta +1)}} \\ &{} \times\frac{\Gamma(i+k+\alpha+\beta+1)}{\Gamma(k+\beta +1)(i-k)!\Gamma(k+\nu+1)} \theta_{kj}\grave{P}^{(\alpha,\beta )}_{T,j}(t) \\ ={}&\sum_{j=0}^{N}\vartheta_{\nu}(i,j, \alpha,\beta)\grave{P}^{(\alpha ,\beta)}_{T,j}(t), \end{aligned} \end{aligned}$$
(26)

where \(\vartheta_{\nu}(i,j,\alpha,\beta)\) is given by

$$\begin{aligned}& \varrho_{\nu}(i,j,k,\alpha,\beta) \\& \quad = \frac{{(-1)}^{i-k}\sqrt{(2i+\alpha +\beta+1) i! \Gamma(i+\beta+1)}\Gamma(i+k+\alpha+\beta+1)}{ \sqrt{T^{2k+\alpha+\beta+1}\Gamma(i+\alpha+1)\Gamma(i+\alpha+\beta +1)}\Gamma(k+\beta+1)(i-k)!\Gamma(k+\nu+1)} \\& \qquad {}\times\sum_{l=0}^{j} \frac{{(-1)}^{j-l}\sqrt{T^{2k+2\nu-\alpha-\beta+1}(2j+\alpha+\beta+1) j! \Gamma(j+\beta+1)}\Gamma{(j+l+\alpha+\beta+1)}}{ \sqrt{ \Gamma(j+\alpha+1)\Gamma(j+\alpha+\beta+1)}\Gamma(l+\beta +1)(j-l)!l! (l+k+\nu+1)}. \end{aligned}$$
(27)

Finally, we can rewrite Eq. (26) in a vector form as

$$ I^{\nu}\grave{P}^{(\alpha,\beta)}_{T,i}(t)\simeq \bigl[\vartheta_{\nu }(i,0,\alpha,\beta), \vartheta_{\nu}(i,1, \alpha,\beta), \ldots, \vartheta_{\nu}(i,N,\alpha,\beta) \bigr] \Psi_{T,N}(t). $$
(28)

Equation (28) completes the proof. □

4 The numerical scheme

In this section, we use the properties of the shifted Jacobi orthonormal polynomials together with the operational matrix of fractional integrals in order to solve the following fractional optimal control problem:

$$ \mathrm{Min.}\quad J=\int_{t_{0}}^{t_{1}}f \bigl(t,x(t),u(t) \bigr)\,dt, $$
(29)

subject to

$$ \begin{aligned} & D^{\nu}x(t)=g \bigl(t,x(t) \bigr)+b(t)u(t), \\ & D^{(i)}x(t_{0})=x_{i},\quad i=0,1,\ldots, n-1, \end{aligned} $$
(30)

where \(n-1 <\nu\leq n\) and \(b(t)\neq0\).

4.1 Shifted Jacobi orthonormal approximation

First, we approximate \(D^{\nu}x(t)\) by the shifted Jacobi orthonormal polynomials \(\grave{P}^{(\alpha,\beta)}_{T,j}(t)\) as

$$ D^{\nu}x(t) \simeq\mathbf{C}^{T} \Psi_{T,N}(t), $$
(31)

where C is an unknown coefficients matrix that can be written as

$$ \mathbf{C} =\left ( \begin{array}{@{}c@{}} c_{ 0} \\ c_{ 1} \\ \vdots\\ c_{ N} \end{array} \right ). $$
(32)

Using (6), we have

$$ I^{\nu}D^{\nu}x(t)=x(t)-\sum _{i=0}^{n-1}x_{i}\frac{t^{i}}{i!}, $$
(33)

from Eq. (19) together with Eq. (31), it is easy to write

$$ I^{\nu}D^{\nu}x(t)\simeq\mathbf{C}^{T} \mathbf{I}^{(\nu)}\Psi_{T,N}(t). $$
(34)

In virtue of Eqs. (31)-(34), we get

$$ x(t)\simeq \mathbf{C}^{T}\mathbf{I}^{(\nu)} \Psi_{T,N}(t)+\sum_{i=0}^{n-1}x_{i} \frac{{t}^{i}}{i!}. $$
(35)

Using (35), we can write the dynamic constraint (30) in the form

$$ \mathbf{C}^{T} \Psi_{T,N}(t) =g \Biggl(t, \mathbf{C}^{T}\mathbf{I}^{(\nu)} \Psi _{T,N}(t)+\sum _{i=0}^{n-1}x_{i}\frac{{t}^{i}}{i!} \Biggr)+b(t)u(t). $$
(36)

The previous equation leads to

$$ u(t)=\frac{1}{b(t)} \Biggl( \mathbf{C}^{T} \Psi_{T,N}(t)-g \Biggl(t,\mathbf {C}^{T}\mathbf{I}^{(\nu)} \Psi_{T,N}(t)+\sum_{i=0}^{n-1}x_{i} \frac {{t}^{i}}{i!} \Biggr) \Biggr). $$
(37)

Using Eqs. (35) and (37), the performance index (29) may be written in the form

$$\begin{aligned} J_{N}[c_{0},c_{1}, \ldots,c_{N}] =&\int_{t_{0}}^{t_{1}}f \Biggl(t, \mathbf{C}^{T}\mathbf {I}^{(\nu)} \Psi_{T,N}(t)+\sum _{i=0}^{n-1}x_{i}\frac{{t}^{i}}{i!}, \\ &\frac{1}{b(t)} \Biggl( \mathbf{C}^{T} \Psi_{T,N}(t)-g \Biggl(t,\mathbf{C}^{T}\mathbf {I}^{(\nu)} \Psi_{T,N}(t)+ \sum_{i=0}^{n-1}x_{i} \frac{{t}^{i}}{i!}\Biggr) \Biggr) \Biggr)\,dt. \end{aligned}$$
(38)

4.2 Legendre-Gauss quadrature

In general, it is more difficult to compute the previous integral exactly, so we use the Legendre-Gauss quadrature formula for this purpose.

First, we suppose the change of variable

$$ t =\frac{t_{1}-t_{0}}{T} \biggl(\grave{t}+\frac{Tt_{0}}{t_{1}-t_{0}} \biggr), $$
(39)

and for simplifying we show

$$\begin{aligned}& x \biggl(\frac{t_{1}-t_{0}}{T} \biggl(\grave{t}+\frac{Tt_{0}}{t_{1}-t_{0}} \biggr) \biggr) \equiv \grave{x}(\grave{t}), \\& u \biggl(\frac{t_{1}-t_{0}}{T} \biggl(\grave{t}+\frac{Tt_{0}}{t_{1}-t_{0}} \biggr) \biggr) \equiv \grave{u}(\grave{t}), \\& b \biggl(\frac{t_{1}-t_{0}}{T} \biggl(\grave{t}+\frac{Tt_{0}}{t_{1}-t_{0}} \biggr) \biggr) \equiv \grave{b}(\grave{t}) \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} &f \Biggl( t, \mathbf{C}^{T}\mathbf{I}^{(\nu)} \Psi_{T,N}(t)+\sum_{i=0}^{n-1}x_{i} \frac{{t}^{i}}{i!}, \frac{1}{\grave{b}(t)} \Biggl( \mathbf{C}^{T} \Psi_{T,N}(t)-g\Biggl(t,\mathbf {C}^{T}\mathbf{I}^{(\nu)} \Psi_{T,N}(t)+\sum_{i=0}^{n-1}x_{i} \frac{{t}^{i}}{i!}\Biggr) \Biggr) \Biggr) \\ &\quad \equiv \grave{f}(\grave{t}). \end{aligned} \end{aligned}$$

Then Eq. (38) is equivalent to

$$ J_{N}[c_{0},c_{1}, \ldots,c_{N}]= \biggl(\frac{t_{1}-t_{0}}{T} \biggr)\int _{0}^{T}\grave {f}(\grave{t})\, d\grave{t}. $$
(40)

Using the Legendre-Gauss quadrature formula, we can write

$$ J_{N}[c_{0},c_{1}, \ldots,c_{N}]\simeq \biggl(\frac{t_{1}-t_{0}}{T} \biggr)\sum _{r=0}^{N}\grave{f}(\grave{t}_{T,N,r}) \varpi_{T,N,r}, $$
(41)

where \(t_{T,N,r}\), \(0\leq r \leq N\), are the zeros of Legendre-Gauss quadrature in the interval \((0,T)\), with \(\varpi_{T,N,r}\), \(0\leq r \leq N\), being the corresponding Christoffel numbers.

As in the Rayleigh-Ritz method, the necessary conditions for the optimality of the performance index are

$$ \frac{\partial J_{N}}{\partial c_{0}}=0, \qquad \frac{\partial J_{N}}{\partial c_{1}}=0,\qquad \ldots, \qquad \frac{\partial J_{N}}{\partial c_{N}}=0. $$
(42)

The system of algebraic equations introduced above can be solved by using any standard iteration method for the unknown coefficients \(c_{j}\), \(j=0,1,\ldots,N\). Consequently, C given in (32) can be calculated.

5 Numerical experiments

In order to show the efficiency and accuracy of the numerical scheme introduced, we applied it to solve some examples and compared the results obtained using our scheme with those obtained using other schemes.

5.1 Example 1

As the first example, we consider the following fractional optimal control problem studied in [39]:

$$ \mathrm{Min.}\quad J=\frac{1}{2}\int_{0}^{1} \bigl(x^{2}(t)+u^{2}(t) \bigr)\,dt, $$
(43)

subjected to the dynamic constraints

$$ \begin{aligned} &D^{\nu}x(t)=-x(t)+u(t),\quad 1\leq\nu\leq2, \\ &x(0)=1. \end{aligned} $$
(44)

The exact solution of this problem for \(\nu=1\) is

$$ \begin{aligned} &x(t)=\cosh(\sqrt{2}t)+\beta\sinh(\sqrt{2}t), \\ &u(t)= (1+\sqrt{2}\beta)\cosh(\sqrt{2}t)+(\sqrt{2}+\beta)\sinh(\sqrt{2}t), \end{aligned} $$
(45)

where

$$\beta=-\frac{\cosh(\sqrt{2}t)+\sqrt{2}\sinh(\sqrt{2}t)}{\sqrt{2}\cosh (\sqrt{2}t)+\sinh(\sqrt{2}t)}. $$

Baleanu et al. [39] approximated the fractional derivative by the modified Grünwald-Letnikov approach and divided the entire time domain into several subdomains for introducing approximate solutions of the control variable \(u(t)\) and the state variable \(x(t)\) and did not achieve reasonable results for the approximate values of \(u(t)\) and \(x(t)\) unless a large number of N (N is increased up to 256) is used, see Figures 1-6 in [39].

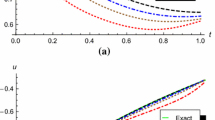
In Figures 1 and 2, we plot the absolute errors of the state variable \(x(t)\) and the control variable \(u(t)\) at \(N=10\), \(\alpha=\beta=0\) and \(\nu=1\), while Figures 3 and 4 present the approximate values of \(x(t)\) and \(u(t)\) as functions of time at \(N=8\), \(\alpha=\beta=0\) and various choices of ν, \(\nu =0.50,0.70,0.90,0.99\mbox{ and }1\). Also, in Tables 1 and 2, we list the absolute errors of \(x(t)\) and \(u(t)\) at \(\alpha=\beta=0\), \(\nu=1\) and various choices of N.

Figure 1
figure 1

Absolute errors of \(\pmb{x(t)}\) at \(\pmb{\alpha=\beta=0}\) , \(\pmb{N=10}\) with \(\pmb{\nu=1}\) for Example 1.

Full size image
Figure 2
figure 2

Absolute errors of \(\pmb{u(t)}\) at \(\pmb{\alpha=\beta=0}\) , \(\pmb{N=10}\) with \(\pmb{\nu=1}\) for Example 1.

Full size image
Figure 3
figure 3

Approximate solution of \(\pmb{x(t)}\) at \(\pmb{\alpha=\beta=0}\) , \(\pmb{N=8}\) and \(\pmb{\nu=1, 0.99, 0.90, 0.70\mbox{ and }0.50}\) for Example 1.

Full size image
Figure 4
figure 4

Approximate solution of \(\pmb{u(t)}\) at \(\pmb{\alpha=\beta=0}\) , \(\pmb{N=8}\) and \(\pmb{\nu=1, 0.99, 0.90, 0.70\mbox{ and }0.50}\) for Example 1.

Full size image
Table 1 Absolute errors of \(\pmb{x(t)}\) at \(\pmb{\nu=1}\) , \(\pmb{\alpha=\beta=0}\) and various choices of N for Example 1
Full size table
Table 2 Absolute errors of \(\pmb{u(t)}\) at \(\pmb{\nu=1}\) , \(\pmb{\alpha=\beta=0}\) and various choices of N for Example 1
Full size table

From Figures 1 and 2 and Tables 1 and 2, it is clear that adding few terms of shifted Jacobi orthonormal polynomials, good approximations of the exact state and control variables were achieved, and from the observation of Figures 3 and 4 we conclude that as ν approaches to 1, the solution for the integer order system is recovered.

5.2 Example 2

Consider the following fractional optimal control problem studied in [40]:

$$ \mathrm{Min.}\quad J=\frac{1}{2}\int_{0}^{1} \bigl(x^{2}(t)+u^{2}(t) \bigr)\,dt, $$
(46)

subjected to the dynamic constraints

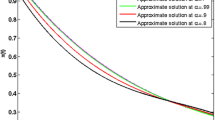
$$ \begin{aligned} &D^{\nu}x(t)=t x(t)+u(t), \quad 1\leq\nu\leq2, \\ &x(0)=1. \end{aligned} $$
(47)

In [40], the authors applied the parameterization method together with the perturbation homotopy method to present a numerical approach to solve this problem. In order to show that our proposed numerical scheme is better than the one introduced in [40], in Table 3 we compare the results of the optimal value of the cost function J obtained using our numerical approach at \(\alpha=\beta=0\) with those obtained in [40]. Figures 5 and 6, present the approximate values of the state variable \(x(t)\) and the control variable \(u(t)\) as functions of time at \(N=8\), \(\alpha=\beta=0\) and various choices of \(\nu, \nu=0.50,0.70,0.90,0.99\mbox{ and }1\).

Figure 5
figure 5

Approximate solution of \(\pmb{x(t)}\) at \(\pmb{\alpha=\beta=0}\) , \(\pmb{N=8}\) and \(\pmb{\nu=1, 0.99, 0.90, 0.70\mbox{ and }0.50}\) for Example 2.

Full size image
Figure 6
figure 6

Approximate solution of \(\pmb{u(t)}\) at \(\pmb{\alpha=\beta=0}\) , \(\pmb{N=8}\) and \(\pmb{\nu=1, 0.99, 0.90, 0.70\mbox{ and }0.50}\) for Example 2.

Full size image
Table 3 Optimal value of J at different choices of ν
Full size table

5.3 Example 3

Consider the following fractional optimal control problem:

$$ \mathrm{Min.}\quad J= \int_{0}^{1} \biggl[e^{t} \bigl(x(t)-t^{4}+t-1 \bigr)+ \bigl(t^{2}+1\bigr)^{2} \biggl(u(t)+1-t+t^{4}- \frac{24t^{4-\nu}}{\Gamma(5-\nu)} \biggr)^{2} \biggr] \,dt, $$
(48)

subjected to the dynamic constraints

$$ \begin{aligned} &D^{\nu}x(t) = x(t)+u(t),\quad 1\leq\nu\leq2, \\ &x(0)=1, \\ &\dot{x}(0)=-1. \end{aligned} $$
(49)

The exact solutions of \(x(t)\) and \(u(t)\) for this problem are

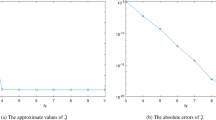
$$ \begin{aligned} &x(t)=1-t+t^{4}, \\ &u(t)=t-t^{4}-1+\frac{24t^{4-\nu}}{\Gamma(5-\nu)}. \end{aligned} $$
(50)

In Table 4, we introduce the maximum absolute errors (MAEs) of the state variable \(x(t)\) at \(\nu=1.9\) and different values of α, β and N while in Table 5 (Table 6), the absolute errors of the state (control) variable are introduced at \(\nu=1.1\), \(\alpha=\beta=1\) (\(\nu=1.5\), \(\alpha=\beta=\frac {1}{2}\)) at various choices of N. In Figure 7 (Figure 8) we plot the absolute errors of the state (control) variable at \(-\alpha=\beta=\frac{1}{2}\), \(\nu=1.3\) (\(\alpha=-\beta=\frac {1}{2}\), \(\nu=1.7\)) at \(N=20\). Finally in Figure 9 (Figure 10) we plot the logarithmic graphs of MAEs (log10 error) of the state (control) variable at \(\alpha=\beta=1\) (\(\alpha=\beta=0\)) at \(\nu=1.1,1.3,1.5,1.7,1.9\) and various choices of N.

Figure 7
figure 7

Absolute errors of \(\pmb{x(t)}\) at \(\pmb{-\alpha=\beta=\frac{1}{2}}\) , \(\pmb{\nu =1.3}\) and \(\pmb{N=20}\) for Example 3.

Full size image
Figure 8
figure 8

Absolute errors of \(\pmb{u(t)}\) at \(\pmb{\alpha=-\beta=\frac{1}{2}}\) , \(\pmb{\nu =1.7}\) and \(\pmb{N=20}\) for Example 3.

Full size image
Figure 9
figure 9

\(\pmb{\log_{10}\mathrm{MAE}}\) of \(\pmb{x(t)}\) at \(\pmb{\alpha=\beta=1}\) for Example 3.

Full size image
Figure 10
figure 10

\(\pmb{\log_{10}\mathrm{MAE}}\) of \(\pmb{u(t)}\) at \(\pmb{\alpha=\beta=0}\) for Example 3.

Full size image
Table 4 MAEs of \(\pmb{x(t)}\) at \(\pmb{\nu=1.9}\) for Example 3
Full size table
Table 5 Absolute errors of \(\pmb{x(t)}\) at \(\pmb{\nu=1.1}\) , \(\pmb{\alpha=\beta=1}\) and various choices of N for Example 3
Full size table
Table 6 Absolute errors of \(\pmb{x(t)}\) at \(\pmb{\nu=1.5}\) , \(\pmb{\alpha=\beta=\frac {1}{2}}\) and various choices of N for Example 3
Full size table